AKADEMIA TECHNICZNO-HUMANISTYCZNA

W BIELSKU-BIAŁEJ

KATEDRA PODSTAW BUDOWY MASZYN

Instrukcje laboratoryjne

Charakterystyki cz stotliwo

ciowe liniowych elementów automatyki

3. Charakterystyki cz

stotliwo

ciowe liniowych elementów automatyki

Cel

wiczenia:

Celem

wiczenia jest zapoznanie z cz stotliwo ciowymi metodami opisu własno ci

dynamicznych elementów automatyki.

Wst

p

Charakterystyki cz stotliwo ciowe sporz dza si dla elementu w stanie ustalonym

dynamicznie, czyli wtedy gdy sygnał wej ciowy ma posta :

( )

t

sin

A

t

u

u

ω

=

gdzie:

A

u

- amplituda wej ciowego sygnału okresowo zmiennego;

ω

- cz sto sygnału wej ciowego

[

)

∞

∈

,

0

ω

.

Wtedy sygnał wyj ciowy ma posta :

( )

(

)

ϕ

ω

+

=

t

sin

A

t

y

y

gdzie:

A

y

- amplituda sygnału wyj ciowego;

ϕ

- przesuni cie fazowe sygnału wyj ciowego wzgl dem sygnału wej ciowego.

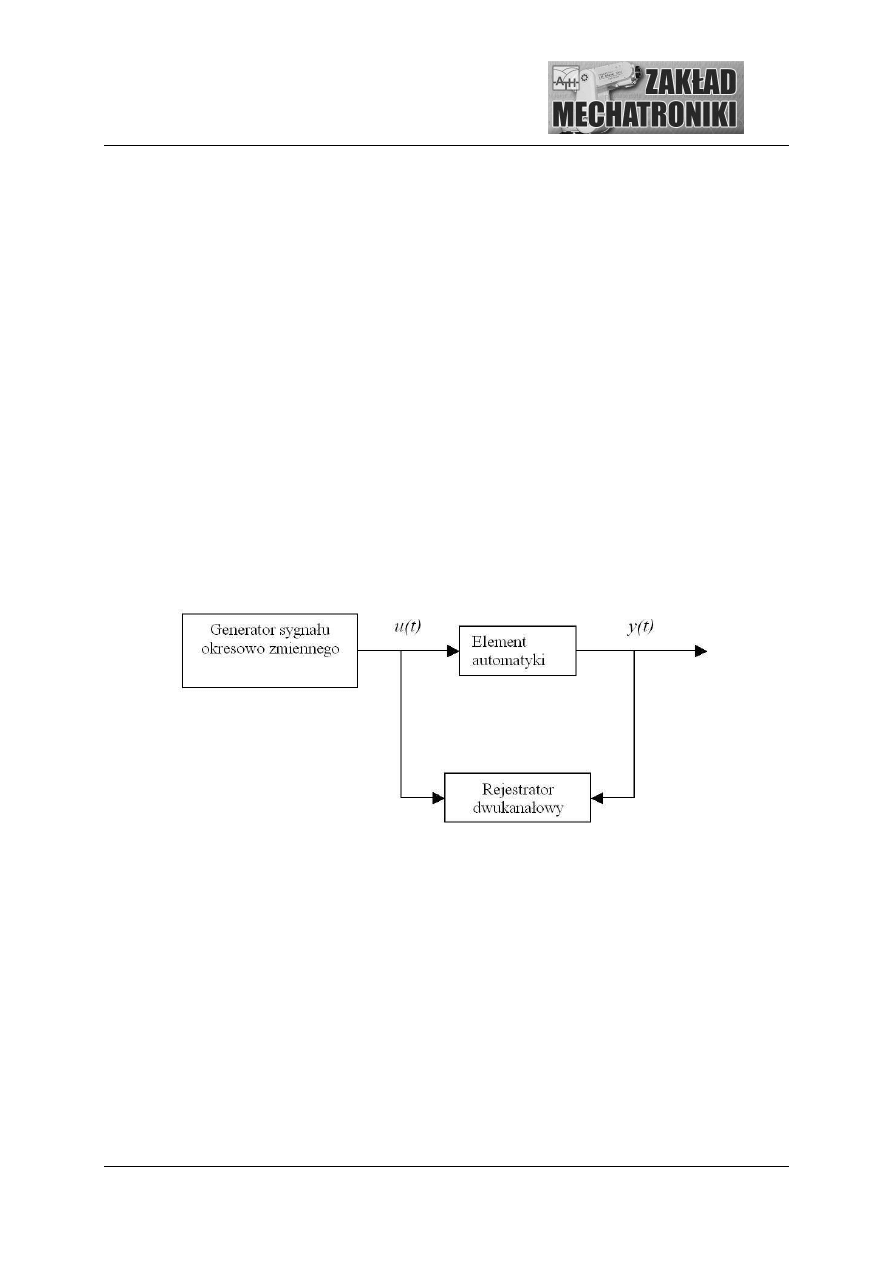
Rys.3.1. Schemat stanowiska pomiarowego do zdejmowania charakterystyk cz stotliwo ciowych

W rejestratorze dwukanałowym (rys.3.6) na jedn o podaje si sygnał wej ciowy a na drug
o sygnał wyj ciowy z elementu automatyki. Dzi ki takiemu podł czeniu na rejestratorze
uzyskamy elips (krzyw Lissajous) [1]. Z zarejestrowanego wykresu (rys. 3.2) odczytujemy
y

1

, A

u

, A

y

.

AKADEMIA TECHNICZNO-HUMANISTYCZNA

W BIELSKU-BIAŁEJ

KATEDRA PODSTAW BUDOWY MASZYN

Instrukcje laboratoryjne

Charakterystyki cz stotliwo

ciowe liniowych elementów automatyki

Rys.3.2. Krzywa Lissajous.

Poniewa równanie sygnału wyj ciowego:

(

)

( )

( )

ϕ

ω

ϕ

ω

ϕ

ω

sin

cos

cos

sin

sin

t

A

t

A

t

A

y

y

y

y

+

=

+

=

gdzie:

( )

u

A

u

t

=

ω

sin

oraz

( )

( )

t

t

ω

ω

2

sin

1

cos

−

=

zatem

ϕ

ϕ

sin

1

cos

2

2

u

y

u

y

A

u

A

A

u

A

y

−

+

=

Dziel c powy sze równanie przez A

y

i odpowiednio przekształcaj c uzyskuje si równanie

elipsy w postaci:

ϕ

ϕ

2

2

2

2

2

sin

cos

2

=

+

−

y

y

u

u

A

y

A

A

uy

A

u

Dla

0

=

u

odczytuje si rz dn y

1

i oblicza si warto przesuni cia fazowego

=

=

y

y

A

y

A

y

1

1

arcsin

sin

ϕ

ϕ

Moduł transmitancji widmowej

( )

u

y

A

A

A

=

ω

Na tej podstawie mo na wyznaczy wykresy Bodego (charakterystyk amplitudowo –
cz stotliwo ciow

L(

ω

)

we współrz dnych półlogarytmicznych i fazowo – cz stotliwo ciow

ϕ

(

ω

)

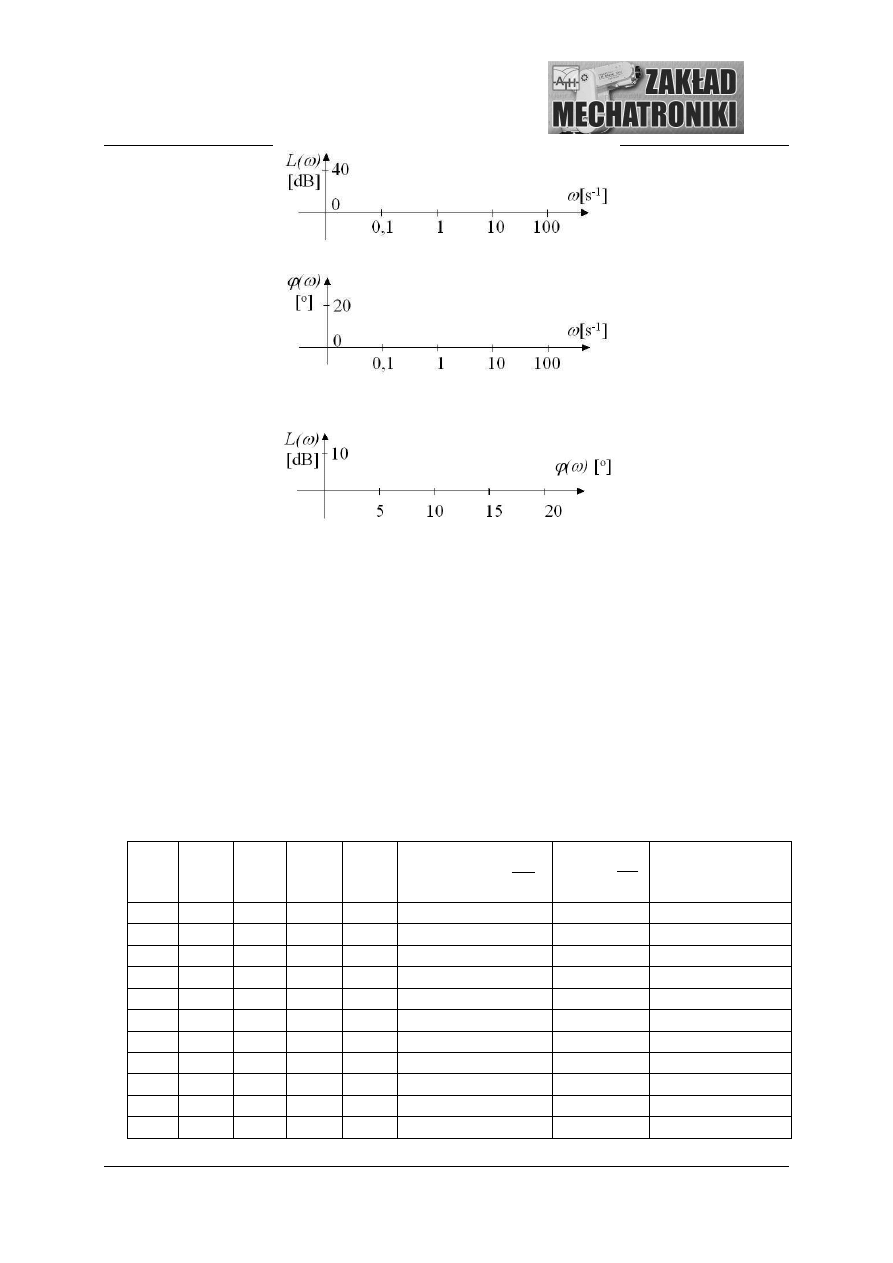
rys.3.3) oraz wykres charakterystyki logarytmicznej amplitudowo – fazowej na

płaszczy nie Black’a

ϕ

(

ω

)

,

L(

ω

),

rys.4

.

AKADEMIA TECHNICZNO-HUMANISTYCZNA

W BIELSKU-BIAŁEJ

KATEDRA PODSTAW BUDOWY MASZYN

Instrukcje laboratoryjne

Charakterystyki cz stotliwo

ciowe liniowych elementów automatyki

Rys.3.3. Współrz dne wykresów Bodego

Rys.3.4. Płaszczyzna Black’a.

Przebieg

wiczenia:

•

zbudowa czwórnik elektryczny wskazany przez prowadz cego (tab.1.1);

•

poł czy układ pomiarowy jak na rys.3.1;

•

ustawi amplitud wej ciowego sygnału sinusoidalnego

A

u

=1[V];

•

ustawi zakresy pomiarowe rejestratora (rys.3.6) X=Y = 100[mV/cm] dla sygnału

u(t)

i

y(t)

;

•

zarejestrowa krzywe Lissajous dla cz stotliwo ci wymuszenia

f

(0,01; 0,02; 0,05;

0,1; 0,2; 0,5; 1; 2; 5; 10 [Hz]);

•

cz sto kołow

ω

wyznacza si z zale no ci:

f

π

ω

2

=

•

z uzyskanych wykresów odczyta

y

1

, A

u

, A

y

,

wyniki zestawi w tabeli 3.1.

Tab. 3.1.

f

[Hz]

ω

[s

-1

]

y

1

[V]

A

u

[V]

A

y

[V]

( )

=

y

A

y

1

arcsin

ω

ϕ

( )

u

y

A

A

A

=

ω

( )

( )

ω

ω

A

L

lg

20

=

0,001

0,01

0,02

0,05

0,1

0,2

0,5

1

2

5

10

AKADEMIA TECHNICZNO-HUMANISTYCZNA

W BIELSKU-BIAŁEJ

KATEDRA PODSTAW BUDOWY MASZYN

Instrukcje laboratoryjne

Charakterystyki cz stotliwo

ciowe liniowych elementów automatyki

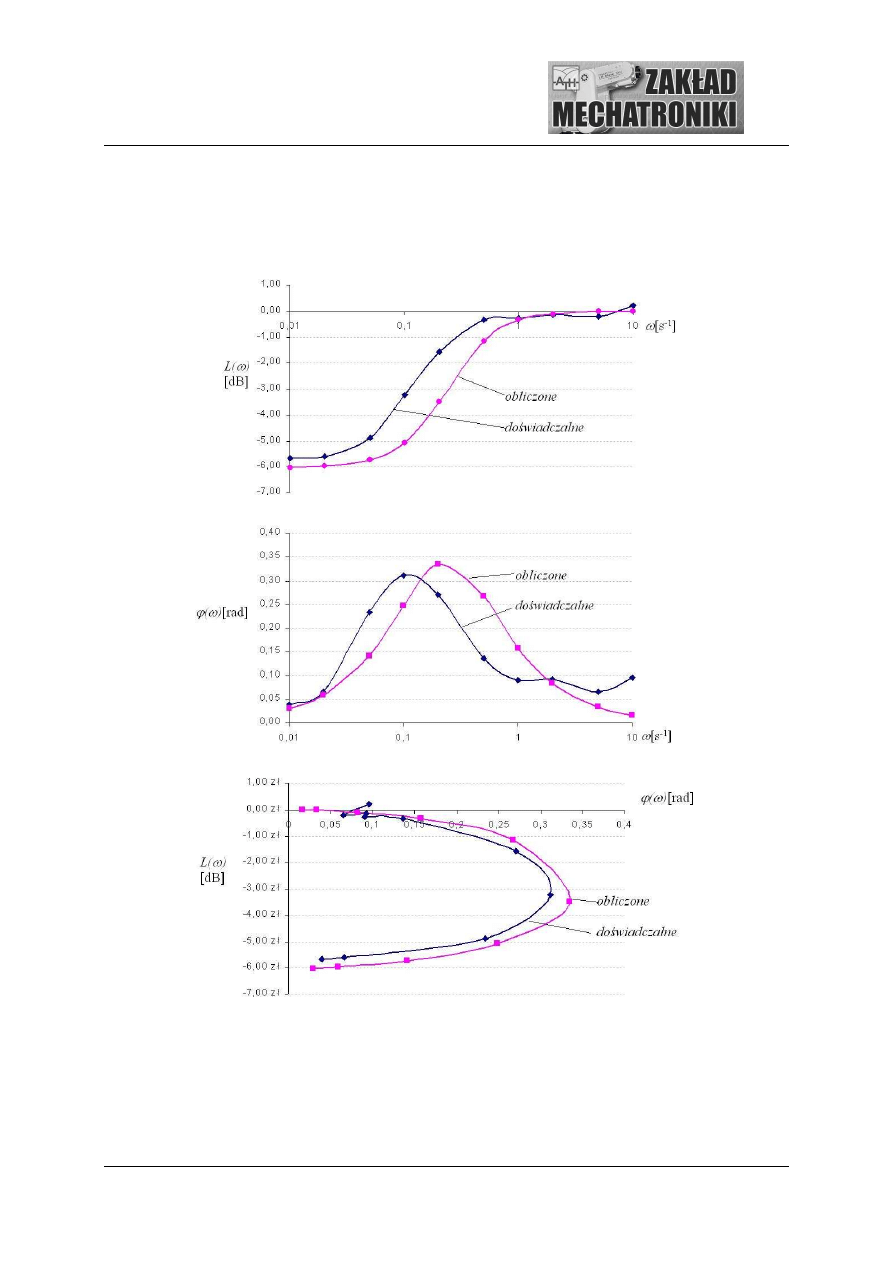
Przykład.
Uzyskane charakterystyki cz stotliwo ciowe dla czwórnika 5.3 z tab. 1.1 przedstawiono na
rys. 3.5.

a)

b)

c)

Rys. 3.5. Charakterystyki cz stotliwo ciowe. a ) amplitudowo-cz stotliwo ciowa, b) fazowo-cz stotliwo ciowa,

c)amplitudowo-fazowa

AKADEMIA TECHNICZNO-HUMANISTYCZNA

W BIELSKU-BIAŁEJ

KATEDRA PODSTAW BUDOWY MASZYN

Instrukcje laboratoryjne

Charakterystyki cz stotliwo

ciowe liniowych elementów automatyki

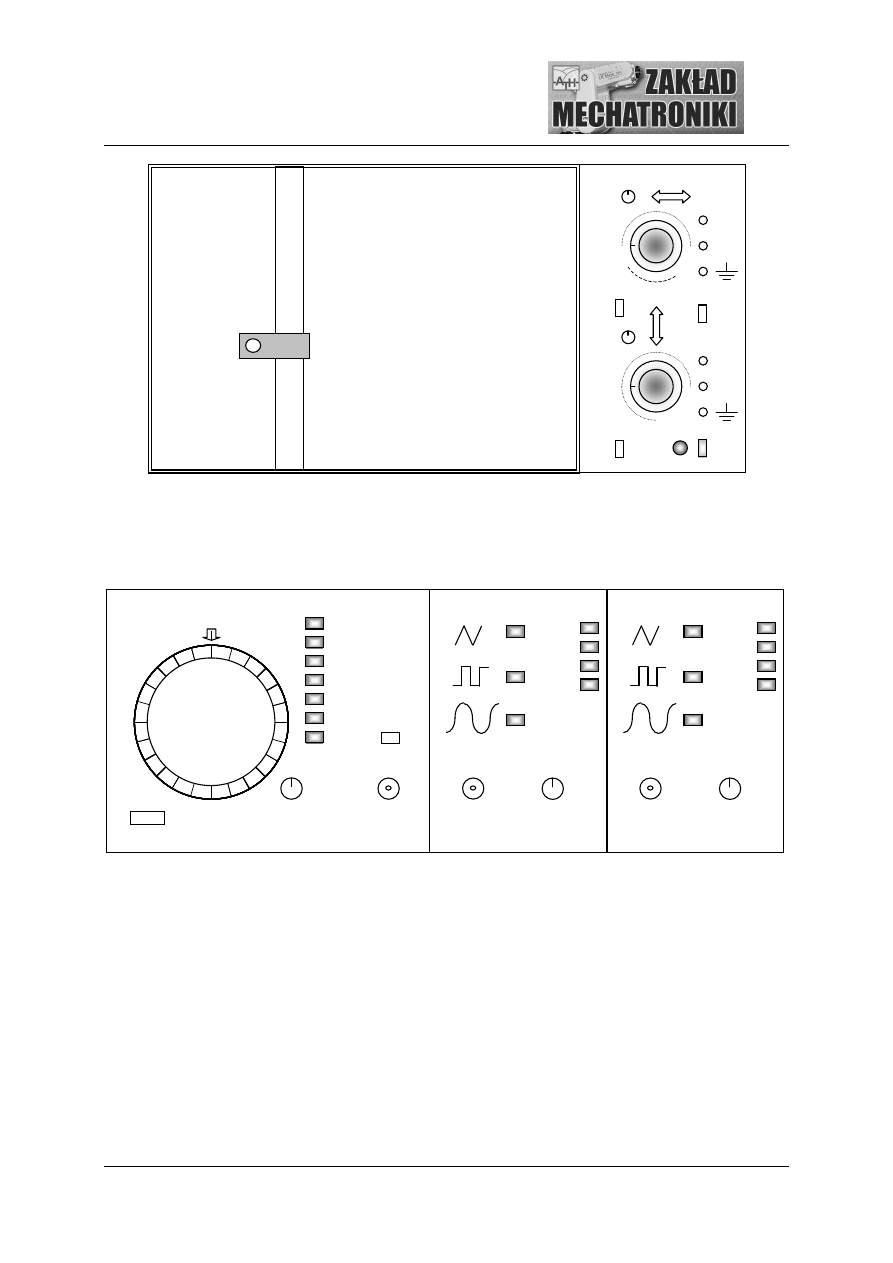
Rys.3.6. Rejestrator dwukanałowy.

Rys.3.7. Generator dwukanałowy.

Uwagi o sprawozdaniu

•

wykona charakterystyki amplitudowo – cz stotliwo ciow i fazowo -
cz stotliwo ciow we współrz dnych półlogarytmicznych (wykresy Bodego);

•

wykona charakterystyk amplitudowo – fazow na płaszczy nie Black’a;

porówna otrzymane na podstawie do wiadczenia charakterystyki z modelowymi.
Literatura

[1]. Dinsdale J., Kłosi ski J.: Podstawy automatyki z elementami mechatroniki. Politechnika Łódzka Filia

w Bielsku-Białej, Bielsko-Biała 1998

X

+

-

Zero

V/cm

s/cm

Y

+

-

Zero

V/cm

Start

VCO

VCO
IN

×

1000

×

100

×

10

×

1

×

0.1

×

0.01

×

0.001

VERNER

FERENQUENCY RANGE

FUNCTION
GENERATOR

POWER

FUNCTION AMPLITUDE

10 V

1 V

0.1 V

0.01 V

OUT CAL

CHANEL A

FUNCTION AMPLITUDE

10 V

1 V

0.1 V

0.01 V

OUT CAL

CHANEL B

AKADEMIA TECHNICZNO-HUMANISTYCZNA

W BIELSKU-BIAŁEJ

KATEDRA PODSTAW BUDOWY MASZYN

Instrukcje laboratoryjne

Charakterystyki cz stotliwo

ciowe liniowych elementów automatyki

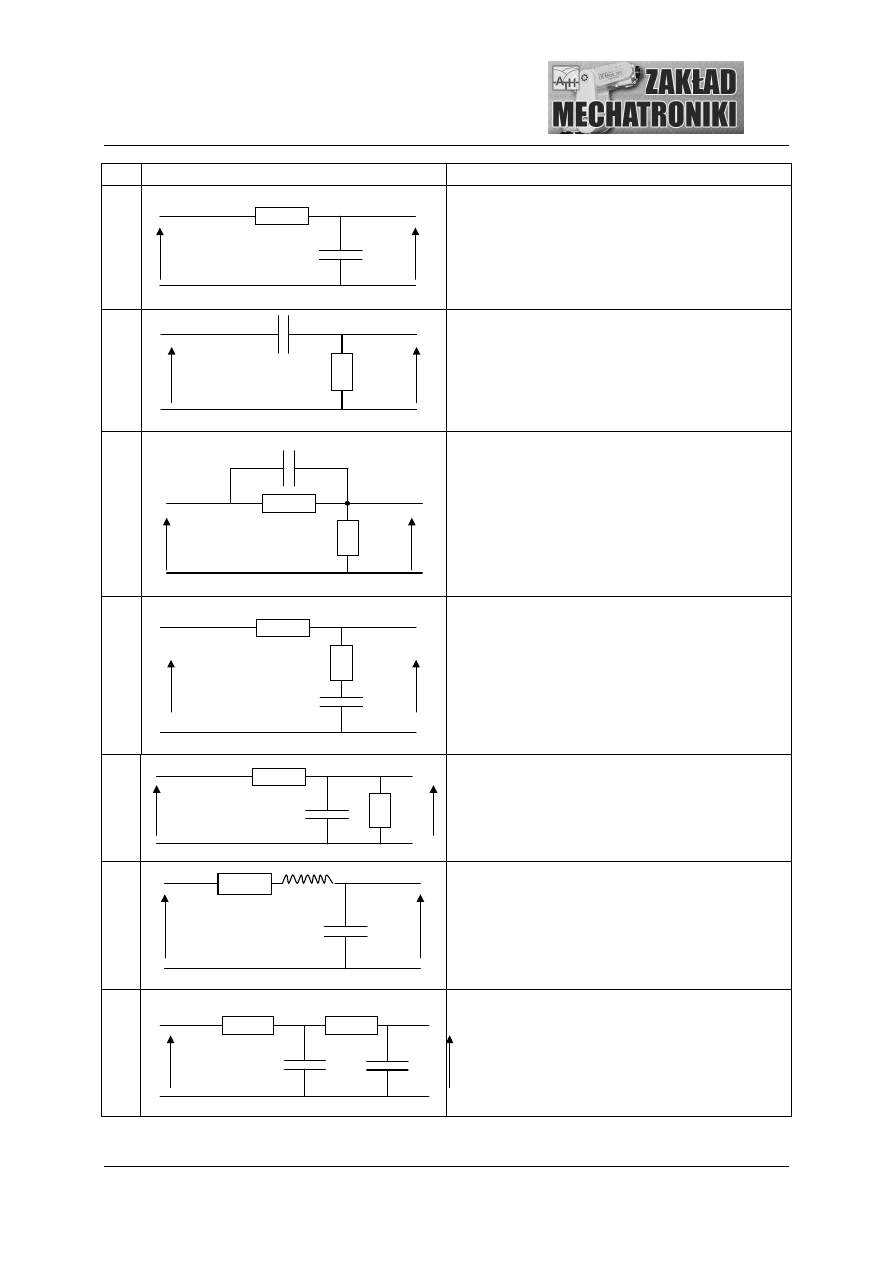
Tab.1.1. Schematy badanych elementów liniowych

Nr

SCHEMAT UKŁADU

WARTO

PARAMETRÓW

1.

1.

R

1

= 1 k

Ω

C=

2200

µ

F

2.

R

1

= 2,5 k

Ω

C=

1470

µ

F

3.

R

1

= 5 k

Ω

C=

1000

µ

F

4.

R

1

= 10 k

Ω

C=

470

µ

F

2.

1.

R

1

= 1 k

Ω

C=

2200

µ

F

2.

R

1

= 2,5 k

Ω

C=

2200

µ

F

3.

R

1

= 5 k

Ω

C=

1000

µ

F

4.

R

1

= 10 k

Ω

C=

1000

µ

F

3.

1.

R

1

=

10 k

Ω

R

2

= 10 k

Ω

C=

1000

µ

F

2.

R

1

= 10 k

Ω

R

2

= 4 k

Ω

C=

2200

µ

F

3.

R

1

= 4 k

Ω

R

2

= 10 k

Ω

C=

2200

µ

F

4.

R

1

= 4 k

Ω

R

2

= 1 k

Ω

C=

4400

µ

F

5.

1.

R

1

=

10 k

Ω

R

2

= 10 k

Ω

C=

1000

µ

F

2.

R

1

= 10 k

Ω

R

2

= 4 k

Ω

C=

2200

µ

F

3.

R

1

= 4 k

Ω

R

2

= 10 k

Ω

C=

2200

µ

F

4.

R

1

= 4 k

Ω

R

2

= 10 k

Ω

C=

1000

µ

F

6.

1.

R

1

= 1 k

Ω

R

2

= 10 k

Ω

C=

2200

µ

F

2.

R

1

= 1 k

Ω

R

2

= 20 k

Ω

C=

2200

µ

F

3.

R

1

= 5 k

Ω

R

2

= 100 k

Ω

C=

2200

µ

F

7.

1.

R

1

=

0

Ω

C=

4400

µ

F

2.

R

1

= 10

Ω

- || -

3.

R

1

= 30

Ω

- || -

4.

R

1

= 50

Ω

- || -

5.

R

1

= 100

Ω

- || -

8.

1.

R

1

=

R

2

= 10 k

Ω

C

1

= C

2

=

1000

µ

F

2.

R

1

= 1 k

Ω

R

2

= 10 k

Ω

C

1

= C

2

=

2200

µ

F

3.

R

1

=

R

2

= 10 k

Ω

C

1

=

470

µ

F

C

1

=

2200

µ

F

R

1

C

U

Y

C

R

1

U

Y

R

1

R

2

C

U

Y

R

1

R

2

C

U

Y

R

1

C

R

2

U

Y

R

1

L

C

U

Y

R

1

C

1

R

2

C

2

U

Y