Wydział : FiTJ |
Imię i nazwisko : Krzysztof Janc, Krzysztof Jankowski Marcin Kieca |
rok II |
Grupa 3 |
Zespół 10 |
||||||
Pracownia fizyczna I |
Temat ćwiczenia :
Moduł Sztywności |
Ćwiczenie nr: 12 |
||||||||
Data wykonania:
|
Data oddania: |
Zwrot do poprawy: |
Data oddania: |
Data zaliczenia: |
Ocena: |
|||||
Cel ćwiczenia:
Wyznaczanie modułu sztywności kilku metali metodą dynamiczną za pomocą pomiaru okresu drgań skrętnych.
Wprowadzenie:
Modułem sztywności G nazywamy stosunek naprężenia stycznego τ do wywołanego przez nie odkształcenia postaci γ.
G=τ/γ
W celu wyznaczenia G wykorzystamy zjawisko skręcenia pręta, gdyż podatność materiału pręta na skręcanie zależy wyłącznie od modułu sztywności G i rozmiarów geometrycznych. Weźmy pręt o promieniu r i długości l. Skręcenie jest odkształceniem wywołanym działaniem pary sił przyłożonej do płaszczyzny przekroju poprzecznego pręta. Należy zauważyć, że podczas skręcania przekroje poprzeczne obracają się dookoła osi pręta, który nie zmienia przy tym swojej długości ani średnicy.
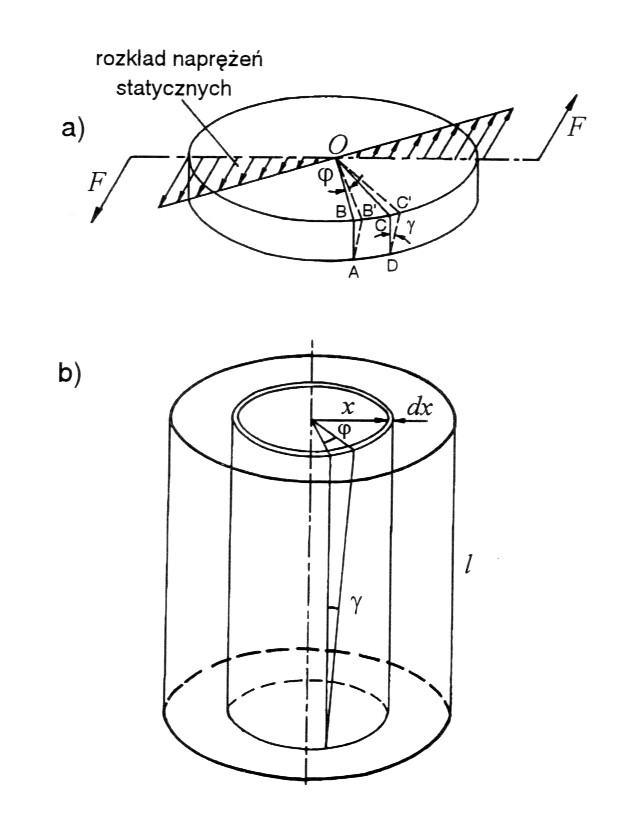
Schemat geometryczny odkształcenia rozpatrywanego pręta przedstawiono na rysunku 1a. Promień OB obróci się o kąt ϕ od położenia OB'. Dwie tworzące AB i DC na powierzchni tej warstwy pochylą się o kąt γ tak, że utworzony element kwadratowy ABCD przekształci się w rąb AB'C'D. Oznacza to, że powstaną odkształcenia postaci, których miarą jest kąt γ. Jest on proporcjonalny do odległości od osi.
Całkowity moment siły można obliczyć przez całkowanie przyczynków pochodzących od niewielkich pierścieni o promieniu x i grubości dx (rys. 1b). Odkształcenie postaci materiału pierścienia wynosi:
γ=(ϕ*x)/l
Zgodnie z prawem Hooke'a wartości naprężeń wynoszą:
![]()
Całkowity moment działający na pręt wynosi:
Wielkość nazywamy stałą skręcenia.
Narzuca się możliwość bezpośredniego wyznaczenia modułu sztywności G przez pomiar wszystkich innych wielkości występujących we wzorze (6). Byłaby to metoda statyczna. Znacznie wygodniejsza jest jednak metoda dynamiczna, która polega na pomiarze okresu drgań skrętnych wibratora, w postaci naszego pręta obciążonego ciałem o momencie bezwładności I0
Przewaga metody dynamicznej polega na zastąpieniu pomiaru siły i kata skręcenia przez łatwiejszy do przeprowadzenia pomiar okresu drgań.
Aby uniknąć trudnego wyznaczania momentu bezwładności Ix wahadła, wykonujemy dwie serie pomiarów okresu drgań. Pierwszą dla wahadła nie obciążonego, drugą dla wahadła obciążonego ciałem geometrycznie prostym, o łatwym do obliczenia momencie bezwładności I0.
Odpowiednie okresy będą wynosić:
Wartość modułu sztywności wynosi:
Opracowanie wyników
Obręcz:
∅wew= 252 ±1 mm
∅zew = 284 ±1 mm
mobr = 1322 ±1 g
Iobr = 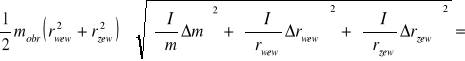
0,02382 ±0,0003 kg⋅m2
Ciężarki
mobc = 556 ± 1 g (sumaryczna)
d = 80 ± 5 mm (odległość jednego ciężarka od osi obrotu)
Iobc = 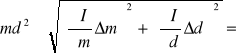
0,00356 ± 0,0004 kg⋅m2
Moduł sztywności liczony był ze wzoru
![]()
,
a błąd liczony był z prawa przenoszenia błędów
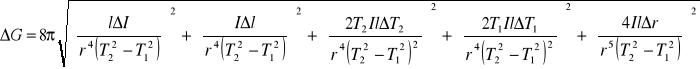
Okresy T1, T2, T2' liczone były jako średnia okresów bez obciązenia, z obciążeniem ciężarkami i obręczą.
![]()
okres bez obciążenia
![]()
okres z obręczą
![]()
okres z obręczą i ciężarkami
Błąd pomiaru okresu był liczony jako odchylenie standardowe średniej
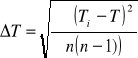
Średnice prętów
Średnica pręta |
|||
Lp. |
miedzianego [mm] |
stalowego [mm] |
mosiężnego [mm] |
1 |
2,44 |
2,47 |
2,45 |
2 |
2,47 |
2,47 |
2,46 |
3 |
2,46 |
2,47 |
2,45 |
4 |
2,46 |
2,46 |
2,50 |
5 |
2,45 |
2,48 |
2,46 |
6 |
2,47 |
2,47 |
2,47 |
7 |
2,47 |
2,47 |
2,46 |
8 |
2,45 |
2,46 |
2,46 |
9 |
2,46 |
2,47 |
2,46 |
10 |
2,46 |
2,45 |
2,45 |
wartość |
2,459 |
2,467 |
2,462 |
średnia |
|
|
|
promień |
1,223 |
1,234 |
1,231 |
Stal
rśr = 1,230 ± 0,003mm
miedź
rśr = 1,234 ± 0,003mm
mosiądz
rśr = 1,231 ± 0,005mm
STAL
l = 706 ± 1 mm
|
nieobciążony [s] |
obręcz [s] |
obręcz i odważniki
[s] |
|||||
i |
i-okresów |
okres |
i-okresów |
okres |
i-okresów |
okres |
||
10 |
22,75 |
2,275 |
33,59 |
3,359 |
34,83 |
3,483 |
||
12 |
27,35 |
2,279 |
40,25 |
3,354 |
41,74 |
3,478 |
||
14 |
31,75 |
2,268 |
47,09 |
3,364 |
48,77 |
3,484 |
||
16 |
36,25 |
2,266 |
53,87 |
3,367 |
55,77 |
3,486 |
||
18 |
40,94 |
2,274 |
60,47 |
3,359 |
62,70 |
3,483 |
||
20 |
45,45 |
2,273 |
67,27 |
3,364 |
69,71 |
3,486 |
||
T1 |
2,272 |
T2 |
3,361 |
T2' |
3,483 |
|||
rśr = 1,230 ± 0,003mm
T1 = 2,272 ± 0,002 s
T2 = 3,361 ± 0,002 s
T2' = 3,483 ± 0,001 s.
Dla pomiaru z obręczą
G = 29,8 ± 0,8 GPa
Dla pomiaru z obręczą i obciążnikami
G = 30 ± 1 GPa
Wartość tablicowa
G = 78 - 81 GPa
MIEDŹ
l = 705 ± 1 mm
|
nieobciążony [s] |
obręcz [s] |
obręcz i odważniki [s] |
|||||
i |
i-okresów |
okres |
i-okresów |
okres |
i-okresów |
okres |
||
10 |
34,52 |
3,452 |
50,63 |
5,063 |
52,81 |
5,281 |
||
12 |
41,39 |
3,449 |
60,72 |
5,060 |
63,15 |
5,263 |
||
14 |
48,30 |
3,450 |
71,15 |
5,082 |
73,71 |
5,265 |
||
16 |
55,11 |
3,444 |
81,21 |
5,076 |
84,21 |
5,263 |
||
18 |
62,05 |
3,447 |
91,40 |
5,078 |
94,74 |
5,263 |
||
20 |
68,89 |
3,445 |
101,59 |
5,080 |
105,24 |
5,262 |
||
T1 |
3,448 |
T2 |
5,073 |
T2' |
5,266 |
|||
rśr = 1,234 ± 0,003mm
T1 = 3,448 ± 0,001 s
T2 = 5,073 ± 0,004 s
T2' = 5,266 ± 0,003 s.
Dla pomiaru z obręczą
G = 13,3± 0,6 GPa
Dla pomiaru z obręczą i obciążnikami
G = 13,4 ± 0,5 GPa
Wartość tablicowa
G = 38 GPa
MOSIĄDZ
l = 705 ± 1 mm
|
nieobciążony [s] |
obręcz [s] |
obręcz i odważniki [s] |
|||||
i |
i-okresów |
okres |
i-okresów |
okres |
i-okresów |
okres |
||
10 |
31,43 |
3,143 |
46,36 |
4,636 |
48,02 |
4,802 |
||
12 |
37,58 |
3,132 |
55,49 |
4,624 |
57,55 |
4,796 |
||
14 |
43,87 |
3,134 |
64,80 |
4,629 |
67,17 |
4,798 |
||
16 |
50,08 |
3,130 |
73,89 |
4,618 |
76,77 |
4,798 |
||
18 |
56,49 |
3,138 |
83,27 |
4,626 |
86,42 |
4,801 |
||
20 |
62,68 |
3,134 |
92,52 |
4,626 |
95,99 |
4,800 |
||
T1 |
3,135 |
T2 |
4,626 |
T2' |
4,799 |
|||
rśr = 1,231 ± 0,005mm
T1 = 3,135 ± 0,002 s
T2 = 4,626 ± 0,002 s
T2' = 4,799 ± 0,001 s.
Dla pomiaru z obręczą
G = 15,9 ± 0,4 GPa
Dla pomiaru z obręczą i obciążnikami
G = 16,0 ± 0,3 GPa
Wartość tablicowa
G = 42 GPa
Wnioski
Otrzymane wartości modułów sztywności są znacznie zaniżone stosunku do wartości tabelowych. Trudno jednoznacznie określić przyczynę ich powstania. Wszystkie wartości były około 2,7 razy mniejsze niż podane w tablicach co może sugerować wadę aparatury pomiarowej bądź błodzy w sposobie obliczania. Trzeba wziąć pod uwagę znaczne dokształcenie pręta (pręt nie był prosty), luzy w mocowaniu (co mogło spowodować znaczne zwiększenie bicia), zmęczenie próbek materiałowych oraz nie uwzględnienie tarci układu.
Rysunek 1
Wyszukiwarka
Podobne podstrony:
12 (2), Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, laborki
12, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, laborki fizy
Kontrola badań laboratoryjnych
badania laboratoryjne 6
ROZRÓD Badanie terenowe i laboratoryjne mleka
Diagnostyka laboratoryjna chorób serca i mięśni poprzecz (2)
Diagnostyka laboratoryjna zaburzen gospodarki lek 2010
medycyna laboratoryjna
Medycyna laboratoryjna 12 13
7) Laboratoria EMG i MMG na pziomach sily i ko
3 1 5 CCNA1 Laboratorium pl
laboratorium2
Laboratorium 7
Laboratorium jezyk c4 2013
więcej podobnych podstron