Sprawozdanie z ćwiczenia A - 22
Kaczorek Paweł Kuczyński Paweł |
Zespół nr 4 |
||
Wydział Elektryczny |
|
||
Czwartek 1100 - 1400 |
Data 21.03.1996 |
Ocena z przygotowania |
|
Prowadzący: dr B.Szymańska |
Ocena z sprawozdania |
|
|
Podpis prowadzącego: |
Zaliczenie
|
|
|
Temat: Ruch ładunku w polu elektrycznym i magnetycznym. Wyznaczanie wartości e/m
PODSTAWY FIZYCZNE
Na ładunek q w polu elektrycznym o natężeniu działa siła :
której wartość nie zależy od prędkości poruszającego się ładunku. Pole magnetyczne natomiast oddziałuje na ładunki elektryczne siłą zwaną siłą Lorentza :
,
gdzie jest prędkością ładunku
jest indukcją pola magnetycznego.
Z własności iloczynu wektorowego otrzymujemy:
.
Wynika z tego, że pole magnetyczne nie działa na ładunek wówczas, gdy ładunek nie porusza się (v=0) lub gdy porusza się w kierunku linii indukcji pola magnetycznego (sin=0). Z wniosku tego stwierdzamy, że stałe pole magnetyczne nie może zmienić energii kinetycznej poruszającego się ładunku, a zatem i wartości prędkości, może tylko zmienić kierunek jego ruchu. Całkowita siła działająca na ładunek znajdujący się jednocześnie w polu elektrycznym i magnetycznym wyraża się wzorem:
Rozważając sytuację w której na poruszający się elektron działają oba pola: magnetyczne i elektryczne. Zakładamy, kierunki wektorów natężeń pól elektrycznego i magnetycznego są do siebie równoległe, natomiast kierunek prędkości elektronu tworzy z kierunkiem wektora natężeń pola kąt α. Wektor prędkości rozkładamy na składowe:
gdzie prostopadły , a równoległy do wektora indukcji magnetycznej .
W kierunku prostopadłym do kierunku linii sił pól elektrycznego i magnetycznego na elektron działa siła Lorentza równa:
Ruch w tej płaszczyźnie ( prostopadłej do kierunku linii pól elektrycznego i magnetycznego ) będzie ruchem po okręgu. Natomiast w kierunku równoległym (wzdłuż linii sił obu pól) na cząstkę poruszającą się z prędkością działa tylko siła pochodząca od pola elektrycznego. W przypadku jego nieobecności elektron poruszałby się w tym kierunku ze stałą prędkością (składowa siły Lorentza wzdłuż tego kierunku jest równa zeru), a założenie ruchu w obu kierunkach dawałoby w efekcie ruch elektronu po linii śrubowej o stałym skoku. Obecności pola elektrycznego powoduje, że elektron w tym kierunku porusza się ruchem jednostajnie przyśpieszonym, co po złożeniu daje ruch po linii śrubowej o zmiennym skoku.
OPIS ĆWICZENIA
Wyznaczanie wartości e/m metodą magnetronu.
Celem przeprowadzonego doświadczenia było oszacowanie wielkości e/m.Doświadczenie polegało na mierzeniu natężenia prądu anodowego IA w zależności od prądu płynącego przez cewkę IC przy stałym napięciu pomiędzy katodą, a anodą UA i przy stałym natężeniu żarzenia IŻ (patrz rys 2).Rozpatrując tę zależność można wyznaczyć e/m. Siłę Lorentza można rozłożyć na dwie składowe (patrz rys 1) w kierunku środka lampy (wzdłuż promienia) Fr i w kierunku prostopadłym do promienia Fa. Całkowita siła działająca na elektron będzie miała składowe Fa i eE+Fr.
Przy obliczaniu wartości e/m korzystamy ze wzoru :
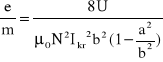
,
gdzie Ikr - natężenie krytyczne prądu anodowego odczytane z wykresu
Rys. 1 SCHEMAT ZESTAWU DOŚWIADCZALNEGO BUDOWA MAGNETRONU
MAGNETRON JEST TO LAMPA ELEKTRONOWA (DIODA) O CYLINDRYCZNEI ANODZIE (A) I OSIOWO UMIESZCZONEJ KATODZIE
Użyliśmy do pomiarów :
mierników uniwersalnych o symbolach:
UM-4a (kl=1.5)
UM-3a (kl=1)
U-110B (kl=1.5)
UM-3b (kl=1)
Rys.2 SIŁY DZIAŁAJĄCE NA ELEKTRON PORUSZAJĄCY SIĘ W MAGNETRONIE
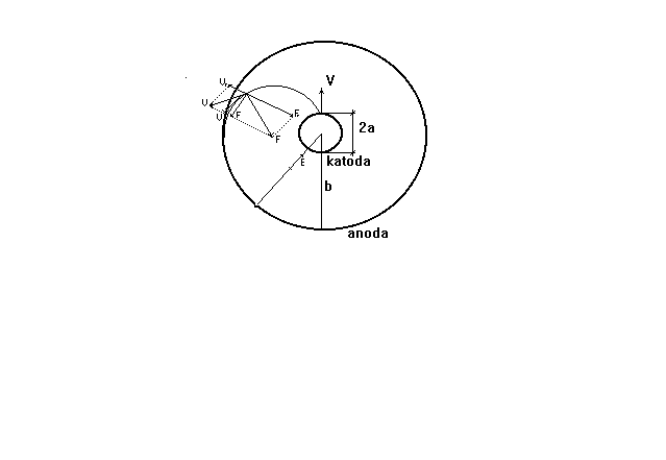
W tabelce zebrano pomiary IA - prądu anody i IC - prądu cewki.
W pomiarze tym napięcie anodowe const UA=1,5V
IA |
[μA] |
52 |
50 |
48 |
44 |
43 |
42 |
40 |
38 |
36 |
32 |
28 |
24 |
20 |
IC |
[A] |
0 |
0,04 |
0,1 |
0,18 |
0,2 |
0,26 |
0,38 |
0,54 |
0,65 |
0,7 |
0,75 |
0,8 |
0,85 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IA |
[μA] |
16 |
12 |
10 |
8 |
6 |
4 |
2 |
||||||
IC |
[A] |
0,95 |
1,1 |
1,2 |
1,35 |
1,6 |
1,9 |
2,8 |
||||||
Zależność e/m. obliczamy ze wzoru :
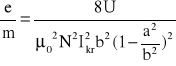
Ikr odczytujemy z wykresu:
Ikr=0,65 [A]
Dane dla pomiarów:
UA=1,5 [V]
IŻ=100 [mA]
N=9250 [zw/m.].
b=0,47 [cm]=4,7*10-3 [m.];a<<b
μ0=4π*10-7 [Tm/a].
.
Po podstawieniu do wzoru wartości podanych wcześniej otrzymaliśmy:
a po uwzględnieniu błędu:
Przeliczenie jednostek:
dla podstawień:
Następnie dokonaliśmy pomiarów dla drugiego sposobu wyznaczania e/m. Metoda ta polegała na założeniu cewki na lampę oscyloskopową, następnie podłączyliśmy zasilanie i miernik.
Pomiary ukazuje tabela:
Ikr |
[A] |
0,5 |
1,1 |
1,8 |
n |
|
1 |
2 |
3 |
Dane do obliczeń dla drugiej części doświadczeńia:
d=11,5 [mm]
2R=89 [mm]
L=127 [mm]
z=1000 [zwojów]
U=760 [V]
Korzystając ze wzoru:
B=μH
czyli po podstawieniu wartości:
dla n=1
dla n=2
dla n=3
Przeliczenie jednostek:
dla podstawień:
DYSKUSJA BŁĘDÓW
W ćwiczeniu liczymy błędy wynikające z użytych przyrządów. W pomiarach używaliśmy miernika analogowego uwzględniamy błąd odczytu wynoszący:
ΔIo=1 [dz] ,
gdzie & - liczba działek, Imax - maksymalny prąd danego zakresu
więc
-dla amperomierza do pomiaru prądu anody :
dla zakresu 100 μ A - ΔIo=2μA
dla zakresu 30 μA - ΔI0=1μA
dla zakresu 10 μA - ΔI0=0,2μA
-dla amperomierza do pomiaru prądu cewki :
dla zakresu 0,6 A - ΔI0=0,02A
dla zakresu 1,5 A - ΔI0=0,05A
dla zakresu 6 A - ΔI0=0,2A
Drugim błędem jaki dotyczy pomiaru prądu jest błąd wynikający z klasy użytego miernika , wynoszący:
ΔIkl= ,
gdzie kl - klasa miernika, Imax - maksymalny prąd danego zakresu.
czyli:
-dla amperomierza do pomiaru prądu anody :
klasa miernika kl=1,5
dla zakresu 100 μ A - ΔIkl=1,5μA
dla zakresu 30 μA - ΔIkl=0,45μA0,5μA
dla zakresu 10 μA - ΔIkl=0,15μA0,2μA
-dla amperomierza do pomiaru prądu cewki :
klasa miernika kl=1
dla zakresu 0,6 A - ΔIkl=0,009A0,01A
dla zakresu 1,5 A - ΔIkl=0,0225A0,02A
dla zakresu 6 A - ΔIkl=0,09A0,1A
Całkowity błąd uzyskany wczasie wykonywania pomiarów równy jest sumie błędów:
czyli błędowi odczytu i błędowi wyńikalącemu z klasy mierników
ΔI=ΔIo+ΔIkl
czyli po podstawieniu wartości:
-dla amperomierza do pomiaru prądu anody :
dla zakresu 100 μ A - ΔI=2,5μA
dla zakresu 30 μA - ΔI=1,5μA
dla zakresu 10 μA - ΔI=0,4μA
-dla amperomierza do pomiaru prądu cewki :
dla zakresu 0,6 A - ΔI=0,03A
dla zakresu 1,5 A - ΔI=0,07A
dla zakresu 6 A - ΔI=0,3A
Błąd dla wartości e/m. :
błąd bezwzględny
błąd względny
wartość tablicowa
a po podstawieniu do wzoru wartości otrzymaliśmy ( dla pierwszej metody pomiarowej ) :
Po podstawieniu wartości otrzymaliśmy ( dla drugiej metody pomiarowej ) :
n=1 ,
n=2 ,
n=3 ,
Błąd dla obliczonej wartości e/m. oszacowuje się za pomocą różniczki zupełnej :
a po podstawieniu wartości :
WNIOSKI
Duża wartość błędu względnego e/m. wynika z małego napięcia emisji elektronów.
Wartość błędu względnego przy drugiej metodzie pomiarowej była obliczona dla poszczególnych n:
n=1
n=2
n=3
jak widać najmniejszy błąd wystąpił przy n=2.
Wartość e/m. jest wielkością stałą gdy bierzemy pod uwagę fizykę klasyczna ( prędkości są dużo mniejsze od prędkości światła), natomiast w fizyce relatywistycznej dla prędkości zbliżonych do c zmienia się masa.
Wyszukiwarka
Podobne podstrony:
A22 , Sprawozdanie z ˙wiczenia A-22.
SP A-22, Sprawozdanie z ˙wiczenia A-22.
sprawozdanie cwiczenie 22, studia, agrobiotechnologie
Sprawozdanie moce"22 (1)
halla2, Sprawozdanie z ˙wiczenia B - 1 (B-14)
Obrabiarki sterowane numery, SPRAWOZDANIE Z ˙WICZE˙ LABORATORYJNYCH
OBROBKA5, SPRAWOZDANIE Z ˙WICZE˙ LABORATORYJNYCH
C 4 A, Sprawozdanie z ˙wiczenia C-4
JUSTC2, Sprawozdanie z ˙wiczenia C2
C 11, Sprawozdanie z ˙wiczenia C-11
Metody nacinania k z baty, SPRAWOZDANIE Z ˙WICZE˙ LABORATORYJNYCH
SPRAWO~2 3, Sprawozdanie z ˙wiczenia B - 1 (B-14)
B-11, Sprawozdanie z ˙wiczenia B-11
SPRAC12, Sprawozdanie z ˙wiczenia C-12
PRAC1FIZ, LAB50, SPRAWOZDANIE Z ˙WICZENIA NR 50
sprawako3, SPRAWOZDANIE Z LABORATORIUM
MF1, Sprawozdanie z ˙wiczenia F-1
więcej podobnych podstron