1. Cel ćwiczenia.

Celem ćwiczenia jest:

• zapoznanie się z opisem ruchu oscylatorów sprzężonych,

• określenie związku między parametrami charakteryzującymi układ oscylatorów sprzężonych z parametrami oscylatora harmonicznego,

• wyznaczenie częstości własnych, częstości dudnień i współczynnika sprzężenia.

2. Wstęp teoretyczny.

Punkt materialny, na który działa siła proporcjonalna do jego wychylenia z położenia równowagi i przeciwnie skierowana, jest oscylatorem harmonicznym, a jego ruch - ruchem harmonicznym. Dlatego też zgodnie z drugą zasadą dynamiki Newtona, równanie ruchu takiego oscylatora wyraża się równaniem:

,

gdzie

m - masa oscylatora,

x - wychylenie z położenia równowagi,

k - współczynnik proporcjonalności (wsp. sprężystości).

Równanie powyższe można zapisać w postaci:

,

przyjmując za,

gdzie

ω₀ - częstość (kołowa) własna oscylatora harmonicznego.

Jeżeli dwa identyczne oscylatory harmoniczne zostaną połączone (sprzężone) w taki sposób, że dodatkowa siła (wynikająca z połączenia) jest proporcjonalna do różnicy wzajemnych wychyleń pojedynczych oscylatorów, to - zgodnie z drugą zasadą dynamiki Newtona - równanie ruchu tych oscylatorów przyjmuje postać:

(**)

Równanie to można uogólnić na większą liczbę oscylatorów harmonicznych o różnych częstościach własnych, przy czym:

x_i - wychylenie i-tego oscylatora z położenia równowagi,

k_S - współczynnik proporcjonalności (współczynnik sprzężenia).

Wówczas rozwiązania równań poszukujemy w postaci:

Po podstawieniu otrzymujemy:

czyli po przekształceniu:

(*)

Powyższy układ równań ma rozwiązanie ze względu na A₁ i A₂ , jeśli wyznacznik tego układu jest równy zeru. Zerowanie się wyznacznika prowadzi do równania:

Z powyższego równania otrzymujemy wyrażenie określające częstości (kołowe) własne oscylatorów sprzężonych:

czyli

lub

Wstawiając ω_I do jednego z równań układu równań (*) otrzymujemy:

czyli k_SA₁= k_SA₂ , stąd ostatecznie A₁=A₂ .

Analogicznie wstawiając ω_II do jednego z równań układu równań (*) otrzymujemy po uproszczeniu . Obydwa oscylatory sprzężone drgają więc z częstością kołową ω_I , jeżeli ich fazy są zgodne lub z częstością ω_II , jeżeli ich fazy są przeciwne.

Jeżeli oscylatorami będą wahadła fizyczne, to

gdzie

D - moment kierujący,

I - moment bezwładności wahadła.

Miarę wychylenia wahadła z położenia równowagi oznaczymy ϕ_i . Sytuacje odpowiadające częstościom kołowym własnym ω₁ i ω₂ są przedstawione na rysunkach. Jeżeli jedno z wahadeł sprzężonych (np. drugi) unieruchomimy ϕ₂=0, a pierwsze pobudzimy do drgań, to równanie oscylatora harmonicznego przyjmie postać:

i drgania odbywać się będą z częstością kołową:

Rozwiązanie równań ruchu dla innych warunków początkowych, np. dla:

można otrzymać wprowadzając nowe zmienne:

Dodając równania (**) stronami i wykorzystując pierwsze równanie otrzymujemy:

Analogicznie z równania drugiego otrzymujemy:

Rozwiązania powyższych równań przy warunkach początkowych mają postać:

tak więc:

Każdy z oscylatorów sprzężonych wykonuje w tym przypadku drgania z częstotliwością kołową

zaś amplituda zeruje się z częstością

gdzie

W omawianym przypadku drgania są więc dudnieniami otrzymanymi przez nałożenie się dwóch drgań własnych o częstościach kołowych ω_I i ω_II

4. Przebieg ćwiczenia.

4.1. Spis przyrządów:

• stoper

• układ wahadeł sprzężonych

4.2.Przebieg pomiarów:

Pomiary wykonujemy dla trzech różnych sprzężeń (trzy różne zawieszenia sprężyny).

4.2.1. Wyznaczenie okresu wahań odpowiadającego częstości własnej ω₁ (zgodne fazy początkowe ϕ₁=ϕ₂).

sprzężenie	ilość okresów n	czas zmierzony t [s]	okres T [s]	częstość ω1 [1/s]	δω1 [%]
1	50	67,61	1,352	4,647	0,015
2	50	67,58	1,352	4,649	0,015
3	50	67,69	1,354	4,641	0,015

4.2.2. Wyznaczenie okresu wahań odp. częstości ω₂ (przeciwne fazy początkowe ϕ₁ = -ϕ₂).

sprzężenie	ilość okresów n	czas zmierzony t [s]	okres T [s]	częstość ω2 [1/s]	δω2 [%]
1	50	66,57	1,331	4,719	0,016
2	50	65,40	1,308	4,804	0,016
3	50	64,54	1,291	4,868	0,016

4.2.3. Wyznaczenie częstości dudnień ω_d (różne fazy początkowe ϕ₁ = -20^o, ϕ₂ = 0^o).

Początkowo wahadło 1 wykonywało drgania o maksymalnej amplitudzie, a wahadło 2 pozostawało w spoczynku. Stopniowo ruch wahadła 1 zaczął zanikać, natomiast wahadło 2 zwiększało amplitudę swoich drgań. Analogiczna sytuacja powtórzyła się teraz dla wahadła 2. Drgania powoli zanikały aż do zatrzymania się wahadła. W tym momencie układ 2 wahadeł wykonał 1 pełny okres dudnień, który został zmierzony.

sprzężenie	ilość okresów n	czas zmierzony t [s]	okres T [s]	częstość ωd [1/s]	δωd [%]
1	1	96,50	96,50	0,065	0,011
2	1	38,47	38,47	0,163	0,026
3	1	25,81	25,81	0,243	0,039

4.2.4. Częstość dudnień:

W poniższej tabeli znajduje się zestawienie wyliczonej częstości dudnień oraz zmierzonej w celu porównania różnic.

sprzężenie	ω1 [1/s]	ω2 [1/s]	ωd = ω2 - ω1 [1/s]	ωd zmierzone [1/s]
1	4,647	4,719	0,072	0,065
2	4,649	4,804	0,155	0,163
3	4,641	4,868	0,227	0,243

4.2.5. Moment kierujący i sprzęgający

Moment kierujący:

Moment sprzęgający:

Po podstawieniu do wzoru na moment sprzęgający wzoru na moment kierujący i odpowiednim uproszczeniu otrzymamy następujące wyrażenie:

gdzie

I - moment bezwładności,

I = 0,2334 kg⋅m² ,

.

Błąd wyznaczenia momentu sprzęgającego:

δD_S= δω₁ + δω_d +δI.

4.3.1 Przykładowe wyliczenia

D₁ =0,2334⋅(4,647)² =5,0402 [Nm]

D₂ =0,2334⋅(4,649)² =5,0445 [Nm]

D₃ =0,2334⋅(4,641)² =5,0272 [Nm]

D_S1 =4,647 ⋅ 0,065 ⋅ 0,2334=0,0705 [Nm]

D_S2 =4,649 ⋅ 0,163⋅0,2334=0,1769 [Nm]

D_S3 =4,641 ⋅ 0,243⋅0,2334=0,2632 [Nm]

4.3.2. Tabela momentów kierujących i sprzęgających

sprzężenie	moment kierujący D [Nm]	moment sprzęgający DS [Nm]
1	5,0402	0,0705
2	5,0445	0,1769
3	5,0272	0,2632

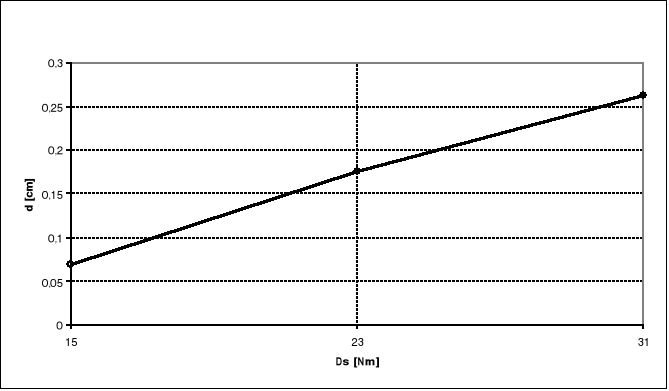
5. Wykres zależności momentu sprzęgającego od odległości punktu zawieszenia sprężyny.

d [cm]	DS [Nm]	δ DS [%]
15	0,0705	0,526
23	0,1769	0,541
31	0,2632	0,554

d - odległość punktu zawieszenia sprężyny (sprzężenia) od punktu zawieszenia wahadła

Wykres zależności momentu sprzęgającego od odległości punktu zawieszenia sprężyny

6. Błędy pomiarów.

Na błędy pomiarów złożyły się następujące błędy:

• Przede wszystkim bardzo znaczący błąd wynikający z czasu reakcji mierzącego - jest on dość znaczny, ale praktycznie niemożliwy do wyliczenia,

• Błąd pomiaru czasu stoperem - jest to błąd dyskretyzacji pomiaru czasu wynikający z cyfrowego charakteru pomiaru czasu,

• Błąd wyznaczenia momentu bezwładności wahadła - podany w instrukcji stanowiska ćwiczenia:

,

• Błąd zaokrąglenia liczby π - pomijalnie mały, gdyż liczba π była wyliczona przez kalkulator z dokładnością do dziewięciu miejsc po przecinku,

• Błąd wyznaczenia kąta wychylenia wahadła - nie istotny, gdyż częstość drgań wahadła nie zależy od początkowego kąta wychylenia.

7. Wnioski:

Jak pokazało ćwiczenie istnieje pewna niewielka różnica pomiędzy częstością dudnień zmierzoną a wyliczoną ze znajomości ω₁ i ω₂ . Związane jest to z błędami jakimi obarczone są wyniki pomiarów. Istotny tu wpływ miał przede wszystkim czas reakcji mierzącego, który musiał w odpowiedniej chwili zastartować i zatrzymać stoper. Jednak błąd ten jest niemożliwy do wyliczenia. Wyeliminowanie, a napewno znaczne zmniejszenie tego błędu mogłoby być zrealizowane za pomocą jakiegoś mechanizmu (np. fotokomórka lub inne czujniki) automatycznie startującego i zatrzymującego stoper.

Celem tego ćwiczenia było poznanie zjawiska dudnień. Sama nazwa „dudnienia” wzięła się prawdopodobnie stąd, iż zjawisko to zachodzi również dla fal dźwiękowych. W przypadku dźwięku zmiany amplitudy przejawiają się jako zmiany głośności. Dobrym przykładem jest równoczesne uderzenie w dwa sąsiednie klawisze fortepianu. Zjawisko to można wykorzystać do nastrojenia dwóch strun na tę samoą częstotliwość metodą naciągania jednej z nich w czasie brzmienia obu, aż do momentu, gdy dudnienia znikną. Ucho ludzkie może rejestrować tylko takie dudnienia między dwoma tonami, których częstość sięga około siedmiu na sekundę. Dudnienia o częstościach wyższych nie są w odbieranym dźwięku rozróżnialne.

Jeżeli ω₁ i ω₂ są prawie równe, amplituda zmienia się powoli. Zjawisko to ma charakter modulacji amplitudy, której zastosowanie mamy w odbiornikach radiowych typu AM (z ang. amplitude modulation).

Wykres zależności momentu sprzęgającego od punktu zawieszenia sprężyny (sprzężenia) sporządzony w trakcie ćwiczenia pozwala przypuszczać, iż charakterystyka ta jest liniowa.

---