
1
Podstawy Konstrukcji Maszyn
Wykład 10
Przekładnie zębate część 3
Koła walcowe o zębach śrubowych
Dr inż. Jacek Czarnigowski
Koła zębate walcowe o zębach
śrubowych
Linia zębów jest pochylona
względem tworzącej walca i jest
linią śrubową
Zęby nacinane są tymi samymi
narzędziami co w przypadku kół
o zębach prostych.
2
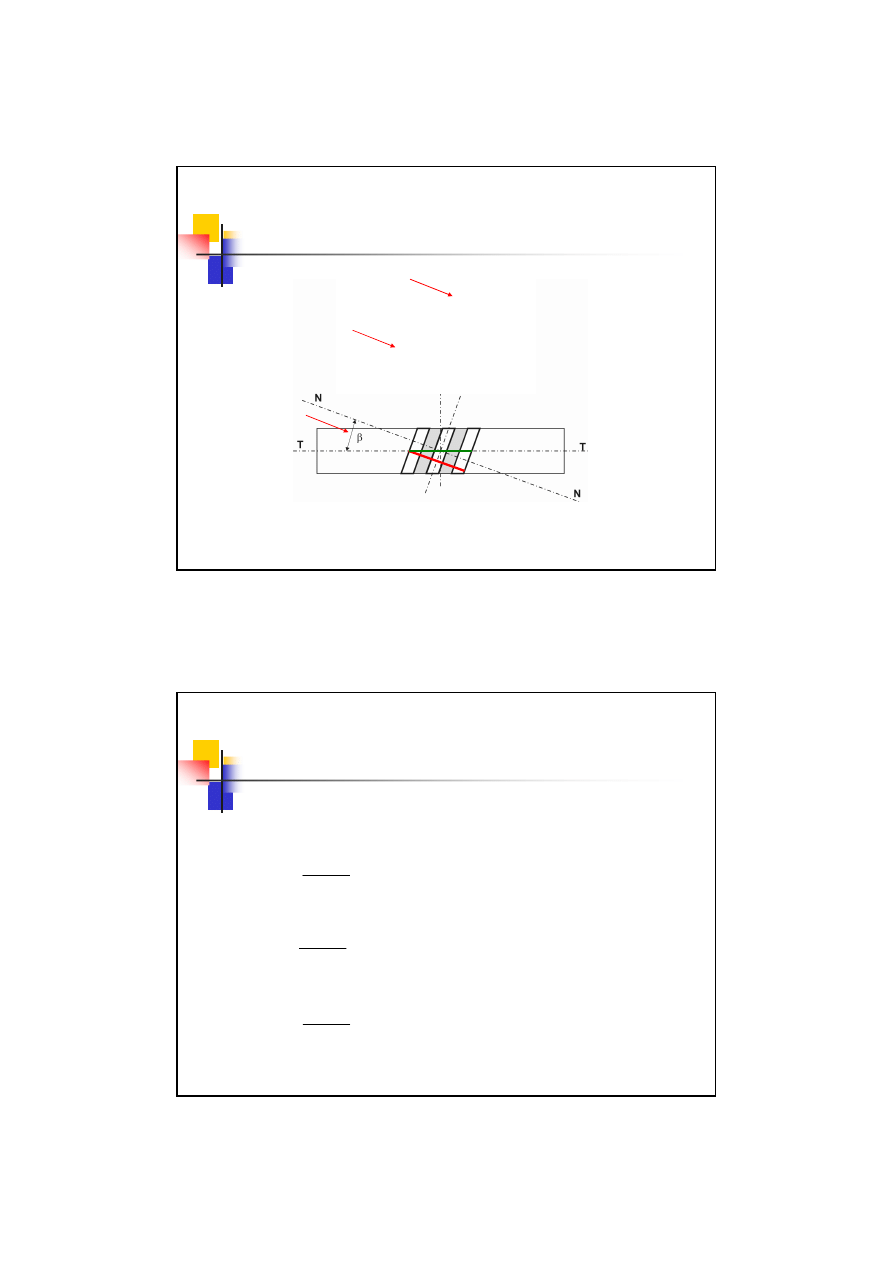
Koła zębate walcowe o zębach
śrubowych
Płaszczyzna normalna
- Płaszczyzna ruchu
narzędzia
Płaszczyzna czołowa
- Płaszczyzna
współpracy zębów
Kąt pochylenia zębów
Wymiary nominalne narzędzia
Wymiary rzeczywiste zębów koła
ββββ
= 8 - 35
°°°°
p
n
p
t
p
n
≠ p
t
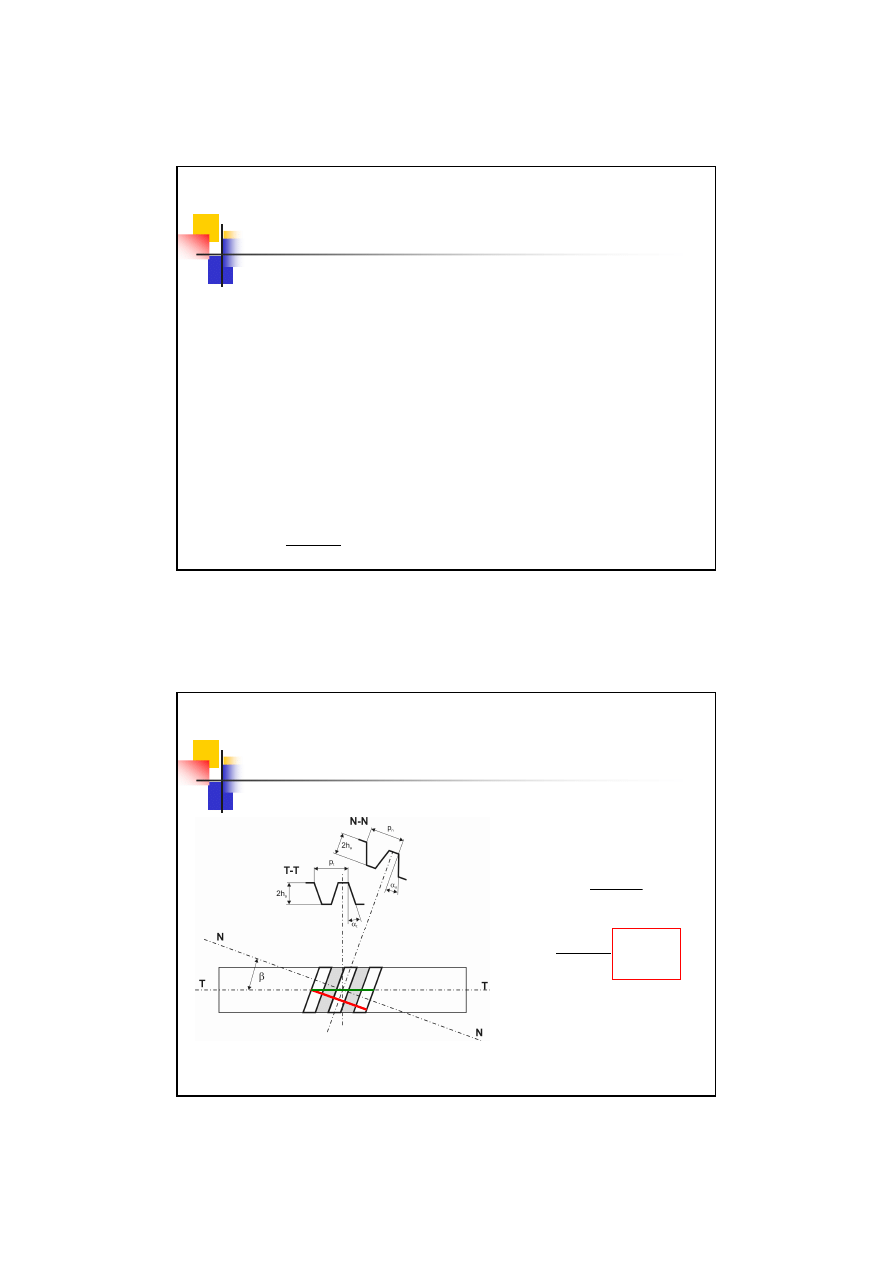
Koła zębate walcowe o zębach
śrubowych
Przeliczenia przekrój czołowy – przekrój normalny
Podziałka:
β
cos
n
t
p
p
=
Moduł:
β
cos
n
t
m
m
=
Kąt przyporu:
β
α
α
cos
n
t
tg
tg
=
Współczynnik wysokości zęba:
β
cos
⋅
=
n
t
y
y
Współczynnik korekcji:
β
cos
⋅
=
n
t
x
x
Współczynnik luzu wierzchołkowego:
β
cos
*
*
⋅
=
n
t
c
c
Współczynnik zeszlifowania głowy zęba:
β
cos
⋅
=
n
t
k
k
3
Koła zębate walcowe o zębach
śrubowych
Wymiary kół
Średnica podziałowa:
z
m
d
t
⋅
=
Średnica głów:
(
)
t
t
t
t
a
k
x
y
z
m
d
⋅
−
⋅
+
⋅
+
⋅
=
2
2
2
Średnica stóp:
(
)
t
t
t
t
f
c
x
y
z
m
d
*
2
2
2
⋅
−
⋅
+
⋅
−
⋅
=
Zerowa odległość osi:
t
m
z
z
a
⋅
+
=
2
2
1
UWAGA!
Całość obliczeń
odbywa się na
płaszczyźnie czołowej
Koła zębate walcowe o zębach
śrubowych
p
n
p
t
p
n
< p
t
Graniczna liczba zębów
Więcej miejsca na wyjście narzędzia
Obliczenia przeprowadza się
na płaszczyźnie czołowej
t
t
gr
y
z
α
β
2
sin
2
⋅
=
β
α
β
3
2
cos
sin
2
⋅
⋅
=
n
n
gr
y
z
Zmniejszenie w stosunku do
kół o zębach prostych
4
Koła zębate walcowe o zębach
śrubowych
Liczba przyporu
β
α
ε
ε
ε
+
=
(
)
(
)
[
]
wt
a
wt
a
tg
tg
z
tg
tg
z
α
α
α
α
π
ε
α
−
⋅
+
−
⋅
⋅
=
2
2
1
1
2
1
Liczba przyporu dla kół o zębach śrubowych składa się z dwóch części:
Czołowa liczba przyporu
Poskokowa liczba przyporu
n
m
b
⋅
⋅
=
π
β
ε
β
sin
Koła zębate walcowe o zębach
śrubowych
Zalety i wady
Zalety:
Długość zęba jest większa od szerokości koła.
Skośna linia przylegania zwiększa wytrzymałość zęba.
Większa liczba przyporu.
Niższa wartość granicznej liczby zębów.
Wady:
Dochodzą siły osiowe zwiększające obciążenia łożysk.
5
Przykład 10.1
– korekcja P-konstrukcyjna
z
1
=19
z
2
=29
m
n
= 2,5
y
n
= 1
α
n
= 20
°°°°
c*
n
= 0,25
ββββ
= 12
°°°°
Obliczyć wymiary kół zębatych przekładni tak aby rzeczywista odległosć
osi wynosiła
a
w
= 60,00 mm
Przykład 10.1
– korekcja P-konstrukcyjna
Przeliczenia przekrój czołowy – przekrój normalny
Moduł:
mm
556
,
2
12
cos
5
,
2
cos
=
=
=
o
n
t
m
m
β
Kąt przyporu:
'
25
20
37210
,
0
12
cos
20
cos
o
t
o
o
n
t
tg
tg
tg
=
⇒
=
=
=
α
β
α
α
Współczynnik wysokości zęba:
9781
,
0
12
cos
1
cos
=
⋅
=
⋅
=
o
n
t
y
y
β
Współczynnik luzu wierzchołkowego:
2445
,
0
12
cos
25
,
0
cos
*
*
=
⋅
=
⋅
=
o
n
t
c
c
β
6
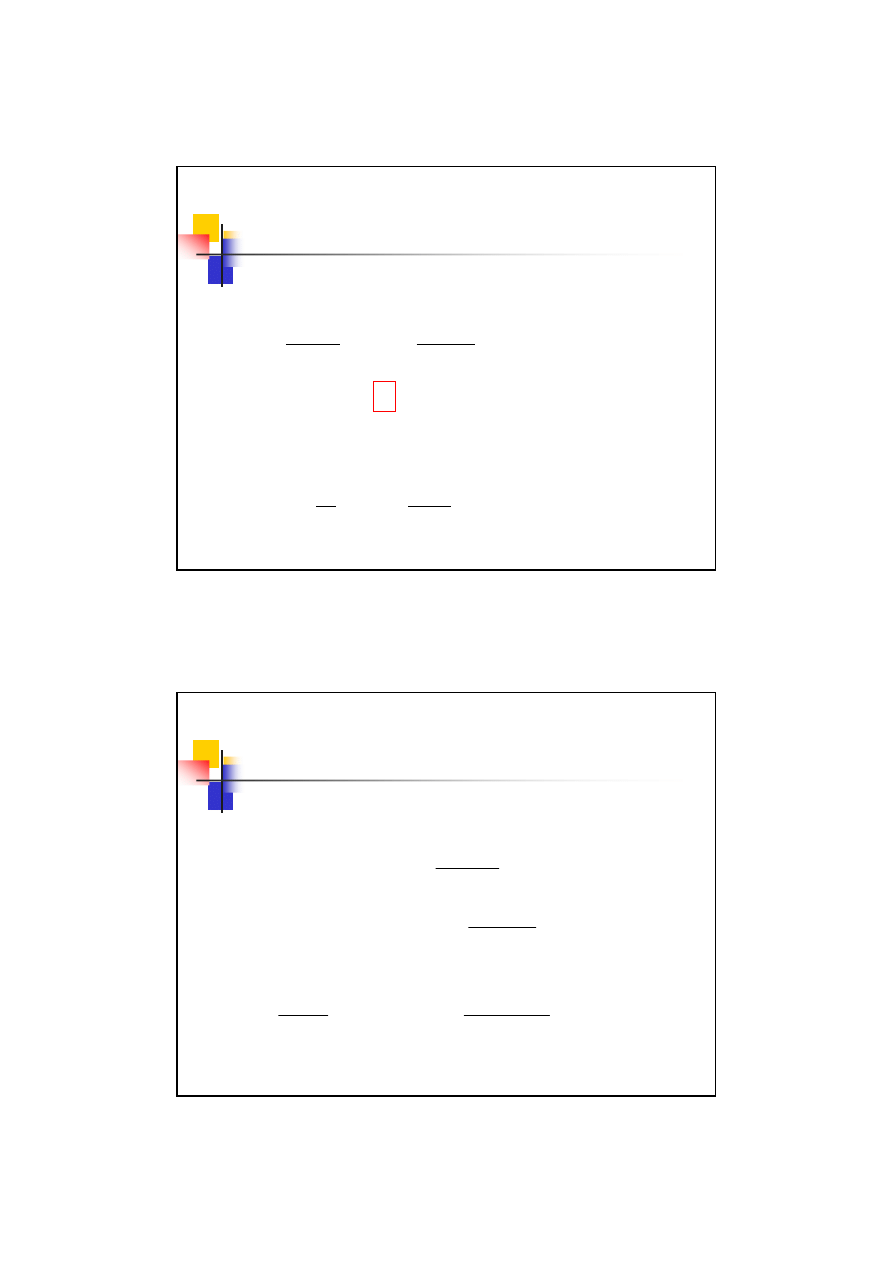
Przykład 10.1
– korekcja P-konstrukcyjna
Sprawdzamy konieczność i rodzaj korekcji:
mm
00
,
60
mm
34
,
61
=
≠
=
w
a
a
mm
34
,
61
2
29
19
556
,
2
2
2
1
=
+
⋅
=
+
⋅
=
z
z
m
a
t
Zatem korekcja P-konstrukcyjna
Obliczamy rzeczywisty toczny kąt przyporu:
'
38
16
9581
,
0
'
25
20
cos
00
,
60
34
,
61
cos
cos
o
w
o
t
w
wt
a
a
=
=
⋅
=
⋅
=
α
α
α
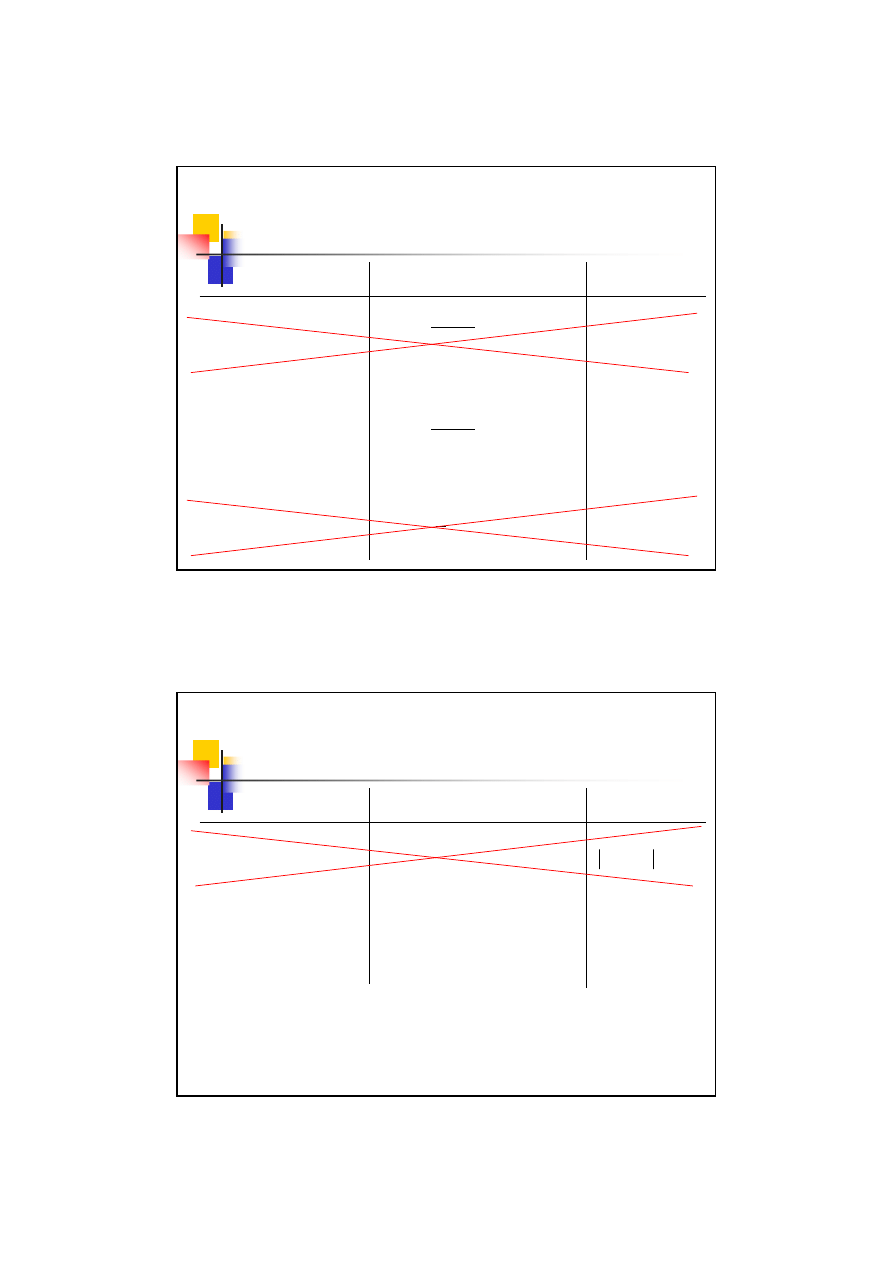
Przykład 10.1
– korekcja P-konstrukcyjna
015890
,
0
180
'
25
20
'
25
20
=
⋅
−
=
−
=
o
o
o
t
t
t
tg
tg
inv
π
α
α
α
Inwoluty kątów:
008440
,
0
180
'
38
16
'
38
16
=
⋅
−
=
−
=
o
o
o
wt
wt
wt
tg
tg
inv
π
α
α
α
Zatem suma współczynników korekcji wyniesie:
(
)
(
)
(
)
(
)
480
,
0
015890
,
0
008440
,
0
'
325
20
2
29
19
2
2
1
2
1
2
1
−
=
+
−
⋅
⋅
+
=
−
⋅
⋅
+
=
+
t
t
o
t
wt
t
t
t
x
x
tg
inv
inv
tg
z
z
x
x
α
α
α
7
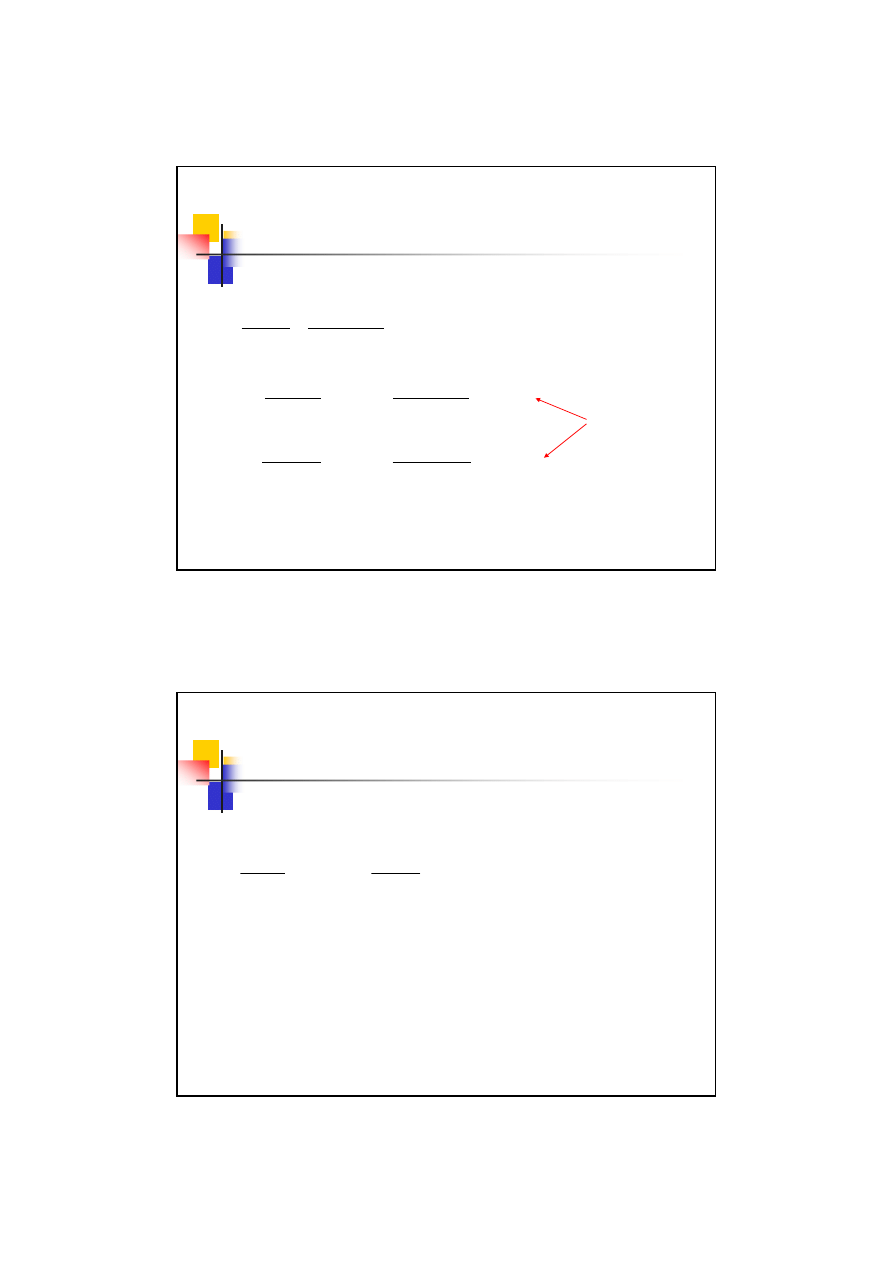
Przykład 10.1
– korekcja P-konstrukcyjna
Nazwa kryterium
Sposób przeprowadzania Zastosowanie
Odwrotnie
proporcjonalnie
(
)
(
)
1
2
1
2
2
1
2
1
2
1
x
x
x
x
x
x
z
z
z
x
−
+
=
+
⋅
+
=
Korekcja
dodatnia
(
)
0
2
1
>
+
x
x
Wprost
proporcjonalnie
(
)
(
)
1
2
1
2
2
1
2
1
1
1
x
x
x
x
x
x
z
z
z
x
−
+
=
+
⋅
+
=
Korekcja
ujemna
(
)
0
2
1
<
+
x
x
Po równo
(
)
1
2
2
1
1
2
1
x
x
x
x
x
=
+
⋅
=
2
1
z
z
≈
√√√√
Przykład 10.1
– korekcja P-konstrukcyjna
(
)
0
2
2
1
1
=
+
=
x
x
x
x
Nazwa kryterium
Sposób przeprowadzania Zastosowanie
Wszystko na jedno
koło
(
)
3
,
0
2
1
<
+
x
x
Niestandardowy
2
2
1
1
gr
gr
x
x
x
x
≥
≥
Zagrożenie
podcięciem
jednego lub
obu kół
?
8
Przykład 10.1
– korekcja P-konstrukcyjna
001
,
16
'
25
20
sin
9781
,
0
2
sin
2
2
2
=
⋅
=
⋅
=
o
t
t
gr
y
z
α
β
gr
gr
z
z
z
z
>
>
2
1
183
,
0
001
,
16
19
001
,
16
9781
,
0
1
1
−
=
−
⋅
=
−
⋅
=
β
β
gr
gr
t
tgr
z
z
z
y
x
438
,
0
001
,
16
29
001
,
16
9781
,
0
2
2
−
=
−
⋅
=
−
⋅
=
β
β
gr
gr
t
tgr
z
z
z
y
x
Granice korekcji
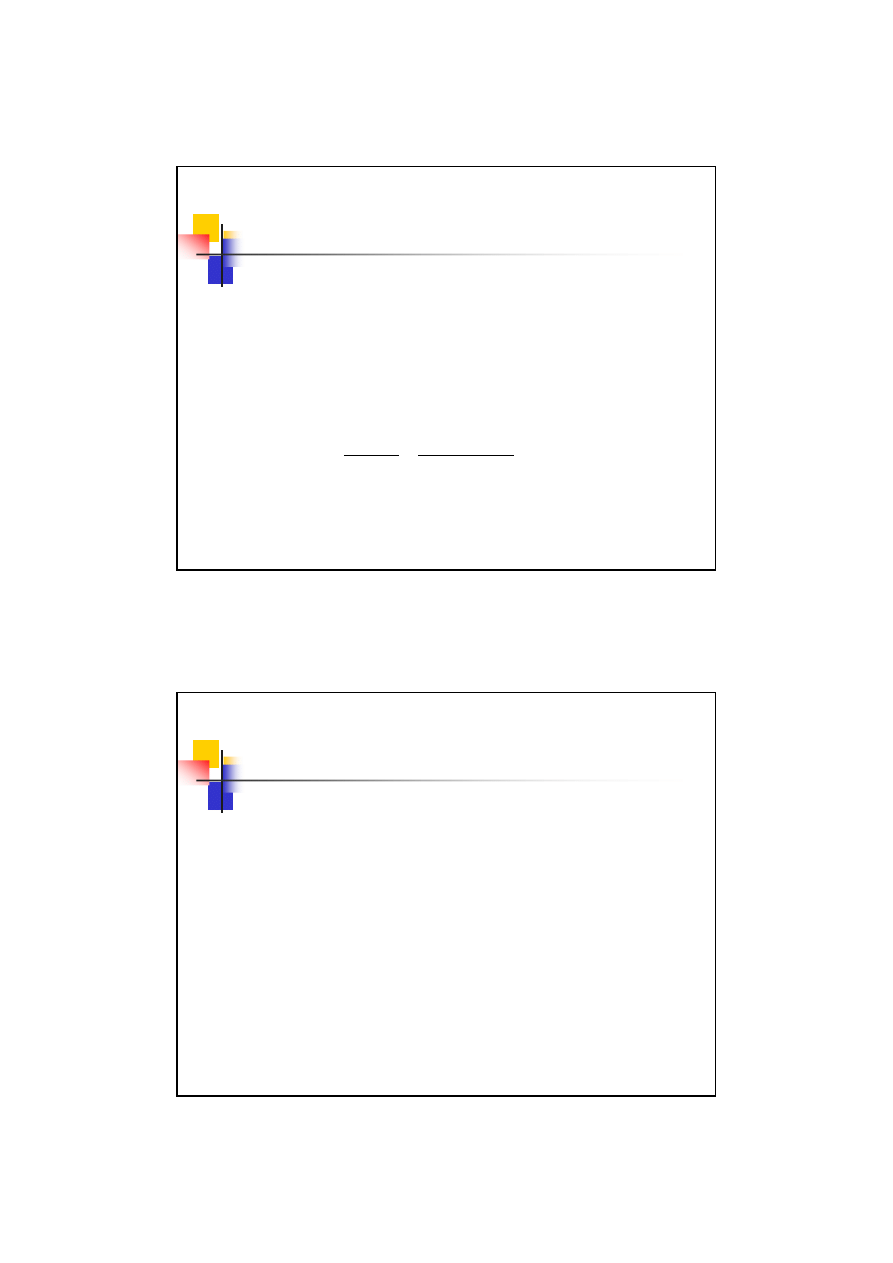
Przykład 10.1
– korekcja P-konstrukcyjna
Z podziału wprost proporcjonalnego:
(
)
(
)
190
,
0
480
,
0
29
19
19
2
1
2
1
1
1
−
=
−
⋅
+
=
+
⋅
+
=
t
t
t
x
x
z
z
z
x
18
,
0
1
−
=
t
x
Przyjmujemy wartość współczynnika na podstawie podziału
niestandardowego:
(
)
(
)
30
,
0
18
,
0
48
,
0
1
2
1
2
−
=
−
−
−
=
−
+
=
t
t
t
t
x
x
x
x
438
,
0
30
,
0
2
2
−
=
>
−
=
tgr
t
x
x
Sprawdzamy:
Ponieważ:
183
,
0
190
,
0
1
1
−
=
<
−
=
tgr
t
x
x
Poprawnie
9
Przykład 10.1
– korekcja P-konstrukcyjna
Oraz obliczamy współczynnik zeszlifowania głowy zęba:
043
,
0
556
,
2
00
,
60
11
,
60
=
−
=
−
=
t
w
p
t
m
a
a
k
(
)
(
)
mm
11
,
60
556
,
2
30
,
0
18
,
0
34
,
61
2
1
=
⋅
−
−
+
=
⋅
+
+
=
t
t
t
p
m
x
x
a
a
Następnie obliczamy pozorną odległość osi:
Przy założonym luzie wierzchołkowym
c*
t
= 0,2445
obniżenie go o 0,046 nie spowoduje wyjścia poza zakres
dopuszczalny (0,15 – 0,25) to przyjmujemy:
0
=
t
k
Przykład 10.1
– korekcja P-konstrukcyjna
Zatem wymiary koła wynoszą
mm
56
,
48
19
556
,
2
1
1
=
⋅
=
⋅
=
z
m
d
t
(
)
(
)
mm
64
,
52
0
2
18
,
0
2
9781
,
0
2
19
556
,
2
2
2
2
1
1
1
=
⋅
+
⋅
−
⋅
+
⋅
=
⋅
−
⋅
+
⋅
+
⋅
=
t
t
t
t
a
k
x
y
z
m
d
(
)
(
)
mm
39
,
41
2445
,
0
2
18
,
0
2
9781
,
0
2
19
556
,
2
*
2
2
2
1
1
1
=
⋅
−
⋅
−
⋅
−
⋅
=
⋅
−
⋅
+
⋅
−
⋅
=
t
t
t
t
f
c
x
y
z
m
d
mm
12
,
74
29
556
,
2
2
2
=
⋅
=
⋅
=
z
m
d
t
(
)
(
)
mm
59
,
77
0
2
30
,
0
2
9781
,
0
2
29
556
,
2
2
2
2
2
2
2
=
⋅
+
⋅
−
⋅
+
⋅
=
⋅
−
⋅
+
⋅
+
⋅
=
t
t
t
t
a
k
x
y
z
m
d
(
)
(
)
mm
34
,
66
2445
,
0
2
30
,
0
2
9781
,
0
2
29
5556
,
2
*
2
2
2
2
2
2
=
⋅
−
⋅
−
⋅
−
⋅
=
⋅
−
⋅
+
⋅
−
⋅
=
t
t
t
t
f
c
x
y
z
m
d
Wyszukiwarka
Podobne podstrony:
10 1 2 Przekl kolowe i zebate
Przekładnie zębate dobór katalogowy wyklad
wyklad 10 MNE
wyklad 10
Wyklady 10 12c PRCz
wyklad 10
Wyklad 10 Wypalenie zawodowe i jego konsekwencje
Wykład 10 dodatek
Wykład 8 10
Wykład 10 12
Wykład 10 Klimatologia, klimaty świata, Europy i Polski
WYKLAD 10
Wyklad 10
więcej podobnych podstron