Wstęp

Niniejsze opracowanie zawiera notatki z ćwiczeń z matematyki prowadzonych na kierunkach: Bu-
downictwo, Mechanika i Budowa Maszyn, Inżynieria Odnawialnych Źródeł Energii. Znajdują się tu
najważniejsze rzeczy z teorii, zrobione przykładowe typowe zadania oraz zestaw zadań do samodziel-
nych ćwiczeń.

Dobre opanowanie materiału zawartego w tym opracowaniu powinno wystarczyć do zaliczenia ćwiczeń,
warto jednak pamiętać, że nie jest to kompletne opracowanie zagadnień omawianych na wykładzie i
ćwiczeniach, w związku z czym zdecydowanie warto zajrzeć też do innych źródeł. W szczególności
warto robić zadania z książek M. Lassaka czy też Krysickiego, Włodarskiego.

W razie zauważenia jakichś błędów w tym tekście proszę o sygnał, na przykład mailowy:
[e-mail]

Michał Musielak

1

1

Funkcje rzeczywiste

Dziedzina funkcji

Dziedzina naturalna funkcji rzeczywistej, to maksymalny zbiór liczb rzeczywistych dla którego funkcja
jest dobrze określona.

W praktyce pewne liczby mogą nam ”wypaść” z dziedziny w następujących wypadkach:

ˆ Aby wyrażenie

1

t

miało sens, musi być t

≠ 0

ˆ Aby wyrażenie

√

t miało sens, musi być t

≥ 0

ˆ Aby wyrażenie

1

√

t

miało sens, musi być t

> 0

ˆ Aby wyrażenie log

a

t miało sens, musi być t

> 0

ˆ Aby wyrażenie log

t

a miało sens, musi być t

> 0 i t ≠ 1

ˆ Aby wyrażenie arcsin t lub arccos t miało sens, musi być

−1 ≤ t ≤ 1

Przykładowe zadanie:
Znaleźć dziedzinę naturalną funkcji:

f

(x) =

arcsin

x
2

√

1

− log

2

(x + 2)

Rozwiązanie:
Muszą być spełnione następujące warunki:
−1 ≤

x
2

≤ 1

x

+ 2 > 0

1

− log

2

(x + 2) > 0

Pierwszy warunek oznacza, że x

∈ [−2, 2]. Drugi, że x ∈ (−2, +∞). W przypadku trzeciego mamy:

1

> log

2

(x + 2)

log

2

2

> log

2

(x + 2)

2

> x + 2

0

> x

czyli x

∈ (−∞, 0). Ponieważ muszą być spełnione wszystkie trzy warunki jednocześnie, więc odpowie-

dzią jest część wspólna tych przedziałów, czyli

(−2, 0)

◇

2

Funkcje różnowartościowe

Funkcję rzeczywistą nazywamy różnowartościową jeśli dla dowolnych x

1

, x

2

z dziedziny funkcji zacho-

dzi wynikanie:

x

1

≠ x

2

⇒ f(x

1

) ≠ f(x

2

)

Inaczej mówiąc: funkcja różnowartościowa różnym argumentom przypisuje różne wartości (jak sama
nazwa wskazuje).

W praktyce wykazać, że funkcja jest różnowartościowa można kilkoma sposobami:

ˆ Można skorzystać z równoważnej definicji różnowartościowości:

f

(x

1

) = f(x

2

) ⇒ x

1

= x

2

ˆ Można narysować wykres funkcji (o ile to możliwe) i sprawdzić czy każda prosta pozioma przetnie

ten wykres co najwyżej raz (wtedy funkcja będzie różnowartościowa) czy też przeciwnie: istnieje
taka prosta pozioma, która przetnie wykres przynajmniej dwa razy (wtedy funkcja nie będzie
różnowartościowa)

ˆ Jeśli wiemy skądinąd, że funkcja jest monotoniczna, to możemy wywnioskować, że jest też róż-

nowartościowa.

ˆ Jeśli badana funkcja jest złożeniem funkcji różnowartościowych, to sama też jest różnowarto-

ściowa.

Przykładowe zadanie:
Sprawdzić czy funkcja

f

(x) =

√

log

2

(2 + arcsin x)

z dziedziną naturalną jest różnowartościowa.
Rozwiązanie:
Nietrudno sprawdzić, że dziedzina naturalna to

[−1, 1]. Jeśli chcemy skorzystać z definicji, to zakła-

damy, że dla pewnych x

1

, x

2

z dziedziny zachodzi równość f

(x

1

) = f(x

2

) i sprawdzamy czy wynika

stąd, że x

1

= x

2

:

√

log

2

(2 + arcsin x

1

) =

√

log

2

(2 + arcsin x

2

)

Podnosimy stronami do kwadratu:
log

2

(2 + arcsin x

1

) = log

2

(2 + arcsin x

2

)

Korzystamy z tego, że funkcja log

2

t jest różnowartościowa:

2

+ arcsin x

1

= 2 + arcsin x

2

Odejmujemy obustronnie dwójkę:
arcsin x

1

= arcsin x

2

Korzystamy z różnowartościowości funkcji arcsin t
x

1

= x

2

Voila!

Inną metodą jest zauważenie, że nasza funkcja to złożenie funkcji

√

x, log

2

x, 2

+x i arcsin x, z których

każda jest różnowartościowa, a zatem nasza funkcja też jest różnowartościowa.

◇

3

Funkcja odwrotna

Jeśli funkcja f

∶ A → B (gdzie A to dziedzina, a B - zbiór wartości) jest różnowartościowa, to istnieje

wtedy funkcja odwrotna do niej (oznaczana przez f

−

1

), której dziedziną jest B, a zbiorem wartości A

oraz jeśli f

(x) = y, to f

−

1

(y) = x.

Można powiedzieć, że funkcja odwrotna zamienia miejscami wartość z argumentem funkcji wyjściowej.

Rozważmy na przykład funkcję f

(x) = log

2

(2x+4). Łatwo sprawdzić (rysując wykres), że jej dziedziną

jest

(−2, +∞), a zbiorem wartości R oraz, że funkcja jest różnowartościowa. Istnieje zatem funkcja do

niej odwrotna.

Funkcja wyjściowa przypisuje argumentowi x wartość y zgodnie z ”przepisem” y

= log

2

(2x + 4), czyli

”weź argument, pomnóż go przez dwa, do wyniku dodaj czwórkę, a całość zlogarytmuj przy podstawie
dwa”. Jeśli szukamy funkcji odwrotnej, to tym razem argumentem jest y, a wartością x, więc choć
zależność między nimi to również y

= log

2

(2x + 4), to tym razem podobnego ”przepisu” nie ma (bo

obliczenie x dla danej wartości y wymagałoby za każdym razem rozwiązania równania).
Skoro więc ”przepisu” na to jak wyliczać wartość x w zależności od y nie ma, to należy go znaleźć.
Mamy:
y

= log

2

(2x + 4)

2

y

= 2x + 4

2

y

− 4 = 2x

2

y−1

− 2 = x

i stąd mamy ”przepis” na x:
x

= 2

y−1

− 2

lub jak kto woli:
f

−

1

(y) = 2

y−1

− 2

Na koniec można jeszcze z przyczyn estetycznych zmienić nazwę zmiennej na x (alternatywnie można
też zamienić miejscami x i y na samym początku):
f

−

1

(x) = 2

x−1

− 2

4

Ćwiczenia

1.1

Narysuj wykres funkcji:

a) f

(x) = (x − 2)

2

+ 3 b) f(x) = 2

x−1

− 1 c) f(x) = 2 − log

3

(x − 3) d) f(x) =

3−4x
2x+1

1.2

Sprawdź czy funkcja jest różnowartościowa:

a) f

(x) = e

x
3

+ 4 b) f(x) = ln(x

2

+ 4) c) f(x) = 2

x

3

− 2 d) f(x) = e

x

+ e

−

x

1.3

Znajdź dziedzinę naturalną oraz zbiór wartości. Sprawdź czy funkcja jest różnowartościowa, a jeśli
tak, to wyznacz funkcję odwrotną. :

a) f

(x) = 2 + log

5

(x + 1) b) f(x) =

√

x−2
1−x

c) f

(x) = 5x

7
4

d) f

(x) =

√

log

2
2

x

− 4 log

2

x

1.4

Wyznacz funkcję odwrotną do podanej:

a) f

(x) = x

2

− 2x + 3 dla x ∈ (1, +∞) b) f(x) = 2

x−5

+ 5 z dziedziną naturalną

c) f

(x) = x +

1

x

dla x

∈ (1, ∞)

d) f

(x) =

√

2

x

− 8 z dziedziną naturalną

e)* f

(x) = cos x dla x ∈ [π, 2π]

5

2

Granice funkcji

Wyrażenia nieoznaczone:

[

0

0

] , [∞

∞]

,

[0 ⋅ ∞] , [∞ − ∞] , [0

0

] , [1

∞

] , [∞

0

] , [

1

0

]

Jeśli w jakiejkolwiek granicy po podstawieniu liczby do której dąży zmienna (lub nieskończoności)
pojawi się którekolwiek z powyższych wyrażeń, oznacza to, że z policzeniem granicy musimy poradzić
sobie jakoś sprytniej.

◇ ◇ ◇

Przykłady obliczania typowych granic

lim

x→∞

3x

3

+ x

2

+ x

2

+ x

3

W wypadku gdy zmienna dąży do

±∞ a funkcja jest wymierna (czyli postaci ”wielomian przez wielo-

mian”), wystarczy wyłączyć przed nawias najwyższą potęgę w liczniku i mianowniku lub też podzielić
licznik i mianownik przez najwyższą potęgę mianownika (w drugim sposobie należy pamiętać, że grani-
ca wielomianu w nieskończoności zależy wyłącznie od najwyższej potęgi tego wielomianu). Ogólniejsza
zasada ”podziel przez największy kawałek mianownika” często sprawdza się też w przypadku funkcji
innych niż wymierne (uwaga: mowa tylko o granicy w nieskończoności!)

. . .

= lim

x→∞

3

+

1

x

2

2

x

3

+

1
x

+ 1

=

3

1

= 3

◇

lim

x→2

x

3

− 8

x

2

− 5x + 6

W wypadku gdy liczymy granicę funkcji wymiernej w punkcie a i wychodzi nam nieoznaczoność typu
[

0
0

] możemy wyłączyć z licznika i mianownika czynnik x − a (co wynika z tw. Bezout) i skrócić

. . .

= lim

x→2

(x − 2)(x

2

+ 2x + 4)

(x − 2)(x − 3)

= lim

x→2

x

2

+ 2x + 4

x

− 3

=

12

−1 = −

12

◇

lim

x→3

√

x

+ 1 − 2

4

−

√

1

+ 5x

6

Jeśli pojawiają się pierwiastki oraz nieoznaczoność typu

[

0
0

], to najczęściej przydatne będzie pomno-

żenie licznika i mianownika przez tzw. sprzężenie. Sprzężeniem wyrażenia

√

a

−

√

b jest

√

a

+

√

b. Dzięki

temu po przekształceniu zerujące się wyrażenia nie będą już zawierały pierwiastka:

. . .

= lim

x→3

(

√

x

+ 1 − 2)(

√

x

+ 1 + 2)(4 +

√

1

+ 5x)

(4 −

√

1

+ 5x)(4 +

√

1

+ 5x)(

√

x

+ 1 + 2)

= lim

x→3

(x − 3)(4 +

√

1

+ 5x)

(15 − 5x)(

√

x

+ 1 + 2)

= lim

x→3

4

+

√

1

+ 5x

−5(

√

x

+ 1 + 2)

= −

2

5

◇

Ważną granicą, którą trzeba zapamiętać jest:

lim

t→0

sin t

t

= lim

t→0

t

sin t

= 1

W miejsce t może stać dowolne wyrażenie, byle było zbieżne do zera.
Przykładowe zadanie:

lim

x→0

sin 4x

sin 3x

Najpierw do każdego sinusa ”dorzucamy” argument tego sinusa, a potem korygujemy wszystko, by
wartość wyrażenia się nie zmieniła:

. . .

= lim

x→0

sin 4x

4x

⋅

3x

sin 3x

⋅

4x

3x

= 1 ⋅ 1 ⋅

4

3

=

4

3

◇

W sytuacji gdy mamy do czynienia z nieoznaczonością typu 1

∞

, będziemy mieć do czynienia z liczbą

e. Najczęściej należy wówczas skorzystać z którejś z granic:

lim

t→±∞

(1 +

1

t

)

t

= e

lim

t→±∞

(1 −

1

t

)

t

=

1

e

Na przykład:

lim

x→∞

(

x

+ 3

x

+ 1)

3x

Wyrażenie w nawiasie dąży do jedynki (dlaczego?), a wykładnik go nieskończoności. Stąd wniosek,
że zapewne gdzieś tu się czai e i trzeba przekształcić naszą funkcję do postaci takiej jak w którejś z
dwóch powyższych podstawowych granic:

. . .

= lim

x→∞

(1 +

2

x

+ 1)

3x

= lim

x→∞

(1 +

1

x+1

2

)

3x

= lim

x→∞

(1 +

1

x+1

2

)

x+1

2

⋅

2

x+1

⋅

3x

= lim

x→∞

⎡⎢

⎢⎢

⎢⎣

(1 +

1

x+1

2

)

x+1

2

⎤⎥

⎥⎥

⎥⎦

6x

x+1

Wyrażenie w nawiasie kwadratowym dąży do e, natomiast wykładnik do 6, dlatego ostatecznie ta
granica jest równa e

6

7

◇ ◇ ◇

Nieoznaczoność typu

[

1
0

] jest nieco innego typu niż pozostałe. W przypadku takiej nieoznaczoności

należy policzyć granice lewo- i prawostronną: jeśli istnieją, to równe są

+∞ lub −∞. Granica funkcji

będzie istniała wyłącznie, jeśli granice jednostronne będą istniały i będą równe.
Przykładowo, jeśli chcemy policzyć:

lim

x→2

1

− x

x

2

− 4

to z uwagi na pojawiającą się nieoznaczoność

[

1
0

] badamy granice jednostronne:

lim

x→2

−

1

− x

x

2

− 4 =

lim

x→2

−

1

− x

(x − 2)(x + 2) = [

−1

(−0) ⋅ 4] = [

−1

−0] = +∞

Skoro dążymy do dwójki z lewej strony, czyli po iksach mniejszych od dwóch, to x

− 2 < 0, czyli x − 2

dąży do zera, ale jest stale ujemne. Ten fakt zapisuje się właśnie w powyższy sposób, stawiając znak
minus przed zerem. Analogicznie:

lim

x→2

+

1

− x

x

2

− 4 =

lim

x→2

+

1

− x

(x − 2)(x + 2) = [

−1

(+0) ⋅ 4] = [

−1

+0] = −∞

Skoro granica lewo- i prawostronna są inne, to znaczy, że wyjściowa granica nie istnieje.

◇ ◇ ◇

Ciągłość funkcji

Mówimy, że funkcja f jest ciągła w punkcie x

0

jeśli:

ˆ Istnieje wartość w tym punkcie, czyli f

(x

0

)

ˆ Istnieje granica w tym punkcie, czyli lim

x→x

0

f

(x)

ˆ Granica jest równa wartości, czyli lim

x→x

0

f

(x) = f(x

0

)

Ponadto, jeśli funkcja jest ciągła w każdym punkcie dziedziny, wtedy mówimy że funkcja jest ciągła.

Przykładowo funkcja:

f

(x) =

⎧⎪⎪

⎨⎪⎪

⎩

sin x

x

dla x

≠ 0

3 dla x

= 0

nie jest ciągła w zerze, bo co prawda ma tam wartość f

(0) = 3 oraz granicę lim

x→0

f

(x) = lim

x→0

sin x

x

= 1,

ale granica nie jest równa wartości.

◇ ◇ ◇

8

Asymptoty funkcji

Granice funkcji są też przydatne do wyznaczania asymptot funkcji, czyli takich prostych, do których
wykres funkcji zbliża się, ale nigdy tych prostych nie osiąga.

By znaleźć asymptoty funkcji, należy wyznaczyć najpierw dziedzinę funkcji i zapisać ją jako sumę
przedziałów, następnie policzyć granice na wszystkich końcach tych przedziałów, a następnie na tej
podstawie rozpoznać asymptoty:

ˆ Jeśli w jakimś punkcie granica funkcji to nieskończoność, czyli:

lim

x→a

±

f

(x) = ±∞

to funkcja ma w tym punkcie asymptotę pionową x

= a

ˆ Jeśli w którejś nieskończoności granica funkcji jest liczbą, czyli:

lim

x→±∞

f

(x) = a

to funkcja ma w tym punkcie asymptotę poziomą y

= a

ˆ Jeśli funkcja nie ma w którejś nieskończoności asymptoty poziomej, to można sprawdzić czy

istnieją asymptoty ukośne. Jeśli poniższa granica jest niezerową liczbą:

lim

x→±∞

f

(x)

x

= a ≠ 0

oraz istnieje granica:

b

= lim

x→±∞

(f(x) − ax)

to wówczas asymptotą ukośną jest prosta y

= ax + b

Prześledźmy to na przykładzie. Załóżmy, że chcemy znaleźć asymptoty funkcji:

f

(x) =

x

2

+ 1

x

− 1

Oczywiście dziedziną funkcji jest D

f

= (−∞, 1)∪(1, +∞). Policzmy więc granice na wszystkich końcach

przedziałów określoności:

lim

x→−∞

x

2

+ 1

x

− 1 =

lim

x→−∞

x

+

1

x

1

−

1
x

= −∞ lim

x→1

−

x

2

+ 1

x

− 1 = [

2

−0] = −∞

lim

x→1

+

x

2

+ 1

x

− 1 = [

2

+0] = +∞

lim

x→+∞

x

2

+ 1

x

− 1 =

lim

x→+∞

x

+

1
x

1

−

1
x

= +∞

Możemy stąd wywnioskować, że funkcja ma asymptotę pionową x

= 1, ale nie ma asymptot poziomych.

Skoro nie ma asymptot poziomych, to sprawdźmy czy są ukośne:

lim

x→±∞

f

(x)

x

= lim

x→±∞

x

2

+ 1

x

2

− x =

lim

x→±∞

1

+

1

x

2

1

−

1
x

= 1

oraz:

b

= lim

x→±∞

(

x

2

+ 1

x

− 1 −

x

) = lim

x→±∞

x

+ 1

x

− 1 =

1

skąd wniosek, że asymptotą ukośną jest y

= x + 1

9

Ćwiczenia

2.1

Oblicz granice:

a) lim

x→∞

x

4

+ x

2

+ 1

x

+ 100x

3

+ 2x

4

b) lim

x→∞

x

2

+ 1

x

3

+ 2

c) lim

x→−∞

x

6

+ x

3

+ 2x + 1

x

3

+ x

2

+ 5x + 3

d) lim

x→−∞

x

2

+ 5x + 2

√

4x

4

+ 3x + 1 + x

2

2.2

Oblicz granice:

a) lim

x→3

x

2

− 5x + 6

x

2

− 9

b) lim

x→2

x

3

− 8

x

2

− 10x + 16

c) lim

x→1

x

3

− 2x

2

+ 1

x

3

− 4x

2

− 2x + 5

d) lim

x→1

x

5

− 1

x

4

− 1

2.3

Oblicz granice:

a) lim

x→1

√

2x

+ 7 − 3

x

2

+ 4x − 5

b) lim

x→1

√

x

+ 3 − 2

x

2

+ 4x − 5

c) lim

x→3

√

3x

+ 7 − x − 1

√

x

+ 1 − 2

d) lim

x→−2

√

2x

+ 8 + x

x

2

− 4

2.4

Oblicz granice:

a) lim

x→0

sin 2x

sin 3x

b) lim

x→0

tg 3x

sin

x
4

c) lim

x→0

ctg 5x

⋅ tg 2x d)* lim

x→0

sin

2

2x

cos

2

3x

− 4 cos 3x + 3

2.5

Oblicz granice:

a) lim

x→∞

(

x

+ 3

x

− 3)

2x+1

b) lim

x→−∞

(

4x

− 1

4x

+ 5)

x−1

c) lim

x→∞

(

x

2

+ 3x

x

2

+ x + 1)

x

d) lim

x→∞

(

2x

− 3

3x

− 1)

2x+1

2.6

Znajdź asymptoty funkcji:

a) f

(x) =

x

2

x

2

−

4

b) f

(x) =

∣

x∣

x+3

c) f

(x) =

x

2

+

2x−3

x+4

d) f

(x) =

√

x

2

+ 1 − x

2.7

a) Sprawdź czy następująca funkcja jest ciągła:

f

(x) =

⎧⎪⎪

⎨⎪⎪

⎩

x

2

+

2x−3

x−1

dla x

≠ 1

1 dla x

= 1

b) Wyznacz wartości parametru a dla którego funkcja jest ciągła w jedynce:

f

(x) =

⎧⎪⎪

⎨⎪⎪

⎩

sin(x

2

−

1)

x−1

dla x

≠ 1

a

2

+ a dla x = 1

10

3

Pochodne

Liczenie pochodnych

Formalnie rzecz biorąc pochodna w punkcie jest granicą ilorazów różnicowych. Jednak do praktycznego
liczenia pochodnych wystarczy znać wyłącznie pochodne funkcji elementarnych oraz kilka podstawo-
wych wzorów.

Pochodne funkcji elementarnych:

ˆ

(x

n

)

′

= nx

n−1

dla n

∈ R, w szczególności:

–

(c)

′

= 0 (x)

′

= 1 (

1
x

)

′

= −

1

x

2

(

√

x

)

′

=

1

2

√

x

ˆ

(e

x

)

′

= e

x

,

(a

x

)

′

= a

x

ln a ,

(ln x)

′

=

1

x

,

(log

a

x

)

′

=

1

x ln a

ˆ

(sin x)

′

= cos x ,

(cos x)

′

= − sin x ,

(tg x)

′

=

1

cos

2

x

,

(ctg x)

′

= −

1

sin

2

x

ˆ

(arcsin x)

′

=

1

√

1−x

2

,

(arccos x)

′

= −

1

√

1−x

2

,

(arctan x)

′

=

1

1+x

2

,

(arc ctg x)

′

= −

1

1+x

2

Tych wzorów warto nauczyć się na pamięć, bo sprawdzanie za każdym razem pochodnej danej funkcji
w tablicach (nawet jeśli te tablice ma się akurat pod ręką) jest czasochłonne. Oprócz tego warto
wiedzieć, że:

ˆ Pochodna sumy (różnicy) funkcji to suma (różnica) pochodnych:

(f(x) ± g(x))

′

= f

′

(x) ± g

′

(x)

ˆ Stałą zawsze można wyłączyć przed pochodną:

(af(x))

′

= af

′

(x)

ˆ Pochodną iloczynu oblicza się według wzoru:

(f(x)g(x))

′

= f

′

(x)g(x) + f(x)g

′

(x)

ˆ Pochodną ilorazu oblicza się według wzoru:

(

f

(x)

g

(x) )

′

=

f

′

(x)g(x) − f(x)g

′

(x)

(g(x))

2

ˆ Pochodną funkcji złożonej oblicza się według wzoru:

[f(g(x))]

′

= f

′

(g(x)) ⋅ g

′

(x)

◇

11

Przykładowe pochodne:

(x

4

+ 5 sin x − ln x)

′

= 4x

3

+ 5 cos x −

1
x

(x

2

e

x

)

′

= (x

2

)

′

e

x

+ x

2

(e

x

)

′

= 2xe

x

+ x

2

e

x

= e

x

(2x + x

2

)

(

x

2

e

x

)

′

=

(

x

2

)

′

e

x

−

x

2

(

e

x

)

′

(

e

x

)

2

=

2xe

x

−

x

2

e

x

e

2x

=

2x−x

2

e

x

Nieznacznie trudniejsze jest obliczanie pochodnej funkcji złożonych:
(sin(ln(x

2

+ 4x)))

′

= . . .

Póki nie nabierze się wprawy można podstawić za ”wnętrze” funkcji zmienną t, tak aby nowa funkcja
od t była funkcją elementarną:
. . .

= (sin t)

′

∣

t=ln(x

2

+

4x)

= . . .

Następnie obliczamy pochodną funkcji elementarnej, pamiętając o domnożeniu przez pochodną funk-
cji wewnętrznej (czyli tej za którą wstawiliśmy zmienną t):
. . .

= cos t ⋅ t

′

∣

t=ln(x

2

+

4x)

= . . .

i wracamy do podstawienia:
. . .

= cos(ln(x

2

+ 4x)) ⋅ (ln(x

2

+ 4x))

′

= . . .

I tak dalej. Jeśli nabierze się już wprawy, to można darować sobie wprowadzanie nowej zmiennej i
liczyć w pamięci - pochodna logarytmu to odwrotność tego co ”w środku” razy pochodna tego co ”w
środku”:
. . .

= cos(ln(x

2

+ 4x)) ⋅

1

x

2

+

4x

⋅ (2x + 4)

Kolejne przykłady:
(2

ln tg x

2

)

′

= 2

ln tg x

2

⋅ ln 2 ⋅

1

tg x

2

⋅

1

cos

2

x

2

⋅ 2x

(najbardziej zewnętrzną funkcją jest 2

t

, stąd zaczynamy od liczenia jej pochodnej, a następnie do-

mnażamy przez pochodną funkcji wewnętrznej)

(e

x

2

arcsin

√

x

)

′

= (e

x

2

)

′

arcsin

√

x

+ e

x

2

(arcsin

√

x

)

′

= e

x

2

⋅ 2x ⋅ arcsin

√

x

+ e

x

2

⋅

1

√

1−x

⋅

1

2

√

x

◇

Jeszcze jednym typem pochodnej jest pochodna z funkcji typu

f

(x)

g(x)

Oblicza się ją korzystając z przekształcenia:

f

(x) = e

ln f (x)

skąd

f

(x)

g(x)

= e

g(x) ln f (x)

i już mamy do czynienia ze zwykłą funkcją złożoną.

Przykładowo:
(x

sin x

)

′

= (e

sin x ln x

)

′

= e

sin x ln x

⋅ (sin x ln x)

′

= x

sin x

⋅ (cos x ln x + sin x ⋅

1

x

)

12

Reguła de l’Hospitala

Jednym z wielu zastosowań pochodnych jest reguła de l’Hospitala, czyli metoda obliczania granic w
przypadku niektórych wyrażeń nieoznaczonych. Reguła ta to jedno z najsilniejszych narzędzi do ob-
liczania granic.

Jeśli obliczamy granicę (w punkcie lub w nieskończoności):

lim

x→a

f

(x)

g

(x)

i obie funkcje f, g dążą jednocześnie do zera lub do nieskończoności, czyli mamy do czynienia z nie-
oznaczonością typu

[

0
0

] lub [

∞

∞

], to granicę można obliczyć według wzoru:

lim

x→a

f

(x)

g

(x) =

lim

x→a

f

′

(x)

g

′

(x)

(o ile granica po prawej stronie istnieje)

◇

Przykłady:

lim

x→0

e

x

− e

−

x

x

= . . . Łatwo widać, że mamy do czynienia z nieoznaczonością typu [

0
0

], zatem możemy

użyć reguły de l’Hospitala:

. . .

= (H) = lim

x→0

(e

x

− e

−

x

)

′

(x)

′

= lim

x→0

e

x

+ e

−

x

1

= 2

lim

x→0

ln sin 2x

ln sin x

= (H) lim

x→0

2 cos 2x

sin 2x

cos x

sin x

= lim

x→0

2 tg x

tg 2x

= (H) =

= lim

x→0

2

cos

2

x

2

cos

2

2x

= lim

x→0

cos

2

2x

cos

2

x

= 1

Niektóre inny typy nieoznaczoności można doprowadzić do postaci w której można użyć reguły de
l’Hospitala:

ˆ Nieoznaczoność typu

[0 ⋅ ∞]

Jeśli w iloczynie dwóch funkcji jedna dąży do zera, a druga do nieskończoności, możemy odwrócić
(w sensie liczbowym) którąkolwiek z nich i w ten sposób otrzymać nieskończoność z założeń
reguły de l’Hospitala:
lim

x→0

(e

x

− 1) ⋅ ctg x = . . .

Oczywiście e

x

− 1 dąży w zerze do zera, a ctg x do nieskończoności. Ale:

ctg x

=

1

tg x

więc nasza granica jest równa:

lim

x→0

e

x

− 1

tg x

= (H) = lim

x→0

e

x

1

cos

2

x

= 1

13

ˆ Nieoznaczoność typu

[∞ − ∞]

W takim wypadku najczęściej można sprowadzić wyrażenie z którego liczymy granicę do wspól-
nego mianownika:

lim

x→0

(

1

x

−

1

sin x

) = lim

x→0

sin x

− x

x sin x

= (H) =

= lim

x→0

cos x

− 1

sin x

+ x cos x = (

H

) = lim

x→0

− sin x

2 cos x

− x sin x =

0

ˆ Nieoznaczoności typu

[0

0

], [∞

0

], [1

∞

]

W takim wypadku używamy podobnego przekształcenia jak w wypadku liczenia pochodnej
funkcji typu f

(x)

g(x)

:

lim

x→0

x

x

= lim

x→0

e

x ln x

= e

lim

x→0

x ln x

(ostatnie przekształcenie wynika z ciągłości funkcji e

x

)

Policzymy osobno granicę z wykładnika:

lim

x→0

x ln x

= lim

x→0

ln x

1

x

= (H) = lim

x→0

1
x

−

1

x

2

= lim

x→0

(−x) = 0

więc nasza granica to: e

0

= 1

Ćwiczenia

3.1

Oblicz pochodne funkcji:

a) f

(x) = e

x

sin x

e) f

(x) = (x

2

+ 1)

2012

j) f

(x) =

√

ln x

⋅ sin(x

2

+ 1)

b) f

(x) =

sin x

e

x

f) f

(x) = arcsin ln arctan x k) f(x) = x

arcsin x

c) f

(x) = 2

√

tg x

g) f

(x) =

√√√

x

i) f

(x) =

e

arcsin x

sin

3

2x

d) f

(x) = sin e

x

2

+

1

h) f

(x) = e

x

2

+

1

⋅ sin cos x

l) f

(x) = (sin x)

x

3.2

Oblicz granice:

a) lim

x→0

1

− cos x

x

2

e) lim

x→0

(

1

x

− ctg x)

i) lim

x→1

(1 − x) tg

1

2

π

b) lim

x→0

e

x

− x − 1

sin

2

x

f) lim

x→0

(e

x

− e

−

x

)

2

x

2

cos x

j) lim

x→∞

(x − x

2

ln

(1 +

1

x

))

c) lim

x→0

x

− arctan x

x

2

g) lim

x→0

(

1

x

2

−

1

sin

2

x

) k) lim

x→0

+

(1 + x)

ln x

d) lim

x→1

x

10

− 9x + 8

x

7

− 6x + 5

h) lim

x→1

x

2

− 1

x

2

tg

1

2

πx

l) lim

x→∞

(

2

π

arctan x

)

x

14

4

Przebieg zmienności funkcji

Badając pierwszą i drugą pochodną funkcji można uzyskać informacje o samej funkcji.

ˆ Pierwsza pochodna

– Jeśli w jakimś przedziale jest f

′

(x) > 0, to w tym przedziale f(x) jest rosnąca.

– Jeśli w jakimś przedziale jest f

′

(x) < 0, to w tym przedziale f(x) jest malejąca.

– Jeśli w jakimś punkcie jest f

′

(x

0

) = 0 oraz w tym punkcie f

′

(x) zmienia znak, to w tym

punkcie jest ekstremum lokalne.

ˆ Druga pochodna

– Jeśli w jakimś przedziale jest f

′′

(x) > 0, to w tym przedziale f(x) jest wypukła.

– Jeśli w jakimś przedziale jest f

′′

(x) < 0, to w tym przedziale f(x) jest wklęsła.

– Jeśli w jakimś punkcie jest f

′′

(x

0

) = 0 oraz w tym punkcie f

′′

(x) zmienia znak, to w tym

punkcie jest punkt przegięcia.

Przykładowo jeśli chcemy znaleźć przedziały monotoniczności i ekstrema funkcji f

(x) =

x

x

2

+

1

, to

(po zauważeniu, że dziedzina to R) liczymy pierwszą pochodną:

f

′

(x) =

x

2

+ 1 − x ⋅ 2x

(x

2

+ 1)

2

=

1

− x

2

(x

2

+ 1)

2

= (

1

− x)(1 + x)

(x

2

+ 1)

2

Widać stąd, że pochodna zeruje się tylko w punktach x

= 1 i w x = −1. Nietrudno też zbadać (metodą

”wężyka”), że f

′

(x) > 0 w przedziale (−1, 1) oraz f

′

(x) < 0 w przedziałach (−∞, −1) i (1, +∞). Wnioski

na temat samej funkcji można sformułować słownie, ale najwygodniej jest przedstawić je w tabelce:

x

(−∞, −1) −1 (−1, 1)

1

(1, ∞)

f

′

(x)

−

0

+

0

−

f

(x)

↘

min

↗

max

↘

Z tabelki można odczytać gdzie funkcja rośnie, a gdzie maleje, a także, że ma minimum lokalne w
x

= −1 (równe f(−1) = −

1
2

) oraz maksimum lokalne w x

= 1 (równe f(1) =

1
2

).

◇

Gdybyśmy natomiast chcieli znaleźć przedziały wypukłości i wklęsłości oraz punkty przegięcia funkcji
f

(x) = x

4

− 6x

2

+ 2x + 5, to trzeba znaleźć drugą pochodną:

f

′

(x) = 4x

3

− 12x + 2

f

′′

(x) = 12x

2

− 12 = 12(x − 1)(x + 1)

Jak poprzednio bardzo łatwo sprawdzić gdzie druga pochodna się zeruje, gdzie jest dodatnia i gdzie
jest ujemna. I jak poprzednio wnioski najwygodniej zamieścić w tabelce:

x

(−∞, −1) −1 (−1, 1)

1

(1, ∞)

f

′′

(x)

+

0

−

0

+

f

(x)

⌣

p.p.

⌢

p.p.

⌣

Jak widać punkty przegięcia są w x

= 1 (wówczas f(1) = 2) oraz w x = −1 (wówczas f(−1) = −2).

15

Uwaga!: w pierwszym wierszu tabelki punktami wyróżnionymi są miejsca zerowe pochodnej (tej

którą akurat badamy) oraz wszystkie punkty, które wypadły z dziedziny.
Natomiast jeśli badamy pełen przebieg zmienności funkcji, to w pierwszym wierszu punktami wyróż-
nionymi muszą być miejsca zerowe obu pochodnych oraz punkty, które wypadły z dziedziny.

◇

Wykorzystując całą zebraną do tej pory wiedzy możemy wyciągnąć wszystkie informacje o zachowaniu
funkcji, czyli zbadać tytułowy przebieg zmienności funkcji. Schemat postępowania wygląda mniej
więcej tak:

1. Zebranie wstępnych informacji o funkcji:

ˆ Dziedzina (koniecznie)
ˆ Miejsca zerowe (niekoniecznie, ale warto wiedzieć gdzie wykres przecina oś OX)
ˆ Parzystość, nieparzystość, okresowość (opcjonalnie)

2. Asymptoty

ˆ Granice na wszystkich końcach przedziałów określoności
ˆ Wnioski na temat asymptot pionowych i poziomych
ˆ Ewentualne szukanie asymptot ukośnych

3. Badanie pierwszej pochodnej

ˆ Doprowadzenie pochodnej do najprostszej postaci (najlepiej iloczynowej)
ˆ Zbadanie miejsc zerowych pochodnej oraz jej znaku

4. Badanie drugiej pochodnej

ˆ Doprowadzenie drugiej pochodnej do najprostszej postaci (najlepiej iloczynowej)
ˆ Zbadanie miejsc zerowych drugiej pochodnej oraz jej znaku

5. Tabelka

ˆ Informacje o obu pochodnych zamieszczamy w tabelce i na ich podstawie wnioskujemy na

temat zachowania funkcji

6. Wykres

◇

Oczywiście redagując rozwiązanie jakiegoś zadania nie trzeba ściśle trzymać się powyższych punktów
- wystarczy, żeby w rozwiązaniu znalazły się wszystkie istotne rzeczy.

Prześledźmy to na przykładzie.

16

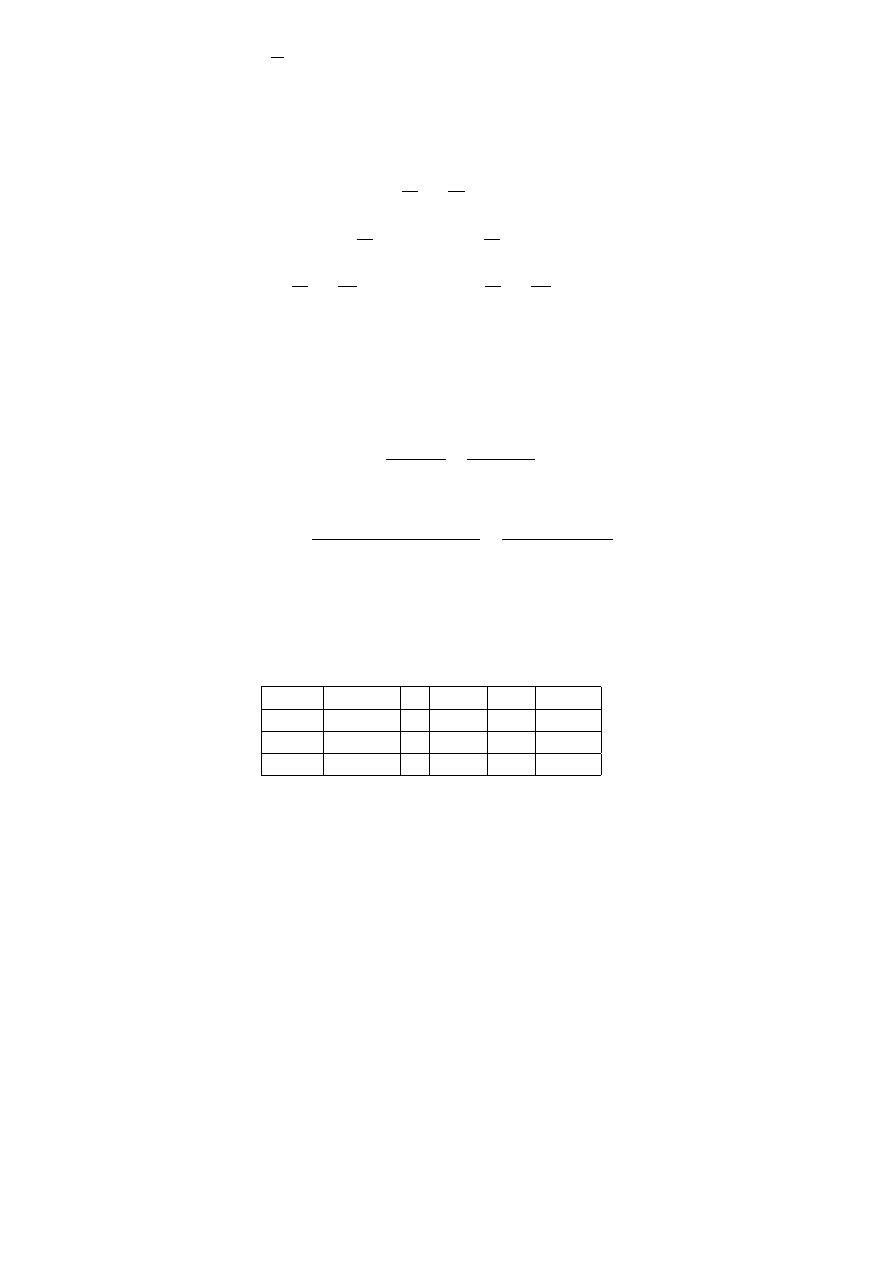
Zbadajmy funkcję f

(x) =

e

x

x

.

Oczywiście jej dziedzina to D

f

= (−∞, 0) ∪ (0, +∞). Widać też, że w dziedzinie funkcja nie ma miejsc

zerowych. Poszukajmy zatem asymptot, zaczynając od liczenia granic na końcach przedziałów okre-
śloności:

lim

x→−∞

e

x

x

= [

0

∞] =

0

lim

x→+∞

e

x

x

= (H) = lim

x→+∞

e

x

1

= +∞

lim

x→0

−

e

x

x

= [

1

−0] = −∞

lim

x→0

+

e

x

x

= [

1

+0] = +∞

Możemy zatem wywnioskować, że obustronną asymptotą pionową jest x

= 0, lewostronną asympto-

tą poziomą jest y

= 0, natomiast nie ma asymptoty poziomej prawostronnej. Analogiczny rachunek

(dwukrotnie użyta reguła de l’Hospitala) pokazuje, że nie ma też prawostronnej asymptoty ukośnej.

Przejdźmy więc do analizy pochodnych. Mamy:

f

′

(x) =

e

x

x

− e

x

x

2

=

e

x

(x − 1)

x

2

oraz

f

′′

(x) =

e

x

x

⋅ x

2

− e

x

(x − 1) ⋅ 2x

x

4

=

e

x

(x

2

− 2x + 2)

x

3

Łatwo widać, że pierwsza pochodna zeruje się w jedynce, dla argumentów mniejszych od jedynki jest
ujemna, a dla większych od jedynki dodatnia. Natomiast druga pochodna nie ma miejsc zerowych,
ale jest dodatnia dla iksów dodatnich i ujemna dla ujemnych.

Zamieśćmy te informacje w tabelce:

x

(−∞, 0) 0 (0, 1)

1

(1, ∞)

f

′

(x)

−

×

−

0

+

f

′′

(x)

−

×

+

+

f

(x)

¿

×

Ç

min

Ä

Minimum lokalne w jedynce jest równe f

(1) = e

Wypełnianie tabelki należy zacząć od pierwszego miejsca - wyróżniamy w nim wszystkie miejsca
zerowe obu pochodnych, punkty które wypadły z dziedziny oraz wszystkie przedziały między tymi
punktami.
Następnie uwzględniamy dziedzinę, to znaczy wykreślamy te miejsca, w których funkcja i jej pochodne
nie istnieją.
Później wypełniamy kolejne wiersze, zapisując w nich informacje uzyskane przy badaniu obu po-
chodnych (tzn. znak i miejsca zerowe), a na koniec uzupełniamy ostatni wiersz na podstawie dwóch
wcześniejszych.

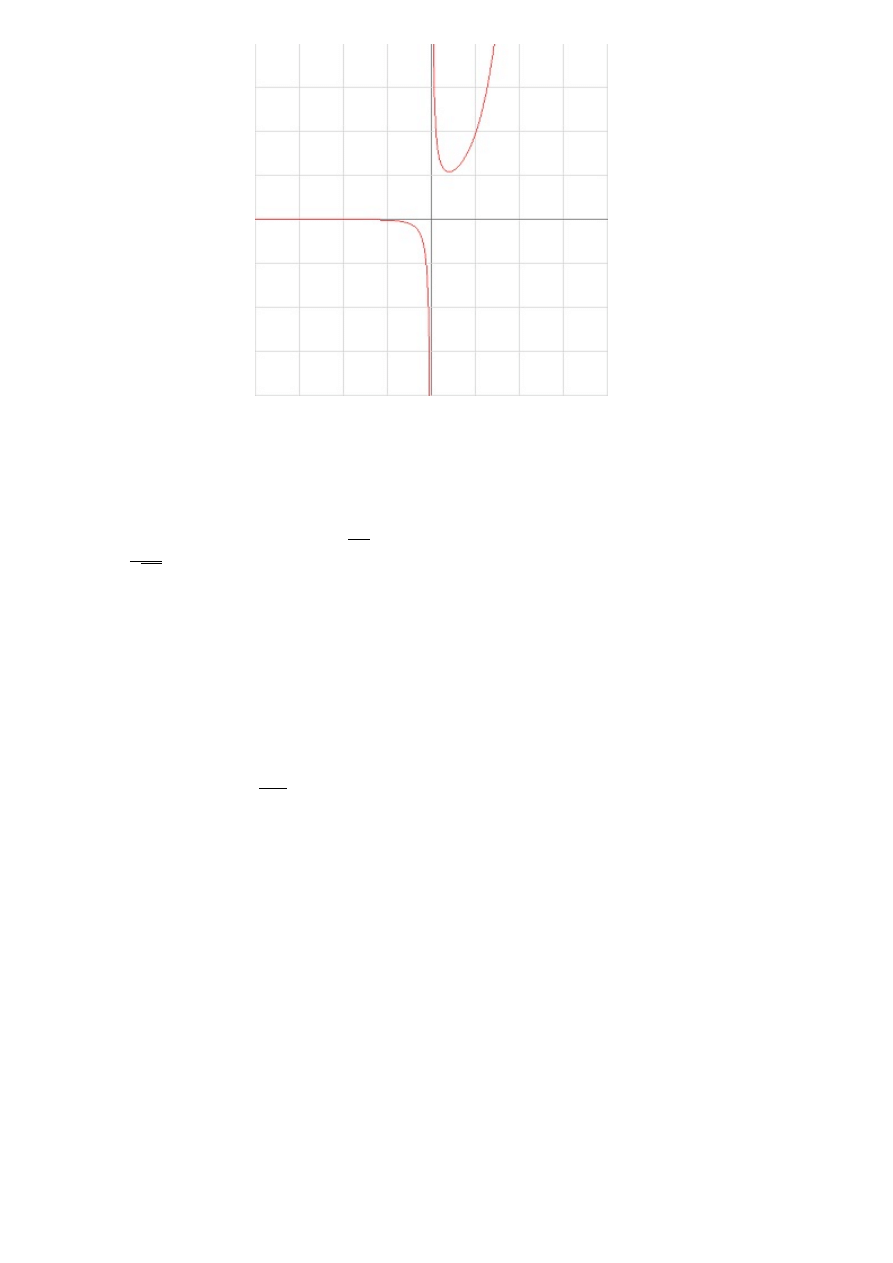
Na końcu na podstawie asymptot i tabelki możemy zrobić wykres funkcji:

17

Ćwiczenia

4.1

Znajdź przedziały monotoniczności i ekstrema lokalne funkcji:

a) f

(x) = x

3

+ 3x

2

− 9x + 2 b) f(x) =

x

3

x+2

c) f

(x) =

x−1

√

x+2

d) f

(x) = (x

2

− 3)e

−

x

4.2

Znajdź przedziały wklęsłości i wypukłości oraz punkty przegięcia funkcji:

a) f

(x) = x

4

− 6x

2

+ x + 3 b) f(x) = ln(x

2

+ 4)

c) f

(x) = (1 + x

2

)e

x

d) f

(x) = x ln x

4.3

Zbadaj przebieg zmienności funkcji:

a) f

(x) = xe

−

x

b) f

(x) =

x

2

x

2

−

1

18

5

Całkowanie przez części i przez podstawienie

Całkowanie to operacja odwrotna do liczenia pochodnych, tzn.:

∫ f(x)dx = F(x) + C ⇔ F

′

(x) = f(x)

Z definicji oraz z tabeli pochodnych funkcji elementarnych od razu wynika tabela całek funkcji ele-
mentarnych:
Całki funkcji elementarnych:

ˆ ∫ x

n

dx

=

x

n+1

n

+ 1

dla n

≠ −1, w szczególności:

–

∫ 1dx = x + C, ∫ xdx =

x

2

2

+ C, ∫

dx

x

2

= −

1

x

+ C, ∫

dx

√

x

= 2

√

x

+ C

ˆ ∫ e

x

dx

= e

x

+ C, ∫ a

x

dx

=

a

x

ln a

+ C, ∫

1

x

dx

= ln ∣x∣ + C

ˆ ∫ sinxdx = −cosx + C, ∫ cosxdx = sinx + C, ∫

dx

cos

2

x

= tg x + C, ∫

dx

sin

2

x

= − ctg x + C

ˆ ∫

dx

√

1

− x

2

= arcsin x + C , ∫

dx

1

+ x

2

= arctan x + C

Podobnie jak przy pochodnych mamy też wzory:

∫ (f(x) + g(x))dx = ∫ f(x)dx + ∫ g(x)dx, ∫ af(x)dx = a ∫ f(x)dx

Wszystkie inne całki będziemy starali się sprowadzić do całek z funkcji elementarnych.

Dwa główne narzędzia, które do tego służą to całkowanie przez części oraz całkowanie przez pod-
stawienie.

Całkowanie przez części
Wzór na całkowanie przez części:

∫ u

′

v

= uv − ∫ uv

′

Jego stosowanie ma sens wtedy gdy całka po prawej stronie równości będzie łatwiejsza do policzenia
niż ta po lewej.

Przykład:

∫ x cos xdx = ∣

u

′

= cos x u = sin x

v

= x

v

′

= 1 ∣ =

x sin x

− ∫ sinx = xsinx + cosx + C

Gdybyśmy przyjęli odwrotnie, tzn. u

′

= x, v = cos x, to nową całką byłaby ∫ x

2

sin x, czyli byłaby

trudniejsza niż wyjściowa.

19

Całkowanie przez podstawienie

Całkowanie przez podstawienie odbywa się według schematu:

∫ f

′

(g(x))g

′

(x)dx = ∣

t

= g(x)

dt

= g

′

(x)dx∣ = ∫

f

′

(t)dt = f(t) + C = f(g(x)) + C

Praktyczna wskazówka jest taka, żeby w funkcji podcałkowej szukać pary: funkcja i jej pochodna sto-
jąca przy dx.

Przykłady:

∫ xe

x

2

dx

=

RRRRR

RRRRR

RRRR

t

= x

2

dt

= 2xdx

1
2

dt

= xdx

RRRRR

RRRRR

RRRR

=

1

2 ∫

e

t

dt

=

1

2

e

t

+ C =

1

2

e

x

2

+ C

∫

dx

x ln x

= ∣

t

= ln x

dt

=

dx

x

∣ = ∫

dt

t

= ln ∣t∣ + C = ln ∣ ln x∣ + C

∫

xdx

1

+ x

4

=

RRRRR

RRRRR

RRRR

t

= x

2

dt

= 2xdx

1
2

dt

= xdx

RRRRR

RRRRR

RRRR

=

1

2 ∫

dt

1

+ t

2

=

1

2

arctan t

+ C =

1

2

arctan x

2

+ C

O ile w przypadku liczenia pochodnych na wszystko jest algorytm, o tyle przy całkowaniu potrzebna
jest odrobina inwencji: po pierwsze trzeba wybrać metodę całkowania, a po drugie przy podstawieniu
trzeba znaleźć odpowiednie podstawienie. Nie ma innej metody na nauczenie się tego niż samodzielne
policzenie n całek dla dostatecznie dużych n (proponowałbym n

≥ 200).

Ćwiczenia

5.1

Oblicz całki stosując metodę całkowania przez części:

a)

∫ x cos xdx b) ∫ x

2

e

x

dx

c)

∫ x ln xdx

d)

∫ ln xdx

e)

∫

arctan xdx

1+x

2

f)

∫ x arctan xdx g) ∫ x ln

2

xdx

h)

∫ e

x

cos 2xdx

5.2

Oblicz całki stosując metodę całkowania przed podstawienie:

a)

∫ x cos x

2

dx

b)

∫ (2x

2

− 5)

2012

xdx

c)

∫

arctan xdx

1+x

2

d)

∫

ln

2

xdx

x

e)

∫

dx

x

√

1−ln

2

x

f)

∫

x

2

dx

x

6

+

1

g)

∫

dx

e

x

+

e

−

x

h)

∫ e

x

sin

2

e

x

cos e

x

dx

5.3

Oblicz całki:

a)

∫ x

3

e

x

2

dx

b)

∫ e

2x

sin e

x

dx

c)

∫

x+1

sin

2

x

dx

d)

∫ arcsin xdx

e)

∫ arccos

2

xdx

f)

∫

sin 2xdx

cos

4

x+1

g)

∫

ln xdx

x

3

h)

∫

x

cos

2

x

dx

20

6

Całkowanie funkcji wymiernych

Funkcje wymierne to funkcje postaci ”wielomian przez wielomian”. Szczególnym przypadkiem funkcji
wymiernych są tzw. ułamki proste czyli funkcje wymierne postaci:

A

(

ax+b)

n

oraz

Ax+B

(

ax

2

+

bx+x)

n

przy czym w mianowniku ∆

< 0

Całkowanie ułamków prostych
Każdy typ ułamka prostego ułamka prostego umiemy scałkować, co łatwo widać na przykładach:

ˆ ∫

2

x−4

= 2 ∫

1

x−4

= 2 ln ∣x − 4∣ + C

ˆ ∫

1

(

x−1)

4

= ∫ (x − 1)

−

4

=

(

x−1)

−

3

−

3

+ C

ˆ ∫

6x+5

x

2

+

4x+8

= . . .

W pamięci liczymy, że pochodną mianownika jest 2x

+ 4, a następnie chcemy ”wyodrębnić” tę

pochodną w liczniku:
. . .

= ∫

3(2x+4)−7

x

2

+

4x+8

= 3 ∫

2x+4

x

2

+

4x+8

− 7 ∫

1

x

2

+

4x+8

W pierwszej całce możemy skorzystać z faktu, że

∫

f

′

f

= ln ∣f∣, co oznacza, że ta całka jest równa

ln

(x

2

+ 4x + 8). Natomiast drugą całkę policzymy korzystając ze wzoru ∫

1

x

2

+

a

2

=

1
a

arctan

x
a

:

∫

1

x

2

+

4x+8

= ∫

1

(

x+2)

2

+

2

2

=

1
2

arctan

x+2

2

Ostatecznie więc nasza całka to:
3 ln

(x

2

+ 4x + 8) −

7
2

arctan

x+2

2

+ C

ˆ ∫

6x+5

(

x

2

+

4x+8)

3

W takim wypadku przekształcamy nawias z mianownika do postaci t

2

+ 1:

x

2

+ 4x + 8 = (x + 2)

2

+ 4 = 4 ⋅ ((

x+2

2

) + 1)

więc nasza całka jest równa:

1

64

∫

6x+5

((

x+2

2

)+

1)

3

dx

i teraz podstawiamy

x+2

2

= t, skąd dx = 2dt oraz x = 2t − 2, więc mamy:

1

32

∫

12t−7

(

t

2

+

1)

3

dt

=

6

32

∫

2t

(

t

2

+

1)

dt

−

7

32

∫

1

(

t

2

+

1)

3

dt

W pierwszej całce wystarczy teraz podstawić t

2

+ 1 = u i 2tdt = du, by sprawdzić, że:

∫

2t

(

t

2

+

1)

dt

= ∫

du
u

3

= −

1

2u

2

+ C = −

1

2(t

2

+

1)

2

+ C = −

1

2((

x+2

2

)+

1)

2

+ C

Natomiast w drugiej całce możemy użyć wzoru rekurencyjnego - jeśli oznaczymy I

n

= ∫

1

(

t

2

+

1)

n

,

to:

I

n

=

t

2

(n − 1)(t

2

+ 1)

n−1

+

2n

− 3

2n

− 1

I

n−1

Widać więc, że nasze szukane I

3

możemy sprowadzić do liczenia I

2

, a to z kolei możemy spro-

wadzić do liczenia I

1

, które oczywiście jest równe arctan t. Policzenie szukanej całki jest więc

wykonalne, ale bardzo żmudne.

Skoro umiemy całkować każdy ułamek prosty, to gdyby dowolną funkcję wymierną dało się przed-

stawić jako sumę ułamków prostych, to udałoby się też ją scałkować. Okazuje się, że takie przedsta-
wienie jest możliwe, o czym mówi nam twierdzenie o rozkładzie funkcji wymiernej na ułamki proste.

21

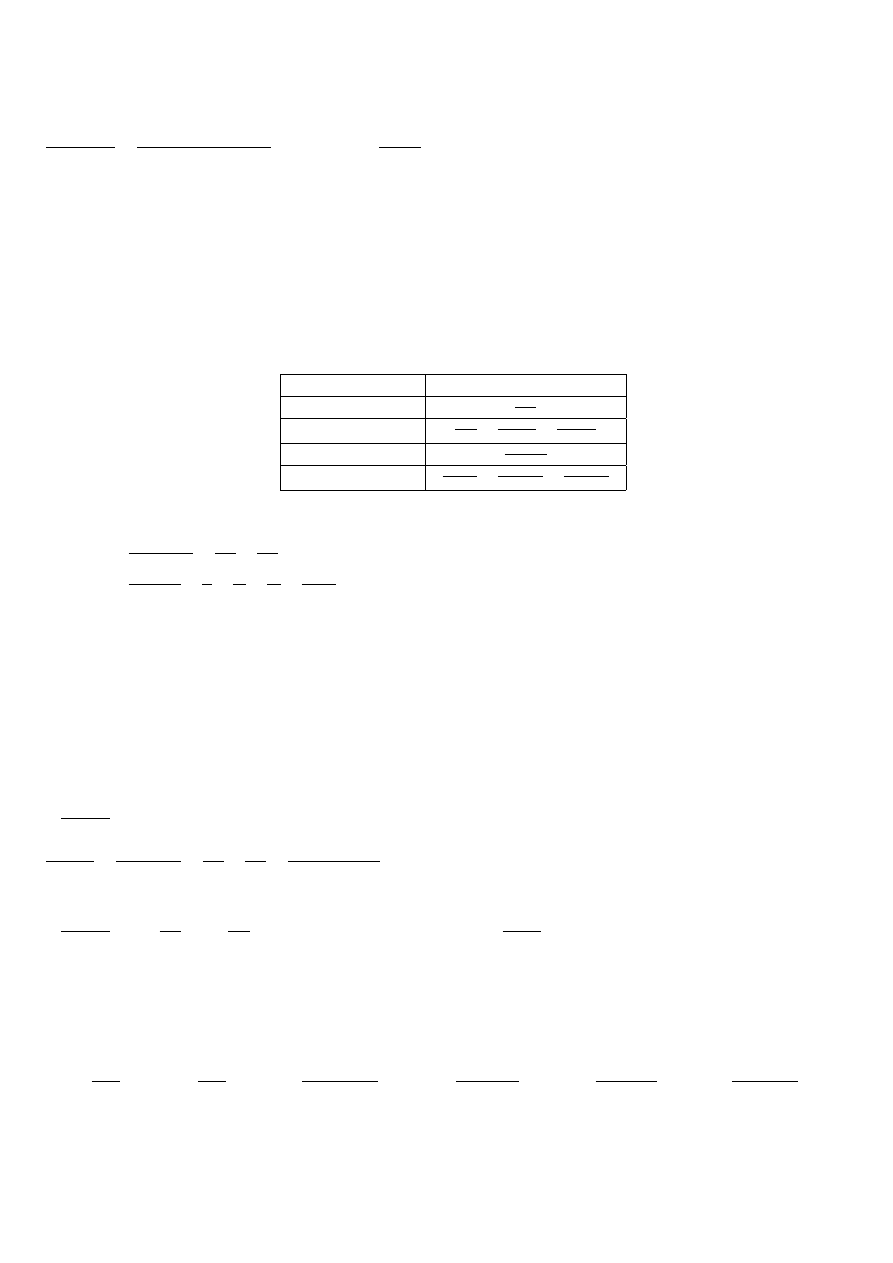
Rozkład funkcji wymiernej na ułamki proste

Aby rozłożyć funkcję wymierną na ułamki proste najpierw musimy zadbać o to by stopień wielomia-
nu w mianowniku był niższy niż stopień wielomianu w liczniku. Jeśli tak nie jest, to zaczynamy od
podzielenia (pisemnie) wielomianu z licznika przez wielomian z mianownika:

x

4

+

2x

3

−

x+1

x

2

−

x+2

=

(

x

2

−

x+2)(x

2

+

3x)−7x+1

x

2

−

x+2

= (x

2

+ 3x) −

7x−1

x

2

−

x+2

Gdybyśmy całkowali wyjściową funkcję, to powyższe przekształcenie sprowadza nam problem do scał-
kowania wielomianu x

2

+ 3x (co umiemy) oraz scałkowania nowej funkcji wymiernej, w której już jest

tak jak chcemy, czyli stopień wielomianu z licznika jest mniejszy niż stopień wielomianu z licznika.

Jeśli już tak jest, to możemy rozłożyć taką funkcję wymierną postępując według schematu:

1. Rozkładamy wielomian z mianownika na czynniki. Jak wiadomo każdy wielomian daje się roz-

łożyć na iloczyn wielomianów stopnia co najwyżej drugiego.

2. Zależnie od postaci czynników przewidujemy jakiego typu ułamki proste znajdą się w rozkładzie:

Rodzaj czynnika

Postać ułamka prostego

x

− 2

A

x−2

(x − 1)

3

A

x−1

+

B

(

x−1)

2

+

C

(

x−1)

3

x

2

+ x + 1

Ax+B

x

2

+

x+1

(x

2

+ 1)

3

Ax+B

x

2

+

1

+

Cx+D

(

x

2

+

1)

2

+

Ex+F

(

x

2

+

1)

3

Przykładowo:

ˆ

x

(

x−3)(x+1)

=

A

x−3

+

B

x+1

ˆ

2x−1

x

3

(

x

2

+

1)

=

A

x

+

B

x

2

+

C

x

3

+

Ex+F

x

2

+

1

3. Znajdujemy wartości stałych A, B, C, . . . z ułamków prostych:

(a) Sprowadzamy ułamki proste do wspólnego mianownika.

(b) Porównujemy licznik tego co wyszło z licznikiem wyjściowej funkcji wymiernej.

(c) Wstawiamy w miejsce x tyle różnych wartości ile mamy stałych A, B, C, . . . do znalezienia

(przy czym wartości te wybieramy tak, by liczyło się najwygodniej)

(d) Rozwiązujemy otrzymany układ równań liniowych

Przykład:
∫

x

x

2

−

3x+2

Rozkładamy funkcję na ułamki proste:

x

x

2

−

3x+2

=

x

(

x−1)(x−2)

=

A

x−1

+

B

x−2

=

A(x−2)+B(x−1)

(

x−1)(x−2)

Porównujemy liczniki: x

= A(x − 2) + B(x − 1) i wstawiając kolejno x = 1 i x = 2 otrzymujemy 1 = −A

(czyli A

= −1) oraz B = 2. Tak więc nasza całka to:

∫

x

x

2

−

3x+2

= − ∫

1

x−1

+ 2 ∫

1

x−2

= − ln ∣x − 1∣ + 2 ln ∣x − 2∣ + C = ln

(

x−2)

2

∣

x−1∣

+ C

Ćwiczenia

6.1

Oblicz całki z funkcji wymiernych:

a)

∫

2x+1
x

2

−

x

dx

b)

∫

x−1

x

3

+

x

dx

c)

∫

9x+1

x

3

+

3x

2

+

7x+5

dx

d)

∫

x

2

+

3

x

3

−

x

2

−

x+1

dx

e)

∫

3x+1

4x

2

+

4x+17

dx

f)

∫

1

(

x

2

+

4x+5)

2

dx

22

7

Całkowanie funkcji niewymiernych

Przez ”funkcje niewymierne” będziemy rozumieć tutaj tylko funkcje, w których występuje pierwiastek
bądź z trójmianu kwadratowego, bądź też z funkcji homograficznej. Oczywiście w istocie klasa funkcji
niewymiernych jest o wiele szersza (w szczególności można by do tego działu dorzucić całkowanie wy-
rażeń dwumiennych oraz całki eliptyczne), ale dla naszych potrzeb wystarczą tylko wymienione typy.

Całki z funkcji z

√

ax

2

+ bx + c

Kluczowe są tutaj dwa wzory:

∫

1

√

x

2

+ q

dx

= ln ∣x +

√

x

2

+ q∣ + C, ∫

1

√

q

− x

2

dx

= arcsin

x

√

q

+ C

lub ogólniej:

∫

1

√

(x − p)

2

+ q

dx

= ln ∣x − p +

√

(x − p)

2

+ q∣ + C, ∫

1

√

q

− (x − p)

2

dx

= arcsin

x

− p

√

q

+ C

Jeśli więc liczymy całkę postaci

∫

dx

√

ax

2

+

bx+c

, to wystarczy sprowadzić trójmian z mianownika do po-

staci kanonicznej.
Przykład:

∫ 3dx

√

4x

2

+ 4x + 9 = ∫ 3dx

√

4

(x +

1
2

)

2

+ 8 =

3
2

∫ ∫ dx

√

(x +

1
2

)

2

+ 2 =

3
2

ln

∣x +

1
2

+

√

(x +

1
2

)

2

+ 2∣

Jeśli w liczniku mamy wyrażenie liniowe, to możemy ”wyodrębnić” z licznika pochodną trójmianu
z mianownika i podzielić szukaną całkę na dwie całki.
Przykład:
∫ 2x + 3

√

4x

2

+ 4x + 9dx = ∫

1
4

(8x + 4) + 2

√

4x

2

+ 4x + 9dx =

1
4

∫ 8x + 4

√

4x

2

+ 4x + 9dx+2 ∫ 1

√

4x

2

+ 4x + 9dx

Druga całka to ta z poprzedniego przykładu. Natomiast, żeby policzyć pierwszą wystarczy scałkować
przez podstawienie:

∫ 8x + 4

√

4x

2

+ 4x + 9dx = ∣

t

= 4x

2

+ 4x + 9

dt

= (8x + 4)dx∣ = ∫

dt

√

t

= 2

√

t

+ C = 2

√

4x

2

+ 4x + 9 + C

Jeśli natomiast w liczniku mamy wielomian stopnia wyższego niż jeden, to możemy przewidzieć postać
rozwiązania. Jeśli W

n

(x) jest wielomianem n-tego stopnia, to dla pewnego wielomianu V

n

1

(x) stopnia

n

− 1 i dla pewnej stałej A zachodzi równość:

∫

W

n

(x)dx

√

ax

2

+ bx + c

= V

n−1

(x)

√

ax

2

+ bx + c + ∫

Adx

√

ax

2

+ bx + c

Ostatnią całkę już umiemy policzyć, wystarczy zatem znaleźć wielomian V

n−1

(x) i stałą A. Można to

zrobić licząc pochodną obu stron, porządkując obie strony i porównując współczynniki przy odpowied-
nich potęgach wielomianów.

23

Całki z funkcji z

n

√

ax+b
cx+d

Jeśli w funkcji podcałkowej występują wyrażenia postaci

n

√

ax+b
cx+d

,

m

√

ax+b
cx+d

, . . ., to używamy podstawienia

t

=

r

√

ax+b
cx+d

, gdzie r to najmniejsza wspólna wielokrotność liczb n, m, . . .. Przykładowo:

ˆ W całce ∫

3

√

x+

√

x

4

√

x+3

dx podstawilibyśmy t

=

12

√

x

ˆ W całce ∫

√

x−2
x+4

dx podstawilibyśmy t

=

√

x−2
x+4

ˆ W całce ∫

dx

√

1

x−1

+

3

√

1

x−1

podstawilibyśmy t

=

6

√

1

x−1

Ideą takiego podstawienia jest sprowadzenie naszej całki do całki z funkcji wymiernej przez pozbycie
się pierwiastków.
Przykłady:

∫

1

2

4

√

x+

3

√

x+

√

x

dx

=

RRRRR

RRRRR

RRRR

t

=

12

√

x

t

12

= x

dx

= 12t

11

dt

RRRRR

RRRRR

RRRR

= ∫

12t

11

2t

3

+

t

4

+

t

6

∫ x

√

x−1
x+2

dx

= ∣t =

√

x−1
x+2

∣ = . . .

Z podstawienia wyznaczamy x: t

2

=

x−1
x+2

, t

2

x

+ 2t

2

= x − 1, x − t

2

x

= 2t

2

+ 1, x =

2t

2

+

1

1−t

2

i obliczamy, że dx

=

6t

(

1−t

2

)

2

dt, więc nasza całka to:

. . .

= ∫

2t

2

+

1

1−t

2

⋅ t ⋅

6t

(

1−t

2

)

2

dt

czyli dostajemy zwykłą całkę z funkcji wymiernej (choć akurat tutaj skomplikowaną rachunkowo).

Ćwiczenia

7.1

Oblicz całki z funkcji niewymiernych:

a)

∫

dx

√

6x−x

2

b)

∫

3x−1

√

5+4x−x

2

dx

c)*

∫

x

2

dx

√

x

2

+

2x+2

d)

∫

3

√

x+1+

3

√

x+1

dx

e)

∫ x

2

√

x

− 3dx f) ∫

√

1−x
1+x

dx

x

8

Całkowanie funkcji trygonometrycznych

Najskuteczniejszą (choć nie zawsze najszybszą) metodą całkowania funkcji w których pojawiają się
funkcje trygonometryczne jest zastosowanie podstawienia uniwersalnego:

Jeśli t

= tg

x

2

to dx

=

2dt

1

+ t

2

, sin x

=

2t

1

+ t

2

, cos x

=

1

− t

2

1

+ t

2

To podstawienie pozwala pozbyć się z funkcji podcałkowej funkcji trygonometrycznych, jeśli więc wyj-
ściowa funkcja podcałkowa była funkcją wymierną od sinusa i cosinusa, to nowa całka będzie całką ze
zwykłej funkcji wymiernej.
Przykład:
∫

1

2 sin x+3 cos x

dx

= ∣t = tg

x
2

∣ = ∫

1

2⋅

2t

1+t2

+

3⋅

1−t2
1+t2

2dt

1+t

2

= ∫

2dt

−

3t

2

+

4t+3

co sprowadza liczenie do takiej całki jaką już umiemy.

24

Czasem jednak można liczyć prościej. Najbardziej typowym przykładem są całki postaci:

∫ sin

n

x cos

m

xdx

Postępujemy wówczas według schematu:

ˆ Jeśli n, m są nieparzyste, to podstawiamy t

= sin x lub t = cos x

ˆ Jeśli n jest nieparzyste, a m parzyste, to podstawiamy t

= cos x

ˆ Jeśli n jest parzyste, a m nieparzyste, to podstawiamy t

= sin x

ˆ Jeśli n, m są parzyste, to mamy trzy możliwości:

– Użyć podstawienia podobnego do uniwersalnego, tzn.:

Jeśli t

= tg x to dx =

dt

1

+ t

2

, sin

2

x

=

t

2

1

+ t

2

, cos

2

x

=

1

1

+ t

2

– Użyć wzorów sin x cos x

=

sin 2x

2

i cos

2

x

=

1+cos 2x

2

– Pozbyć się jednej z funkcji sin, cos i zastosować wzory rekurencyjne

Przykłady:

ˆ ∫ sin

2

x cos

3

xdx

= ∫ sin

2

x

(1 − sin

2

x

) cos xdx = ∣

t

= sin x

dt

= cos dx∣ = ∫ (

t

2

− t

4

)dt =

=

t

3

3

−

t

5

5

+ C =

sin

3

x

3

−

sin

5

x

5

+ C

ˆ ∫ sin

2

x cos

4

xdx

= ∣t = tg x∣ = ∫

t

2

t

2

+

1

⋅

1

(

1+t

2

)

2

⋅

dt

1+t

2

W ten sposób otrzymujemy całkę z funkcji wymiernej, a to już umiemy (choć akurat w tym
przypadku trzeba się mocno nagimnastykować ze wzorami na I

n

)

ˆ ∫ sin

2

x cos

4

xdx

= ∫ (sinxcosx)

2

cos

2

xdx

=

1
4

∫ sin

2

2x

(1 + cos 2x)dx =

= ∣

t

= 2x

dx

=

1
2

dt∣ =

1
8

∫ (sin

2

t

+ sin

2

t cos t

)dt

Scałkować sin

2

t cos t oczywiście umiemy, natomiast w przypadku całki z sin

2

t wystarczy zasto-

sować:

∫ sin

2

xdx

=

1

2

x

+ sin x cos x + C, ∫ cos

2

xdx

=

1

2

x

− sin x cos x + C

Ćwiczenia

8.1

Oblicz całki z funkcji trygonometrycznych:

a)

∫

1+sin x

sin x(1+cos x)

dx

b)

∫

1

sin

3

x

dx

c)

∫ sin

5

x cos

4

xdx

d)

∫ sin

2

x cos

2

xdx

25

9

Całki oznaczone

Całkę oznaczoną definiuje się jako granicę sum pól pod krzywą, z czego wynika geometryczna inter-

pretacja - całka oznaczona

b

∫

a

f

(x)dx jest równa (co do modułu) polu figury między krzywą f(x) a

osią OX i znajdującej się między prostymi x

= a i x = b. Równie ważny co interpretacja geometryczna

jest fakt wynikający z Podstawowego Twierdzenia Rachunku Całkowego:

Jeśli

∫ f(x)dx = F(x) + C to

b

∫

a

f

(x)dx = F(x)∣

b
a

= F(b) − F(a)

Przykładowo:

e

∫

1

ln xdx

= (x ln x − x)∣

e
1

= (e ln e − e) − (1 ⋅ ln 1 − 1) = 1

Niektóre zastosowania całek oznaczonych

1) Pole figury płaskiej:
a) współrzędne kartezjańskie - jeśli figura jest ograniczona przez y

= f(x) (z góry), y = g(x) (z dołu)

oraz x

= a, x = b, to jej pole to: S =

b

∫

a

(f(x) − g(x))dx

b) współrzędne biegunowe - jeśli figura składa się z punktów o kącie należącym do przedziału

[α, β] i

promieniu mniejszym od r

= r(φ), to jej pole to: S =

1

2

β

∫

α

(r(φ))

2

dφ

c) postać parametryczna - jeśli figura ograniczona jest krzywą x

= x(t), y = y(t) gdzie t ∈ [t

1

, t

2

], to jej

pole to: S

=

t

2

∫

t

1

∣y(t)x

′

(t)∣dt

2) Długość krzywej:

a) współrzędne kartezjańskie - długość krzywej y

= f(x) dla x ∈ [a, b] to: l =

b

∫

a

√

1

+ (f

′

(x))

2

dx

b) współrzędne biegunowe - długość krzywej r

= r(φ) dla φ ∈ [α, β] (gdzie α, beta ∈ [0, 2π)) to:

l

=

β

∫

α

√

(r(φ))

2

+ (r

′

(φ))

2

dφ

c) postać parametryczna - długość krzywej x

= x(t), y = y(t) dla t ∈ [t

1

, t

2

] to: l =

t

2

∫

t

1

√

(x

′

(t))

2

+ (y

′

(t))

2

dt

3) Objętość bryły obrotowej:
a) współrzędne kartezjańskie - bryła powstała przez obrót figury płaskiej ograniczonej krzywymi

y

= f(x), y = 0, x = a, x = b wokół osi OX ma objętość: V = π

b

∫

a

(f(x))

2

dx

b) postać parametryczna - bryła powstała przez obrót figury płaskiej ograniczonej krzywą x

= x(t),

y

= y(t) (gdzie x

′

(t) i y(t) są ciągłe, a x

′

(t) jest stałego znaku) dla t ∈ [t

1

, t

2

] i osią OX wokół osi OX

26

ma objętość: V

= π

t

2

∫

t

1

(y(t))

2

∣x

′

(t)∣dx

4) Pole powierzchni bocznej bryły obrotowej:
a) współrzędne kartezjańskie - bryła powstała przez obrót figury płaskiej ograniczonej krzywymi

y

= f(x), y = 0, x = a, x = b wokół osi OX ma pole powierzchni bocznej: P

p

= π

b

∫

a

∣f(x)∣

√

1

+ (f

′

(x))

2

dx

b) postać parametryczna - bryła powstała przez obrót figury płaskiej ograniczonej krzywą x

= x(t), y =

y

(t) dla t ∈ [t

1

, t

2

] i osią OX wokół osi OX ma pole powierzchni bocznej: P

p

= π

t

2

∫

t

1

∣y(t)∣

√

(x

′

(t))

2

+ (y

′

(t))

2

dx

Zadania przy których potrzebny jest któryś z powyższych wzorów robi się schematycznie - podsta-
wiamy do stosownego wzoru (być może czasem trzeba najpierw znaleźć granice całkowania), a potem
liczymy stosowną całkę nieoznaczoną (co zazwyczaj jest najtrudniejszą częścią zadania) i wstawiamy
na koniec granice całkowania. Prawie zawsze wygodnie jest zacząć rozwiązanie od zrobienia rysunku
(czasem jest to wręcz niezbędne).

Najbardziej typowe zadanie to policzenie pola figury ograniczonej przez dwie krzywe. Niech jedną
krzywą ograniczającą naszą figurę będzie y

= x

2

, a drugą y

= 4. Po zrobieniu rysunku widać, że figura

ma kształt ”miski” oraz górna krzywa to y

= 4, a dolna y = x

2

. Pozostaje znaleźć granice całkowania

- są to pierwsze współrzędne punktów wspólnych tych dwóch krzywych, czyli takich punktów, które
spełniają oba równania naraz. Z porównania igreków dostajemy x

2

= 4, czyli x = −2 lub x = 2, stąd

nasze pole to:

S

=

2

∫

−

2

(4 − x

2

) = (4x −

x

3

3

) ∣

2
−

2

=

48

3

Używając powyższych wzorów można też łatwo wyprowadzić wiele zależności geometrycznych. Wy-
prowadźmy dla przykłady wzór na obwód koła o promieniu R. We współrzędnych biegunowych okrąg
o takim promieniu ma równanie r

(φ) = R gdzie φ ∈ [0, 2π]. W takim razie r

′

(φ) = 0 i ze wzoru 2b

mamy:

Obw

=

2π

∫

0

√

R

2

+ 0

2

dφ

= Rφ∣

2π
0

= 2πR

czyli rzeczywiście wzór poznany w szkole średniej jest prawdziwy.

Ćwiczenia

9.1

Znajdź pola figur ograniczonych krzywymi:
a)y

= sin x, y = cos x, x = 0, x =

π

2

b) y

= x

2

− 2, y = x

9.2

Wyprowadź wzory na pole i obwód koła o promieniu R, objętość i pole powierzchni bocznej kuli o
promieniu R, objętość i pole powierzchni bocznej stożka o wysokości H i promieniu podstawy R.
Porównaj złożoność rachunków przy użyciu poszczególnych układów współrzędnych.

27

10

Całki niewłaściwe

Najogólniej (choć nie do końca ściśle) rzecz biorąc - całka niewłaściwa to całka oznaczona, w której
funkcja podcałkowa nie istnieje na którymś końcu przedziału całkowania. Przez ”nieistnienie” rozu-
miemy tu także sytuację, gdy którymś końcem przedziału całkowania jest

±∞. Formalne definicje to:

Całka niewłaściwa I rodzaju
Jeśli funkcja f

(x) jest określona i całkowalna na każdym odcinku [a, T], to:

∞

∫

a

f

(x)dx = lim

T →∞

T

∫

a

f

(x)dx

Jeśli funkcja f

(x) jest określona i całkowalna na każdym odcinku [T, b], to:

b

∫

−∞

f

(x)dx = lim

T →−∞

b

∫

T

f

(x)dx

Całka niewłaściwa I rodzaju
Jeśli funkcja f

(x) jest określona, ograniczona i całkowalna na każdym odcinku [a, T] dla T < b, a w b

ucieka do nieskończoności to:

b

∫

a

f

(x)dx = lim

T →b

−

T

∫

a

f

(x)dx

Jeśli funkcja f

(x) jest określona, ograniczona i całkowalna na każdym odcinku [T, a] dla a < T, a w

a ucieka do nieskończoności to:

b

∫

a

f

(x)dx = lim

T →a

+

b

∫

T

f

(x)dx

Jeśli te granice istnieją i są skończone to mówimy, że całka jest zbieżna, w przeciwnym wypadku
mówimy, że jest rozbieżna.

Przykładowo:

∞

∫

1

dx

x

2

= lim

T →∞

T

∫

1

dx

x

2

= lim

T →∞

(−

1

x

) ∣

T
1

= lim

T →∞

(1 −

1

T

) = 1

1

∫

0

dx

√

x

= lim

T →0

+

1

∫

T

dx

√

x

= lim

T →0

+

(2

√

x

) ∣

1
T

= lim

T →0

+

(2 − 2

√

T

) = 2

(obie całki są zbieżne)

W przypadku kiedy funkcja podcałkowa nie istnieje w kilku punktach, całkę podzielić na kilka speł-
niających założenia definicji, na przykład:

1

∫

−

1

dx

√

1

− x

2

=

0

∫

−

1

dx

√

1

− x

2

+

1

∫

0

dx

√

1

− x

2

= lim

T →0

−

T

∫

−

1

dx

√

1

− x

2

+ lim

T →0

+

1

∫

T

dx

√

1

− x

2

= . . .

i dalej jak w zwykłym przypadku.

28

11

Szeregi liczbowe

Szeregiem liczbowym nazywamy wyrażenie postaci

∞

∑

n=0

a

n

i definiujemy jako:

∞

∑

n=0

a

n

= lim

N →∞

N

∑

n=0

a

n

Intuicyjnie należy przez szereg rozumieć sumę wszystkich wyrazów dowolnego ciągu liczbowego.
Jeśli powyższa granica jest skończona, to mówimy, że szereg jest zbieżny, a jeśli granica jest nieskoń-
czona lub w ogóle nie istnieje, to mówimy, że szereg jest rozbieżny.

Przykłady:

Szereg

∞

∑

n=0

1

3

n

jest zbieżny, ponieważ jest to suma nieskończonego ciągu geometryczny o ilorazie q ta-

kim, że

∣q∣ < 1 - granica z definicji zatem istnieje i jest skończona.

Szereg

∞

∑

n=0

3

n

jest rozbieżny, ponieważ jest to suma nieskończonego ciągu geometryczny o ilorazie q

takim, że

∣q∣ > 1 - granica z definicji zatem co prawda istnieje, ale jest nieskończona.

Szereg

∞

∑

n=0

(−1)

n

jest rozbieżny, ponieważ granica z definicji nie istnieje - suma skończona na zmia-

nę jest jedynką i zerem, więc do niczego nie zbiega.

Przydatne granice: lim

n→∞

(1 +

1

n

)

n

= e lim

n→∞

n

√

a

= 1 lim

n→∞

n

√

n

= 1

W przypadku szeregów liczbowych najczęściej szukamy odpowiedzi na pytanie czy szereg jest zbieżny
czy rozbieżny. Do jej znalezienia możemy użyć kilku kryteriów zbieżności.
Uwaga: od tej pory zakładamy, że ciąg a

n

ma wyrazy nieujemne!

ˆ Warunek konieczny zbieżności

Jeśli

∞

∑

n=0

a

n

jest zbieżny, to lim

n→∞

a

n

= 0. Inaczej mówiąc: jeśli lim

n→∞

a

n

nie istnieje lub istnieje, ale

jest różna od zera, to szereg

∞

∑

n=0

a

n

jest rozbieżny.

ˆ Kryterium Cauchy’ego.

Niech lim

n→∞

n

√

a

n

= g. Jeśli g > 1 to szereg

∞

∑

n=0

a

n

jest rozbieżny, jeśli g

< 1 szereg jest zbieżny, a

jeśli g

= 1, to kryterium nie daje rozstrzygnięcia.

ˆ Kryterium d’Alemberta

Niech lim

n→∞

a

n+1

a

n

= g. Jeśli g > 1 to szereg

∞

∑

n=0

a

n

jest rozbieżny, jeśli g

< 1 szereg jest zbieżny, a

jeśli g

= 1, to kryterium nie daje rozstrzygnięcia.

ˆ Kryterium porównawcze

Niech dla ciągów

(a

n

) i (b

n

) od pewnego miejsca zachodzi nierówność a

n

≤ b

n

. Wówczas:

- jeśli szereg

∞

∑

n=0

b

n

jest zbieżny, to

∞

∑

n=0

a

n

też

- jeśli szereg

∞

∑

n=0

a

n

jest rozbieżny, to

∞

∑

n=0

b

n

też.

29

Inaczej mówiąc: ze zbieżności sumy większego ciągu wynika zbieżność sumy mniejszego ciągu, a
z rozbieżności sumy mniejszego ciągu wynika zbieżność sumy większego ciągu.
W przypadku używania kryterium porównawczego warto wiedzieć, że:

- szereg

∞

∑

n=0

1

n

α

jest zbieżny dla α

> 1 oraz rozbieżny dla α ≤ 1

- szereg

∞

∑

n=0

q

n

jest zbieżny dla

∣q∣ < 1 i rozbieżny dla ∣q∣ ≥ 1

Przykłady zastosowań:

ˆ Szereg

∞

∑

n=0

(−1)

n

jest rozbieżny, ponieważ nie spełnia warunku koniecznego zbieżności.

ˆ Szereg

∞

∑

n=0

(

2n

+ 1

n

+ 3 )

n

jest rozbieżny na mocy kryterium Cauchy’ego, ponieważ:

lim

n→∞

n

√

(

2n

+ 1

n

+ 3 )

n

= lim

n→∞

2n

+ 1

n

+ 3 =

lim

n→∞

2

+

1

n

1

+

3

n

= 2 > 1

ˆ Szereg

∞

∑

n=0

2

n

n!

jest zbieżny na mocy kryterium d’Alemberta, ponieważ mamy:

lim

n→∞

a

n+1

a

n

= lim

n→∞

2

n+1

(

n+1)!

2

n

n!

= lim

n→∞

2

n

⋅ 2

n!

⋅ (n + 1) ⋅

n!

2

n

= lim

n→∞

2

n

+ 1 =

0

< 1

ˆ Szereg

∞

∑

n=0

n

+ 1

n

2

+ 1

jest rozbieżny na mocy kryterium porównawczego.

By to stwierdzić możemy zacząć od ocenienia rzędu wielkości ciągu - w liczniku dominującym
składnikiem jest n, a w mianowniku n

2

, tak więc całość jest rzędu

n

n

2

=

1

n

. Dzięki temu wiemy, że w

ogóle będziemy chcieli pokazywać rozbieżność. A żeby pokazać rozbieżność wystarczy wskazać
jakiś mniejszy ciąg, którego suma jest rozbieżna. Czyli musimy oszacować ciąg

n+1

n

2

+

1

z dołu.

Szacując ułamek z dołu mamy prawo zmniejszyć licznik i zwiększyć mianownik, a szacując
ułamek z góry mamy prawo zwiększyć licznik i zmniejszyć mianownik, co symbolicznie można
zapisać:

zmniejszamy

zwiększamy

≤

licznik

mianownik

≤

zwiększamy

zmniejszamy

U nas mamy:

n+1

n

2

+

1

≥

n

n

2

+

n

2

=

1
2

⋅

1

n

. Suma mniejszego szeregu jest rozbieżna, zatem suma wyjścio-

wego również, co właśnie chcieliśmy pokazać.

Warto zwrócić uwagę, że kryterium d’Alemberta opłaca się stosować gdy w ciągu pojawiają się silnie,
a kryterium Cauchy’ego gdy w ciągu pojawiają się n-te potęgi (i nie ma silni).

Ćwiczenia

11.1

Rozstrzygnij czy następujące szeregi są zbieżne:

a)

∞

∑

n=0

n

3

n

b)

∞

∑

n=0

n!

2

n

c)

∞

∑

n=0

(

2

+ n

1

+ n)

n

2

d)

∞

∑

n=0

n

+

√

n

+ 1

n

3

+ n + 2

e)

∞

∑

n=0

n!

n

n

f)

∞

∑

n=0

√

n

n

+ 1

30