www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
P
RÓBNY
E
GZAMIN
M
ATURALNY
Z
M
ATEMATYKI
Z
ESTAW PRZYGOTOWANY PRZEZ SERWIS
WWW
.
ZADANIA
.
INFO
POZIOM PODSTAWOWY
22
MARCA
2014
C
ZAS PRACY
: 170
MINUT
Zadania zamkni˛ete
Z
ADANIE
1
(1
PKT
)
Dwadzie´scia dziewcz ˛
at stanowi 62,5% uczniów klasy IB. Ilu chłopców jest w tej klasie?
A) 12
B) 6
C) 32
D) 9
R
OZWI ˛
AZANIE
Je ˙zeli przez n oznaczymy liczb˛e chłopców, to mamy równanie
62, 5%
· (
20
+
x
) =
20
/ : 0, 625
20
+
x
=
32
⇒
x
=
12.
Odpowied´z: A
Z
ADANIE
2
(1
PKT
)
Wszystkie liczby spełniaj ˛
ace warunek x
−
1
<
2x 6 3x
+
3 mo ˙zna zapisa´c za pomoc ˛
a prze-
działu:
A)
(−
1,
+
∞
)
B)
(−
∞,
−
3
i
C)
h−
3,
−
1
)
D)
h−
3,
+
∞
)
R
OZWI ˛
AZANIE
Musimy rozwi ˛
aza´c dwie nierówno´sci
x
−
1
<
2x
i
2x 6 3x
+
3
−
1
<
x
i
−
3 6 x.
Zatem x
∈ (−
1,
+
∞
)
.
Odpowied´z: A
Materiał pobrany z serwisu
www.zadania.info
1
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
3
(1
PKT
)
Liczba log
3,5
12, 25
−
log
0,5
8 jest równa
A) 5
B)
−
1
C)
−
1
2
D) 1
R
OZWI ˛
AZANIE
Liczymy
log
3,5
12, 25
−
log
0,5
8
=
log
7
2
49
4
−
log
1
2
8
=
=
log
7
2
7
2
2
−
log
1
2
1
2
−
3
=
2
− (−
3
) =
5.
Odpowied´z: A
Z
ADANIE
4
(1
PKT
)
Rozwi ˛
azaniem układu równa ´n
(
5x
+
3y
=
0
2y
+
x
=
14
jest para
(
x, y
)
liczb takich, ˙ze
A) x
<
0 i y
<
0
B) x
<
0 i y
>
0
C) x
>
0 i y
<
0
D) x
>
0 i y
>
0
R
OZWI ˛
AZANIE
Odejmuj ˛
ac do pierwszego równania drugie pomno ˙zone przez 5 ( ˙zeby skróci´c x) mamy
5x
+
3y
−
10y
−
5x
=
0
−
70
⇐⇒
−
7y
= −
70
⇐⇒
y
=
10.
Zatem z drugiego równania mamy
x
=
14
−
2y
= −
6.
Odpowied´z: B
Z
ADANIE
5
(1
PKT
)
Wska ˙z zbiór rozwi ˛
aza ´n nierówno´sci
p
(−
5
−
x
)
2
6 3.
A) x
∈ h−
8, 2
i
B) x
∈ h−
2, 8
i
C) x
∈ h
2, 8
i
D) x
∈ h−
8,
−
2
i
Materiał pobrany z serwisu
www.zadania.info
2
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Zapisujemy nierówno´s´c w postaci nierówno´sci z warto´sci ˛
a bezwzgl˛edn ˛
a
| −
5
−
x
|
6 3
|
x
+
5
|
6 3
|
x
− (−
5
)|
6 3.
Rozwi ˛
azaniem tej nierówno´sci jest zbiór liczb, które s ˛
a odległe od
−
5 o nie wi˛ecej ni ˙z 3, czyli
przedział
h−
5
−
3,
−
5
+
3
i = h−
8,
−
2
i
.
Odpowied´z: D
Z
ADANIE
6
(1
PKT
)
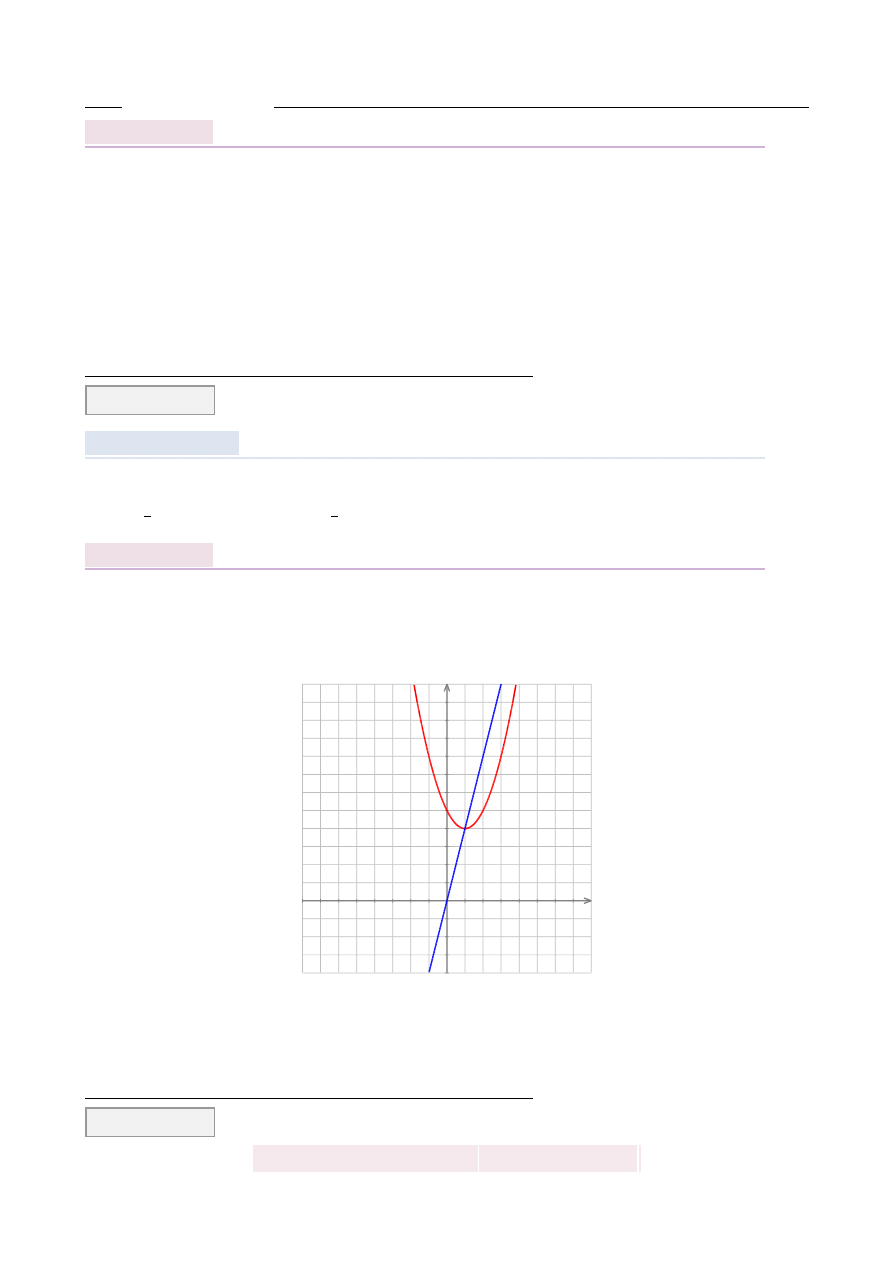
Wierzchołek paraboli o równaniu y
= (
x
−
1
)
2
+
2c le ˙zy na prostej o równaniu y
=
4x.
Wtedy
A) c
=
1
2
B) c
= −
1
2
C) c
= −
2
D) c
=
2
R
OZWI ˛
AZANIE
Wierzchołek paraboli w postaci kanonicznej
y
=
a
(
x
−
x
w
)
2
+
y
w
ma współrz˛edne
(
x
w
, y
w
)
. Zatem w naszej sytuacji jest to punkt
(
1, 2c
)
.
-5
-1
+3
+5
x
-1
+1
+5
+10
y
y=4x
y=(x-1)
2
+2c
Z drugiej strony wiemy, ˙ze punkt ten le ˙zy na prostej y
=
4x. W takim razie
2c
=
4
⇒
c
=
2.
Odpowied´z: D
Materiał pobrany z serwisu
www.zadania.info
3
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
7
(1
PKT
)
K ˛
at α jest ostry i sin α
=
2
3
. Warto´s´c wyra ˙zenia 1
−
tg α
·
cos α jest równa
A)
4
9
B)
2
3
C)
1
3
D)
11
9
R
OZWI ˛
AZANIE
Poniewa ˙z
tg α
=
sin α
cos α
,
mamy
1
−
tg α
·
cos α
=
1
−
sin α
cos α
·
cos α
=
1
−
sin α
=
1
−
2
3
=
1
3
.
Odpowied´z: C
Z
ADANIE
8
(1
PKT
)
Wyra ˙zenie 4x
2
− (
x
−
y
)
2
po rozło ˙zeniu na czynniki przyjmuje posta´c:
A)
(
x
+
y
)(
3x
+
y
)
B)
(
x
−
y
)(
3x
+
y
)
C)
(
3x
−
y
)(
x
−
y
)
D)
(
3x
−
y
)(
x
+
y
)
R
OZWI ˛
AZANIE
Liczymy (korzystamy ze wzoru skróconego mno ˙zenia na ró ˙znic˛e kwadratów).
4x
2
− (
x
−
y
)
2
= (
2x
)
2
− (
x
−
y
)
2
=
= (
2x
+ (
x
−
y
))(
2x
− (
x
−
y
)) = (
3x
−
y
)(
x
+
y
)
.
Odpowied´z: D
Z
ADANIE
9
(1
PKT
)
Liczba
√
40
−
√
10
√
5
jest równa
A)
√
2
B) 2
√
2
C) 4
D)
√
20
−
√
5
R
OZWI ˛
AZANIE
Liczymy
√
40
−
√
10
√
5
=
√
40
√
5
−
√
10
√
5
=
r
40
5
−
r
10
5
=
=
√
8
−
√
2
=
2
√
2
−
√
2
=
√
2.
Odpowied´z: A
Materiał pobrany z serwisu
www.zadania.info
4
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
10
(1
PKT
)
Liczba
1
2
+
log
5
√
20 jest równa:
A) log
5
5
√
20
B) log
5
√
5
C)
1
4
D) log
5
10
R
OZWI ˛
AZANIE
Liczymy (korzystamy ze wzoru na sum˛e logarytmów)
1
2
+
log
5
√
20
=
log
5
5
1
2
+
log
5
√
20
=
log
5
√
5
·
√
20
=
log
5
10.
Odpowied´z: D
Z
ADANIE
11
(1
PKT
)
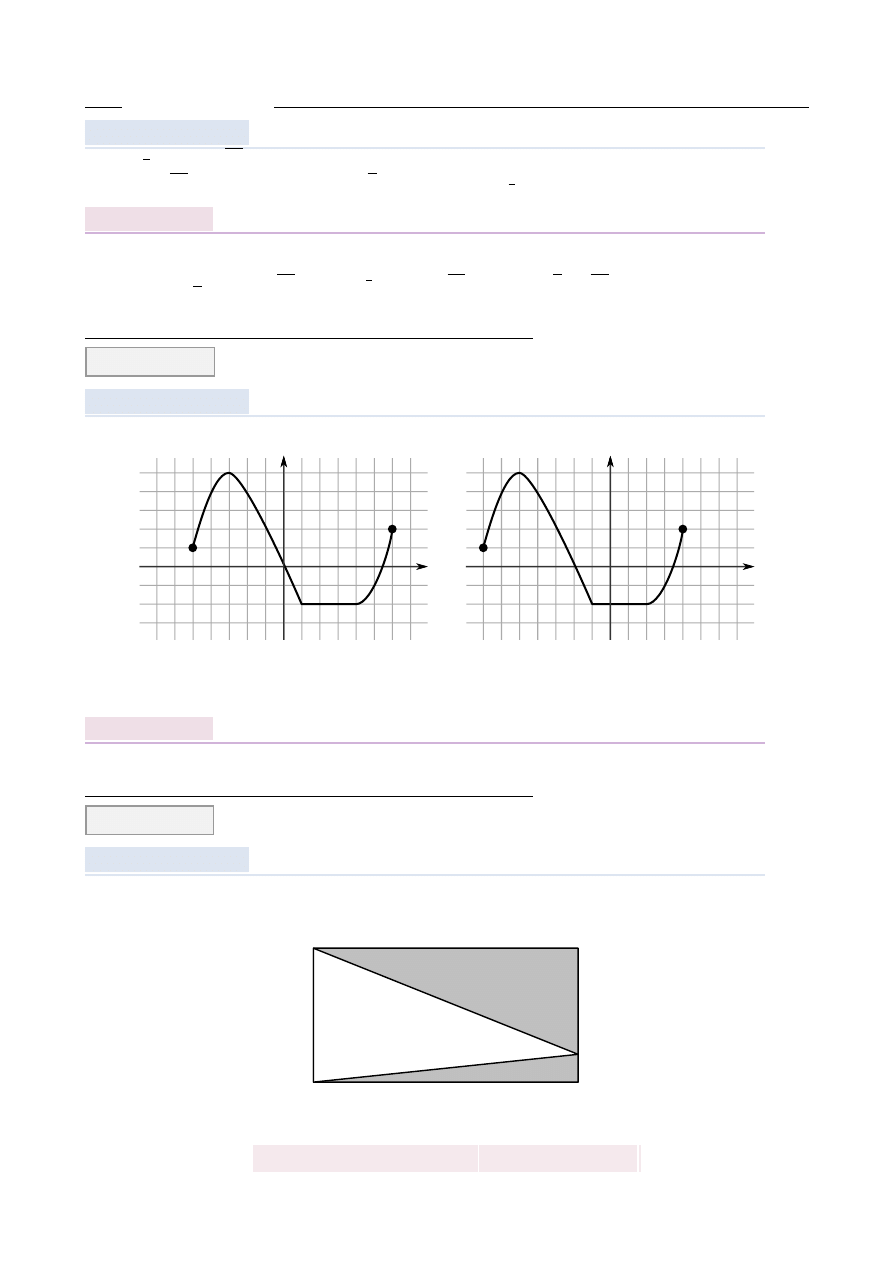
Na rysunku 1 przedstawiony jest wykres funkcji y
=
f
(
x
)
okre´slonej dla x
∈ h−
5, 6
i
.
0
1
2
3
4
5
y
x
-1
-2
-3
1
2
3
4
5
6
7
-1
-2
-3
-4
-5
-6
-7
0
1
2
3
4
5
y
x
-1
-2
-3
1
2
3
4
5
6
7
-1
-2
-3
-4
-5
-6
-7
Rysunek 2 przedstawia wykres funkcji
A) y
=
f
(
x
+
2
)
B) y
=
f
(
x
) −
2
C) y
=
f
(
x
−
2
)
D) y
=
f
(
x
) +
2
R
OZWI ˛
AZANIE
Wykres na drugim rysunku jest przesuni˛ety wzgl˛edem wykresu na pierwszym rysunku o
dwie jednostki w lewo. Jest to wi˛ec wykres funkcji y
=
f
(
x
+
2
)
.
Odpowied´z: A
Z
ADANIE
12
(1
PKT
)
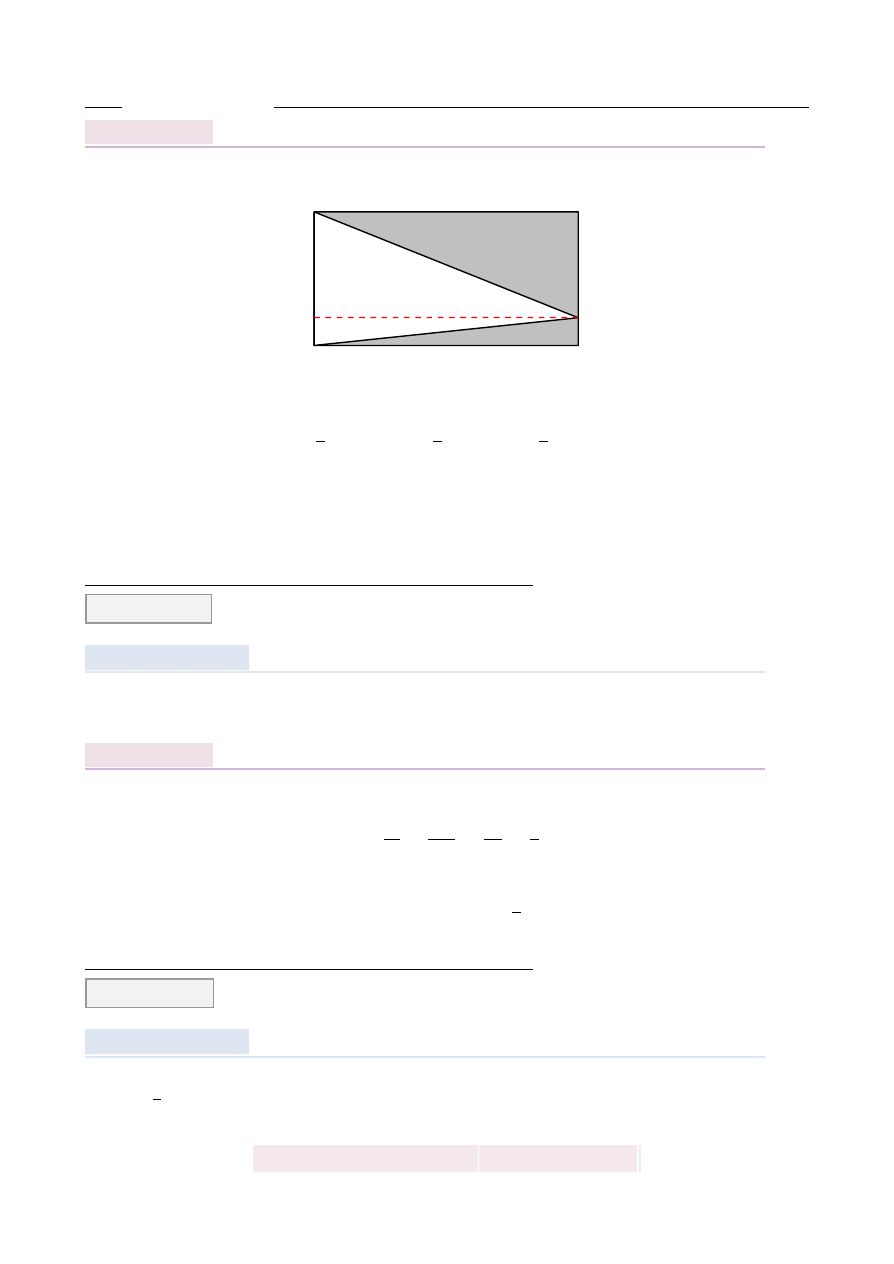
Z prostok ˛
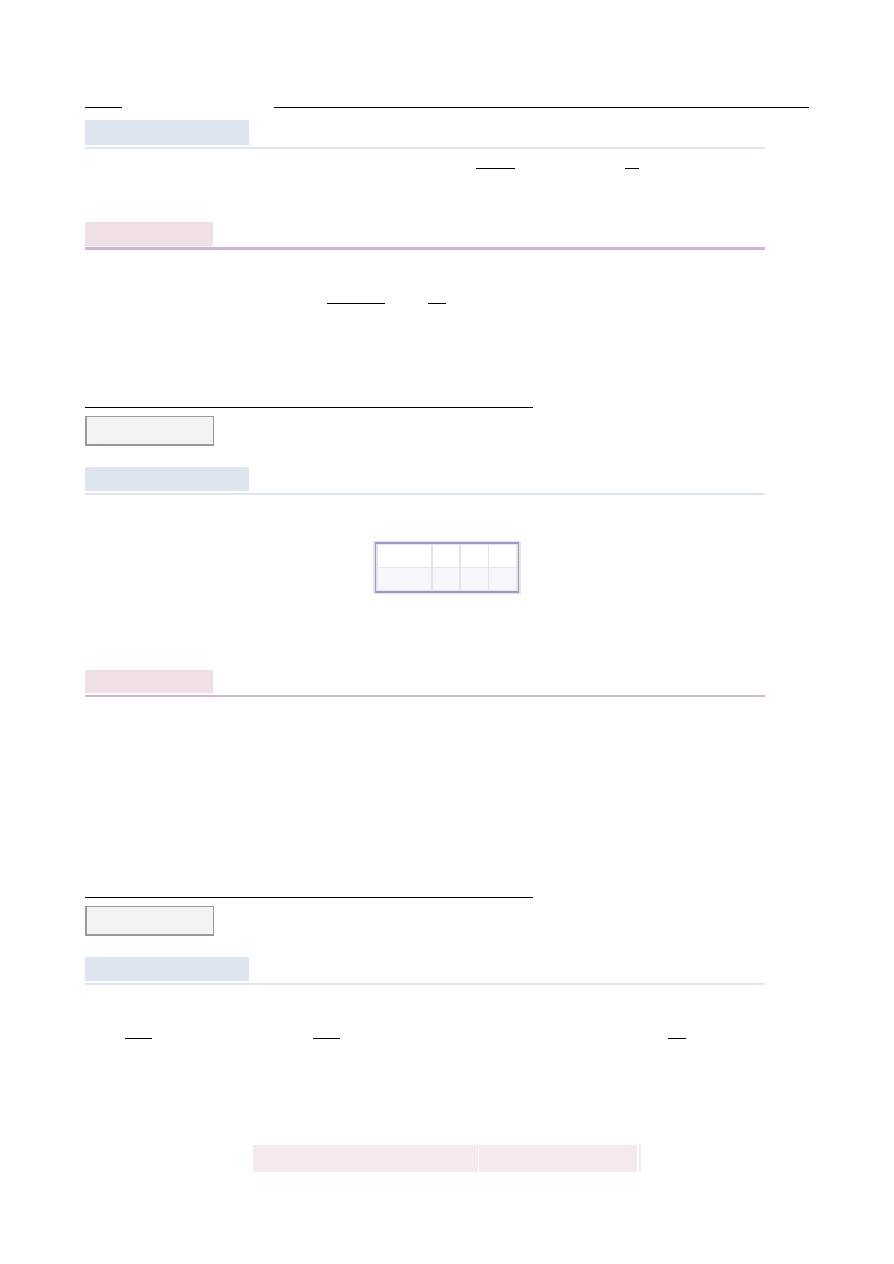
ata ABCD o polu 30 wyci˛eto trójk ˛
at AOD (tak jak na rysunku). Pole zacieniowanej
figury jest równe
A
B
D
C
O
A) 7,5
B) 15
C) 20
D) 25
Materiał pobrany z serwisu
www.zadania.info
5
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Niech OE b˛edzie wysoko´sci ˛
a wyci˛etego trójk ˛
ata opuszczon ˛
a z wierzchołka O.
A
B
D
C
O
E
Pole wyci˛etego trójk ˛
ata jest wi˛ec równe
P
AOD
=
1
2
·
AD
·
OE
=
1
2
AD
·
AB
=
1
2
P
ABCD
=
15.
Zatem zacieniowana cz˛e´s´c ma pole równe
30
−
15
=
15.
Odpowied´z: B
Z
ADANIE
13
(1
PKT
)
Ci ˛
ag
(
147, 42, x
−
3
)
jest geometryczny. Wtedy
A) x
=
15
B) x
=
12
C) x
=
9
D) x
=
6
R
OZWI ˛
AZANIE
Iloraz danego ci ˛
agu jest równy
q
=
a
2
a
1
=
42
147
=
6
21
=
2
7
.
Zatem
x
−
3
=
a
3
=
a
2
q
=
42
·
2
7
=
12.
St ˛
ad x
=
12
+
3
=
15.
Odpowied´z: A
Z
ADANIE
14
(1
PKT
)
Ci ˛
agiem arytmetycznym jest ci ˛
ag o wyrazie ogólnym a
n
równym:
A) a
n
=
4
n
B) a
n
=
2
n
C) a
n
= −
3n
−
3
D) a
n
=
3
+
n
2
Materiał pobrany z serwisu
www.zadania.info
6
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
W´sród podanych ci ˛
agów, tylko ci ˛
ag
a
n
= −
3n
−
3
= −
6
−
3
(
n
−
1
)
jest ci ˛
agiem arytmetycznym (z a
1
= −
6 i r
= −
3).
Odpowied´z: C
Z
ADANIE
15
(1
PKT
)
Liczba rzeczywistych rozwi ˛
aza ´n równania
(
x
+
1
)(
x
+
2
)(
x
2
−
3
) =
0 jest równa
A) 0
B) 1
C) 2
D) 4
R
OZWI ˛
AZANIE
Poniewa ˙z x
2
−
3
= (
x
−
√
3
)(
x
+
√
3
)
równanie ma cztery rozwi ˛
azania:
x
∈ {−
2,
−
1,
−
√
3,
√
3
}
.
Odpowied´z: D
Z
ADANIE
16
(1
PKT
)
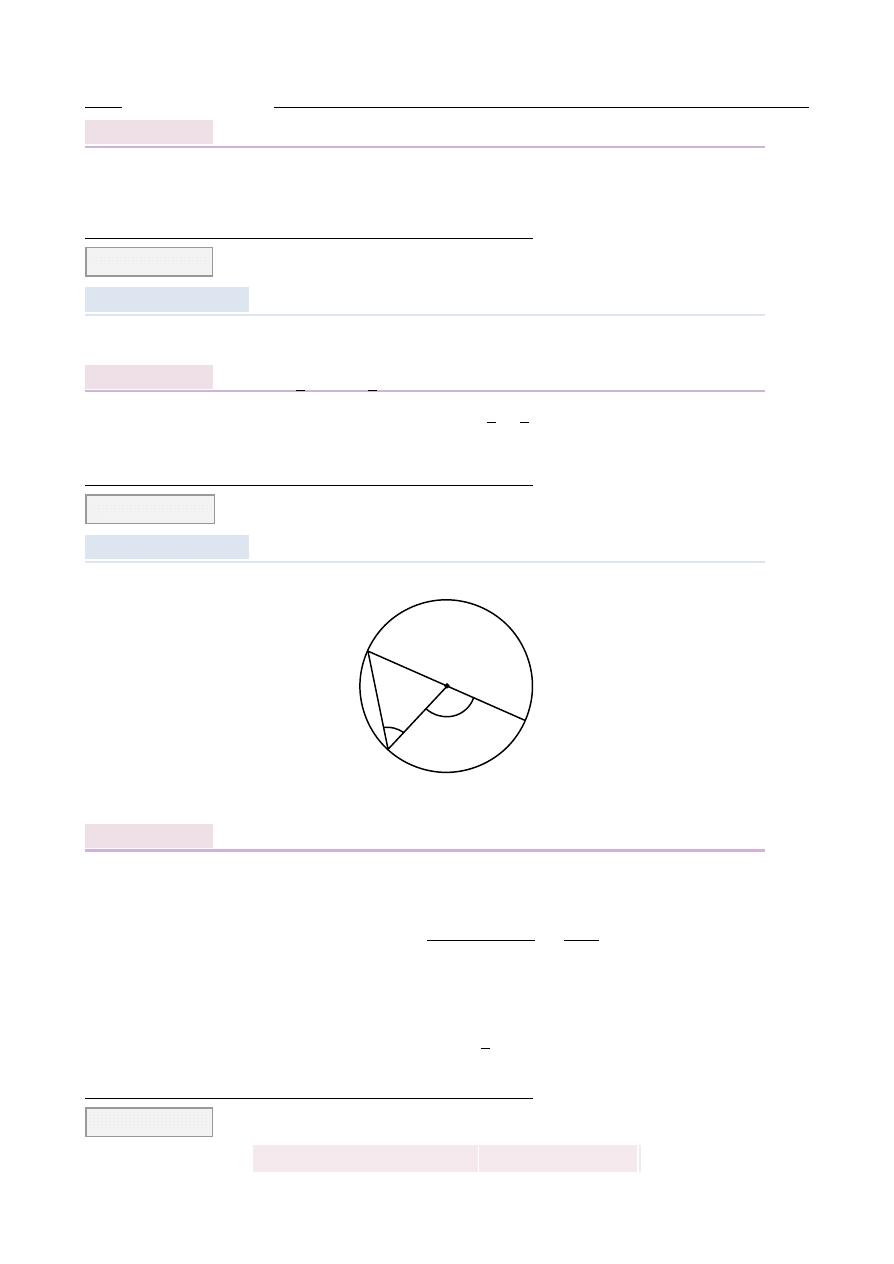
Punkt O jest ´srodkiem okr˛egu o ´srednicy AB (tak jak na rysunku). K ˛
at α ma miar˛e
A
B
C
O
120
o
α
A) 40
◦
B) 50
◦
C) 60
◦
D) 80
◦
R
OZWI ˛
AZANIE
Sposób I
Zauwa ˙zmy, ˙ze trójk ˛
at BOC jest równoramienny, wi˛ec
α
=
]OCB
=
]OBC
=
180
◦
−
]BOC
2
=
120
◦
2
=
60
◦
.
Sposób II
Korzystaj ˛
ac z twierdzenia o k ˛
atach wpisanym i ´srodkowym, mamy
α
=
]OCB
=
]OBC
=
1
2
]AOC
=
60
◦
.
Odpowied´z: C
Materiał pobrany z serwisu
www.zadania.info
7
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
17
(1
PKT
)
Który wyraz ci ˛
agu
(
a
n
)
o wyrazie ogólnym a
n
=
3n
2
−
5
1
−
2n
2
jest równy
−
10
7
?
A) pi ˛
aty
B) dwudziesty pi ˛
aty
C) siódmy
D) dziewi ˛
aty
R
OZWI ˛
AZANIE
Liczymy
3n
2
−
5
1
−
2n
2
= −
10
7
/
·
7
(
1
−
2n
2
)
21n
2
−
35
= −
10
+
20n
2
n
2
=
25
⇒
n
=
5.
Odpowied´z: A
Z
ADANIE
18
(1
PKT
)
Poni ˙zej zamieszczono fragment tabeli warto´sci funkcji liniowej
x
1
2
4
f
(
x
)
4
1
W pustym miejscu w tabeli powinna znajdowa´c si˛e liczba:
A)
−
5
B) 5
C)
−
2
D) 2
R
OZWI ˛
AZANIE
Je ˙zeli f
(
x
) =
ax
+
b to wiemy, ˙ze
(
4
=
a
+
b
1
=
2a
+
b.
Odejmuj ˛
ac od drugiego równania pierwsze mamy a
= −
3. St ˛
ad b
=
4
−
a
=
7 i f
(
x
) =
−
3x
+
7. Zatem
f
(
4
) = −
12
+
7
= −
5.
Odpowied´z: A
Z
ADANIE
19
(1
PKT
)
Dany jest trójk ˛
at o wierzchołkach A
= (
4,
−
3
)
, B
= (
4, 1
)
, C
= (−
6,
−
2
)
. Długo´s´c ´srodkowej
poprowadzonej z wierzchołka C jest równa
A)
√
101
B)
√
102
C) 10
D)
√
10
Materiał pobrany z serwisu
www.zadania.info
8
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Zaczynamy od rysunku
x
4
y
6
3
0
-2
-3
A
-4
B
C
S
Liczymy współrz˛edne ´srodka odcinka AB
S
=
4
+
4
2
,
−
3
+
1
2
= (
4,
−
1
)
.
Obliczamy długo´s´c odcinka CS
|
CS
| =
q
(
4
+
6
)
2
+ (−
1
+
2
)
2
=
√
101.
Odpowied´z: A
Z
ADANIE
20
(1
PKT
)
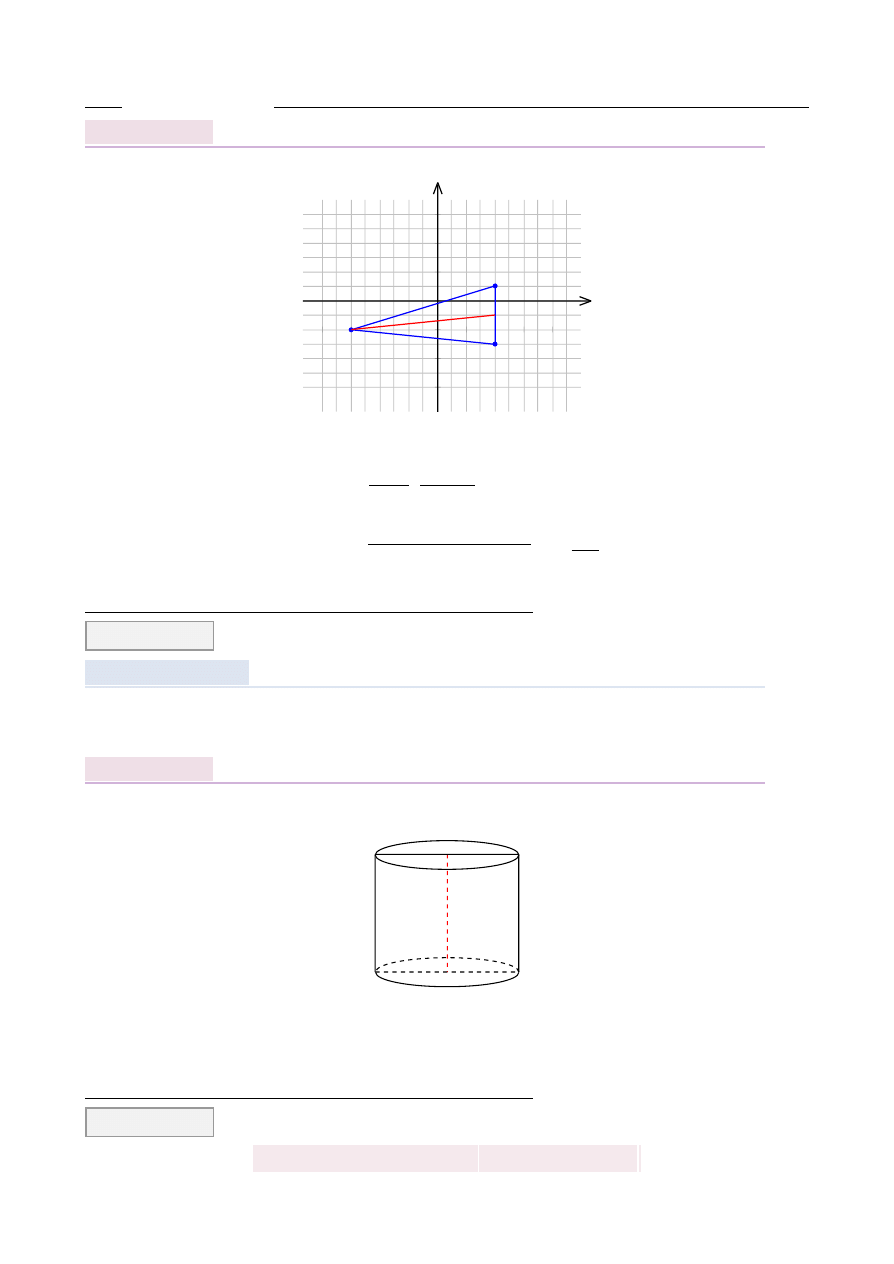
Prostok ˛
at o bokach 3 i 5 obracaj ˛
ac si˛e dookoła prostej zawieraj ˛
acej dłu ˙zszy bok wyznacza
brył˛e o obj˛eto´sci równej
A) 45π
B) 15π
C) 180π
D) 90π
R
OZWI ˛
AZANIE
Z obrazka wida´c, ˙ze w wyniku opisanej operacji otrzymamy walec o promieniu podstawy
r
=
3 i wysoko´sci H
=
5.
3
5
3
Zatem obj˛eto´s´c jest równa
V
=
πr
2
·
H
=
9π
·
5
=
45π.
Odpowied´z: A
Materiał pobrany z serwisu
www.zadania.info
9
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
21
(1
PKT
)
´Srednia arytmetyczna zestawu danych: 2, 3, x, 9, 4, 5, 1, 5 wynosi 4,5. Wynika z tego, ˙ze:
A) x
=
6
B) x
=
3
C) x
=
7
D) x
=
5
R
OZWI ˛
AZANIE
Liczymy
2
+
3
+
x
+
9
+
4
+
5
+
1
+
5
8
=
4, 5
/
·
8
29
+
x
=
36
x
=
7.
Odpowied´z: C
Z
ADANIE
22
(1
PKT
)
Prawdopodobie ´nstwo zdarzenia, ˙ze w rzucie dwiema symetrycznymi kostkami do gry otrzy-
mamy iloczyn oczek równy 4, wynosi
A)
1
4
B)
1
9
C)
1
12
D)
1
18
R
OZWI ˛
AZANIE
Wyniki rzutów b˛edziemy zapisywa´c jako pary
(
k, n
)
, gdzie k jest wynikiem na pierwszej
kostce, a n wynikiem na drugiej. Najpierw obliczamy ile jest zdarze ´n elementarnych
|
Ω
| =
6
·
6
=
36.
Wypiszmy zdarzenia sprzyjaj ˛
ace
(
1, 4
)
,
(
2, 2
)
,
(
4, 1
)
.
Zatem prawdopodobie ´nstwo wynosi
3
36
=
1
12
.
Odpowied´z: C
Z
ADANIE
23
(1
PKT
)
K ˛
at α jest ostry i cos α
=
√
3
3
. Wtedy warto´s´c wyra ˙zenia 2
−
sin
2
α
jest równa
A) 0
B)
2
3
C)
4
3
D) 1
Materiał pobrany z serwisu
www.zadania.info
10
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Na mocy jedynki trygonometrycznej
sin
2
α
+
cos
2
α
=
1
mamy
2
−
sin
2
α
=
2
− (
1
−
cos
2
α
) =
1
+
cos
2
α
=
1
+
1
3
=
4
3
.
Odpowied´z: C
Z
ADANIE
24
(1
PKT
)
Równania 9
−
5y
=
0 i 3x
+
7
=
0 opisuj ˛
a proste w układzie współrz˛ednych, które
A) s ˛
a prostopadłe
B) s ˛
a równoległe
C) przecinaj ˛
a si˛e pod k ˛
atem 60
◦
D) przecinaj ˛
a si˛e pod k ˛
atem 45
◦
R
OZWI ˛
AZANIE
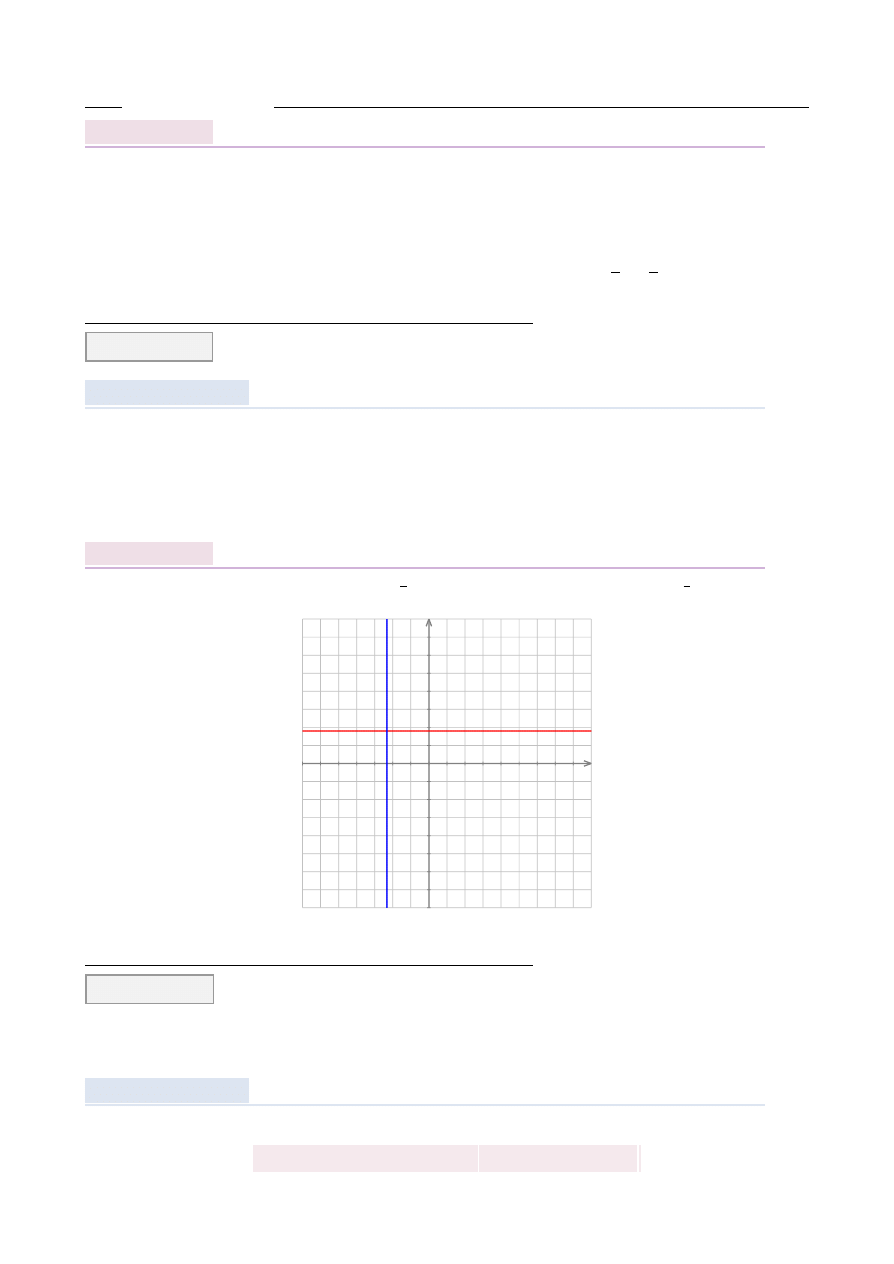
Pierwsza prosta to pozioma prosta y
=
9
5
, a druga to pionowa prosta x
= −
7
3
.
-5
-1
+5
x
-5
-1
+1
+5
y
Proste te s ˛
a wi˛ec prostopadłe.
Odpowied´z: A
Zadania otwarte
Z
ADANIE
25
(2
PKT
)
Rozwi ˛
a ˙z równanie 6x
3
−
8x
2
−
9x
+
12
=
0.
Materiał pobrany z serwisu
www.zadania.info
11
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Gdy si˛e przyjrzymy równaniu to mo ˙zna zauwa ˙zy´c, ˙ze mo ˙zemy łatwo wył ˛
aczy´c
(
3x
−
4
)
przed nawias.
6x
3
−
8x
2
−
9x
+
12
=
0
2x
2
(
3x
−
4
) −
3
(
3x
−
4
) =
0
(
2x
2
−
3
)(
3x
−
4
) =
0
6
x
−
r
3
2
!
x
+
r
3
2
!
x
−
4
3
=
0.
Zatem x
∈
n
−
√
6
2
,
√
6
2
,
4
3
o
.
Odpowied´z: x
∈
n
−
√
6
2
,
√
6
2
,
4
3
o
Z
ADANIE
26
(2
PKT
)
Oblicz warto´s´c wyra ˙zenia 2 sin
2
α
+
1
−
tg
2
α
1
+
tg
2
α
, gdzie α jest k ˛
atem ostrym.
R
OZWI ˛
AZANIE
Skorzystamy z definicji tangensa
tg α
=
sin α
cos α
i jedynki trygonometrycznej
sin
2
α
+
cos
2
α
=
1.
Liczymy
2 sin
2
α
+
1
−
tg
2
α
1
+
tg
2
α
=
2 sin
2
α
+
1
−
sin
2
α
cos
2
α
1
+
sin
2
α
cos
2
α
=
=
2 sin
2
α
+
cos
2
α
−
sin
2
α
cos
2
α
+
sin
2
α
=
2 sin
2
α
+
cos
2
α
−
sin
2
α
=
=
sin
2
α
+
cos
2
α
=
1.
Odpowied´z: 1
Z
ADANIE
27
(2
PKT
)
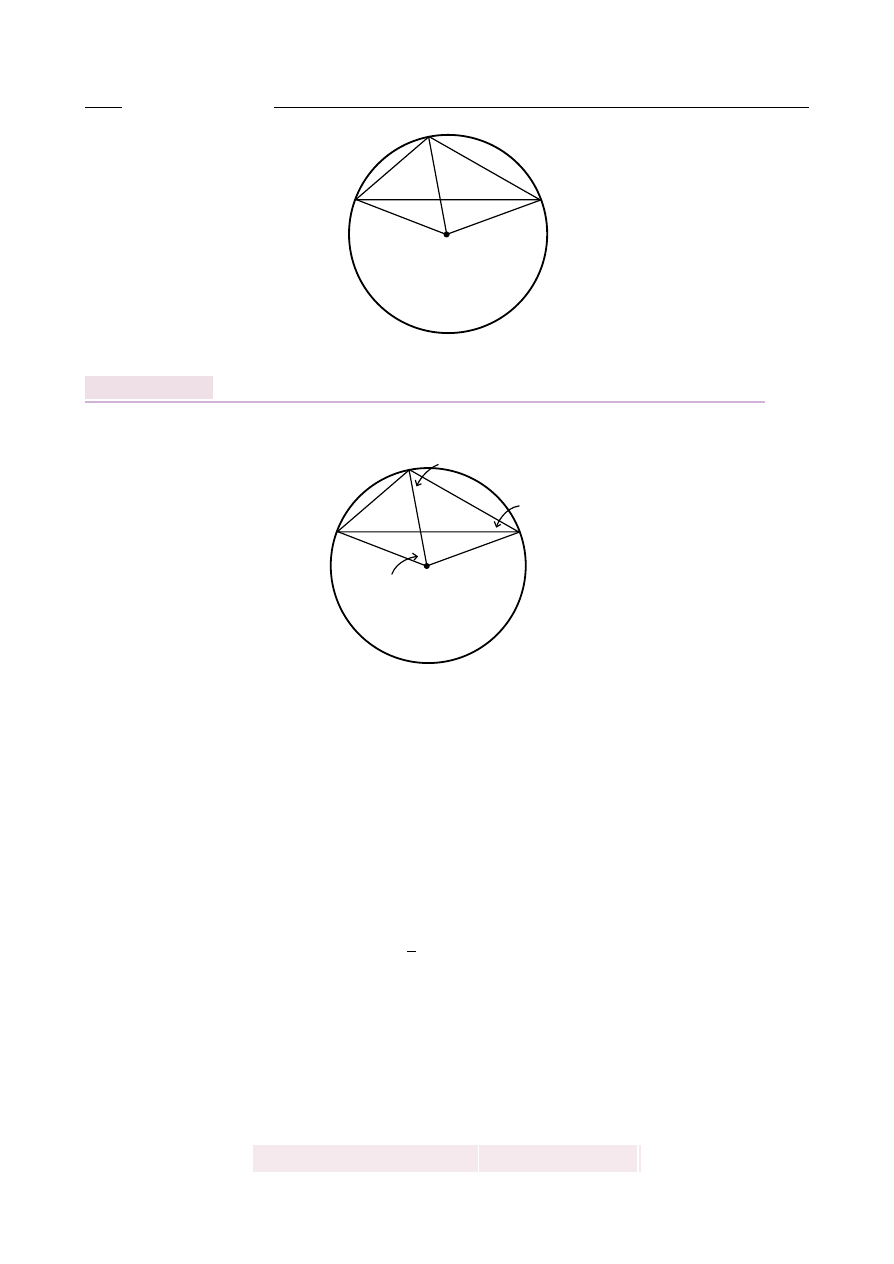
Punkt S jest ´srodkiem okr˛egu opisanego na trójk ˛
acie rozwartok ˛
atnym ABC. K ˛
at CAB jest
dwa razy wi˛ekszy od k ˛
ata BAS, a k ˛
at CBA jest o 10
◦
wi˛ekszy od k ˛
ata BAS. Oblicz k ˛
aty
trójk ˛
ata ABC.
Materiał pobrany z serwisu
www.zadania.info
12
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
A
B
C
S
R
OZWI ˛
AZANIE
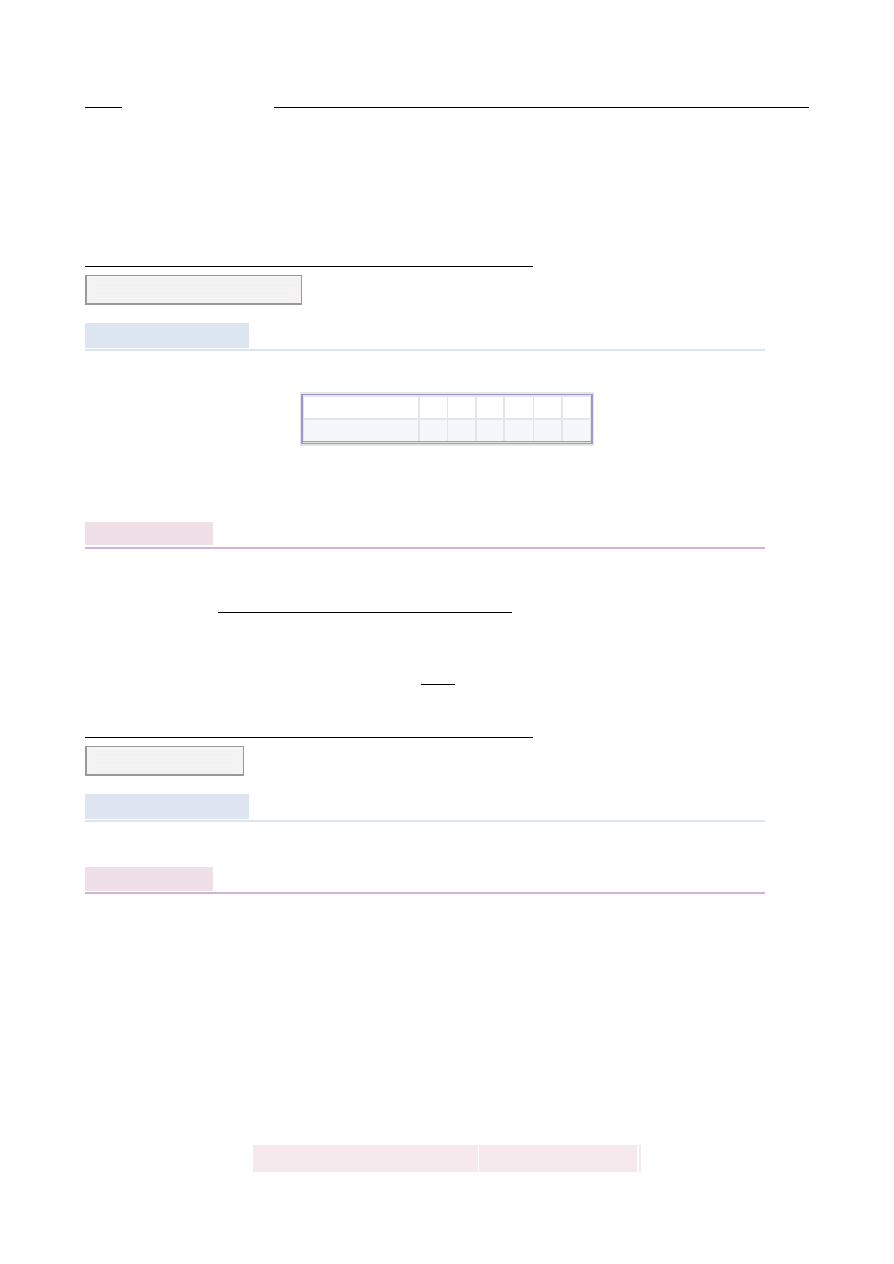
Oznaczmy α
=
]BAS.
α
A
B
C
S
α
2α
3α
180
o
-6α
90
o
-3α
90
o
-2α
Trójk ˛
aty ABS, BSC i ASC s ˛
a równoramienne, wi˛ec z podanych informacji mamy
]ABS
=
]BAS
=
α
]CAB
=
2α
]ACS
=
]CAS
=
3α.
Suma k ˛
atów trójk ˛
ata ASC jest równa 180
◦
, wi˛ec
]ASC
=
180
◦
−
6α.
Teraz korzystamy z własno´sci k ˛
atów wpisanych i ´srodkowych opisanych na tym samym
łuku.
]ABC
=
1
2
]ASC
=
90
◦
−
3α.
Trójk ˛
at CSB jest równoramienny, wi˛ec
]SCB
=
]SBC
=
90
◦
−
2α.
Z drugiej strony wiemy, ˙ze ]CBA
=
α
+
10
◦
. Mamy zatem
90
◦
−
3α
=
α
+
10
◦
80
◦
=
4α
⇒
α
=
20
◦
.
Materiał pobrany z serwisu
www.zadania.info
13
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
W takim razie k ˛
aty trójk ˛
ata ABC maj ˛
a miary
]A
=
2α
=
40
◦
]B
=
90
◦
−
3α
=
30
◦
]C
=
90
◦
+
α
=
110
◦
.
Odpowied´z: 40
◦
, 30
◦
, 110
◦
Z
ADANIE
28
(2
PKT
)
W tabeli przedstawiono oceny ze sprawdzianu z matematyki w klasie 1B.
Ocena
1
2
3
4
5
6
Liczba ocen
3
3
6
x
4
2
´Srednia arytmetyczna tych ocen jest równa 3,48. Oblicz liczb˛e x ocen dobrych (4) otrzyma-
nych przez uczniów na tym sprawdzianie.
R
OZWI ˛
AZANIE
Wszystkich ocen jest 3
+
3
+
6
+
x
+
4
+
2
=
x
+
18, wi˛ec z podanej ´sredniej mamy równanie
1
·
3
+
2
·
3
+
3
·
6
+
4
·
x
+
5
·
4
+
6
·
2
x
+
18
=
3, 48
/
· (
x
+
18
)
3
+
6
+
18
+
4x
+
20
+
12
=
3, 48x
+
62, 64
0, 52x
=
3, 64
⇒
x
=
3, 64
0, 52
=
7.
Odpowied´z: x
=
7
Z
ADANIE
29
(2
PKT
)
Wyka ˙z, ˙ze 7
16
−
1 jest liczb ˛
a podzieln ˛
a przez 2
7
.
R
OZWI ˛
AZANIE
Korzystamy ze wzoru a
2
−
b
2
= (
a
−
b
)(
a
+
b
)
7
16
−
1
= (
7
8
−
1
)(
7
8
+
1
) = (
7
4
−
1
)(
7
4
+
1
)(
7
8
+
1
) =
= (
7
2
−
1
)(
7
2
+
1
)(
7
4
+
1
)(
7
8
+
1
) =
=
48
(
7
2
+
1
)(
7
4
+
1
)(
7
8
+
1
)
.
Zauwa ˙zmy teraz, ˙ze 48 dzieli si˛e przez 2
4
=
16, a liczby w pozostałych nawiasach to liczby
parzyste. Zatem 7
16
−
1 jest liczb ˛
a podzieln ˛
a przez
2
4
·
2
·
2
·
2
=
2
7
.
Materiał pobrany z serwisu
www.zadania.info
14
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
30
(2
PKT
)
Wyka ˙z, ˙ze je ˙zeli a
>
1, to
a
4
+
a
2
+
1
2
>
a
3
−
1
a
2
−
1
.
R
OZWI ˛
AZANIE
Przekształcamy równowa ˙znie dan ˛
a nierówno´s´c
a
4
+
a
2
+
1
2
>
a
3
−
1
a
2
−
1
/
·
2
(
a
2
−
1
)
(
a
4
+
a
2
+
1
)(
a
2
−
1
)
> 2a
3
−
2
a
6
+
a
4
+
a
2
−
a
4
−
a
2
−
1 > 2a
3
−
2
a
6
−
2a
3
+
1 > 0
(
a
3
−
1
)
2
> 0.
Otrzymana nierówno´s´c jest oczywi´scie spełniona, a przekształcali´smy przy pomocy równo-
wa ˙zno´sci, wi˛ec wyj´sciowa nierówno´s´c równie ˙z musi by´c prawdziwa.
Z
ADANIE
31
(4
PKT
)
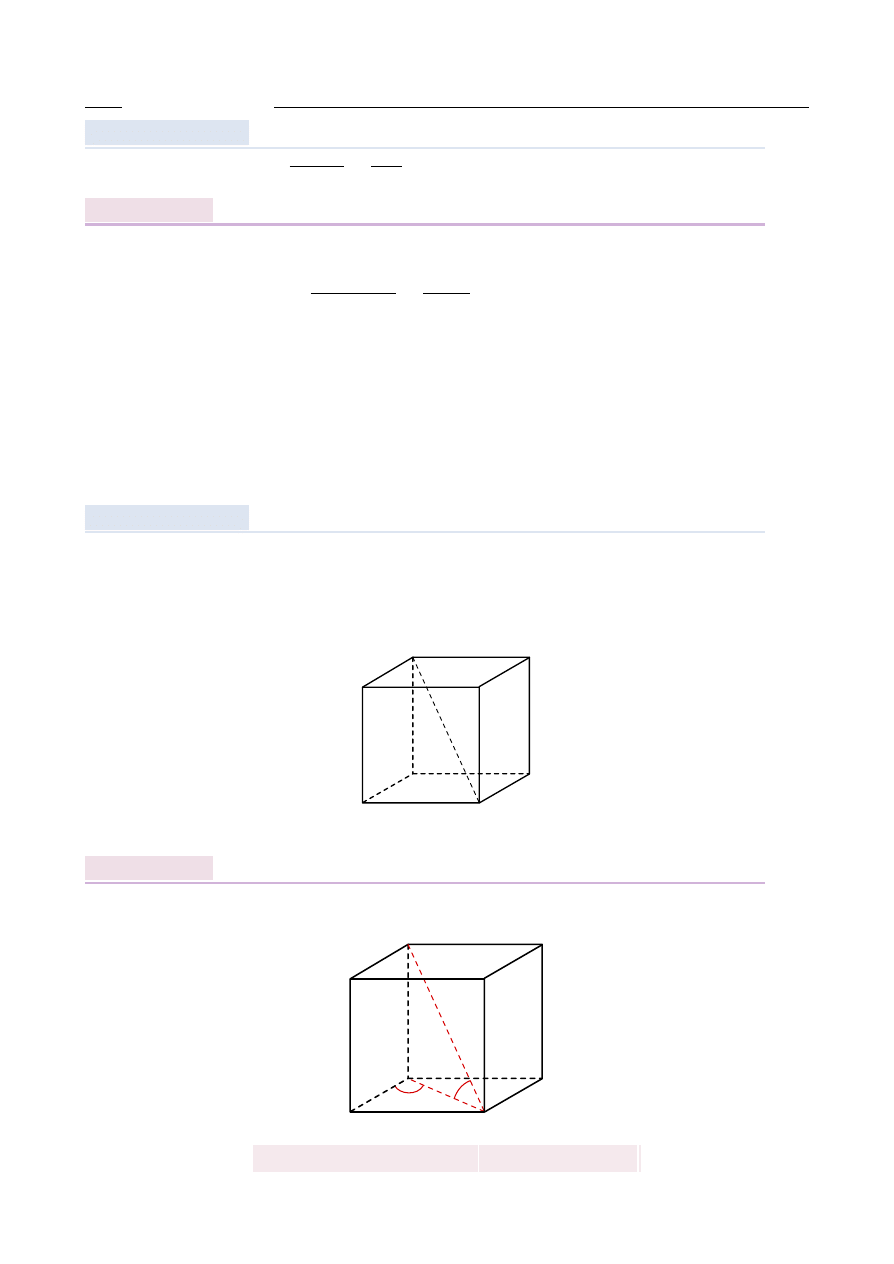
Podstaw ˛
a graniastosłupa ABCDEFGH jest prostok ˛
at ABCD (zobacz rysunek), którego dłu ˙z-
szy bok ma długo´s´c 6. Przek ˛
atna prostok ˛
ata ABCD tworzy z jego krótszym bokiem k ˛
at 60
◦
.
Przek ˛
atna HB graniastosłupa tworzy z płaszczyzn ˛
a jego podstawy k ˛
at 45
◦
stopni. Oblicz
obj˛eto´s´c tego graniastosłupa.
A
B
C
D
E
F
G
H
R
OZWI ˛
AZANIE
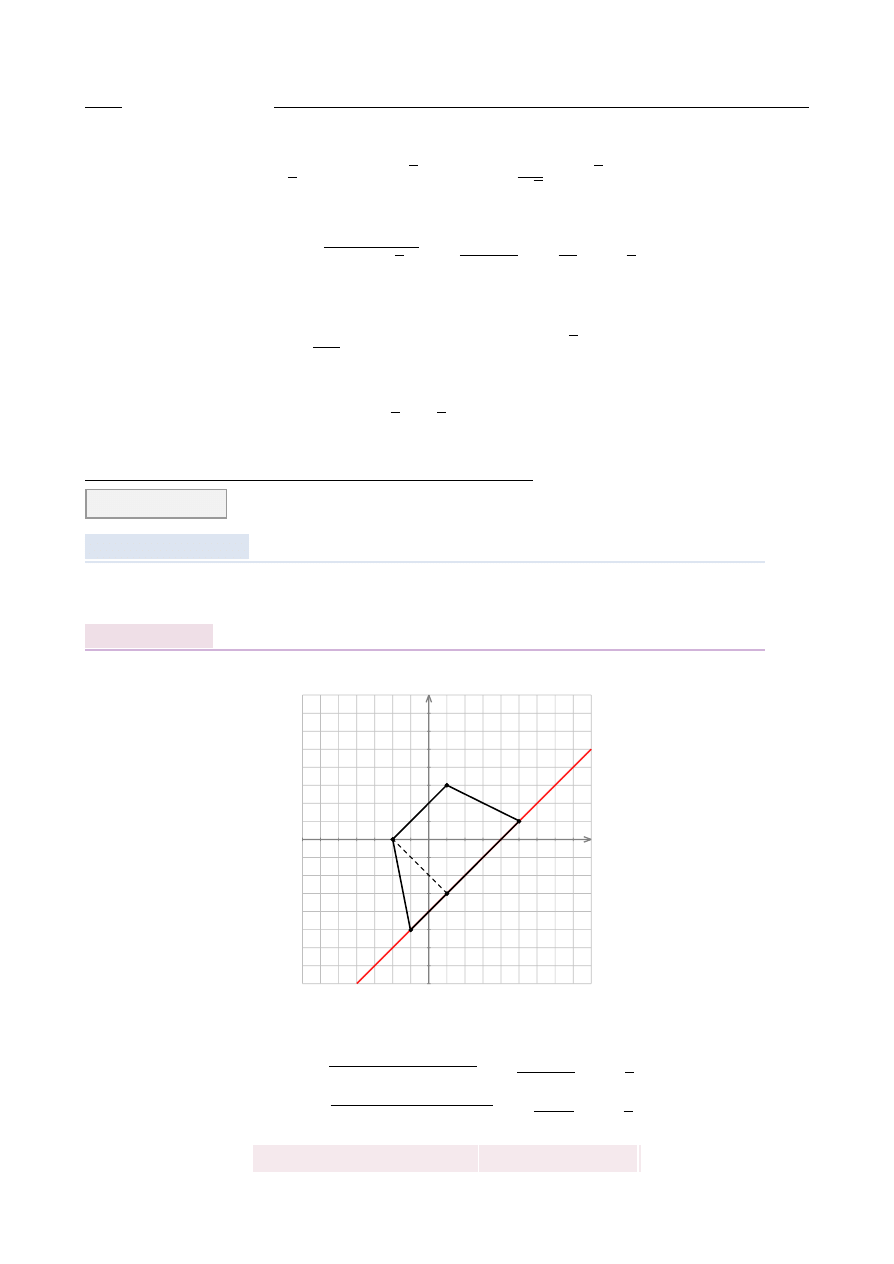
Zacznijmy od zaznaczenia na rysunku podanych k ˛
atów.
A
B
C
D
E
F
G
H
6
6
60
o
45
o
a
h
h
a
Materiał pobrany z serwisu
www.zadania.info
15
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z trójk ˛
ata prostok ˛
atnego ABD obliczamy długo´s´c a drugiej kraw˛edzi podstawy.
6
a
=
tg 60
◦
=
√
3
⇒
a
=
6
√
3
=
2
√
3.
Obliczmy jeszcze długo´s´c przek ˛
atnej podstawy
DB
=
q
6
2
+ (
2
√
3
)
2
=
√
36
+
12
=
√
48
=
4
√
3.
Z trójk ˛
ata prostok ˛
atnego DBH obliczamy długo´s´c wysoko´sci graniastosłupa.
h
DB
=
tg 45
◦
=
1
⇒
h
=
4
√
3.
Pozostało obliczy´c obj˛eto´s´c graniastosłupa.
V
=
6
·
2
√
3
·
4
√
3
=
12
·
4
·
3
=
144.
Odpowied´z: 144
Z
ADANIE
32
(5
PKT
)
Punkty A
= (−
1,
−
5
)
, B
= (
5, 1
)
, C
= (
1, 3
)
, D
= (−
2, 0
)
s ˛
a kolejnymi wierzchołkami
trapezu ABCD. Oblicz pole tego trapezu.
R
OZWI ˛
AZANIE
Rozpoczynamy oczywi´scie od szkicowego rysunku.
-5
-1
+5
x
-5
-1
+1
+5
y
A
C
D
h
B
E
Aby obliczy´c pole trapezu musimy zna´c długo´sci jego podstaw oraz długo´s´c wysoko´sci.
Długo´sci podstaw łatwo obliczy´c.
AB
=
q
(
5
+
1
)
2
+ (
1
+
5
)
2
=
√
36
+
36
=
6
√
2
CD
=
q
(−
2
−
1
)
2
+ (
0
−
3
)
2
=
√
9
+
9
=
3
√
2.
Materiał pobrany z serwisu
www.zadania.info
16
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Napiszmy teraz równanie prostej AB. Szukamy prostej w postaci y
=
ax
+
b. Podstawiamy
współrz˛edne punktów A i B.
(
−
5
= −
a
+
b
1
=
5a
+
b.
Odejmujemy od drugiego równania pierwsze i mamy 6a
=
6, czyli a
=
1. St ˛
ad b
= −
5
+
a
=
−
4 i prosta AB ma równanie: y
=
x
−
4.
Dalsz ˛
a cz˛e´s´c rozwi ˛
azania poprowadzimy na dwa sposoby.
Sposób I
Wysoko´s´c trapezu mo ˙zemy łatwo obliczy´c ze wzoru na odległo´s´c punktu P
= (
x
0
, y
0
)
od
prostej Ax
+
By
+
C
=
0:
|
Ax
0
+
By
0
+
C
|
√
A
2
+
B
2
.
W naszej sytuacji mamy P
=
D
= (−
2, 0
)
, a prosta to: x
−
y
−
4
=
0. Mamy zatem
h
=
| −
2
−
4
|
√
1
+
1
=
6
√
2
.
Pole trapezu jest wi˛ec równe
P
=
AB
+
CD
2
·
h
=
6
√
2
+
3
√
2
2
·
6
√
2
=
27.
Sposób II
Je ˙zeli kto´s nie chce korzysta´c ze wzoru na odległo´s´c punktu od prostej, to wysoko´s´c trapezu
mo ˙zemy wyznaczy´c bardziej wprost, wyznaczaj ˛
ac równanie wysoko´sci DE opuszczonej z
wierzchołka D na bok AB.
Prosta DE jest prostopadła do prostej AB, wi˛ec ma równanie postaci y
= −
x
+
b. Współ-
czynnik b wyznaczamy podstawiaj ˛
ac współrz˛edne punktu D.
0
=
2
+
b
⇒
b
= −
2.
Szukamy teraz punku wspólnego prostych AB i DE.
(
y
=
x
−
4
y
= −
x
−
2.
Odejmuj ˛
ac od pierwszego równania drugie ( ˙zeby skróci´c y), mamy 0
=
2x
−
2, czyli x
=
1 i
y
=
x
−
4
= −
3. Zatem E
= (
1,
−
3
)
i
h
=
DE
=
q
(
1
+
2
)
2
+ (−
3
−
0
)
2
=
√
9
+
9
=
3
√
2.
Pole trapezu jest równe
P
=
AB
+
CD
2
·
h
=
6
√
2
+
3
√
2
2
·
3
√
2
=
27.
Odpowied´z: 27
Materiał pobrany z serwisu
www.zadania.info
17
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
33
(5
PKT
)
Pole ka ˙zdej z dwóch prostok ˛
atnych działek jest równe 2400 m
2
. Szeroko´s´c pierwszej działki
jest o 8 m wi˛eksza od szeroko´sci drugiej, ale jej długo´s´c jest o 10 m mniejsza. Oblicz szeroko´s´c
i długo´s´c ka ˙zdej z działek.
R
OZWI ˛
AZANIE
Niech x oznacza szeroko´s´c pierwszej działki, a y jej długo´s´c. W takim razie druga działka
ma szeroko´s´c x
−
8 i długo´s´c y
+
10. Podane pola powierzchni daj ˛
a układ równa ´n.
(
xy
=
2400
(
x
−
8
)(
y
+
10
) =
2400.
Podstawmy y
=
2400
x
z pierwszego równania do drugiego.
(
x
−
8
)
2400
x
+
10
=
2400
/
·
x
10
(
x
−
8
)(
240
+
x
) =
240x
240x
+
x
2
−
1920
−
8x
=
240x
x
2
−
8x
−
1920
=
0
∆
=
64
+
7680
=
7744
=
88
2
x
=
8
−
88
2
<
0
∨
x
=
8
+
88
2
=
48.
Ujemne rozwi ˛
azanie odrzucamy i mamy x
=
48. St ˛
ad y
=
2400
x
=
50. Druga działka ma
wymiary x
−
8
=
40 i y
+
10
=
60.
Odpowied´z: 48 m
×
50 m oraz 40 m
×
60 m
Materiał pobrany z serwisu
www.zadania.info
18