39

INTERFERENCJA ŚWIATŁA SIATKA DYFRAKCYJNA

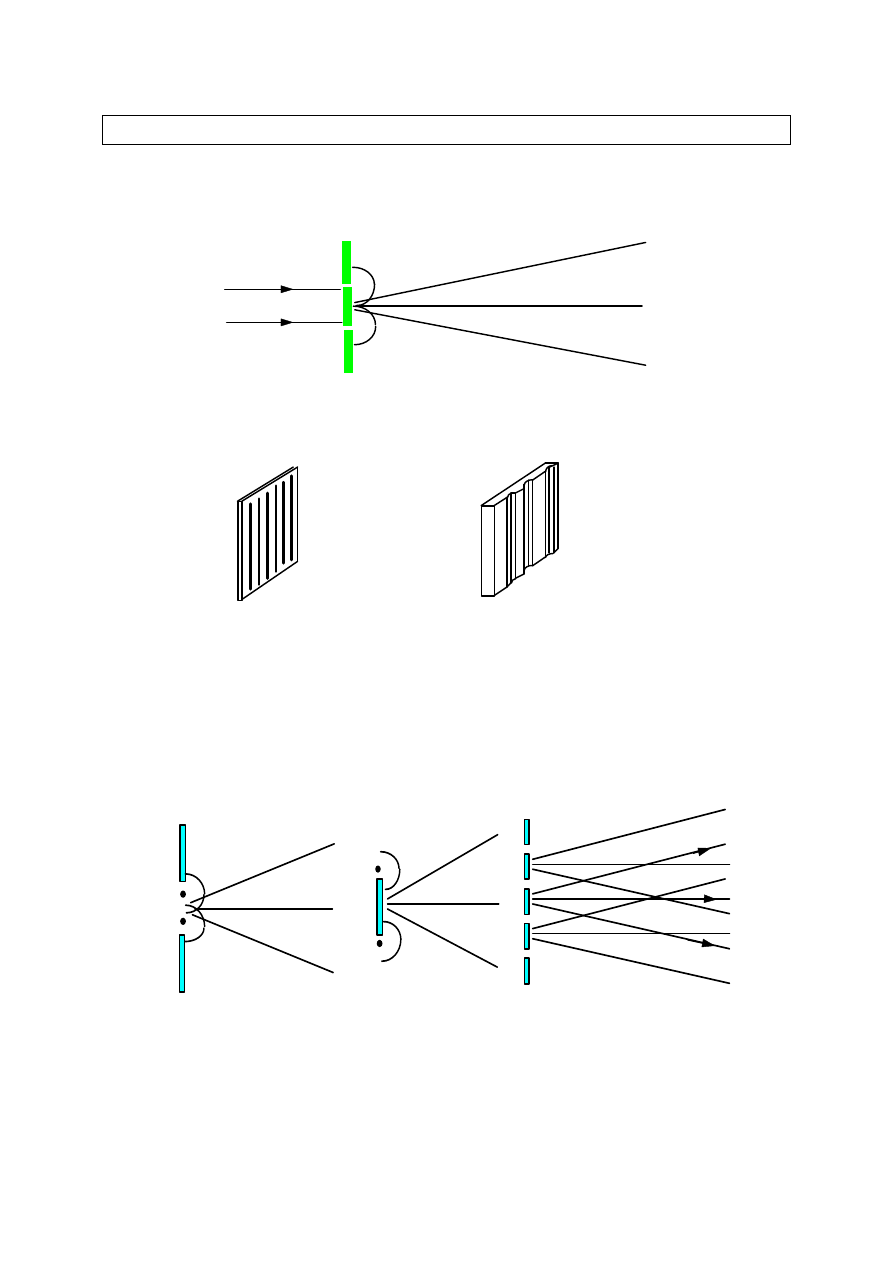
W wyniku nałożenia się fal o jednakowych okresach powstają charakterystyczne
maksima interferencyjne.

Wzmocnienie ma miejsce na takich kierunkach, na których różnica dróg

przebytych przez fale stanowi wielokrotność długości fal. Kształt maksimów
interferencyjnych jest niezależny od tego, czy nakładające się fale są
wytworzone przez dwie szczeliny, punkty brzegowe jednej szczeliny, punkty
brzegowe przeszkody, czy układ regularnie rozmieszczonych szczelin.
Wyraźnie widoczne maksima powstają wtedy, gdy odległość sąsiednich źródeł
fal cząstkowych jest porównywalna z długością fali. Długość fali świetlnej jest
rzędu 10

-7

m. Przez dwie szczeliny ustawione w takiej odległości, których

szerokość jest tego samego rzędu, przechodzi niewiele światła i obraz
interferencyjny jest ciemny. Aby uzyskać jasny obraz interferencyjny stosuje się
tzw. siatki dyfrakcyjne .

siatka wykonana

siatka wykonana

metodą fotogra-

mechanicznie

ficzną

40

Najprostsza siatka dyfrakcyjna, to klisza fotograficzna o dużej rozdzielczości, na
której uzyskano szereg równoległych linii, na przemian ciemnych i jasnych.
Przeciętnie na jednym milimetrze szerokości siatki jest około 200 takich linii.
Siatka wykonana mechanicznie to płytka szklana, na której wykonano
diamentem szereg równoległych rys około 200 na milimetr szerokości siatki.
Rysy, względnie ciemne linie na siatce wykonanej metodą fotograficzną
stanowią zasłony, między którymi są szczeliny przepuszczające światło.

Ś

wiatło tworzące wiązkę o szerokości rzędu milimetra przechodzi przez setki

szczelin siatki dyfrakcyjnej, w wyniku czego wiązka światła rozdziela się na
szereg wiązek tworzących poszczególne maksima.

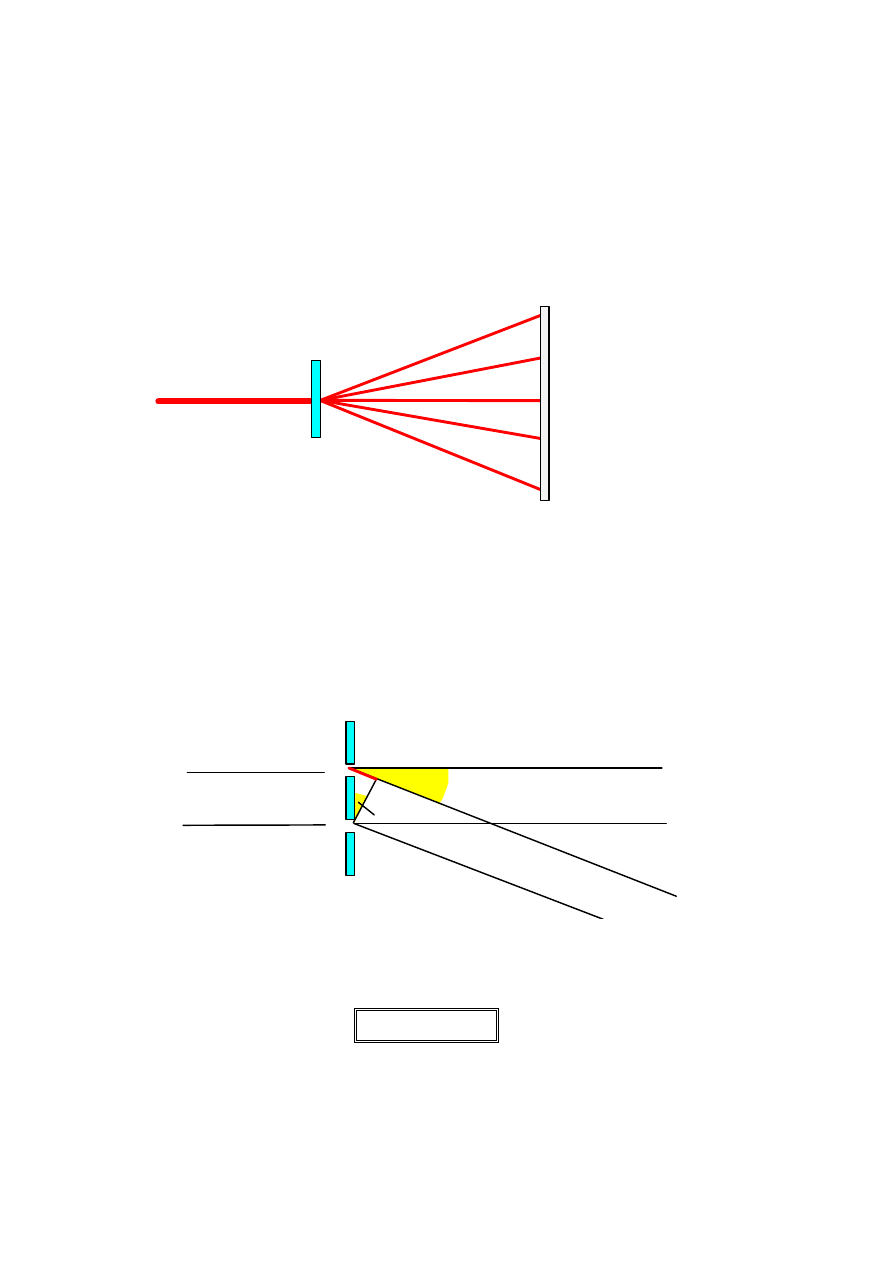
Jeśli na kierunku tworzącym kąt

α

n

z kierunkiem wiązki zerowego rzędu

powstaje maksimum n - tego rzędu, to różnica dróg przebytych przez fale
cząstkowe pochodzące z sąsiadujących szczelin wynosi :

∆

∆

∆

∆

x = d sin

αααα

n

d - stała siatki

Korzystając z warunku interferencyjnego wzmocnienia otrzymujemy:

Z powyższej zależności wynika, że dla światła o różnej długości fali maksima
tego samego rzędu wypadają na różnych kierunkach.

0

ekran, na którym są
widoczne maksima
interferencyjne różnych
rzędów

II

II

I

I

siatka

wiązka światła
padająca na
siatkę

∆

X

α

n

α

n

d

n

λ =

λ =

λ =

λ =

d sin

αααα

n

41

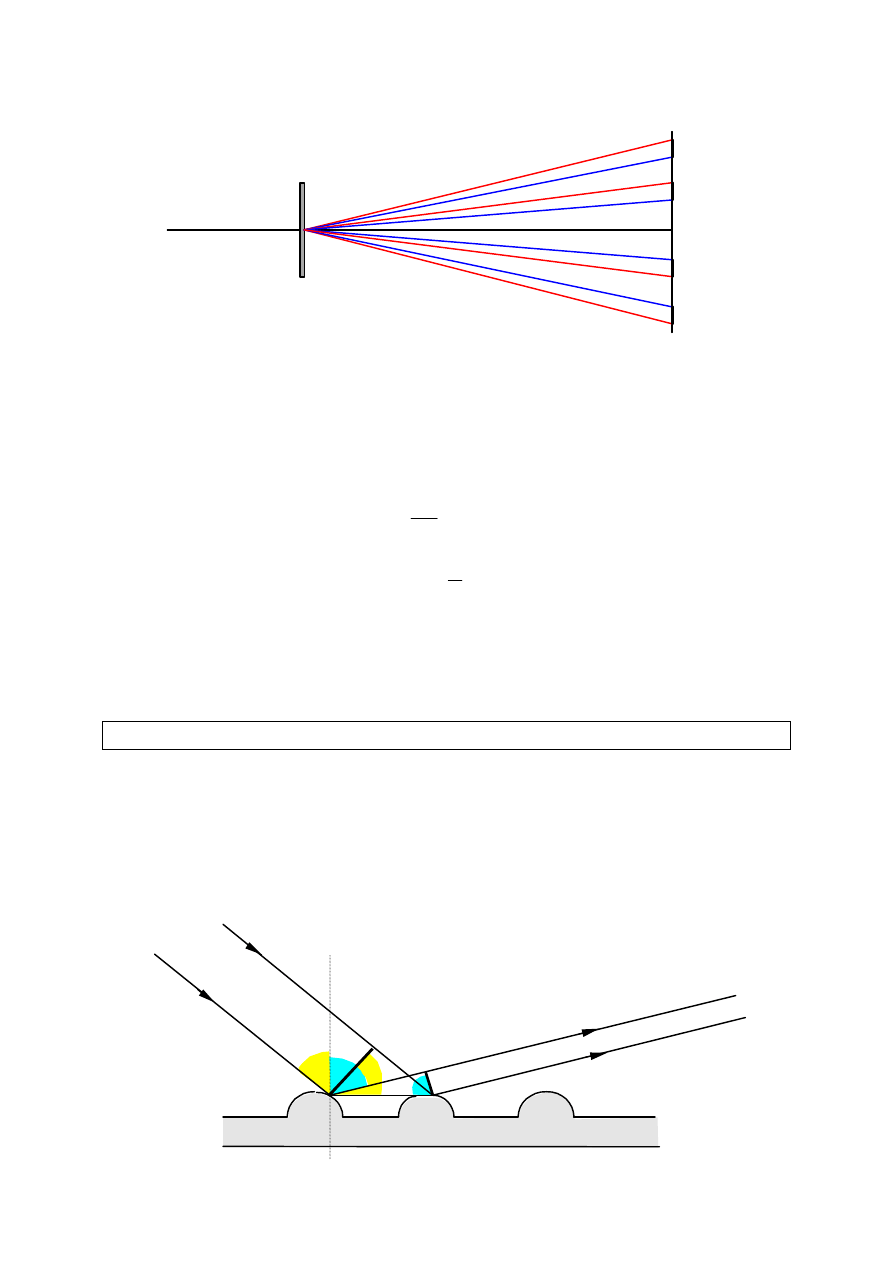
Siatka dyfrakcyjna rozszczepia światło, przy czym promienie o większej
długości fali są bardziej odchylone. Każda siatka daje ściśle określoną ilość
rzędów widma, bowiem kąt odchylenia maksimum ostatniego rzędu nie może
być większy od 90

0

.

sin

α

α

α

α

n

∠

∠

∠

∠

1

n

d

λλλλ ∠∠∠∠

1

λλλλ

<<<<

d

n

Największa liczba naturalna spełniająca powyższy warunek określa
maksymalny rząd widma, jaki można otrzymać przy użyciu danej siatki,
przyjmując że promienie padają na siatkę prostopadle.

ODBICIOWA SIATKA DYFRAKCYJNA

Ś

wiatło odbite od powierzchni płyty kompaktowej mieni się barwami tęczy.

Podobne efekty można obserwować przy odbiciu światła od każdej powierzchni
pokrytej drobnymi, regularnymi rowkami. Przyczyną tego zjawiska jest
interferencja światła.

Promienie padają na rozpatrywaną powierzchnię pod kątem

αααα

,

a po odbiciu

λλλλ

2222

>>>> λ

λ

λ

λ

1

1

1

1

λλλλ

1111

ο

ο

ο

ο

λλλλ

1111

λλλλ

2

2

2

2

>>>> λ

λ

λ

λ

1

1

1

1

C

αααα α

α

α

α

D

d

Β

ΒΒ

Β

Α

Α

Α

Α

ββββ

ββββ

42

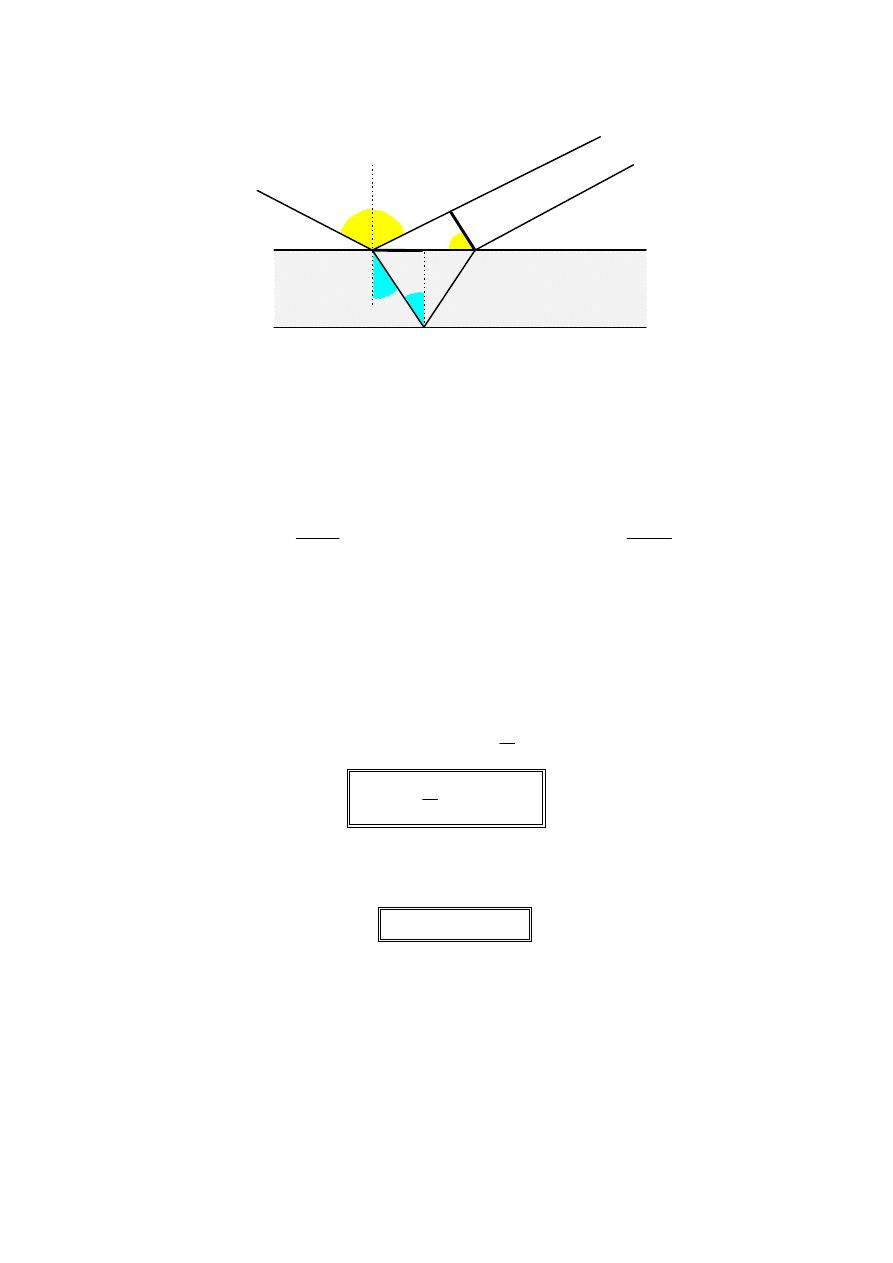
rozchodzą się pod kątem

ββββ

. Różnica dróg przebytych przez te promienie

wynosi:

∆

∆

∆

∆

x = A D - C B

∆

∆

∆

∆

x = d sin

- d sin

αααα

∆∆∆∆

x = d (

sin

β

β

β

β

- sin

α )

α )

α )

α )

Ś

wiatło po odbiciu ulega wzmocnieniu jeśli jest spełniony warunek:

∆

∆

∆

∆

x = k

λλλλ

; k

∈

∈

∈

∈

C

k

λ =

λ =

λ =

λ =

d ( sin

β −

β −

β −

β −

sin

α )

α )

α )

α )

INTERFERENCJA

Ś

WIATŁA W CIENKICH BŁONKACH

Bańki mydlane są kolorowe. Kolorowe są również plamy oleju na wodzie
.Przyczyną tego zjawiska jest interferencja światła odbitego, względnie
przechodzącego przez cienkie warstwy różnych ośrodków.

Jeśli fala przechodzi z jednego ośrodka
do drugiego, to zmianie prędkości
towarzyszy analogiczna zmiana długości
fali.

n

C

V

====

====

λλλλ

λλλλ

0

Zmiana fazy fali świetlnej po przebyciu

w próżni pewnej drogi jest taka sama, jak przy przebyciu w ośrodku o
współczynniku załamania

n

, drogi

n

razy mniejszej. Iloczyn drogi

geometrycznej i współczynnika załamania nazywamy drogą optyczną.
Podczas odbicia fali świetlnej od granicy z ośrodkiem optycznie gęstszym
(o większym współczynniku załamania) następuje odwrócenie fazy fali, co

odpowiada różnicy dróg

λλλλ

2

.Zjawiska tego nie ma przy odbiciu od granicy z

ośrodkiem rzadszym (o mniejszym współczynniku załamania).

43

C = d tg

ββββ

a = 2 C sin

αααα

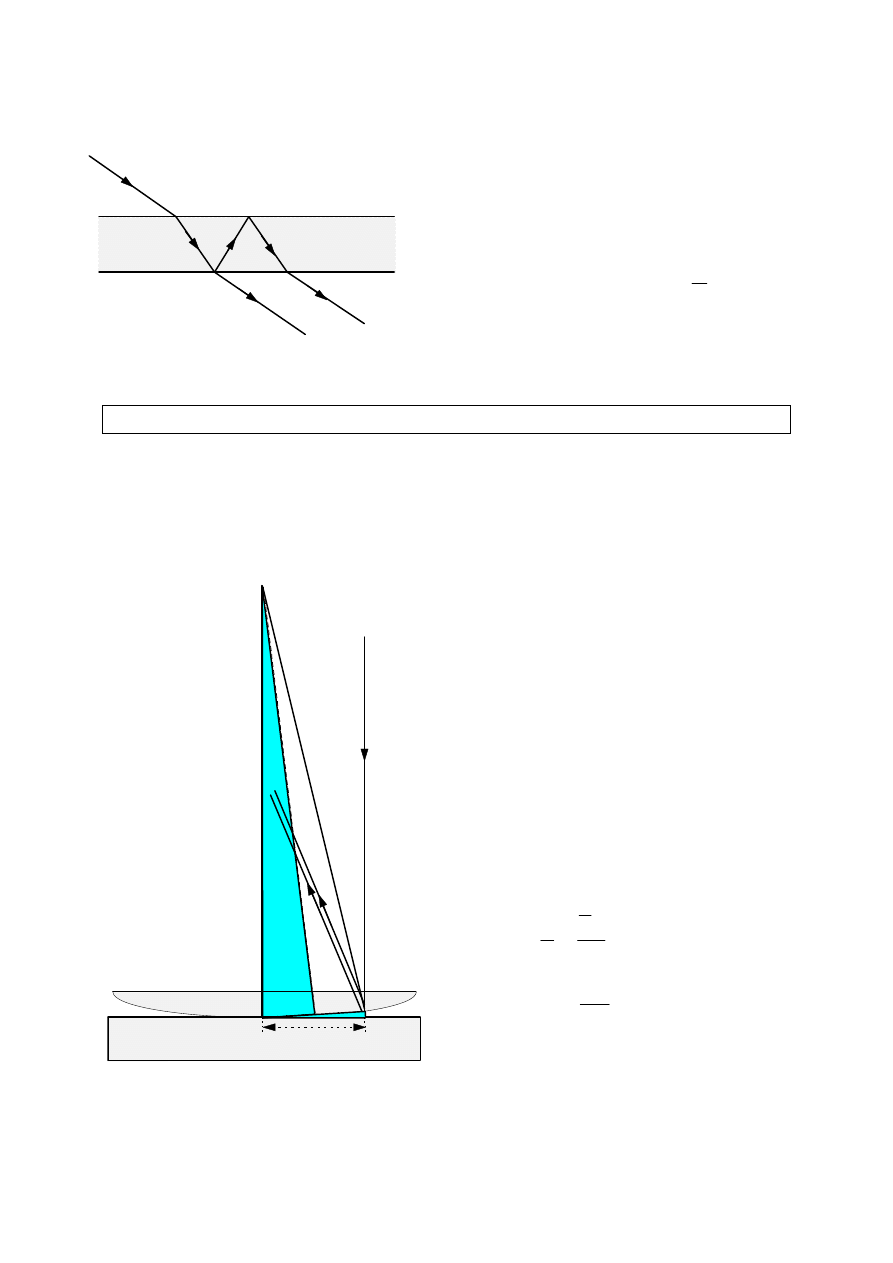
Jeśli część światła odbija się od górnej powierzchni błonki, a część - od dolnej,
to różnica dróg optycznych dla obu promieni wynosi:

∆

∆

∆

∆

X = 2 b n - a

∆∆∆∆

X

n

d

dtg

====

−−−−

2

2

cos

sin

ββββ

ββββ

αααα

;

n

====

sin

sin

αααα

ββββ

∆∆∆∆

X = 2 d n cos

ββββ

Uwzględniając fakt, że przy odbiciu światła od górnej powierzchni warstwy
następuje odwrócenie fazy fali, warunkiem wzmocnienia dla promieni odbitych
od różnych powierzchni warstwy odbijającej jest:

((((

))))

∆∆∆∆

X

k

====

++++

2

1

2

λλλλ

((((

))))

2

1

2

2

k

dn

++++

====

λλλλ

ββββ

cos

Warunkiem wygaszenia promieni odbitych jest:

Analogicznie można wykazać, że dla promieni przechodzących przez warstwę
warunki wzmocnienia i wygaszenia przyjmują postać:

α α

α α

α α

α α

a

c c

αααα

β

β

β

β

d

n

b

k

λ =

λ =

λ =

λ =

2dn cos

ββββ

44

2 d n cos

β =

β =

β =

β =

k

λ

λ

λ

λ

wzmocnienie

((((

))))

2

2

1

2

dn

k

cos

ββββ

λλλλ

====

++++

wygaszenie

PIERŚCIENIE NEWTONA

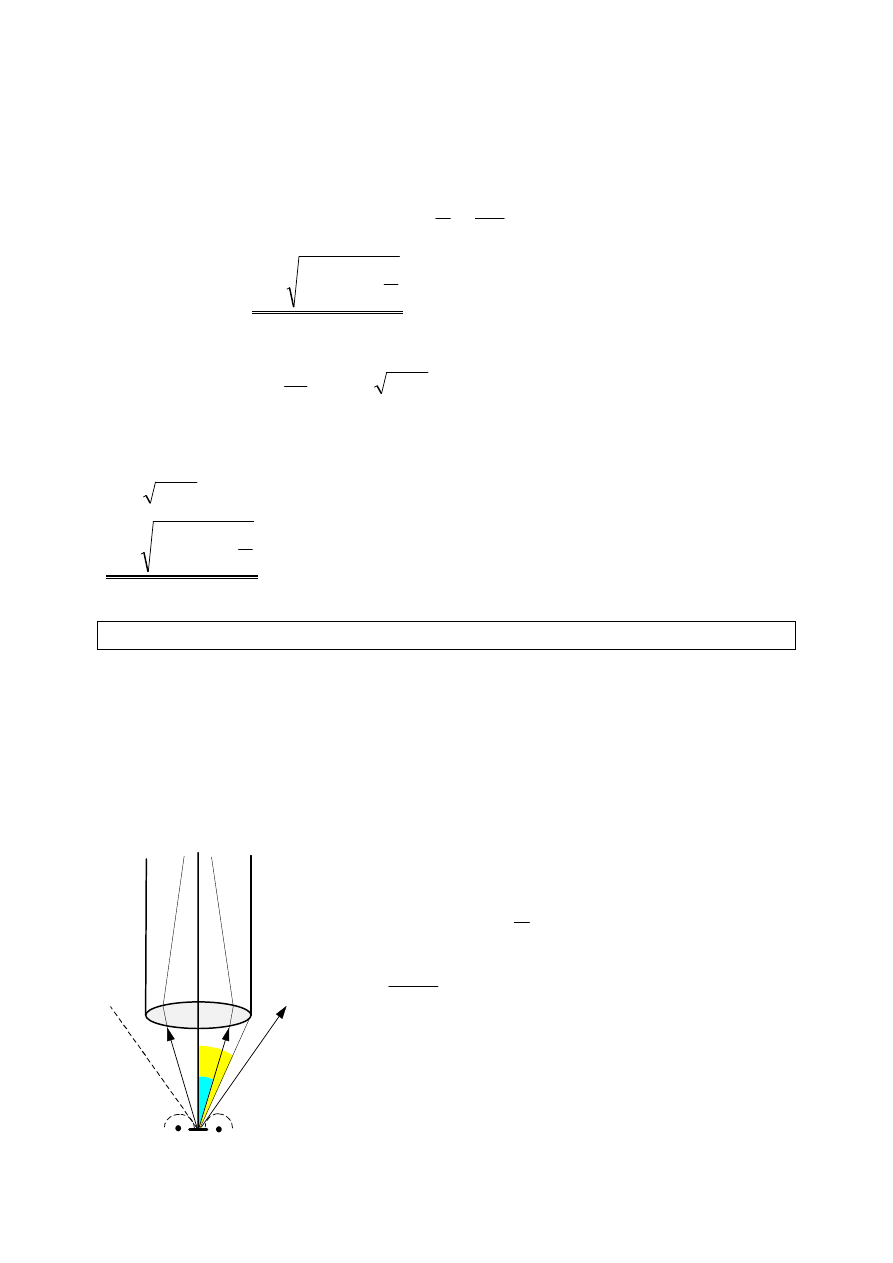
Na płytce szklanej P spoczywa szklana soczewka S. Promień światła pada na
płaską stronę soczewki. Część tego promienia odbija się od wewnętrznej,
wypukłej powierzchni soczewki. Druga część tego promienia ulega odbiciu od
powierzchni szklanej płytki. Następuje przy tym odwrócenie fazy fali. Ta część
promienia przechodzi ponownie przez soczewkę. Obydwa promienie po wyjściu

z soczewki interferują. O efektach
interferencji

decyduje

różnica

dróg

optycznych. Przyjmując, że soczewka ma
znaczny

promień

krzywizny,

a

rozpatrywany promień pada na soczewkę
blisko jej środka, to różnica dróg
przebytych przez poszczególne promienie
jest równa 2d, gdzie d - szerokość
szczeliny powietrznej między soczewką i
płytką w miejscu padania promienia.

Korzystając z podobieństwa
zaznaczonych trójkątów otrzymujemy :

d

r

r

R

====

1

2

d

r

R

====

2

2

Ś

wiatło odbite od układu trafia do oka

obserwatora. Warunkiem
interferencyjnego wzmocnienia jest, aby

różnica dróg stanowiła nieparzystą liczbę połówek długości fali. (Odwrócenie

R

S

d

P

r

45

fazy fali przy odbiciu od powierzchni płytki daje efekt przesunięcia o połowę
długości fali.) Obserwator widzi zatem jasny pierścień o promieniu

r

spełniającym warunek :

((((

))))

2

1

2

2

2

2

k

r

R

++++

====

⋅⋅⋅⋅

λλλλ

((((

))))

2

R

1

k

2

r

λλλλ

++++

====

;

k= 0 ,1 ,2........

Promienie ciemnych pierścieni interferencyjnych są określone równaniem :

k

r

R

r

kR

λλλλ

λλλλ

====

⇒

⇒

⇒

⇒

====

2

;

k = 0 , 1 , 2 .......

Jeśli obserwacja jest prowadzona w świetle przechodzącym, to warunki te są
odwrócone .

r

kR

====

λλλλ

- promienie jasnych pierścieni w świetle przechodzącym

((((

))))

2

R

1

k

2

r

λλλλ

++++

====

- promienie ciemnych pierścieni w świetle przechodzącym.

ZDOLNOŚĆ ROZDZIELCZA MIKROSKOPU.

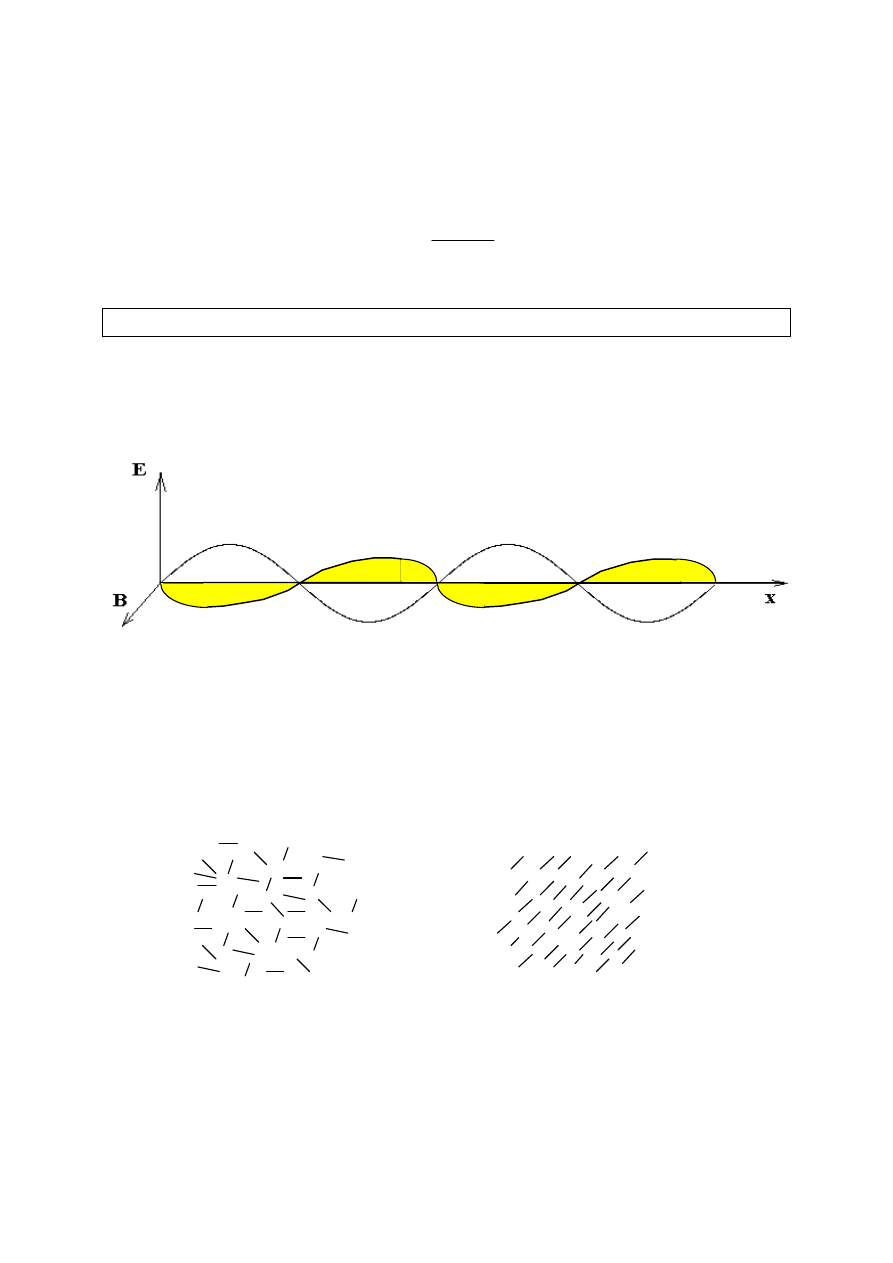
Niewielki przedmiot o średnicy d znajduje się w polu widzenia obiektywu
mikroskopu. Promienie świetlne ugięte na brzegach tego przedmiotu tworzą
maksima interferencyjne. Obraz przedmiotu powstanie w mikroskopie wtedy,
gdy wiązki tworzące maksima co najmniej pierwszego rzędu są odchylone pod
kątem mniejszym od apertury obiektywu mikroskopu

Ψ

Ψ

Ψ

Ψ

. Warunkiem powstania

obrazu jest zatem spełnienie nierówności :

αααα

αααα

λλλλ

1

1

<<<<

<<<<

<<<<

Ψ

Ψ

Ψ

Ψ

Ψ

Ψ

Ψ

Ψ

Ψ

Ψ

Ψ

Ψ

sin

sin

sin

d

d

==== λλλλ

sin

Ψ

Ψ

Ψ

Ψ

- zdolność rozdzielcza mikroskopu

Ponieważ kąt

Ψ

Ψ

Ψ

Ψ

jest mniejszy od 90

0

, to jego sinus jest

mniejszy od 1. Oznacza to że przez mikroskop można
zobaczyć przedmioty o średnicy większej od długości fali
ś

wietlnej.

d

>>>>

λλλλ

Ψ

Ψ

Ψ

Ψ

α

α

α

α

1111

46

Zdolność rozdzielczą mikroskopu można nieco zwiększyć wprowadzając
między przedmiot i obiektyw mikroskopu tzw. ciecz immersyjną, tj. ciecz o
możliwie dużym współczynniku załamania, która zmniejsza wartość kąta

αααα

1111

....

Zdolność rozdzielcza mikroskopu staje się wtedy równa:

d

n

====

λλλλ

sin

Ψ

Ψ

Ψ

Ψ

POLARYZACJA ŚWIATŁA

Ś

wiatło jest strumieniem fotonów. Każdy foton powstaje przy przejściu jakiegoś

atomu ze stanu wzbudzonego do stanu podstawowego. Czas emisji fotonu jest
rzędu 10

-8

s

. W tym czasie światło przebywa drogę ok. 3 m.

Foton jest zatem dokładniej paczką fal elektromagnetycznych. Każda fala
elektromagnetyczna ma dwie prostopadłe do siebie płaszczyzny zmian
wektorów: elektrycznego (E) i magnetycznego (B).

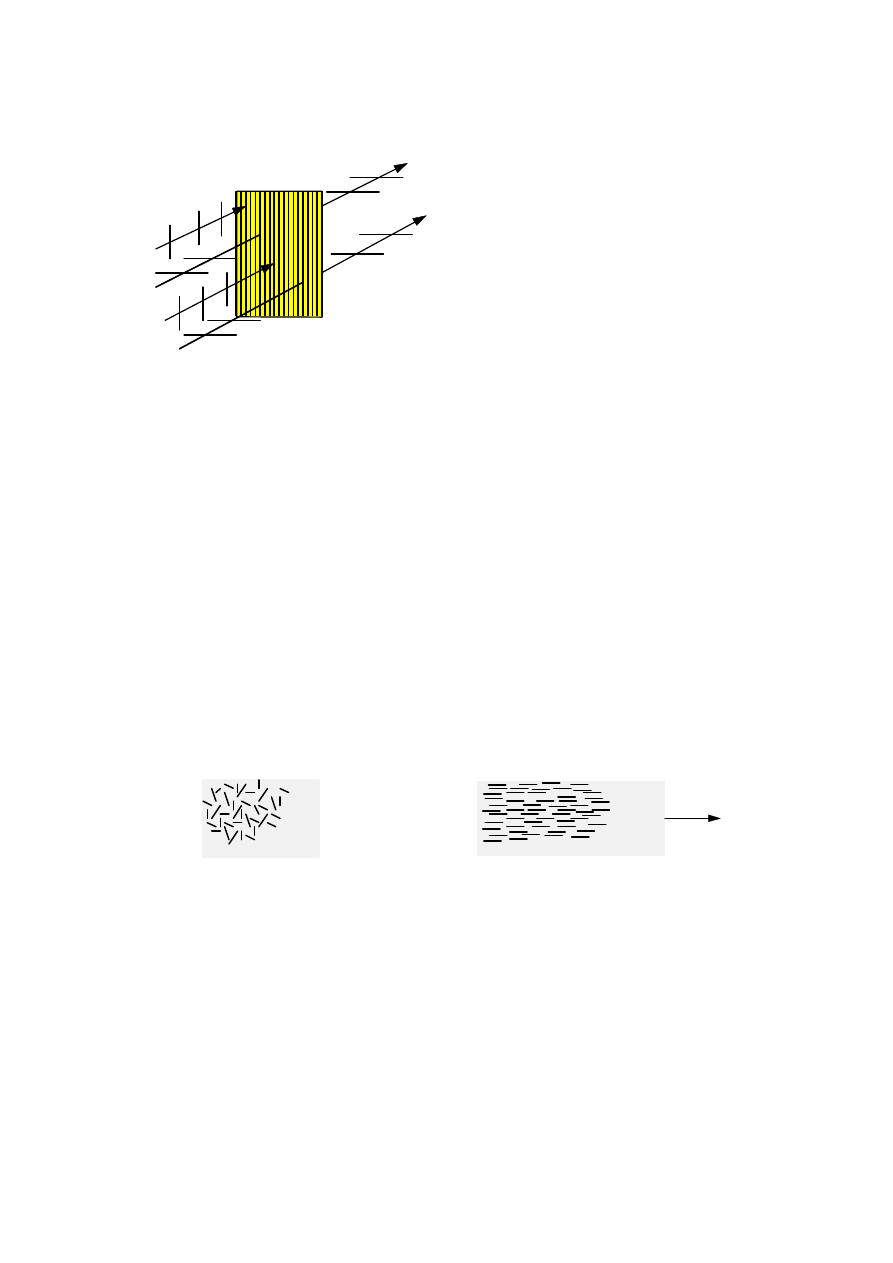
Jeśli fotony padające na płaszczyznę kartki mają różne płaszczyzny zmian
wektora elektrycznego, to takie światło nazywamy niespolaryzowanym. światło
spolaryzowane zawiera fotony o jednakowej płaszczyźnie zmian wektora
elektrycznego.

ś

wiatło niespolaryzowane

ś

wiatło spolaryzowane

1. Polaryzator siatkowy.

Wyobraźmy sobie siatkę równolegle ułożonych przewodzących pręcików.

ź

ródło

ś

wiatła

47

Odległości między sąsiednimi pręcikami są rzędu długości fali świetlnej (10

-7

m

) Jeśli na taką siatkę pada foton

którego płaszczyzna zmian wektora
elektrycznego jest równoległa do
pręcików siatki, to pole elektryczne
fotonu spowoduje ruch elektronów
zawartych

w

przewodzących

pręcikach siatki w wyniku czego
taki foton zostanie pochłonięty.
Fotony, których płaszczyzna zmian
wektora

elektrycznego

jest

prostopadła do pręcików siatki nie

tracą energii, gdyż ich pole elektryczne mogłoby jedynie wywołać ruch
elektronów w kierunku poprzecznym do pręcików siatki, ale w tym kierunku
elektrony nie mają swobody przemieszczania się. Takie fotony przechodzą przez
siatkę.
Wykonanie takiej siatki jest bardzo trudne. Dopiero w 1963 r. wykonano
szklaną siatkę dyfrakcyjną zawierającą 2000 rys na jednym milimetrze. Na
krawędzie rys napylono atomy złota, w wyniku czego uzyskano szereg
równolegle ułożonych przewodzących pasków o szerokości zaledwie kilkuset
atomów.

2. Polaroid H .

W tym polaroidzie rolę cienkich, przewodzących pręcików pełnią cząsteczki
polimeru. Ich równoległe ułożenie można uzyskać przez rozciąganie .

Do wytwarzania takich polaroidów stosuje się najczęściej przeźroczyste błony z
alkoholu poliwinylowego. Przewodnictwo elektryczne uzyskuje się przez
zanurzenie błony w roztworze bogatym w jod.

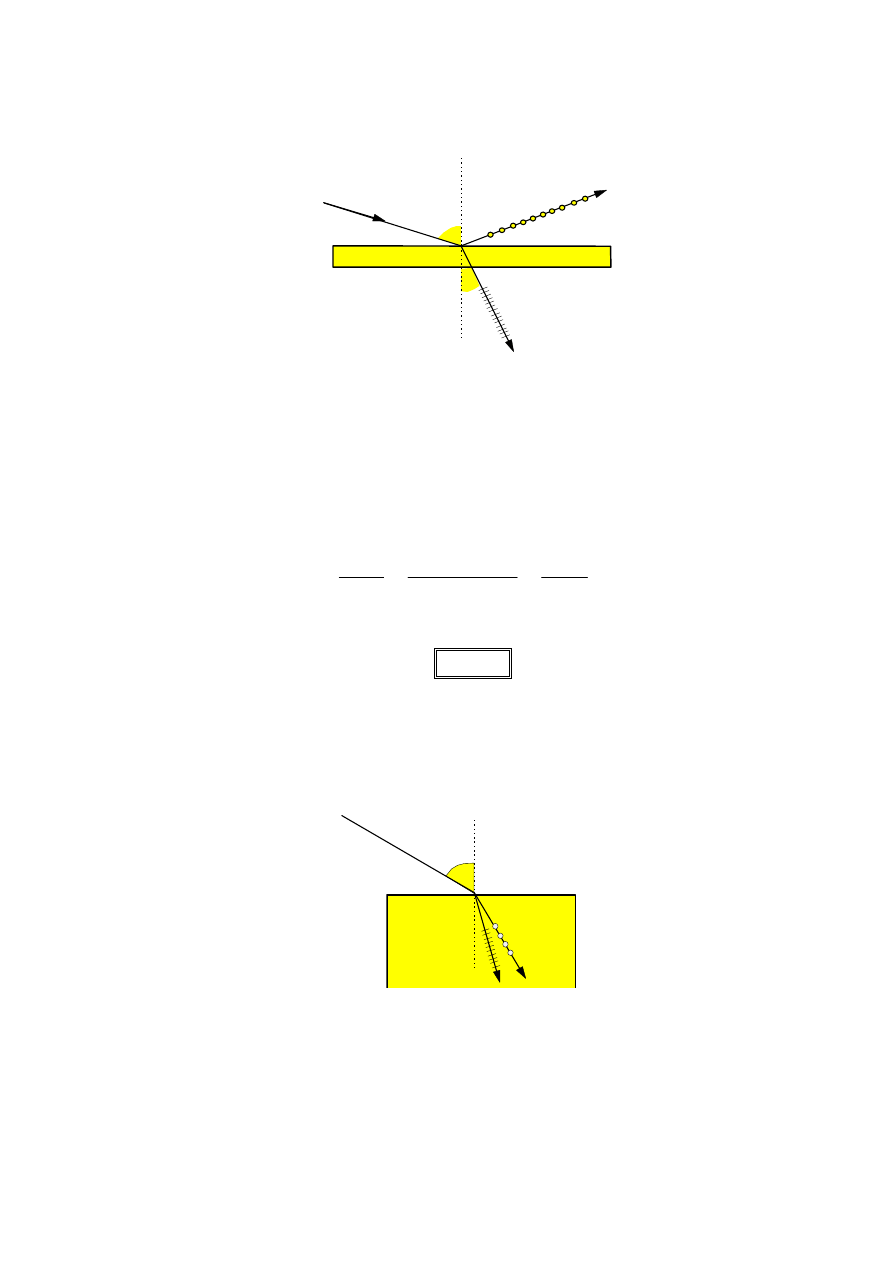
3. Polaryzacja przez odbicie i załamanie.

48

Podczas odbicia i załamania światła również zachodzi oddziaływanie między
polem elektrycznym fotonu i ładunkami zawartymi w ośrodku. Zarówno światło
odbite jak i załamane jest spolaryzowane. Płaszczyzny polaryzacji obu promieni
są wzajemnie prostopadłe. Jeśli promień odbity jest prostopadły do promienia
załamanego, to promień odbity jest całkowicie spolaryzowany, a promień
załamany - częściowo, chociaż w maksymalnym stopniu.

((((

))))

n

====

====

−−−−

====

sin

sin

sin

sin

sin

cos

αααα

ββββ

αααα

αααα

αααα

αααα

90

0

n

tg

==== αααα

Kąt padania a przy którym polaryzacja jest maksymalna nazywamy kątem
Brewstera.

4. Polaryzacja w kryształach dwójłomnych.

Jeśli skierujemy wiązkę światła na kryształ kalcytu lub inny jednoosiowy
kryształ dwójłomny, zauważymy, że zwykle wewnątrz kryształu powstają dwie
wiązki. Wyjątek stanowi przypadek, gdy wiązka światła ma akurat kierunek osi
optycznej. W jednej z tych wiązek kierunek czoła fali jest zazwyczaj ukośny w
stosunku do promienia fali, a nie prostopadły. Obie wiązki mają zwykle różne
prędkości rozchodzenia, rozchodzą się w różnych kierunkach, przy czym każda

αααα

ββββ

αααα

49

jest spolaryzowana. Kierunki polaryzacji promieni zwanych zwyczajnym i
nadzwyczajnym są wzajemnie prostopadłe.

5. Skręcenie płaszczyzny polaryzacji.

Szereg materiałów organicznych i nieorganicznych ma własność skręcania
płaszczyzny polaryzacji, co oznacza, że podczas przechodzenia światła
spolaryzowanego liniowo przez warstwę takiej substancji następuje zmiana
orientacji wektora elektrycznego. Związki skręcające płaszczyznę polaryzacji są
przeważnie związkami węgla. W podobny sposób zachowują się także związki
azotu, krzemu, cyny i fosforu.
Własność skręcania płaszczyzny polaryzacji ma między innymi roztwór cukru.

Kąt skręcenia płaszczyzny polaryzacji jest wprost proporcjonalny do grubości
warstwy roztworu (d) i do jego stężenia (c). Współczynnik proporcjonalności
(

αααα

0000

))))

zależy od rodzaju ośrodka.

6. Zastosowanie światła spolaryzowanego.

Jedno z najważniejszych zastosowań światła spolaryzowanego umożliwiają tzw.
ciekłe kryształy. Są to ciecze anizotropowe, których cząsteczki mają kształt
wydłużony i ulegają samorzutnemu uporządkowaniu. Orientację cząsteczek
można łatwo zmienić przy pomocy pola elektrycznego. Światło przechodzące
przez warstewkę ciekłego kryształu ulega polaryzacji. Przy pomocy polaroidu,
można uzyskać wygaszenie światła spolaryzowanego, co umożliwia uzyskanie
napisów w kalkulatorach, zegarkach elektronicznych, na ekranach przenośnych
komputerów czy uzyskanie obrazu w niektórych typach kineskopów
telewizyjnych.
W fotografii znajdują zastosowanie filtry polaryzacyjne, które służą do
wygaszania niekorzystnych refleksów jakie powstają przy odbiciu światła od
dużych, błyszczących powierzchni.
Wykorzystując pole elektryczne można wywoływać zmiany natężenia
strumienia

ś

wiatła

(komórka

Kerra).

Modulowanie

fali

ś

wietlnej

wykorzystywane jest w optycznym zapisie dźwięku i w przesyłaniu informacji
przy użyciu światłowodów.
Ś

wiatło spolaryzowane jest także wykorzystywane w filmie trójwymiarowym.

Przy użyciu polaroidów można uzyskać wygaszenie światła nie przeznaczonego
dla lewego lub prawego oka.
Istnieje możliwość wykorzystania światła spolaryzowanego przy użyciu
specjalnych, polaryzacyjnych okularów przeciwsłonecznych. Wygaszają one
głównie promieniowanie odbite od poziomych płaszczyzn. Oglądany przez takie

d

αααα αααα

====

o

cd

roztwór cukru

50

okulary krajobraz ma delikatniejsze i głębsze barwy. Ułatwiają one również
oglądanie przedmiotów znajdujących się pod powierzchnią wody.
Szereg materiałów przeźroczystych staje się dwójłomnymi pod wpływem
naprężeń. Oglądając modele przedmiotów w świetle spolaryzowanym można
wykryć istnienie naprężeń oraz ocenić ich wielkość. Umożliwia to właściwą
konstrukcję narzędzi o odpowiedniej wytrzymałości. Przedmioty szklane
oglądane w świetle spolaryzowanym ujawniają istniejące w nich naprężenia.

Niektóre owady a prawdopodobnie i inne zwierzęta rozróżniają
ś

wiatło spolaryzowane i niespolaryzowane. Dzięki temu np. pszczoły nawet w

dni pochmurne mogą kierować się Słońcem. Światło słoneczne przechodząc
przez chmury ulega częściowej polaryzacji. Pszczoły określają położenie
Słońca po azymucie polaryzacji światła nieba.