Zad 7. Opracowanie na podstawie książki „Fizyka dla politechnik” A.Januszajtis.

Równanie falowe:

Fala harmoniczna biegnąca opisana jest wzorem y(x, t)=Asink(x - ct)=Asin(kx-kct)

Lub wzorem y(x, t)=Acosk(x - ct)=Acos(kx-kct) (gdy fale biegną w przeciwnym kierunku

we wzorach będą znaki `+”)

Dowód dla funkcji sinusoidalnej:

;

;

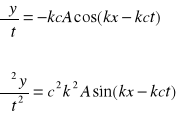
- funkcja spełnia równanie falowe.

Zależność prędkości fali od gęstości i położenia:

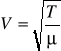
gdzie T - naprężenie, μ - gęstość liniowa

zad8. Rozpatruje przypadek nieograniczonego ośrodka sprężystego, na który nie działają żadne siły zewnętrzne. Jedynymi siłami SA siły bezwładności - ms^''. Jeżeli gęstość ośrdkda jest równa R to gęstość siły bezwładności f= -Rs^'' s równania ruchu maja postać :

Przykładem Fali w ośrodku sprężystym jest fala w pręcie.

Wyprowadzenie gęstości energii:

---