
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
ÓWNANIA WIELOMIANOWE STOPNIA
3
Wszyscy znamy bardzo wygodne wzory na rozwi ˛
azania równania kwadratowego. Z dru-
giej strony
, ˙ze takie wzory nie mog ˛
a istnie´c dla równa ´n stopnia wi˛ekszego od 4.
Znana jest ponadto metoda sprowadzania równa ´n stopnia 4 do równa ´n stopnia 3 (jest ona
do´s´c skomplikowana, wi˛ec nie wchodzimy w szczegóły). W takiej sytuacji jedyny ciekawy
przypadek, to przypadek równania stopnia 3:
ax
3
+
bx
2
+
cx
+
d
=
0.
Wzory w tym przypadku nosz ˛
a nazw˛e wzorów Cardano i wła´snie im b˛edzie po´swi˛econy
ten poradnik.
Podkre´slmy, ˙ze w wielu sytuacjach s ˛
a prostsze metody rozwi ˛
azywania równa ´n stopnia
3, o czym mo ˙zecie dokładnie poczyta´c w
o rozwi ˛
azywaniu równa ´n wielomiano-
wych.
x
2
mówimy: pa,pa
Posta´c wzorów Cardano w przypadku napisanego wy ˙zej, ogólnego równania, jest bardzo
skomplikowana, dlatego na pocz ˛
atku spróbujemy je troch˛e upro´sci´c.
Po pierwsze mo ˙zemy równanie podzieli´c stronami przez a, co sprowadza nas do sytuacji
ze współczynnikiem równym 1 przy x
3
:
x
3
+
bx
2
+
cx
+
d
=
0.
Kolejny krok to podstawienie x
=
y
−
b
3
. Sprawd´zmy jak zmieni si˛e równanie po takim
podstawieniu.
0
=
y
−
b
3
3
+
b
y
−
b
3
2
+
c
y
−
b
3
+
d
=
=
y
3
−
y
2
b
+
y
b
2
3
−
b
3
27
+
by
2
−
2b
2
y
3
+
b
3
9
+
cy
−
bc
3
+
d
=
=
y
3
+
c
−
b
2
3
y
+
2b
3
27
+
d
−
bc
3
.
Wprawdzie współczynniki troch˛e si˛e nam skomplikowały, ale za to znikn˛eła niewiadoma w
kwadracie, co pozwala nam zajmowa´c si˛e równaniem postaci
y
3
+
py
+
q
=
0
(jest to spore uproszczenie, bo zostały nam ju ˙z tylko dwa parametry).
Podstawmy x
=
y
−
b
3
=
y
+
1 w równaniu x
3
−
3x
2
+
5x
−
4
=
0.
Liczymy
0
= (
y
+
1
)
3
−
3
(
y
+
1
)
2
+
5
(
y
+
1
) −
4
=
=
y
3
+
3y
2
+
3y
+
1
−
3y
2
−
6y
−
3
+
5y
+
5
−
4
=
y
3
+
2y
−
1.
Wida´c zatem, ˙ze zamienili´smy wyj´sciowe równanie na równanie, w którym nie ma
y
2
.
Materiał pobrany z serwisu
1

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Wyró˙znik
Podobnie jak dla równania kwadratowego, definiujemy wyró˙znik równania
y
3
+
py
+
q
=
0
wzorem
∆
=
p
3
3
+
q
2
2
.
Nie powinno by´c zaskoczeniem, ˙ze znak wyró ˙znika pozwala stwierdzi´c ile rozwi ˛
aza ´n ma
równanie, dokładny opis mo ˙zliwych sytuacji zrobimy jednak odrobin˛e pó´zniej.
Wzór Cardano
Nie przedłu ˙zaj ˛
ac, liczba
y
=
3
r
−
q
2
−
√
∆
+
3
r
−
q
2
+
√
∆,
jest zawsze pierwiastkiem równania y
3
+
py
+
q
=
0. Jest to wła´snie wspominany ju ˙z wzór
Cardano
. Zanim omówimy dokładnie ró ˙zne niuanse zwi ˛
azane z tym wzorem sprawd´zmy,
˙ze rzeczywi´scie jest on poprawny. ˙Zeby ułatwi´c sobie zapis, oznaczmy a
= −
q
2
−
√
∆ i b
=
−
q
2
+
√
∆. W szczególno´sci
a
+
b
= −
q
2
−
√
∆
−
q
2
+
√
∆
= −
q
ab
=
−
q
2
−
√
∆
−
q
2
+
√
∆
=
q
2
4
−
∆
= −
p
3
3
.
Teraz ju ˙z jeste´smy gotowi do rachunków. Sprawdzimy, ˙ze y
3
= −
py
−
q.
3
√
a
+
3
√
b
3
=
a
+
3
3
√
a
2
b
+
3
3
√
ab
2
+
b
=
= (
a
+
b
) +
3
3
√
ab
(
3
√
a
+
3
√
b
) = −
q
+
3y
3
r
−
p
3
3
= −
q
−
py.
Czyli wszystko cacy.
Znak wyró˙znika
a) Je ˙zeli
∆
>
0 to równanie y
3
+
py
+
q
=
0 ma dokładnie jeden pierwiastek i jest on
równy
y
=
3
r
−
q
2
−
√
∆
+
3
r
−
q
2
+
√
∆.
Rozwi ˛
a ˙zmy równanie x
3
+
3x
−
6
=
0.
Liczymy
∆-˛e.
∆
=
p
3
3
+
q
2
2
=
1
3
+
9
=
10.
Zatem jest jeden pierwiastek i jest on równy
x
=
3
q
3
−
√
10
+
3
q
3
+
√
10.
Materiał pobrany z serwisu
2

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Rozwi ˛
a ˙zmy równanie x
3
+
3x
−
14
=
0.
Liczymy dokładnie tak samo jak poprzednio.
∆
=
p
3
3
+
q
2
2
=
1
+
49
=
50.
Zatem jedyny pierwiastek jest równy
x
=
3
q
7
−
√
50
+
3
q
7
+
√
50
=
3
q
7
−
5
√
2
+
3
q
7
+
5
√
2.
Zaraz, zaraz, przecie ˙z pierwiastek wyj´sciowego równania mo ˙zna łatwo zgadn ˛
a´c
bez wzorów Cardano: jest to x
=
2! Nie jest to ˙zadna sprzeczno´s´c, po prostu
3
q
7
−
5
√
2
+
3
q
7
+
5
√
2
=
2.
Powinno by´c teraz dla was jasne sk ˛
ad bior ˛
a si˛e zadania takie jak
b) Je ˙zeli
∆
=
0 i q
=
0 to mamy równanie y
3
=
0, które ma jeden pierwiastek potrójny.
Je ˙zeli natomiast
∆
=
0 i q
6=
0 to równanie ma dwa ró ˙zne pierwiastki
y
=
3
r q
2
∨
y
= −
2
3
r q
2
i jeden z nich jest podwójny.
Rozwi ˛
a ˙zmy równanie x
3
−
12x
+
16
=
0.
Liczymy
∆-˛e.
∆
=
p
3
3
+
q
2
2
= −
64
+
64
=
0.
Zatem równanie ma dwa rozwi ˛
azania
x
=
3
r q
2
=
2,
y
= −
2
3
r q
2
= −
4.
Mo ˙zna sprawdzi´c, ˙ze x
=
2 jest pierwiastkiem podwójnym, czyli
x
3
−
12x
+
16
= (
x
−
2
)
2
(
x
+
4
)
.
c) No i została nam najciekawsza sytuacja, gdy
∆
<
0. Równanie ma wtedy trzy pier-
wiastki. S ˛
a ró ˙zne triki, ˙zeby w tym miejscu udawa´c, ˙ze mo ˙zna si˛e obej´s´c bez liczb ze-
spolonych, ale my jak zwykle staramy si˛e pisa´c jak jest naprawd˛e, a prawda jest taka,
˙ze wła´snie znale´zli´smy si˛e w historycznej sytuacji, w której ludzie zdali sobie spra-
w˛e, ˙ze „nie da si˛e ˙zy´c” bez pierwiastków kwadratowych z liczb ujemnych. Sytuacj˛e t˛e
omówimy w nast˛epnym rozdziale.
Materiał pobrany z serwisu
3

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Casus irreducibilis
Idea jest taka: wiemy, ˙ze równanie ma trzy pierwiastki rzeczywiste, wi˛ec wystarczy zna´c
jeden z nich i dalej ju ˙z poradzimy sobie jak w szkole, dziel ˛
ac przez dwumian itd. Jak zatem
znale´z´c jeden pierwiastek? Jest nim dokładnie pierwiastek ze wzoru Cardano, czyli liczba
y
=
3
r
−
q
2
−
√
∆
+
3
r
−
q
2
+
√
∆.
Przypomnijmy, ˙ze sprawdzili´smy (nie przejmuj ˛
ac si˛e
∆- ˛a), ˙ze po wstawieniu tej liczby do
równo´sci x
3
+
px
+
q otrzymujemy 0.
No i fajnie, wi˛ec jaki jest problem? Problem jest taki, ˙ze jeste´smy w przypadku
∆
<
0,
wi˛ec w powy ˙zszym wyra ˙zeniu mamy dwa razy pierwiastek kwadratowy z liczby ujemnej
∆! Oczywi´scie od pocz ˛atku si˛e to ludziom (matematykom) nie podobało, wi˛ec bardzo si˛e
starali jako´s ten wzór zapisa´c tak, aby nie było tych dziwnych pierwiastków. Okazuje si˛e
jednak, ˙ze nie da si˛e tego zrobi´c. Co gorsza wiemy, ˙ze pierwiastki równania s ˛
a liczbami rze-
czywistymi, wi˛ec to dziwaczne wyra ˙zenie jest tak naprawd˛e „magicznym” zapisem zwykłej
liczby rzeczywistej.
Rozwi ˛
a ˙zmy równanie x
3
−
15x
−
4
=
0.
Mamy
∆
=
p
3
3
+
q
2
2
= −
125
+
4
= −
121
= −
11
2
.
Zatem jeden z pierwiastków równania jest równy
3
q
2
−
p
−
11
2
+
3
q
2
+
p
−
11
2
=
3
q
2
−
11
√
−
1
+
3
q
2
+
11
√
−
1.
Liczba ta oczywi´scie wygl ˛
ada podejrzanie, ale przykład ten jest tak dobrany, ˙ze
mo ˙zemy bezpo´srednio sprawdzi´c, ˙ze jest to tak naprawd˛e liczba rzeczywista: wy-
ra ˙zenia pod oboma pierwiastkami s ˛
a pełnymi sze´scianami.
3
q
2
−
11
√
−
1
+
3
q
2
+
11
√
−
1
=
3
q
8
−
12
√
−
1
−
6
+
√
−
1
+
3
q
8
+
12
√
−
1
−
6
−
√
−
1
=
3
q
8
−
3
·
4
·
√
−
1
+
3
·
2
· (
√
−
1
)
2
− (
√
−
1
)
3
+
+
3
q
8
+
3
·
4
·
√
−
1
+
3
·
2
· (
√
−
1
)
2
+ (
√
−
1
)
3
=
=
3
q
(
2
−
√
−
1
)
3
+
3
q
(
2
+
√
−
1
)
3
=
2
−
√
−
1
+
2
+
√
−
1
=
4.
Nie było łatwo, ale wida´c, ˙ze wzory Cardano dały nam po prostu bardzo orygi-
nalny sposób na zapisanie liczby 4. Łatwo sprawdzi´c, ˙ze x
=
4 jest rzeczywi´scie
pierwiastkiem oryginalnego równania.
Powy ˙zsze przekształcenie nie powinno nas dziwi´c, widzieli´smy ju ˙z w przypadku
∆
>
0, ˙ze wzory Cardano potrafi ˛
a prost ˛
a liczb˛e zapisa´c w skomplikowany sposób.
Materiał pobrany z serwisu
4

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Je ˙zeli lekko zmodyfikujemy poprzedni przykład: x
3
−
15x
−
2
=
0 to mamy
∆
=
p
3
3
+
q
2
2
= −
125
+
1
= −
124
i jeden z pierwiastków jest równy
3
q
2
−
√
−
124
+
3
q
2
+
√
−
124.
Teraz jednak nie ma ju ˙z łatwego sposobu na pozbycie si˛e pierwiastków z liczb
ujemnych i mamy w takiej sytuacji dwa wyj´scia:
a) albo jeste´smy konserwatywni i uwa ˙zamy, ˙ze pierwiastki z liczb ujemnych nie
maj ˛
a sensu; w tym przypadku musimy si˛e pogodzi´c z faktem, ˙ze nie umie-
my rozwi ˛
aza´c równania x
3
−
15x
−
2
=
0 (bo uwa ˙zamy powy ˙zszy wzór za
bezsensowny);
b) albo jeste´smy post˛epowi i uaktualniamy nasze poj˛ecie liczby tak, aby powy ˙z-
szy wzór był OK; w ten sposób odkrywamy ´swiat liczb zespolonych.
Oczywi´scie matematycy obrali drug ˛
a drog˛e (w XVI wieku).
Zadania
.info
Podoba Ci się ten poradnik?
Pokaż go koleżankom i kolegom ze szkoły!
T
IPS
& T
RICKS
1
Historia prób rozwi ˛
azania równania trzeciego stopnia jest bardzo długa i si˛ega staro ˙zytnego
Babilonu. Prawdopodobnie pierwszym znacz ˛
acym post˛epem było znalezienie na pocz ˛
atku
XVI wieku przez włoskiego matematyka Scipione del Ferro metody na rozwi ˛
azanie rów-
nania postaci x
3
+
mx
=
n. Z dzisiejszej perspektywy wiemy, ˙ze ka ˙zde równanie trzeciego
stopnia mo ˙zna sprowadzi´c do tej postaci, ale del Ferro nie mógł tego wiedzie´c, bo w ów-
czesnych czasach nie były jeszcze u ˙zywane liczby ujemne (a s ˛
a one potrzebne aby wykona´c
wspomnian ˛
a redukcj˛e). Del Ferro utrzymywał swoj ˛
a metod˛e w sekrecie i ujawnił j ˛
a dopiero
na krótko przed ´smierci ˛
a swojemu uczniowi Antonio Fiore.
Prawdopodobnie niezale ˙znie, w roku 1530 Niccolò Tartaglia oznajmił, ˙ze umie rozwi ˛
a-
zywa´c równania stopnia 3, co do prowadziło do pojedynku (na równania) mi˛edzy Tartagli ˛
a,
a Fiore. Zawody wygrał Tartagila. W 1539 roku Tartaglia wyjawił swój sekret rozwi ˛
azywania
równa ´n sze´sciennych Gerolamowi Cardano, warunkiem była jednak obietnica, ˙ze Cardano
nie ujawni publicznie tej metody. W 1540, asystent Cardana, Lodovico Ferrari, odkrył meto-
d˛e redukcji równa ´n 4 stopnia do równa ´n sze´sciennych, co w poł ˛
aczeniu z metod ˛
a Tartaglii
dawało metod˛e rozwi ˛
azania dowolnych równa ´n stopni 3 i 4. Wyniki te jednak wci ˛
a ˙z nie
mogły zosta´c opublikowane ze wzgl˛edu na obietnic˛e dan ˛
a Tartagli.
Materiał pobrany z serwisu
5

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
W 1543 roku Cardano dowiedział si˛e, ˙ze pierwszym matematykiem, który umiał rozwi ˛
a-
za´c równania trzeciego stopnia był del Ferro i uznał, ˙ze w ten sposób przestaje obowi ˛
azy-
wa´c go obietnica dana Tartagli. W 1545 opublikował w ksi ˛
a ˙zce Ars Magna metod˛e rozwi ˛
aza ´n
równa ´n stopnia 3 i 4, co doprowadziło do wyzwania go przez Tartagli˛e na (matematyczny)
pojedynek. Cardano odmówił, ale w zamian do pojedynku stan ˛
ał jego ucze ´n Ferrari. Ferrari
pojedynek wygrał, co pozbawiło Tartagli˛e zarówno presti ˙zu jak i pieni˛edzy.
Cardano zauwa ˙zył ju ˙z w Ars Magna, ˙ze wzory Tartaglii prowadz ˛
a do pierwiastków kwa-
dratowych z liczb ujemnych, ale nie potrafił tego w ˙zaden sposób zinterpretowa´c. Dokład-
niejsze badania tego problemu przeprowadził pó´zniej Rafael Bombelli i 1569 roku wpro-
wadził symbol
±
i
=
√
−
1, co uwa ˙za si˛e dzi´s za moment odkrycia liczb zespolonych.
2
Wró´cmy jeszcze do problemu niemo ˙zno´sci zapisania pierwiastków równania stopnia 3 bez
u ˙zycia liczb zespolonych. Problem ten nosi nazw˛e casus irreducibilis. Przypomnijmy raz jesz-
cze, ˙ze np. równanie x
3
−
15x
−
2
=
0 ma trzy pierwiastki rzeczywiste i jeden z nich jest
równy
3
q
2
−
√
−
124
+
3
q
2
+
√
−
124.
Jak ju ˙z pisali´smy nie da si˛e tej liczby upro´sci´c tak, aby nie było w jej zapisie pierwiastków z
liczb ujemnych.
Filozoficznie nale ˙zy o tej sytuacji my´sle´c nast˛epuj ˛
aco. Badamy pewien ´swiat: ´swiat liczb
rzeczywistych. Okazuje si˛e jednak, ˙ze nie jeste´smy w stanie prowadzi´c tych bada ´n nie wy-
chodz ˛
ac poza ten ´swiat, w naszej sytuacji musimy poszerzy´c nasze horyzonty o liczby ze-
spolone (pomimo, ˙ze w problemie, którym si˛e zajmujemy nie ma ˙zadnych liczb zespolo-
nych).
Tego typu sytuacja jest bardzo cz˛esta w matematyce i z tego powodu matematycy wci ˛
a ˙z
„odkrywaj ˛
a nowe ´swiaty”.
Sytuacj˛e podobn ˛
a do casus irreducibilis, ale chyba prostsz ˛
a do zrozumienia, mo ˙zna za-
obserwowa´c na granicy liczb wymiernych i niewymiernych. Mo ˙ze nigdy si˛e nad tym nie
zastanawiali´scie, ale problem istnienia liczb niewymiernych wcale nie jest prostszy od pro-
blemu istnienia liczb zespolonych (czyli pierwiastków kwadratowych z liczb ujemnych).
Czy jakikolwiek odcinek mo ˙ze mie´c długo´s´c niewymiern ˛
a? Wiem, ˙ze zaraz powiecie, ˙ze
przek ˛
atna kwadratu o boku długo´sci 1 ma długo´s´c
√
2, ale jaki to ma sens praktyczny? Je-
˙zeli my´slimy o liczbach, jak o długo´sciach wyst˛epuj ˛
acych w przyrodzie, to jaki sens maj ˛
a
liczby niewymierne? Przecie ˙z w wyniku pomiaru długo´sci nigdy nie otrzymamy wyniku
√
2.
Powy ˙zszy akapit miał w was zaszczepi´c w ˛
atpliwo´s´c, ˙ze by´c mo ˙ze fakt istnienia liczb nie-
wymiernych wcale nie jest tak oczywisty, jak by si˛e mogło wydawa´c. Z drugiej strony, liczby
niewymierne s ˛
a bardzo wygodne (bez nich nie dałoby si˛e stworzy´c analizy matematycznej)
i cz˛esto pojawiaj ˛
a si˛e w problemach, które na pierwszy rzut oka dotycz ˛
a tylko i wył ˛
acznie
liczb wymiernych.
Materiał pobrany z serwisu
6
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
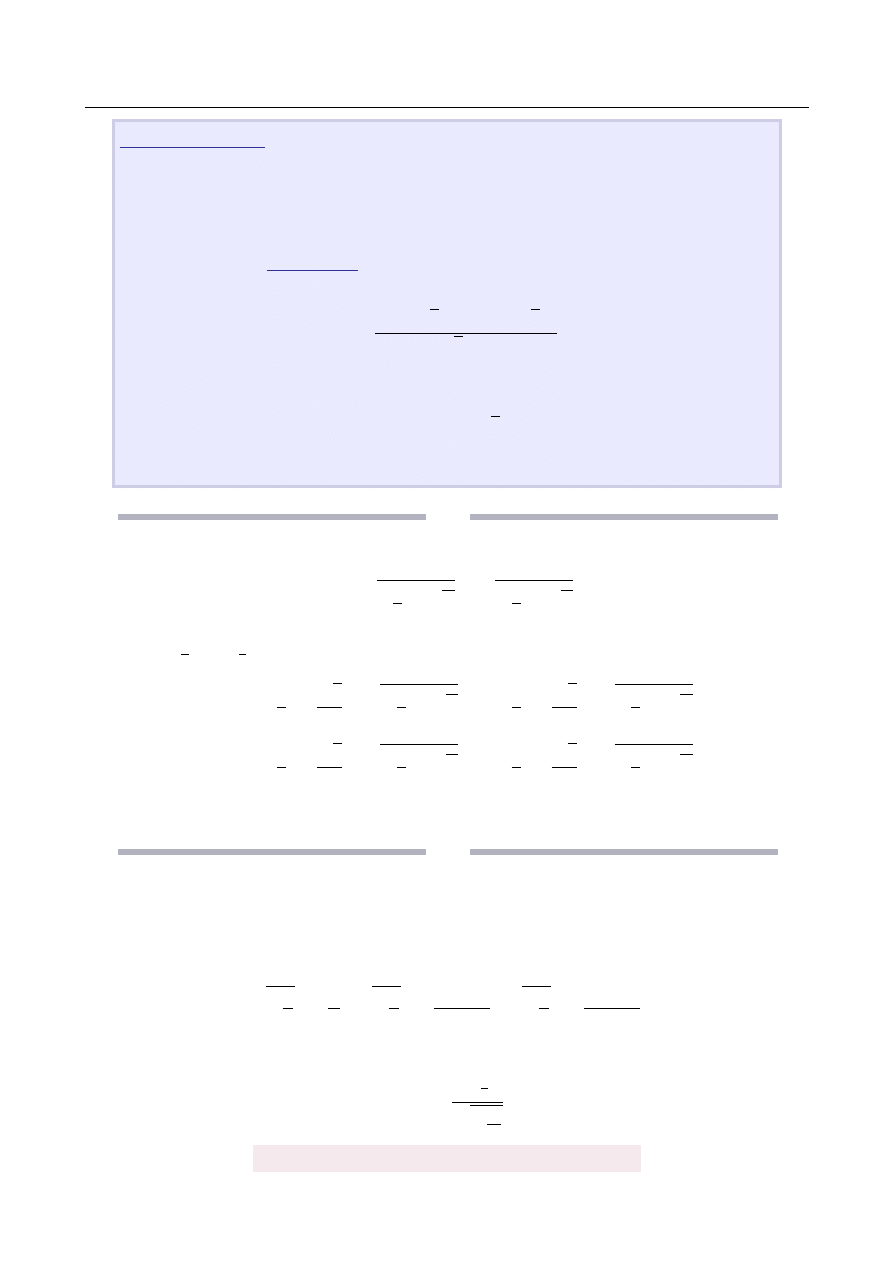
jest to ci ˛
ag liczb naturalnych
1, 1, 2, 3, 5, 8, 13, 21, 34, . . . ,
w którym ka ˙zdy kolejny wyraz powstaje jako suma dwóch poprzednich. Oczywi-
´scie ten ci ˛
ag nie ma nic wspólnego z liczbami niewymiernymi.
Hmm, naprawd˛e?
, ˙ze mo ˙zna wyznaczy´c wzór na n-ty wyraz tego ci ˛
agu
i wzór ten wygl ˛
ada nast˛epuj ˛
aco
a
n
=
(
1
+
√
5
)
n
+ (
1
−
√
5
)
n
√
5
·
2
n
.
Mamy w tym przypadku sytuacj˛e zupełnie analogiczn ˛
a do wzorów Cardano: ka ˙z-
da z liczb a
n
jest liczb ˛
a całkowit ˛
a, ale nie jeste´smy w stanie zapisa´c (przyzwoitego)
wzoru na a
n
bez u ˙zycia liczby niewymiernej
√
5!
Tak wi˛ec nawet je ˙zeli nic nas nie obchodz ˛
a liczby niewymierne, nie mo ˙zemy si˛e bez
nich obej´s´c.
3
Wyliczyli´smy, ˙ze jeden z pierwiastków równania x
3
+
px
+
q
=
0 jest równy
y
1
=
3
r
−
q
2
−
√
∆
+
3
r
−
q
2
+
√
∆,
gdzie
∆
=
p
3
3
+
q
2
2
. A ile s ˛
a równe pozostałe? Oto odpowied´z:
y
2
=
−
1
2
+
i
√
3
2
!
3
r
−
q
2
−
√
∆
+
−
1
2
−
i
√
3
2
!
3
r
−
q
2
+
√
∆
y
3
=
−
1
2
−
i
√
3
2
!
3
r
−
q
2
−
√
∆
+
−
1
2
+
i
√
3
2
!
3
r
−
q
2
+
√
∆
Liczby te s ˛
a rzeczywiste, o ile
∆
<
0.
4
Korzystaj ˛
ac ze wzoru na pierwiastki z liczb zespolonych, mo ˙zna wyliczy´c, ˙ze pierwiastki
równania
x
3
+
px
+
q
=
0
w przypadku
∆
<
0 s ˛
a równe
r
−
p
3
cos
ϕ
3
,
r
−
p
3
cos
ϕ
+
2π
3
,
r
−
p
3
cos
ϕ
+
4π
3
,
gdzie k ˛
at ϕ zdefiniowany jest przez równo´s´c
cos ϕ
=
−
q
2
q
−
p
3
27
.
Materiał pobrany z serwisu
7

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Wzory te maj ˛
a t˛e przewag˛e nad wzorami Cardano, ˙ze nie ma w nich jawnie pierwiastków
z liczb ujemnych. Z drugiej strony, pojawiaj ˛
a si˛e cosinusy i funkcja odwrotna do cosinusa
(potrzebna przy wyliczeniu ϕ).
Rozwi ˛
a ˙zmy równanie x
3
−
3
4
x
−
1
8
=
0.
Sprawd´zmy, ˙ze w tym przypadku
∆
<
0.
∆
=
p
3
3
+
q
2
2
=
−
1
64
+
1
256
<
0.
Szukamy teraz k ˛
ata ϕ, który spełnia warunek
cos ϕ
=
−
q
2
q
−
p
3
27
=
−
1
16
q
1
64
= −
1
2
.
Mo ˙zemy wi˛ec przyj ˛
a´c ϕ
=
2π
3
i rozwi ˛
azania równania s ˛
a równe:
x
1
=
2
r
1
4
cos
2π
9
=
cos
2π
9
x
2
=
cos
2π
3
+
2π
3
=
cos
8π
9
x
3
=
cos
2π
3
+
4π
3
=
cos
14π
9
.
5
W pierwszej chwili mo ˙ze wydawa´c si˛e dziwne, ˙ze dla równania 3 stopnia te ˙z mo ˙zna zdefi-
niowa´c wyró ˙znik (którego znak ma bezpo´sredni zwi ˛
azek z liczb ˛
a pierwiastków równania),
dlatego spróbujemy wyja´sni´c sk ˛
ad si˛e on bierze. W ogólnej sytuacji, dla równania stopnia n
x
n
+
a
n
−
1
x
n
−
1
+ · · · +
a
1
x
+
a
0
=
0
definiujemy wyró˙znik
∆ jako iloczyn kwadratów wszystkich mo˙zliwych ró˙znic
(
x
i
−
x
j
)
,
gdzie i
<
j oraz x
1
, x
2
, . . . , x
n
s ˛
a wszystkimi pierwiastkami wielomianu napisanego z lewej
strony równania. Zwró´cmy uwag˛e, ˙ze zało ˙zyli´smy, ˙ze pierwiastków jest n, co oznacza, ˙ze
dopuszczamy pierwiastki zespolone i pierwiastki wielokrotne. Okazuje, ˙ze dzi˛eki wzorom
Viète’a wyró ˙znik zawsze mo ˙zna wyliczy´c jak wzór od współczynników wielomianu (pomi-
mo, ˙ze jest zdefiniowany przy pomocy pierwiastków, a tych na ogół nie mo ˙zna wyliczy´c).
Materiał pobrany z serwisu
8

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Zgodnie z powy ˙zszym opisem wyró ˙znik równania kwadratowego
x
2
+
bx
+
c
=
0
jest równy
∆
= (
x
1
−
x
2
)
2
.
Przekształcimy teraz to wyra ˙zenie korzystaj ˛
ac ze wzorów Viète’a.
∆
= (
x
1
−
x
2
)
2
= (
x
1
+
x
2
)
2
−
4x
1
x
2
=
b
2
−
4c,
co daje nam szkoln ˛
a
∆-˛e. Zauwa˙zmy jeszcze, ˙ze z równo´sci
∆
= (
x
1
−
x
2
)
2
jest oczywiste, ˙ze
∆
=
0 je ˙zeli x
1
=
x
2
, oraz
∆
>
0 je ˙zeli x
1
6=
x
2
i oba pierwiastki s ˛
a
rzeczywiste (bo wtedy prawa strona jest dodatnia).
Wyró ˙znik równania
x
3
+
px
+
q
=
0
jest równy
∆
= (
x
1
−
x
2
)
2
(
x
1
−
x
3
)
2
(
x
2
−
x
3
)
2
.
Je ˙zeli pracowicie przekształcimy to wyra ˙zenie korzystaj ˛
ac ze
dla
równania stopnia 3 to otrzymamy
∆
= −
4p
3
−
27q
2
.
Szczerze mówi ˛
ac nie jest to dokładnie definicja jak ˛
a zamie´scili´smy przy wzorach
Cardano, ale ró ˙znica polega tylko na mno ˙zeniu przez
−
4
·
27, co praktycznie nie-
istotnie zmienia interpretacj˛e
∆-y. W zamian wzór Cardano wygl ˛ada wyj ˛atkowo
elegancko.
Podobnie jak dla równania stopnia dwa, z równo´sci
∆
= (
x
1
−
x
2
)
2
(
x
1
−
x
3
)
2
(
x
2
−
x
3
)
2
wida´c, ˙ze
∆
=
0 gdy równanie ma pierwiastki wielokrotne, oraz
∆
>
0, gdy s ˛
a trzy
pierwiastki rzeczywiste.
Materiał pobrany z serwisu
9
Wyszukiwarka
Podobne podstrony:
RÓWNANIA PROSTEJ, układy równań 1-go stopnia, FUNKCJA LINIOWA
Rozwiązywanie równań pierwszego stopnia z jedną niewiadomą
rownania wielomianowe, Matematyka
równania wielomianowe, Matematyka, Liceum
matematyka, RÓWNANIE DRUGIEGO STOPNIA Z DWIEMA NIEWIADOMYMI, RÓWNANIE DRUGIEGO STOPNIA Z DWIEMA NIEW
Rownania wielomianowe
3 rownania wielomianowe+odp, matematyka srednia
rownania wielomianowe z parametrem
Układy równań wyższych stopni, układy nierówności
Spline wielomianem 3 stopnia
APROKSYMACJA CHARAKTERYSTYK WIELOMIANEM DRUGIEGO STOPNIA
Funkcja kwadratowa, wielomiany, równania
Lista zadań 4 Drgania o dwóch stopniach swobody (Równania Lagrange'a II rodzaju)
Drgania mechaniczne, Drgania 4, Równania drgań układu o n - stopniach swobody układamy korzystając
Algebra 2 08 równania stopnia 2, 3 i 4
więcej podobnych podstron