„Równania są dla mnie

ważniejsze, gdyż polityka
jest czymś istotnym tylko

dzisiaj, a równania są

wieczne.”

Albert Einstein

ROZWIĄZYWANIE RÓWNAŃ

PIERWSZEGO STOPNIA Z

JEDNĄ NIEWIADOMĄ

Z tej lekcji dowiesz się jak rozwiązać równanie
pierwszego stopnia z jedną niewiadomą
metodą

równań

równoważnych.

Brzmi

strasznie uczenie? Nie martw się, na pewno
zrozumiesz o co chodzi. Rozwiązywanie
równań z jedną niewiadomą nie jest trudne, a
raz pojęte zasady znajdowania niewiadomej
pamięta się całe życie…

ODROBINA TEORII.

PRZYKŁAD:

Każde z poniższych równań spełnia liczba 20:
2x + 15 = 3x – 5;

15 + 5 = 3x – 2x;

20 = x

Rozwiązywanie równań metodą równań
równoważnych polega na zapisywaniu
coraz prostszych równań równoważnych
danemu.
Niektóre

operacje

matematyczne

nie

zmieniają

zbioru

rozwiązań

równania,

możemy więc je wykonywać, aby uzyskać
równanie równoważne danemu.

Równania nazywamy równaniami

równoważnymi, gdy mają ten sam zbiór

rozwiązań.

OPERACJE KTÓRE NIE

ZMIENIAJĄ ZBIORU

ROZWIĄZAŃ RÓWNANIA.

Przypomnijmy, każde równanie ma dwie
strony: prawą i lewą.

3x + 9 = 13 + x

Lewa strona

równania

Prawa strona
równania

Operacje które nie zmieniają zbioru rozwiązań
równania:

• dodanie do obu stron równania tego
samego wyrażenia

• odjęcie od obu stron równania tego samego
wyrażenia

• pomnożenie obu stron równania przez tę
samą liczbę różną od zera

• podzielenie obu stron równania przez tę
samą liczbę różną od zera

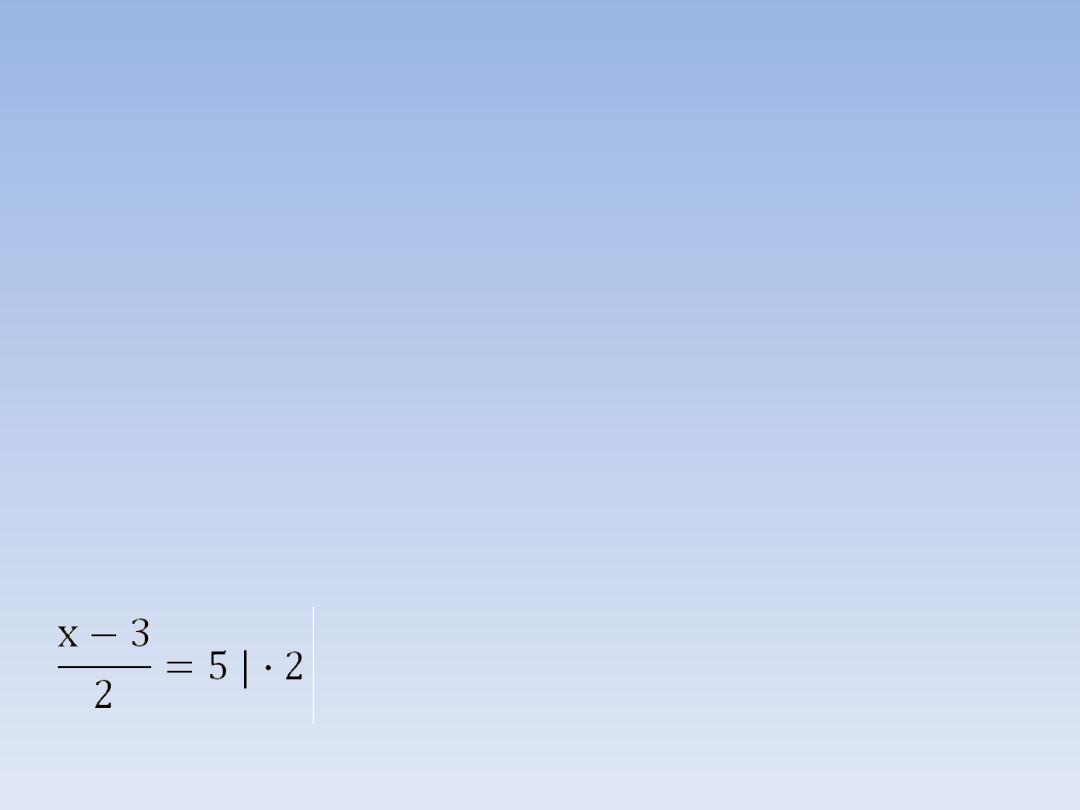
PRZYKŁADY.

PRZYKŁAD 1.
3x – 5 = 16 | +5

(do obu stron równania dodajemy 5 – to

oznacza zapis | +5)

3x – 5 + 5 = 16 + 5
3x = 21
PRZYKŁAD 2.
6x + 15 = -45 | -15

(od obu stron równania odejmujemy

15)

6x + 15 – 15 = -45 – 15
6x = -60
PRZYKŁAD 3.

(obie strony równania mnożymy przez 2)

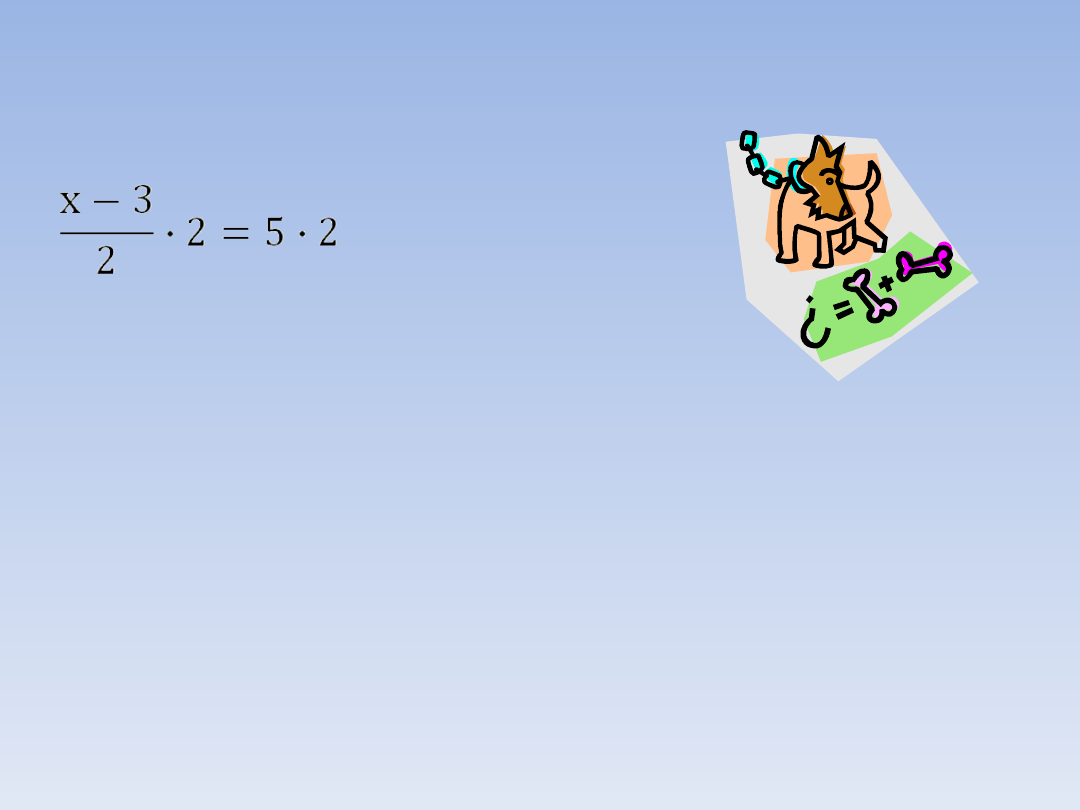
PRZYKŁADY.

PRZYKŁAD 3 – ciąg dalszy.

x – 3 = 10
PRZYKŁAD 4.
5(x + 7) = 55 | : 5

(obie strony równania dzielimy przez 5)

5(x + 7) : 5 = 55 : 5
x + 7 = 11
We wszystkich przykładach otrzymaliśmy
równania które łatwo rozwiązać w pamięci,
jednak przy rozwiązywaniu równania dążymy
do otrzymania postaci x = liczba.

ROZWIĄZYWANIE RÓWNAŃ.

Oto przykłady rozwiązywania równań metodą
równań równoważnych:
PRZYKŁAD 1.
7x – 6 = 3x + 14 | + 6

(do obu stron równania dodajemy

6)

7x = 3x + 20 | - 3x

(od obu stron równania odejmujemy 3x)

4x = 20 | : 4

(obie strony równania dzielimy przez 4)

x = 5

(rozwiązaniem równania jest liczba 5)

Sprawdźmy czy rozwiązanie jest prawidłowe:
L = 7 ∙ 5 – 6 = 35 – 6 = 29
P = 3 ∙ 5 + 14 = 15 + 14 = 29
L = P a więc nasze równanie jest prawidłowo
rozwiązane.

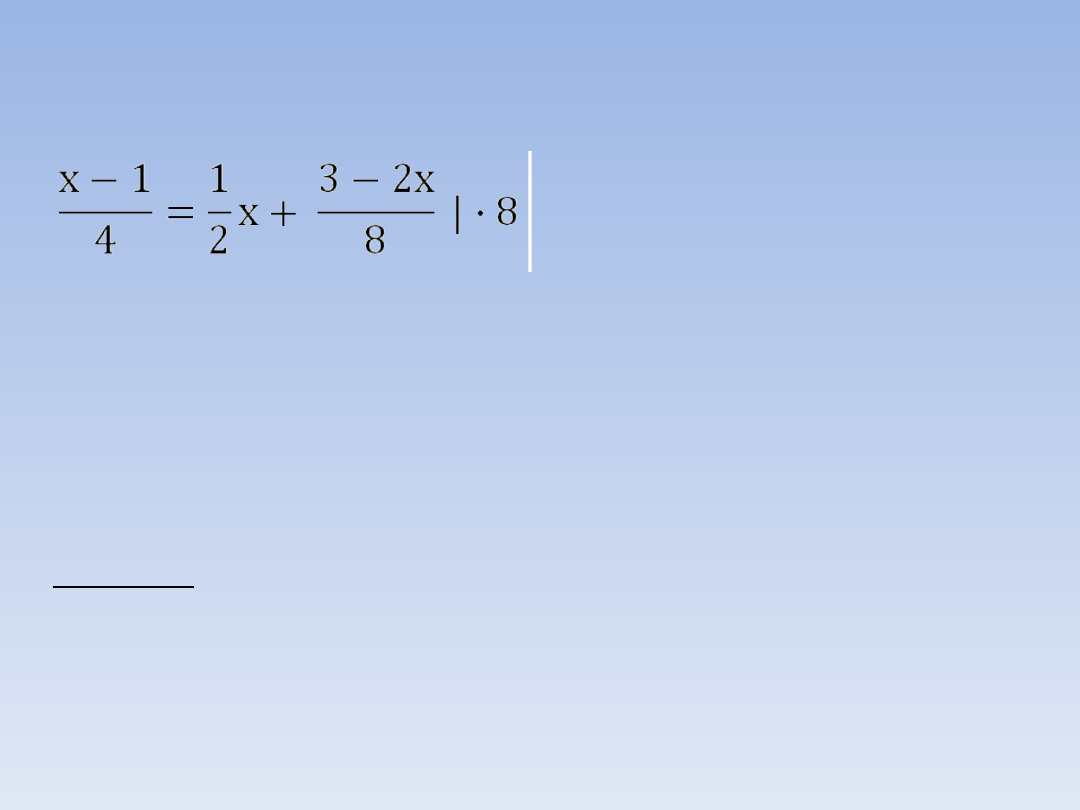
ROZWIĄZYWANIE RÓWNAŃ.

PRZYKŁAD 2.

(mnożymy obie

strony równania przez 8 –

ogólnie: przez liczbę dzięki

której
„pozbędziemy się”
ułamków)

2(x – 1) = 4x + 3 – 2x

(upraszczamy obie strony

równania)

2x – 2 = 2x + 3 | - 2x

(odejmujemy od obu stron

równania 2x)

-2 = 3

(oczywiście jest to sprzeczność, co świadczy o tym, że

dane równanie nie ma
rozwiązania – jest równaniem sprzecznym)

Zawsze, kiedy po rozwiązaniu równania
otrzymamy

sprzeczność,

będzie

to

oznaczało, że dane równanie jest równaniem
sprzecznym – nie ma rozwiązań.

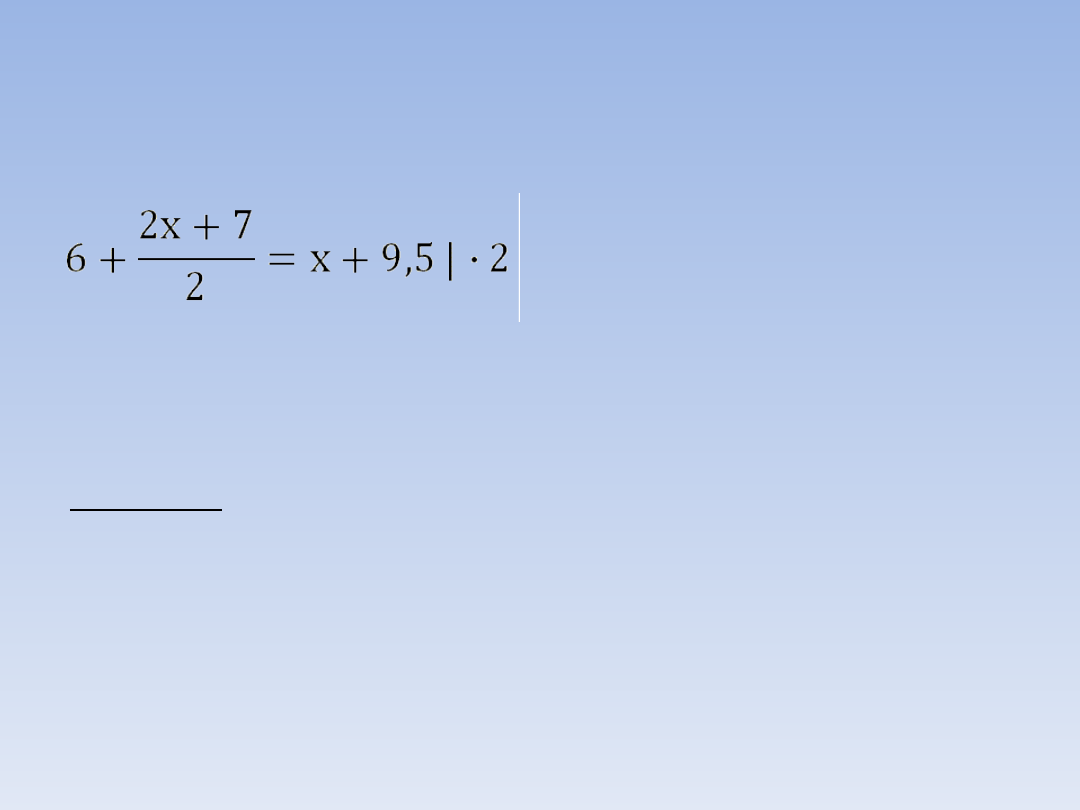
ROZWIĄZYWANIE RÓWNAŃ.

PRZYKŁAD 3.

(mnożymy obie strony

równania przez 2)

12 + 2x + 7 = 2x + 19

(upraszczamy co się da)

2x + 19 = 2x + 19 | - 2x

(od obu stron równania odejmujemy

2x)

19 = 19

(otrzymaliśmy tożsamość, a więc nasze równanie spełnia

każda liczba –
- jest to równanie tożsamościowe)

Zawsze, kiedy po rozwiązaniu równania
otrzymamy tożsamość, oznaczać to będzie, że
dane równanie jest tożsamościowe – spełnia je
każda liczba.

PRZENOSZENIE.

Dodawanie do obu stron równania i
odejmowanie od obu stron równania tych
samych wyrażeń można interpretować także
jako przenoszenie tych wyrażeń na drugą
stronę równania ze znakiem zmienionym na
przeciwny (jeśli był +, po drugiej stronie
równania będzie -, jeśli był – będzie +).
Przy

rozwiązywaniu

bardziej

skomplikowanych

równań

przenoszenie

wyrazów jest o wiele wygodniejsze .

PRZYKŁAD.

Sposób I (jak
wcześniej)

Sposób II
(przenoszenie)

4x + 2 = 3x -1 | - 2

4x + 2 – 2 = 3x – 1 –
2

4x = 3x - 3 | - 3x

4x – 3x = 3x – 3 – 3x

x = - 3

4x

+ 2

=

3x – 1

(przenosimy 2)

4x

=

3x – 1

– 2

4x

=

3x

– 3

(przenosimy

3x)

4x

– 3x

=

-3

x

=

-3

(po zmianie znaku
jest – 2)

(po zmianie znaku
jest – 3x)

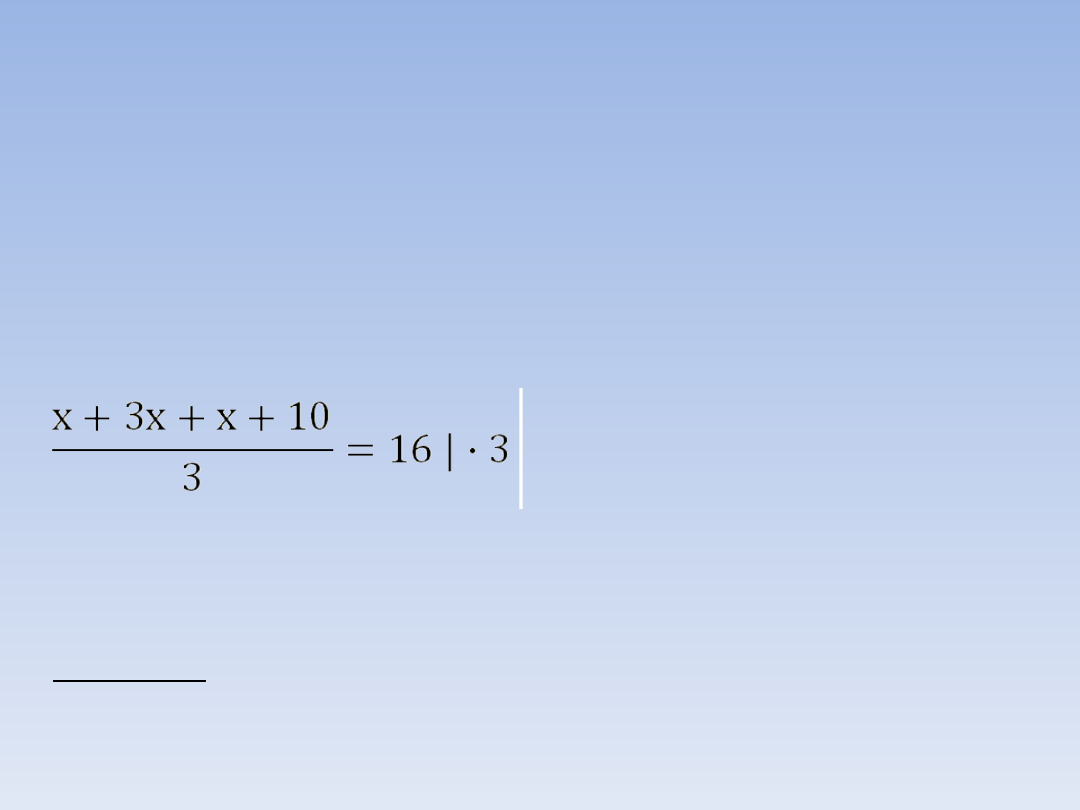
PRZYKŁADOWE ZADANIA.

ZADANIE 1.
Zapisz i rozwiąż odpowiednie równanie.
Średnia arytmetyczna trzech liczb: liczby x,

trzykrotności liczby x i liczby o 10 większej
od x wynosi 16. Co to za liczby?

5x + 10 = 48 | - 10
5x = 38 | : 5
x = 7,6
Te liczby to 7,6; 22,8 oraz 17,6.

PRZYKŁADOWE ZADANIA.

ZADANIE 2.
Dla jakich całkowitych wartości a rozwiązanie
równania ax + 26 = 31 jest liczbą całkowitą?
ax = 31 – 26
ax = 5
Żeby x było całkowite a musi być dzielnikiem
5, a więc mogą to być liczby: 5, -5, 1, -1.

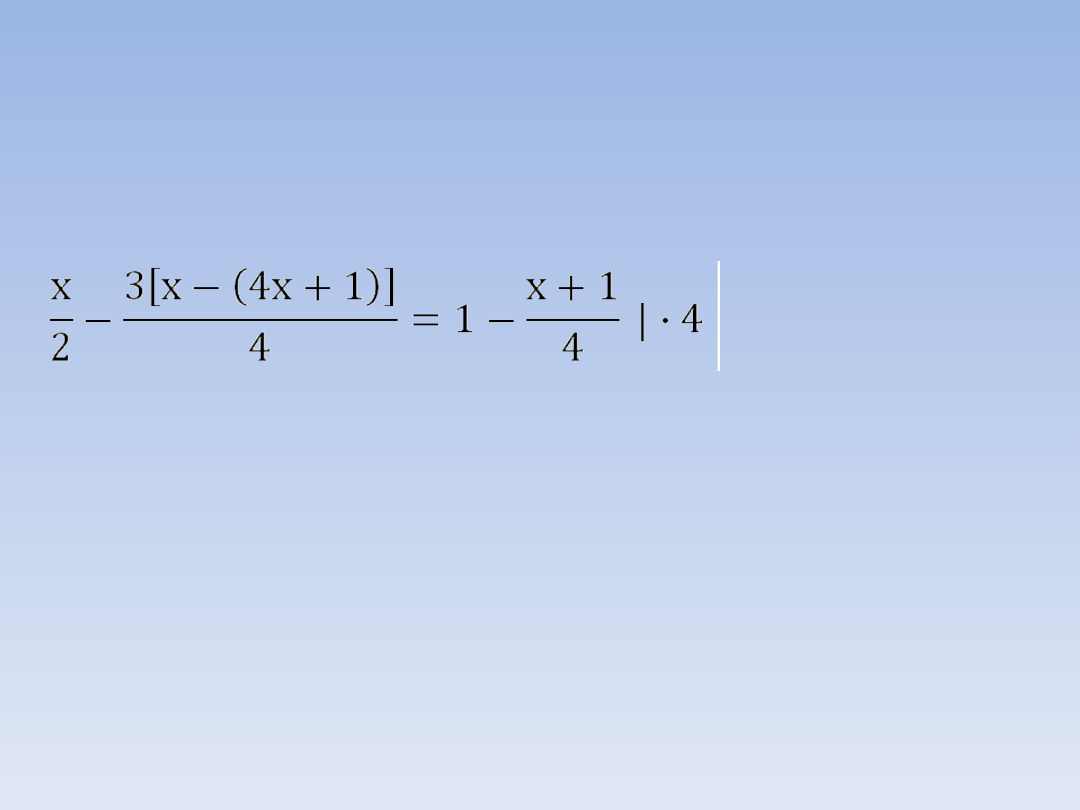
PRZYKŁADOWE ZADANIA.

ZADANIE 3.
Rozwiąż równanie i sprawdź poprawność
rozwiązania.

2x – 3[x – (4x + 1)] = 4 – (x + 1)

(upraszczamy co się da)

2x – 3(x – 4x – 1) = 4 – x – 1
2x – 3(-3x – 1) = -x + 3
2x + 9x + 3 = -x +3
11x + 3 = -x + 3
11x + x = 3 – 3
12x = 0 | : 12

(przenosimy niewiadome na jedną
stronę równania, a liczby na drugą
stronę)

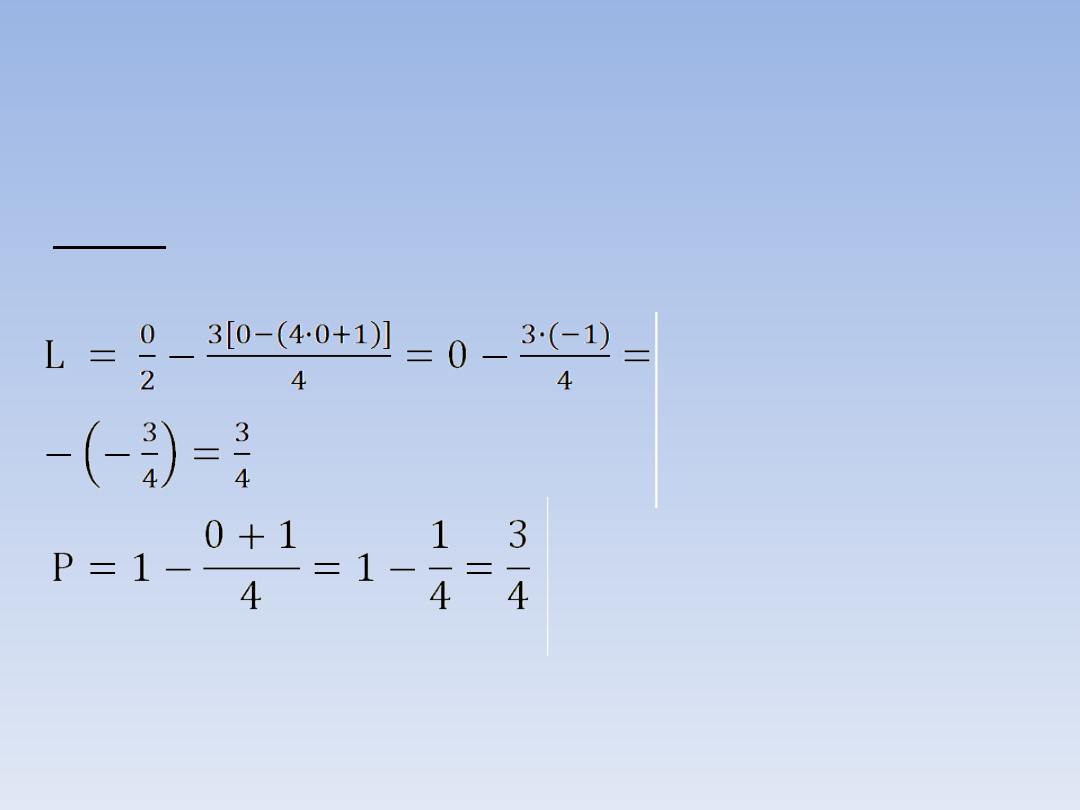
PRZYKŁADOWE ZADANIA.

ZADANIE 3 – ciąg dalszy.
x = 0
Sprawdzamy:

L = P a więc nasze rozwiązanie jest
prawidłowe.