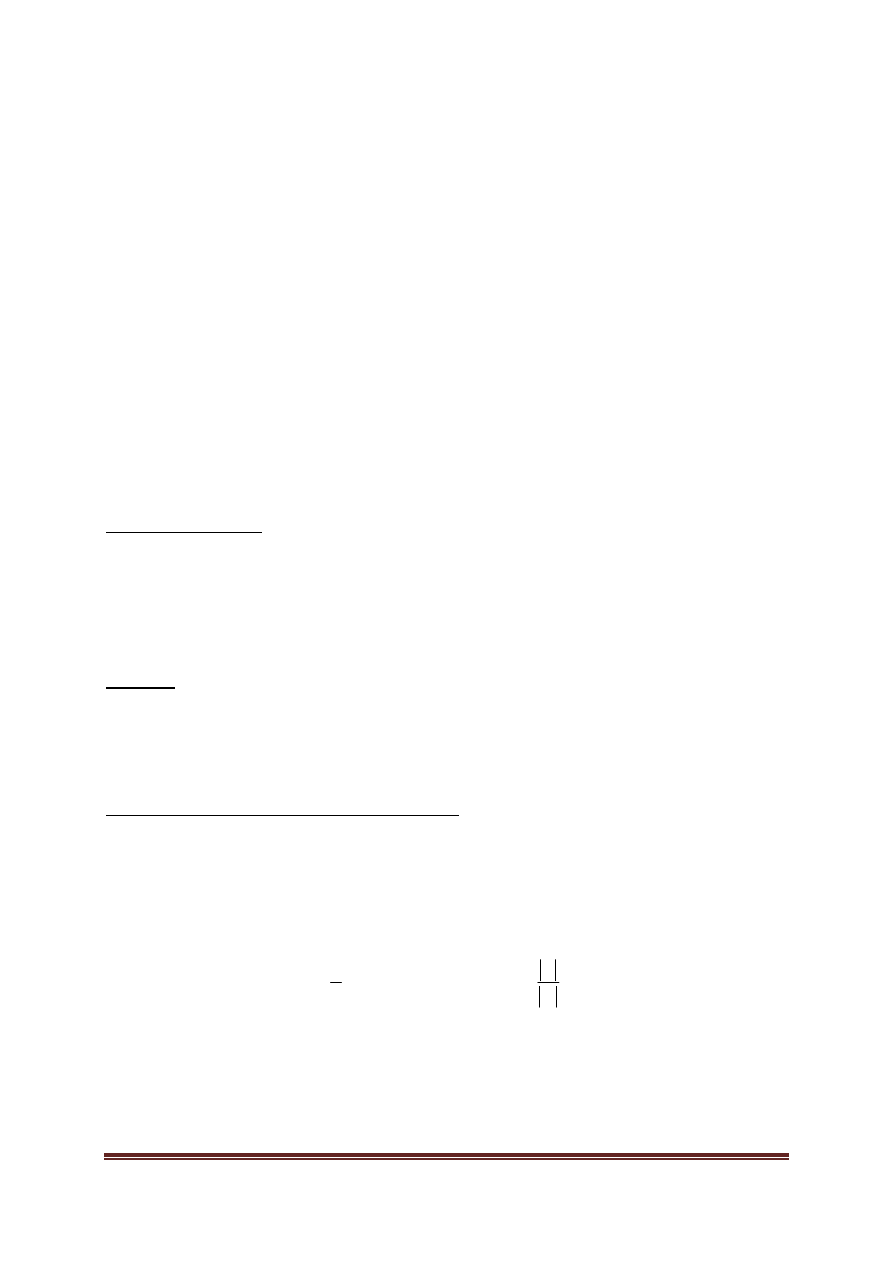
Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację. fraczek@meil.pw.edu.pl . Wersja 07
Strona 1
1 Wykład pierwszy
1.1 Piśmiennictwo
• Oderfeld J.: Statystyczne podstawy prac doświadczalnych, Wydawnictwo Politechniki
Warszawskiej, 1990
• Plucińska A., Pluciński E.: Probabilistyka, WNT, Warszawa 2000
• Gajek L., Kałuszka M.: Wnioskowanie statystyczne, modele i metody. WNT 1996.
• Bobrowski D.: Probabilistyka w zastosowaniach technicznych, WNT 1986
• Majsnerowska Małgorzata: Elementarny wykład z rachunku prawdopodobieństwa
z zadaniami. Skrypt UW, Wrocław 2002.
• Zieliński R.: Tablice statystyczne, PWN, W-wa 1972.
• Pakiety komputerowe: MATLAB – Statistical toolbox, Statistica, Statgraphics
1.2 Pojęcia wstępne
Prawdopodobieństwo:
Niech Ω będzie zbiorem możliwych wyników w doświadczeniu losowym czyli
przestrzenią zdarzeń, elementy Ω to zdarzenia elementarne. Podzbiór
Ω
A
⊂
to zdarzenie, a
jego elementy to zdarzenia elementarne
Φ – zdarzenie niemożliwe,
Ω\A
A'
=
zdarzenie
przeciwne,
B
A
∩ - jednocześnie zaszło A i B,
B
A
∪ - zaszło co najmniej jedno z nich. Jeśli
Φ
B
A
=
∩
- zdarzenia się wykluczają.
Definicje:
1.
{
}
n
Ω
ω
ω
ω
,...,
,
2
1
=
- skończona przestrzeń zdarzeń
Funkcja
( )
n
i
i
i
,...,
2
,
1
P
:
P
=
→
ω
ω
taka, że
( )
( )
1
P
0
P
=
≥
∀
∑
n
i
i
i
i
oraz
ω
ω
, nazywa się
prawdopodobieństwem dyskretnym skończonym.
Dla dowolnego zdarzenia
Ω
A
⊂ :
( )
( )
{
}
∑
⊂
=
A
i
i
P
A
ω
ω
:
1
P
(1.1)
Jeżeli
( )
( )
Ω
=
⇒
=
=
A
A
n
i
n
i
P
,...,
2
,
1
1
P
ω
(1.2)
Jest to klasyczna definicja prawdopodobieństwa.
Sprawdzamy, że:
a)
( )
0
P
≥
A
b) Prawdopodobieństwo sumy skończonej liczby zdarzeń parami wykluczających
się jest równe sumie prawdopodobieństw
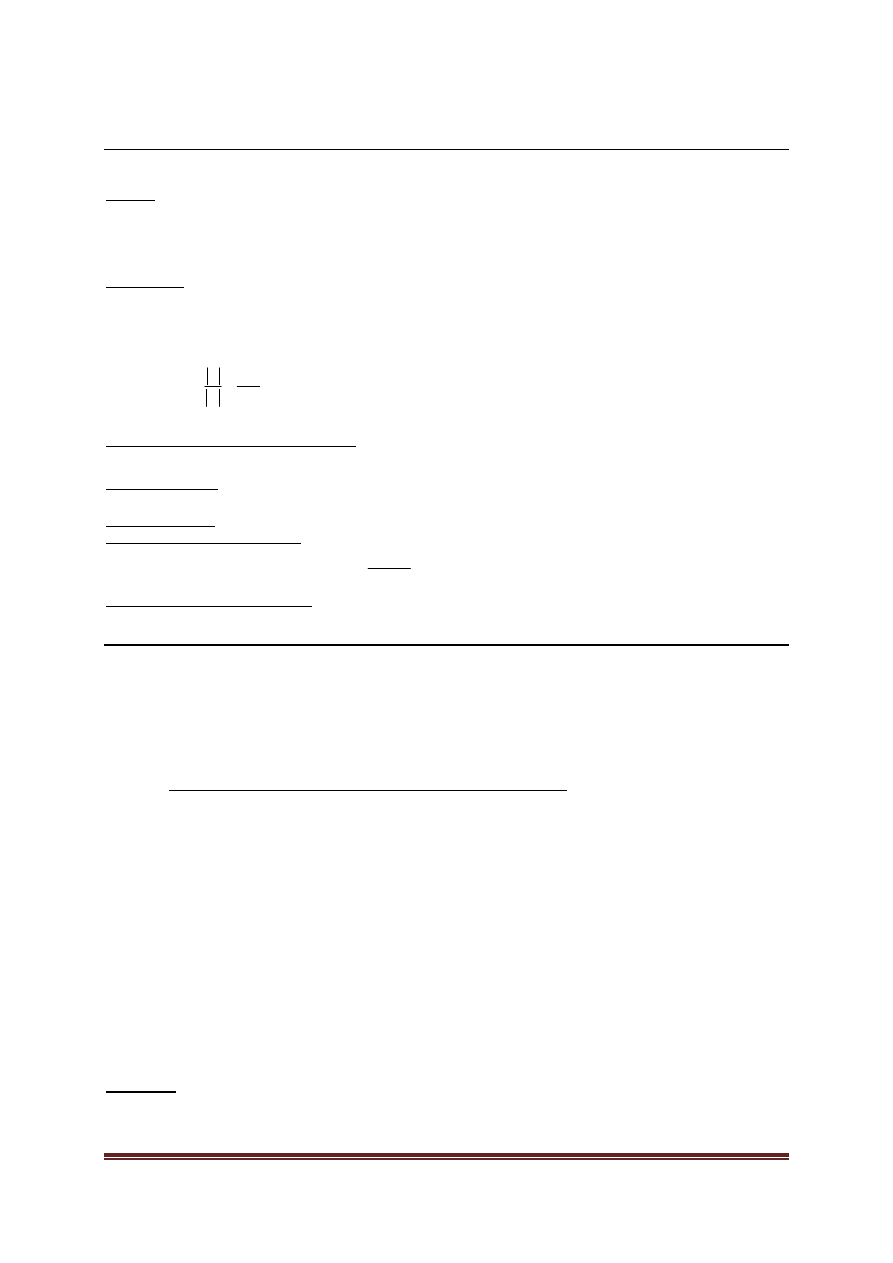
Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację. fraczek@meil.pw.edu.pl . Wersja 07
Strona 2
c)
( )
1
P
=
Ω
PRZYKŁAD 1.1
Zadanie (Bobrowski str. 101)
Dwie radiostacje tego samego typu położone w pewnej odległości od siebie mogą być nastrojone na
jedną z 10 częstotliwości. Jakie jest prawdopodobieństwo, że obie radiostacje nastrojone i włączone niezależnie
będą miały tę samą częstotliwość?
Rozwiązanie
( )
{
}
10
,
,
2
,
1
,
,
K
=
=
Ω
j
i
e
ij
,
e
ij
– zdarzenie elementarne, że pierwsza radiostacja ma częstotliwość i
a druga ma j.
{
}
j
i
e
A
ij
=
=
,
,
( )
%
10
%
100
1
,
0
100
10
P
=
⋅
=
=
Ω
=
A
A
Przypomnienie wzorów z kombinatoryki:
Liczba kombinacji (podzbiorów k elementowych zbioru n-elementowego) k z n:
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
k
n
Liczba permutacji (możliwych wszystkich uporządkowań zbioru zbioru n elementowego):
n!
Liczba wariacji bez powtórzeń (uporządkowań k elementowych wybranych ze zbioru n-elementowego bez
możliwości powtórzeń):
(
)
!
!
!
k
n
n
k
k
n
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
Liczba wariacji z powtórzeniami (uporządkowań k-elementowych wybranych ze zbiorów n-elementowych z
możliwością powtórzeń) :
n
k
2. Jeżeli:
{
}
( )
( )
∑
∞
=
=
=
≥
=
1
2
1
1
,
,
2
,
1
0
P
,
,
i
i
i
P
i
oraz
Ω
ω
ω
ω
ω
K
K
.
(1.3)
to P jest prawdopodobieństwem dyskretnym nieskończonym.
3. Definicja „nowoczesna”
Dana niepusta rodzina F podzbiorów Ω spełniająca warunki:
a) Jeśli:
F
A
∈ , to
F
A
∈
'
b)
Jeśli
K
,
2
,
1
=
∈
i
F
A
i
, to
F
A
i
i
∈
∞
U
nazywa się σ – ciałem.
W przypadku skończonego zbioru
Ω, σ ciało to rodzina wszystkich podzbiorów. Jest
to rodzina
Definicja
Funkcja rzeczywista P określona na podzbiorach przestrzeni
Ω, tworzących σ ciało F
mająca własności:
Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację. fraczek@meil.pw.edu.pl . Wersja 07
Strona 3
a.
( )
0
P
≥
A
b.
j
i
Φ
A
A
j
i
j
i
≠
=
∩
∀
≠
to
∑
∞
=
∞
=
=
1
1
)
(
P
)
(
P
i
i
i
i
A
A
U
c.
( )
1
P
=
Ω
nazywa się prawdopodobieństwem.
Trójka
(Ω,F,P) – to przestrzeń probabilistyczna, a własności a, b, c, to aksjomaty
prawdopodobieństwa
.
Łatwo wykazać, że definicje 1 i 2 są szczególnym przypadkiem definicji 3.
Własności
a)
( ) ( )
B
A
B
A
P
P
≤
⇒
⊂
- monotoniczność
b)
( )
( )
A
A
P
1
'
P
−
=
,
( )
1
P
≤
A
c)
(
) ( ) ( ) (
)
B
A
B
A
B
A
∩
−
+
=
∪
P
P
P
P
d)
( )
∑
=
=
≤
⎟
⎠
⎞
⎜
⎝
⎛
n
i
i
n
i
i
A
A
1
1
P
P
U
- nierówność Boole’a
Dowody pomijamy (zobacz piśmiennictwo)
Prawdopodobieństwo warunkowe
Rozważmy doświadczenie losowe i zwiążmy z nim przestrzeń (
Ω ,F,P). Jeśli
interesuje nas wynik doświadczenia należącego do podzbioru
Ω
⊂
B
, dla którego
P(B)>0 to
możemy zredukować wyjściową przestrzeń probabilistyczną do przestrzeni
(B, F
B
,
)
( B
P
⋅
),
gdzie F
B
={
B
A
∩ ,
F
A
∈ } oraz
(
)
(
)
( )
F
A
dla
B
B
A
B
A
∈
∩
=
P
P
|
P
(1.4)
Jest to prawdopodobieństwo warunkowe zdarzenia A pod warunkiem, że zaszło B lub
krócej, prawdopodobieństwem A pod warunkiem B.
Zauważmy, że wzór (1.4) jest równoważny zależności:
(
) (
) ( )
B
P
B
A
B
A
⋅
=
∩
|
P
P
o ile
( )
0
P
>
B
(1.5)
Prawdopodobieństwo całkowite
Jeżeli ciąg zdarzeń
{
}
n
i
B
i
,...,
1
,
=
tworzy zupełny układ zdarzeń w przestrzeni
Ω
(tzw. rozbicie przestrzeni) tzn. spełnione są trzy warunki:
U
n
i
i
B
1
=
=
Ω
, P(B
i
)>0 oraz
Φ
B
B
j
i
j
i
=
∩
∧
≠
to dla dowolnego
F
A
∈ zachodzi:
( )
(
) ( )
i
n
i
i
B
B
A
A
P
|
P
P
1
∑
=
⋅
=
(1.6)
Jest to wzór na prawdopodobieństwo całkowite.
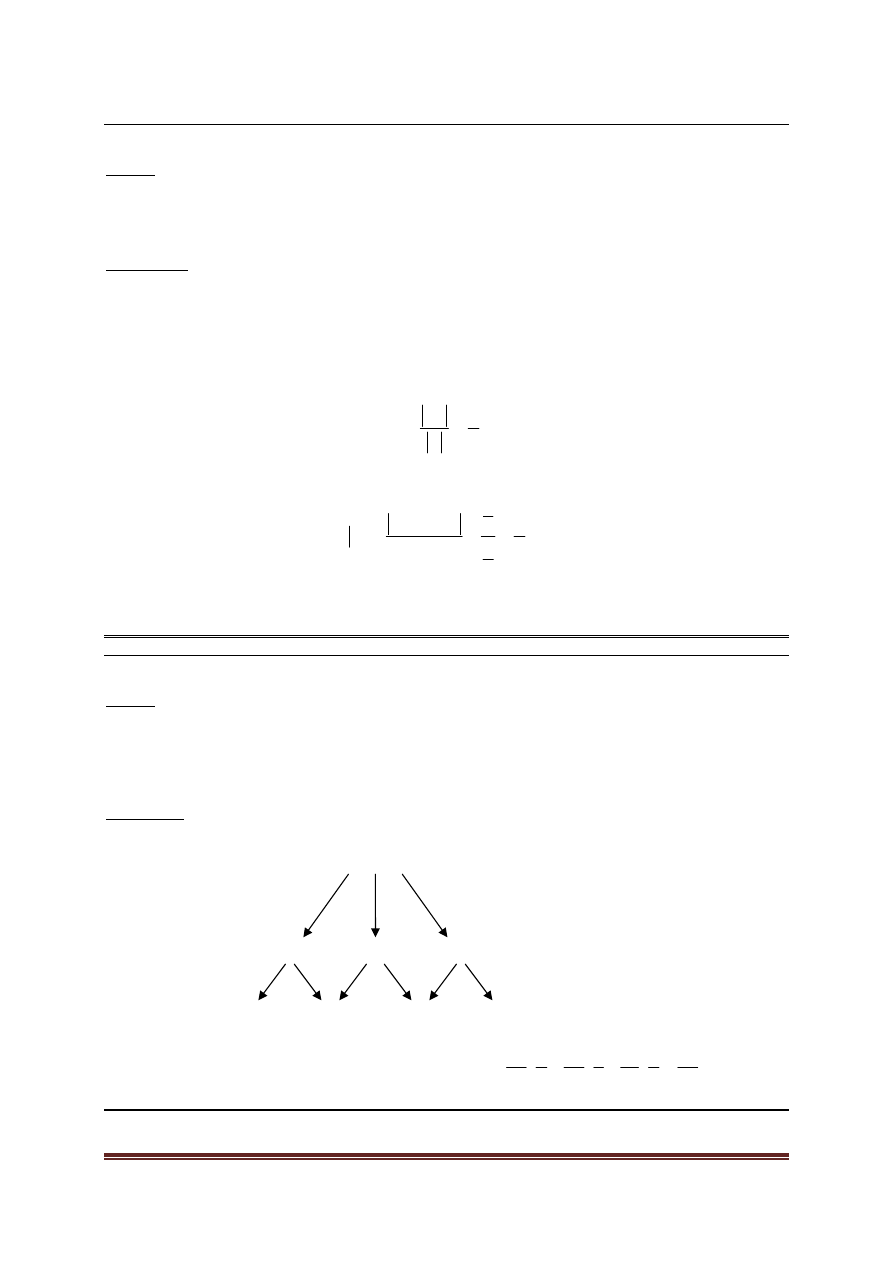
Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację. fraczek@meil.pw.edu.pl . Wersja 07
Strona 4
PRZYKŁAD 1.2
Zadanie (ilustrujące wzór na prawdopodobieństwo warunkowe)
„Podpatrzyliśmy”, że ktoś wpisuje trzyliterowe hasło do komputera korzystając tylko z klawiszy a oraz
b. Ponadto zauważyliśmy, że pierwszy znak hasła jest litera a. Jaka jest szansa, że trafimy wybierając jako drugą
literę znak b i jako trzecią literę znak b ?
Rozwiązanie:
Zadanie rozwiążemy na dwa sposoby.
1. Zauważmy, że:
(
) (
) (
) (
) (
) (
) (
) (
)
{
}
b
b
b
a
b
b
b
a
b
a
a
b
b
b
a
a
b
a
b
a
a
a
a
a
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
=
Ω
(a)
Rozważmy nową przestrzeń zdarzeń elementarnych
(
) (
) (
) (
)
{
}
b
b
a
a
b
a
b
a
a
a
a
a
S
,
,
,
,
,
,
,
,
,
,
,
=
i jej podzbiór
zdarzenie
(
)
{
}
b
b
a
D
S
,
,
=
. W takim razie:
4
1
)
(
=
=
S
D
D
P
S
S
(b)
2. Wykorzystamy teraz wzór (1.4):
4
1
8
4
8
1
)
(
)
(
)
(
=
=
∩
=
S
P
S
D
P
S
D
P
S
(b)
A zatem wynik jest ten sam.
PRZYKŁAD 1.3
Zadanie ( prawdopodobieństwo całkowite)
Student na zajęcia dojeżdża rowerem raz na dwa dni (zdarzenie R), autobusem raz na trzy dni
(zdarzenie A) oraz tramwajem raz na sześć dni (zdarzenie T). Jeśli jedzie rowerem spóźnia się raz na 60
przypadków, jeśli autobusem raz na 20 przypadków, jeśli tramwajem raz na 10 przypadków. Jakie jest
prawdopodobieństwo spóźnienia się studenta (zdarzenie S)?
Rozwiązanie
Drzewo modelu – dendryt.
( ) (
) ( ) (
) ( ) (
) ( )
24
1
6
1
10
1
3
1
20
1
2
1
60
1
|
|
|
=
⋅
+
⋅
+
⋅
=
⋅
+
⋅
+
⋅
=
T
P
T
S
P
A
P
A
S
P
R
P
R
S
P
S
P
1/2
R
1/3
A
1/6
T
1/60
S
Z
S
Z
S
Z
1/20 1/10
R – rower
A – autobus
T – tramwaj
S – spóźnienie
Z – zdążenie

Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację. fraczek@meil.pw.edu.pl . Wersja 07
Strona 5
Wzór Bayesa
Przy założeniach poprzedniego twierdzenia dla dowolnego zdarzenie
F
A
∈ takiego,
że
( )
0
>
A
P
. Zachodzi:
(
)
(
) ( )
(
) ( )
∑
=
⋅
⋅
=
n
i
i
i
i
i
i
B
B
A
B
B
A
A
B
1
P
|
P
P
|
P
|
P
n
i
,...,
1
=
(1.7)
Nomenklatura:
P(B
i
|A) - prawdopodobieństwo a'posteriori
1
P(B
i
) - prawdopodobieństwo a'priori
2
Wzór (1.7) nosi nazwę wzoru na prawdopodobieństwo przyczyny
PRZYKŁAD 1.4
Zadanie
W magazynie znajdują się monitory komputerowe wyprodukowane w trzech różnych oddziałach firmy,
w tym: 50% z oddziału w Polsce (R), 30% z oddziału w Chinach (C), 20% z oddziału w Japoni (J). Wiadomo, że
prawdopodobieństwo wyprodukowania monitora wadliwego (plamki na ekranie) jest równe 0,05 dla oddziału
(R) i (C) oraz 0,12 dla oddziału w (J). Odbiór odbywa się na podstawie kontroli wyrywkowej. Załóżmy, że
wylosowany wyrywkowo monitor okazał się wadliwy, jakie jest prawdopodobieństwo, że jest to monitor
wyprodukowany w Polsce.
Rozwiązanie
a) a’priori,
A - monitor jest wadliwy:
P(R) = 0,5
P(C) = 0,3
P(J) = 0,2
P(A|R) = 0,05 = P(A|C)
P(A|J) = 0,12
b) a’posteriori:
(
)
(
) ( )
(
) ( ) (
) ( ) (
) ( )
391
,
0
064
,
0
025
,
0
2
.
0
12
,
0
3
.
0
05
,
0
5
.
0
05
,
0
5
.
0
05
,
0
P
|
P
|
P
|
|
P
|
P
=
=
⋅
+
⋅
+
⋅
⋅
=
⋅
+
⋅
+
⋅
⋅
=
J
J
A
C
P
C
A
R
P
R
A
P
R
P
R
A
A
R
Niezależność zdarzeń
Niech
F
B
A
∈
,
będą zdarzeniami takimi, że P(A|B) =P(A), czyli zajście B nie zmienia
prawdopodobieństwa zajścia A. Czyli A jest niezależne, od B tzn:
(
) ( ) ( )
B
P
A
B
A
⋅
=
∩
P
P
(1.8)
Uogólnienie:
Niech C będzie dowolną rodziną zdarzeń. Jeśli dla skończonej podrodziny {A
1
,A
2
,...,A
n
}
zdarzeń z C spełniony jest warunek:
1
a'posteriori – na podstawie faktów, z następstwa,
2
a'priori – bez zapoznania się z faktami, uprzedzając fakty, przed doświadczeniem, z góry.

Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację. fraczek@meil.pw.edu.pl . Wersja 07
Strona 6
( )
∏
=
=
=
⎟
⎠
⎞
⎜
⎝
⎛
n
i
i
n
i
i
A
A
1
1
P
P
I
(1.9)
to C nazywamy rodziną zdarzeń niezależnych.
Uwaga:
Niezależność wg wzoru (1.9) jest własnością silniejszą, niż niezależność parami.
PRZYKŁAD 1.5
Zadanie
Mamy dużą partię uszkodzonych dysków. Dyski są uszkodzone bo ¼ z nich piszczy, ¼ pracuje
niestabilnie, 1/4 się grzeje a ¼ ma wszystkie wymienione wady. Niech: A zdarzenie, że pierwszy losowo
wybrany dysk piszczy a B i C, że pracuje niestabilnie lub się grzeje. Czy zdarzenia A, B i C stanowią rodzinę
zdarzeń wzajemnie niezależnych?
Rozwiązanie
( ) ( ) ( )
2
1
P
P
P
=
=
=
C
B
A
(
) (
) (
)
4
1
P
P
P
=
∩
=
∩
=
∩
C
B
C
A
B
A
(
) ( ) ( ) (
) ( ) ( ) (
) ( ) ( )
;
P
P
P
;
P
P
P
;
P
P
C
B
C
B
C
A
C
A
B
P
A
B
A
⋅
=
∩
⋅
=
∩
⋅
=
∩
(
) ( ) ( ) ( )
8
1
P
P
P
P
4
1
=
⋅
⋅
≠
∩
∩
=
C
B
A
C
B
A
Czyli zdarzenia A, B i C nie stanowią rodziny zdarzeń wzajemnie niezależnych
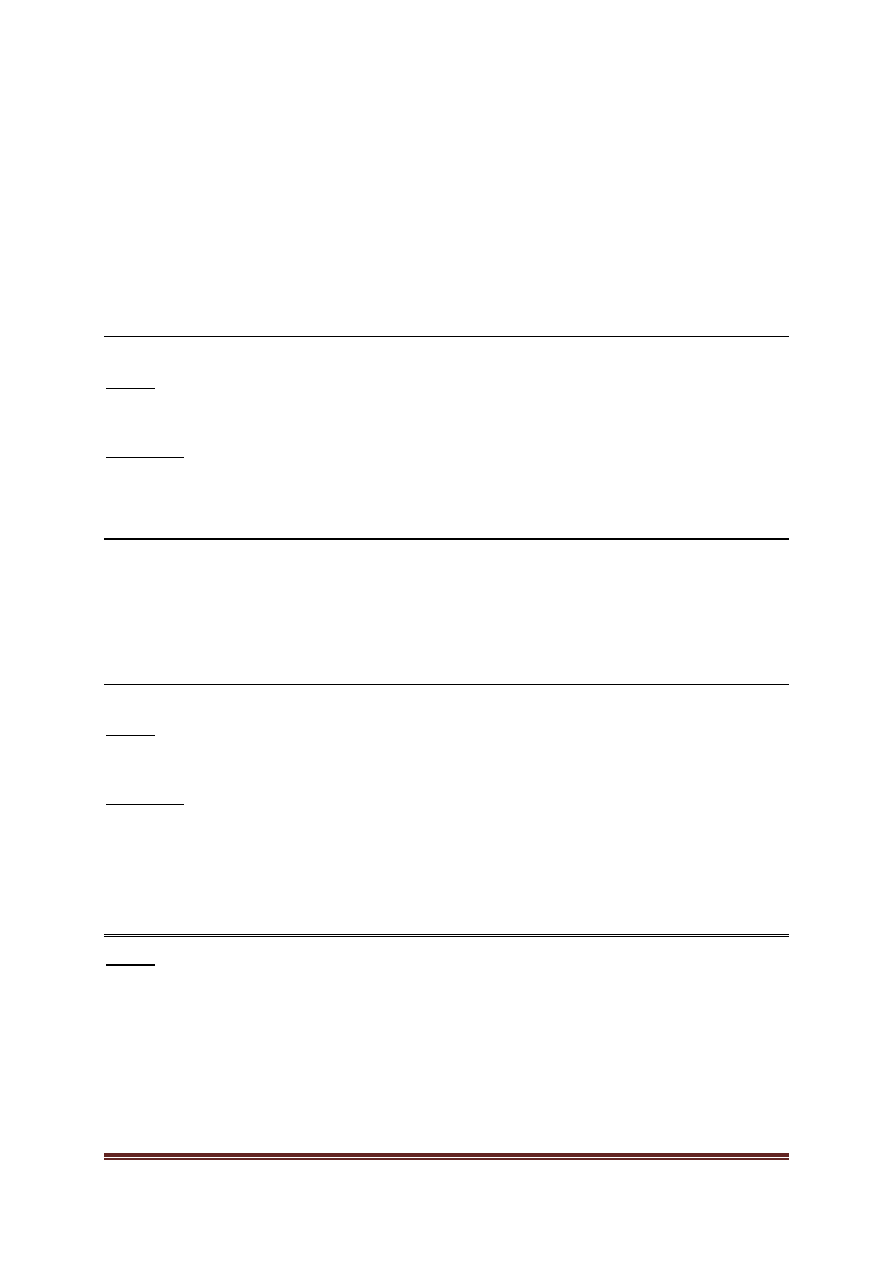
Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację. fraczek@meil.pw.edu.pl . Wersja 07
Strona 7
2 Wykład drugi
2.1 Zmienna losowa jednowymiarowa.
Weźmy trojkę probabilistyczną ( Ω ,F,P). Wprowadzimy definicję:
Funkcję
R
→
X:Ω
nazywamy zmienną losową jednowymiarową, jeśli dla
każdego
R
∈
a
zbiór
((
)
)
,
1
a
X
∞
−
−
jest zdarzeniem, czyli:
((
)
F
a
X
∈
∞
−
−
)
,
1
. Realizacją
zmiennej losowej nazywa się wartość funkcji X w punkcie i oznacza małą literą x.
PRZYKŁAD 2.6
Zadanie
Weźmy dyski komputerowe. Losujemy z partii jeden i sprawdzamy, czy jest sprawny. Jeśli jest
stawiamy 1 jeśli nie 0.
Rozwiązanie
{
}
nsp
sp
ω
ω
,
=
Ω
, a zbiorem wartości jest zbiór {0,1}. Zmienna losowa przyjmuje wartość z pewnym
prawdopodobieństwem.
W przypadku pomiarów fizycznych obarczonych błędem przypadkowym jako
zmienną losową przyjmuje się wprost funkcję, której realizacjami są wyniki pomiaru.
Rozkładem zmiennej losowej X nazywamy funkcję prawdopodobieństwa
przyporządkowującą zadanemu przedziałowi
(
)
x
,
∞
−
wartości
( )
{
}
(
)
x
X
<
ω
ω
:
P
, gdzie P jest
funkcją prawdopodobieństwa.
PRZYKŁAD 2.7
Zadanie
Dla danych z przykładu 2.6 zakładamy, że
( )
8
,
0
P
=
sp
ω
,
( )
2
,
0
P
=
nsp
ω
Rozwiązanie
Rozkład zmiennej losowej X definiuje się więc według wzoru:
(
)
⎪⎩
⎪
⎨
⎧
<
≤
<
≤
=
<
x
gdy
x
gdy
x
gdy
x
X
1
1
1
0
2
,
0
0
0
P
Uwagi
• Zmienne losowe przyjmujące tę samą wartość, ale z różnym prawdopodobieństwem (o
różnych rozkładach) uważamy za różne.
• W niektórych przypadkach wygodne jest posługiwanie się funkcją prawdopodobieństwa,
którą określa się na zbiorach punktowych w następujący sposób:
( ) (
)
x
X
x
=
= P
P
(2.10)
Funkcję taką nazywa się funkcją prawdopodobieństwa zmiennej losowej X.

Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację. fraczek@meil.pw.edu.pl . Wersja 07
Strona 8
2.2 Typy zmiennych losowych
W klasycznych wykładach rachunku prawdopodobieństwa i statystyki wyróżniamy zwykle:
1. Zmienne losowe typu skokowego (dyskretną) (oznaczymy SK)
2. Zmienną losową typu ciągłego (albo w skrócie ciągłą) (oznaczymy C)
3. Zmienne losowe mieszane
Zmienna typu skokowego (SK)
przyjmuje ściśle określone, dyskretne wartości
liczbowe ,...
3
,
2
,
1
=
i
x
i
(może być skończone, albo nie), czyli
(
)
i
i
p
x
X
P
=
=
. Z własności
prawdopodobieństwa 1
1
=
∑
=
n
i
i
p
dla zmiennej o skończonej liczbie wartości, oraz
1
1
=
∑
∞
=
i
i
p
gdy ma nieskończoną liczbę wartości.
Znając pary uporządkowane (x
i
, p
i
) mamy pełną informacje o rozkładzie zmiennej
losowej skokowej.
Funkcję prawdopodobieństwa skokowej zmiennej losowej można zapisać w postaci:
( )
(
)
⎩
⎨
⎧
=
=
=
=
poza
x
x
dla
p
x
X
x
i
i
i
0
P
P
(2.11)
Zmienna losowa typu ciągłego (C)
Mówimy, że zmienna losowa jest typu ciągłego jeżeli istnieje nieujemna funkcja
( )
x
f
taka, że
( )
0
≥
x
f
, całka
( )
1
=
∫
R
x
f
(lub
( )
1
=
∫
∞
∞
−
x
f
) i dla każdego przedziału
2
1
, x
x
{
}
(
)
∫
=
≤
≤
2
1
)
(
)
(
:
P
2
1
x
x
dx
x
f
x
X
x
ω
ω
(2.12)
Dystrybuanta
Dla zmiennej losowej X jest to funkcja (zwyczajowo oznaczana dużą literą F albo F
X
)
1
,
0
→
R
F:
taka, że:
( ) (
)
x
X
x
F
<
= P
(2.13)
Własności dystrybuanty:
1. Dystrybuanta jest funkcją niemalejącą tzn:
( )
( )
2
1
2
1
2
1
,
x
F
x
F
x
x
x
x
≤
⇒
<
∈
∀
R
2.
(
)
( ) ( )
1
2
2
1
2
1
P
,
x
F
x
F
x
X
x
x
x
−
=
<
≤
∈
∀
R
3.
( )
( )
0
lim
1
lim
=
=
−∞
→
∞
→
x
F
x
F
x
x
4. Jest funkcją co najmniej lewostronnie ciągłą
( )
( )
0
0
lim
x
F
x
F
x
x
=
−
→
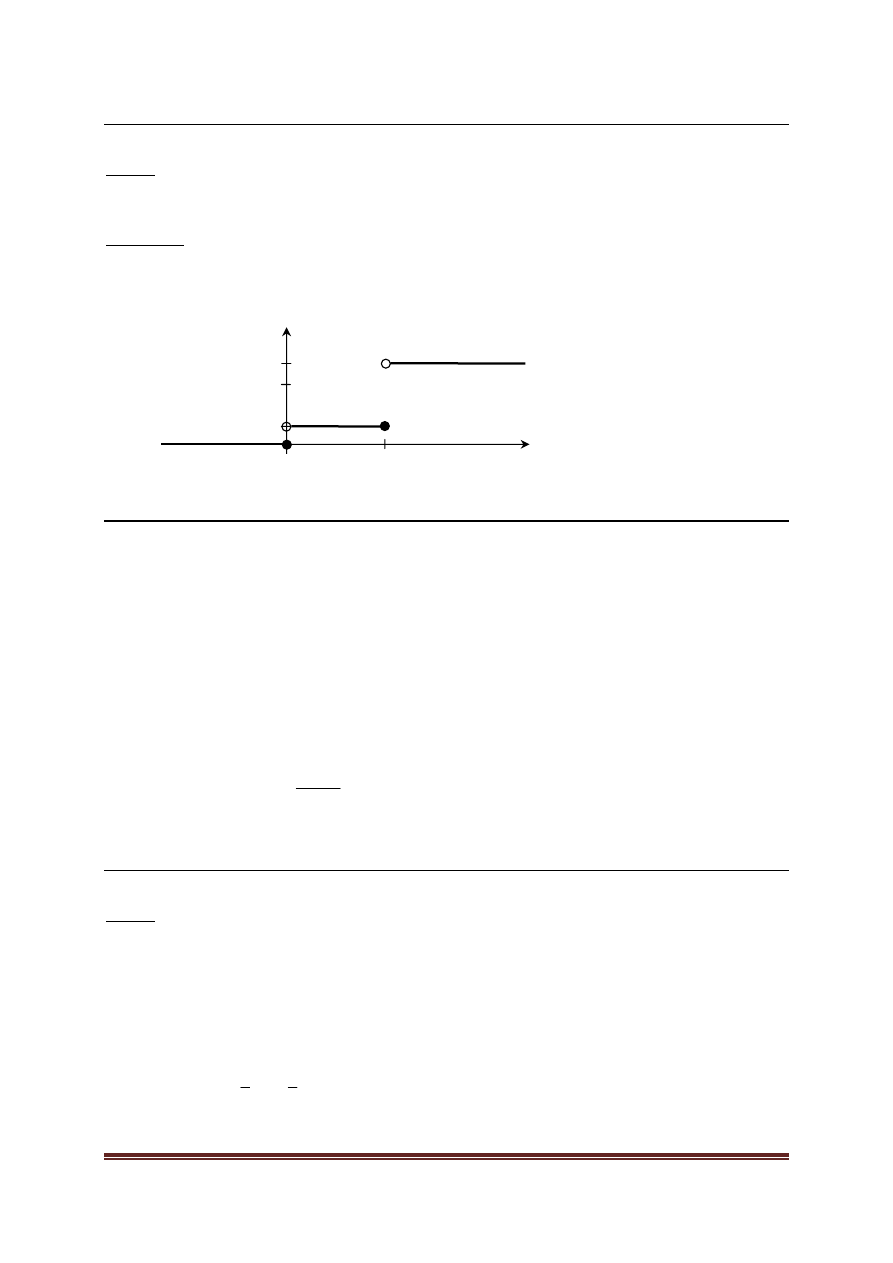
Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację. fraczek@meil.pw.edu.pl . Wersja 07
Strona 9
PRZYKŁAD 2.8
Zadanie
Narysować wykres dystrybuanty zmiennej losowej (SK) z przykładu 2.7
Rozwiązanie
⎪⎩
⎪
⎨
⎧
<
≤
<
≤
=
x
gdy
x
gdy
x
gdy
x
F
1
1
1
0
2
,
0
0
0
)
(
Na ogół dystrybuanta nie jest w każdym punkcie ciągła prawostronnie, Różne zmienne
losowe mogą tę samą dystrybuantę. Jeśli X jest zmienną losową ciągłą to dodatkowo
zachodzą następujące własności dla dystrybuanty:
5.
( )
( )
0
0
0
lim
x
F
x
F
x
x
x
=
∀
+
→
prawostronna ciągłość
6.
(
)
0
P
0
0
=
=
∈
∀
x
X
x
R
7.
(
)
( )
∫
−
=
=
≤
≤
∈
∀
2
1
)
(
)
(
P
,
1
2
2
1
2
1
x
x
x
F
x
F
dt
t
f
x
X
x
x
x
R
8. W każdym punkcie ciągłości gęstości prawdopodobieństwa f(x) dystrybuanta F jest
różniczkowalna i:
( )
( )
x
f
dx
x
dF
=
Zwróćmy uwagę, że z uwagi 6 wynika, że fakt iż prawdopodobieństwo zdarzenia jest
równe zero nie oznacza, zdarzenie nie jest możliwe.
PRZYKŁAD 2.9
Zadanie
Zmienna losowa (C) ma funkcję gęstości
( )
⎩
⎨
⎧
≤
≤
=
poza
x
cx
x
f
0
1
0
3
Należy:
1. Obliczyć stałą c
2. Znaleźć dystrybuantę
3. Narysować wykres gęstości i dystrybuanty
4. Znaleźć
⎟
⎠
⎞
⎜
⎝
⎛
≤
≤
−
2
1
2
1
P
x
F(x)
x
0,2
0,8
1
1
0.2

Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację. fraczek@meil.pw.edu.pl . Wersja 07
Strona 10
Rozwiązanie
Ad 1. Ponieważ
( )
1
=
∫
R
x
f
to:
4
1
4
1
0
3
=
⇒
=
=
∫
c
c
dx
cx
Ad 2.
( )
( )
⎪
⎩
⎪
⎨
⎧
≥
<
<
≤
=
=
=
∫
∫
∞
−
∞
−
1
1
1
0
0
0
4
4
3
x
dla
x
dla
x
x
dla
dt
t
x
f
x
F
x
x
Ad 3.
Ad 4.
( )
( ) ( )
16
1
2
1
2
1
2
1
2
1
2
1
P
4
2
1
2
1
=
=
−
−
=
=
⎟
⎠
⎞
⎜
⎝
⎛
≤
≤
−
∫
−
F
F
dx
x
f
x
x
1
x
1
F(x)
f(x)
4 1

Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację. fraczek@meil.pw.edu.pl . Wersja 07
Strona 11
3 Wykład trzeci
3.1 Charakterystyki liczbowe zmiennych losowych
Rozkład zmiennej losowej może być jednoznacznie określony przez podanie
prawdopodobieństwa każdej możliwej wartości zmiennej losowej, bądź przez podanie
analitycznej postaci dystrybuanty lub gęstości prawdopodobieństwa. W praktyce zamiast
pełnej informacji o rozkładzie prawdopodobieństwa podaje się kilka charakterystycznych
parametrów, które opisują własności zmiennych losowych. Do najważniejszych
charakterystyk należą miary położenia i miary rozrzutu. Do miar położenia należą wartość
oczekiwana i kwantyle (w szczególności mediana i kwartale) natomiast do miar rozrzutu
wariancja i odchylenie standardowe. Ponadto omówimy pojęcia momentów zwykłych i
centralnych.
Wartość oczekiwana
( inaczej nadzieja matematyczna, wartość przeciętna, wartość średnia)
Wartość oczekiwana to jest liczba określona wzorem:
( )
( )
( ) ( )
⎪
⎩
⎪
⎨
⎧
=
∫
∑
R
i
i
i
C
dx
x
xf
SK
p
x
X
E
(3.14)
o ile szereg i całka są bezwzględnie zbieżne.
Uwaga
W piśmiennictwie wartość oczekiwaną zapisuje się EX, E[X] lub E(X). Przyjmiemy
zapis E(X).
W przypadku jeśli funkcja Y jest funkcją złożoną X tzn. Y = g(X) to wartość
oczekiwaną oblicz się ze wzoru:
( )
( )
[
]
( )
( )
( ) ( )
( )
⎪
⎩
⎪
⎨
⎧
=
=
∫
∑
R
i
i
i
C
dx
x
f
x
g
SK
p
x
g
X
g
Y
E
E
(3.15)
PRZYKŁAD 3.10
Zadanie
Dana jest zmienna losowa (SK) określona następująco (funkcja prawdopodobieństwa):
(
)
⎪⎩
⎪
⎨
⎧
−
=
=
−
=
=
−
=
=
=
=
pozostało
x
x
x
x
x
x
dla
x
X
P
i
0
4
;
3
;
5
;
4
;
1
;
2
6
1
6
5
4
3
2
1
Należy obliczyć wartość oczekiwaną zmiennej losowej X.
Rozwiązanie
( )
(
)
6
1
4
3
5
4
1
2
6
1
6
1
−
=
−
+
−
+
−
=
=
∑
=
i
i
i
p
x
X
E
Wynik można interpretować następująco.

Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację. fraczek@meil.pw.edu.pl . Wersja 07
Strona 12
Gramy w kości, jeśli wypadnie 1 to dostajemy 2 zł, jeśli wypadnie 2 to płacimy 1 zł, jeśli wypadnie 3 to
dostajemy 4zł, itd. W grę gramy bardzo długo. Pytanie jaka jest średnia wygrana przypadająca na grę?
(
)
6
1
6
4
3
5
4
1
2
6
−
=
−
=
−
+
−
+
−
n
n
n
n
PRZYKŁAD 3.11
Zadanie
Podamy analogię mechaniczną do wartości oczekiwanej.
Pytanie: Jakie jest położenie środka masy układu?
Rozwiązanie
Masa układu wynosi
∑
=
i
i
m
M
,
Więc położenie środka ciężkości można wyznaczyć jako:
i
i
i
c
i
i
i
c
x
M
m
x
x
m
x
M
⋅
=
⇒
=
⋅
∑
∑
Wyrażenie
M
m
i
jest odpowiednikiem
i
p
, bo
1
=
∑
i
i
M
m
Własności wartości oczekiwanej
Ponieważ wartość oczekiwana jest określana jako suma lub całka, to ma następujące
własności:
1) gdy
(
)
R
∈
=
c
c
X
to
( )
( )
c
c
X
=
= E
E
(3.16)
2) Dla dowolnych stałych
n
i
a
i
,...
2
,
1
=
∈ R
( )
i
n
i
i
n
i
i
i
X
a
X
a
E
E
1
1
∑
∑
=
=
=
⎟
⎠
⎞
⎜
⎝
⎛
(3.17)
Momenty zmiennej losowej
Momentem zwykłym rzędu
(
)
N
k
k
∈
zmiennej losowej
X nazywamy liczbę
( )
k
k
X
m
E
=
tzn.
( )
( ) ( )
⎪
⎩
⎪
⎨
⎧
=
∫
∑
C
dx
x
f
x
SK
p
x
m
R
k
i
k
k
i
k
(3.18)
Jeśli suma i całka istnieją
m
1
m
2
m
3
x
1
x
2
x

Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację. fraczek@meil.pw.edu.pl . Wersja 07
Strona 13
Dla
( )
( )
X
X
m
k
E
E
1
1
1
=
=
=
jest momentem rzędu pierwszego. Jest widoczne, że
moment rzędu pierwszego jest wartością . Czasem stosuje się oznaczenie
μ
=
1
m
.
Momentem centralnym rzędu k zmiennej losowej X nazywamy liczbę:
( )
[
]
{
}
(
)
[
]
k
k
k
X
X
X
μ
μ
−
=
−
=
E
E
E
(3.19)
Moment centralny rzędu 2,
2
μ nazywamy wariancją i oznaczamy
( )
X
D
2
, czasem
( )
X
Var
. Pierwiastek kwadratowy z wariancji nazywany odchyleniem standardowym
i oznaczamy
σ .
( )
X
2
2
D
=
σ
lub
( )
X
2
D
=
σ
(3.20)
Można zauważyć, że:
( )
(
)
[
]
(
)
( )
( )
( )
2
1
2
2
2
2
2
2
2
2
E
E
2
E
2
E
E
D
m
m
X
X
X
X
X
X
k
−
=
+
−
=
+
−
=
−
=
=
=
μ
μ
μ
μ
μ
σ
μ
(3.21)
Własności wariancji
1) Gdy
(
)
R
∈
=
c
c
X
to
( )
( )
0
D
D
2
2
=
=
c
X
2) Jeżeli c jest dowolną stałą to
( )
( )
X
c
cX
2
2
2
D
D
=
3) Jeśli
R
∈
c
to
(
)
( )
X
c
X
2
2
D
D
=
+
(przesunięcie)
(3.22)
Wariancja i odchylenie standardowe są miarą rozproszenia zmiennej losowej.
PRZYKŁAD 3.12
Zadanie
W teorii niezawodności i w teorii masowej obsługi stosuje się zmienne losowe o rozkładzie
wykładniczym. Są to zmienne losowe ciągłe o funkcji ciągłości określonej wzorem:
⎩
⎨
⎧
>
≥
<
=
−
0
0
0
0
)
(
λ
λ
λ
i
x
e
x
x
f
x
Należy obliczyć wartość oczekiwaną i odchylenie standardowe zmiennej losowej o rozkładzie wykładniczym.
Rozwiązanie
Wartość oczekiwana (całkowanie przez części)
f(x)
λ
x
0

Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację. fraczek@meil.pw.edu.pl . Wersja 07
Strona 14
( )
( )
λ
λ
λ
λ
λ
λ
λ
λ
λ
1
1
lim
2
0
2
0
0
=
=
⎥⎦
⎤
⎢⎣
⎡
−
−
=
=
=
−
−
∞
→
∞
−
∞
∫
∫
T
x
x
T
x
e
e
x
dx
xe
dx
x
xf
X
E
bo:
x
x
x
x
x
x
e
e
x
dx
e
e
x
x
v
e
u
dx
xe
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
−
−
−
−
−
−
−
−
=
−
−
=
=
=
=
∫
∫
2
1
Wariancja:
( )
2
1
2
2
2
2
m
m
X
D
−
=
=
=
σ
μ
( )
( )
2
0
0
2
0
2
0
2
2
2
2
2
lim
λ
λ
λ
λ
λ
λ
λ
λ
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
⎥
⎦
⎤
⎢
⎣
⎡
−
⋅
=
=
=
=
∫
∫
∫
∞
−
−
∞
→
∞
−
∞
dx
e
x
e
x
dx
e
x
dx
x
f
x
m
X
E
x
T
x
T
x
( )
2
2
2
2
1
2
2
2
2
1
1
2
λ
λ
λ
σ
μ
=
⎟
⎠
⎞
⎜
⎝
⎛
−
=
−
=
=
=
m
m
X
D
Kwantyle
Liczbę
(
)
1
0
<
< p
x
p
nazywamy kwantylem rzędu p zmiennej losowej X, gdy
spełnione są następujące warunki:
(
)
p
x
X
p
≥
≤
P
oraz
(
)
p
x
X
p
−
≥
≥
1
P
(3.23)
Nierówności
(3.23)
nie wyznaczają kwantyli jednoznacznie. Jeżeli zmienna losowa jest ciągła,
to kwantyl rzędu p można wyznaczyć z równania:
( )
p
x
F
p
= .
Kwantyl rzędu ½ nazywa się medianą, a kwantyle rzędu ¼ i ¾ nazywa się kwartynami
(czasem kwartylami rzędu 1 i 3).
Graficzna interpretacja kwantyli
Pole równe p tzn.
( )
(
)
p
p
x
X
P
p
x
F
≤
=
=
Pole równe 1- p tzn.
(
)
p
x
X
P
≥
Rysunek 3.1 Graficzna interpretacja kwantyli
f(x)
x
0
x
p
Pole równe p
Pole równe 1-p

Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację. fraczek@meil.pw.edu.pl . Wersja 07
Strona 15
4 Wykład czwarty
4.1 Zmienna losowa dwuwymiarowa
Niech dana będzie trójka probabilistyczną ( Ω ,F,P). Zmienna losowa dwuwymiarowa
(lub inaczej dwuwymiarowy wektor losowy) jest to uporządkowana para zmiennych
losowych (X,Y) określona na przestrzeni zdarzeń elementarnych
2
:
)
,
(
R
→
Ω
Y
X
. Zmienne
X, Y nazywa się składowymi wektora losowego. Rozkład prawdopodobieństwa zmiennej
dwuwymiarowej (X,Y) nazywa się łącznym rozkładem zmiennych losowych, a rozkłady
składowych wektora losowego nazywa się rozkładami brzegowymi.
Zwykle rozpatrujemy zmienne losowe skokowe (dyskretne) i ciągłe.
Zmienna losowa dwuwymiarowa skokowa
Jest to zmienna taka, że wszystkie składowe są dyskretnymi zmiennymi losowymi tzn
funkcja prawdopodobieństwa jest określona wzorem:
( )
( )
]
,
)
,
[(
P
,
P
y
x
Y
X
y
x
=
=
.
(4.24)
Jeśli oznaczymy:
(
)
(
)
],
,
,
[
P
k
i
ij
y
x
Y
X
p
=
=
i,k=1,2,…
(4.25)
to funkcja prawdopodobieństwa określa się wzorem:
( )
⎩
⎨
⎧
=
=
=
poza
y
y
i
x
x
p
y
x
j
i
ij
0
,
P
przy czym
1
=
∑
ij
ij
p
(4.26)
Zmienna losowa dwuwymiarowa typu ciągłego
Określa się ja na podstawie nieujemnej funkcji gęstości f(x,y) takiej, że:
( )
0
,
≥
y
x
f
i
( )
1
,
2
=
∫∫
R
y
x
f
(4.27)
Dystrybuanta dwuwymiarowej zmiennej losowej jest to funkcja
1
,
0
:
2
→
R
F
taka, że:
{
}
)
,
(
P
)
)
(
,
)
(
:
(
P
)
,
(
y
Y
x
X
y
Y
x
X
y
x
F
<
<
=
<
<
=
ω
ω
ω
(4.28)
( )
}
{
}
{
( )
( )
( )
⎪
⎪
⎩
⎪⎪
⎨
⎧
=
∫ ∫
∑ ∑
∞
−
∞
−
<
<
y
x
x
x
i
y
y
j
ij
C
dudv
v
u
f
SK
p
y
x
F
i
j
,
,
:
:
(4.29)
Dla zmiennej losowej ciągłej zachodzą własności:
Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację. fraczek@meil.pw.edu.pl . Wersja 07
Strona 16
1.
(
)
( )
∫ ∫
=
≤
≤
≤
≤
d
c
b
a
dxdy
y
x
f
d
Y
c
b
X
a
,
,
P
2.
( )
( )
y
x
f
y
x
y
x
F
F
xy
,
,
2
=
∂
∂
∂
=
tam, gdzie f(x,y) ciągła
Rozkład brzegowy
Rozkłady brzegowe zmiennych losowych powstają gdy interesuje nas rozkład jednej ze
składowych wektora losowego.
Definicje dla zmiennej losowej skokowej:
(
)
∑
=
=
=
•
j
ij
i
i
p
p
x
X
P
,
(
)
∑
=
=
=
•
i
ij
j
i
p
p
y
Y
P
(4.30)
Dla dwuwymiarowej zmiennej losowej (X,Y) typu ciągłego definiuje się rozkłady brzegowe
zmiennej za pomocą brzegowych gęstości prawdopodobieństwa:
( )
( )
∫
=
R
X
dy
y
x
f
x
f
,
(4.31)
analogicznie
( )
y
f
Y
:
( )
( )
∫
=
R
Y
dx
y
x
f
y
f
,
(4.32)
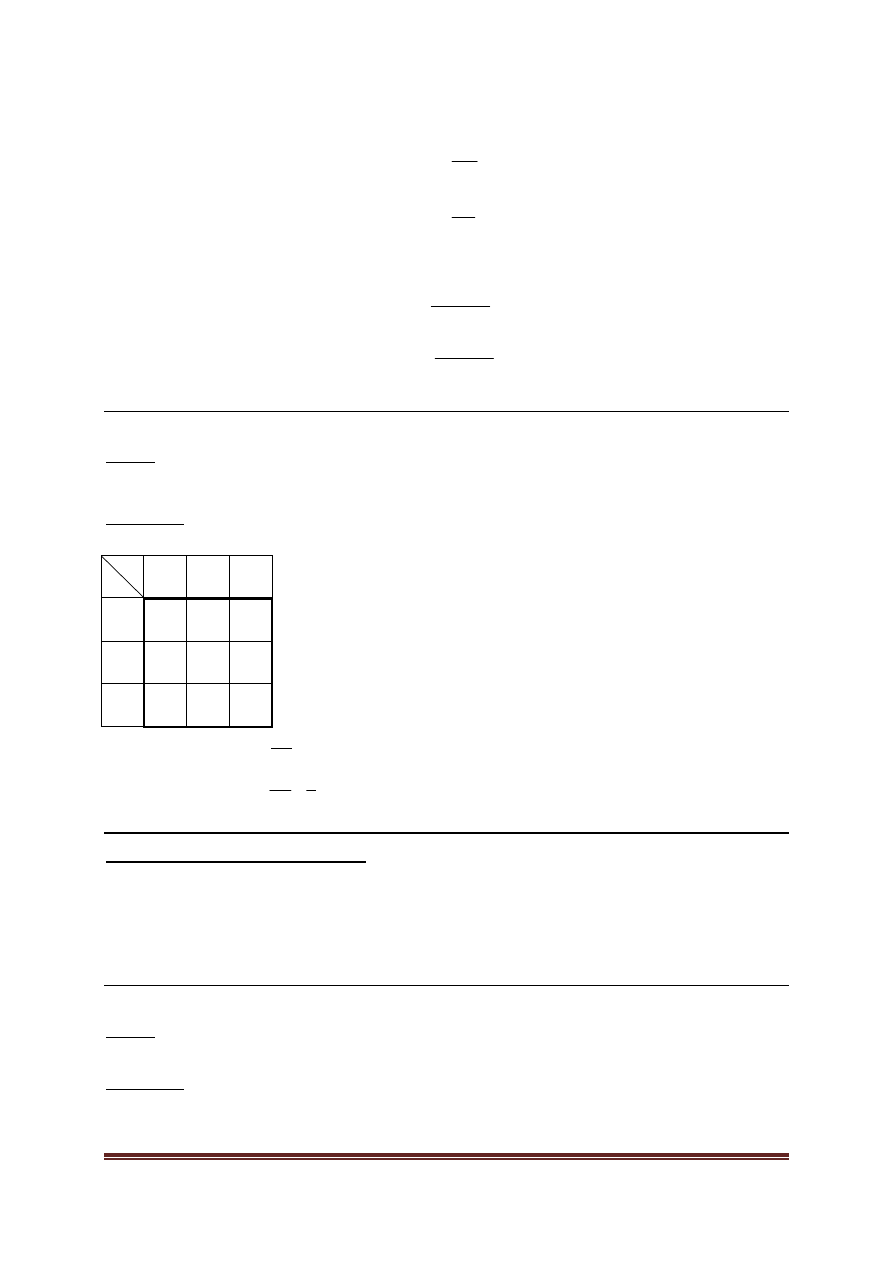
PRZYKŁAD 4.13
Zadanie
Znaleźć rozkłady brzegowe zmiennej losowej dwuwymiarowej (SK) określonej poniższą tabelką.
Rozwiązanie
Rozkłady brzegowe określono w ostatniej kolumnie i ostatnim wierszu tabeli.
x
i
y
j
1 2 3
j
p
•
1 0 1/6 1/6 1/3
2 1/6 0 1/6 1/3
3 1/6 1/6 0 1/3
•
i
p
1/3 1/3 1/3 1
Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację. fraczek@meil.pw.edu.pl . Wersja 07
Strona 17
x
1
y
6
D
PRZYKŁAD 4.14
Zadanie
Zmienna losowa dwuwymiarowa ciągła określona jest funkcją:
( )
⎩
⎨
⎧
>
=
−
−
poza
y
x
dla
e
y
x
f
y
x
0
0
,
,
Znaleźć rozkłady brzegowe zmiennych X i Y.
Rozwiązanie
( )
x
y
x
y
x
X
e
dy
e
e
dy
e
x
f
−
∞
−
−
∞
−
−
=
=
=
∫
∫
0
0
oraz przez symetrię:
( )
y
y
x
Y
e
dx
e
y
f
−
∞
−
−
=
=
∫
0
PRZYKŁAD 4.15
Zadanie
Dwuwymiarowa zmienna losowa ciągła ma funkcję gęstości:
( )
⎪⎩
⎪
⎨
⎧
∈
−
−
=
poza
D
y
x
dla
y
x
y
x
f
0
,
6
1
,
Należy wyznaczyć funkcje brzegowych gęstości porawdopodobeństwa:
Rozwiązanie
Opis obszaru:
( )
(
)
{
}
x
y
i
x
y
x
D
−
≤
≤
≤
≤
1
6
0
1
0
:
,
:
albo
( )
{
}
6
1
0
6
0
:
,
:
y
x
i
y
y
x
D
−
≤
≤
≤
≤
Obliczenie rozkładów brzegowych:
( )
(
)
(
)
(
)
(
)
(
)
[
]
(
)
(
)
(
)
2
1
6
0
2
1
6
0
1
6
0
1
6
0
1
6
0
1
3
12
1
6
1
6
1
x
y
y
x
dy
y
dy
x
dy
y
x
x
f
x
x
x
x
x
X
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
⎟
⎠
⎞
⎜
⎝
⎛
−
−
=
⎟
⎠
⎞
⎜
⎝
⎛
−
−
=
−
−
−
−
−
∫
∫
∫
( )
2
6
1
0
2
6
1
0
6
1
2
1
2
6
1
6
1
⎟
⎠
⎞
⎜
⎝
⎛ −
=
⎥
⎦
⎤
⎢
⎣
⎡
−
⎟
⎠
⎞
⎜
⎝
⎛ −
=
⎟
⎠
⎞
⎜
⎝
⎛
−
−
=
−
−
∫
y
x
x
y
dx
y
x
y
f
y
y
Y
Wykresy rozkładów brzegowych:
Rozkłady warunkowe zmiennych losowych
Są to rozkłady jednych ze składowych wektora losowego pod warunkiem, że druga przyjęła
określoną wartość.
x
1
y
6
f
Y
(y)
f
X
(x)
3
½
Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację. fraczek@meil.pw.edu.pl . Wersja 07
Strona 18
Dla zmiennej losowej skokowej
(
)
(
)
0
|
P
0
|
P
>
=
=
=
>
=
=
=
•
•
•
•
i
i
ij
i
i
j
j
ij
i
i
p
gdy
p
p
x
X
y
Y
p
gdy
p
p
y
Y
x
X
(4.33)
Dla zmiennej losowej ciągłej
(
)
(
)
( )
( )
(
)
(
)
( )
( )
0
,
|
0
,
|
0
0
0
0
0
0
0
0
>
=
=
>
=
=
x
f
x
f
y
x
f
x
X
y
f
y
f
y
f
y
x
f
y
Y
x
f
X
X
X
Y
Y
X
(4.34)
PRZYKŁAD 4.16
Zadanie
Wyznaczyć prawdopodobieństwa warunkowe P(X=x
i
|Y=y
i
) dla zmiennych losowych z przykładu 4.13.
Rozwiązanie
x
i
y
i
1 2 3
1 0 1/2
1/2
2 1/2 0 1/2
3 1/2 1/2 0
Bo np.
(
)
0
|
1
11
1
1
=
=
=
=
•
p
p
y
Y
x
X
P
(
)
2
1
|
1
21
1
2
=
=
=
=
•
p
p
x
X
y
Y
P
Niezależność zmiennych losowych
Zmienne losowe są niezależne (NZ) wtedy, gdy:
(
) (
) (
)
j
i
i
i
i
i
j
i
p
p
y
Y
x
X
y
Y
x
X
•
•
⋅
=
=
⋅
=
=
=
=
∀
∀
P
P
|
P
(SK)
( )
( ) ( )
y
f
x
f
y
x
f
Y
X
y
x
⋅
=
∀
∀
,
(C)
(4.35)
PRZYKŁAD 4.17
Zadanie
Zbadać niezależność zmiennych losowych z przykładu 4.13.
Rozwiązanie
Zmienne losowe nie są niezależne, bo np. dla i=j=2 mamy:
0
22
=
p
Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację. fraczek@meil.pw.edu.pl . Wersja 07
Strona 19
3
1
;
3
1
2
2
=
=
•
•
p
p
22
2
2
0
9
1
3
1
3
1
p
p
p
=
≠
=
⋅
=
⋅
•
•
PRZYKŁAD 4.18
Zadanie
Do danych z przykładu 4.15 sprawdzić, czy zmienne losowe są niezależne.
Rozwiązanie
Sprawdźmy dla
2
1
=
x
i
1
=
y
3
1
6
1
2
1
1
1
,
2
1
=
−
−
=
⎟
⎠
⎞
⎜
⎝
⎛
f
( )
72
25
1
;
4
3
2
1
=
=
⎟
⎠
⎞
⎜
⎝
⎛
Y
X
f
f
( )
3
1
72
25
4
3
1
2
1
≠
⋅
=
⋅
⎟
⎠
⎞
⎜
⎝
⎛
Y
X
f
f
Czyli:
( )
⎟
⎠
⎞
⎜
⎝
⎛
≠
⋅
⎟
⎠
⎞
⎜
⎝
⎛
∃
∃
=
=
1
,
2
1
1
2
1
1
2
1
f
f
f
Y
X
y
x
Charakterystyki liczbowe zmiennej losowej dwuwymiarowej
Moment zwykły rzędu (k,l) oznaczany
kl
m
,
gdzie
N
l
k
∈
,
dwuwymiarowej zmiennej (X,Y)
jest to liczba określona wzorem:
( )
( )
( )
( )
( )
⎪
⎩
⎪
⎨
⎧
=
=
∫
∑∑
C
dxdy
y
x
f
y
x
SK
p
y
x
Y
X
m
R
l
k
i
j
ij
l
j
k
i
l
k
kl
2
,
)
(
E
jeśli szereg i całka są zbieżne
(4.36)
Łatwo zauważyć, że momenty zwykłe rzędu (1,0) oraz (0,1) są to średnie rozkładów
brzegowych
Y
X
m
m
μ
μ
=
=
01
10
gdzie
X
μ - średnia rozkładu brzegowego zmiennej X i
Y
μ to średnia rozkładu brzegowego
zmiennej Y.
Moment centralny
Moment centralny rzędu (k,l) gdzie
N
l
k
∈
,
jest to liczba określona następująco:
(
) (
)
[
]
l
k
kl
m
Y
m
X
01
10
E
−
⋅
−
=
μ
(4.37)
Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację. fraczek@meil.pw.edu.pl . Wersja 07
Strona 20
Uwaga
Momenty centralne rzędu (2,0) i (0,2) są to wariancje
2
2
,
Y
X
σ
σ
rozkładów brzegowych
zmiennych losowych X i Y.
Kowariancja i współczynnik koleracji
Moment centralny rzędu (1,1) nazywa się kowariancją zmiennych losowych X i Y i oznacza
Cov(X,Y) tzn:
(
)(
)
[
]
01
10
11
E
)
,
(
Cov
m
Y
m
X
Y
X
−
−
=
=
μ
(4.38)
Kowariancję można przedstawić jako funkcję momentów zwykłych:
(
)(
)
[
]
)
(
)
(
E
)
(
E
)
E(
E
)
,
(
Cov
01
10
11
01
10
10
01
01
10
Y
E
X
XY
m
m
m
m
m
Y
m
Xm
XY
m
Y
m
X
Y
X
−
=
−
=
=
+
−
−
=
−
−
=
(4.39)
W wyprowadzeniu powyższych zależności wykorzystano własności wartości oczekiwanej.
Zauważmy, że:
X
X
X
2
D
)
,
(
Cov
=
(4.40)
Czasem w rachunku prawdopodobieństwa wprowadza się pojęcie zmiennych
standaryzowanych zdefiniowanych wzorem:
X
X
X
X
σ
μ
−
=
~
,
Y
Y
Y
Y
σ
μ
−
=
~
(4.41)
Prawdziwe jest następujące twierdzenie:
Jeśli zmienne losowe są niezależne to E(XY)=E(X)E(Y) oraz
0
)
,
(
Cov
=
Y
X
.
Ale twierdzenie odwrotne nie jest prawdziwe. Ilustruje to poniższy przykład.
PRZYKŁAD 4.19
Dana jest dwuwymiarowa zmienna losowa typu skokowego, której rozkład łączny opisany jest tabelką:
x
i
y
j
6 8 10
j
p
•
1 0.2 0 0.2 0.4
2 0 0.2 0 0.2
3 0.2 0 0.2 0.4
•
i
p
0.4 0.2 0.4 1
Obliczymy kowariancję. Kolejno:
∑∑
=
=
=
=
3
1
3
1
11
16
i
j
ij
j
i
p
y
x
m
8
4
.
0
10
2
.
0
8
4
.
0
6
)
(
E
3
1
10
=
⋅
+
⋅
+
⋅
=
=
=
•
=
∑
i
i
i
p
x
X
m
Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację. fraczek@meil.pw.edu.pl . Wersja 07
Strona 21
2
4
.
0
3
2
.
0
2
4
.
0
1
)
(
E
3
1
01
=
⋅
+
⋅
+
⋅
=
=
=
•
=
∑
j
j
j
p
y
Y
m
Zatem:
0
8
2
16
)
,
(
Cov
01
10
11
=
⋅
−
=
−
=
m
m
m
Y
X
.
Ale zmienne nie są niezależne bo np.:
0
21
=
p
oraz
4
.
0
2
.
0
1
2
=
=
•
•
p
i
p
. Jest widoczne, że
1
2
21
•
•
≠
p
p
p
Współczynnikiem korelacji zmiennych losowych X i Y oznaczanym
ρ
albo
XY
ρ
nazywamy
liczbę:
Y
X
02
20
11
)
,
(
Cov
σ
σ
μ
μ
μ
ρ
Y
X
=
=
(4.42)
Czasem w rachunku prawdopodobieństwa wprowadza się pojęcie zmiennych
standaryzowanych zdefiniowanych wzorem:
X
X
X
X
σ
μ
−
=
~
,
Y
Y
Y
Y
σ
μ
−
=
~
(4.43)
Współczynnik korelacji można zdefiniować przy tych oznaczeniach następująco:
)
~
,
~
(
Cov
)
,
(
Cov
Y
X
Y
X
Y
X
=
=
σ
σ
ρ
(4.44)
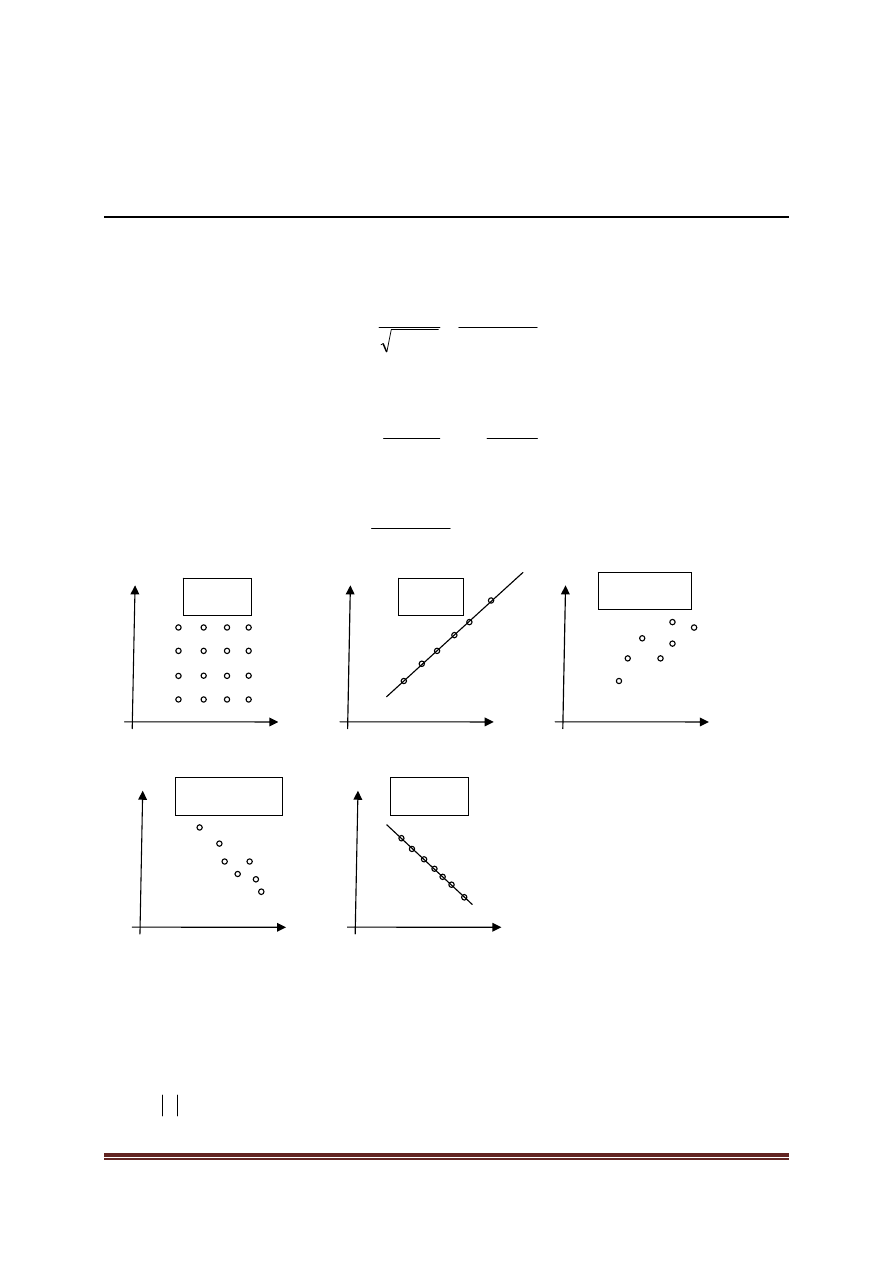
Rysunek 4.2
Przykładowe realizacje wektorów losowych dwuwymiarowych (X,Y) przy
rożnych wartościach współczynnika korelacji pomiędzy składowymi.
Współczynnik korelacji ma następujące własności:
•
1
≤
ρ
(o ile istnieje)
x
1
−
=
ρ
y
x
0
1
<
<
−
ρ
y
x
1
0
<
<
ρ
y
x
1
=
ρ
y
0
=
ρ
y
x
Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację. fraczek@meil.pw.edu.pl . Wersja 07
Strona 22
•
1
=
ρ
wtedy i tylko wtedy gdy
1
)
(
P
=
+
=
b
aX
Y
Z drugiej zależności wynika, że współczynnik korelacji może służyć jako miara liniowej
zależności zmiennych losowych X i Y.
Znaczenie wartości bezwzględnej i znaku współczynnika korelacji ilustruje rys.
4.2
.
Mówimy, że zmienne losowe są nieskorelowane jeśli 0
=
ρ
oraz, że są skorelowane
w przeciwnym przypadku (oczywiście to, że zmienne są nieskorelowane nie oznacza jeszcze,
że są niezależne).
Jeśli zmienne losowa Y jest funkcją liniową zmiennej X to prostą o równaniu:
b
ax
y
+
=
(4.45)
nazywamy prostą regresji.
Jeśli nie jest spełniony warunek
1
=
ρ
to znaczy, że nie zachodzi równość
1
)
(
P
=
+
=
b
aX
Y
to często szukamy takiej funkcji liniowej aby prawdopodobieństwo )
(
P
b
aX
Y
+
=
było
możliwie duże. Zazwyczaj przyjmuje się jako kryterium tzw. oczekiwany kwadratowy błąd
aproksymacji:
]
)
-
-
E[(
2
b
aX
Y
e
=
(4.46)
Wartości a i b, dla których e jest minimalne wyznaczają prostą nazywaną prostą regresji II
rodzaju
.
Można pokazać, że współczynnik korelacji jest miarą dokładności, z jaka jedną zmienna
losową Y można aproksymować przez liniową funkcję innej zmiennej losowej, której
współczynniki dobrano tak aby błąd e był minimalny. Jeśli 0
=
ρ
to błąd ten jest największy,
jeśli natomiast
1
=
ρ
to jest najmniejszy.
Wyszukiwarka
Podobne podstrony:
MiTE wykład 1 7 wersja 02
MiTE wykład 1 4 wersja 07
MiTE wykład 7 8 wersja 01
Wyklad 2 TM 07 03 09
Materiały pomocne przy nauce podsumowanie powyższych wykładów wersja mini
Owoce i warzywa wykłady (wersja 4)
Systemy Eksploatacji Złóż Wykłady 2 wersja
EIE, Wykład IX 07
Filozofia wykłady wersja2
polityka pieniezna wyklady wersja komputerowa, POLITYKA PIENIEZNA2
polityka pieniezna wyklady wersja komputerowa, POLITYKA PIENIEZNA2
Metody badań minerałów i skał – wykłady wersja 1
WYKŁAD 05 07 01 05
Wykład 1 wersja studencka
Microsoft PowerPoint WYKŁAD1 KOS 07(2)
Wykład 10 [07.12.05], Biologia UWr, II rok, Zoologia Kręgowców
więcej podobnych podstron