G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

1

SPIS TREŚCI

1. Metody przybliżone w mechanice konstrukcji

2

2. Metoda Różnic Skończonych

9

3. Metoda Elementów Brzegowych

17

3.1

MEB dla równania Poissona

17

3.2

Zagadnienia teorii sprężystości (poza programem)

21

4. Koncepcja MES na przykładzie równania Poissona

35

5. MES w analizie konstrukcji prętowych

38

5.1.Belki

38

5.2. Pręty rozciągane i skręcane. Sprężyny

52

5.3. Kratownice i ramy płaskie

59

5.4. Przestrzenne kratownice i ramy

63

6. Dwuwymiarowe i trójwymiarowe zadania teorii sprężystości

66

6.1. Element skończony trójkątny CST (constant strain triangle)

77

6.2. Izoparametryczny 8-węzłowy element skończony

84

6. 3. Całkowanie numeryczne

89

7. MES w praktyce inżynierskiej

91

7.1.Uwagi o dokładności obliczeń MES ...

91

7.2. Wykorzystanie profesjonalnych systemów obliczeniowych .....

96

Literatura

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

2

1. METODY PRZYBLIŻONE W MECHANICE

KONSTRUKCJI

Konstrukcje odkształcalne mogą być badane doświadczalnie lub metodami

teoretycznymi; analitycznymi i numerycznymi. Poważną wadą analiz eksperymentalnych jest

ich koszt i czasochłonność. Dotyczy to zarówno większości badań modelowych jak i badań

obiektów rzeczywistych. Pracochłonność metod doświadczalnych jest szczególnie odczuwana

w trakcie prac projektowych, gdzie analizie poddawane są różne warianty konstrukcji.

Dlatego rozwój metod teoretycznych, przede wszystkim metod numerycznych, wpływał

zawsze na jakość projektowanych konstrukcji inżynierskich. Przykładem może być postęp w

konstrukcjach statków, dźwigów, wysokich budynków, samochodów, samolotów.

Badania teoretyczne polegają na sformułowaniu odpowiedniego opisu matematycznego i

następnie rozwiązaniu postawionego problemu. Niestety, dla bardzo wielu praktycznych

problemów mechaniki konstrukcji można zbudować wiarygodny model matematyczny, ale

nie są znane odpowiednie ścisłe rozwiązania analityczne. Prostym przykładem takich

zagadnień jest wyznaczanie współczynników koncentracji naprężeń. Tylko w bardzo

szczególnych przypadkach znane są rozwiązania dokładne.

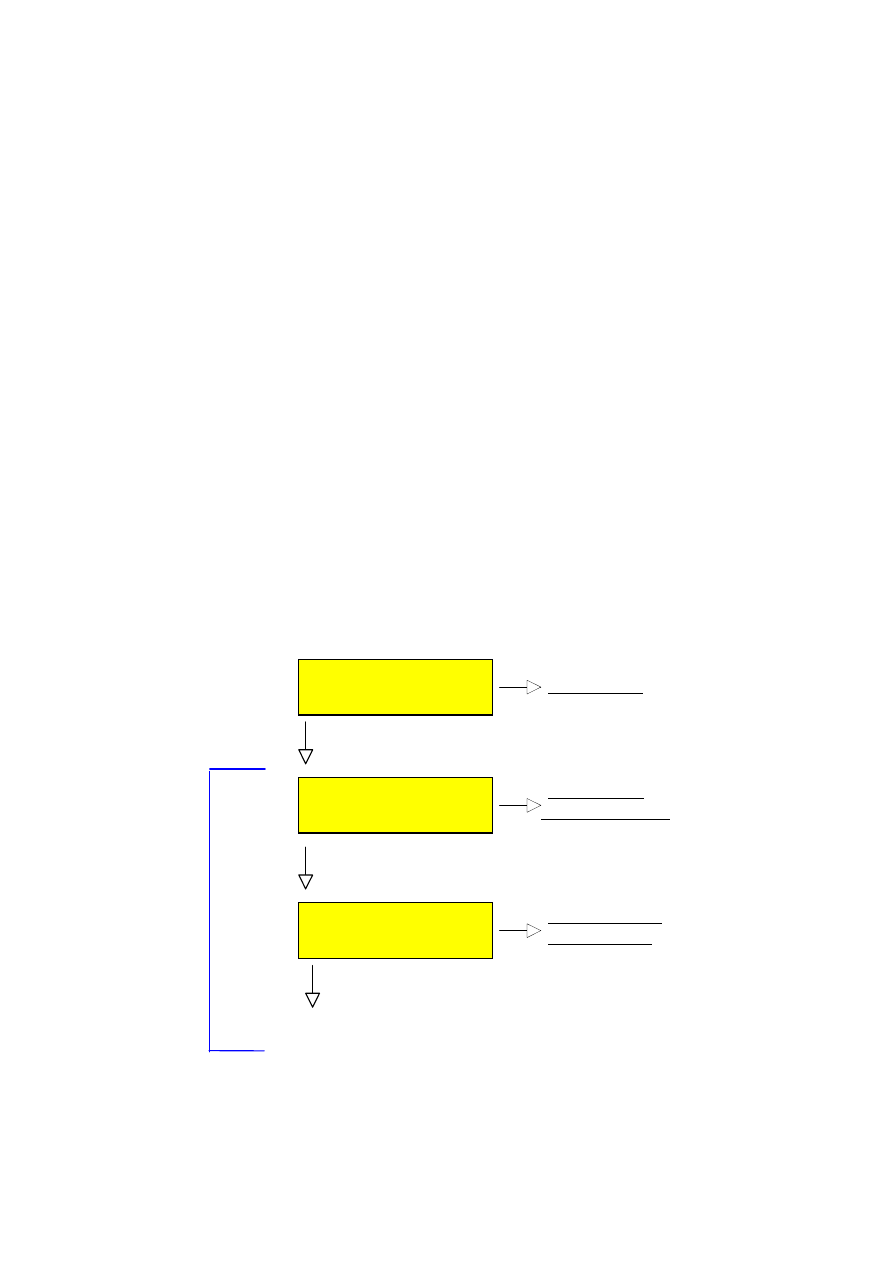
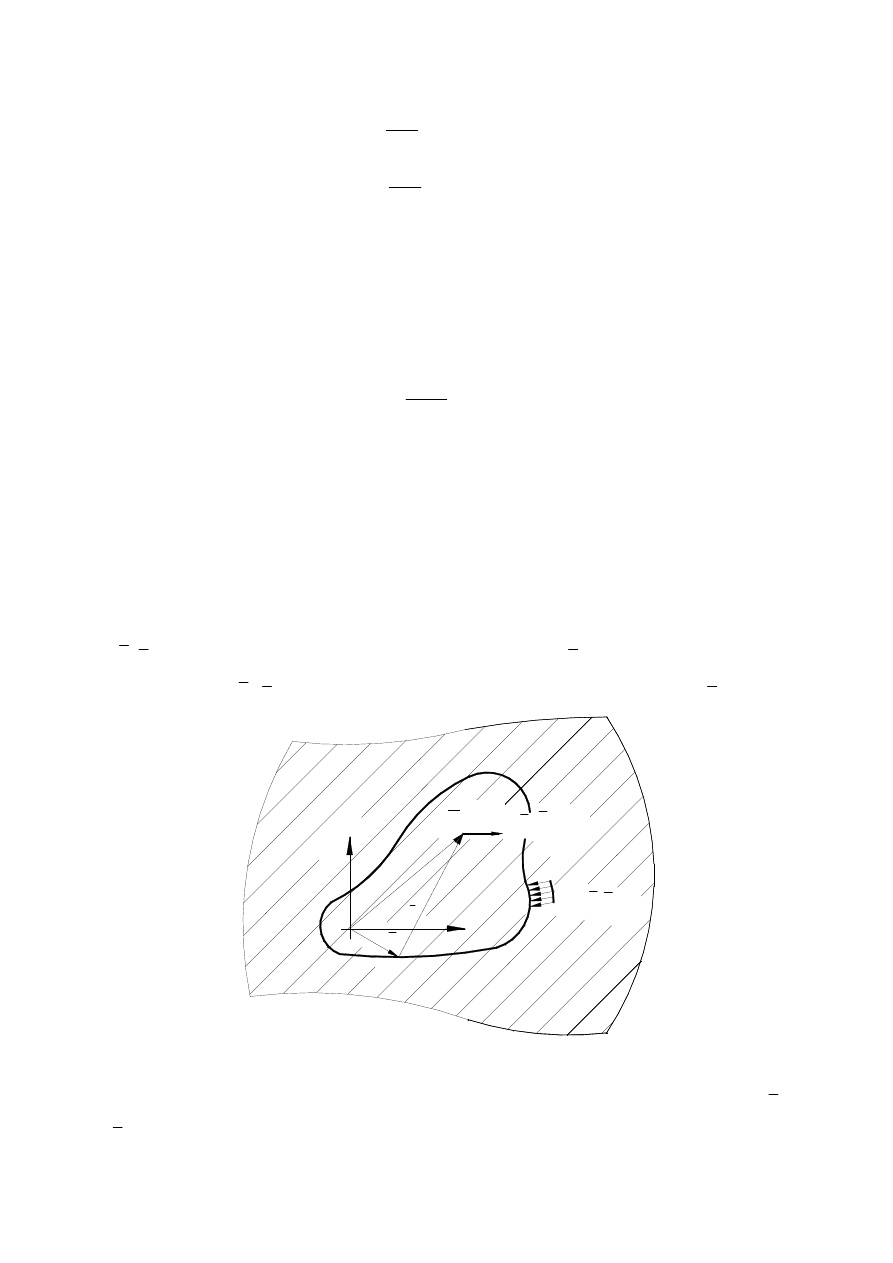
Rzeczywiste zjawisko

Model matematyczny

ci

ą

gły

Model

dyskretny

Rzeczywisty wynik

Rozwi

ą

zanie

ś

cisłe

modelu matematycznego

Rozwi

ą

zanie dokładne

modelu dyskretnego

Prawa fizyki
Własno

ś

ci materiałowe, geometria,

Dyskretyzacja

Aproksymacja

Realizacja oblicze

ń

Wynik numeryczny

Warunki brzegowe

M

E

T

O

D

A

P

R

Z

Y

B

L

I

Ż

O

N

A

Rys. 1. Rozwiązywanie zagadnień analizy ośrodków ciągłych metodami przybliżonymi.

Schemat postępowania

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

3

Dlatego równolegle do rozwoju analitycznych metod znajdowania rozwiązań ścisłych

były opracowywane i doskonalone metody przybliżone. Większość zadań analizy

wytrzymałościowej konstrukcji rozwiązuje się współcześnie za pomocą metod przybliżonych,

przy wykorzystaniu obliczeń komputerowych.

Ogólny schemat postępowania przy zastosowaniu metod przybliżonych przedstawiony jest na

rysunku 1.

Pierwszym krokiem na drodze poszukiwania rozwiązania jest budowa modelu

matematycznego. Potrzebna jest do tego znajomość odpowiednich praw fizyki,

sformalizowany opis własności materiałowych, kształtu konstrukcji, jej warunków podparcia i

obciążenia. Dla każdego rzeczywistego problemu możemy zbudować wiele różnych modeli

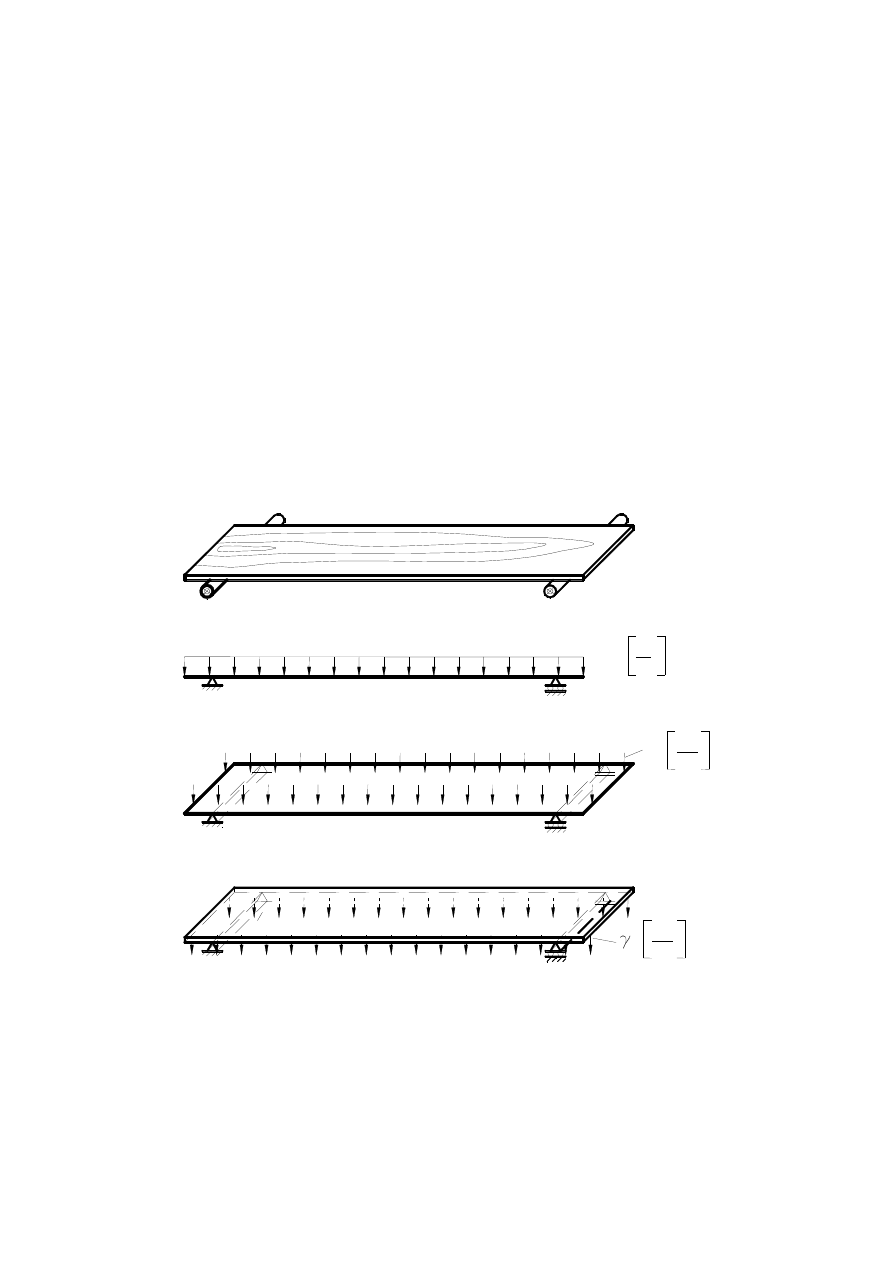
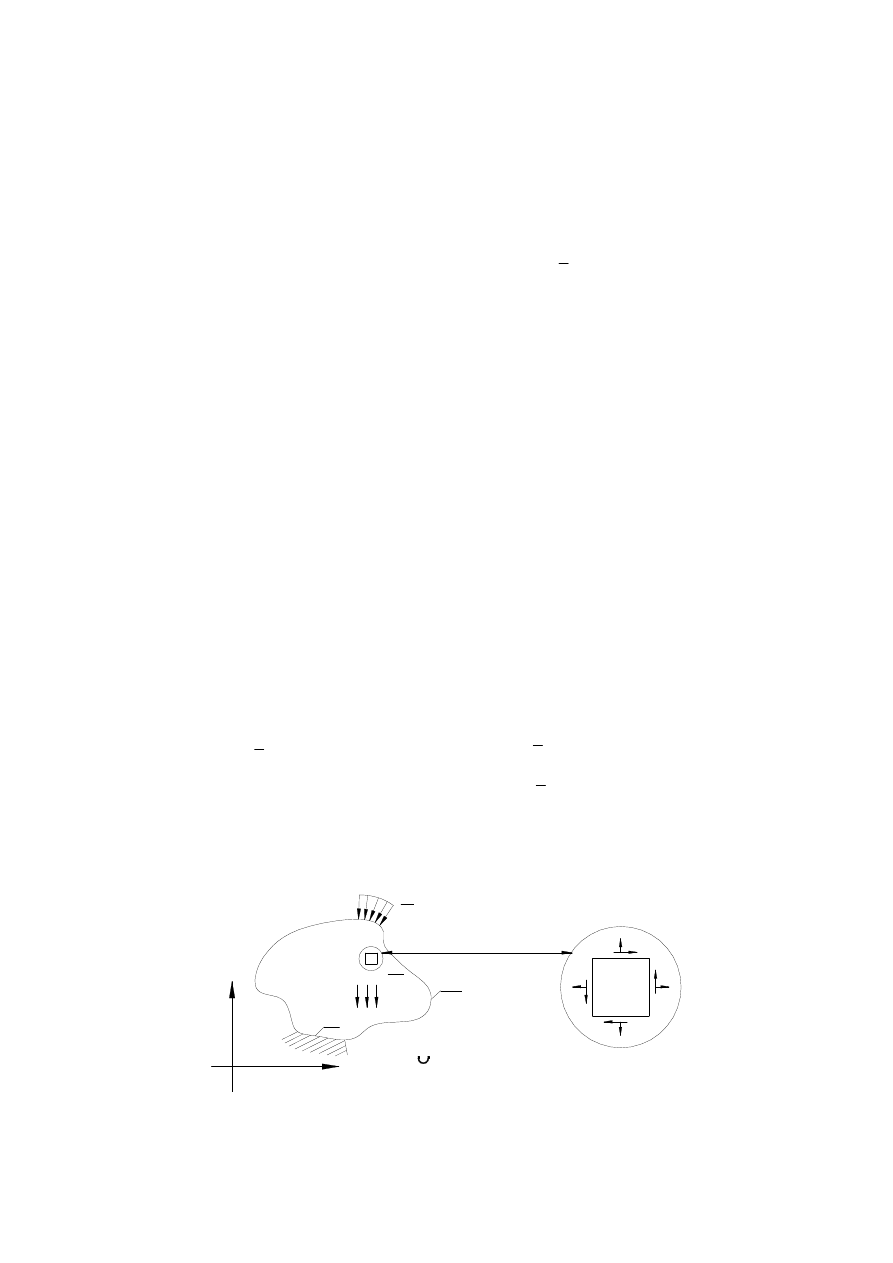
matematycznych. Bardzo prostą ilustracją może być tu zadanie określenia ugięcia pod

wpływem sił ciężkości swobodnie podpartej drewnianej deski (rys. 2).

a) model belki

b) model płyty

c) model trójwymiarowy bryły

q

0

N

m

p

0

m

N

2

N

m

0

3

Rys. 2. Różne modele w analizie wytrzymałościowej zginanej deski

Dla takiego zagadnienia można przedstawić typowy jednowymiarowy model

matematyczny

belki,

dwuwymiarowy

model

zginanej

płyty

lub

pełny

model

trójwymiarowego zadania mechaniki ciał odkształcalnych. Własności materiału i równania

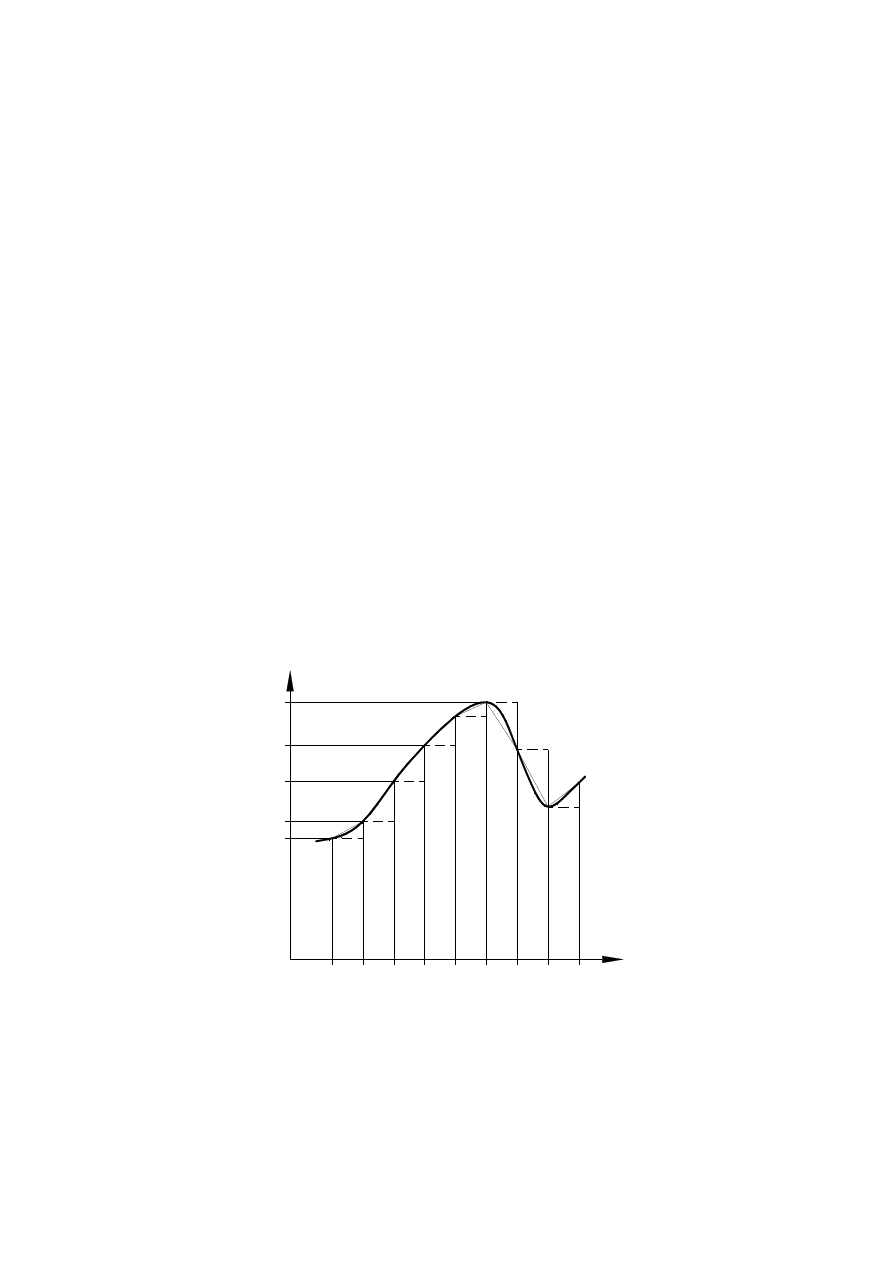
G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

4

opisujące konstrukcję mogą w najprostszym przypadku zakładać izotropową liniową

sprężystość. Mogą również uwzględniać anizotropię, lepkosprężystość czy duże ugięcia i w

konsekwencji nieliniowość zjawisk. Również warunki brzegowe można przyjąć w postaci

uproszczonej lub uwzględnić na przykład zjawiska kontaktowe. Przykład ten pokazuje, że

zwykle nie ma jednego, najlepszego modelu obliczeniowego dla analizy wytrzymałości

elementów konstrukcyjnych. Właściwy model obliczeniowy zależy od celu analizy, wymagań

stawianych konstrukcji, żądanej dokładności wyników, dostępności danych materiałowych,

ale także - w dużym stopniu - od dostępnych narzędzi obliczeniowych.

Ponadto opis matematyczny wybranego modelu można przedstawić w różnych

sformułowaniach, na przykład równań różniczkowych, odpowiadających im równań

całkowych lub w ujęciu wariacyjnym, w postaci problemu minimalizacji odpowiedniego

funkcjonału [5]. Budowa modelu matematycznego stanowi najważniejszy element analizy

obliczeniowej, w którym bardzo trudno zastąpić bezpośrednią decyzję człowieka przez

sformalizowane algorytmy postępowania.

W metodach przybliżonych problem poszukiwania nieznanych funkcji (opisujących

pole przemieszczeń, odkształceń i naprężeń) zastępujemy przez problem poszukiwania

skończonej liczby parametrów, za pomocą których można opisać – w pewnym przybliżeniu-

poszukiwane funkcje.

x

f(x)

x

1

x

2

b

x =a

h

0

x =a+ih

i

h

h

h

f

1

f

2

f

0

3

f

f

i

Rys. 3. Dyskretyzacja i aproksymacja na przykładzie funkcji jednej zmiennej

Dokonujemy tego poprzez dyskretyzację, czyli wybór skończonej liczby parametrów

opisujących w przybliżeniu analizowany problem oraz aproksymację poszukiwanych funkcji

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

5

za pomocą innych z góry założonych prostych funkcji, które uzależnione są od wybranych

parametrów.

Najprostszym przykładem dyskretyzacji i aproksymacji jest numeryczna reprezentacja

dowolnej funkcji f(x) w przedziale <a,b>. Zrealizować możemy to przez podział przedziału

<a,b> na n równych podprzedziałów o długości h=(b-a)/n.

Funkcję ciągłą f(x) reprezentować będzie wtedy zbiór (n+1) wartości f(a+ih), i=0,1,2, n.

Przybliżone wartości funkcji dla dowolnej wartości x z przedziału <a,b> wyznaczać możemy

za pomocą aproksymacji funkcją w podprzedziałach stałą (schodkową), liniową (łamaną) lub

na przykład wielomianowymi funkcjami sklejanymi (rys. 3).

Metody przybliżone analizy ośrodków ciągłych stanowią intensywnie rozwijaną część

współczesnej matematyki. Wiążą się z problemami analizy funkcjonalnej, metod

numerycznych i rachunku wariacyjnego. Prezentuje się je czasem jako szczególne warianty

tak zwanych technik residuów ważonych dla przybliżonego rozwiązywania zagadnień

opisywanych przez równania różniczkowe cząstkowe [5,7].

W naukach technicznych metody przybliżone opisywane są zazwyczaj od strony zastosowań,

jako wyspecjalizowane procedury obliczeniowe dla określonych zagadnień, na przykład pól

deformacji sprężystej, pól temperatury, pół elektrycznych i magnetycznych. Istnieje wiele

metod przybliżonych, stosowanych od dawna w mechanice ciała odkształcalnego i mechanice

konstrukcji, np. metoda Ritza, Galerkina, Trefftza, kollokacji, Kantorowicza [2,6]. Metody te

różnią się postacią modelu matematycznego, sposobem dyskretyzacji i aproksymacji, a także

stosowanym algorytmem obliczeń. Jednak współcześnie dominują te metody przybliżone,

które charakteryzuje łatwość pełnej automatyzacji i które rozwinęły się wraz z rozwojem

technik komputerowych. Najbardziej znane z nich to metoda różnic skończonych (MRS),

metoda elementów skończonych (MES) i metoda elementów brzegowych (MEB). Nazywamy

je metodami numerycznymi lub komputerowymi. Każda z tych metod ma bardzo bogatą

literaturę i prezentowana może być w wielu odmiennych sformułowaniach.

Metoda różnic skończonych bezpośrednio wykorzystuje model matematyczny w

postaci równań różniczkowych opisujących rozwiązywane zagadnienie [4,5]. Dyskretyzacja

polega na ustaleniu w analizowanym obszarze siatki węzłów, np. w przypadku

dwuwymiarowym prostokątnej lub trójkątnej. Przyjmujemy, że w każdym węźle pochodne

można przybliżyć przez tak zwane ilorazy różnicowe, czyli wyrażenia algebraiczne

uzależnione od wartości funkcji w węzłach przyległych. Równanie różniczkowe w każdym

węźle zastępowane jest przez odpowiednie równanie algebraiczne wiążące wartości funkcji w

najbliższych węzłach. W rezultacie otrzymujemy układ równań, których liczba odpowiada

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

6

liczbie węzłów. Niewiadomymi są wartości poszukiwanej funkcji w tych węzłach. Warunki

brzegowe przedstawiane są jako dodatkowe związki łączące wartości funkcji w węzłach

przylegających do konturu analizowanego obszaru.

W metodzie elementów skończonych [6,7] zamiast rozwiązywać równania

różniczkowe poszukujemy przybliżonego rozwiązania sformułowania alternatywnego w

postaci problemu minimalizacji odpowiedniego funkcjonału

1

. Zagadnieniami minimalizacji

funkcjonałów i ich związkami z odpowiednimi równaniami różniczkowymi zajmuje się dział

matematyki nazywany rachunkiem wariacyjnym. W MES analizowany obszar dzielony jest

na podobszary, nazywane elementami skończonymi. W przypadku dwuwymiarowym mogą to

być np. trójkąty lub czworokąty. Elementy skończone łączą się ze sobą w węzłach. Położenie

węzłów elementu wyznacza jego kształt. Przebieg poszukiwanej funkcji u wewnątrz każdego

elementu wyznacza się za pomocą z góry ustalonych funkcji aproksymujących nazywanych

funkcjami kształtu:

( )

( )

i

i

i

u x

N x u

=

∑

gdzie

i

u stanowią wartości funkcji w węzłach, x jest wektorem współrzędnych, a

i

N

są

funkcjami kształtu.

Minimalizowany funkcjonał przedstawić wtedy można jako funkcję wielu zmiennych

Niewiadomymi są zwykle wartości poszukiwanej funkcji w węzłach całego obszaru. Warunek

minimum prowadzi do układu równań liniowych, którego rozwiązanie określa nieznane

wartości funkcji w węzłach.

Metoda elementów brzegowych

[5] wymaga znajomości tak zwanych brzegowych

równań całkowych, które w innej formie wyrażają związki znane w postaci równań

różniczkowych lub w postaci problemu minimalizacji odpowiedniego funkcjonału. Dla wielu

zagadnień tak zwane brzegowe sformułowanie, które wyraża całkowe zależności między

wartościami funkcji i jej pochodnych dla punktów brzegowych jest znane z analizy

matematycznej.

Dyskretyzacja polega na podziale brzegu na małe segmenty zwane elementami brzegowymi.

W przypadku dwuwymiarowym mogą to być odcinki prostych lub też krzywych, których

kształt opisany jest przez wielomiany. Zapisanie dyskretnego odpowiednika równania

całkowego dla każdego węzła prowadzi do układu równań algebraicznych, z którego można

wyznaczyć wartości poszukiwanej funkcji na brzegu.

1

Metoda elementów skończonych może być prezentowana jako oparta na innych sformułowaniach]

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

7

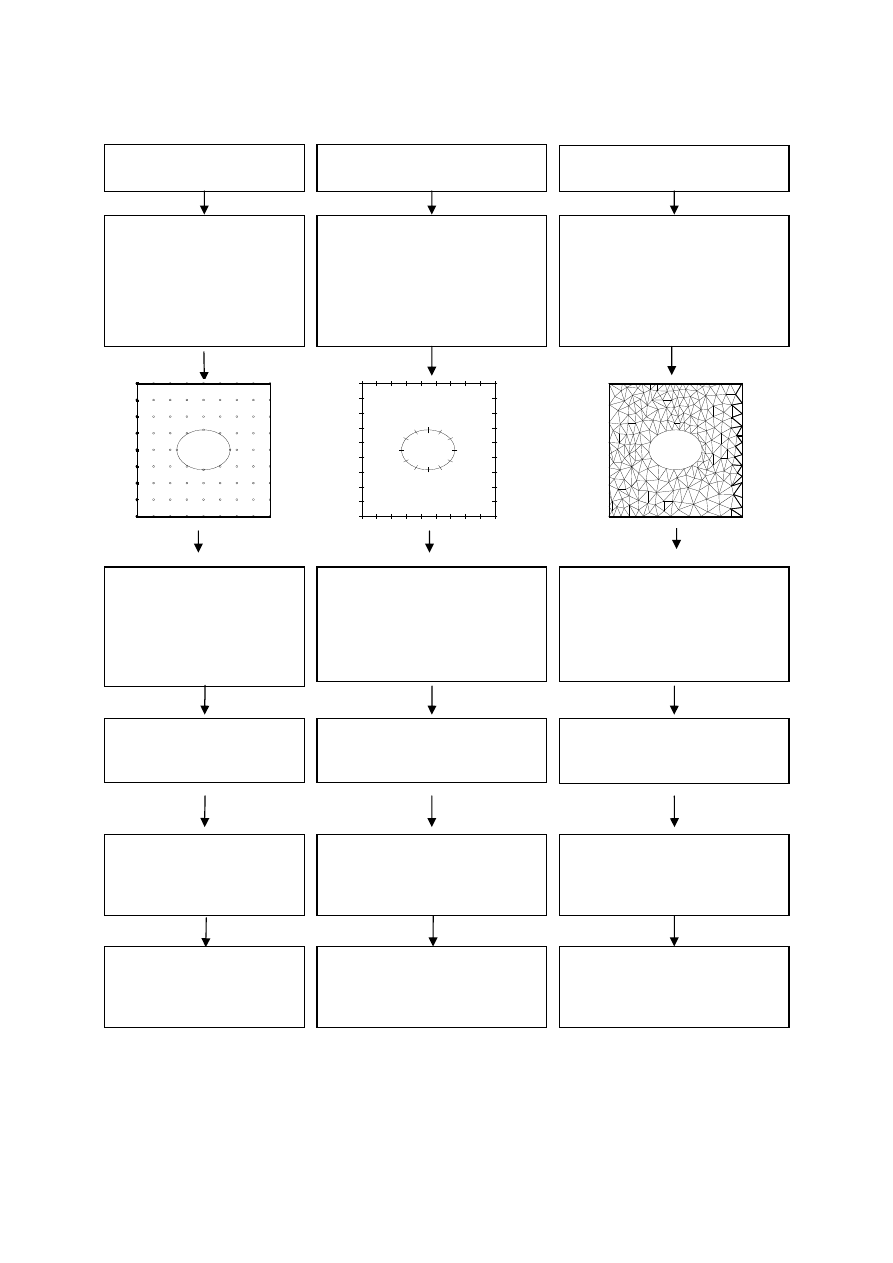
Rys. 4. Ogólny schemat postępowania przy obliczeniach metodą różnic skończonych, metodą

elementów brzegowych i metodą elementów skończonych

Równania różniczkowe

cząstkowe

Budowa siatki węzłów i

przyjęcie wybranych

schematów różnicowych

Całkowe równania brzegowe

Problem minimalizacji

funkcjonału

Podział brzegu na segmenty

(elementy brzegowe) i założenie

odpowiednich funkcji aproksymują-

cych na elementach – funkcji

kształtu

Podział obszaru na małe

podobszary (elementy skończone) i

przyjęcie odpowiednich funkcji

aproksymujących na elementach –

funkcji kształtu

Zastąpienie równań

różniczkowych przez równania

różnicowe dla kolejnych

węzłów obszaru.

Formowanie układu

równańliniowych

Budowa dyskretnej reprezentacji

równania całkowego dla kolejnych

węzłów brzegu.

Formowanie układu równań

liniowych

Budowa macierzy sztywności

kolejnych elementów.

Formowanie układu równań

liniowych

Rozwiązanie układu równań

liniowych (macierz rzadka,

pasmowa, zwykle

symetryczna)

Rozwiązanie układu równań

liniowych (macierz pełna,

niesymetryczna)

Rozwiązanie układu równań

liniowych (macierz rzadka,

pasmowa, zwykle symetryczna)

Modyfikacja układu równań –

wprowadzenie warunków

brzegowych

Modyfikacja układu równań –

wprowadzenie warunków

brzegowych

Modyfikacja układu równań –

wprowadzenie warunków

brzegowych

Obliczenia uzupełniające, np.

poszukiwanych funkcji i ich

pochodnych w wybranych punktach

obszaru

Obliczenia uzupełniające, np.

funkcji i jej pochodnych funkcji

wewnątrz elementów skończonych

Obliczenia uzupełniające, np.

pochodnych poszukiwanych

funkcji w węzłach

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

8

Rysunek 4 przedstawia ogólny szkic algorytmów MRS MEB i MES dla typowego

problemu liniowego, na przykład dla zagadnienia Laplace’a, zagadnienia Poissona lub

liniowego zadania teorii sprężystości.

Porównanie powyższych trzech metod jest w ogólnym przypadku bardzo trudne.

Istnieją pewne szczególne zagadnienia, dla których za najbardziej efektywną można uznać

metodę różnic skończonych lub metodę elementów brzegowych. Jednak niewątpliwie

najbardziej uniwersalną jest metoda elementów skończonych. Fakt ten potwierdza

powszechność zastosowań inżynierskich programów komputerowych MES.

Metoda elementów skończonych powstała w latach pięćdziesiątych XX wieku jako technika

obliczeniowa stosowana praktycznie, bez formalnych podstaw teoretycznych. Podwaliny dało

opracowanie metody analizy wytrzymałościowej poprzez podział złożonych konstrukcji

nośnych na skończoną liczbę uproszczonych elementów składowych. Związki, które musiał

spełniać tak zbudowany model zapisywano w postaci macierzowej. Otrzymywano układy

równań z wieloma niewiadomymi, których liczba związana była z dokładnością przyjętego

modelu.

Czynnikiem wpływającym na gwałtowny rozwój MES był postęp w technice komputerowej i

potrzeby intensywnie rozwijanego wówczas przemysłu zbrojeniowego i lotniczego. Analiza

podstaw teoretycznych metody, jej systematyzowanie i zwiększanie efektywności

doprowadziło do korzystania z MES jako ogólnej metody obliczeń problemów ciągłych w

matematyce, a także do szerokich zastosowań w praktyce inżynierskiej przy analizie pól

naprężeń odkształceń i przemieszczeń, pól elektrycznych, magnetycznych, termicznych,

zagadnień przepływowych a także pól sprzężonych (np. zagadnień naprężeń temperaturowych

czy problemów elektryczno-cieplnych).

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

9

2. METODA RÓŻNIC SKOŃCZONYCH

Metoda różnic skończonych (MRS) jest jedną z najstarszych metod numerycznych

rozwiązywania

zagadnień

opisywanych

równaniami

różniczkowymi

cząstkowymi.

Przyjmujemy w niej, że poszukiwana funkcja określona jest przez zbiór jej wartości w

wybranych punktach (tzw. węzłach), dostatecznie gęsto rozłożonych w analizowanym

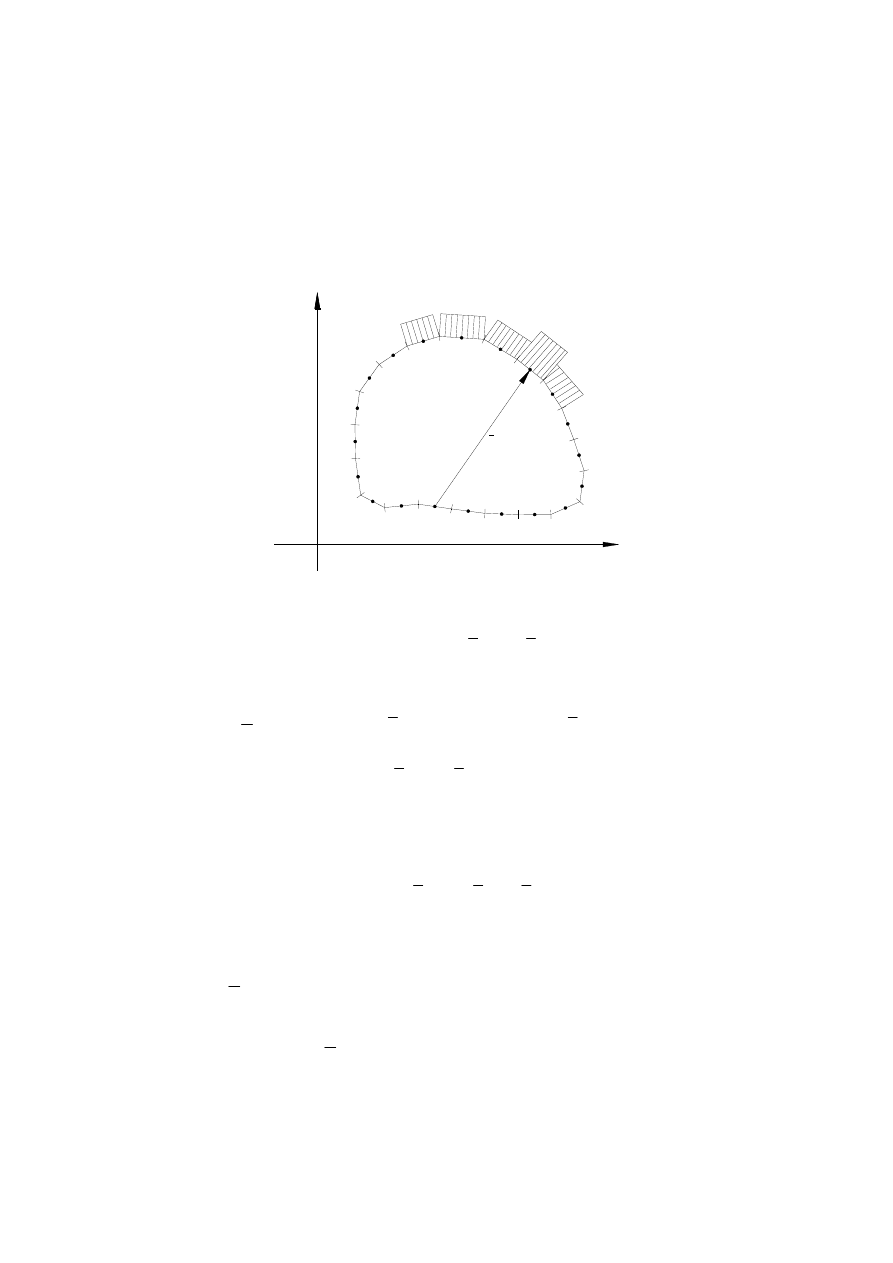
obszarze. Punkty te dobierane są zazwyczaj tak. że tworzą regularne siatki, z których

najprostszymi są siatka prostokątna w przypadku dwuwymiarowym lub prostopadłościenna w

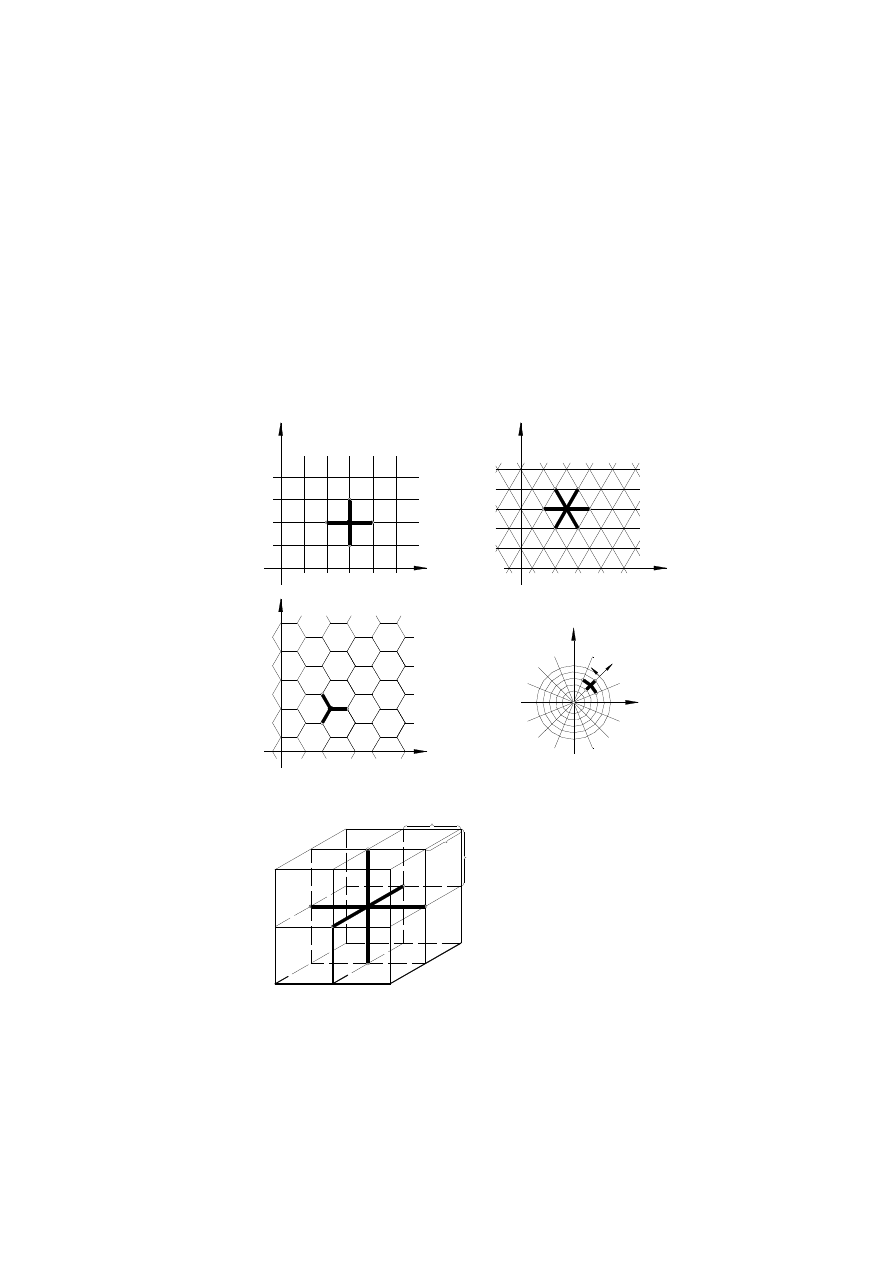
przypadku trójwymiarowym (rys. 5).

x

y

y

a)

r

θ

1

2

3

4

5

6

h

g

0

x

b)

x

y

c)

x

y

d)

e)

l

Rys. 5. Przykłady regularnych siatek MRS: a) prostokątna, b) trójkątna, c) sześciokątna, d) w

układzie biegunowym, e) prostopadłościenna

W metodzie różnic skończonych operatory różniczkowania funkcji zastępowane są

odpowiednimi operatorami różnicowymi. Oznacza to, że wartości pochodnych w punkcie

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

10

zastępowane są przez odpowiednie przyrosty (różnice) funkcji w sąsiadujących węzłach.

Zamieniamy w ten sposób równania różniczkowe na równania algebraiczne, tak zwane

równania różnicowe. W efekcie, zamiast równania różniczkowego, otrzymujemy układ

równań z niewiadomymi będącymi wartościami funkcji w węzłach. Każde równanie

odpowiada odpowiedniemu węzłowi siatki. Otrzymany układ równań jest modyfikowany w

wyniku uwzględnienia warunków brzegowych. Rozwiązaniem układu są wartości

poszukiwanej funkcji we wszystkich węzłach siatki.

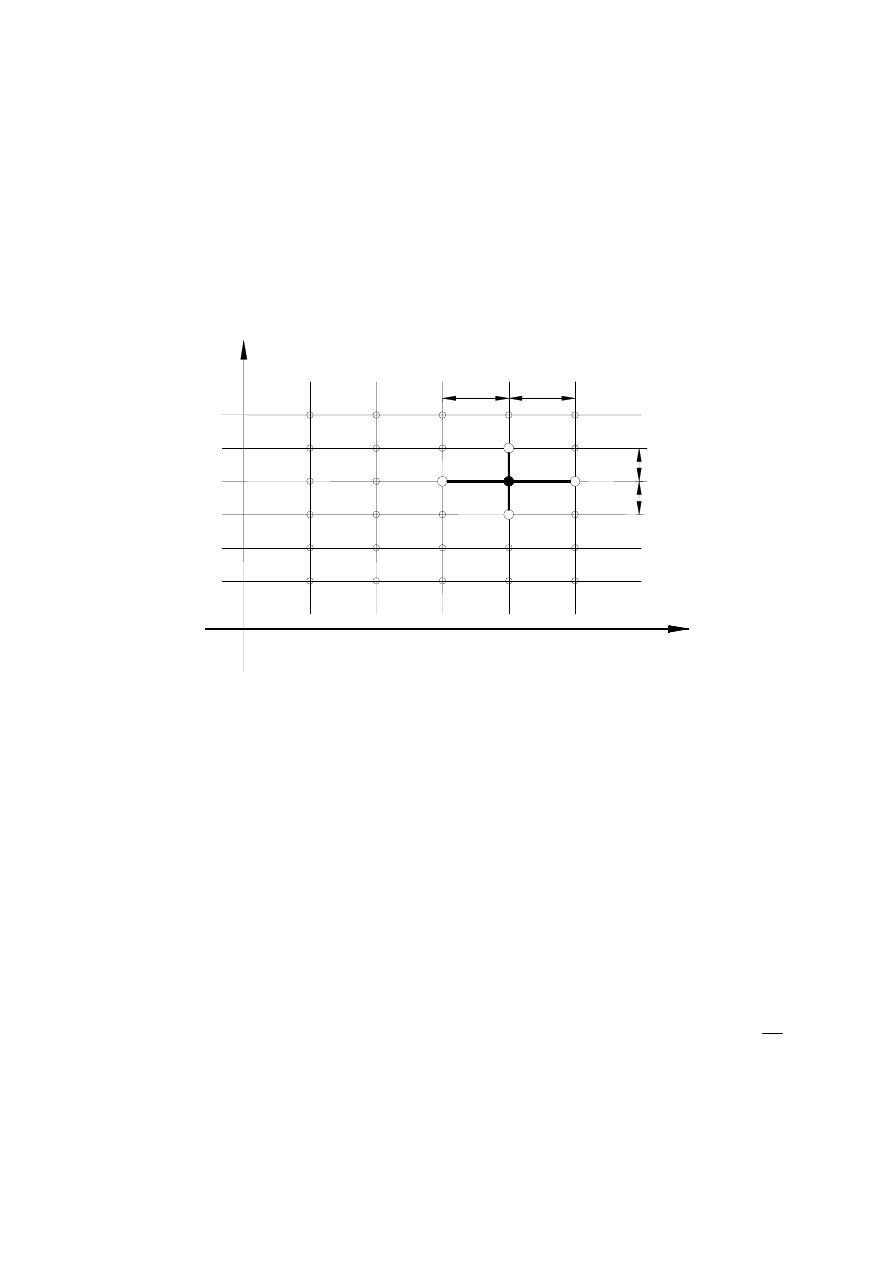
Rys. 6. Dwuwymiarowa siatka prostokątna metody różnic skończonych

Załóżmy, że mamy do czynienia z zagadnieniem dwuwymiarowym we współrzędnych

kartezjańskich xy i stosujemy typową siatkę prostokątną (rys. 6) opisaną przez formuły:

,

,

i

o

k

o

x

x

ih

y

y

kg

= +

=

+

(1)

gdzie

,

o

o

x y

są współrzędnymi wybranego punktu odniesienia.

Przyjmijmy oznaczenie

,

( ,

)

i k

i

k

u

u x y

=

,

(2)

gdzie ( , )

u x y

jest poszukiwaną funkcją.

Możemy wówczas definiować różne schematy różnicowe, na przykład pierwszą pochodną

u

y

∂

∂

można zastąpić przez trzy różne operatory różnicowe:

h

h

g

g

u

u

u

u

i,k+1

i,k

i,k-1

i-1,k

u

i+1,k

x

x

x

y

y

y

0

i

0

k

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

11

,

1

,

,

,

1

,

1

,

1

a)

,

b)

,

c)

.

2

i k

i k

i k

i k

i k

i k

u

u

u

u

y

y

g

u

u

u

u

y

y

g

u

u

u

u

y

y

g

+

−

+

−

−

∂

∆

≈

=

∂

∆

−

∂

∆

≈

=

∂

∆

−

∂

∆

≈

=

∂

∆

(3)

Pierwszy z operatorów (3) nazywany ilorazem różnicowym przednim, drugi ilorazem

różnicowym tylnym, a trzeci ilorazem różnicowym centralnym. Ilorazy różnicowe

odpowiadające drugim pochodnym możemy otrzymać stosując analogiczne schematy

powtórnie, tym razem w stosunku do pierwszych pochodnych. Typowe formuły to na

przykład:

2

2

1,

,

1,

2

2

2

2

2

,

1

,

,

1

2

2

2

2

,

2

.

i

k

i k

i

k

i k

i k

i k

u

u

u

u

u

x

x

h

u

u

u

u

u

y

y

g

+

−

+

−

−

+

∂

∆

≈

=

∂

∆

−

+

∂

∆

≈

=

∂

∆

(4)

Podobnie uzyskamy również wyrażenia na ilorazy różnicowe odpowiadające innym

pochodnym np.

4

4

2,

1,

,

1,

2,

4

4

4

4

6

4

i

j

i

j

i j

i

j

i

j

u

u

u

u

u

u

u

x

x

h

+

+

−

−

−

+

−

+

∂

∆

≈

=

∂

∆

(5)

Szczegóły dalszego postępowania czytelnik znajdzie w przykładach.

P

RZYKŁAD

1

Belka o długości l jest utwierdzona sztywno na obu końcach. Znane jest początkowe (dla chwili

0

t

=

) ugięcie

belki

( )

o

w x

oraz rozkład prędkości początkowej

0

0

( , )

( )

( ,

0)

t

w x t

v x

v x t

t

=

∂

=

= =

∂

. Należy obliczyć jak

zmienia się linia ugięcia belki dla

0

t

>

.

Rozwiązanie.

Funkcja

( , )

w x t

opisująca ugięcie belki spełnia równanie różniczkowe.

4

2

4

2

2

1

0

w

w

x

a

t

∂

∂

+

=

∂

∂

,

(6)

gdzie

EJ

a

A

ρ

=

oraz warunki brzegowe

0

(0, )

( , )

0

dla

0,

dla

0,

x

x l

w

t

w l t

t

w

w

t

x

x

=

=

=

=

≥

∂

∂









=

≥









∂

∂









(7)

i warunki początkowe

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

12

0

0

0

( , 0)

( )

dla

(0, ),

( )

dla

(0, ).

t

w x

w x

x

l

w

v x

x

l

t

=

=

∈

∂





=

∈





∂





(8)

Analizujemy obszar

(0, ) (0, )

l

T

×

, gdzie

T

oznacza czas końcowy procesu

(

0)

T

>

. Przyjmijmy prostokątną

siatkę węzłów dla metody różnicowej

,

.

i

j

x

ih

t

jg

=

=

Pochodnym w równaniu (6) odpowiadają ilorazy różnicowe:

4

2,

1,

,

1,

2,

4

4

2

,

,

1

,

2

2

2

4

6

4

,

2

.

i

j

i

j

i j

i

j

i

j

i j

i j

i j

w

w

w

w

w

w

x

h

w

w

w

w

t

g

+

+

−

−

−

−

−

+

−

+

∆

=

∆

−

+

∆

=

∆

(9)

W ten sposób otrzymujemy układ równań liniowych stanowiący przybliżoną, różnicową postać równania
różniczkowego (6):

2

2

4

2,

1,

,

1,

2,

,

,

1

,

2

(

4

6

4

)

(

2

2

)

0,

0,1, 2,..., ,

0,1, 2,... .

i

j

i

j

i j

i

j

i

j

i j

i j

i j

a g w

w

w

w

w

h w

w

w

i

n

j

m

−

−

+

+

−

−

−

+

−

+

+

−

+

=

=

=

(10)

Z warunków brzegowych mamy

,

,

0

dla

0,...,

o j

n j

w

w

j

m

=

=

=

(11)

i z warunków początkowych

,

,1

( )

1, 2,...,

1,

( )

( )

1, 2,...,

1.

i o

o

i

i

o

i

o

i

w

w x

i

n

w

w x

v x

g

i

n

=

=

−

=

+

⋅

=

−

(12)

Układ równań (10) wraz z warunkami (11) i (12) może być rozwiązywany dla kolejnych kroków czasowych
j=2,3,4....[10].

Rozwiązaniem jest wektor

j

w

opisujący w przybliżeniu linię ugięcia belki w chwili

j

t

(

)

2

2

1

2

4

2

j

j

j

a

g

w

A I

w

w

n

−

−





⋅

=

+

−









,

(13)

gdzie

I

jest macierzą jednostkową,

6

4

1

0

0

...

0

0

4

6

4

1

0

...

0

0

1

4

6

4

1

...

0

0

0

1

4

6

4 ...

0

0

0

0

0

0

0

...

6

4

0

0

0

0

0

...

4

6

A

−









−

−









−

−





=

−

−













−









−





⋮

⋮

⋮

⋮

⋮

⋮

⋮

⋮

,

(14)

jest macierzą nieosobliwą a wektor

j

w

ma postać

2,

3,

2,

j

j

j

n

j

w

w

w

w

−













=

















⋮

.

(15)

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

13

Wektory

j

w

oblicza się korzystając ze znajomości wektorów linii ugięcia dla poprzedzających punktów

czasowych

1

j

w

−

i

2

j

w

−

, przy czym

0

w

i

1

w

wynikają z warunków początkowych

0

2

0

2

0

2

0

3

0

3

0

3

0

1

0

2

0

2

0

(

)

(

)

(

)

( )

( )

( )

(

)

(

)

(

)

n

n

n z

w x

w x

v x

g

w x

w x

v x

g

w

w

w x

w x

v x

g

−

−

−

+

⋅

















+

⋅









=

=

























+

⋅









⋮

⋮

(16)

Wymiar wektorów

j

w

jest zmniejszony, ponieważ warunki brzegowe dają nam

0,

0

j

w

=

,

1,

0

j

w

=

,

1,

0

n

j

w

−

=

,

,

0

n j

w

=

.

P

RZYKŁAD

2

Przedstawić równania różnicowe dla siatki prostokątnej opisanej przez związki (1) dla

a)

równania Poissona

2

2

2

2

( , )

0

u

u

f x y

x

y

∂

∂

+

+

=

∂

∂

,

(17)

b)

równania Helmholtza

2

2

2

2

2

0

u

u

k u

x

y

∂

∂

+

+

=

∂

∂

,

(18)

c)

równania przewodnictwa ciepła

2

2

2

1

0

u

u

x

a

t

∂

∂

+

=

∂

∂

.

(19)

Rozwiązanie:
a)

Zastępując pochodne w równaniach różniczkowych przez odpowiednie ilorazy różnicowe otrzymamy:

(

)

(

) (

)

1,

,

1,

,

1

,

,

1

2

2

1

1

2

2

,

0

i

j

i j

i

j

i j

i j

i j

i

j

u

u

u

u

u

u

f x y

h

g

+

−

+

−

−

+

+

−

+

+

=

.

(20)

Jeśli przyjmiemy

h

g

=

(siatka kwadratowa) i

0

f

≡

(równanie Laplace’a) to uzyskamy wynik:

1,

1,

,

1

,

1

,

4

i

j

i

j

i j

i j

i j

u

u

u

u

u

+

−

+

−

+

+

+

=

.

(21)

Wartość funkcji w węźle jest wtedy równa średniej arytmetycznej z wartości funkcji w 4 najbliższych węzłach,
oddalonych o

h

.

b)

Sprowadzenie do postaci różnicowej daje

(

)

2

2

,

1,

1,

,

1

,

1

4

i j

i

j

i

j

i j

i j

u

g h

u

u

u

u

+

−

−

+

⋅ −

=

+

+

+

.

(22)

c)

Przyjmując

x

h

∆ =

,

t

g

∆ =

otrzymamy

(

)

2

2

2

2

2

1,

,

1,

,

1

2

i

j

i j

i

j

i j

a gu

h

a g u

a gu

h u

+

−

−

−

+

+

= −

.

(23)

P

RZYKŁAD

3

Jednowymiarowy model zginania belki jest opisany równaniem różniczkowym (patrz cz. I, wzór (1.75))

4

4

d w

p

dx

EJ

=

,

(24)

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

14

gdzie

( )

w x

jest funkcją ugięcia belki,

p

obciążeniem ciągłym (N/m),

E

modułem Younga a

J

odpowiednim momentem bezwładności przekroju.
Po zastosowaniu dyskretyzacji: określeniu położenia węzłów dla metody różnic skończonych wg formuły

i

x

a ih

= +

, możemy zastosować centralny iloraz różnicowy dla czwartej pochodnej i równanie różniczkowe

(24) zastąpimy przez równanie

2

1

1

2

4

4

6

4

i

i

i

i

i

i

w

w

w

w

w

p

h

EJ

−

−

+

+

−

+

−

+

=

,

(25)

gdzie

( )

i

i

p

p x

=

.

Możliwe są różne typy warunków brzegowych, które zapisujemy, uwzględniając, że :

a)

wielkość ugięcia w punkcie odpowiada wartości funkcji

( )

w x

,

b)

kąt ugięcia, w zakresie małych deformacji odpowiada wartości pochodnej

dw

dx

,

c)

moment gnący w przekroju

x

jest związany z funkcją ugięcia wzorem

2

2

( )

d w

M x

EJ

dx

=

,

(26)

d)

siła tnąca w przekroju

x

jest związana z linią ugięcia

( )

w x

wzorem

3

3

( )

d w

T x

EJ

dx

=

.

(27)

Uwzględniając powyższe stwierdzenia możemy rozpatrzyć typowe warunki brzegowe (rys. 7) zakładając w
każdym przypadku, że węzeł

k

odpowiada przekrojowi belki z narzuconym warunkiem brzegowym

Przekrój utwierdzony
Odpowiednie warunki brzegowe mają postać:

(

)

0,

(

)

0,

k

k

dw

w x

x

dx

=

=

co po dyskretyzacji prowadzi do zależności

1

1

0,

0.

2

k

k

k

w

w

w

h

+

−

−

=

=

(28)

Jeżeli punkt

k

jest początkiem (końcem) rozpatrywanego przedziału

x

możemy przyjąć odpowiednio

1

0

k

w

+

=

(

1

0

k

w

−

=

).

Przekrój przegubowo podparty, nieobciążony
Odpowiednie warunki brzegowe mają postać

(

)

0

k

w x

=

oraz

(

)

0

k

M x

=

.

Po dyskretyzacji otrzymamy

1

1

2

2

0

i

0

k

k

k

k

w

w

w

w

h

+

−

−

+

=

=

(29)

Przekrój swobodny i obciążony momentem

g

M

Warunki brzegowe odpowiadające temu przypadkowi to

(

)

0

k

T x

=

i

(

)

k

g

M x

M

=

.

Odpowiednie równania różnicowe mają postać:

2

1

1

2

3

2

2

0

k

k

k

k

w

w

w

w

h

+

+

−

−

−

+

−

=

i

1

1

2

2

k

k

k

g

w

w

w

EJ

M

h

+

−

−

+

=

.

(30)

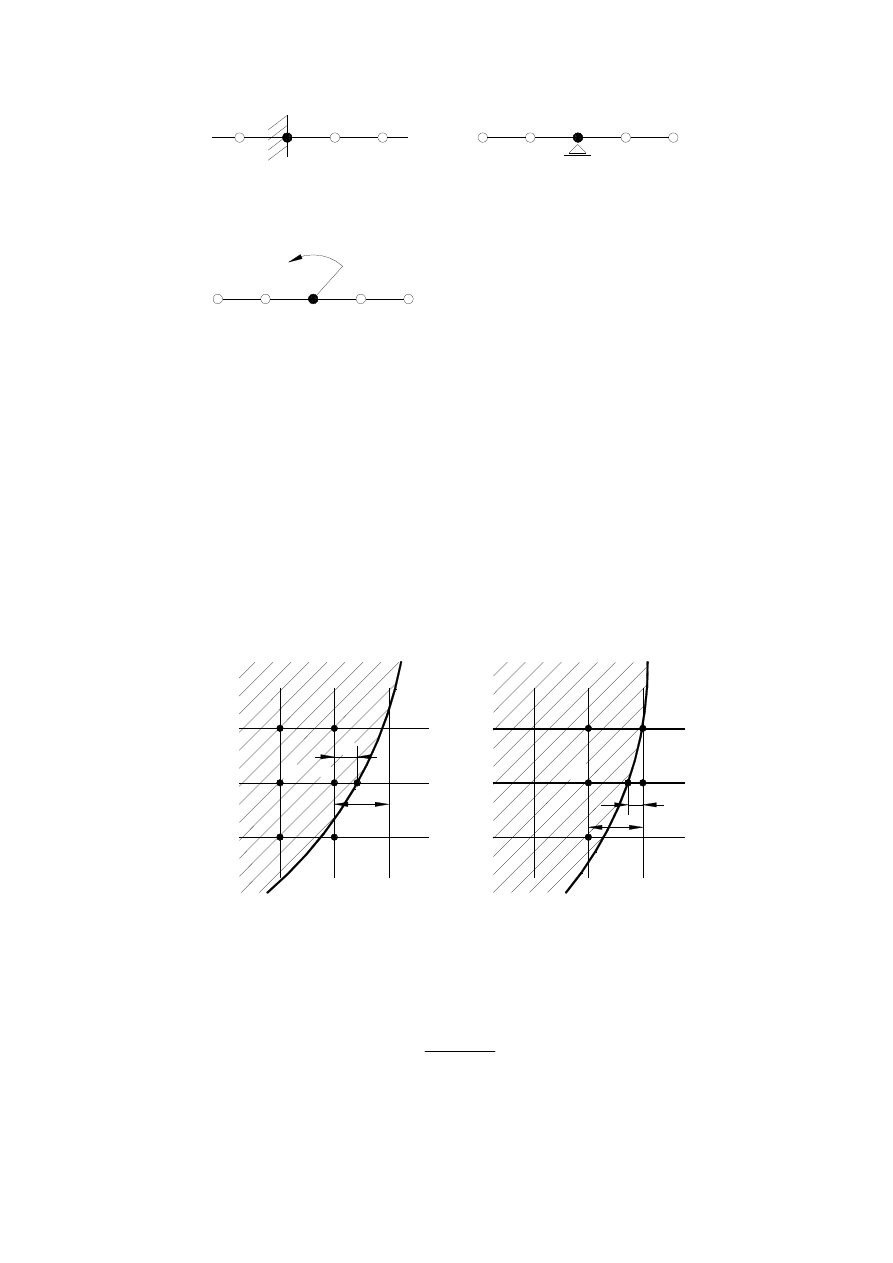
G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

15

Mg

k - 1

k

k + 1

k + 2

k

k + 1

k + 2

k - 1

k - 2

k

k + 1

k + 2

k - 1

k - 2

Rys. 7. Warianty warunków brzegowych w modelu MRS belki zginanej (przykład 3)

W metodzie różnic skończonych siatka węzłów obejmuje często zarówno węzły leżące

wewnątrz analizowanego obszaru, jak i dodatkowe węzły zewnętrzne, które ułatwiają

wprowadzanie warunków brzegowych.

W przypadkach dwu- i trójwymiarowych często zdarza się, że brzeg obszaru przebiega

między węzłami regularnej siatki (rys. 8). W takim przypadku węzłom leżącym najbliżej

konturu przypisujemy wartości wynikające z interpolacji lub ekstrapolacji.

1

2

0

1

2

0

h

h

δ

δ

a)

b)

Rys. 8. Interpolacja i ekstrapolacja warunku brzegowego w MRS

Jeśli ostatni węzeł siatki (1) leży wewnątrz konturu (rys. 8a), to zamiast narzuconego

warunku na wartość funkcji

0

u

u

=

wprowadzamy związek

0

2

1

hu

u

u

h

δ
δ

+

=

+

.

(31)

W przeciwnym przypadku (rys. 8b) mamy

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

16

0

2

1

hu

u

u

h

δ
δ

−

=

−

.

(32)

Metoda różnic skończonych ma wiele zalet, dzięki którym w przeszłości uważana była

za najbardziej efektywną metodę obliczeń zautomatyzowanych. Do najważniejszych z nich

należą prostota algorytmów i bezpośrednie wykorzystanie równań różniczkowych problemu.

W pewnych obszarach jest do dziś praktycznie stosowana, np. w analizie tarcz i płyt, czy w

zagadnieniach przepływowych.

MRS napotyka na szereg trudności w przypadku obszarów o złożonych kształtach i

skomplikowanych warunków brzegowych. Dla poprawienia jej efektywności opracowano

pewne modyfikacje i udogodnienia mające na celu ułatwienie budowy modelu dyskretnego,

np. algorytmy MRS dla nieregularnych siatek węzłów.

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

17

3. METODA ELEMENTÓW BRZEGOWYCH

Metoda elementów brzegowych (MEB) jest stosunkowo nową komputerową metodą

rozwiązywania zagadnień opisywanych równaniami różniczkowymi cząstkowymi. Jej

podstawą jest sprowadzenie zadania brzegowego lub brzegowo-początkowego opisanego za

pomocą układu równań różniczkowych cząstkowych z odpowiednimi warunkami

granicznymi do tak zwanych brzegowych równań całkowych. Równania te są rozwiązywane

w sposób przybliżony przez podział brzegu na segmenty zwane elementami brzegowymi i

przyjęcie odpowiedniej aproksymacji analizowanych funkcji na elementach brzegowych za

pomocą z góry założonych funkcji modelujących. Warto podkreślić, że w MEB zwykle

niezbędna jest dyskretyzacja tylko brzegu obszaru a nie całego analizowanego obszaru, co

prowadzi do znacznego zmniejszenia liczby niewiadomych w porównaniu do metody różnic

skończonych i metody elementów skończonych. Mówimy, że MRS i MES należą do tzw.

metod obszarowych przybliżonego rozwiązywania zagadnień brzegowo-początkowych a

MEB reprezentuje metody brzegowe.

Metodę elementów brzegowych omówimy najpierw na przykładzie równania różniczkowego

Poissona w przypadku dwuwymiarowym. W poprzednim rozdziale przedstawiony był sposób

rozwiązania tego równania metodą różnic skończonych. Rozwiązanie zagadnienia Poissona

metodą elementów skończonych omówione będzie w rozdziale następnym.

3.1. METODA ELEMENTÓW BRZEGOWYCH DLA RÓWNANIA

POISSONA

Rozpatrzmy równanie Poissona:

2

2

1

2

2

2

1

2

( ,

)

0

u

u

f x x

x

x

∂

∂

+

+

=

∂

∂

,

(33)

gdzie

1

2

( ,

)

x

x x

=

∈Ω

z warunkami brzegowymi

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

18

0

0

( )

,

( )

( )

,

u

q

u x

u

x

u x

q x

q

x

n

=

∈Γ

∂

=

=

∈Γ

∂

(34)

Równanie Poissona i Laplace’a (gdy

1

2

( ,

)

0

f x x

=

) opisuje wiele zjawisk o dużym znaczeniu

w technice: stacjonarny przepływ ciepła, stacjonarny bezwirowy przepływ nieściśliwej i

nielepkiej cieczy, proste pola magnetyczne i elektryczne [4]. W teorii sprężystości równanie

Poissona opisuje rozkłady naprężeń w przekroju pręta skręcanego .

Dla takiego zagadnienia przedstawić można brzegowe równanie całkowe

2

, które stanowi

sformułowanie równoważne problemowi opisanemu przez związki (33) i (34).

( )

( ) ( )

( )

( , )

( )

( , )

( )

( )

( , )

( )

u x

c

u

u x q

x d

x

u

x d

x

f x u

x dR x

n

ξ

ξ

ξ

ξ

ξ

∗

∗

∗

Γ

Γ

Ω

∂

=

Γ

−

Γ

+

∂

∫

∫

∫

(35)

W równaniu (35) ( )

c

ξ

jest współczynnikiem liczbowym, którego wartość jest równa

1

2

jeśli

ξ

leży na gładkim konturze, a 1 dla

ξ

leżącego wewnątrz obszaru. W przypadku naroża

współczynnik ten należy specjalnie obliczać.

Funkcje u

∗

i q

∗

zależą od położenia dwóch punktów: punktu

ξ

zwanego punktem

ź

ródłowym i punktu x zwanego punktem obserwacyjnym (rys. 9).

x

x

2

1

r

r

r

1

2

Ω

Γ

Γ

u

Γ Γ =Γ

u

q

q

n

n

n

1

2

ξ

x

Rys. 9. Oznaczenia pomocnicze do brzegowego sformułowania zagadnienia Poissona

Funkcja u

∗

znana w teorii równań całkowych, jako tak zwane rozwiązanie fundamentalne ma

postać:

1

1

( , )

ln

2

u

x

r

ξ

π

∗

 

=

=

 

 

,

(36)

2

wyprowadzenie równania (35) znaleźć można w monografiach teorii spręzystości

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

19

gdzie

2

2

1

1

2

2

(

)

(

)

r

x

x

ξ

ξ

=

−

+

−

.

Funkcja q

∗

określona jest przez pochodną kierunkową u

∗

:

( , )

( , )

u

x

q

x

n

ξ

ξ

∗

∗

∂

=

∂

.

(37)

Dokonując różniczkowania otrzymamy

1

2

1

2

1

1

2

2

2

,

(

)

,

2

u

u

q

n

n

x

x

r n

r n

q

r

π

∗

∗

∗

∗

∂

∂

=

⋅ +

⋅

∂

∂

− ⋅ + ⋅

=

(38)

gdzie

,

i

i

i

r

x

ξ

= −

1, 2

i

=

, a

1

2

,

n

n n

=

jest jednostkowym wektorem zewnętrznie normalnym

do brzegu

Γ

.

Wzór (38) można łatwo otrzymać, zauważając, że

i

i

i

i

x

r

r

x

r

r

ξ

−

∂ =

=

∂

.

(39)

Brzegowe równanie całkowe (35) wiąże ze sobą nieznane funkcje

( )

u x i jej pochodną

normalną

( )

( )

u x

q x

n

∂

=

∂

na konturze obszaru. W trzeciej całce, obszarowej, funkcje

podcałkowe są znane. Równanie (35) można rozwiązać numerycznie w sposób przybliżony,

realizując następujący schemat:

1.

Brzeg

Γ

dzielimy na LE elementów brzegowych, będących odcinkami lub

krzywoliniowymi segmentami z węzłami wyznaczającymi ich kształt.

2.

Na każdym elemencie brzegowym funkcje

( )

u x i

( )

( )

u x

q x

n

∂

=

∂

aproksymujemy za

pomocą wartości w węzłach i odpowiednich, z góry założonych funkcji interpolacyjnych.

3.

Wykorzystując przyjętą dyskretyzację przekształcamy równania całkowe formułowane

dla każdego węzła (punktu

ξ

) w algebraiczne równanie liniowe.

4.

Otrzymujemy układ równań liniowych wiążący ze sobą wartości

i

u i

i

q funkcji ( )

u x i

( )

q x dla wszystkich węzłów konturu. Układ ten rozwiązujemy po wprowadzeniu

warunków brzegowych (w każdym węźle znamy albo

i

u albo

i

q ). Rozwiązaniem jest

wektor nieznanych wartości funkcji ( )

u x i jej pochodnych w węzłach brzegu.

5.

Jeśli chcemy wyznaczyć wartości funkcji u dla punktów wewnętrznych wykorzystujemy

ponownie wzór (35) przenosząc punkt

ξ

do wewnątrz obszaru. Wtedy

( ) 1

c

ξ

=

i

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

20

ponieważ znane są już wartości funkcji i jej pochodnych na konturze zadanie sprowadza

się do zwykłego numerycznego całkowania.

Rozpatrzmy na przykład przebieg obliczeń dla najprostszych elementów brzegowych, tzw.

elementów stałych (rys. 10). Element brzegowy jest w tym przypadku odcinkiem a węzeł tego

elementu usytuowany jest w środku.

x

x

2

1

P

P

j

i

r

Rys. 10. Podział brzegu na elementy stałe (o stałych wartościach funkcji aproksymowanych)

Zakładamy, że na każdym elemencie funkcje ( )

u x i ( )

q x przybliżamy funkcjami stałymi.

Otrzymamy wtedy dla każdego węzła i związek

1

1

1

( )

( , ) (

)

( , ) (

)

2

( )

( , )

1, 2,..

j

j

LE

LE

i

i

j

j

i

j

j

j

j

i

u P

u P x q P d

q P x u P d

f x u P x dR

i

LE

∗

∗

=

=

Γ

Γ

∗

Ω

=

Γ −

Γ

+

=

∑

∑

∫

∫

∫

(40)

Dla obliczenia wartości trzeciej całki, ze znanymi funkcjami podcałkowymi, niezbędna jest

pomocnicza dyskretyzacja obszaru. Przyjmijmy oznaczenie

( )

( , )

( )

i

i

f

f x u P x d

x

∗

Ω

=

Ω

∫

.

(41)

Po numerycznym całkowaniu dla każdego punktu węzłowego otrzymujemy związek

1

1

1

( )

(

)

(

)

,

1, 2...

2

LE

LE

i

ij

j

ij

j

i

j

j

u P

U

q P

Q u P

f

i

LE

∗

∗

=

=

=

⋅

−

⋅

+

=

∑

∑

.

(42a)

{ }

{ }

{ } { }

1

2

u

U

q

Q

n

f

∗

∗









=

−

+









.

(42b)

Otrzymamy więc LE równań liniowych, w których niewiadome (42b) stanowią nieznane

wartości (

)

j

u P (jeśli węzeł

j

P leży na części

q

Γ

konturu) i ( )

i

q P (jeśli węzeł

i

P leży na

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

21

części

u

Γ

konturu). Oznaczając te niewiadome jako

{ }

y

układ (42) możemy doprowadzić do

postaci:

[ ]

{ } { }

A

y

b

=

(43)

gdzie macierz

[ ]

A

i wektor prawych

{ }

b

stron są znane.

W rezultacie otrzymujemy kompletną informację o funkcji ( )

u x i jej pochodnych na brzegu.

W odróżnieniu do MRS i MES, gdzie analogiczna macierz jest zazwyczaj pasmowa i

symetryczna, w metodzie elementów brzegowych otrzymujemy macierz A pełną i

niesymetryczną.

3.2. DWUWYMIAROWE ZAGADNIENIE TEORII SPRĘŻYSTOŚCI.

BRZEGOWE RÓWNANIE CAŁKOWE

Opis matematyczny MEB dla zagadnień teorii sprężystości może być formułowany na

wiele sposobów [5] i jest bardziej złożony niż w metodzie różnic skończonych, czy metodzie

elementów skończonych. W tym rozdziale prezentowany jest skrótowy obraz tak zwanego

podejścia bezpośredniego, w którym niewiadomymi w równaniach całkowych są

przemieszczenia i naprężenia.

Rozpatrujemy izotropowe, jednorodne ciało liniowo sprężyste zajmujące w przestrzeni

2

R obszar

Ω

i znajdujące się w stanie równowagi pod działaniem sił zewnętrznych:

powierzchniowych

1

2

1

2

( ,

)

(

,

)

p x x

p p

=

i objętościowych

1

2

1

2

( ,

)

(

,

)

X x x

X X

=

. Obciążenia te

powodują powstanie odpowiedniego pola przemieszczeń

1

2

1

2

( ,

)

( ,

)

u x x

u u

=

i pola naprężeń

1

2

( ,

),

ij

x x

σ

,

1, 2

i j

=

(rys. 11).

X

p

22

11

12

11

22

x

x

2

1

Γ Γ =Γ

u

q

Γ

u

Ω

Γ

q

σ

σ

σ

σ

σ

Rys. 11. Analizowane ciało sprężyste

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

22

Polu przemieszczeń u odpowiada tensor odkształcenia:

(

)

,

,

1

2

ij

i j

j i

u

u

ε

=

+

.

(44)

Różniczkowe równanie równowagi w układzie kartezjańskim

1 2

x x

ma postać:

,

0

ji j

i

X

σ

+

=

,

(45)

gdzie

ij

σ

jest symetrycznym tensorem naprężenia.

Ciało jest podparte na części

u

Γ

brzegu (znane przemieszczenia

1

2

ˆ ˆ

( ,

)

u u u

∆

) i obciążone na

Części

p

Γ

(znane obciążenia

1

2

ˆ

ˆ

(

,

)

p

p p

∆

=

). Mamy więc warunki brzegowe:

ˆ ,

(

)

i

ji

j

i

p

p

n

p

x

σ

=

=

∈Γ

,

(46)

gdzie

1

2

( ,

)

n

n n

=

jest wersorem normalnym zewnętrznie do konturu oraz

ˆ ,

(

)

i

i

u

u

u

x

=

∈Γ

.

(47)

Związek między tensorami odkształcenia i naprężenia określają poniższe zależności,

wyrażające uogólnione prawo Hooke’a. Dla płaskiego stanu naprężenia (PSN):

2

1

1

ij

ij

ij

kk

E

Ev

v

v

σ

ε

δ ε

=

+

+

−

,

(48)

a dla płaskiego stanu odkształcenia (PSO):

1

(1

)(1 2 )

ij

ij

ij

kk

E

vE

v

v

v

σ

ε

δ ε

=

+

+

+

−

,

(49)

gdzie E jest modułem Younga a v – stałą Poissona.

Zauważyć można, że związki konstytutywne (48) i (49) różnią się wyłącznie

współczynnikami określonymi przez stałe materiałowe. Przez podstawienie do (48)

zmodyfikowanych wartości stałych:

2

,

1

1

E

v

E

v

v

v

′

′

=

=

−

−

,

(50)

otrzymamy związek (49), a przez podstawienie do (49)

2

(1 2 )

,

(1

)

1

E

v

v

E

v

v

v

+

′

′

=

=

+

+

,

(51)

otrzymamy związek (48).

W przypadku wykorzystania w prawie Hooke’a modułu sprężystości postaciowej

2(1

)

E

G

v

=

+

i stałej Poissona, podstawienia (50) i (51) przejdą odpowiednio w (52) i (53):

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

23

,

1

v

v

G

G

v

′

′

=

=

−

,

(52)

,

1

v

v

G

G

v

′

′

=

=

+

.

(53)

Powyższe związki pozwalają na proste dostosowanie algorytmów numerycznych do realizacji

obliczeń zarówno dla PSN jak i PSO w zależności od określającego stan parametru

sterującego. Dalsze zależności przedstawiane będą dla płaskiego stanu odkształcenia.

Podstawiając (44) do (49) a następnie do (45) otrzymujemy przemieszczeniowe

równania różniczkowe Naviera:

,

,

0

1 2

j kk

k kj

j

G

Gu

u

X

v

+

+

=

−

.

(54)

Punktem wyjścia dla bezpośredniej metody elementów brzegowych są wzory

Somigliany. Wzory Somigliany wyprowadzić można ze znanego twierdzenia Bettiego o

wzajemności prac:

i

i

i

i

i

i

i

i

X u dV

p u dA

X u dV

p u dA

Ω

Γ

Ω

Γ

′

′

′

′

+

=

+

∫

∫

∫

∫

.

(55)

Twierdzenie to można wyrazić następująco:

Jeśli na ciało działają kolejno dwa układy obciążeń to praca pierwszego układu obciążeń

( , )

X p na przemieszczeniach wywołanych przez drugi układ ( )

u

′

jest równa pracy drugiego

układu obciążeń (

,

)

X p

′ ′

na przemieszczeniach wywołanych przez układ pierwszy ( )

u .

x

r

ξ

X = (x

ξ

i

i k

(k=1)

P (x

ξ

i

δ

x

2

x

1

δ

- )

(k)

, )

Rys. 12. Pomocniczy stan równowagi: siła w przestrzeni nieograniczonej

Aby otrzymać wzory Somigliany przyjmijmy, że dany jest układ obciążeń ciała p ,

X . Drugi stan równowagi konstruujemy wyodrębniając w nieograniczonej przestrzeni

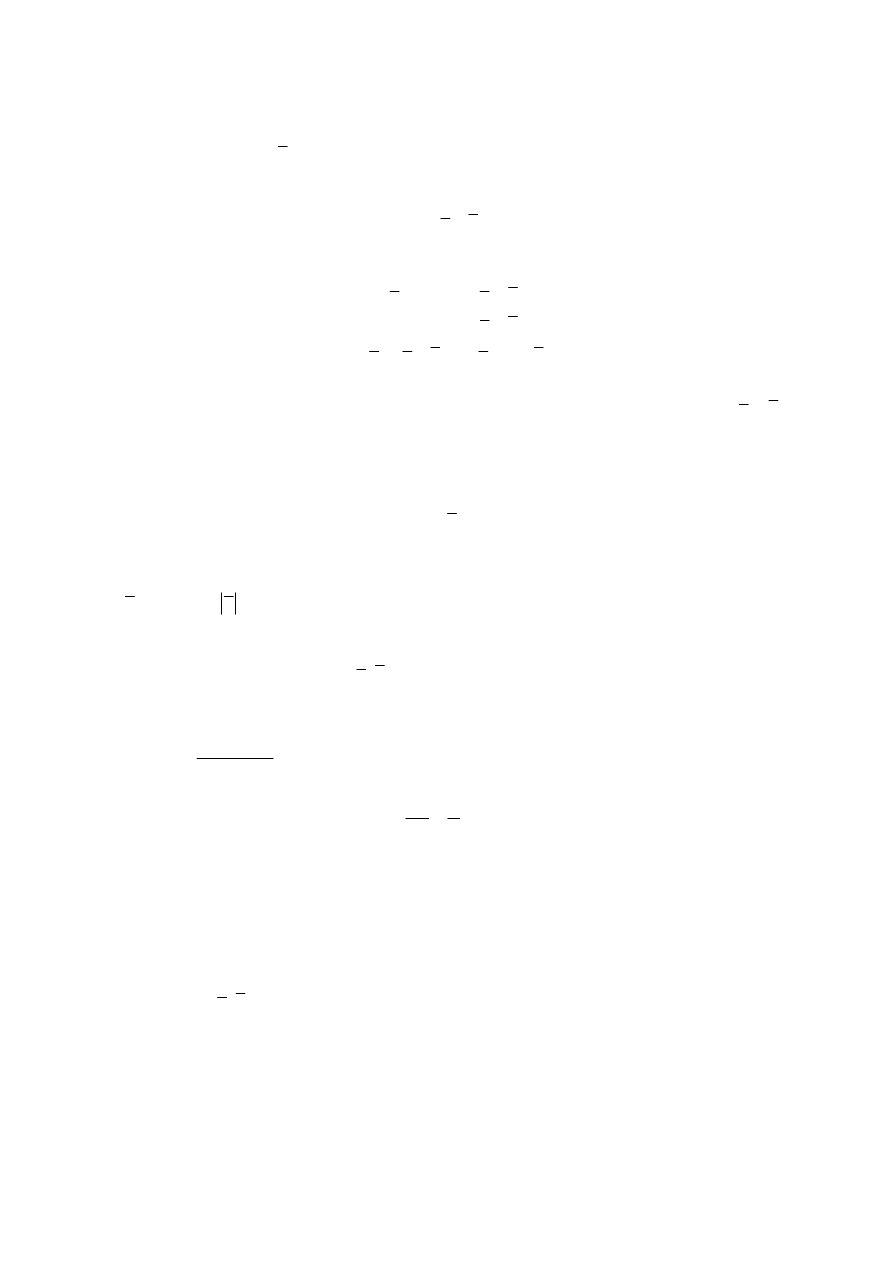
G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

24

sprężystej

∞

Ω

obszar

Ω

odpowiadający obszarowi zajmowanemu przez analizowane ciało

(rys. 12). W punkcie

ξ

∈Ω

przykładamy jednostkową, objętościową siłę skupioną X

′

o

kierunku k:

(

)

i

ik

X

x

δ

ξ δ

′ =

−

.

(56)

W powyższym wzorze (

)

x

δ

ξ

−

jest funkcją (dystrybucją) Diraca o własnościach:

( )

0,

0,

( )

,

0,

( ) (

)

( )

( ).

x

x

x

x

f x

x

d

x

f

σ

δ

δ

ξ

ξ

Ω

=

≠

→ ∞

=

−

Ω

=

∫

(57)

Wynika stąd, że

i

X

′

określone wzorem (56) jest wszędzie równe zeru poza punktem x

ξ

=

,

gdzie ma jedną składową (k) o wartości nieskończonej. Siłę określoną przez funkcję

i

X

′

możemy traktować jako siłę jednostkową, gdyż:

( )

i

ik

X dV x

δ

Ω

′

=

∫

.

(58)

Rozwiązanie układu równań przemieszczeniowych (54) dla takiej siły, z warunkiem

( )

0

u x

→

dla

x

→ ∞

, daje w rezultacie w przypadku płaskiego stanu odkształceń pole

tensorowe przemieszczeń [2]:

( )

( )

1

, ,

2

( , )

ln

k

i

i k

ik

U

x

C r r

C

r

ξ

δ





=

−



 ,

(59)

gdzie:

1

1

8

(1

)

C

G

v

π

=

−

,

2

3 4

C

v

= −

,

(

)

1/ 2

(

)(

)

i

i

i

i

r

x

x

ξ

ξ

=

−

−

,

,

i

i

i

r

r

r

x

r

∂

=

=

∂

,

i

i

i

r

x

ξ

= −

.

Funkcje

( )

k

i

U

nazywane są rozwiązaniami (funkcjami) fundamentalnymi Kelvina równań

elastostatyki lub funkcjami przemieszczeniowymi Greena dla przestrzeni nieograniczonej [4,

16].

Znajomość tensora przemieszczeniowego Greena (59) pozwala na określenie pola

naprężeń

( )

( )

,

k

ji

x

σ

ξ

i następnie obciążeń

( )

k

i

P

odpowiadających brzegowi

Γ

. Korzystając ze

związku (44) mamy:

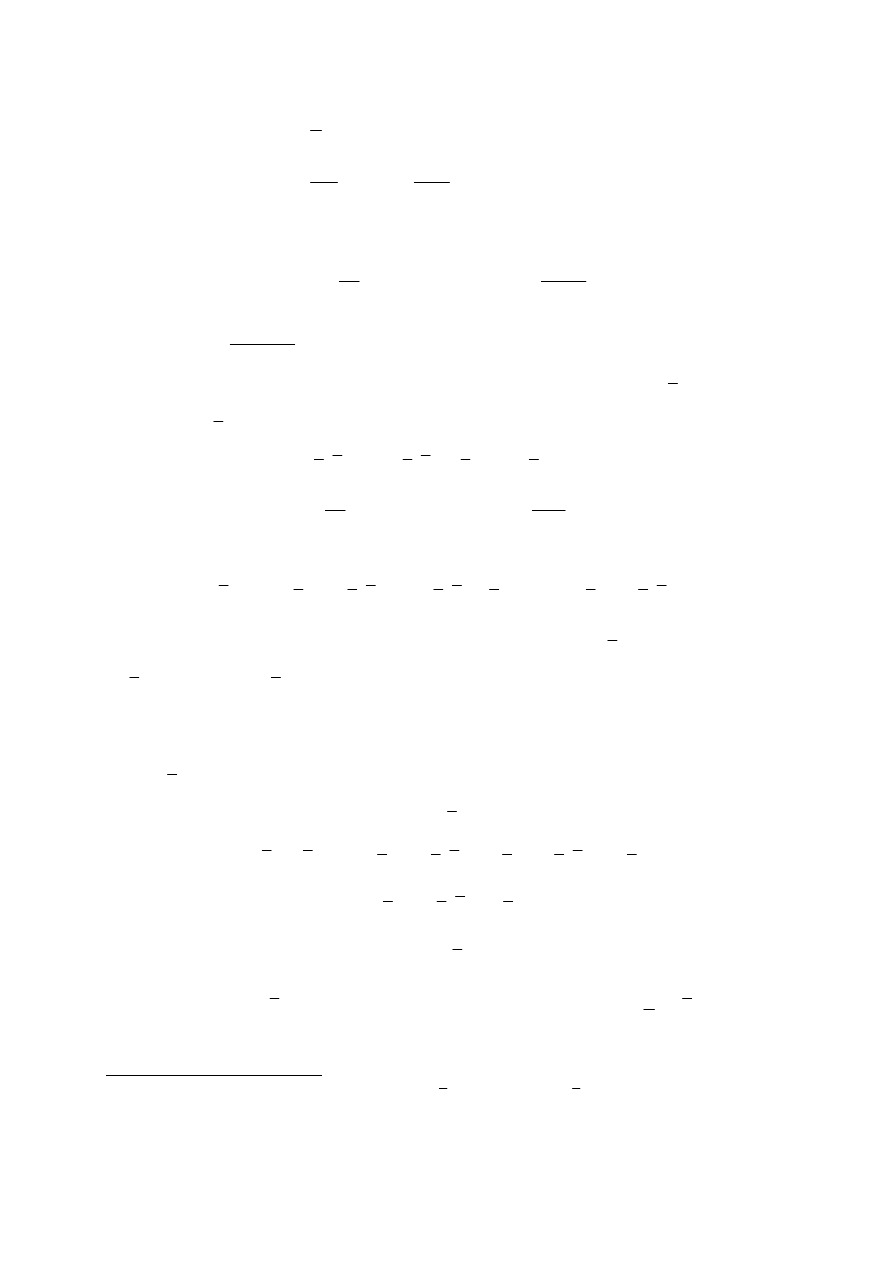
G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

25

(

)

(

)

( )

( )

( )

,

,

( )

1

2

2

2

1

,

2

2

4

(

1)

.

2

k

k

k

ij

i j

j i

i j k

k

ij

ij k

jk i

ik j

U

U

r r r

C

r

C

r

r

r

r

ε

ε

δ

δ

δ

=

+





=

−

−

−

+









(60)

Wyznaczony z prawa Hooke’a wzór określający składowe tensora naprężeń ma postać:

(

)

( )

3

4

2

2

2

i j k

k

ij

ij k

ik i

ik j

r r r

C

C

r

r

r

r

r

σ

δ

δ

δ





=

−

−

−









,

(61)

gdzie:

3

1

4 (1

)

C

v

π

=

−

,

4

1 2

C

v

= −

.

Mając dany tensor naprężeń odpowiadający przyłożeniu w punkcie

1

2

( ,

)

ξ

ξ ξ

=

siły

jednostkowej X

′

można wyznaczyć obciążenia linii konturu

Γ

:

( )

( )

( )

3

4

4

2

2

( , )

( , )

( ),

,

2

(

)

.

k

k

i

ij

j

k

i k

i

i k

k i

ik

l

l

P

x

x

n x

x

A

C

r r

P

C n r

n r

C

r n

r

r

ξ

σ

ξ

δ

=

∈









=

−

−

+

















(62)

Wstawiając wyrażenia (59) i (62) do (55) otrzymujemy wzory Somigliany:

(

)

( )

( )

( )

( )

( )

( , )

( , ) ( )

( )

( , )

k

k

k

k

i

i

i

i

i

i

u

p x U

x

P

x

u x d

X x U

x

d

ξ

ξ

ξ

ξ

Γ

Ω

=

−

Γ +

Ω

∫

∫

(63)

Ze wzorów Somigliany wynika, że znając rozkład sił masowych

( )

i

X x oraz przemieszczenia

( )

i

u x i obciążenia

( )

i

p x brzegu ciała

Γ

możemy obliczyć przemieszczenia

k

u w dowolnym

punkcie wewnętrznym tego ciała

3

.

Praktyczne zastosowanie wzorów Somigliany stało się możliwe przez przeniesienie

punktu

ξ

(leżącego wewnątrz obszaru ciała i w którym określane jest przemieszczenie) na

brzeg ciała

Γ

. Można wykazać, że dla punktu

ξ

∈Γ

otrzymujemy

(

)

( )

( )

( )

( )

( )

( )

( , )

( )

( , )

( )

( )

( , )

( ),

k

k

kj

j

i

i

i

i

k

i

i

c

u

p x U

x

u x P

x

d

x

X x U

x

d

x

ξ

ξ

ξ

ξ

ξ

Γ

Ω

=

−

Γ

+

+

Ω

∫

∫

(64)

gdzie

kj

c zależy od kształtu konturu w punkcie

ξ

i od współczynnika Poissona.

Gdy brzeg w punkcie

ξ

jest gładki, lewa strona równania (64) ma postać

1

( )

2

k

u

ξ

.

3

Konieczność znajomości zarówno przemieszczeń

( )

i

u x jak i obciążeń

( )

i

p x brzegu dla zastosowania zasady

Somigliany powodowała, że przed rozwojem metody elementów brzegowych uważano, że „wzory Somigliany
mają jedynie teoretyczne znaczenie, bowiem na brzegu ciała mogą być znane albo przemieszczenia albo
obciążenia, ale każdy z tych typów warunków brzegowych oddzielnie” (Nowacki W., Teoria sprężystości)

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

26

W dalszych rozważaniach przyjmiemy

0

i

X

≡

. Siły masowe mogą być uwzględnione

w MEB. Jednak w takim przypadku wymagana jest pomocnicza dyskretyzacja obszaru by

obliczyć wartość trzeciej całki w równaniu (64). Przyjęcie odpowiedniej dyskretyzacji brzegu

i aproksymacji warunków brzegowych sprowadza zadanie rozwiązania równania (64) do

układu równań liniowych z niewiadomymi określającymi nieznaną część warunków

brzegowych. Po wykonaniu tego zadania można obliczać przemieszczenia, odkształcenia i

naprężenia w wybranych punktach wewnętrznych obszaru. Przemieszczenia obliczane są

bezpośrednio ze zdyskretyzowanych wzorów Somigliany (63).

Wyrażenia na składowe tensorów odkształcenia i naprężenia otrzymamy po

zróżniczkowaniu równania względem

i

ξ

i wykorzystaniu wzorów (44) i (49). Otrzymujemy

([2,4]):

( )

( , )

( )

( )

( , )

( )

( )

ij

kij

k

kij

k

A

x

p x d

x

B

x

u x d

x

ε ξ

ξ

ξ

Γ

Γ

=

Γ

−

Γ

∫

∫

,

(65)

gdzie:

(

)

( )

( )

1

, ,

,

2

,

,

1

( , )

,

2

2

4

(1

)(

) ,

2

i

j

k

k

kij

j

i

kij

ij jk

i

j

k

jk

i

ik

j

U

U

A

x

C

A

r

r r r

C

r

r

r

ξ

ξ

ξ

δ

δ

δ







∂

∂

=

+













∂

∂









= −

−

+ −

+



(66)

(

)

(

) (

)

}

( )

( )

3

,

,

,

, ,

,

2

4

, ,

,

,

,

,

,

1

( , )

,

2

2

4

2

2

,

i

j

k

k

kij

j

i

kij

ij

k

ik

j

jk

i

i

j

k

ik

j

jk

i

ij

k

i

j

k

k

j

i

k

i

j

P

P

B

x

C

r

B

r

v

r

r

r r r

r

n

C

n

n

n

r r n

v r r n

r r n

ξ

ξ

ξ

δ

δ

δ

δ

δ

δ







∂

∂

=

+











∂

∂









∂









=

+

+

−

+









∂







+

+

−

+

+

+





(67)

oraz

( )

( , )

( )

( )

( , )

( )

( )

ij

kij

k

kij

k

A

A

D

x

p x dA x

S

x

u x dA x

σ ξ

ξ

ξ

=

−

∫

∫

,

(68)

gdzie

(

)

3

4

,

,

,

, ,

,

2

kij

ik

j

jk

i

ij k

i

j

k

C

D

C

r

r

r

r r r

r

δ

δ

δ





=

+

−

+



 ,

(69)

(

)

(

)

(

)

(

)

(

)

3

,

,

,

, ,

,

2

, ,

,

,

,

,

2

2

1 2 )

(

4

1 2

2

4

1

2

.

kijh

ij

k

ik

jk

jk

i

i

j

k

i

j

k

ik

j

jk

i

ij

k

k

j

i

k

i

j

C G

r

S

v

r v

r

r

r r r

r

n

v

r r n

n

n

v

n

v r r n

r r n

δ

δ

δ

δ

δ

δ

∂









=

−

+

−

+









∂





+ −

+

+

+

−

+

+

+

(70)

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

27

We wzorach (3.21)÷(3.25)

,

i

i

i

i

i

i

x

r

r

r

r

x

r

r

ξ

ξ

−

∂

∂

=

= −

=

=

∂

∂

.

3.3. ALGORYTMY NUMERYCZNE MEB W DWUWYMIAROWYM

ZADANIU TEORII SPRĘŻYSTOŚCI

Najważniejsze elementy postępowania, jakie możemy wyróżnić w analizie metodą

elementów brzegowych to:

a)

Dyskretyzacja brzegu na elementy brzegowe. Przyjmijmy oznaczenia: LE – liczba

elementów brzegowych, LW – liczba węzłów konturu, LWE – liczba węzłów elementu

brzegowego.

b)

Przyjęcie funkcji modelujących przebieg przemieszczeń ( )

i

u i obciążeń (

)

i

p na

elemencie w zależności od ich wartości w punktach węzłowych,

c)

Przedstawienie związków (64) dla wszystkich punktów węzłowych jako układu 2· LW

równań liniowych typu

[ ]{ } [ ]{ }

P u

U

p

=

z nieznanymi 2· LW składowymi przemieszczeń i obciążeń węzłowych pozostałymi po

uwzględnieniu znanych warunków brzegowych,

d)

Rozwiązanie przekształconego układu równań

[ ]{ } { }

A x

b

=

a więc określenie nieznanych obciążeń i przemieszczeń w węzłach brzegowych,

e)

Obliczenie składowych tensora naprężeń na brzegu, odpowiadających znanym już

obciążeniom i przemieszczeniom,

f)

Obliczenie przemieszczeń i naprężeń w wybranych punktach wewnętrznych ze

zdyskretyzowanych wzorów (65) i (68).

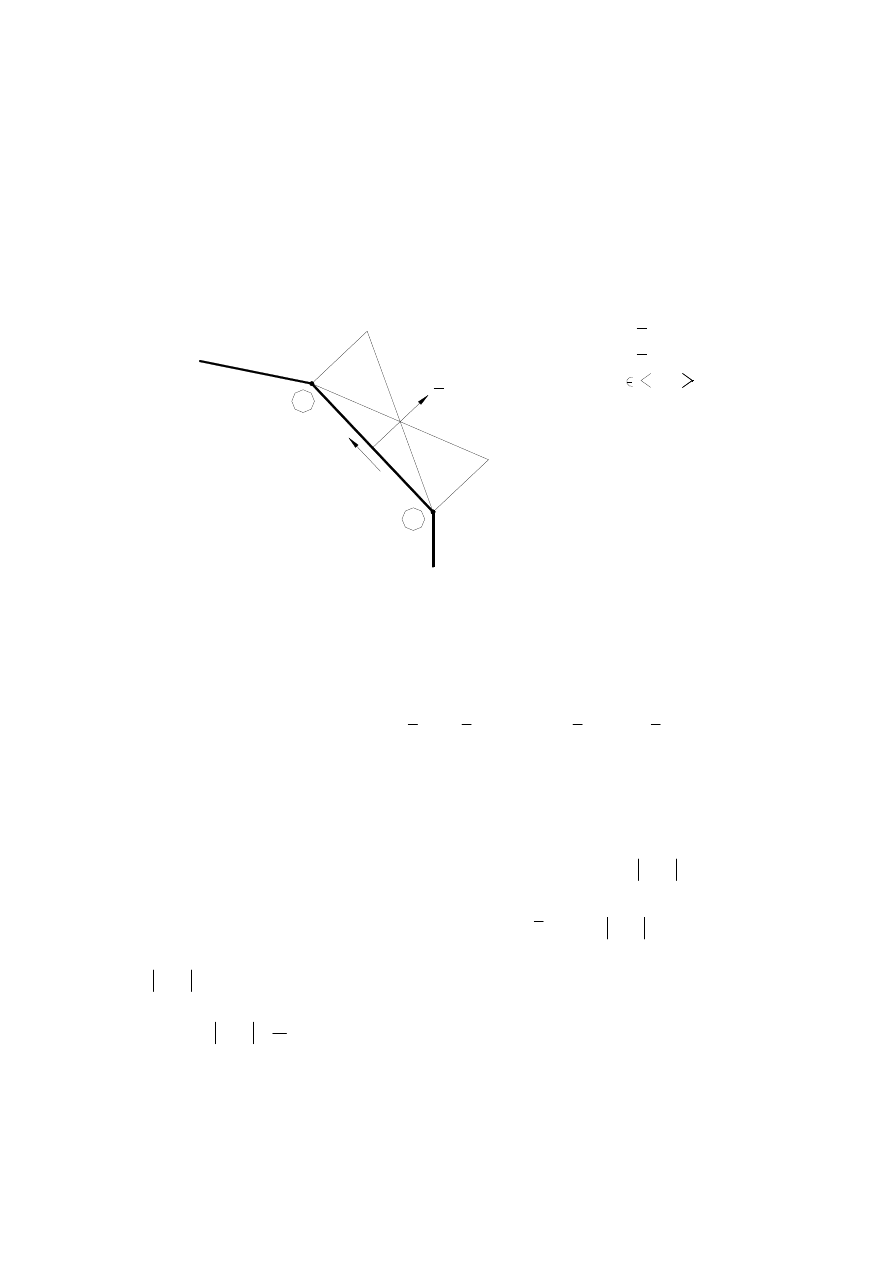
Aproksymacja kształtu elementu, przemieszczeń i obciążeń określone mogą być wzorami

1

1

1

( )

( ) ( ),

( )

( ) ( ),

( )

( )

( ),

LWE

G

i

l

i

l

LWE

u

i

l

i

l

LWE

p

i

l

i

l

x

x l

u

u l

p

p l

η

ψ η

η

ψ η

η

ψ η

=

=

=

=

=

=

∑

∑

∑

(71)

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

28

gdzie LWE – jest liczbą węzłów elementu,

η

– lokalną współrzędną określającą położenie na

linii elementu (

1,1 )

η

∈< −

>

,

( )

i

x l ,

( )

i

u l ,

( )

i

p l oznaczają współrzędne, przemieszczenia i

obciążenia węzła l a

ψ

∗

∗

są założonymi z góry funkcjami modelującymi. Zazwyczaj

przyjmuje się ten sam sposób aproksymacji wszystkich przybliżanych funkcji:

,

1, 2.

G

u

P

l

l

l

l

l

ψ

ψ

ψ

ψ

=

=

=

=

η = 1

1

2

η = −1

η

n

Ψ = 1

2

Ψ = 1

1

Ψ = ( 1−η)
Ψ = ( 1+η)

η −1,1

1
2

1

2

1
2

Rys. 13. Liniowy element brzegowy

Rysunek 13 ilustruje przypadek, gdy funkcje

l

ψ

są liniowe. W takim przypadku równanie

(64) dla wybranego węzła

j

M konturu przybiera postać

( )

( )

1

(

) (

)

(

( )

( ,

)

( ,

)

( )

l

LE

k

k

ki

j

i

j

i

i

j

i

i

j

l

l

L

c

M u M

p x U

x M

u P

x M dL x

=





=

−













∑ ∫

,

(72)

gdzie LE jest liczbą elementów konturu a

l

L oznacza l-ty element konturu (rys. 13).

Po uwzględnieniu związków (71) i odpowiednich przekształceniach mamy:

(

)

(

)

(

)

}

1

1

2

1

1

1

1

1

2

1

1

(

)

( )

(

)

( )

(

)

( ),

( )

( ) (

)

( ) (

)

( ( ),

)

( )

LE

k

ki

i

j

i

l

i

l

i

j

l

k

i

l

i

l

i

j

c u M

p M

p M

U

x

M

J

d

u M

u M

P x

M

J

d

ψ η

ψ η

η

η η

ψ η

ψ η

η

η η

+

=

+

−



=

+

+





−

+

∑ ∫

∫

(73)

gdzie

( )

J

η

jest jakobianem przejścia z układu

1 2

x x

na zmienną

η

. Dla przypadku elementu

liniowego jest

( )

2

j

l

J

η

=

, gdzie

j

l oznacza długość elementu j.

Po dalszych przekształceniach równanie (73) można doprowadzić do postaci:

(

)

( )

(

)

( )

( )

( )

1

1

(

)

,

,

LW

LW

k

k

ki

i

j

i

n

j

i

n

i

n

j

i

n

n

n

c u M

U

M M

p M

P

M M

u M

=

=

=

∆

−

∆

∑

∑

(74)

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

29

gdzie LW jest liczbą węzłów konturu a współczynniki

(

)

( )

,

k

i

n

j

U

M M

∆

i

(

)

( )

,

k

i

n

j

P

M M

∆

są

wynikiem odpowiednich całkowań w związku (73). Całkowania te przeprowadzane są

numerycznie. Dla

j

n

=

całki składające się na

(

)

(

)

( )

( )

,

,

k

k

i

n

j

i

j

j

U

M M

U

M M

∆

= ∆

i zawierające osobliwości funkcji podcałkowych obliczane są ze wzorów analitycznych a

całki składające się na

(

)

(

)

( )

( )

,

,

k

k

i

n

j

i

j

j

P

M M

P

M M

∆

= ∆

obliczane są łącznie ze

współczynnikami

ki

c w dalszym etapie z warunku ruchu ciała jako bryły sztywnej.

Zapisując związek (74) w postaci macierzowej otrzymamy

(1)

(1)

(1)

1

1

2

1

1

11

(2)

(2)

(2)

1

1

2

1

1

21

(

,

)

(

,

)

(

,

)

(

)

(

,

)

(

,

)

(

,

)

(

)

j

j

j

j

j

j

j

j

j

j

P

M M

P

M M

P

M M

c

M

P

M M

P

M M

P

M M

c

M



∆

∆

∆

+



∆

∆

∆

+



……

……

1

1

2

1

(1)

(1)

(1)

1

2

12

1

2

(2)

(2)

(2)

2

2

22

1

2

1

2

(

)

(

)

(

)

(

,

)

(

)

(

,

)

(

,

)

(

)

(

,

)

(

)

(

,

)

(

,

)

(

)

(

)

j

j

j

j

LW

j

LW

j

j

j

j

j

LW

j

LW

j

LW

LW

u M

u M

u M

P

M M

c

M

P

M

M

P

M

M

u M

P

M M

c

M

P

M

M

P

M

M

u M

u M























∆

+

∆

∆





=

 



∆

+

∆

∆

 

























⋮

……

……

⋮

(1)

(1)

(1)

(1)

1

1

2

1

1

1

2

(2)

(2)

(2)

(2)

1

1

2

1

1

1

2

(

,

)

(

,

)

(

,

)

(

,

)

(

,

)

(

,

)

(

,

)

(

,

)

j

j

j

j

j

j

j

j

j

j

U

M M

U

M M

U

M M

U

M M

U

M M

U

M M

U

M M

U

M M



∆

∆

∆

∆



∆

∆

∆

∆



……

…

……

…

1

1

2

1

(1)

(1)

1

1

2

(2)

(2)

2

1

2

1

2

(

)

(

)

(

)

(

,

)

(

,

)

(

)

(

,

)

(

,

)

(

)

(

)

j

LW

j

LW

j

j

LW

j

LW

j

LW

LW

p M

p M

p M

U

M

M

U

M

M

p M

U

M

M

U

M

M

p M

p M























∆

∆





 



∆

∆

 

























⋮

…

…

⋮

(75)

Związek ten stanowi układ dwóch równań z 2 LW

⋅

niewiadomymi sformułowany dla węzła

j

M (rys. 14). Niewiadomymi jest część elementów wektora

{ }

u

i część elementów

wektora

{ }

p

. Jeśli warunek brzegowy dotyczy przemieszczenia znane jest

i

u a niewiadomą

stanowi

i

p a jeśli znane jest obciążenie

i

p do wyznaczenia zostaje

i

u .

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

30

x

x

2

1

M ( )

M

M

M

x

n

η

j

l-1

l

l+1

L

i

r ( , )

x

ξ

ξ

Rys. 14. Sposób przeprowadzania całkowania po konturze

Formułując analogiczne związki dla pozostałych węzłów otrzymujemy układ 2 LW

⋅

równań

z 2 LW

⋅

niewiadomymi:

[ ]

{ }

[ ]

{ }

P u

U

p

=

.

(76)

Uwzględniając, że warunki brzegowe zadania określają nam 2 LW

⋅

wartości składowych

wektorów

{ }

u

i

{ }

p

równanie (76) można przekształcić do postaci:

[ ]

{ } { }

A

y

b

=

,

(77)

gdzie

{ }

y

zawiera nieznane wartości węzłowe przemieszczeń i obciążeń.

Dla modelowania nieciągłości obciążeń na brzegu wprowadza się tzw. węzły podwójne

(rys. 15). Węzeł podwójny stanowią dwa węzły o identycznych współrzędnych, w których

niezależnie określane są obciążenia

i

p a przemieszczenia z założenia są identyczne.

k+3

k+2

k+1,k

k-1

P

Rys. 15. Węzeł podwójny (k+1,k) na konturze analizowanego obszaru

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

31

Określenie, po rozwiązaniu układu równań (77), wszystkich składowych obciążeń i

przemieszczeń węzłowych pozwala na łatwe wyznaczenie stanu naprężeń w węzłach

brzegowych. Naprężenia obliczane są w układzie lokalnym

1

2

,

x x

′ ′

związanym z elementem

brzegowym (rys. 16). Tak na przykład dla węzła n mamy

11

1

2

12

1

2

( ) cos

( ) sin ,

( ) sin

( ) cos .

p n

p n

p n

p n

σ

α

α

σ

α

α

′ =

+

′ = −

+

(78)

Naprężenie normalne w kierunku stycznym do brzegu obliczamy wykorzystując definicje

odkształceń i prawo Hooke’a (44) i (49):

2

22

11

2

2

1

1

E

u

v

v

x

v

σ

σ

∂

′

′

=

+

′

−

∂

−

.

(79)

Uwzględniając, że przemieszczenie jest zmienne liniowo wzdłuż elementu możemy zapisać

2

2

22

11

2

(

1)

( )

( )

( )

1

1

1

E

u n

u n

v

n

n

v

v

σ

σ

′

′

+ −

′

′

=

+

−

+

.

(80)

Otrzymane składowe stanu naprężenia transformowane są następnie do układu globalnego

1

2

,

x x

.

x

x

2

1

α

22

σ

22

σ

11

σ

12

σ

'

'

'

'

11

σ

'

x

2

x

1

'

'

n+2

n+1

n-1

Rys. 16. Wyznaczanie naprężeń w węzłach konturu

Dla każdego węzła naprężenia liczone są dwukrotnie przy wykorzystaniu wyników z

obu elementów zawierających dany węzeł. Końcowe naprężenia w węźle stanowią średnią

arytmetyczną z rezultatów otrzymanych dla obu elementów.

Określenie naprężeń brzegowych kończy zwykle proces obliczeń. W dowolnym,

wybranym punkcie wewnętrznym można jednak określić przemieszczenie i naprężenia

bezpośrednio za pomocą wzorów (63) i (68). Wzory te są dyskretyzowane zgodnie z

opisanymi powyżej zasadami. Odpowiedni algorytm automatyzujący określenie siatki

punktów wewnętrznych może umożliwiać otrzymywanie rozwiązania dla całego

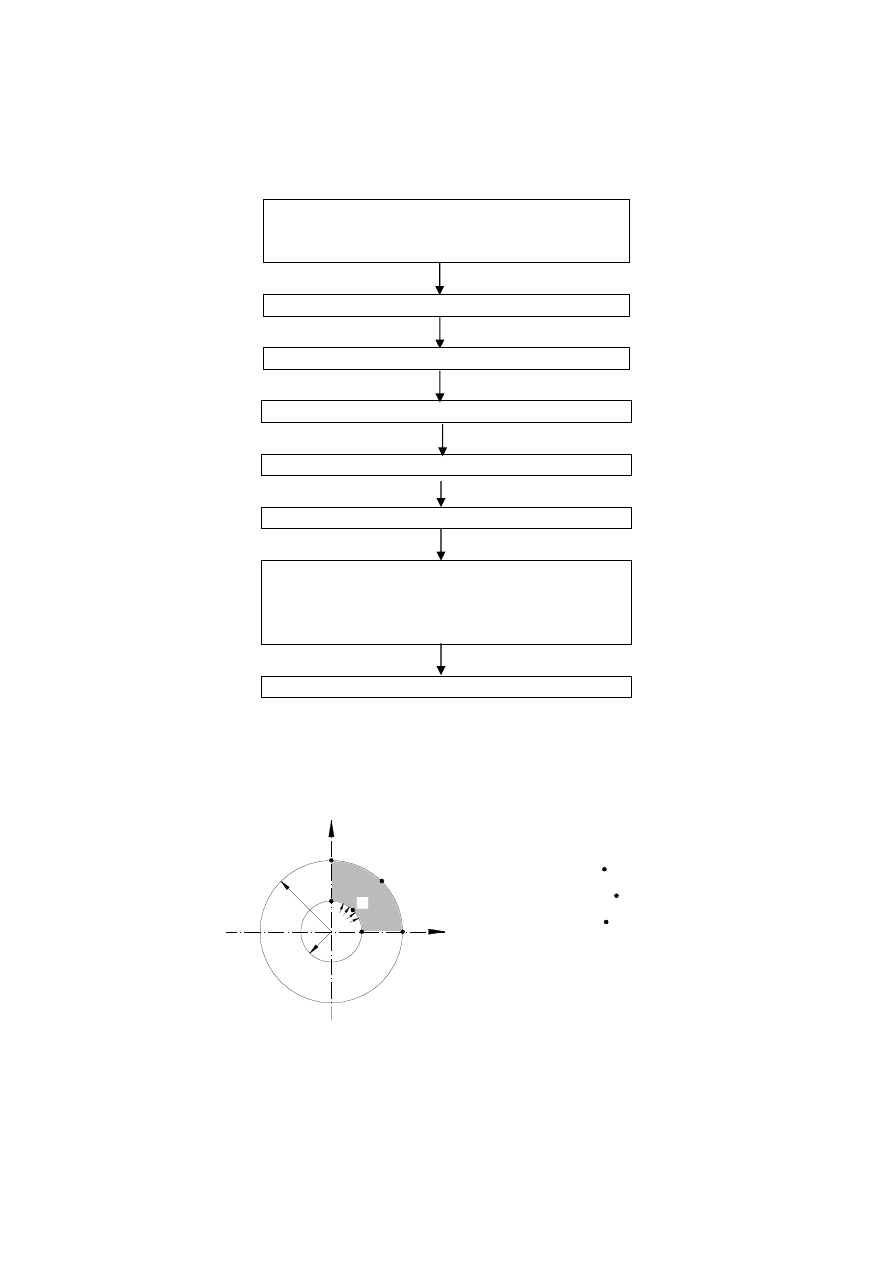
G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

32

analizowanego obszaru. Schemat działania typowego programu metody elementów

brzegowych dla dwuwymiarowych zadań teorii sprężystości przedstawia rys. 17.

1. Wprowadzenie informacji o geometrii

konturu, warunkach brzegowych i stałych
materiałowych.

2. Interakcyjna prezentacja graficzna danych.

3. Budowa układu równań.

4. Rozwiązanie układu równań.

5. Obliczanie naprężeń brzegowych.

6. Interakcyjna prezentacja graficzna wyników.

7. Obliczenia dla wybranych punktów

wewnętrznych lub dla automatycznie
wygenerowanej siatki punktów
wewnętrznych.

8. Prezentacja izolinii wybranych wielkości.

Rys. 17. Schemat podstawowych działań w programie MEB dla dwuwymiarowych zagadnień

teorii sprężystości

P

RZYKŁAD

4

Rura grubościenna

Analizie poddano zagadnienie płaskiego stanu odkształceń przedstawione na rys. 18.

a = 1 10 m

b = 2.5 10 m

E = 2 10 MPa

= 0.3

p = 100 MPa

-2

5

-2

o

a

b

C

D

E

F

A

p

B

o

ν

x

2

x

1

Rys. 18. Rura grubościenna poddana ciśnieniu wewnętrznemu (przekrój)

Obliczenia przeprowadzono dla fragmentu ABCD obszaru przyjmując symetryczne warunki brzegowe na odcinkach AB

1

(

0)

u

=

i CD

2

(

0)

u

=

. Przyjęto trzy stopnie dyskretyzacji w modelu numerycznym MEB: 18 elementów brzegowych

(A), 36 elementów brzegowych (B) i 72 elementy brzegowe (C). Wyniki obliczeń komputerowych (naprężenia zredukowane

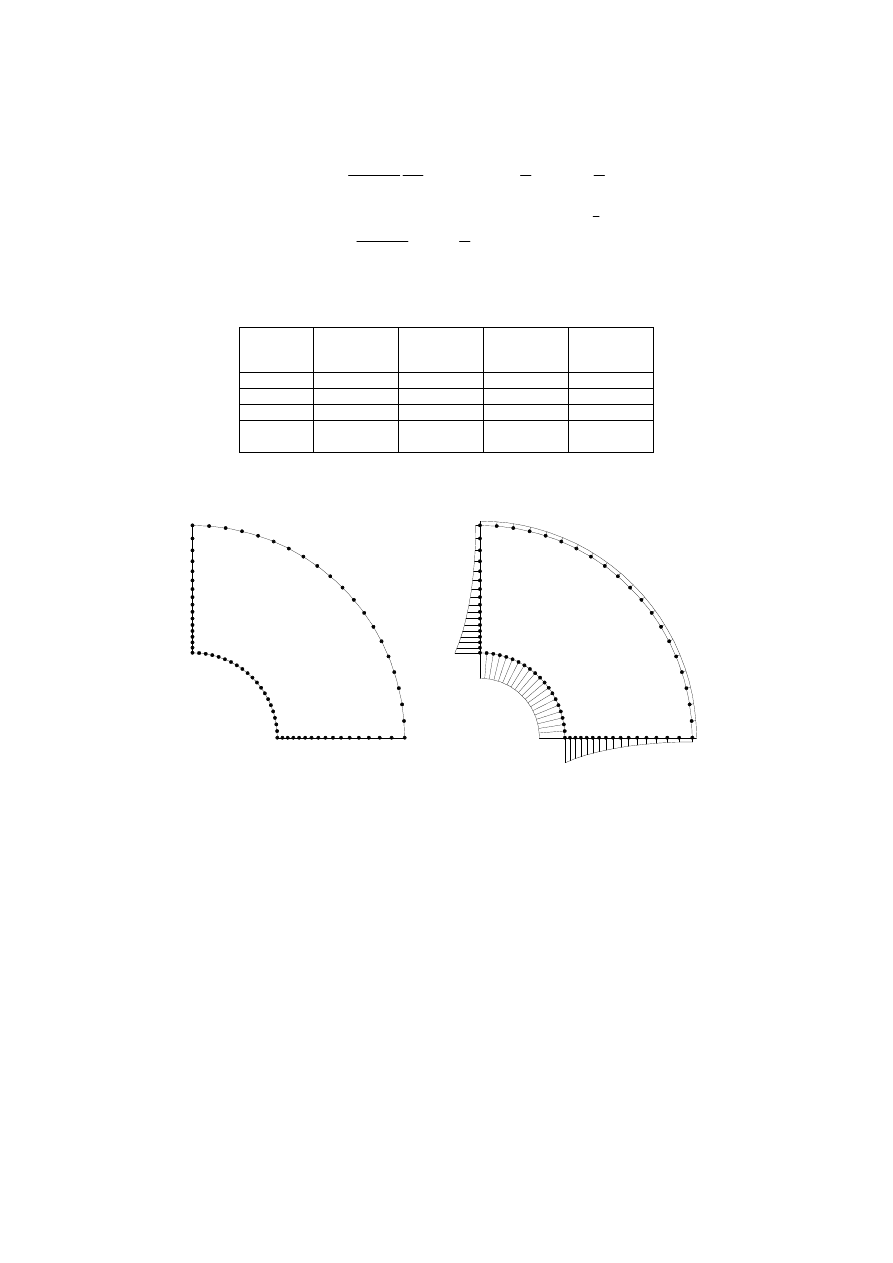
G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

33

Hubera-Misesa

red

σ

i przemieszczenia promieniowe

r

u

w punktach E i F) porównano z wynikami rozwiązania ścisłego, w

którym mamy:

(

)

(

)

2

2

0

2

2

( )

1 2

1

r

p

ab

r

b

u

r

v

v

v

b

a

E

b

r





=

=

−

−

+ +





−





,

1

4

2

2

0

2

2

( )

3

1 4 (1

)

red

a

b

r

p

v

v

b

a

r

σ





 

=

+ −

−





 





−

 





.

Otrzymane rezultaty prezentuje tablica 1.

Tablica 1.

Przykład 4 – wyniki obliczeń

( )

red

E

σ

[MPa]

( )

red

F

σ

[MPa]

( )

r

u E

4

[10

m]

−

( )

r

u F

4

[10

m]

−

A

211,6

32,7

0,845

0,453

B

209,0

33,6

0,831

0,441

C

207,2

33,8

0,826

0,435

Wartości

dokładne

206,3

33,9

0,823

0,443

Rysunek 19 prezentuje przyjęty podział brzegu i obraz rozkładu naprężeń zredukowanych na konturze dla przykładu C.

Rys. 19. Rura grubościenna pod ciśnieniem wewnętrznym – dyskretyzacja i rozkład

naprężenia zredukowanego Hubera-Misesa na konturze analizowanego obszaru

Metoda elementów brzegowych rozwijała się najbardziej intensywnie w latach

siedemdziesiątych i osiemdziesiątych ubiegłego wieku. Duże nadzieje wiązano z nią głównie

z powodu możliwości ograniczenia dyskretyzacji jedynie do brzegu (konturu) ciała. Dzięki

temu w porównaniu do MRS i MES dyskretny model obliczeniowy MEB opisany może być

przez znacznie mniejszą liczbę niewiadomych. Tak na przykład podział sześcianu określony

przez siatkę n

x

n

x

n=n

3

węzłów w metodach obszarowych (MRS i MES) odpowiada liczbie

2

6

12

8

n

n

−

+

węzłów w metodzie elementów brzegowych. Jeśli przyjmiemy

40

n

=

mamy

odpowiednio 64000 węzłów w porównaniu do 9128 . Korzyści z dyskretyzacji jedynie brzegu

są jednak znacznie mniejsze dla obszarów wielospójnych lub obszarów o złożonym kształcie.

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

34

Dodatkowo należy pamiętać, że macierz układu równań MEB jest niesymetryczna i pełna,

więc rozwiązanie wymaga znacznie większej liczby operacji arytmetycznych niż w MRS lub

MES, gdzie mamy do czynienia z macierzami pasmowymi i zwykle również symetrycznymi.

Algorytmy numeryczne MEB są znacznie bardziej złożone niż dwóch pozostałych

metod i nie wykazują uniwersalizmu, ułatwiającego różnorodność zastosowań. W rezultacie

metoda elementów brzegowych nie znalazła takiej popularności w praktyce obliczeniowej jak

MES czy nawet MRS. Stosowana zwykle jest w analizie takich zagadnień, gdzie ograniczenie

dyskretyzacji do brzegu ma szczególne znaczenie, na przykład w analizie problemów

kontaktowych, obliczaniu współczynników koncentracji naprężeń i analizie obszarów o

zmiennym kształcie. Szersze informacje na temat zastosowań metody elementów brzegowych

w mechanice konstrukcji znaleźć można na przykład w pracy [5].

Dominująca obecnie w zastosowaniach inżynierskich jest jednak metoda elementów

skończonych, która dzięki swym zaletom, a głównie prostocie i uniwersalizmowi

algorytmów, stała się powszechnie używanym narzędziem w analizie i projektowaniu

konstrukcji inżynierskiej.

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

35

4. KONCEPCJA METODY ELEMENTÓW SKOŃCZONYCH

NA PRZYKŁADZIE RÓWNANIA POISSONA

MES opiera się na podziale analizowanego obszaru na typowe, małe podobszary nazywane elementami

skończonymi. Wewnątrz każdego elementu skończonego poszukiwane funkcje przybliżane są za pomocą z góry

założonych funkcji aproksymujących nazywanych funkcjami kształtu.

Koncepcję metody przeanalizujemy na przykładzie równania Poissona (33). Wykazać można, że rozwiązanie

równania (33) z warunkami brzegowymi (34) jest równoważne rozwiązaniu zadania minimalizacji funkcjonału

2

2

1

2

0

1

2

1

( )

2 ( ,

)

,

2

q

u

u

I u

f x x u d

q ud

x

x

Ω

Γ













∂

∂





=

+

−

Ω −

Γ









∂

∂

















∫

∫

(81)

gdzie funkcja u spełnia warunek Dirchleta

0

( )

,

u x

u

=

u

x

∈Γ

(82)

W metodzie elementów skończonych dyskretyzacja prowadzi do zamiany zadania minimalizacji funkcjonału

(81) na zadanie minimalizacji funkcji wielu zmiennych.

obszar

kontur

e

w

ę

zły

elementy

x

2

x

1

2

1

u(x ,x )

2

x

x

1

u

1

u

2

u

3

u

8

u

7

u

6

u

5

u

4

e

1

2

3

4

5

6

7

8

LWE=8

Rys. 20. Podział obszaru analizy

Ω

na elementy skończone i aproksymacja analizowanej funkcji wewnątrz

elementu za pomocą wartości węzłowych.

W tym celu dzielimy obszar

Ω

na elementy

i

Ω

(rys. 20)

1

LE

e

i

=

Ω = Ω

∪

i

0

i

j

Ω Ω =

∩

j

i

≠

,

(83)

gdzie LE oznacza liczbę elementów skończonych w obszarze

Ω

.

Zakładamy, że wartość funkcji poszukiwanej

( )

u x

w dowolnym punkcie wewnętrznym każdego elementu

możemy określić za pomocą jej wartości w węzłach tego elementu zgodnie z formułą

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

36

1

2

1

2

1

( ,

)

( ,

)

LWE

i

i

i

u x x

N x x u

=

=

∑

(84)

gdzie

LWE oznacza liczbę węzłów elementu,

i

u

, i = 1,...,LWE są wartościami poszukiwanej funkcji w węzłach,

N

i

(x

1

,x

2

) są założonymi z góry funkcjami aproksymującymi, tak zwanymi funkcjami kształtu.

Elementy skończone łączą się ze sobą w węzłach, dzięki czemu zachowana może być ciągłość analizowanej

funkcji na granicach między elementami. Funkcje kształtu N

i

z reguły definiowane są w lokalnych układach

współrzędnych, związanych z węzłami elementu, dzięki czemu ich postać jest uniezależniona od wielkości

elementu i usytuowania jego węzłów.

Wartość funkcjonału po dyskretyzacji obszaru można przedstawić jako:

2

2

1

2

0

1

1

1

2

1

( )

2 ( ,

)

2

i

j

LE

LK

i

j

i

j

u

u

I u

f x x u d

q ud

x

x

=

=

Ω

Γ













∂

∂





≅

+

−

Ω −

Γ









∂

∂

















∑

∑

∫

∫

(85)

gdzie LK oznacza liczbę krawędzi elementów leżących na części

q

Γ

konturu, a funkcja u określona jest w

każdym podobszarze

i

Ω

przez związki typu (84).

Wewnątrz każdego elementu, zgodnie z (84) mamy:

1

1

1

1

2

2

,

.

LWE

i

i

i

LWE

i

i

i

N

u

u

x

x

N

u

u

x

x

=

=

∂

∂ =

∂

∂
∂

∂ =

∂

∂

∑

∑

(86)

Po podstawieniu (86) do (85) i po przeprowadzeniu całkowania

( )

I u

staje się funkcją wartości węzłowych

,

1, 2,...,

i

u

i

LW

=

, gdzie LW oznacza liczbę węzłów podzielonego obszaru.

Jeśli funkcję tę przedstawimy w postaci macierzowej otrzymamy:

11

12

13

1

1

1

21

22

23

2

2

31

32

1

2

3

1

2

3,

3

3

1

1

( )

,

,

,...,

,

,

,

2

LW

LW

LW

LW

LW LW

LW

LW

k

k

k

k

u

b

k

k

k

u

b

k

k

I u

u u u

u

u u u

u

u

b

k

k

u

b



 









 









 























≈

−























 









 









 



















…

…

…

…

…

Związek ten można zapisać w skróconej formie:

[ ]

{ }

{ }

1

1

1

1

1

2

LW

LW

LW

LW

LW LW

I

u

u

u b

K

×

×

×

×

×

≈

−

 

 

 

 

.

(87)

Indeksy na dole poszczególnych symboli oznaczają wymiary wektorów i macierzy.

Warunkiem koniecznym minimum tej funkcji jest zerowanie się jej wszystkich pochodnych cząstkowych:

0

i

I

u

∂ =

∂

,

1,

,

i

LW

=

…

.

(88)

Otrzymamy stąd

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

37

[ ]

{ } { }

K

u

b

=

,

(89)

czyli układ liniowych z nieznanym wektorem wartości węzłowych funkcji

u

. Przed rozwiązaniem tego układu

należy uwzględnić jeszcze znane z brzegowego warunku Dirchleta niektóre wartości

i

u

.

Po rozwiązaniu układu otrzymujemy wszystkie wartości węzłowe

i

u

. Możemy wtedy wyznaczyć przybliżone

wartości funkcji

u

i jej pochodnych wewnątrz każdego elementu korzystając ponownie ze związków (84) i (86).

Macierz

[ ]

K

jest macierzą symetryczną, dodatnio określoną, pasmową (rys. 21).

zerowe

elementy

LW - liczba stopni swobody

m - szeroko

ść

półpasma macierzy

LW

m

Rys. 21. Symetryczna macierz układu równań MES

Szerokość półpasma m macierzy

[ ]

K

zależy od przyjętej w wektorze

{ }

u

numeracji węzłów obszaru. Zwykle

możemy tak zmienić numerację aby uzyskać

m

LW

<<

.

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

38

5.

MES W ANALIZIE KONSTRUKCJI PRĘTOWYCH

Metoda elementów skończonych w statyce konstrukcji przedstawiana zwykle jest jako

metoda przybliżona wykorzystująca twierdzenie o minimum całkowitej energii potencjalnej

układu odkształcalnego.

Całkowita energia potencjalna (V) jest różnicą energii potencjalnej odkształcenia sprężystego (U) i energii

potencjalnej obciążeń zewnętrznych (-

z

W

), gdzie

z

W

nazywane jest pracą obciążeń zewnętrznych

min!

z

V

U

W

= −

=

,

(90)

Całkowita energia potencjalna jest funkcjonałem, którego argumentem jest funkcja opisująca przemieszczenia

ciała odkształcalnego. Pod wpływem obciążenia w ciele powstaje takie pole przemieszczeń, dla którego V

przyjmuje wartość minimalną. Wówczas układ odkształcalny pozostaje w stanie równowagi.

Funkcje opisujące pole przemieszczeń muszą dodatkowo spełniać przemieszczeniowe warunki brzegowe.

Wówczas warunek minimum całkowitej energii potencjalnej jest warunkiem koniecznym i dostatecznym

równowagi sprężystego ustroju odkształcalnego poddanego obciążeniu zewnętrznemu.

Prezentację metody elementów skończonych zaczniemy od konstrukcji belkowych, należących do

najprostszych prętowych elementów konstrukcyjnych.

5.1.

BELKI

W przypadku belek obciążonych obciążeniem ciągłym

N

m

p













całkowitą energię potencjalną określa wzór:

2

0

0

1

(

)

2

l

l

V

EI w

dx

pwdx

′′

=

−

∫

∫

,

(91)

gdzie w(x) jest funkcją ugięcia belki o długości l.

W przypadku występowania dodatkowych obciążeń skupionych w postaci sił

i

P

i momentów sił

i

M

wzór (91)

przyjmie postać

2

0

0

1

(

)

2

l

l

i

i

j

j

i

j

V

EI w

dx

pwdx

Pw

M

θ

′′

=

−

−

−

∑

∑

∫

∫

(92)

gdzie

i

w

i

j

θ

oznaczają odpowiednio przemieszczenie w punkcie przyłożenia siły

i

P

i kąt ugięcia w punkcie

przyłożenia momentu siły

j

M

.

Metoda elementów skończonych jest przybliżoną metodą znajdowania minimum funkcjonału V i ma wiele

wspólnego ze znaną od dawna metodą Ritza.

Przypomnijmy najpierw schemat postępowania w metodzie Ritza:

1. Linię ugięcia opisujemy za pomocą rozwiązania przybliżonego

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

39

1

( )

( )

n

i

i

i

w x

a

x

ϕ

=

=

∑

ɶ

,

(93)

gdzie a

i

są nieznanymi parametrami, a

i

ϕ

są z góry założonymi funkcjami.

Funkcje

i

ϕ

muszą być liniowo niezależne, to znaczy żadna z nich nie może być kombinacją liniową

pozostałych a

)

(

~ x

w

spełniać powinna przemieszczeniowe warunki brzegowe (dotyczą one

poszukiwanej funkcji przemieszczeń i jej pochodnych do rzędu o 1 mniejszego niż największy rząd

pochodnej funkcji poszukiwanej w minimalizowanym funkcjonale)

2. Podstawiamy

)

(

~ x

w

do funkcjonału całkowitej energii potencjalnej (92). Otrzymujemy energię

potencjalną jako funkcję nieznanych parametrów

n

a

a

a

…

,

,

2

1

.

3. Warunek minimum funkcjonału zastępujemy przez warunek minimum funkcji wielu zmiennych

0

i

V

a

∂ =

∂

,

1,...,

i

n

=

.

(94)

Ponieważ V jest funkcją kwadratową, dodatnio określoną, to warunek (94) jest wystarczający dla

wyznaczenia minimum.

Warunek minimum (94) stanowi układ n równań liniowych z niewiadomymi

n

a

a

a

…

,

,

2

1

.

4. W wyniku rozwiązania układu (94) otrzymujemy wartości parametrów a

i

, które jednocześnie

określają otrzymane rozwiązanie przybliżone (93).

Stąd łatwo wyznaczyć przebieg momentu gnącego i siły tnącej

( )

( ),

( )

( ).

q

M

x

EIw x

T x

EIw x

′′

=

′′′

= −

ɶ

ɶ

ɶ

ɶ

(95)

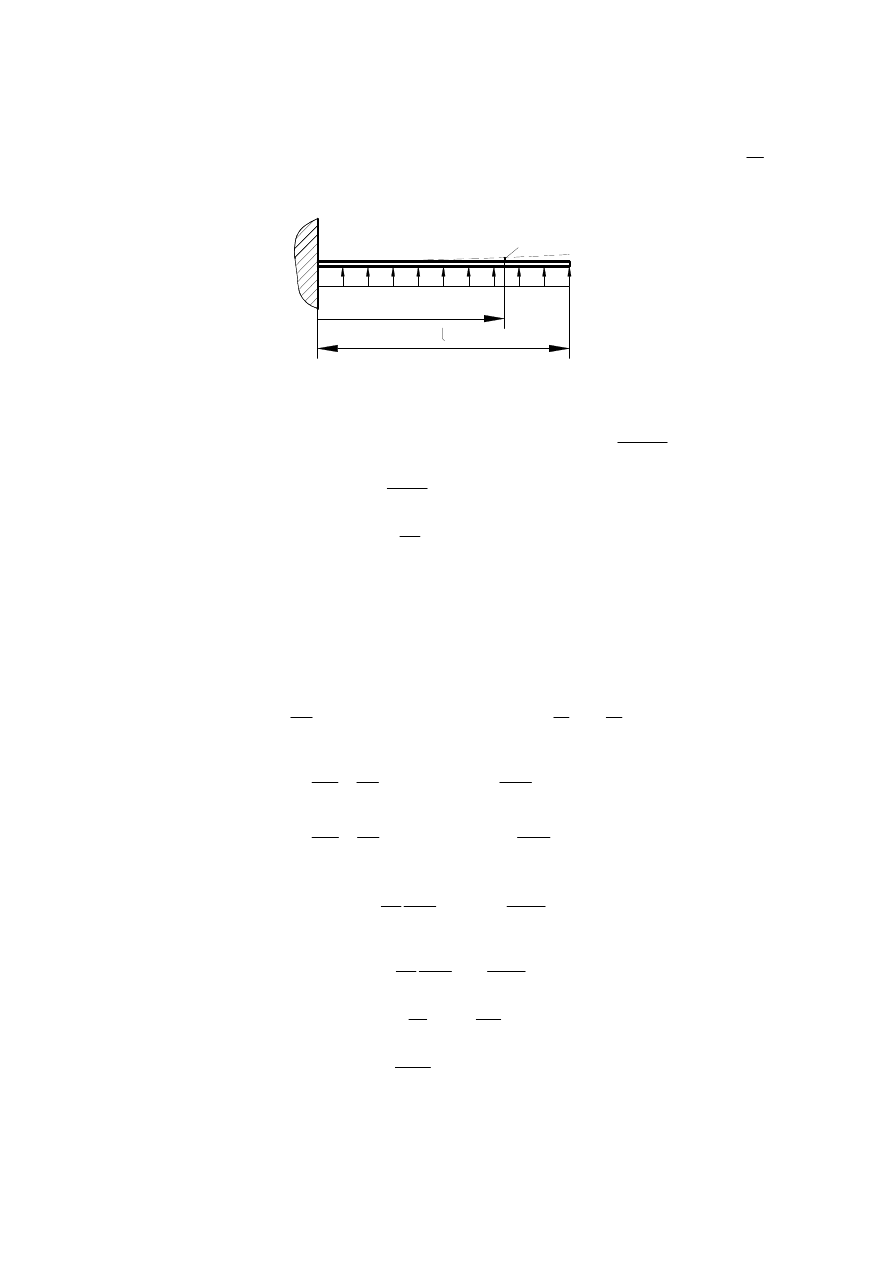
G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

40

P

RZYKŁAD

5.

Porównać rozwiązanie ścisłe dla belki wspornikowej (rys. 22) o długości

l obciążonej stałym rozkładem sił

0

N

p

m













z

rozwiązaniem metodą Ritza zakładając, że

3

4

2

3

2

1

)

(

~

x

a

x

a

x

a

a

x

w

+

+

+

=

.

w(x)

p

0

x

Rys. 22. Belka wspornikowa obciążona obciążeniem ciągłym p

0

[N/m] (przykład 5)

Rozwiązanie

Rozwiązanie ścisłe, otrzymane na przykład z całkowania równania różniczkowego

( )

( )

g

M

x

w x

EI

′′

=

ma postać:

2

2

2

0

2

0

0

( )

(6

4

)

,

24

( )

(

) ,

2

( )

(

).

q

p

w x

l

lx

x x

EI

p

M

x

l

x

T x

p l

x

=

−

+

=

−

= −

−

(96)

Funkcja przybliżona

w

ɶ

powinna spełniać warunki brzegowe:

(

0)

0,

w x

= =

ɶ

(

0)

0

w x

′ = =

ɶ

.

(97)

Stąd otrzymamy

3

4

2

3

)

(

~

x

a

x

a

x

w

+

=

.

(98)

Całkowita energia potencjalna V , zgodnie ze wzorem (92) jest równa:

)

4

3

(

)

12

12

4

(

2

4

4

3

3

3

2

4

2

4

3

2

3

l

a

l

a

p

l

a

l

a

a

l

a

EI

V

+

−

+

+

=

.

(99)

Warunek minimum przyjmie postać:

(

)

(

)

3

2

0

3

4

3

4

2

3

0

3

4

4

8

12

0,

2

3

12

24

0.

2

4

p l

V

EI

la

l a

a

p l

V

EI

l a

l a

a

∂ =

+

−

=

∂

∂ =

+

−

=

∂

(100)

Stąd

2

0

0

3

4

5

,

24

12

p l

p l

a

a

EI

EI

=

= −

(101)

Rozwiązaniem przybliżonym jest więc

2

2

3

0

0

2

0

0

0

5

( )

,

24

12

5

( )

,

12

2

( )

.

2

q

p l

p

w x

x

x

EI

EI

p l

M

x

p l

x

p l

T x

=

−

=

−

−

=

ɶ

ɶ

ɶ

(102)

Porównanie rozwiązania ścisłego i przybliżonego przedstawione jest na rys. (23).

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

41

x

W(x)

x

W(x)

~

l

l

4

2

l

4

3l

10

-2

pl

EJ

1.318

1.172

4.427

8.35

12.5

12.5

8.203

4.167

W(x)

~

W(x)

M (x)

M (x)

~

g

g

4

l

2

l

4

3l

l

0.417

0.5

0.292

0.167

0.42

-0.083

0.281

0.125

0.031

pl

*

2

*

T(x)
~

T(x)

pl

*

x

4

l

2

l

4

3l

l

g

M (x)

~

M (x)

g

0.5

1

T(x)

T(x)

~

Rys. 23. Rozwiązanie ścisłe i przybliżone dla zadania belki wspornikowej (przykład 5)

Wykresy na rys. 23 wskazują, że rozwiązanie przybliżone

w

ɶ

jest bardzo bliskie rozwiązaniu ścisłemu

( )

w x

.

Dokładność rozwiązania przybliżonego jest gorsza, gdy porównamy

( )

g

M

x

i

( )

q

M

x

ɶ

, a zupełnie

niezadowalająca w przypadku porównania rozkładu sił tnących

( )

T x

i

( )

T x

ɶ

. Taka cecha rozwiązania

przybliżonego jest charakterystyczna dla wielu metod przybliżonych, także dla MES. Kolejne pochodne funkcji

aproksymującej są w metodach przybliżonych coraz bardziej odległe od odpowiednich pochodnych w

rozwiązaniu ścisłym.

Rozwiązanie metodą elementów skończonych przebiega w sposób podobny do przyjętego w metodzie

Ritza. Zasadnicza różnica polega na innej koncepcji doboru funkcji aproksymujących. W metodzie Ritza mamy

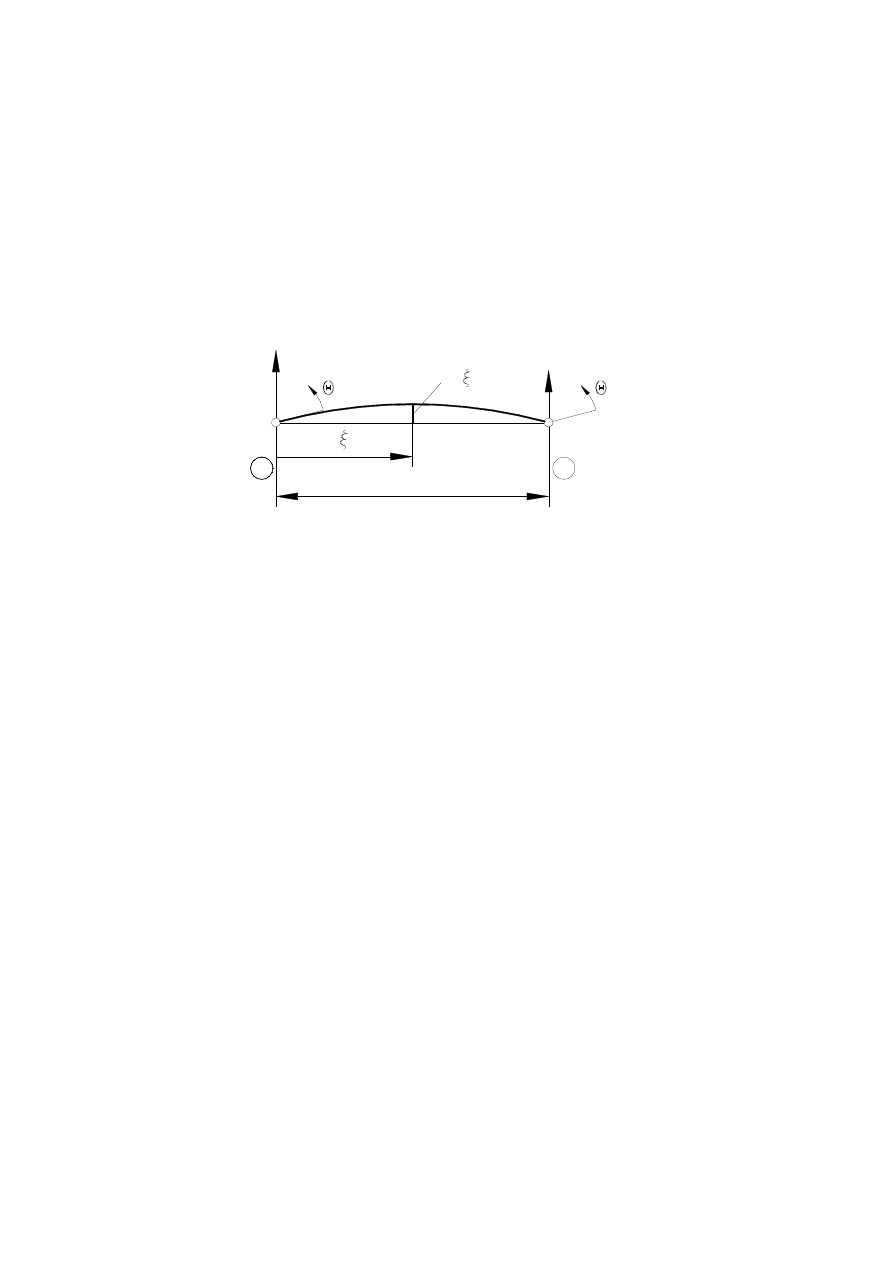
G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

42

do czynienia z aproksymacją globalną, parametryczną. Funkcje aproksymujące są określone w całym obszarze a

ich przebieg uzależniony jest od wartości parametrów występujących we wzorach definiujących. W rezultacie

zmiana dowolnego parametru prowadzi do zmiany przebiegu poszukiwanej funkcji w całym obszarze.

W metodzie elementów skończonych stosuje się aproksymację lokalną, węzłową. Oznacza to, że funkcje

aproksymujące definiowane są lokalnie w elementach skończonych, a ich przebieg określany jest przez wartość

funkcji w węzłach siatki podziału. W efekcie zmiana jednego parametru (wartości funkcji w jednym węźle)

zmienia rozwiązanie tylko w bezpośrednim otoczeniu tego węzła. Postępowanie jest zbliżone do przyjmowanego

w grafice komputerowej i programach CAD przy aproksymacji kształtu za pomocą funkcji sklejanych.

l

1

2

e

w( )

w =q

1

1

=q

2

1

=q

4

2

w =q

2

3

Rys. 24. Element skończony belki

Typowy element skończony belki (rys. 24) stanowi segment o długości l

e

, w którym założona postać funkcji

ugięcia wyraża się wzorem

3

4

2

3

2

1

)

(

ξ

α

ξ

α

ξ

α

α

ξ

+

+

+

=

w

(103)

Taki wielomian jest określony przez cztery parametry

i

α

. W MES dążymy jednak do tego, aby funkcja ugięcia

była definiowana przez przemieszczenia węzłowe. Przyjmijmy, że cztery niezależne przemieszczenia węzłowe:

w

1

i w

2

czyli przemieszczenia węzłów oraz

1

2

i

θ θ

czyli kąty obrotu w węzłach tworzą wektor (macierz-

kolumnę):

{ }

























=

























=

2

2

1

1

4

3

2

1

θ

θ

w

w

q

q

q

q

q

e

e

.

(104)

Wektor

{ }

e

q

nazywamy wektorem przemieszczeń węzłowych elementu skończonego lub też wektorem stopni

swobody elementu. Ugięcia

)

(

ξ

w

przedstawimy jako uzależnione od przemieszczeń węzłowych q

i

wg formuły

4

1

( )

( )

i

i

i

w

N

q

ξ

ξ

=

=

∑

.

(105)

Potrzebne jest więc wyznaczenie związków między stopniami swobody

4

3

2

1

,

,

,

α

α

α

α

funkcji

)

(

ξ

w

(103) a

nowymi stopniami swobody

4

3

2

1

,

,

,

q

q

q

q

(105).

Zauważmy, że:

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

43

1

1

2

2

2

3

3

1

2

3

4

2

4

2

3

4

(0)

,

(0)

,

( )

,

( )

2

3

.

e

e

e

e

e

q

w

dw

q

d

q

w l

l

l

l

dw

q

l

l

l

d

α

α

ξ

α α

α

α

α

α

α

ξ

=

=

=

=

=

= +

+

+

=

=

+

+

(106)

Równania (106) możemy zapisać w postaci macierzowej

1

1

2

2

2

3

3

3

2

4

4

1

0

0

0

0

1

0

0

.

1

0

1

2

3

e

e

e

e

e

q

q

l

l

l

q

l

l

q

α

α
α
α





 









 





 









=

 









 









 









 









(107)

Stąd wyznaczyć można zależność odwrotną

1

1

2

2

3

3

2

2

4

4

3

3

2

1

0

0

0

0

1

0

0

3

2

3

1

2

1

2

1

e

e

e

e

e

e

e

e

q

q

q

l

l

l

l

q

l

l

l

l

α

α
α
α





















 









 





 





=





 





−

−

−





 









 





 









−













.

(108)

Podstawiając (108) do (103) otrzymamy

1

1

2

2

2

3

1

2

3

4

3

3

4

4

( )

1, ,

,

( ),

( ),

( ),

( )

q

q

w

N

N

N

N

q

q

α

α

ξ

ξ ξ ξ

ξ

ξ

ξ

ξ

α
α





 





 





 





=

=









 













 





 





 

,

(109)

gdzie

2

3

1

2

3

2

3

2

2

2

3

3

2

3

2

3

4

2

( ) 1 3

2

,

( )

2

,

( )

3

2

,

( )

.

e

e

e

e

e

e

e

e

N

l

l

N

l

l

N

l

l

N

l

l

ξ

ξ

ξ

ξ

ξ

ξ

ξ

ξ

ξ

ξ

ξ

ξ

ξ

= −

+

= −

+

=

−

−

=

+

(110)

Funkcje

( )

i

N

ξ

nazywamy funkcjami kształtu elementu belkowego. Są one oczywiście, tak jak założona

wstępnie funkcja ugięcia (103), wielomianami trzeciego stopnia. Ze związku (109) wynika, że każda z funkcji

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

44

( )

i

N

ξ

opisuje linie ugięcia elementu belki, w którym przemieszczenia węzłowe są:

1

i

q

=

, a dla

0

j

j

i

q

≠

=

(rys. 25).

N ( )

1

1

1

2

N ( )

N ( )

4

N ( )

3

tg =1

e

tg =1

e

e

e

Rys. 25. Funkcje kształtu elementu belki

Znając funkcję ugięcia (109) możemy wyznaczyć rozkłady pochodnych linii ugięcia

( )

w

ξ

jako funkcję

położenia i przemieszczeń węzłowych. Mamy więc

{ }

{ }

{ }

( )

( )

,

( )

( )

,

( )

( )

.

e

e

e

w

N

q

w

N

q

w

N

q

ξ

ξ

ξ

ξ

ξ

ξ

=









′

′

=









′′

′′

=









(111)

Także całkowitą energię potencjalną elementu belki można przedstawić jako uzależnioną od przemieszczeń

węzłowych. Całkowita energia potencjalna elementu belki o długości

e

l

obciążonego obciążeniem ciągłym

( )

p

ξ

jest zgodnie z (92) określona wzorem:

2

0

0

(

( ))

( ) ( )

2

e

e

l

l

e

e

ze

i

i

j

j

i

j

EI

V

U

W

w

d

p

w

d

Pw

M

ξ

ξ

ξ

ξ ξ

ϑ

′′

=

−

=

−

−

−

∑

∑

∫

∫

.

(112)

Wykorzystując (111) możemy po kolejnych przekształceniach uzyskać wyrażenie na energię sprężystą

e

U

w

formie macierzowej:

{ }

{ }

0

0

1

1

1

2

1

3

1

4

2

1

2

2

2

3

2

4

3

1

3

2

3

3

3

4

4

1

4

2

4

3

4

4

( )

( )

2

2

2

e

e

l

l

e

e

e

e

EI

EI

U

w

w

d

q

N

N

q

d

N N

N N

N N

N N

N N

N N

N N

N N

EI

q

N N

N N

N N

N N

N N

N N

N N

N N

ξ

ξ ξ

ξ

′′

′′

′′

′′

=

=

=

 





 









′′ ′′

′′ ′′

′′ ′′

′′ ′′





′′ ′′

′′ ′′

′′ ′′

′′ ′′



=

 

 



′′ ′′

′′ ′′

′′ ′′

′′ ′′





′′ ′′

′′ ′′

′′ ′′

′′ ′′



∫

∫

{ }

0

.

e

l

e

d

q

ξ















∫

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

45

Wynik możemy zapisać w postaci

[ ]

{ }

1

2

e

e

e

e

U

q

k

q

=

 

 

,

(113)

gdzie

[ ]

1

1

1

2

1

3

1

4

0

0

0

0

2

1

2

2

2

3

2

4

0

0

0

0

3

1

3

2

3

3

3

4

0

0

0

0

4

1

4

2

0

0

e

e

e

e

e

e

e

e

e

e

e

e

e

e

l

l

l

l

l

l

l

l

e

l

l

l

l

l

l

N N d

N N d

N N d

N N d

N N d

N N d

N N d

N N d

k

EI

N N d

N N d

N N d

N N d

N N d

N N d

ξ

ξ

ξ

ξ

ξ

ξ

ξ

ξ

ξ

ξ

ξ

ξ

ξ

ξ

′′ ′′

′′ ′′

′′ ′′

′′ ′′

′′ ′′

′′ ′′

′′ ′′

′′ ′′

=

′′ ′′

′′ ′′

′′ ′′

′′ ′′

′′ ′′

′′ ′′

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

4

3

4

4

0

0

e

e

l

l

N N d

N N d

ξ

ξ













































′′ ′′

′′ ′′













∫

∫

∫

.

(114)

Macierz

[ ]

e

k

w wyrażeniu (113) nazywamy macierzą sztywności elementu skończonego belki. Po podstawieniu

do wzoru (114) drugich pochodnych funkcji

( )

i

N

ξ

i obliczeniu wartości całek otrzymamy:

[ ]

2

2

3

2

2

6

3

6

3

3

2

3

2

6

3

6

3

3

3

2

e

e

e

e

e

e

e

e

e

e

e

e

e

e

l

l

l

l

l

l

EI

k

l

l

l

l

l

l

l

−









−





=





−

−

−





−









.

(115)

Podobnie przekształcamy pracę obciążenia ciągłego działającego na element skończony:

{ }

{ }

0

0

1

2

3

4

0

( ) ( )

( )

( )

( ) ( )

,

( ) ( )

,

( ) ( )

,

( ) ( )

,

e

e

e

l

l

p

ze

e

l

e

W

p

w

d

p

N

q

d

N

p

d

N

p

d

N

p

d

N

p

d

q

d

ξ

ξ ξ

ξ

ξ

ξ

ξ

ξ ξ

ξ

ξ ξ

ξ

ξ ξ

ξ

ξ ξ

ξ

=

=

=









=









∫

∫

∫

{ }

1

2

1

2

3

4

3

4

,

,

,

p

e

e

e

e

ze

e

e

e

q

q

W

F F F F

F

q

q

q

 

 

 





=

=

 

 

 





 

 

 

,

(116)

0

( ) ( )

e

l

e

i

i

F

N

p

d

ξ

ξ ξ

=

∫

.

(117)

Wzór (116) wskazuje, że wartości

e

i

F

możemy traktować jako wartości uogólnionych sił węzłowych

równoważnych obciążeniu ciągłemu

( )

p

ξ

działającemu na analizowany element skończony. Elementy

1

e

F

i

3

e

F

wektora

{ }

e

F

są siłami skupionymi działającymi w węzłach elementu a

2

e

F

i

4

e

F

są wartościami

momentów sił działających w tych węzłach.

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

46

P

RZYKŁAD

6.

Znaleźć wartości równoważnych sił węzłowych odpowiadających obciążeniu ciągłemu o stałej wartości

0

( )

p

p

ξ

=

.

Rozwiązanie

Obliczając wartości kolejnych całek (117) otrzymamy:

0

1

3

2

0

2

2

0

4

2

12

12

e

e

e

e

e

e

e

p l

F

F

p l

F

p l

F

=

=

=

−

=

(118)

Interpretację geometryczną otrzymanego wyniku przedstawia rysunek 26.

1

2

0

p

p

2

0 e

0 e

2

0 e

12

2

12

2

e

0

p

p

p

Rys. 26. Siły węzłowe w elemencie belki równoważne obciążeniu ciągłemu

0

p

Związki (113) i (116) pozwalają napisać wyrażenie na całkowitą energię potencjalną elementu skończonego

belki w postaci

 

[ ] { }

 

{ }

4 4

4 1

1 4

1 4

4 1

1

2

e

e

ze

V

U

W

q

q

q

F

k e

e

e

e

e

×

×

×

×

×

=

−

=

−

.

(119)

Indeksy na dole oznaczają wymiary poszczególnych wektorów i macierzy.

Jeżeli belka została podzielona na

LE

elementów skończonych i

LW

węzłów, to jej ugięcie opisane jest przez

2

n

LW

=

stopni swobody, tworzących tak zwany globalny wektor stopni swobody modelu belki:

{ }

1

2

n

q

q

q

q

 

 

 

=

 

 

 

 

…

.

Każdemu elementowi belki odpowiadają cztery spośród stopni swobody

(

1, 2,

, )

i

q i

n

=

…

.

Energia sprężysta elementu skończonego

e

U

może być więc zapisana w postaci

 

[ ] { }

*

1

1

1

2

e

n n

n

n

e

U

q

q

k

×

×

×

=

,

(120)

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

47

gdzie rozszerzona macierz sztywności elementu o wymiarze

n n

×

*

e

k

 

 

ma, tak jak macierz (115), tylko 16

niezerowych elementów. Ich miejsca w macierzy uzależnione są od pozycji jaką mają kolejne stopnie swobody

elementu w globalnym wektorze stopni swobody

{ }

q

.

1

2

0

p

3

4

P

M

1

2

3

1

q

q

3

q

5

q

7

q

2

4

q

q

6

q

8

=

3

e

e

e

e

Rys. 27. Model utwierdzonej jednostronnie belki obciążonej siłami skupionymi

,

P M

oraz obciążeniem ciągłym

0

p

P

RZYKŁAD

7

Model belki przedstawionej na rysunku 27 składa się z trzech elementów skończonych i czterech węzłów. Globalny wektor
stopni swobody ma więc 8 elementów:

{ }

1

1

2

1

3

2

4

2

5

3

6

3

7

4

8

4

q

w

q

q

w

q

q

q

w

q

q

w

q

θ

θ

θ

θ

  



  



  



  



  



  



=

=

  



  



  



  



  



  







 

.

Stopniami swobody elementu pierwszego są

1

2

3

,

,

q q q

,

4

q

elementu drugiego:

3

4

5

,

,

q q q

,

6

q

a elementu trzeciego

5

6

7

,

,

q q q

,

8

q

. Kolejne macierze

i

k

∗

 

 

mają więc postać:

1

k

∗

 

=

 

2

k

∗

 

=

 

3

k

∗

 

=

 

gdzie niezerowe elementy macierzy wypełniają jedynie obszar przyciemniony i określone są przez wzór (115).

Przedstawienie

e

U

w postaci (120) daje możliwość łatwego zsumowania energii dla całej analizowanej

konstrukcji

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

48

{ }

[ ]

{ }

1

1

1

1

2

2

LE

LE

e

e

e

i

U

U

q

k

q

q

K

q

∗

=

=





 

=

=

=

 

 

 

 





 





∑

∑

.

(121)

Współczynniki macierzy

[ ]

K

stanowią, zgodnie z regułami dodawania macierzy, sumy odpowiednich

współczynniki macierzy

e

k

∗

 

 

.

W rezultacie całkowita energia potencjalna całej konstrukcji może być zapisana jako:

[ ]

{ }

{ }

1

2

z

V

U

W

q

K

q

q

F

= −

=

−

 

 

 

 

,

(122)

gdzie

{ }

F

oznacza wektor sił węzłowych modelu. Wyliczając elementy wektora

{ }

F

uwzględniamy

równoważne siły węzłowe od obciążenia ciągłego oraz istniejące siły skupione. W ten sposób otrzymaliśmy

całkowitą energię potencjalną belki jako funkcję nieznanych przemieszczeń węzłowych

{ }

q

. Ponieważ jest to

kwadratowa, dodatnio określona funkcja wielu zmiennych więc twierdzenie o minimum całkowitej energii

potencjalnej prowadzi do warunku:

0

i

V

q

∂ =

∂

,

1, 2, 3,

,

i

n

=

…

Dokonując różniczkowania wyrażenia (122) otrzymamy układ równań liniowych

[ ]

{ } { }

K

q

F

=

.

(123)

Przed rozwiązaniem (123) należy uwzględnić przemieszczeniowe warunki brzegowe, czyli warunki podparcia

konstrukcji. Warunki te oznaczają narzucenie wartości niektórych elementów wektora

{ }

q

. Macierz

[ ]

K

układu równań przed uwzględnieniem warunków podparcia jest, podobnie jak każda z macierzy sztywności

elementów, macierzą osobliwą. Jest to odzwierciedleniem faktu, że bez narzucenia przynajmniej takich

warunków podparcia, które uniemożliwiają ruch modelu konstrukcji jako bryły sztywnej, rozwiązanie w postaci

przemieszczeń byłoby niejednoznaczne. Uwzględnienie warunków podparcia prowadzi do modyfikacji układu

równań. Po rozwiązaniu przekształconego układu (123) otrzymujemy wartości wszystkich przemieszczeń

węzłowych

{ }

q

. W końcowej fazie obliczeń możemy wyznaczyć rozkłady sił wewnętrznych w każdym

elemencie skończonym.

1

2

1

2

3

4

3

4

1

2

1

2

3

4

3

4

( )

( )

,

,

,

,

( )

( )

,

,

,

.

q

e

e

q

q

M

EIw

EI N

N

N

N

q

q

q

q

T

EIw

EI N

N

N

N

q

q

ξ

ξ

ξ

ξ

 

 

 





′′

′′

′′

′′

′′

=

=

 







  

 

 

 

 

 





′′′

′′′

′′′

′′′

′′′

= −

=

 







  

 

 

(124)

Po wyznaczeniu kolejnych pochodnych funkcji kształtu

( )

i

N

ξ

określonych przez wzory (110) otrzymamy

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

49

1

2

3

4

3

3

3

2

1

3

2

4

3

2

12

6

2

12

6

( )

(

)

(

)

(

)

(

)

,

2

3

2

3

12

6

( )

(

)

(

)

.

e

e

e

q

e

e

e

e

e

e

e

l

l

l

M

q

l q

q

q

EI

l

l

l

l

T

q

q

q

q

EI

l

l

ξ

ξ

ξ

ξ

ξ

ξ





=

−

+

−

−

−

+

−













= −

−

+

+









(125)

Ze wzorów (125) wynika, że przy założonych funkcjach kształtu

( )

q

M

ξ

jest zawsze funkcją liniową na

prezentowanym elemencie skończonym belki a

( )

T

ξ

jest funkcją stałą.

P

RZYKŁAD

8

Model belki przestawiony w przykładzie 7 i na rysunku (27) prowadzi do układu równań

1

11

k

1

12

k

1

13

k

1

14

k

0

0

0

0

1
21

k

1
22

k

1
23

k

1
24

k

0

0

0

0

1

31

k

1

32

k

1

2

33

11

k

k

+

1

2

34

12

k

k

+

2

13

k

2

14

k

0

0

1
41

k

1
42

k

1

2

43

21

k

k

+

1

2

44

22

k

k

+

2

23

k

2

24

k

0

0

0

0

2

31

k

2

32

k

2

3

33

11

k

k

+

2

3

34

12

k

k

+

3

13

k

3

14

k

0

0

2

41

k

2

42

k

2

3

43

21

k

k

+

2

3

44

22

k

k

+

2

23

k

3

24

k

0

0

0

0

3

31

k

3

32

k

3

33

k

3

34

k

0

0

0

0

3

41

k

3

42

k

3

43

k

3

44

k

1

1

2

2

3

3

4

4

5

5

6

6

7

7

8

8

q

F

q

F

q

F

q

F

q

F

q

F

q

F

q

F

 





 





 





 





 





 





=

 





 





 





 





 





 





 





gdzie

e

ij

k

oznacza współczynnik

( , )

i j

macierzy elementu skończonego o numerze

e

.

Uwzględniając podane warunki podparcia i obciążenia oraz podstawiając wartości współczynnika

e

ij

k

mamy:

6

3

e

l

–6

3

e

l

0

0

0

0

3

e

l

2

2

e

l

3

e

l

−

2

e

l

0

0

0

0

–6

3

e

l

−

12

0

–6

3

e

l

0

0

3

e

l

2

e

l

0

2

4

e

l

3

e

l

−

2

e

l

0

0

0

0

–6

3

e

l

−

12

0

–6

3

e

l

0

0

3

e

l

2

e

l

0

2

4

e

l

3

e

l

−

2

e

l

0

0

0

0

–6

3

e

l

−

6

3

e

l

−

3

2

e

EI

l

0

0

0

0

3

e

l

2

e

l

3

e

l

−

2

2

e

l

1

2

0

3

4

0

5

6

0

7

2

8

0

0

0

0

2

12

e

e

e

e

F

F

p l

q

q

p l

q

M

q

p l

P

q

q

p l









 





 





 





 





 





  



=

  



  



  



  



+

  



  



−

  











G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

50

Do układu równań wprowadziliśmy jako znane

1

0

q

=

i

2

0

q

=

(warunki utwierdzenia węzła pierwszego). Nieznane są

natomiast wartości

1

F

i

2

F

, ponieważ nieznane są wartości reakcji.

P

RZYKŁAD

9

Jeśli model belki z rysunku 22 składać się będzie tylko z jednego elementu skończonego otrzymamy układ równań:

1

2

2

2

0

3

3

2

2

2

4

0

0

6

3

6

3

0

3

2

3

2

6

3

6

3

2

3

3

2

12

F

l

l

F

l

l

l

l

EI

p l

q

l

l

l

q

l

l

l

l

p l









−

 





 

−

  



=

  



−

−

−

  



  



−

−

 









Rozwiązanie możemy otrzymać przekształcając powyższy układ równań do postaci

[ ]

{ }

1

2

3

4

F

F

A

b

q

q













=

















,

lub, co prostsze, redukując go do dwóch ostatnich równań (po przyjęciu

1

0

q

=

i

2

0

q

=

)

0

3

4

3

2

2

0

3

4

3

2

(6

3

)

,

2

2

( 3

2

)

,

12

p l

EI

q

lq

l

p l

EI

lq

l q

l

−

=

−

−

+

=

Rozwiązaniem jest:

4

0

3

3

0

4

1

8

1

6

p l

q

EI

p l

q

EI

=

=

Wyznaczając ugięcie, zgodnie ze wzorem (109) otrzymamy

2

2

2

3

2

3

0

0

0

0

3

1

2

1

5

( )

8

6

8

6

24

12

p l

p l

p l

p l

w

EI

EI

EI

EI

ξ

ξ

ξ

ξ

ξ

−









=

−

+

+

=

−

















czyli rozwiązanie identyczne z uzyskanym metodą Ritza – przykład 5. Wynik jest oczywisty jeśli zauważymy, że w obu
przypadkach stosowaliśmy jako funkcję przybliżającą linię ugięcia wielomian trzeciego stopnia. Różnica polega na przyjęciu
różnej parametryzacji (103) o metodzie Ritza i (105) w MES.

W metodzie elementów skończonych nieistotna jest statyczna wyznaczalność lub statyczna

niewyznaczalność konstrukcji. Stwierdziliśmy poprzednio, że minimalna liczba odebranych stopni swobody

odzwierciedlających warunki podparcia odpowiada odebraniu możliwości ruchu modelu jako ciała sztywnego.

Większa liczba warunków podparcia ułatwia jedynie rozwiązanie ponieważ zmniejsza liczbę niewiadomych, a w

dużych zadaniach dodatkowo „stabilizuje” rozwiązanie i poprawia dokładność wyników (poprawia

uwarunkowanie numeryczne zadania-patrz podrozdział 8.1).

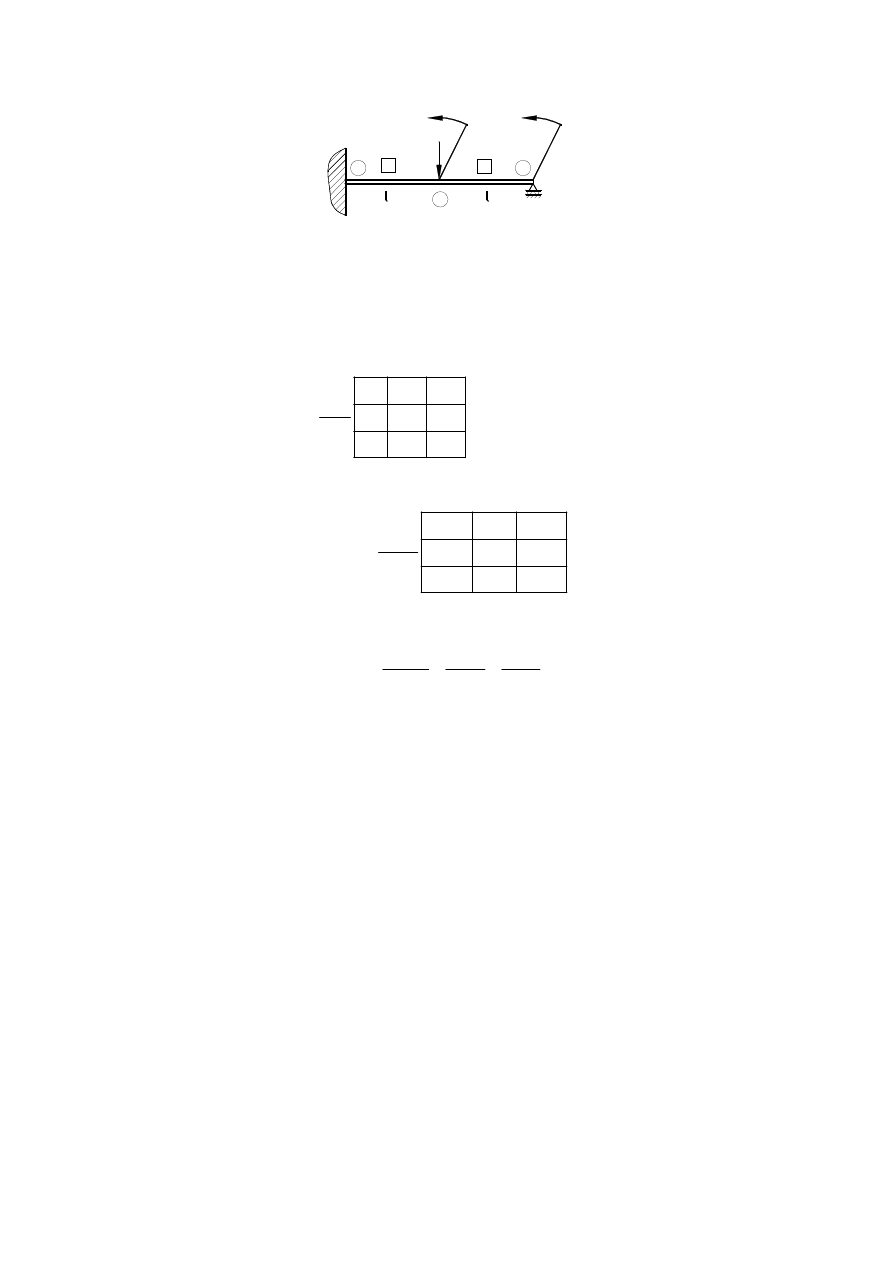
G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

51

1

2

2

3

P

M

1

M

1

2

A

B

C

Rys. 28. Belka o długości

2l

podparta w sposób statycznie niewyznaczalny (przykład 10)

P

RZYKŁAD

10

Obliczyć metodą elementów skończonych ugięcie punktu

B

belki z rysunku 28.

Rozwiązanie

Przyjmując model obliczeniowy złożony z dwóch elementów skończonych otrzymamy

3

2

2

4

1

3

2

2

6

2

12

0

3

2

0

4

3

2

l

q

P

EI

l

l

q

M

l

l

l

l

q

M

−

  



  



=

  



  



  



.

Odwracając macierz powyższego układu równań dostaniemy

2

3

2

4

2

1

6

3

2

7

3

12

3

15

12

96

12

12

48

q

w

l

l

l

P

l

q

l

M

EI

q

l

M

θ
θ

−

−

  







  







=

=

−

  







  







−

−

  







.

Poszukiwane ugięcie punktu B jest więc równe

3

2

2

1

2

2

7

96

32

8

Pl

M l

M l

w

EI

EI

EI

−

=

+

−

Jest to rozwiązanie dokładne, ponieważ rozwiązaniem dokładnym dla segmentu belki nie obciążonej obciążeniem ciągłym
jest wielomian trzeciego stopnia, a taki właśnie wielomian jest założoną z góry funkcją ugięcia na elemencie skończonym.

5.2.

PRĘTY ROZCIĄGANE I SKRĘCANE. SPRĘŻYNY

Podstawą do zbudowania układu równań metody elementów skończonych jest sformułowanie związków

obowiązujących w elemencie skończonym, a także umiejętność budowy macierzy sztywności elementu i

wyznaczania równoważnych sił węzłowych od obciążenia ciągłego. Bardzo proste zależności otrzymamy

stosując przedstawiony wcześniej sposób postępowania w przypadku rozciągania i skręcania. Przeanalizujemy

najpierw najprostszy element pręta rozciąganego lub ściskanego (rys. 29).

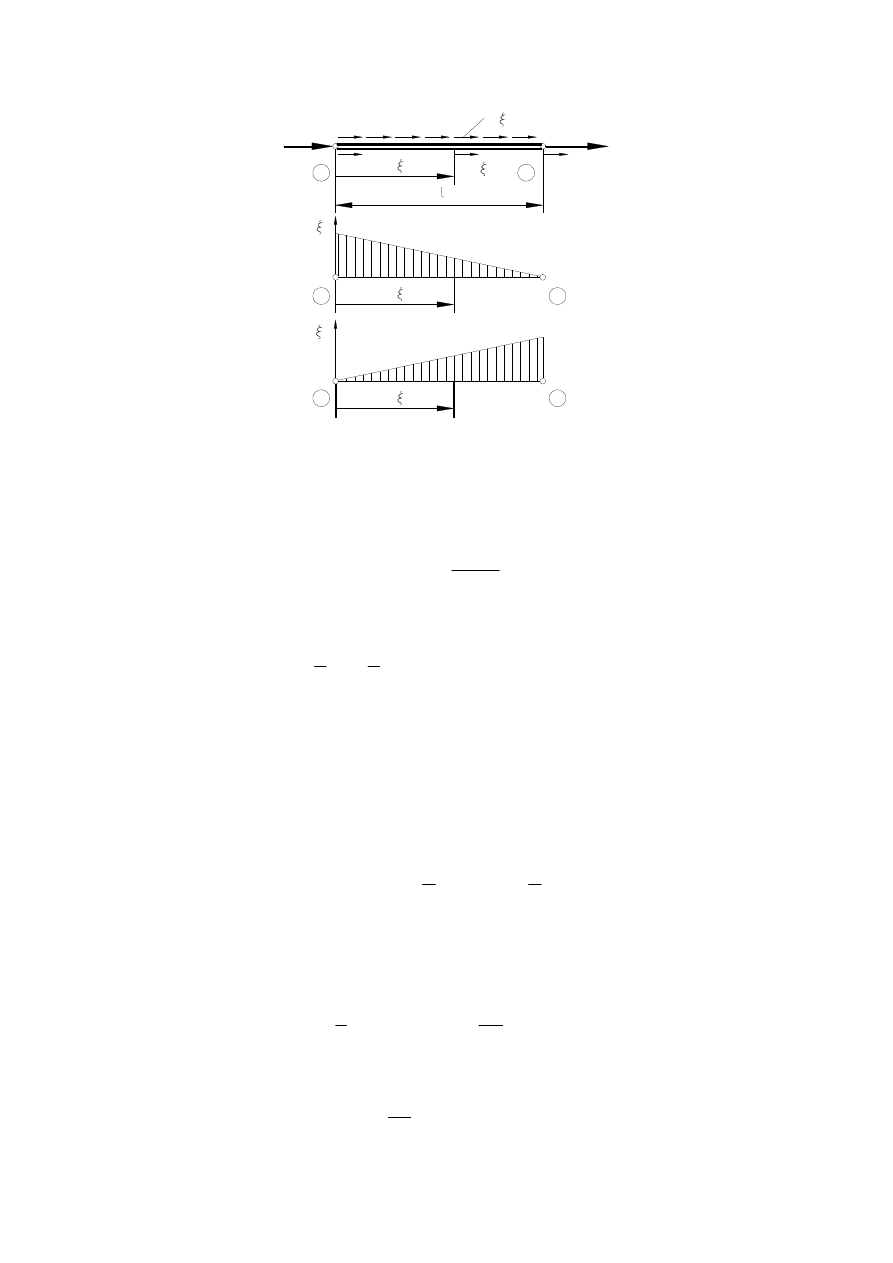
G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

52

2

1

1

1

e

N ( )

1

N ( )

2

u( )

p( )

u1

2

u

1

2

1

2

F

2

1

F

Rys. 29. Dwuwęzłowy element skończony pręta rozciąganego i funkcje kształtu

1

2

( ),

( )

N

N

ξ

ξ

Jeżeli przemieszczenie wewnątrz elementu

( )

u

ξ

ma być jednoznacznie określone przez przemieszczenia

węzłowe

1

u

i

2

u

to przyjąć można, że

( )

u

ξ

jest funkcją liniową

2

1

1

( )

e

u

u

u

u

l

ξ

ξ

−

= +

.

(126)

Przekształcając

( )

u

ξ

do postaci analogicznej jak (105) otrzymamy:

{ }

1

1

2

1

2

2

( )

1

( ),

( )

e

e

q

u

u

u

N

N

N

q

q

l

l

ξ

ξ

ξ

ξ

ξ

 





= −

+

=

=





 

 





 









 

,

(127)

gdzie

{ }

1

1

2

2

e

e

e

q

u

q

q

u

 

 

=

=

 

 

 

 

,

oznacza wektor stopni swobody elementu a

1

2

( ),

( )

N

N

N

ξ

ξ

=

 





 





,

gdzie

1

( ) 1

,

e

N

l

ξ

ξ

= −

2

( )

e

N

l

ξ

ξ

=

,

(128)

oznacza wektor funkcji kształtu.

Aby znaleźć macierz sztywności wyznaczamy energię odkształcenia sprężystego zgromadzoną w elemencie

skończonym. Mamy:

2

0

0

1

( ) ( )

( ( ))

2

2

e

e

l

l

e

EA

U

A

d

d

σ ξ ε ξ ξ

ε ξ

ξ

=

=

∫

∫

.

(129)

Ze wzoru (127) otrzymamy

1

1

2

2

( )

,

.

e

q

du

N

N

q

d

ε ξ

ξ

 





′

′

=

=

 







  

(130)

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

53

Energię sprężystą

e

U

przedstawić więc można jako

[ ]

{ }

1

1

1

2

1

2

2

0

2

1

1

1

2

1

1

2

2

0

2

1

2

2

,

,

2

1

,

,

2

2

e

e

l

e

e

e

l

e

e

e

e

e

N

q

EA

U

q q

N

N

d

q

N

N N

N N

q

EA

q q

d

q

k

q

q

N N

N N

ξ

ξ





′

 



 



′

′

=

=



 



 













′

 













′ ′

′ ′

 





=

=





 

 





 





′ ′

′ ′

 





∫

∫

(131)

gdzie

[ ]

1

1

1

1

e

e

EA

k

l

−





=





−





,

(132)

jest macierzą sztywności elementu pręta rozciąganego.

Znajdziemy teraz formuły na wyznaczenie równoważnych sił węzłowych dla dowolnego obciążenia ciągłego

N

( )

m

p

ξ













działającego na element skończony. W tym celu obliczmy drugi człon w wyrażeniu na całkowitą

energię potencjalną

1

1

2

2

0

0

1

1

2

2

0

0

( ) ( )

( ) ( ),

( ) ( )

( ) ( ),

( ) ( )

.

e

e

e

e

l

l

p

ze

e

l

l

e

q

W

p

u

d

N

p

N

p

d

q

q

N

p

N

p

d

q

ξ ξ ξ

ξ

ξ

ξ

ξ

ξ

ξ

ξ

ξ

ξ ξ

 

=

=

=



  





 



  

=



  



  





∫

∫

∫

∫

Wynik możemy zapisać jako

1

1

2

2

,

p

e

e

ze

e

e

q

W

F F

q

 





=

 





 

,

gdzie

0

( ) ( )

e

l

e

i

i

F

N

p

d

ξ ξ ξ

=

∫

,

(133)

e

i

F

nazywamy równoważnymi siłami węzłowymi od obciążenia ciągłego

p

rozłożonego na danym elemencie.

Budowa układu równań w przypadku pręta rozciąganego przebiega w sposób analogiczny do przedstawionego

poprzednio dla belek. W wyniku składania macierzy sztywności elementu dostajemy globalną macierz

sztywności

[ ]

K

. Po określeniu znanych elementów wektora sił węzłowych

{ }

F

dochodzimy do układu

równań:

{ } { }

[ ]

K

q

F

=

.

(134)

Elementy

i

F

wektora sił węzłowych oznaczają w równaniu (134) całkowite oddziaływanie zewnętrzne

odpowiadające i–temu stopniowi swobody. Ponieważ przed rozwiązaniem układu nie znamy wartości reakcji to

te spośród sił

i

F

, które odpowiadają odebranym stopniom swobody pozostają nieznane. Znane są natomiast

odpowiednie wartości przemieszczeń

i

q

. Po rozwiązaniu(134) znamy wszystkie składowe wektorów

{ }

q

i

{ }

F

, a więc przemieszczenia wszystkich węzłów i ich obciążenia, w tym reakcje podpór.

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

54

Jeśli interesują nas naprężenia w kolejnych elementach wykorzystujemy wzór

1

2

1

1

2

2

(

)

( ),

( )

e

e

q

E q

q

E

E N

N

q

l

σ

ε

ξ

ξ

 

−





′

′

=

=

=

 







  

.

(135)

Naprężenie w omawianym elemencie pręta rozciąganego jest więc zawsze stałe.

a

1

1

q =0

2

q

2

3

q =0

3

1

2

a

P

P

p

0

1

1

q =0

1

2

0

2

p (l-a)

3

q =0

2

2

a)

b)

Rys. 30. Obustronnie utwierdzony pręt obciążony: a) siłą skupioną

P

; b) obciążeniem ciągłym

0

p

(przykład 11)

P

RZYKŁAD

11

Obustronnie utwierdzony pręt o długości

l

jest obciążony siłą

P

przyłożoną w odległości

a

od jednej z podpór (rys. 30a).

Obliczyć przemieszczenie punktu przyłożenia siły i reakcje podpór.

Rozwiązanie:

Przyjmujemy najprostszy model, składający się z dwóch elementów skończonych. Ich macierze sztywności są równe:

[ ]

1

1

1

1

1

e

EA

k

a

−





=





−





[ ]

2

1

1

1

1

e

EA

k

l

a

−





=





−

−





.

Układ równań równowagi ma więc postać:

1

1

2

2

3

3

1

1

0

1

1

1

1

1

1

a

a

q

F

EA

q

F

a

a

l

a

l

a

q

F

l

a

l

a





−







    

  







−

+

−

=

  







−

−

  





    





−





−

−





.

Uwzględniając, że

1

3

0

q

q

=

=

a

2

F

P

=

2

1

3

(

)

,

(

)

,

.

P l

a a

q

EAl

P l

a

F

l

Pa

F

l

−

=

−

−

=

−

=

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

55

Ponieważ w węzłach 1 i 3 nie ma innych oddziaływań zewnętrznych to

1

F

i

3

F

stanowią wartości reakcji podpór.

Jeśli zmodyfikujemy zadanie przez zmianę obciążenia (rys. 30b) otrzymamy ze wzoru (133) równoważną siłę węzłową

0

2

(

)

2

p l

a

F

−

=

,

i po rozwiązaniu układu

2

0

2

(

)

2

p l

a a

q

lEA

−

=

,

2

0

1

(

)

2

p l

a

F

l

−

−

=

,

0

3

(

)

2

p a l

a

F

l

−

−

=

.

Reakcja w węźle pierwszym jest równa

1

F

natomiast żeby wyliczyć reakcję w węźle trzecim należy uwzględnić wartość

równoważnej siły węzłowej od obciążenia ciągłego przypadającą na ten węzeł:

0

0

0

1

1

(

)

(

)

(

)(

)

2

2

2

p a l

a

p l

a l

p l

a l

a

R

F

l

l

l

−

−

−

−

−

+

= =

−

=

.

Suma reakcji jest więc równa

1

3

0

(

)

R

R

p l

a

+

= −

−

.

Warto zauważyć, że rozwiązanie dla pręta z rysunku 30a jest rozwiązaniem ścisłym a dla pręta z rysunku 30b rozwiązaniem
przybliżonym.

Macierz sztywności sprężyny o sztywności

k

(rys. 31) możemy określić w podobny sposób jak dla pręta

rozciąganego.

1

2

q =u

1

1

q =u

2

2

k

F=k u=k(u -u )

*

[k] =k 1 -1

-1 1

2

1

e

Rys. 31. Sprężyna jako element skończony

Energia odkształcenia sprężystego jest równa

2

2

1

2

1

1

1

1

(

)

(

)(

)

2

2

2

e

U

F u

k

u

k u

u

u

u

=

∆ =

∆

=

−

−

.

(136)

Wynik możemy zapisać w postaci

[ ]

{ }

1

1

2

2

1

,

,

2

1

,

2

e

e

e

e

e

u

k

k

U

u u

u

k

k

U

q

k

q

−

 





=





 



 



−



  

=

 

 

gdzie

[ ]

e

k

k

k

k

k

−





=





−





,

(137)

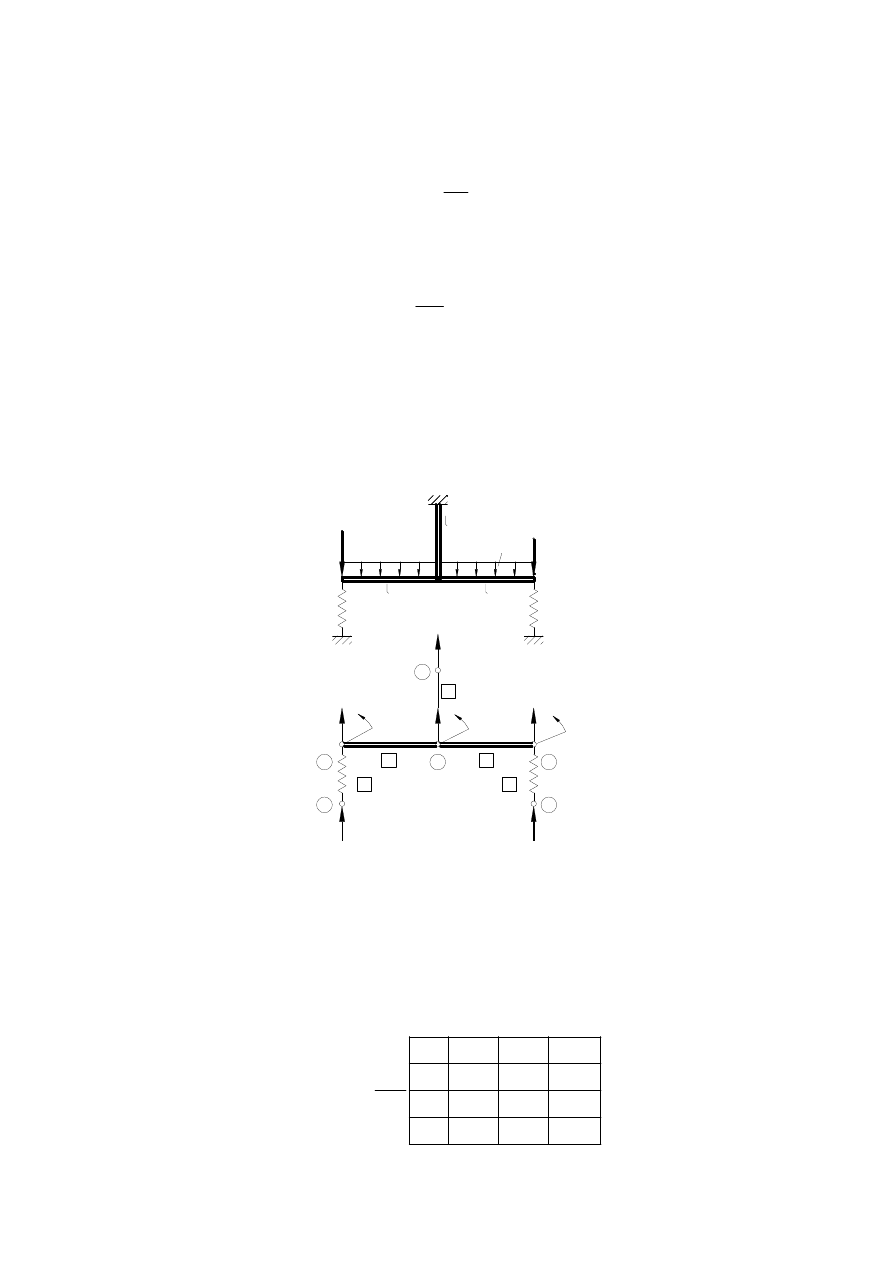
G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

56

jest macierzą sztywności elementu skończonego sprężyny. Macierz (137) można też otrzymać

bezpośrednio z macierzy sztywności pręta rozciąganego (132) podstawiając

k

l

EA

e

=

.

Postępując w podobny sposób łatwo znajdziemy macierz sztywności elementu pręta skręcanego, w którym

mamy dwa stopnie swobody kąty skręcenia końców:

[ ]

1

1

1

1

s

e

e

GI

k

l

−





=





−





,

(138)

gdzie

s

GI

jest sztywnością pręta na skręcanie.

Znając formuły określające macierze sztywności dla różnych elementów konstrukcyjnych możemy w

standardowy sposób analizować konstrukcje złożone. Macierz

[ ]

K

układu równań metody elementów

skończonych jest budowana z uwzględnieniem przyjętej numeracji węzłów i stopni swobody. Zmiana numeracji

stopni swobody zmieni sam układ równań nie zmieniając oczywiście wyników zadania.

1

3

0

p

k

1

1

1

2

k

2

2

1

q

7

q

q

2

3

q

4

q

5

q

6

q

4

8

q

q

9

5

6

1

2

3

P

P

1

2

4

5

Rys. 32. Model MES konstrukcji złożonej z różnych elementów konstrukcyjnych

(przykład 12)

P

RZYKŁAD

12

Sformułować układ równań

[ ]

{ } { }

F

q

K

=

dla konstrukcji składającej się z belki, dwóch sprężyn i pręta rozciąganego

(rys. 32).

Rozwiązanie

Przyjmijmy podział belki na 2 elementy skończone. Model konstrukcji obejmuje dodatkowe 2 elementy skończone

odpowiadające sprężynom oraz element pręta rozciąganego. Model opisany jest przez 9 stopni swobody

i

q

. Macierze

sztywności elementów belkowych są określone przez wzór:

[ ] [ ]

2

1

1

2

1

1

2

1

1

2

1

1

2

1

1

1

1

3

1

2

1

2

3

3

3

6

3

6

3

2

3

3

6

3

6

2

l

l

l

l

l

l

l

l

l

l

l

l

l

EI

k

k

e

e

−

−

−

−

−

−

=

=

.

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

57

Stopnie swobody elementu pierwszego to

1

2

3

4

,

,

,

q q q q

, a elementu drugiego

6

5

4

3

,

,

,

q

q

q

q

.

Macierz sztywności elementu pręta rozciąganego jest równa

[ ]













−

−

=

1

1

1

1

2

3

l

EA

k

e

.

Stopnie swobody tego elementu w globalnym wektorze to

3

q

i

7

q

.

Macierze sztywności sprężyn są równe:

[ ]













−

−

=

1

1

1

1

1

4

k

k

e

[ ]

5

2

1

1

1

1

e

k

k

−





=





−





,

a odpowiadające im stopnie swobody to

8

q

i

1

q

oraz

9

q

i

5

q

.

Układ równań

[ ]

{ } { }

K

q

F

=

dla przyjętej numeracji stopni swobody będzie miał postać:

1

2

3

4

5

6

7

8

9

1

2

3

4

5

6

7

8

9

0 1

1

2

1

0 1

2

0 1

3

4

0 1

5

2

6

2

0 1

7

8

9

2

12

0

2

0

12

0

0

p l

P

q

p l

q

p l

q

q

p l

q

P

q

p l

F

F

F

−





−









 

−





 





 





 





 





 





 





= −

 





−

 





 





 





 





 





 





 

















–

elementy macierzy szt. elementu 1 (belka),

–

elementy macierzy szt. elementu 2 (belka),

–

elementy macierzy szt. elementu 3 (pręt),

–

elementy macierzy szt. elementu 4 (sprężyna),

–

elementy macierzy szt. elementu 5 (sprężyna).

Macierz układu równań

[ ]

K

można zapisać stosując symbole

m

ij

k

, oznaczające składowe

)

,

( j

i

macierzy sztywności

elementu skończonego

m

.

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

58

[ ]

1

4

1

1

1

4

11

22

12

13

14

12

1

1

1

1

21

22

23

24

1

1

1

2

3

1

2

2

2

3

31

32

33

11

11

34

12

13

14

12

1

1

1

2

1

2

2

2

41

42

43

21

44

22

23

24

2

2

2

5

2

5

31

32

33

22

34

12

2

2

2

2

9 9

41

42

43

44

3

3

21

11

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

K

×

+

+

+

+

+

+

=

+

4

4

21

11

5

5

21

11

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

k

k

k

k

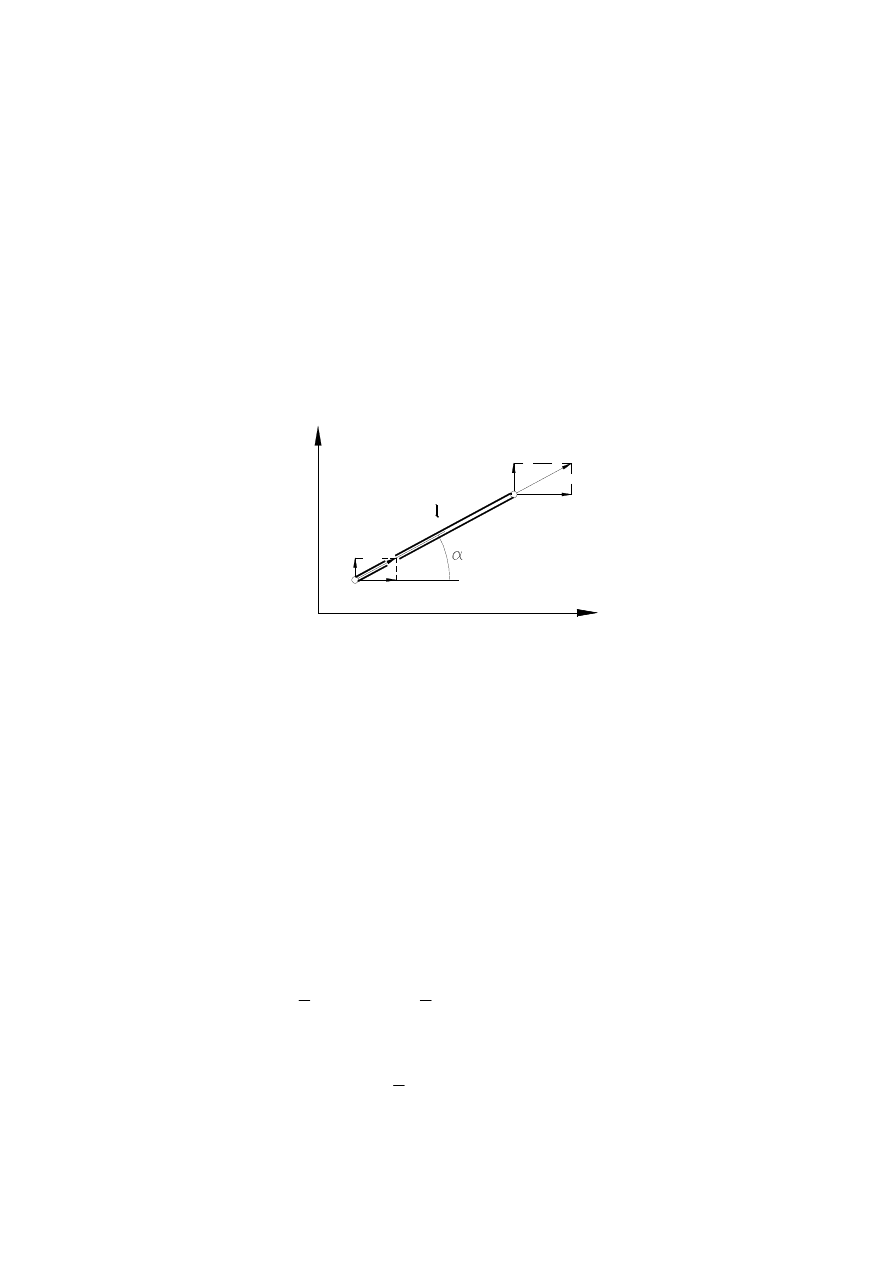
G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

59

5.3. KRATOWNICE I RAMY PŁASKIE

Związki obowiązujące w poszczególnych prętowych elementach skończonych, a także kierunki przemieszczeń

uogólnionych opisywane były dotychczas w lokalnych, elementowych układach współrzędnych. W takich

konstrukcjach jak na przykład kratownica, gdzie musimy zapewnić ciągłość przemieszczeń na połączeniach

między różnie nachylonymi prętami wygodniejsze jest stosowanie globalnego układu współrzędnych. Załóżmy,

ż

e analizowany pręt (element) kratownicy jest nachylony pod kątem

α

w stosunku do osi

x

globalnego

kartezjańskiego układu współrzędnych (rys. 33). Poszukujemy związków między lokalnymi stopniami swobody

elementu

1

2

,

e

e

q

q q

=

 





 





(przemieszczenia wzdłuż osi pręta), a stopniami swobody tego elementu w

globalnym układzie współrzędnych

1

1

2

2

, ,

,

g

e

e

q

u

u

υ

υ





=













.

x

y

q

1

q

2

v

1

v

2

u

2

u

1

e

Rys. 33. Element skończony pręta kratownicy

Dla obu węzłów elementu

)

2

,

1

(

=

i

otrzymujemy

1

cos

sin

i

i

q

u

α υ

α

=

+

.

(139)

Poszukiwany związek ma więc postać:

1

1

1

2

2

2

cos

sin

0

0

0

0

cos

sin

e

e

u

q

q

u

υ

α

α

α

α

υ

 

 

 



  

=

 

 









 

 

 

 

,

(140)

czyli

{ }

[ ]

{ }

e

q

k

e

q

T

q

=

.

(141)

Energię sprężystą elementu można więc zapisać w formie

[ ]

{ }

[ ] [ ] [ ]

{ }

1 2

4 2

2 4

2 1

2 2

2 2

4 1

1 4

1

1

2

2

T

T

q

e

q

k

k

e

e

e

e

e

q

U

q

k

q

q

k

T

T

×

×

×

×

×

×

×

×

 

=

=

 

 

 

,

(142)

lub

{ }

1

2

e

q

g

q

e

e

e

U

q

k

q

  



=

  



,

(143)

gdzie

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

60

2

2

2

2

2

2

2

2

sin ,

cos

g

e

e

c

sc

c

sc

sc

s

sc

s

EA

k

c

sc

c

sc

l

sc

s

sc

s

s

c

α

α

−

−

−

−





=





−

−

−

−

=

=

.

(144)

Otrzymaliśmy więc macierz sztywności elementu kratownicy w globalnym układzie współrzędnych

kartezjańskich. Kratownica płaska o

LW

węzłach ma więc

LW

2

stopnie swobody odpowiadające pionowym

i poziomym przemieszczeniom wszystkich węzłów.

P

RZYKŁAD

13.

Zbudować układ równań MES dla kratownicy z rysunku 34. Jakie jest przemieszczenie węzła 4 jeśli

2

1

β

β

=

a siła

P

przyłożona jest poziomo

)

0

(

=

γ

.

Rozwiązanie

Ustrój składa się z trzech elementów.

Element 1 określany przez węzły 1i 4 jest nachylony pod kątem

1

1

β

α

=

i ma długość

1

1

cos

α

l

l

=

.

Element 2 określony przez węzły 2 i 4 jest nachylony pod kątem

0

2

=

α

i ma długość

2

2

cos

α

l

l

=

.

Element 3 określony przez węzły 3 i 4 jest nachylony pod kątem

2

3

β

α

−

=

i ma długość

3

3

cos

α

l

l

=

.

Każda z macierzy sztywności tych elementów

[ ] [ ] [ ]

3

2

1

,

,

e

ij

e

ij

e

ij

k

k

k

jest zdefiniowana przez wzór (144) gdzie

e

l

i

α

są

długością i kątem nachylenia odpowiednich elementów.
Pełny układ równań ma więc postać:

1

1

1

1

11

12

13

14

1

1

1

1

21

22

23

24

2

2

2

2

11

12

13

14

2

2

2

2

21

22

23

24

3

3

3

3

11

12

13

14

3

3

3

3

21

22

23

24

1

1

2

2

3

3

1

2

3

1

2

3

31

32

31

32

31

32

33

33

33

34

34

34

1

1

2

2

3

3

1

41

42

41

42

41

42

43

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

+

+

+

+

1

2

3

4

5

6

7

2

3

1

2

3

8

43

43

44

44

44

0

0

0

0

0

0

cos

sin

F

F

F

F

F

F

q

P

q

k

k

k

k

k

P

γ

γ

  



  



  



  



  



  



=

  



  



  



  



  



  



+

+

+

+





 

.

Uwzględniając, że

0

j

q

=

dla

1, 6

j

=

możemy układ zredukować do

2

3

3

7

1

1

2

3

3

8

1

1

sin

cos

i

i i

i

i

i

i

i i

i

i

i

i

i

c

s c

q

P

l

l

EA

s c

s

q

P

l

l

γ

γ

=

=

=

=





  







  







=

  







  





   











∑

∑

∑

∑

.

Zakładając, że

1

2

β

β

β

=

=

i

0

γ

=

mamy

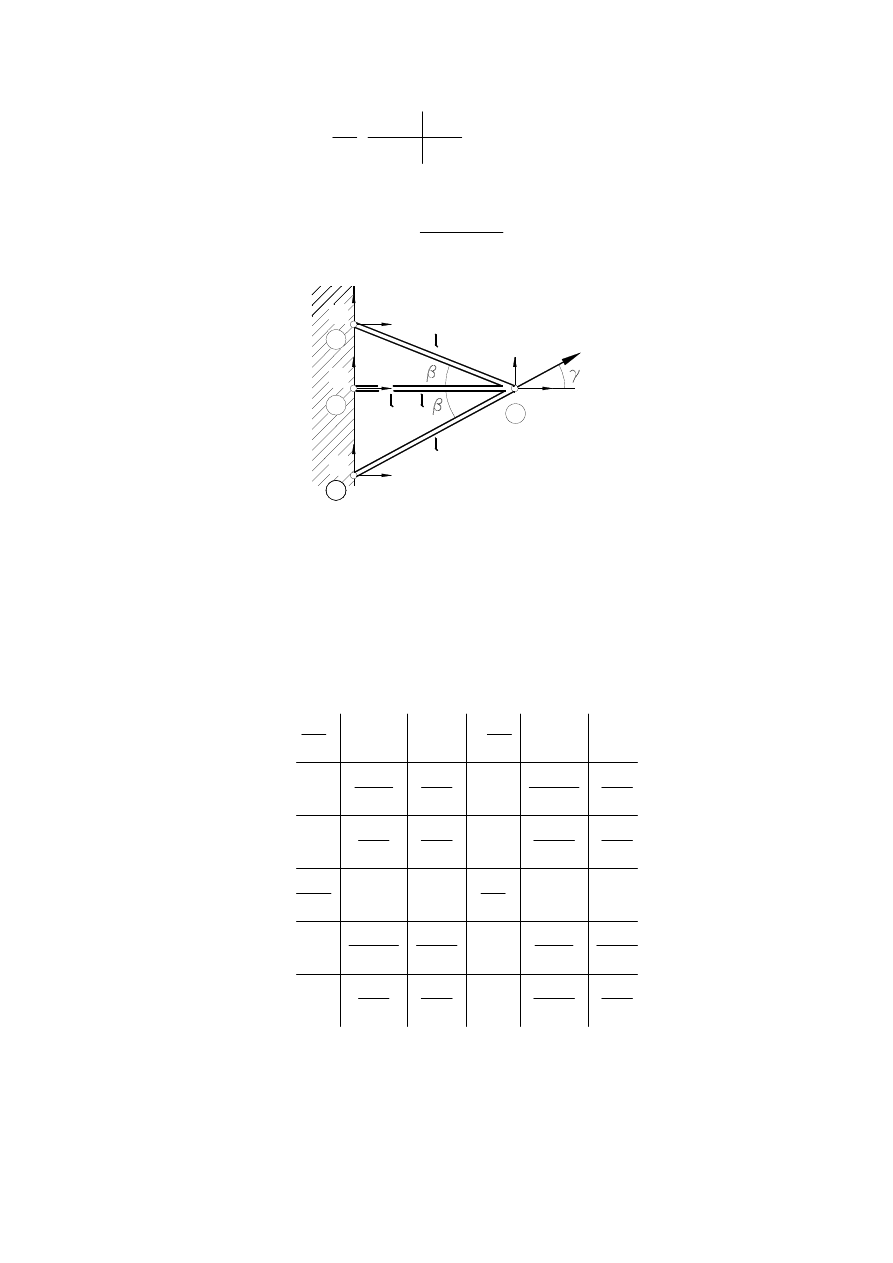
G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

61

3

7

2

8

1 2

0

0

2

0

c

q

P

EA

s c

q

l





+

   

=



    

 

 









,

gdzie

cos

c

β

=

,

sin

s

β

=

.

Stąd

7

3

(1 2 )

Pl

q

EA

c

=

+

,

8

0

q

=

.

q

1

1

q

2

8

q

q

7

4

q

q

3

6

q

q

5

3

2

=

2

1

1

4

2

3

P

Rys. 34. Kratownica z przykładu 13

Związki otrzymane dla elementu pręta rozciąganego i belki mogą być wykorzystane do budowy elementu

skończonego ramy dwuwymiarowej. Element ramy możemy potraktować jako strukturę będącą połączeniem

elementu belki i pręta. Przyjmując numerację stopni swobody z rysunku 35a i wykorzystując znane macierze

sztywności belki (115) i pręta rozciąganego (132) otrzymamy macierz sztywności elementu ramy płaskiej:

[ ]

3

2

3

2

2

2

3

2

3

2

2

2

0

0

0

0

12

6

12

6

0

0

6

4

6

2

0

0

0

0

0

0

12

6

12

6

0

0

6

2

6

4

0

0

e

e

e

e

e

e

e

e

e

e

e

e

e

e

e

e

e

e

e

e

e

EA

EA

l

l

EI

EI

EI

EI

l

l

l

l

EI

EI

EI

EI

l

l

l

l

k

EA

EA

l

l

EI

EI

EI

EI

l

l

l

l

EI

EI

EI

EI

l

l

l

l





−









−

















−









=





−













−

−

−













−













.

(145)

Element ten ma więc 6 stopni swobody a jego deformacja jest określona przez przemieszczenia

( )

u

ξ

i

( )

w

ξ

w lokalnym układzie współrzędnych związanym z węzłami 1 i 2 (rys. 35b).

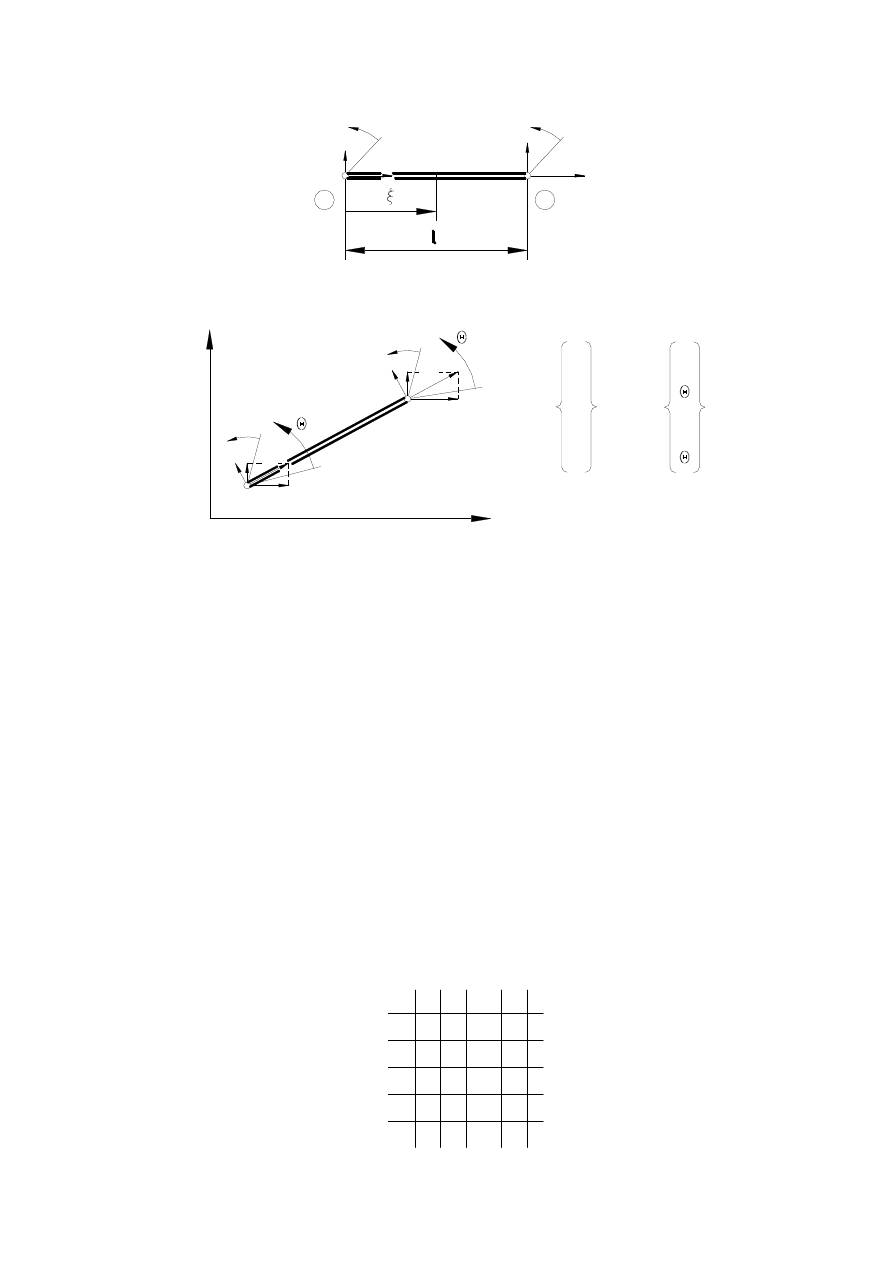
G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

62

x

y

q

1

q

4

v

1

v

2

u

2

u

1

l

e

q

2

1

2

5

q

q

3

6

q

q

1

q

2

q

3

q

4

q

5

q

6

{q} =

e

v

2

2

u

e

{q } =

v

u

2

1

1

1

g

q

1

q

4

e

q

2

5

q

q

3

6

q

1

2

a)

b)

Rys. 35. Element ramy dwuwymiarowej (a); Stopnie swobody elementu ramy w układzie lokalnym {q}

e

i

globalnym {q

g

}

e

(b)

Łatwo stwierdzić, że przemieszczenia uogólnione np. węzła 1 w lokalnym i globalnym układzie współrzędnych

wiążą zależności:

1

1

1

2

1

1

3

1

cos

sin ,

sin

cos ,

.

q

u

q

u

q

α υ

α

α υ

α

θ

=

+





= −

+





=



Otrzymamy stąd zależności:

[ ]

[ ]

{ }

1

1

2

1

3

1

4

2

5

2

6

2

r

r

g

e

e

q

u

q

q

T

T

q

q

u

q

q

υ
θ

υ
θ

 

 

 

 

 

 

 

 

 

 

=

=

⋅

 

 

 

 

 

 

 

 

 

 

 

 

,

(146)

gdzie macierz transformacji

[ ]

r

T

ma postać

[ ]

0

0

0

0

0

0

0

0

0

0

1

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

1

r

c

s

s

c

T

c

s

s

c









−









=













−













.

(147)

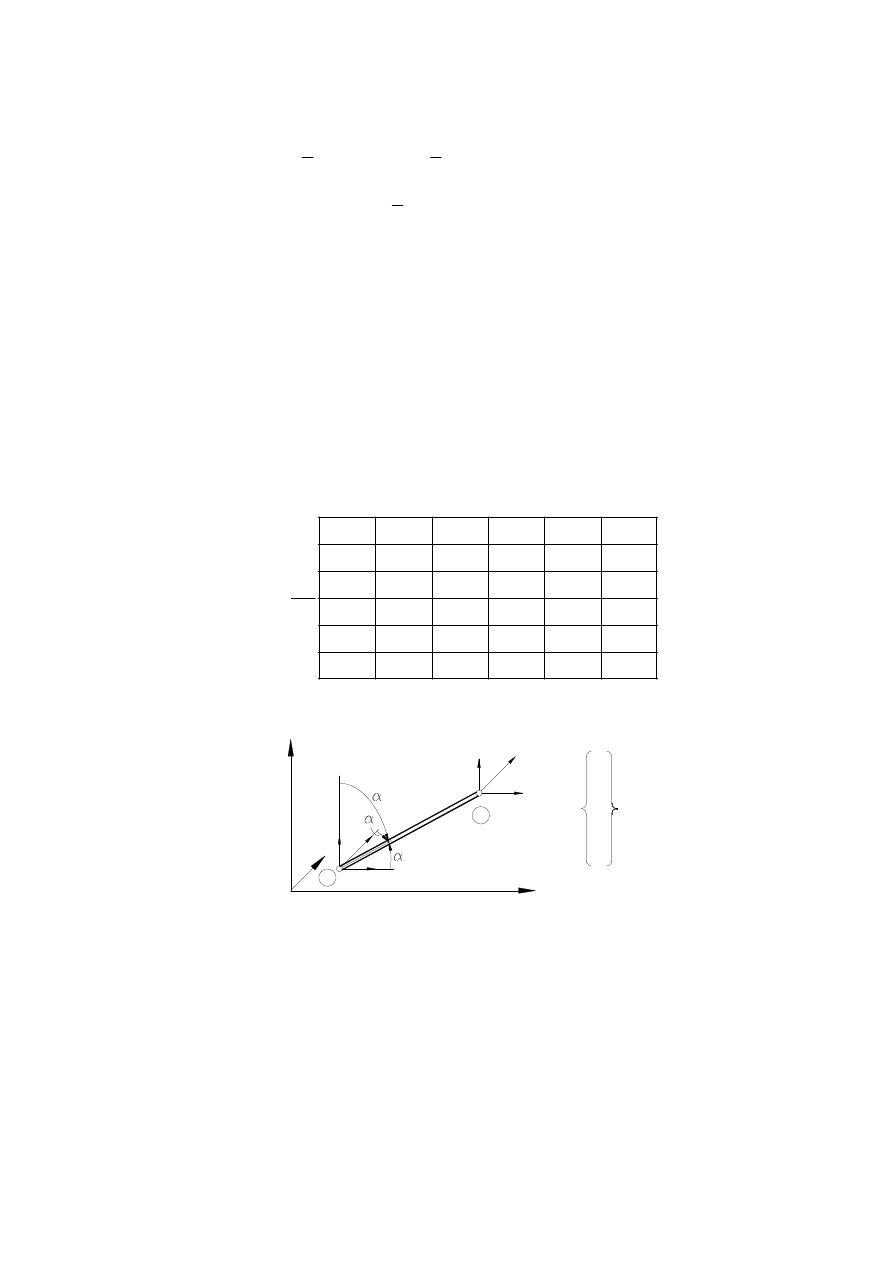
G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

63

Energia sprężysta zgromadzona w elemencie jest równa

[ ]

{ }

[ ] [ ] [ ]

{ }

{ }

1

1

,

2

2

1

,

2

T

e

g

r

r

g

e

e

e

e

e

e

g

e

g

g

e

e

e

U

q

k

q

q

T

k

T

q

U

q

k

q





=

=

 

 













=



 



(148)

gdzie

[ ] [ ] [ ]

T

g

r

e

e

k

T

k

T





=





,

(149)

jest macierzą sztywności elementu ramy dwuwymiarowej w globalnym układzie współrzędnych.

5.4. PRZESTRZENNE KRATOWNICE I RAMY

Związki otrzymane dla kratownic i ram dwuwymiarowych można stosunkowo łatwo uogólnić na

konstrukcje trójwymiarowe. Przyjmijmy oznaczenia dla elementu kratownicy trójwymiarowej przedstawione na

rysunku 36. Postępując podobnie jak w przypadku dwuwymiarowym otrzymamy macierz sztywności w układzie

globalnym x,y,z:

2

2

2

2

2

2

2

2

2

2

2

2

x

x

y

x z

x

x

y

x z

x

y

y

y z

x

y

y

y z

x z

y

z

z

x z

y

z

z

g

e

x

x

y

x z

x

x

y

x z

e

x

y

y

y z

x

y

y

y z

x z

y

z

z

x z

y z

z

c

c c

c c

c

c c

c c

c c

c

c c

c c

c

c c

c c

c c

c

c c

c c

c

EA

k

c

c c

c c

c

c c

c c

l

c c

c

c c

c c

c

c c

c c

c c

c

c c

c c

c

−

−

−

−

−

−

−

−

−





=





−

−

−

−

−

−

−

−

−

,

(150)

gdzie

cos

x

x

c

α

=

,

cos

y

y

c

α

=

,

cos

z

z

c

α

=

.

x

z

w

1

w

2

u

2

u

1

{q} =

e

v
w

2

2

u
v
w
u

2

1

1

1

y

v

1

2

v

x

y

z

1

2

Rys. 36. Element skończony kratownicy trójwymiarowej

Macierz sztywności elementu belki 3-wymiarowej (rys. 37) można zbudować przez złożenie znanych już

macierzy sztywności dla rozciągania (132), skręcania (138) i zginania (115).

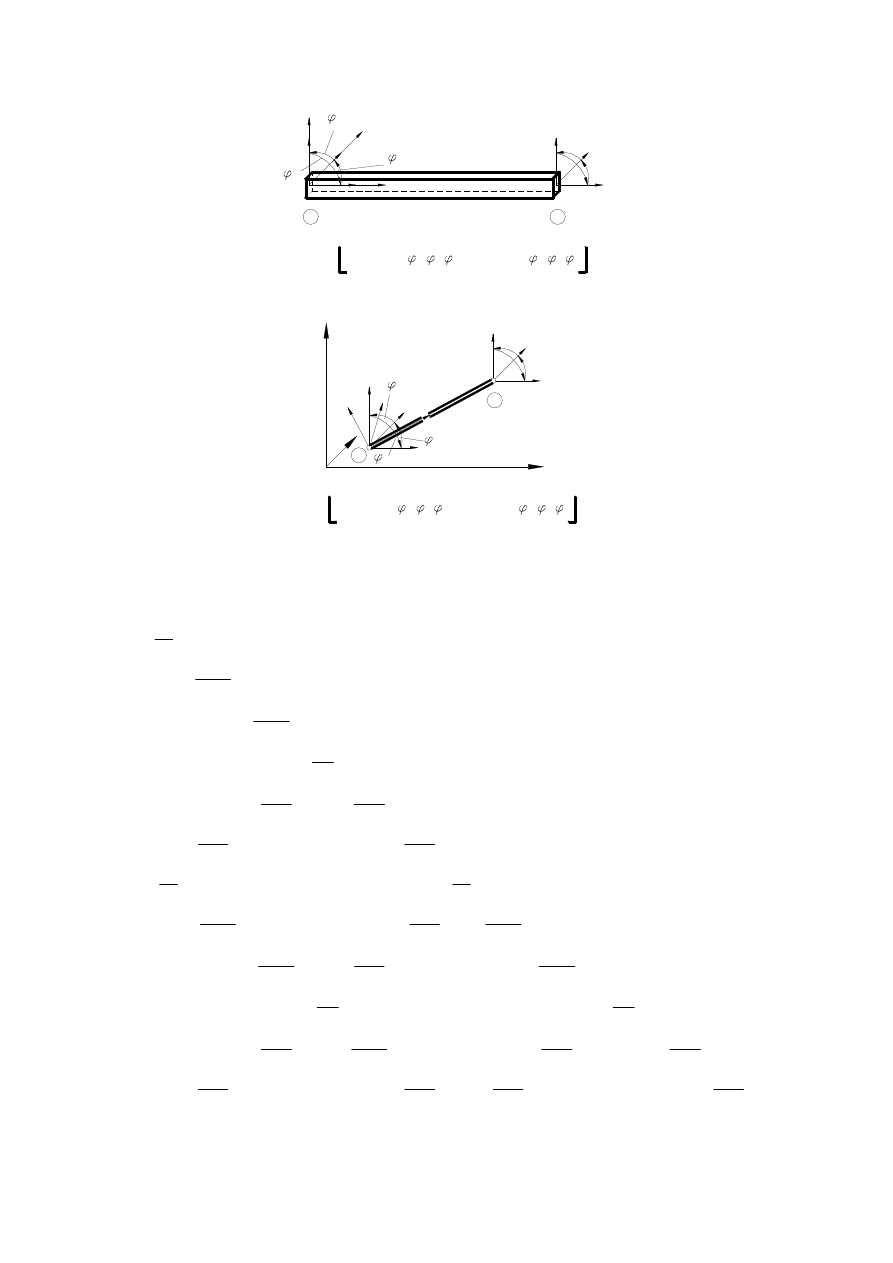
G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

64

x

z

w

1

w

2

u

2

u

1

{q} = u , v , w , , , , u , v , w , , ,

e

y

v

1

2

v

1

1

z

1

2

x'

z'

y'

x

1

y

1

y

1

z

1

x

1

1

1

2

2

2

x

y

z

2

2

2

{q} = u , v , w , , , , u , v , w , , ,

e

1

1

x'
1

1

y'

z'

1

1

2

2

2

x'

y'

2

2

z'
2

'

'

'

'

'

'

2

v

u

2

w

2

w'

v'

1

u'

1

2

1

1

x'

z'

y'

x'

1

z'
1

y'
1

T

T

Rys. 37. Element ramy trójwymiarowej w układzie lokalnym współrzędnych

x y z

′ ′ ′

w układzie globalnym xyz

W układzie lokalnym

z

y

x

′

′

′

,

,

, związanym z osią wzdłużną pręta i położeniem głównych osi bezwładności

przekroju ma ona postać:

[ ]

3

3

2

2

3

2

3

3

2

3

macierz

symetryczna

12

0

12

0

0

0

0

0

6

4

0

0

0

6

4

0

0

0

0

0

0

0

0

0

12

6

12

0

0

0

0

0

12

12

6

0

0

0

0

0

0

0

0

0

0

0

0

0

0

6

0

0

e

z

e

y

e

s

e

y

y

e

e

z

z

e

e

e

e

e

z

z

z

e

e

e

y

y

z

e

e

e

s

s

e

e

y

EA

l

EI

l

EI

l

GI

l

EI

EI

l

l

EI

EI

l

l

k

EA

EA

l

l

EI

EI

EI

l

l

l

EI

EI

EI

l

l

l

GI

GI

l

l

EI

l

′

′

′

′

′

′

′

′

′

′

′

′

′

−

=

−

−

−

−

−

−

2

2

2

2

2

6

4

12

0

0

0

0

0

6

2

6

4

0

0

0

0

0

0

0

0

y

y

z

e

e

e

z

z

z

z

e

e

e

e

EI

EI

EI

l

l

l

EI

EI

EI

EI

l

l

l

l

′

′

′

′

′

′

′





















































































































































−

















(151)

G

RZEGORZ

K

RZESIŃSKI

.

MES_1.

C

ZĘŚĆ

1.

MATERIAŁY DO WYKŁADU

.

65

Rozwiązywanie trójwymiarowych konstrukcji prętowych metodą elementów skończonych jest

obliczeniowo złożone: jeden element skończony kratownicy ma 6 stopni swobody, a ramy 12 stopni swobody.

Dlatego nawet proste obliczenia wykonywane są technikami komputerowymi. Warto tu podkreślić, że

wykonywanie wszelkich obliczeń metodą elementów skończonych bez zastosowania komputera jest zwykle

nieefektywne i ma jedynie znaczenie dydaktyczne, poznawcze. Atutem metody jest uniwersalizm podejścia i

prosta automatyzacja obliczeń uzyskane kosztem dużej liczby operacji arytmetycznych potrzebnych do

otrzymania rozwiązania.