OPTYKA KWANTOWA

Wykład dla 5. roku Fizyki

c

!Adam Bechler 2006

Instytut Fizyki Uniwersytetu Szczecińskiego

Lasery i zasada ich działania

Absorpcja promieniowania w ośrodku

Promieniowanie elektromagnetyczne
przy przejściu przez ośrodek
materialny jest przeważnie
pochłaniane. Miarą pochłaniania jest
spadek natężenia światła na
jednostkę drogi przebytej przez
światło w ośrodku.

!"#$%&'()*&%$+,-.,$/).,)*/*

$0%$123

!

"

#

!

#

#

$%

$#

!

!

"

=

"

=

4

5

6

7

!

Makroskopowy współczynnik
pochłaniania

Oznaczając natężenie światła przez
I , równanie różniczkowe opisujące
pochłanianie na poziomie
makroskopowym zapiszemy w
postaci

dI (x)

dx

=

−αI (x).

(7.1)

gdzie

α

nosi nazwę

makroskopowego współczynnika
absorpcji

.

Lasery i zasada ich działania

Mechanizm absorpcji

Równanie to ma proste rozwiązanie

I (x) = I

0

e

−αx

,

(7.2)

gdzie

I

0

jest natężeniem padającej

wiązki światła.
Pochłanianie światła zachodzi na
skutek absorpcji na centrach
pochłaniających - atomach lub
cząsteczkach ośrodka. Padające
światło wzbudza przejścia kwantowe
między parą poziomów
energetycznych 1 i 2. Wzbudzony
poziom 2 rozpada się następnie do
poziomu 1 na skutek:

1.

rozproszenia energii do innych
stopni swobody ośrodka,

2.

emisji spontanicznej,

3.

emisji wymuszonej.

Osłabianie promieniowania powodują
procesy 1 i 2, natomiast emisja
wymuszona powoduje wzmocnienie
promieniowania.
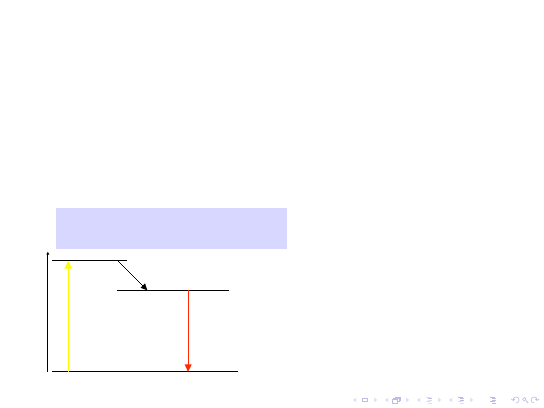
Oznaczmy przez

n

1

liczbę atomów

(cząsteczek) w jednostce objętości,
w których elektron zajmuje poziom
energetyczny 1, a przez

n

2

- liczbę

atomów (cząsteczek) w jednostce
objętości, gdzie elektron znajduje się
na poziomie 2.

Lasery i zasada ich działania

Mechanizm absorpcji

Dodatni wkład do makroskopowego współczynnika absorpcji dadzą te
atomy (cząsteczki), w których elektron zajmuje poziom 1 o niższej
energii, a ujemny wkład te atomy (cząsteczki), gdzie elektron obsadza
poziom 2 o wyższej energii.Wynika stąd, że

α jest proporcjonalny do

różnicy n

1

− n

2

. Oznaczając współczynnik proporcjonalności przez

σ

zapiszemy makroskopowy współczynnik absorpcji w postaci

α = σ(n

1

− n

2

).

(7.3)

Jaki jest wymiar współczynnika proporcjonalności σ ? Ze względu na to,
że

[n

1

] = [n

2

] = m

−3

, a współczynnik absorbcji ma wymiar odwrotności

długości

4

,

[α] = m

−1

,

wymiar σ wynosi m

2

, czyli wymiar powierzchni.

Współczynnik σ ma fizyczny sens

przekroju czynnego na absorpcję

.

Możemy sobie wyobrazić, że jeśli otoczylibyśmy centrum pochłaniające
tarczką o powierzchni σ, to promień świetlny, który trafi w tę tarczkę,
ulegnie absorpcji.

4

αx ma wymiar jeden jako wykładnik funkcji wykładniczej

Lasery i zasada ich działania

Absorpcja i ujemna absorpcja

W zwykłej sytuacji liczba atomów lub cząsteczek z obsadzeniem poziomu
o niższej energii znacznie przewyższa liczbę atomów lub cząsteczek, w
których obsadzony jest poziom o wyższej energii:

n

1

>> n

2

.

Makroskopowy współczynnik absorpcji jest dodatni, a emisja wymuszona
odgrywa zaniedbywalną rolę.
Gdyby jednak udało się doprowadzić do

inwersji obsadzeń

, czyli sytuacji

w której

n

2

> n

1

,

(7.4)

to z równości (7.3) wynika, że wówczas

α < 0

. Mielibyśmy wtedy do

czynienia z

ujemną absorpcją

i natężenie światła przechodzącego przez

taki ośrodek ulagałoby wzmocnieniu, a nie osłabianiu. Z równania (7.2)
mamy bowiem przy ujemnym współczynniku pochłaniania

I (x) = I

0

e

|α|x

,

(7.5)

i zależność natężenia światła od drogi przebytej w ośrodku opisana

byłaby przez rosnącą, a nie malejącą, funkcję wykładniczą.

Lasery i zasada ich działania

Wzmocnienie światła można osiągnąć jeżeli uda się doprowadzić w
ośrodku czynnym do

inwersji obsadzeń

. Wzmocnienie zachodzi wtedy

dzięki

emisji wymuszonej

, która ma tę własność, że promieniowanie

emitowane ma ten sam kierunek co promieniowanie padające i jest z nim
spójne. Mamy więc do czynienia z

interferencją konstruktywną

promieniowania padającego i emitowanego.
Pochodzenie nazwy LASER

L

ight

A

mplification

(by)

S

timulated

E

mission

(of)

R

adiation

Lasery i zasada ich działania

Laser rubinowy

Substancją czynną jest

rubin

, czyli tlenek glinu

Al

2

O

3

domieszkowany

atomami chromu

Cr

. Jako domieszki atomy chromu zachowują w

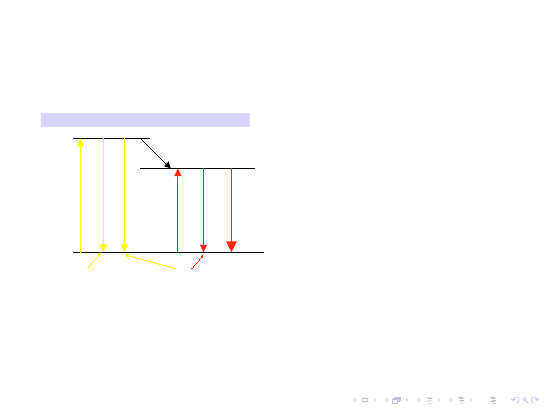
przybliżeniu taki układ poziomów energetycznych jak w próżni.

Uproszczony schemat
poziomów energetycznych
chromu

!"#"$"%$&'"(")'"%*"#+,"%

,-.')/0+1/

!

!

"

!

#

!

$

!"#!"$%&'(
"!)*+,&(

%&

'(

)

234

5

6

5

=

=

!

"

-,*./'(0!1,(23+'(0.(,!1"#'(&'-)(

%/+2%04%-(1"$%

%&

'(

)

7

6

389

:

6

;

=

=

!

"

<=,/#&>&/)?%#>@+A"B%=/&'/AC0%+)+,1+B?>&)?>@

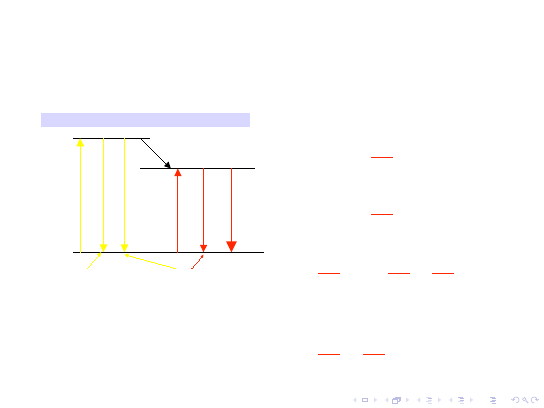
Poziom 1 - poziom podstawowy
Poziom 3 - krótkotrwały poziom
pośredni
Poziom 2 - poziom

metatrwały

Szybkie przejście

3 → 2

jest

przejściem

bezpromienistym

. Akcja

laserowa polega na przejściu między
poziomami

2 i 1

. Inwersja obsadzeń

jest możliwa do osiągnięcia dzięki
długiemu czasowi życia poziomu 2
(rzędu 10

−3

s).

Lasery i zasada ich działania

Laser rubinowy

!

"

!

#

!"#!"$%&'(
"!)*+,&(

$%

&'

(

!"#

$

%

$

=

=

!

"

-,*./'(0!1,(23+'(0.(,!1"#'(&'-)(

%/+2%04%-(1"$%

$%

&'

(

&

%

"'(

)

%

*

=

=

!

"

*&

)

&*

)

&*

*

+,-./0123,4.5670

+,-./01.867907-:570

+,-./0
23,4.5670

0;.6<8:/0

*$

)

$*

*

$*

)

!

+

&$

,

=<5+/>:-01?207962+121@0.+<5+1<4;-7623,

-

.

/

)

)

*&

&*

*&

=

=

0

.

/

)

)

*$

$*

*$

=

=

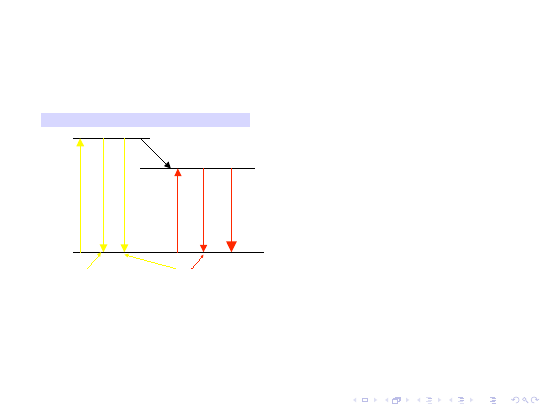
Symbolami

W

oznaczamy

prawdopodobieństwa na jednostkę
czasu przejść wymuszonych, tj.

absorpcji i emisji wymuszonej

.

Przejście

1 → 3

następuje poprzez

wzbudzenie światłem żółtym lampy
błyskowej. Następuje potem szybkie
przejście bezpromieniste

3 → 2

do

poziomu 2 o długim czasie życia.
Emisja spontaniczna z poziomu 2 do
1 zapoczątkowuje

akcję laserową

,

która jest podtrzymywana dzięki
emisji wymuszonej.

U

p

oznacza

natężenie promieniowania
pompującego, a

U

"

- natężenie

promieniowania laserowego.

Lasery i zasada ich działania

Laser rubinowy

!

"

!

#

!"#!"$%&'(
"!)*+,&(

$%

&'

(

!"#

$

%

$

=

=

!

"

-,*./'(0!1,(23+'(0.(,!1"#'(&'-)(

%/+2%04%-(1"$%

$%

&'

(

&

%

"'(

)

%

*

=

=

!

"

*&

)

&*

)

&*

*

+,-./0123,4.5670

+,-./01.867907-:570

+,-./0
23,4.5670

0;.6<8:/0

*$

)

$*

*

$*

)

!

+

&$

,

=<5+/>:-01?207962+121@0.+<5+1<4;-7623,

-

.

/

)

)

*&

&*

*&

=

=

0

.

/

)

)

*$

$*

*$

=

=

Symbolami

A

oznaczamy niezależne

od natężenia promieniowania
prawdopodobieństwa na jednostkę
czasu emisji spontanicznej.

S

32

jest

szybkością rozpadu poziomu 3.
Oznaczmy przez

n

1

, n

2

, n

3

ilości

atomów chromu w jednostce
objętości z obsadzonymi poziomami,
odpowiednio, 1, 2, 3.

n

1

+n

2

+n

3

= n

0

= const. (7.6)

Szybkości zmian liczby atomów z

obsadzonymi poziomami 1, 2, 3
opisywane są przez

równania

kinetyczne (rate equations)

.

Lasery i zasada ich działania

Laser rubinowy

!

"

!

#

!"#!"$%&'(
"!)*+,&(

$%

&'

(

!"#

$

%

$

=

=

!

"

-,*./'(0!1,(23+'(0.(,!1"#'(&'-)(

%/+2%04%-(1"$%

$%

&'

(

&

%

"'(

)

%

*

=

=

!

"

*&

)

&*

)

&*

*

+,-./0123,4.5670

+,-./01.867907-:570

+,-./0
23,4.5670

0;.6<8:/0

*$

)

$*

*

$*

)

!

+

&$

,

=<5+/>:-01?207962+121@0.+<5+1<4;-7623,

-

.

/

)

)

*&

&*

*&

=

=

0

.

/

)

)

*$

$*

*$

=

=

dn

2

dt

= W

12

n

1

−

(W

12

+ A

21

)n

2

+ S

32

n

3

,

(7.7)

dn

3

dt

= W

13

n

1

−

(W

13

+ A

31

+ S

32

)n

3

,

(7.8)

dn

1

dt

=

−

!

dn

2

dt

+

dn

3

dt

"

.

(7.9)

W stanie równowagi w laserze

dn

2

dt

=

dn

3

dt

= 0,

(7.10)

Lasery i zasada ich działania

Laser rubinowy

czyli

W

13

n

1

= (W

13

+ A

31

+ S

32

)n

3

,

(7.11)

W

12

n

1

− (W

12

+ A

21

)n

2

=

−S

32

n

3

,

(7.12)

co po podzieleniu stronami daje

W

12

n

1

− (W

12

+ A

21

)n

2

W

13

n

1

=

−

S

32

W

13

+ A

31

+ S

32

,

(7.13)

i dalej

W

12

− (W

12

+ A

21

)

n

2

n

1

W

13

=

−

S

32

W

13

+ A

31

+ S

32

.

(7.14)

Lasery i zasada ich działania

Laser rubinowy

Rozwiązując względem

n

2

/n

1

otrzymujemy

n

2

n

1

=

W

12

+ W

13

S

32

W

13

+A

31

+S

32

W

12

+ A

21

.

(7.15)

Ze względu na to, że przejście 3 → 2 jest bardzo szybkie, współczynnik

tego przejścia jest dużo większy od W

13

i A

31

;

W

13

<< S

32

i A

31

<< S

32

.

Rozwiązanie (7.15) możemy dzięki temu przybliżyć przez

n

2

n

1

≈

W

12

+ W

13

W

12

+ A

21

.

(7.16)

Lasery i zasada ich działania

Laser rubinowy - warunek inwersji obsadzeń

Z inwersją obsadzeń mamy do czynienia, gdy

n

2

/n

1

> 1

, co daje

W

12

+ W

13

W

12

+ A

21

> 1.

(7.17)

Otrzymujemy stąd

warunek inwersji obsadzeń w laserze rubinowym

W

13

> A

21

(7.18)

Inwersja obsadzeń jest warunkiem koniecznym wystąpienia akcji laserowej.

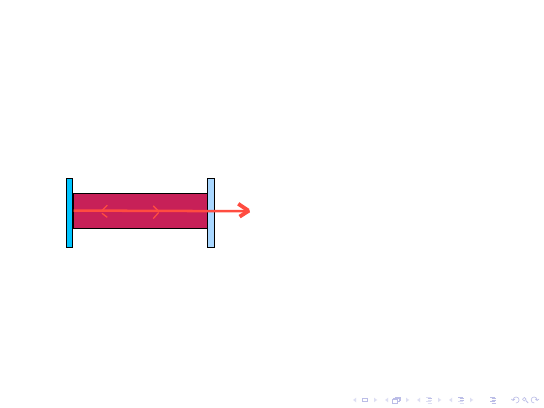
Lasery i zasada ich działania

Schemat lasera

Po osiągnięciu inwersji obsadzeń
dochodzi do emisji spontanicznej
dzięki przejściu

2 → 1

.

!"#!$%&'()*++*

),-%#(-.$/!

),-%#(-.$/!'

01/0#)%023)().4+%

Fotony pochodzące z emisji
spontanicznej trafiając na atomy
chromu z obsadzonym poziomem 2
indukują emisję wymuszoną, która
prowadzi do wzmocnienia światła.
Na końcach

rezonatora optycznego

znajdują się zwierciadła. Wiązka
światła odbijając sie od zwierciadeł
wielikrotnie przechodzi przez
ośrodek czynny, co potęguje efekt
wzmocnienia. Jedno ze zwierciadeł
jest częściowo przepuszczalne, dzięki
czemu wzmocniona wiązka światłą
może opuścić rezonator i wyjść na
zewnątrz.

Lasery i zasada ich działania

Rubin

Źródło: http://pl.wikipedia.org/wiki/Rubin/

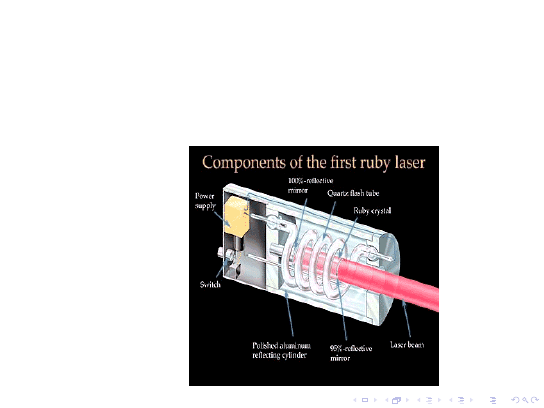
Lasery i zasada ich działania

Budowa lasera rubinowego

Źródło: http://www.llnl.gov/nif/library/aboutlasers/how.html

Lasery i zasada ich działania

Laser helowo - neonowy

Ażeby uzyskać akcję laserową można doprowadzić do inwerssji obsadzeń
dwóch poziomów wzbudzonych, jak to ma miejsce np. w

laserze helowo -

neonowym

.

Uproszczony schemat
poziomów

!"#$%&'

!"#(%&'

)*

!*

)

!

+&

,&

&'

"

!$

$

)"

)$

!"

!! = "#$%&&'
" -%./!#0%12

34526%7489:&

/

W rurze wyładowczej lasera znajduje
się mieszanina helu i neonu w
proporcji ≈ 10:1 pod ciśnieniem ok.

10

2

Pa. W gazie zostaje wywołane

wyładowanie elektryczne, które
wzbudza przede wszystkim atomy
helu z poziomu 1’ do poziomu 2’.
Atomy helu przekazują w
zderzeniach energię atomom neonu
zwiększając obsadzenie poziomu 3.
Akcja laserowa zachodzi w atomach
neonu. Jedną z emitowanych linii
jest pokazana na rysunku linia
czerwona.

Lasery i zasada ich działania

!"#$%#&'#()%*+"%,&#-,(./,0+(1#2+(%(

./,0#0(&#,&+

!"3

#"

#"$

!"

4$%#"(%"#$%#&'#0

4,(%"#$%#&'+

Lasery i zasada ich działania

Laser helowo - neonowy

Źródło: http://pl.wikipedia.org/wiki/Laser