
Wyznaczenie undulacji geoidy
Systemy wysokości w geodezji
2
2
Zastosowanie anomalii grawimetrycznych do wyznaczania odchylenia linii pionu
ds
dN
P
0
W
0
(geoida)
U
0
(elipsoida)
Q
0
ds
dN<0
d
R
ds
Rd
ds
cos
;
)
2
(
;
)
0
(
N
R
N
R
cos
1
1
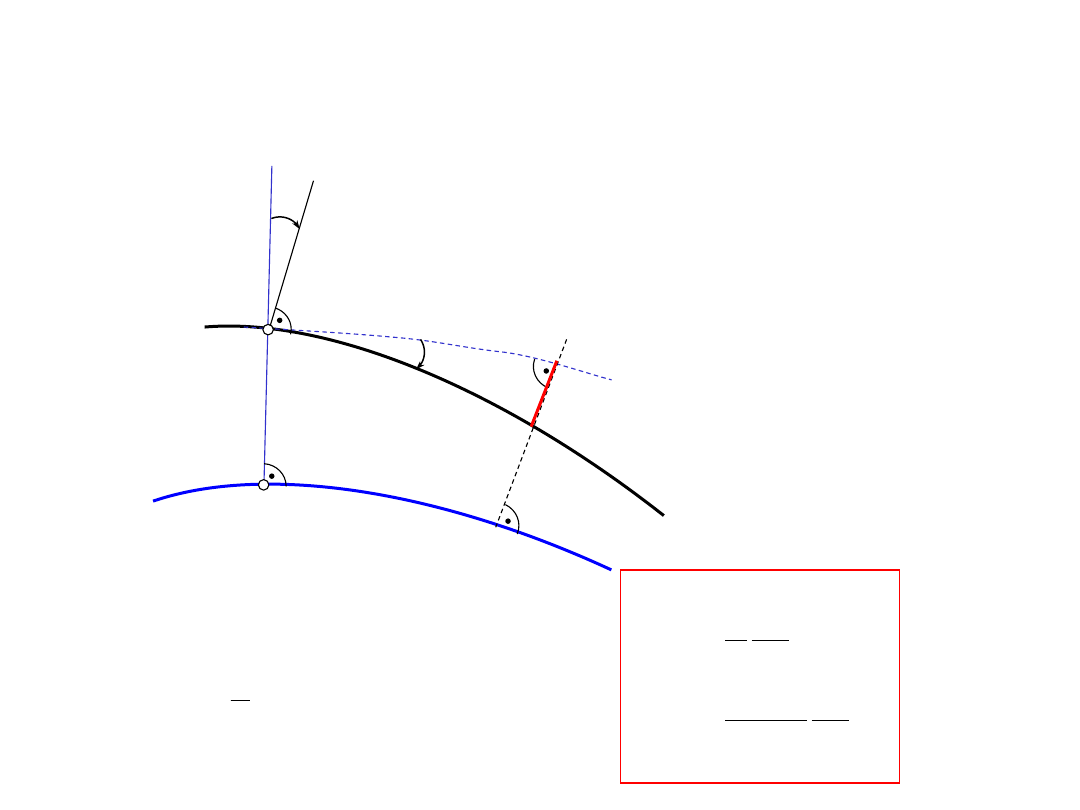
1. Na rys. przedstawiono związek między odstępem geoidy od elipsoidy (N) a
odchyleniem linii pionu (
) w dowolnym kierunku (
). Dla tego przypadku
można zapisać związek między przyrostem odstępu N, katem odchylenia
oraz
odległością s:
N
0
2. Rzut kąta
na płaszczyznę południka (
=0) jest
składową południkową
, a rzut na płaszczyznę do niej
prostopadłą (1-go wertykału) jest składową poprzeczną
(
):
4. Sposób obliczenia odstępu N decyduje
o metodzie wyznaczenia składowych
odchylenia linii pionu. W metodzie
grawimetrycznej do obliczenia odstępu
wykorzystuje się sumowanie wartości
anomalii grawimetrycznych
3. Zakłada się, że składowa
>0, gdy linia pionu wychyla się od normalnej
na północ, składowa
>0, gdy linia pionu wychyla się na wschód.
n
e
l.p.
3
3
N
N
.
1
Uwzględnienie 1, 2 i 3 we wzorach na składowe (poprzedni slajd) wraz z podstawowym równaiem
geodezji fizycznej prowadzi do wzorów Veniga-Meinesza (V-M) na składowe o.l.p. w metodzie
grawimetrycznej.
2. aby wyznaczyć
- wzór cosinusowy dla boku
w trójkącie PBd
.
90
-
90
-
P
-
d
B
d
d
R
d
sin
.
3
2
.
sin
cos
)
(
2
1
0
2
0
d
d
Q
Ag
2
sin
2
sin
ln
2
sin
12
2
sin
1
3
2
sin
32
2
sin
12
2
cos
1
2
cos
2
)
(
2
2
2
2
Q
gdzie Q(
) jest funkcją Venig-Meinesza (pochodna funkcji Stokesa).
1. Na rysunku przedstawiono położenie elementu powierzchni (sfery) d
we
współrzędnych azymutalnych (
,
) oraz w układzie geograficznym (
,
). Pozwala to
przedstawić pochodną odstępu po
,
w funkcji położenia na sferze. Zróżniczkowanie
wzoru Stotesa na N prowadzi do odpowiednich wzorów na składowe (
,
) odchylenia
linii pionu – wzory Veniga-Meinesza.
Wzory V-M wymagają sumowania anomalii po całej powierzchni sfery (Ziemi). Praktyczne jego zastosowanie sprowadza się do
podziału obszaru całkowania na strefy o różnym promieniu. Dzięki temu możliwe jest uproszczenie zagadnienia wyznaczania
odchylenia jeśli sumowanie anomalii ograniczy się do najbliższych obszarów.
- element powierzchni

4
4
Podział obszaru na strefy i zsumowanie wpływu segmentów.
Strefy dalekiej
>10
Strefy bliskiej 0<r<1000km
Strefy centralnej 0<r<5km
r
B
r
Q
Q
c
)
(
)
(
D
Cr
r
B
r
Q
Q
)
(
)
(
1
)
(
Q
]
44
[
5
10
.
0
y
Ag
x
Ag
r
c
(B = 1339.6
; C = 0.000066
; D = 0.315
)
Zsumowanie wyników obliczonych dla kolejnych stref (dalekiej, bliskiej i centralnej) daje całkowitą wartość składowych odchylenia linii pionu.
dla r,x,y [km] i Ag[mGal]

5
Temat 3
Wykorzystanie mapy anomalii grawimetrycznych do
obliczenia składowych odchylenia linii pionu.
......................................

6
Odstęp powierzchni geoidy od elipsoidy wynika z podstawowego równania
geodezji fizycznej uzupełnionego o zależność Brunsa:
]
3
[
)
,
(
4
1
s
ds
S
Ag
R
N
2
2
2
1
2
cos
ln
cos
3
3
cos
5
1
2
)
(cos
1
1
2
)
,
(
n
n
n
n
R
r
R
r
R
r
P
R
n
n
S
]
2
[
]
1
[
1
0
0
0
0
P
Q
T
N
T
n
n
T
Ag
Dla sferycznej powierzchni ekwipotencjalnej i dowolnego stanowiska (wz.Stokesa):
R – promień sfery,
- promień wodzący stanowiska centrum masy bryły (geoidy),
-
odległość sferyczna stanowiska od elementu powierzchni ds.
2
sin
2
R
r
dA
d
R
ds
sin
2
funkcja Stokesa
1 wyraz: tzw. anomalia właściwa spowodowana zakłóceniami
w rozkładzie masy
2 wyraz: wpływ niepokrycia się elipsoidy z geoidą
7
Konieczne założenia:
1.
Anomalie dotyczące geoidy zregularyzowanej, co oznacza pozbawionej
masy ponad poziomem morza,
2.
Geoida i elipsoida powinny mieć ten sam środek ciężkości.
3.
Geoida i elipsoida powinny obejmować całą masę Ziemi.
4.
(2) i (3) oznacza, że objętości obu brył muszą być jednakowe.
5.
Geoida i elipsoida muszą mieć tą samą oś obrotu.
6.
(W
0
=U
0
).
7.
Suma przyrostów odstępów na całej powierzchni powinna być równa zeru.
Uproszczenie dla stanowiska na geoidzie (
=R):
)
sin
ln(sin
2
cos
5
1
sin
6
cos
1
)
(
2
S
2
dA
d
R
ds
sin
2
A – azymut kierunku (stanowisko-ds)
]
3
[
)
(
4
1
s
ds
S
Ag
R
N

8
Odstęp dla ogólnych warunków:
1. W
0
U
0
i spełnione pozostałe warunki (Pizzetti):
s
Pizeetti
ds
S
Ag
R
N
2
1
)
(
4
1
1
_
2. W
0
U
0
, różne środki mas i różne masy geoidy i elipsoidy (T
1
) (Pizzetti):
)
(
2
1
)
(
4
1
0
0
1
2
_
U
W
T
ds
S
Ag
R
N
s
Pizeetti
T – dodatkowy potencjał zakłócający wynikający z niepokrywania się środków mas

9
Odstęp dla funkcji Helmarta i współrzędnych biegunowych (
,A):
0
2
0
)
(
2
dA
d
F
Ag
R
N
2
sin
)
(
2
1
)
sin(
)
2
(
2
1
)
(
S
S
F
Uzupełnienie dla Ziemi elipsoidalnej (R
(a,b)):
2
2
4
sin
3
1
e
N
N
N
e
Dla obszaru Polski i elipsoidy GRS80 drugi składnik osiąga wartość ok. 5 cm
dA
d
R
ds
sin
2

10
Praktyczne wykorzystanie wzoru Stokesa:
n
i
m
j
A
A
ij
i
i
j
j
dA
d
F
Ag
R
N
0
1
1
1
)
(
2
Podział obszaru na i-strefy i j-sektory tworząc segmenty, dla których oblicza
się średnią anomalię.
Wydzielenie składowych odstępu geoidy od elipsoidy:
DTM
Ag
GM
N
N
N
N
N
GM
– pasmo długofalowe, geopotencjalny model geoidy z rozwinięcia potencjału w
szereg funkcji kulistych do składnika n
max
,
N
ag
– pasmo średniofalowe – całkowanie anomalii zgodnie z wzorem Stokesa,
N
DTM
– pasmo krótkofalowe, wpływ rzeźby terenu na wartość odstępu, utożsamiane z
redukcją topograficzną.
DTM
GM
wp
Ag
Ag
Ag
Ag
Anomalie grawimetryczne, które powinny być stosowane do badania figury
Ziemi w myśl teorii Stokesa
)
2
;
0
(
)
;
0
(
A

11
)
sin
cos
(
)
(sin
)
1
(
max
2
0
,
nm
nm
P
nm
n
n
n
m
P
nm
P
GM
m
S
m
C
P
n
G
Ag
)
sin
cos
(
)
(sin
max
2
0
,
nm
nm
P
nm
n
n
n
m
P
nm
P
GM
m
S
m
C
P
R
N
Ag
DTM
= Rg
T-DTM
Uproszczenie dla niewielkiego obszaru -
aproksymacja geoidy płaszczyzną w bliskim otoczeniu (s):
s
R
S
pł
2
)
(
P
w
Ag
G
s
N
wpływ najbliższej strefy na wartość odstępu
2
2
(
2
y
x
G
Ag
N
xy
0
2
0
)
(
2
dA
d
F
Ag
R
N
w funkcji lokalnych współrzędnych (x,y)

12
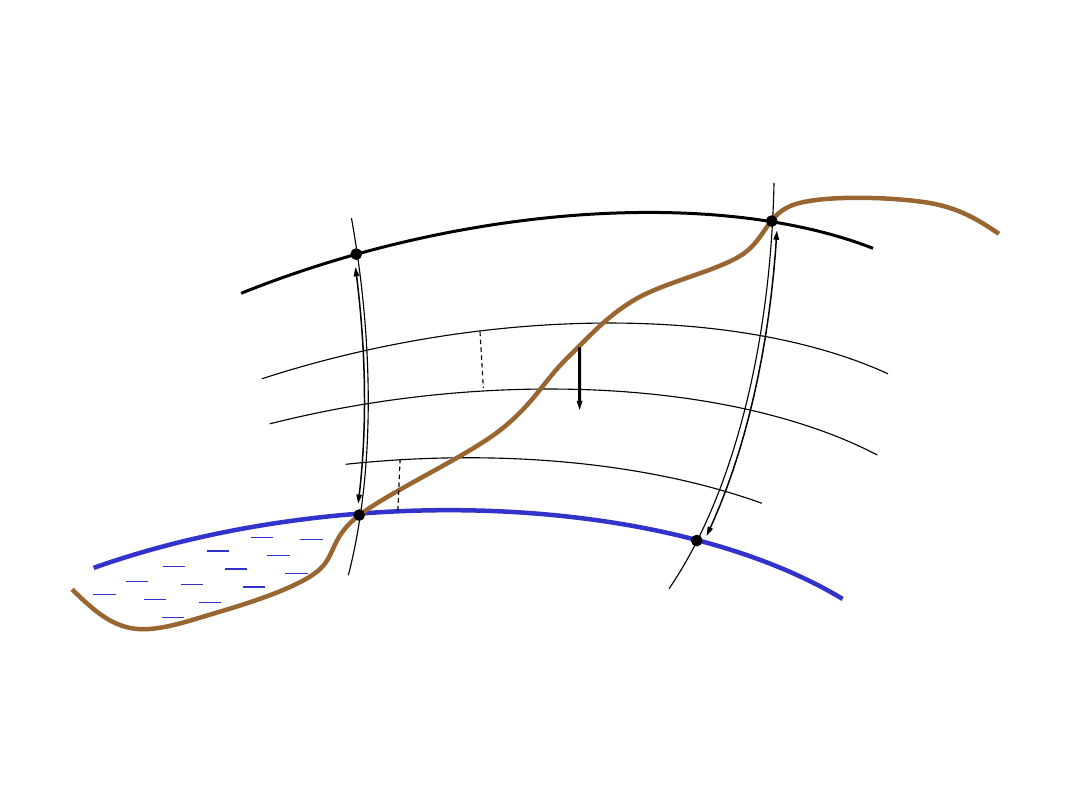
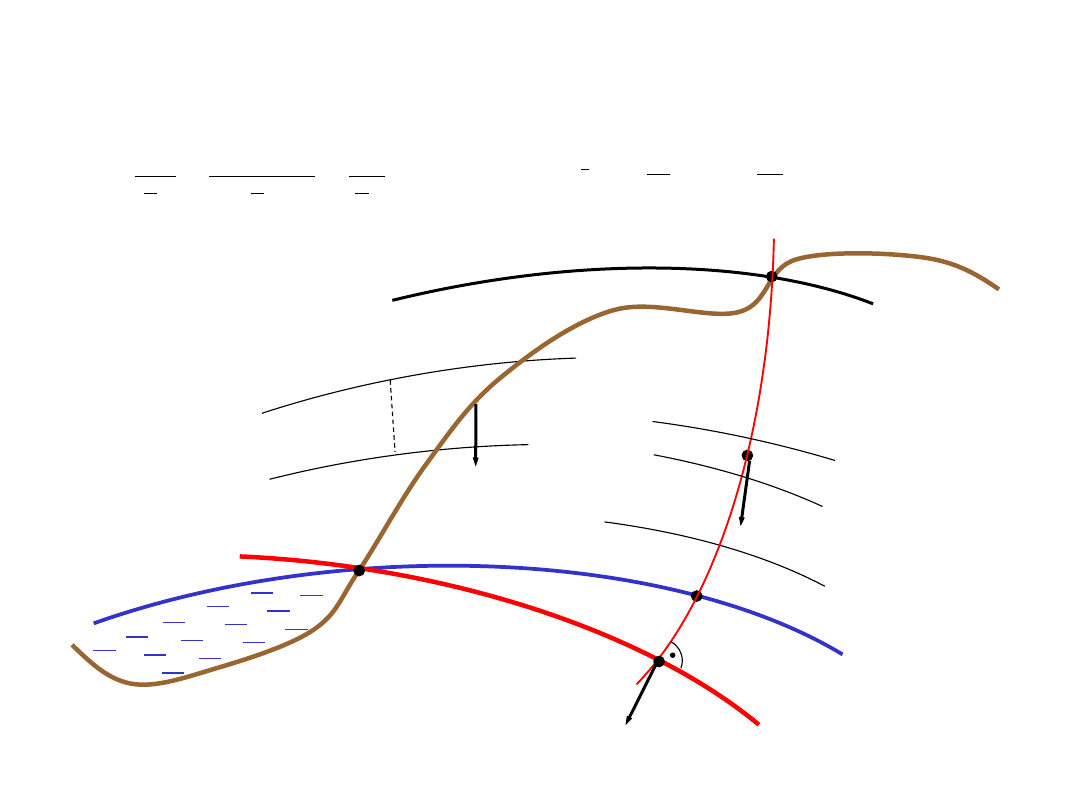
Systemy wysokości w geodezji
Precyzyjne wyznaczenie wysokości wymaga uwzględnienia własności pola siły
ciężkości i wyboru systemu wysokościowego. Wybór systemu powinien
uwzględniać:
1.
Wyznaczane wysokości powinny być niezależne od trasy ciągu niwelacyjnego,
2.
Wysokości punktów nie powinny być zależne od czynników określanych w
sposób przybliżony np. rozkładu masy, topografii, itp.
3.
Poprawki przenoszące pomierzone przewyższenie do określonego systemu
powinny być na tyle małe aby nie było potrzeby ich uwzględnienia ich w
niwelacji niższej dokładności,
4.
W wysokości (przewyższeniu) należy wydzielić część geometryczną (niwelacja) i
geoidalną (poprawka),
5.
Wysokości punktów z tej samej powierzchni ekwipotencjalnej powinny być jak
najbliższe sobie (np. hydrotechnika)
Postulaty dla wyboru systemu wysokościowego
13
W
0
W
A
A
P
O
B
W
i+1
W
i
f.p.Z.
g
i
dh
i
dh
1
dH
A
dH
P
geoida
geop
i
(mareograf)
Niwelacja: OAP lub OBP lub OP(dh)
różne wyniki
)
(
0
0
0
P
P
P
dh
H
H
dh - część geometryczna,
- część geoidalna
wynikająca z krzywizny powierzchni
ekwipotencjalnych, możliwa do wyznaczenia
ścisłego tylko w polu normalnym

14
Wartość geopotencjalna punktu P:
P
P
P
gdh
W
W
C
0
0
Wartość geopotencjalna – to praca w polu ciężkościowym przeciwko sile
ciężkości jaką należy wykonać przenosząc masę 1kg z powierzchni
geoidy do punktu P. Jest uniwersalnym miernikiem wysokości
(MAG,1954). Jednostka 1g.p.u. = 10 m/s
2
m
= 1 kGal·m
Podzielenie wartości geopotencjalnej przez
k
=10m/s
2
daje odstęp powierzchni
ekwipotencjalnych (N=dW/
) – wysokość geopotencjalną
P
k
k
P
g
P
gdh
C
H
0
1
Podział na część geometryczną i geoidalną (g=
k
+(g-
k
)):
P
k
k
P
g
P
dh
g
dh
H
0
0
)
(
1
P
k
k
P
dh
g
G
P
0
)
(
1
.
.
Wartość geopotencjalna i wysokość (cecha) geopotencjalna

15
S
P
R
P
g
R
P
G
P
h
H
.
.
R
P
i
i
k
k
R
P
h
g
G
P
)
(
1
.
.
Dla przewyższenia:
Własności:
1.
Wysokości geopotencjalne są mierzone od geoidy wzdłuż linii pionu,
2.
Punkty położone na tym samym geopie mają jednakową wysokość
geopotencjalną,
Teoretyczna odchyłka ciągu zamkniętego
W ciągu zamkniętym z P do P suma odczytów na łacie wstecz i wprzód nie
będzie różna od zera, zerować się będzie praca dla jednostkowej masy
przenoszonej wzdłuż tego ciągu. Poprawka geopot. wyraża zatem
teoretyczną odchyłkę ciągu zamkniętego. Stąd zamkniecie ciągów w sieci
niwelacji precyzyjnej musi poprzedzić wprowadzenie do wyników
pomiarów poprawki geopotencjalnej wynikającej z zakrzywienia
powierzchni ekwipotencjalnych.
16
Wysokość (cecha) dynamiczna – redukcja wysokości
P
P
d
P
gdh
C
H
0
45
0
45
0
1
Wysokość jest zatem odniesiona do powierzchni elipsoidy poziomowej na
równoleżniku 45
.
Aby osiągnąć dokładność różnicy wysokości rzędu 1mm/1000km wystarczy
zastosować do powyższego wzoru średnie wartości pomierzonego g
miedzy punktami P i R .
R
P
R
P
d
R
P
gdh
C
C
H
45
0
45
0
45
0
1
Redukcja różnicy poziomów do poziomu średniego
=45

17
Część geometryczna i geoidalna a także teoretyczna odchyłka zamknięcia
ciągu niwelacyjnego (poprawka dynamiczna) – podobnie jak w przypadku
wysokości geopotencjalnych.
R
P
R
P
i
i
d
R
P
h
g
h
H
)
(
1
45
0
45
0
R
P
i
R
P
h
g
D
P
)
(
1
.
45
0
45
0
Własności
1.
Wysokości mierzone od geoidy
2.
Punkty położone na tym samym geopie mają jednakową wysokość
dynamiczną,
3.
Wysokości dynamiczne nie mają interpretacji geometrycznej,
4.
P.D. osiągają duże wartości,
5.
Możliwość zastosowania lokalnej wysokości dynamicznej (
L
),
6.
Możliwość zastąpienia (gdh) przez (
dh)

18
Wysokości ortometryczne
P
P
P
P
o
P
gdh
g
g
W
W
H
0
0
1
W
0
W
A
A
P
O
B
W
i+1
W
i
f.p.Z.
g
i
dh
i
dh
1
H
o
P
geoida
geop
i
(mareograf)
g
p
g
Pi
M
Bruns 1878, Helmert 1884,
C
p
– nie zależy od trany obliczenia więc H jest jednoznaczne

19
Problem obliczenia przeciętnej wartości przyspieszenia:
1.
Metoda Helmerta
)
)(
2
(
2
)
(
M
P
M
P
P
M
H
H
G
H
H
h
g
g
g
R
g
h
g
P
2
.
2
Z
M
P
P
Z
M
P
P
P
M
P
R
H
H
g
H
H
g
g
G
H
H
G
2
3
)
(
2
)
(
2
Z
Z
Z
Z
P
R
G
R
GM
g
3
4
.
1
2
Wykorzystanie jednorodnej kulistej Ziemi (R
Z
,
Z
):
Z
M
P
Z
Z
M
P
P
M
R
H
H
R
H
H
g
g
3
2
1
20
Przeciętna wartość przyspieszenia:
P
M
P
Z
M
P
Z
Z
M
P
o
P
P
P
M
M
o
P
M
G
dH
R
H
H
R
H
H
H
g
dH
g
H
g
0
0
3
2
1
1
Z
o
P
P
Z
o
P
Z
Z
o
P
P
P
R
H
g
R
H
R
H
g
G
1
2
3
1
Z
2
3
1
P
P
o
P
gdh
G
H
0
1
Wysokość ortometryczna:
Wydzielenie części geometrycznej i geoidalnej:
)
(
)
(
C
i
P
C
P
i
g
g
G
g
G
g
n
i
i
C
i
P
n
i
i
P
P
C
n
i
i
o
P
h
g
g
G
h
G
G
g
h
H
1
1
1
)
(
1
)
(
.
0
m
np
const
g
C
Po scałkowaniu

21
Różnica wysokości ortometrycznych oraz teoretyczna odchyłka zamknięcia
ciągu niwelacyjnego
R
P
R
P
i
i
R
Z
R
P
Z
P
i
o
R
P
g
h
G
H
R
H
R
h
H
1
2
2
R
P
i
i
R
R
P
P
Z
R
P
g
h
G
H
H
R
O
P
1
1
.
2
2
Metodę Helmerta bazującą na pewnych uproszczeniach: model kuli, brak
uwzględniania topografii można używać dla większości obszarów
(nizinnych) Polski.
h
i
– średnia wysokość odcinka

22
2. Metoda Ramsayera i Niethammera – dla obszarów górskich i wysokogórskich
a) Inny sposób obliczania przyspieszenia przeciętnego na drodze geoida-f.p.Z.
n
i
i
C
i
P
n
i
i
P
P
C
n
i
i
o
P
h
g
g
G
h
G
G
g
h
H
1
1
1
)
(
1
R
P
P
c
P
R
c
R
R
P
c
Hdg
H
g
g
H
g
g
dh
g
g
)
(
)
(
)
(
T
T
B
wp
R
R
Rg
Rg
g
G
2
dla M czyli 1/2H; brak R
T
we wzorach Helmerta
b) Inny sposób sumowania
n
i
i
C
i
h
g
g
1
)
(
R
P
P
C
P
R
C
R
R
P
C
Hdg
H
g
g
H
g
g
dh
g
g
)
(
)
(
)
(
g
c
– dowolna
wartość bliska
przyspieszeniu np..
normalnemu

23
n
i
i
c
i
R
R
P
i
R
R
c
P
R
R
P
n
i
i
R
P
h
g
g
G
h
G
G
g
H
G
G
G
h
H
1
1
)
(
1
R
P
i
i
R
TR
P
TP
R
Z
R
P
Z
P
n
i
i
R
P
g
H
G
H
G
g
H
G
g
H
R
H
R
h
H
1
2
2
1
P.O. - Ramsayer
P.O. - Niethammer
-funkcja gęstości
Aby obliczyć poprawkę wg. Niethammera należy znać wartość przyspieszenia wzdłuż
ciągu niwelacyjnego(g) oraz średnie wartości przyspieszenia wzdłuż linii pionu dla obu
punktow (G
P
,
G
R
), czego pomierzyć się nie da.
24
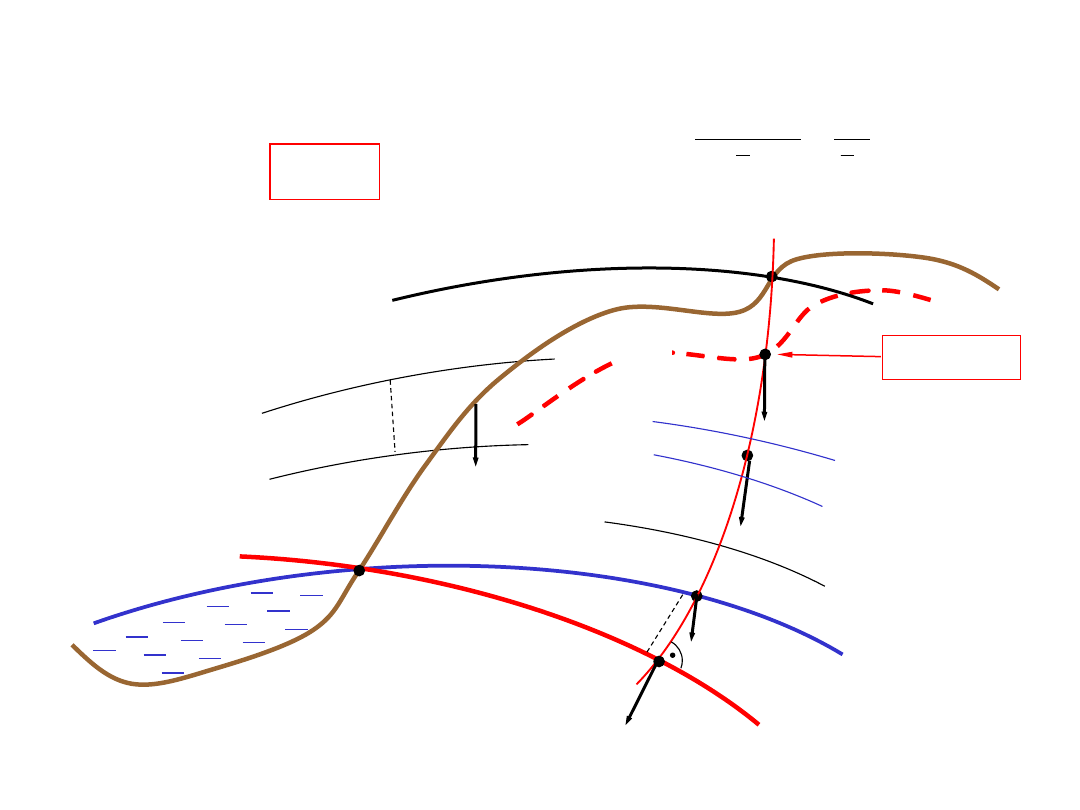
Wysokości normalne Mołodeńskiego
P
P
P
P
P
P
n
P
gdh
W
W
C
H
0
0
1
W
0
W
P
P
O
B
W
2
W
1
f.p.Z.
g
i
dh
i
dH
n
geoida
elipsoida
(mareograf)
U
1
i
U
2
U
0
0
Z
n
R
H
h
2
0
0

25
Wysokości normalne Mołodeńskiego
T
P
U
U
W
W
0
0
W
0
W
P
P
O
B
W
2
W
1
f.p.Z.
g
i
dh
i
dH
n
geoida
elipsoida
(mareograf)
U
1
i
T
T
U
2
U
0
0
U
T
= W
P
N
P
26
Wysokości normalne Mołodeńskiego
T
P
U
U
W
W
0
0
W
0
W
P
P
O
B
W
2
W
1
f.p.Z.
g
i
dh
i
dH
n
geoida
elipsoida
(mareograf)
U
1
i
T
T
U
2
U
0
0
U
T
= W
P
(t)
0P
N
P
P
P
P
T
n
P
gdh
U
U
H
0
0
1
27
dh
g
dh
dh
gdh
dC
)
(
)
(
tożsamość +
na telluroidzie
d
H
dC
d
C
dC
d
C
dC
dH
n
n
1
1
1
2
P
P
P
P
P
P
n
P
gdh
W
W
C
H
0
0
1
dh
g
d
H
dh
dh
dH
n
n
dC
dh
g
dh
dh
gdh
)
(
)
(
Własności telluroidy (t):
1.
Powierzchnia utworzona z punktów dla których U
T
=W
fpZ
2.
Nie jest powierzchnią ekwipotencjalną,
3.
Jest „kopią” f.p.Z.

28
dh
g
d
H
dh
dh
dH
n
n
T
P
g
Ag
g
anomalia mieszana
P
P
P
P
dh
dh
0
0
0
0
)
(
)
(
-w punkcie bieżącym terenu
0
-na geoidzie dla pkt bieżącego
0P
-na geoidzie dla pionu pkt P
0
d
h
d
H
dh
n
0
2
)]
(
)
[(
)
(
)
(
0
0
0
0
0
0
0
0
P
P
P
P
P
P
P
P
P
dh
h
h
h
h
dh
dh
dh
Po wprowadzeniu normalnego gradientu przyspieszenia
29
dh
g
d
h
dh
dH
n
0
1.
nierównoległość p.e. pola normalnego
2.
anomalność pola normalnego na
odcinku dh
.
.N
P
h
H
i
R
P
n
R
P
i
R
P
i
R
P
i
i
P
R
P
h
g
h
N
P
)
(
1
)
(
1
.
.
0
0
h
i
– średnia wysokość odcinka (i)
R
B
P
A
i
R
P
P
i
R
P
H
H
h
g
N
P
0
0
0
0
)
(
.
.
R
B
P
A
R
P
R
P
H
H
D
P
N
P
45
0
45
0
45
0
45
0
.
.
.
.
Przyspieszenie dla średniej
szerokości geodezyjnej
30
P
n
P
P
H
h
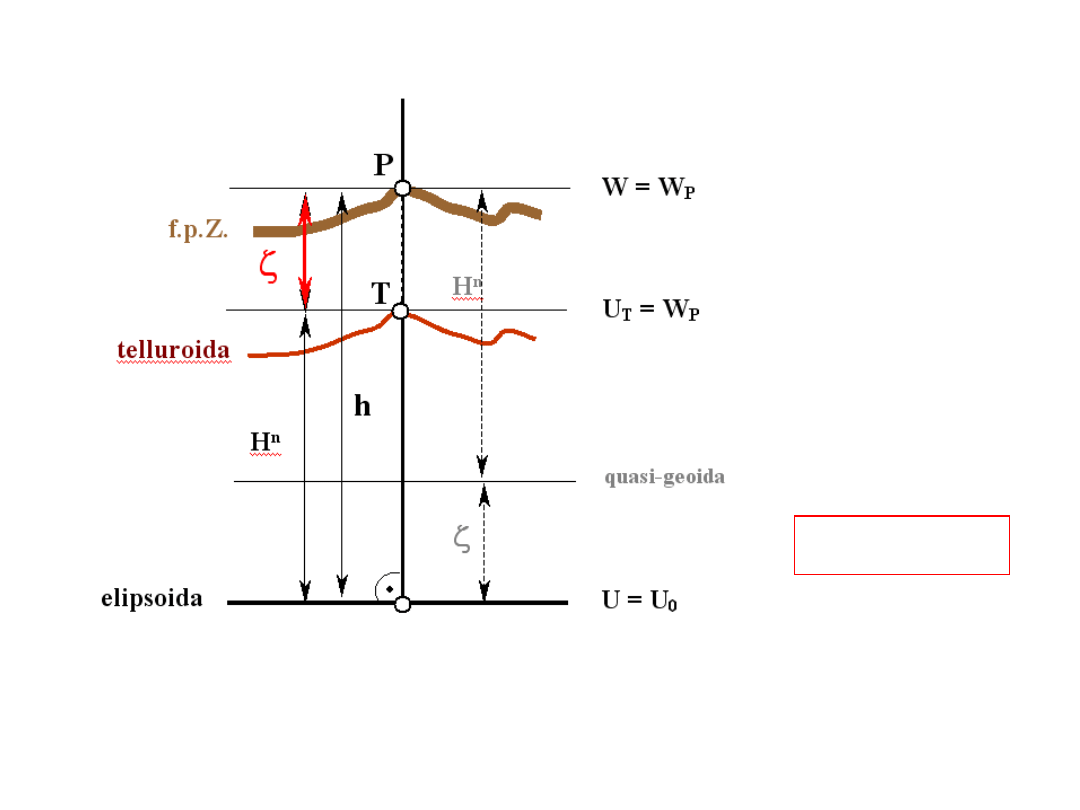
Schemat dla wysokości normalnej i elipsoidalnej
Własności quasi-geoidy:
1.
Nie jest powierzchnią ekwipotencjalną
2.
Utworzona ze spadków wysokości normalnych odmierzonych od f.p.Z.
3.
Anomalia wysokości (
) odpowiada odstępowi (N) geoidy od elipsoidy

31
Zamiana wysokości w różnych systemach wysokościowych
X
P
X
P
enie
przyspiesz
C
H
)
(
X
X
P
P
enie
przyspiesz
H
C
)
(
P
n
P
P
o
P
d
P
P
H
G
H
H
C
45
,
0
P
d
P
P
P
P
d
P
P
P
n
P
o
P
G
H
G
H
G
H
H
45
,
0
45
,
0
Podobnie jest dla wysokości geopotencjalnej

32
AB
niw
AB
n
AB
N
P
h
H
.
.
AB
niw
AB
o
AB
O
P
h
H
.
.
AB
AB
o
AB
n
AB
O
P
N
P
H
H
.
.
.
.
A
A
n
A
h
H
B
B
n
B
h
H
B
A
n
AB
H
A
A
o
A
N
h
H
B
B
o
B
N
h
H
B
A
o
AB
N
N
H
Odstęp quasi-geoidy od geoidy
A
N
B
N
A
A
B
B
B
A
B
A
o
AB
n
AB
N
N
N
N
H
H
)
(
)
(
)
(
)
(
AB
AB
A
N
B
N
O
P
N
P
.
.
.
.
)
(
)
(
B
B
B
A
A
A
A
N
B
N
H
G
H
G
45
0
45
0
)
(
)
(
o
N
H
G

33
Rozwinięcie i uproszczenie:
o
n
B
o
o
N
H
H
h
Rg
H
h
g
g
H
G
)
2
(
2
0
h
G
h
g
;
o
n
B
o
o
o
n
B
o
N
H
H
Rg
H
G
GH
g
H
H
Rg
H
G
g
)
2
(
2
)
2
(
2
0
0
o
o
o
B
o
o
n
B
wp
H
H
G
N
H
Ag
H
H
G
H
Rg
Rg
g
2
2
2
2
)
(
0
o
o
o
B
H
N
H
G
H
Ag
2
)
(
2
)
(
2
o
N
o
o
B
N
H
H
G
H
Ag
2
2
)
(
2
(przyspieszenie przeciętne liczone
w połowie wysokości H)

34
Zasadniczy wpływ na wartość odstępu quasi-geoidy od geoidy zawarty jest w pierwszym składniku
powyższej sumy. Maksymalną jego wartość można oszacować następująco:
dla Ag
B
rzędu 10
2
mGal (podgórskie i górskie obszary Polski) oraz H
o
10
3
m (obszary górskie) oraz
10
6
mGal składnik ten osiągnie wartość rzędu 10 cm. Na obszarach nizinnych wartość ta jednak
będzie zdecydowanie mniejsza często nie przekraczając 1 cm i stąd często pozostałe mniejsze składniki
pomija się.
Ze względu na wartość ułamka i niewielką różnicę między H
o
a H
n
zasadne staje się
zastąpienie wartością H
n
lub przybliżoną H.
Drugi składnik osiągnie istotną wartość jedynie w obszarach górskich. Występująca w nim tzw.
anomalia gradientu (
-G) jak wskazują badania (Grybów) może dochodzić do 0.1 mGal. Zatem przy
wysokościach rzędu 500 m
700 m a nawet 1000 m może osiągnąć wartość rzędu 1 cm
5 cm. Na
obszarach nizinnych wartość ta będzie zdecydowanie mniejsza (dla rejonu Krakowa przy
-G
0.1
mGal i H
300 m będzie to ok. 5 mm).
Ostatni składnik sumy jest dla obszaru Polski zdecydowanie do pominięcia. Dla maksymalnych wartości
0.1 m i H
1000 m osiągnie wartość nie więcej niż 0.02 mm.
3
10
B
Ag
N
Analiza wpływu poszczególnych składników wzoru:

35
Wnioski:
§ Odstęp qusi-geoidy od geoidy na obszarach nizinnych można obliczać
wyłącznie na podstawie anomalii Bouguera:
§ Dla obszarów podgórskich i górskich należałoby do obliczenia
wykorzystać wartości rzeczywistego gradientu p.s.c. a następnie anomalii
gradientu.
B
N
Ag
Wyszukiwarka
Podobne podstrony:
(31 Wyznaczenie odstepu geoidy Nieznany (2)
Wyznaczenie odstępu geod od elip
Wyznaczenie odstępu geod od elip Praktyka 2013
Wyznaczenie odstępu geod od elip Praktyka 2013A
(Temat 2 Wyznaczenie odstępu quasi geoidy od geoidy na punktach sieci geodynamicznej)
Temat2 wyznaczenie odstepu quasi geoidy od geoidy na pkt sieci geodynamicznej
Systemy wysokości w niwelacji precyzyjnej
OII04 Wyznaczanie logarytmicznego dekrementu tlumienia przy pomocy wahadla fizycznego
Wyznaczanie zależności przewodnictwa od temperatury, AGA, Nr ćw.
hkf, ROZWOJ SYSTEMOW WF W XIX W, ROZWÓJ SYSTEMÓW WYCHOWANIA FIZYCZNEGO W XIX WIEKU NA TLE ZMIAN POLI
spraw, LAB 44, Wyznaczenie zależności rezystancji od temperatury dla metalu i półprzewodnika
Badanie zależności temperatury wrzenia wody od ciśnienia, ćwiczenie14+, LABORATORIUM FIZYCZNE
List motywacyjny Referent w Dziale Podatkow od Dzialalnosci Gospodarczej Osob Fizycznych
Wyznaczanie lepkości cieczy metodą stokesa, Wyznaczanie lepkości cieczy metodą Stokesa 1, ?I" P
sciaga od borysa, AWF Wychowanie fizyczne, studiaa, STUDIA, Sciagi metodyka
więcej podobnych podstron