Metody numeryczne dla fizyk ´

ow

Krzysztof Golec–Biernat

(December 4, 2006)

Wersja robocza nie do dystrybucji

Krak ´ow

2005/06

2

Spis tre´sci

1

Liczby

6

1.1

Systemy liczbowe . . . . . . . . . . . . . . . . . . . . . . . . . .

6

1.2

Zapis liczb w komputerze . . . . . . . . . . . . . . . . . . . . . .

8

1.2.1

Liczby całkowite . . . . . . . . . . . . . . . . . . . . . .

8

1.2.2

Liczby rzeczywiste . . . . . . . . . . . . . . . . . . . . .

9

2

Błe¸dy

11

2.1

Dokładno´s´c zapisu . . . . . . . . . . . . . . . . . . . . . . . . .

11

2.2

Bła¸d wzgle¸dny zapisu . . . . . . . . . . . . . . . . . . . . . . . .

12

2.3

´

Zr´odła błe¸d´ow . . . . . . . . . . . . . . . . . . . . . . . . . . . .

13

2.4

Stabilno´s´c numeryczna . . . . . . . . . . . . . . . . . . . . . . .

16

3

Interpolacja

18

3.1

Wielomian interpolacyjny Lagrange’a . . . . . . . . . . . . . . .

18

3.2

Interpolacja Lagrange’a znanej funkcji . . . . . . . . . . . . . . .

20

3.3

Wielomiany Czebyszewa . . . . . . . . . . . . . . . . . . . . . .

21

3.4

Optymalny wyb´or we¸zł´ow interpolacji . . . . . . . . . . . . . . .

23

3.5

Interpolacja przy pomocy funkcji sklejanych . . . . . . . . . . . .

24

3

4

Aproksymacja

25

4.1

Regresja liniowa . . . . . . . . . . . . . . . . . . . . . . . . . . .

25

4.2

Aproksymacja ´sredniokwadratowa . . . . . . . . . . . . . . . . .

26

4.3

Aproksymacja Czebyszewa . . . . . . . . . . . . . . . . . . . . .

28

4.3.1

Aproksymacja Czebyszewa w dowolnym przedziale . . .

30

4.4

Aproksymacja trygonometryczna . . . . . . . . . . . . . . . . . .

31

4.4.1

Wzory dla dowolnego okresu

. . . . . . . . . . . . . . .

32

5

R´o˙zniczkowanie

33

5.1

Metody z aproksymacja¸ . . . . . . . . . . . . . . . . . . . . . . .

33

5.2

Metody z rozwinie¸ciem Taylora

. . . . . . . . . . . . . . . . . .

33

5.3

Wy˙zsze pochodne . . . . . . . . . . . . . . . . . . . . . . . . . .

34

6

Całkowanie

36

6.1

Podstawowe metody

. . . . . . . . . . . . . . . . . . . . . . . .

36

6.1.1

Metoda prostokat´ow . . . . . . . . . . . . . . . . . . . .

36

6.1.2

Metoda trapez´ow . . . . . . . . . . . . . . . . . . . . . .

37

6.1.3

Metoda parabol Simpsona . . . . . . . . . . . . . . . . .

37

6.1.4

Bła¸d przybli˙zenia . . . . . . . . . . . . . . . . . . . . . .

38

6.2

Kwadratura i jej rza¸d . . . . . . . . . . . . . . . . . . . . . . . .

39

6.3

Wielomiany ortogonalne . . . . . . . . . . . . . . . . . . . . . .

41

6.4

Kwadratura Gaussa . . . . . . . . . . . . . . . . . . . . . . . . .

43

6.4.1

Popularne kwadratury Gaussa . . . . . . . . . . . . . . .

44

7

Zera funkcji

48

7.1

Metoda połowienia . . . . . . . . . . . . . . . . . . . . . . . . .

48

7.2

Metoda Newtona . . . . . . . . . . . . . . . . . . . . . . . . . .

50

7.3

Metoda siecznych i metoda falsi . . . . . . . . . . . . . . . . . .

52

4

8

Macierze

54

8.1

Układ r´owna´n liniowych . . . . . . . . . . . . . . . . . . . . . .

54

8.2

Metoda eliminacji Gaussa . . . . . . . . . . . . . . . . . . . . . .

56

8.3

Rozkład LU macierzy . . . . . . . . . . . . . . . . . . . . . . . .

58

8.3.1

Wyznacznik . . . . . . . . . . . . . . . . . . . . . . . . .

61

9

R´ownania r´o˙zniczkowe zwyczajne

62

9.1

Metody Eulera

. . . . . . . . . . . . . . . . . . . . . . . . . . .

64

9.2

Stabilno´s´c numeryczna rozwia¸za´n . . . . . . . . . . . . . . . . .

66

9.3

Metoda Rungego-Kutty . . . . . . . . . . . . . . . . . . . . . . .

67

10 Metody Monte Carlo

70

10.1 Zmienna losowa i jej rozkład . . . . . . . . . . . . . . . . . . . .

70

10.1.1 Rozkład wielu zmiennych losowych . . . . . . . . . . . .

73

10.1.2 Niezale˙zno´s´c zmiennych losowych

. . . . . . . . . . . .

74

10.2 Generowanie liczb losowych . . . . . . . . . . . . . . . . . . . .

75

10.2.1 Metoda transformacji . . . . . . . . . . . . . . . . . . . .

75

10.2.2 Metoda odwracania dystrybunaty . . . . . . . . . . . . .

77

10.2.3 Metoda odrzucania . . . . . . . . . . . . . . . . . . . . .

78

10.3 Centralne twierdzenie graniczne . . . . . . . . . . . . . . . . . .

80

10.4 Całkowanie metoda¸ Monte Carlo . . . . . . . . . . . . . . . . . .

81

10.4.1 Metoda importance sampling . . . . . . . . . . . . . . . .

83

5

Rozdział 1

Liczby

1.1

Systemy liczbowe

Przypomnijmy zapis liczby całkowitej w systemie dziesie

‘

tnym, na przykład

1234

= 4 · 10

0

+ 3 · 10

1

+ 2 · 10

3

+ 1 · 10

4

.

(1.1)

Do zapisu u˙zywamy dziesie

‘

´c cyfr

{0,1,2,...,9}, a 10 to podstawa systemu licz-

bowego. Warto´s´c cyfry zale˙zy od pozycji w liczbie.

W og´olno´sci, dowolna

‘

liczbe

‘

całkowita

‘

mo˙zna zapisa´c w systemie pozycyjnym

o podstawie p przy pomocy cyfr c

i

∈ {0,1,..., p − 1}:

(c

k

. . . c

1

c

0

)

p

= c

0

· p

0

+ c

1

· p + ... + c

k

· p

k

(1.2)

Szczeg´olnie wa˙zna

‘

role

‘

odgrywa system dw´ojkowy o podstawie p

= 2 i cyfrach

c

i

∈ {0,1}. Przykładowo

(11010)

2

= 0 · 2

0

+ 1 · 2

1

+ 0 · 2

2

+ 1 · 2

3

+ 1 · 2

4

= 2 + 8 + 16 = 26

(1.3)

Znaczenie tego systemu dla maszyn cyfrowych wynika z faktu, ˙ze podstawowa

‘

jednostka

‘

informacji jest bit przyjmuja

‘

cy jedna

‘

z dw´och mo˙zliwych warto´sci: 0

lub 1. Maja

‘

c n bit´ow mo˙zemy zapisa´c wszystkie liczby całkowite dodatnie od 0 do

2

n

− 1.

6

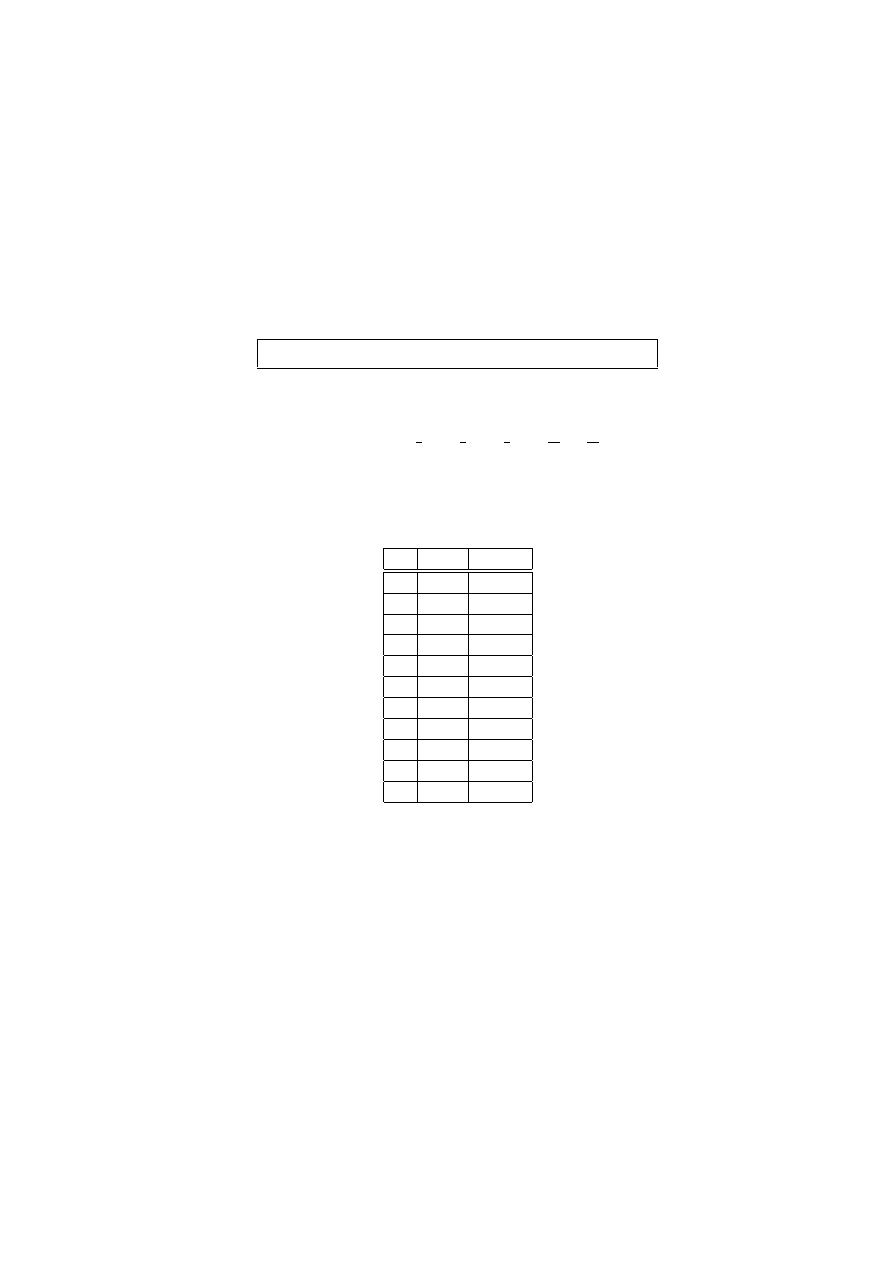
Przykładowo, dysponuja

‘

c 1 bajtem

= 8 bit´ow, najwie

‘

ksza

‘

liczba

‘

jest

(11111111)

2

= 1 · 2

0

+ . . . + 1 · 2

7

= 2

8

− 1 = 255.

(1.4)

Podobnie dowolna

‘

liczbe

‘

ułamkowa

‘

z przedziału

(0, 1) mo˙zemy zapisa´c w sys-

temie dw´ojkowych przy pomocy (na og´oł niesko´nczonego) rozwinie

‘

cia

(0. c

−1

c

−2

. . . c

−n

)

2

= c

−1

· 2

−1

+ c

−2

· 2

−2

+ . . . + c

−n

· 2

−n

(1.5)

Przykładowo

(0.1101)

2

= 1 ·

1
2

+ 1 ·

1
4

+ 0 ·

1
8

+ 1 ·

1

16

=

13
16

.

(1.6)

Wygodnie jest zapamie

‘

ta´c naste

‘

puja

‘

ca tabelke

‘

ułatwiaja

‘

ca

‘

zamiane

‘

liczby z

systemu dw´ojkowego na dziesie

‘

tny.

n

2

n

2

−n

0

1

1

1

2

1/2

2

4

1/4

3

8

1/8

4

16

1/16

5

32

1/32

6

64

1/64

7

128

1/128

8

256

1/256

9

512

1/512

10

1024

1/1024

Konwersje

‘

odwrotna

‘

(10

→ 2) dla liczb całkowitych realizuje sie

‘

zauwa˙zaja

‘

c,

˙ze

x

= c

0

+ c

1

· 2

1

+ . . . + c

k

· 2

k

= c

0

+ 2 · (c

1

+ . . . + c

k

· 2

k

−1

)

(1.7)

Tak wie

‘

c c

0

to reszta z dzielenia x przez 2. Podobnie c

1

jest reszta

‘

z dzielenia

(c

1

+ . . . + c

k

· 2

k

−1

) przez 2, itd.

Przykładowo, konwertuja

‘

c 31 otrzymamy

7

31

2

· 15 + 0

15

2

· 7 + 1

7

2

· 3 + 1

3

2

· 1 + 1

1

2

· 0 + 1

Odczytuja

‘

c reszty od dołu do g´ory otrzymujemy: 31

= (11110)

2

.

Podobnie, dla liczb ułamkowych x

∈ (0,1), po pomno˙zeniu przez dwa otrzy-

mamy

2x

= c

−1

+ (c

−2

· 2

−1

+ . . . + c

−n

· 2

−n+1

)

|

{z

}

r

(1.8)

Jak łatwo zauwa˙zy´c c

−1

jest cze

‘

´scia

‘

całkowita

‘

liczby 2x (r´owna

‘

0 lub 1) natomiast

r

< 1 jest cze

‘

´scia

‘

ułamkowa

‘

. Mno˙zymy wtedy r przez dwa by wydoby´c c

−2

, itd.

Przykładowo, dla 0

.375 otrzymujemy

0

.375

×2 = 0.750

0

.750

×2 = 1.500

0

.500

×2 = 1.000

Odczytuja

‘

c cze

‘

´sci całkowite liczb po prawej stronie r´owno´sci od g´ory do dołu,

dostajemy 0

.375 = (0.011)

2

La

‘

cza

‘

c dwie przedstawione metody konwersji 10

→ 2, mo˙zemy znale´z´c repre-

zentacje

‘

dw´ojkowa

‘

dowolnej liczby rzeczywistej, na przykład:

31

.375 = 31 + 0.375 = (11110.011)

2

(1.9)

1.2

Zapis liczb w komputerze

1.2.1

Liczby całkowite

Zał´o˙zmy, ˙ze mamy do dyspozycji n bit´ow. Pierwszy z nich przeznaczamy na znak
liczby:

(0) dla znaku dodatniego i (1) dla znaku ujemnego. Pozostałe (n−1) bit´ow

słu˙zy do zapisu liczb całkowitych z przedziału:

(−2

n

−1

+ 1 , 2

n

−1

− 1)

(1.10)

8

Przykładowo, dysponuja

‘

c 4 bajtami czyli 32 bitami (zapis w pojedynczej precyzji),

mo˙zemy zapisa´c wszystkie liczby całkowite pomie

‘

dzy:

±(2

31

− 1) = ±2147483647.

Operacje arytmetyczne na tych liczbach moga

‘

prowadzi´c do przekroczenia za-

kresu. Chwilowym wyj´sciem z problemu jest zwie

‘

kszenie liczby bajt´ow przezna-

czonych do zapisu jednej liczby całkowitej, np. do 8 bajt´ow czyli 64 bit´ow (zapis
w podw´ojnej precyzji). Wtedy zakres wynosi:

±(2

63

− 1).

1.2.2

Liczby rzeczywiste

Najbardziej efektywny zapis liczb rzeczywistych wykorzystuje reprezentacje

‘

zmie-

nnoprzecinkowa

‘

. W reprezentacji tej nie ustala sie

‘

maksymalnej liczby cyfr po

przecinku przy zapisie liczby.

Przykładowo, rozwa˙zmy liczbe

‘

x

= 0.00045. Mo˙zemy ja zapisa´c w naste

‘

puja

‘

cy

spos´ob

x

= 45 · 10

−5

= 4.5 · 10

−4

= 0.45 · 10

−3

.

Liczba stoja

‘

ca przez pote

‘

ga

‘

dziesia

‘

tki to mantysa M, natomiast wykładnik pote

‘

gi

to cecha C. Dowolna

‘

liczbe

‘

rzeczywista

‘

mo˙zna wie

‘

c zapisa´c w postaci

x

= M · 10

C

.

(1.11)

Przyjmujemy konwencje

‘

, ˙ze mantysa zawiera sie

‘

w przedziale:

1

≤ |M| < 10.

(1.12)

Dla przykładowej liczby: M

= 4.5 i C = −4.

Przyjmuja

‘

c za podstawe

‘

p

= 2 dostajemy analogiczny zapis w systemie dw´oj-

kowym

x

= M · 2

C

,

(1.13)

gdzie tym razem dla mantysy zachodzi:

1

≤ |M| < 2.

(1.14)

Reprezentacja (1.13) jest podstawa

‘

zapisu liczb rzeczywistych w komputerze.

Dzielimy n bit´ow przeznaczonych do zapisu liczby rzeczywistej na n

M

bit´ow słu-

˙za

‘

cych do zapisu mantysy i n

C

bit´ow dla zapisu cechy, łacznie ze znakiem,

n

= n

M

+ n

C

.

(1.15)

9

Przykładowo, dla podziału 8

= 4 + 4 najmniejsza liczba dodatnia to

(0)100
| {z }

M

(1)111
| {z }

C

= (1 · 2

0

+ 0 · 2

−1

+ 0 · 2

−2

) · 2

−(1·2

0

+1·2

1

+1·2

2

)

= 1 · 2

−7

=

1

128

.

gdzie liczby odczytujemy od lewa do prawa. Pierwsze bity mantysy i cechy (w
nawiasie) sa

‘

zarezerwowane na znak:

(0) = (+) oraz (1) = (−). Zauwa˙zmy, ˙ze

ze wzgle

‘

du na warunek M

≥ 1 nie musieliby´smy rezerwowa´c jednego bitu dla

zapisu mantysy, zachowamy go jednak ze wzgle

‘

du jednak na klarowno´s´c dyskusji.

Najwie

‘

ksza liczba to

(0)111(0)111 = (1 · 2

0

+ 1 · 2

−1

+ 1 · 2

−2

) · 2

(1·2

0

+1·2

1

+1·2

2

)

=

7
4

· 2

7

= 224 .

Liczba 1 jest reprezentowana przez

(0)100(0)000 = 1 · 2

0

= 1 ,

natomiast liczba 0 nie jest reprezentowana i na jej zapis musi by´c przeznaczone
dodatkowe osiem bit´ow.

Podsumowuja

‘

c, przy ustalonym podziale o´smiu bit´ow mo˙zemy zapisa´c 2

8

=

256 liczb rzeczywistych z przedziału

−224, −

1

128

∪

1

128

, 224

.

Oczywistym jest, ˙ze prawie wszystkie liczby rzeczywiste sa

‘

reprezentowane z

pewnym przybli˙zeniem.

10

Rozdział 2

Błe¸dy

2.1

Dokładno´s´c zapisu

Miara

‘

przybli˙zonego zapisu liczby rzeczywistej jest epsilon maszynowy, zdefinio-

wany w naste

‘

puja

‘

cy spos´ob. Rozwa˙zmy najmniejsza liczbe

‘

mo˙zliwa

‘

do zapisu w

komputerze wie

‘

ksza od 1 i oznaczny ja

‘

przez x. Epsilon maszynowy to r´o˙znica:

ε

m

= x − 1.

(2.1)

W naszym przykładzie z podziałem 8

= 4 + 4 bit´ow najmniejsza

‘

zapisana

‘

liczba

‘

wie

‘

ksza

‘

od 1 to

(0)101(0)000 = (1 · 2

0

+ 0 · 2

−1

+ 1 · 2

−2

) · 2

0

= 1 +

1
4

(2.2)

i sta

‘

d

ε

m

= 2

−2

= 0.25. W og´olno´sci, przeznaczaja

‘

c n

M

bit´ow do zapisu mantysy

(z czego jeden bit jest po´swie

‘

cony na znak), mamy

ε

m

=

1

2

(n

M

−2)

(2.3)

Zdefiniujmy tak˙ze precyzje

‘

p zmiennoprzecinkowego systemu liczbowego.

Jest to liczba bit´ow u˙zyta do zapisu mantysy (bez znaku)

p

= n

M

− 1.

(2.4)

Tak wie

‘

c

ε

m

= 1/2

p

−1

. Zwie

‘

kszaja

‘

c liczbe

‘

bit´ow mantysy n

M

zwie

‘

kszamy pre-

cyzje

‘

. Odbywa sie

‘

to kosztem zmniejszenia maksymalnej liczby mo˙zliwej do za-

pisania, gdy˙z przy ustalonej całkowitej liczbie bit´ow n, mniej bit´ow mo˙zna przez-
naczy´c do zapisu cechy: n

C

= n − n

M

. Jest to ilustracja wymienno´sci pomie

‘

dzy

dokładno´scia

‘

a zakresem reprezentowanych liczb zmiennoprzecinkowych w kom-

puterze.

11

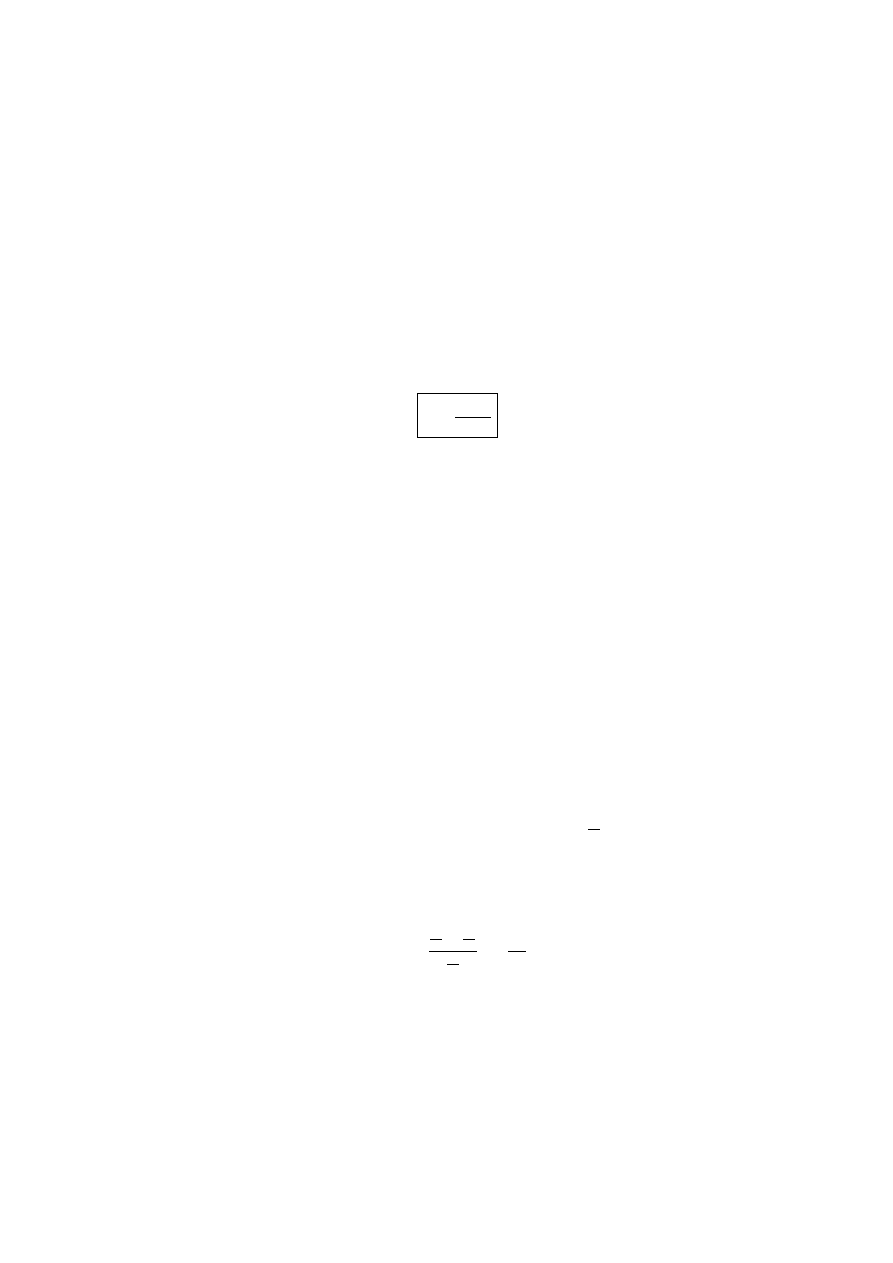
2.2

Bła¸d wzgle¸dny zapisu

Na og´oł dowolona liczba zmiennoprzecinkowa x nie mo˙ze by´c reprezentowana w
komputerze dokładnie. Je˙zeli najbli˙zsza

‘

liczba

‘

zapisana

‘

dokładnie jest x

′

, to bła

‘

d

bezwgle

‘

dny jest zdefiniowany jako r´o˙znica

δ

x

= x

′

− x ,

(2.5)

natomiast bła

‘

d wzgle

‘

dny to stosunek błe

‘

du bezwzgle

‘

dnego do warto´sci dokładnej

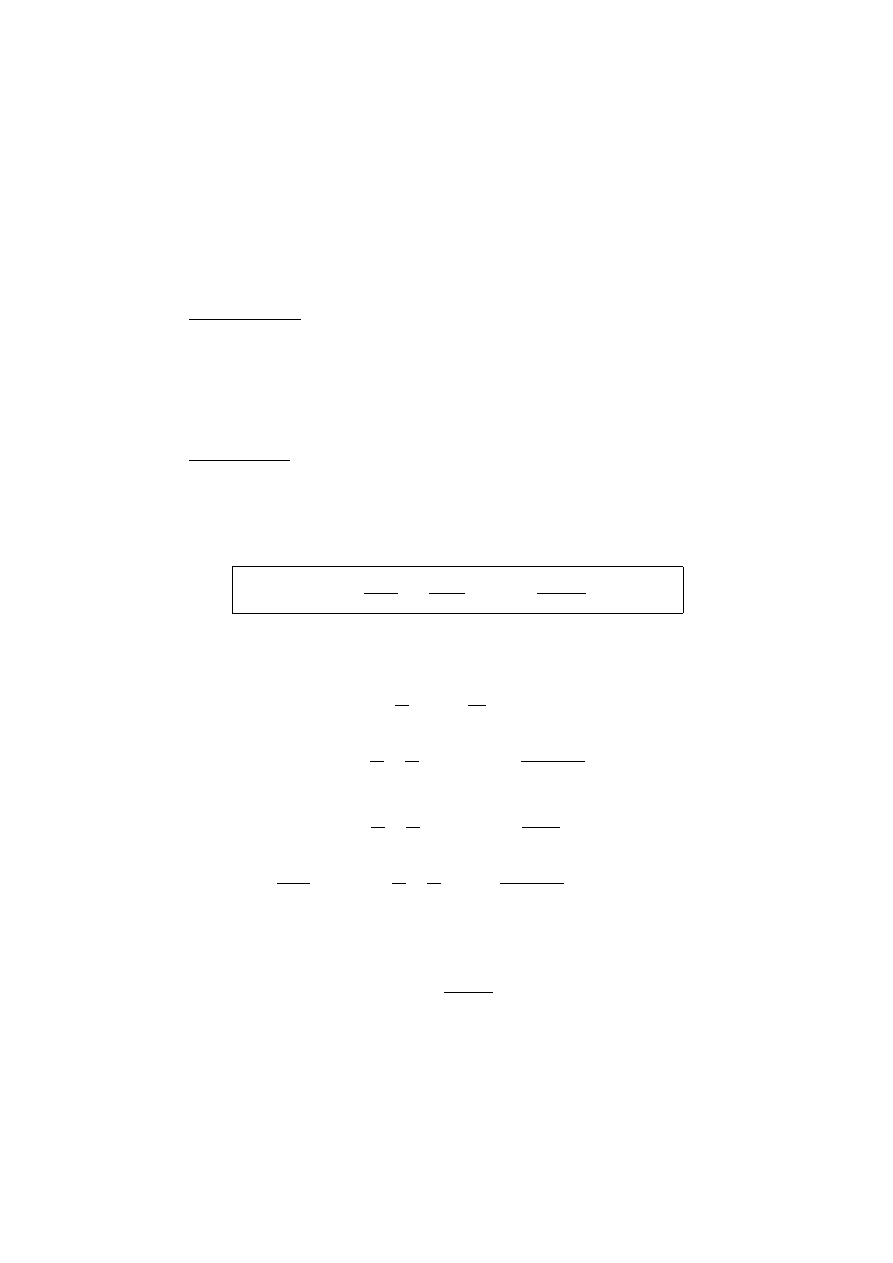
liczby

ε

=

x

′

− x

x

(2.6)

Z ostatniego wzoru wynika

x

′

= x (1 +

ε

).

(2.7)

Mo˙zna pokaz´c, ˙ze moduł błe

‘

du wzgle

‘

dnego jest mniejszy od epsilona maszyno-

wego

|

ε

| ≤

ε

m

.

(2.8)

Przyklad

Chcemy zapisa´c liczbe

‘

0

.48 = 12/25 przy pomocy 8 = 4 + 4 bit´ow. Zapiszmy

ja

‘

w reprezentacji cecha-mantysa, przyjmuja

‘

c podstawe

‘

p

= 2:

0

.48 = 1.92/4 = (1.92) · 2

−2

.

Mantysa zapisana w systemie dw´ojkowym to

1

.92 = (1.111010 . . .)

2

.

(2.9)

W reprezentacji 8

= 4 + 4 pozostawiamy pierwsze trzy bity w rozwinie

‘

ciu dw´oj-

kowym mantysy. Sta

‘

d

0

.48 ≈ (0)111(1)010 = (1 · 2

0

+ 2

−1

+ 2

−2

) · 2

−2

=

7

16

= 0.4375 .

Jest to ilustracja zaokra

‘

glania, polegaja

‘

cego na odrzuceniu cyfr w rozwinie

‘

ciu

dw´ojkowym mantysy wykraczaja

‘

cych poza przyje

‘

ta

‘

liczbe

‘

bit´ow (w tym przy-

padku trzech). Powstały w ten spos´ob bła

‘

d wzgle

‘

dny to

|

ε

| =

7

16

−

12
25

12
25

=

17

192

.

Jak wida´c

|

ε

| < 1/4 =

ε

m

, zgodnie z warunkiem (2.8).

12

2.3

´

Zr´odła błe¸d´ow

Przy obliczeniach komputerowych mamy do czynienia z trzema rodzajami błe

‘

d´ow.

Błe

‘

dy wej´sciowe.

Sa

‘

one spowodowane tym, ˙ze dane wej´sciowe (punkty eksperymentalne, liczby

niewymierne) ju˙z sa

‘

obarczone błe

‘

dem niezale˙znym od komputera lub u˙zytej pro-

cedury numerycznej.

Błe

‘

dy obcie

‘

cia.

Powstaja

‘

na skutek niemo˙zno´sci wykonania w obliczeniach numerycznych nie-

sko´nczonych sumowa´n lub ´scisłych przej´s´c granicznych. Dla przykładu, obliczaja

‘

c

warto´s´c funkcji przy pomocy rozwinie

‘

cia Taylora,

f

(x + h) = f (x) +

f

′

(x)

1!

h

+

f

′′

(x)

2!

h

2

+ . . . +

f

(N)

(x)

N!

h

N

+ R

N

(x, h)

popełniamy bła

‘

d zadany przez odrzucana

‘

reszte

‘

R

N

(x, h). W szczeg´olno´sci, dla

kilku podstawowych funkcji u˙zywamy naste

‘

puja

‘

cych przybli˙zonych rozwinie

‘

´c:

exp x

≈ 1 + x +

x

2

2!

+ . . . +

x

N

N!

sin x

≈ x −

x

3

3!

+

x

5

5!

+ . . . + (−1)

N

x

2N

+1

(2N + 1)!

(2.10)

cos x

≈ 1 −

x

2

2!

+

x

4

4!

+ . . . + (−1)

N

x

2N

(2N)!

ln

1

+ x

1

− x

≈ 2

x

+

x

3

3!

+

x

5

5!

+ . . . +

x

2N

+1

(2N + 1)!

|x| < 1.

Z ostatniego wzoru korzystamy obliczaja

‘

c logarytm dowolnej liczby dodatniej w

=

(1 + x)/(1 − x), odwracaja

‘

c najpierw te

‘

relacje

‘

:

x

=

(w − 1)
(w + 1)

,

13

a naste

‘

pnie podstawiaja

‘

c po prawej stronie.

Błe

‘

dy zaokra

‘

gle´n.

To błe

‘

dy wynikaja

‘

ce z niedokładno´sci zapisu liczb rzeczywistych, propagu-

ja

‘

cych sie

‘

przy wykonywaniu wielokrotnych działa´n arytmetycznych. Je´sli przez

fl

(x) oznaczymy wynik oblicze´n numerycznych r´o˙znia

‘

cy sie

‘

od dokładnej warto´sci

x na skutek błe

‘

d´ow zaokra

‘

gle´n, to zgodnie z (2.6) dla pojedynczej liczby mamy:

fl

(x) = x (1 +

ε

) .

(2.11)

W przypadku wykonywania działa´n arytmetycznych obowia

‘

zuje:

Lemat Wilkinsona

Błe

‘

dy zaokra

‘

gle´n powstaja

‘

ce przy wykonywaniu działa´n zmiennoprzecinko-

wych sa

‘

r´ownowa˙zne zaste

‘

pczemu zaburzaniu liczb, na kt´orych wykonujemy dzia-

łania. W przypadku pojedynczych działa´n zachodzi

fl

(x

1

± x

2

) = x

1

(1 +

ε

1

) ± x

2

(1 +

ε

2

)

fl

(x

1

· x

2

) = x

1

(1 +

ε

3

) · x

2

= x

1

· x

2

(1 +

ε

3

)

(2.12)

fl

(x

1

/x

2

) = x

1

(1 +

ε

4

)/x

2

= x

1

/(x

2

(1 +

ε

5

)) ,

gdzie mo˙zna tak dobra´c zaburzenia, ˙ze wszystkie liczby

|

ε

i

| <

ε

m

.

(2.13)

Przyklad

Zilustrujmy lemat Wilkinsona dodaja

‘

c do siebie dwie liczby w reprezentacji

8

= 4 + 4 bit´ow:

0

.48 + 0.24 =

12
25

+

12
50

.

Na podstawie przykładu z poprzedniego rozdziału:

0

.48 = 1.92 · 2

−2

≈ (0)111(1)010 = (1 · 2

0

+ 2

−1

+ 2

−2

) · 2

−2

=

7

16

0

.24 = 1.92 · 2

−3

≈ (0)111(1)110 = (1 · 2

0

+ 2

−1

+ 2

−2

) · 2

−3

=

7

32

.

Po dodaniu

fl

(0.48 + 0.24) =

7

16

+

7

32

=

21
32

= 1.625 · 2

−1

≈ (0)110(1)100 =

3
4

14

gdy˙z 1

.625 = (1.101)

2

. Ten sam wynik mo˙zna otrzyma´c zaburzaja

‘

c dodawane do

siebie liczby

12
25

(1 +

ε

1

) +

12
50

(1 +

ε

2

) =

3
4

,

ska

‘

d wynika relacja

2

ε

1

+

ε

2

=

1
8

.

Wyb´or liczb

ε

i

nie jest jednoznaczny, np.

ε

1

=

ε

2

= 1/24. Mo˙zna wie

‘

c tak dobra´c

te parametry, ˙ze oba

|

ε

i

| ≤

ε

m

= 1/4, zgodnie z lematem Wilkinsona.

Obliczmy bła

‘

d wzgle

‘

dny r´o˙znicy dw´och liczb. Zgodnie z lematem Wilkinsona

|

ε

| =

fl

(x

1

− x

2

) − (x

1

− x

2

)

x

1

− x

2

=

x

1

·

ε

1

− x

2

·

ε

2

x

1

− x

2

.

(2.14)

Bła

‘

d wzgle

‘

dny mo˙ze by´c dowolnie du˙zy w sytuacji gdy odejmowane liczby niewiele

sie

‘

od siebie r´o˙znia

‘

. Na przkład dla x

1

= x

2

(1 +

δ

) otrzymujemy

|

ε

| ≃

|

ε

1

−

ε

2

|

|

δ

|

→

∞

dla

δ

→ 0.

(2.15)

Nale˙zy wie

‘

c unika´c odejmowania mało r´o˙znia

‘

cych sie

‘

od siebie liczb.

Nieograniczony wzrost (2.15) nie jest sprzeczny z warunkiem (2.13) w lemacie

Wilkinsona, gdy˙z epsilony w tym lemacie to zaburzenia indywidualnych liczb, a
nie bła

‘

d wzgle

‘

dny (2.14) wyniku działa´n arytmetycznych.

Przyklad

Obliczaja

‘

c jeden z pierwiastk´ow r´ownania kwadratowego dla b

2

≫ 4ac,

x

=

−b +

√

b

2

− 4ac

2a

,

(2.16)

nale˙zy wykorzysta´c r´ownowa˙zna

‘

posta´c

x

=

−b +

√

b

2

− 4ac

2a

·

(−b −

√

b

2

− 4ac)

(−b −

√

b

2

− 4ac)

=

−2c

b

+

√

b

2

− 4ac

.

(2.17)

Dodajemy wtedy dwie wielko´sci tego samego rze

‘

du w mianowniku, zamiast odej-

mowa´c dwie bliskie liczby w liczniku.

15

2.4

Stabilno´s´c numeryczna

Zagadnienie to dotyczy wpływu błe

‘

d´ow zaokra

‘

gle´n lub błe

‘

d´ow obcie

‘

´c na sta-

bilno´s´c algorytm´ow numerycznych. Wynikaja

‘

ce sta

‘

d niebezpiecze´nstwa przed-

stawimy analizuja

‘

c przykład zaczerpnie

‘

ty z Numerical Recipes [2].

Rozwa˙zmy liczbe

‘

φ

=

√

5

− 1

2

≈ 0.618033989.

(2.18)

Chcemy obliczy´c kolejne pote

‘

gi

φ

n

. Poniewa˙z

φ

2

= 1−

φ

, wydaje sie

‘

, ˙ze najprostsza

‘

metoda

‘

jest skorzystanie z relacji rekurencyjnej

φ

n

+2

=

φ

n

−

φ

n

+1

.

(2.19)

Okazuje sie

‘

, ˙ze numeryczna realizacja tej relacji prowadzi do szybko rosna

‘

cych

kolejnych warto´sci

φ

n

, co jest sprzeczne z warunkiem

lim

n

→

∞

φ

n

= 0 .

(2.20)

Jest to spowodowane nieuniknionym błedem zaokra

‘

glenia niewymiernej liczby

(2.18). Aby to zrozumie´c, rozwa˙zmy og´olna

‘

relacje

‘

rekurencyjna

‘

F

n

+2

= F

n

− F

n

+1

(2.21)

z warunkami F

0

= 1 oraz F

1

=

φ

. Rozwia

‘

˙zemy te

‘

relacje

‘

posługuja

‘

c sie

‘

funkcja

‘

tworza

‘

ca

‘

F

(z) =

∞

∑

n

=0

F

n

z

n

+1

.

(2.22)

Otrzymujemy

F

(z) = z +

φ

z

2

+

∞

∑

n

=2

F

n

z

n

+1

= z +

φ

z

2

+

∞

∑

n

=0

F

n

+2

z

n

+3

(2.23)

= z +

φ

z

2

+

∞

∑

n

=0

(F

n

− F

n

+1

) z

n

+3

= z +

φ

z

2

+ z

2

F

(z) − z

∞

∑

n

=0

F

n

+1

z

n

+2

= z +

φ

z

2

+ z

2

F

(z) − z

∞

∑

n

=1

F

n

z

n

+1

= z +

φ

z

2

+ z

2

F

(z) − z(F(z) − z)

(2.24)

16

Sta

‘

d znajdujemy

F

(z) =

(1 + z (1 +

φ

)) z

1

+ z − z

2

.

(2.25)

Wyra˙zenie to mo˙zemy zapisa´c w naste

‘

puja

‘

cy spos´ob

F

(z) =

1

+ z (1 +

φ

)

(a − b)

1

1

− az

−

1

1

− bz

,

(2.26)

gdzie a

+ b = −1 oraz ab = −1, co prowadzi do rozwia

‘

zania

a

=

√

5

− 1

2

b

= −

√

5

+ 1

2

.

(2.27)

Tak wie

‘

c

F

(z) =

1

+ z (1 +

φ

)

√

5

∞

∑

n

=0

(a

n

− b

n

) z

n

=

1

√

5

(

∞

∑

n

=1

(a

n

− b

n

) z

n

+ (1 +

φ

)

∞

∑

n

=0

(a

n

− b

n

) z

n

+1

)

=

1

√

5

(

∞

∑

n

=0

(a

n

+1

− b

n

+1

) z

n

+1

+ (1 +

φ

)

∞

∑

n

=0

(a

n

− b

n

) z

n

+1

)

=

1

√

5

∞

∑

n

=0

(a

n

+1

− b

n

+1

) + (1 +

φ

)(a

n

− b

n

)

z

n

+1

=

∞

∑

n

=0

F

n

z

n

+1

.

Sta

‘

d rozwia

‘

zanie rekurencji (2.21) z zadanymi warunkami pocza

‘

tkowym

F

n

=

1

√

5

{a

n

(1 + a +

φ

) − b

n

(1 + b +

φ

)}

(2.28)

Je˙zeli

φ

= a to po podstawieniu do (2.28) otrzymujemy zgodnie z oczekiwa-

niami:

F

n

= a

n

.

(2.29)

Jednak w obliczeniach numerycznych liczba niewymierna

φ

jest zawsze zadana z

przybli˙zeniem, tak wie

‘

c

φ

= a +

ε

(2.30)

i po podstawieniu do (2.28), otrzymujemy

F

n

= a

n

1

+

ε

√

5

− b

n

ε

√

5

.

(2.31)

Poniewa˙z a

< 1 oraz |b| > 1, drugie wyra˙zenie dominuje dla du˙zych warto´sci n,

prowadza

‘

c do niestabilnej rekurencji spowodowanej błe

‘

dem zaokra

‘

glenia liczby

φ

.

17

Rozdział 3

Interpolacja

3.1

Wielomian interpolacyjny Lagrange’a

Poszukujemy og´olnej zale˙zno´sci funkcyjnej w sytuacji gdy znamy te

‘

zale˙zno´s´c w

(n + 1) punktach:

x

0

x

1

... x

n

y

0

y

1

... y

n

.

(3.1)

Punkty x

i

nazywamy we

‘

złami interpolacji, przy czym x

i

< x

j

dla i

< j. Problem ten

ma jednoznaczne rozwia

‘

zanie je´sli poszukiwana

‘

funkcja

‘

jest wielomian stopnia n

W

n

(x) = a

0

+ a

1

x

+ ... + a

n

x

n

.

(3.2)

Wsp´ołczynniki wielomianu a

i

musza

‘

by´c tak dobrane by wielomian W

n

przechodził

przez ka˙zdy punkt

(x

i

, y

i

):

y

i

= W

n

(x

i

)

i

= 0, 1, . . ., n .

(3.3)

Warunek ten prowadzi do układu liniowego

(n + 1) r´owna´n na (n + 1) niewia-

domych wsp´ołczynnik´ow wielomianu a

i

:

a

0

+ a

1

x

0

+ ... + a

n

x

n
0

= y

0

a

0

+ a

1

x

1

+ ... + a

n

x

n
1

= y

1

...

a

0

+ a

1

x

n

+ ... + a

n

x

n
n

= y

n

,

(3.4)

18

lub zapisuja

‘

c w postaci macierzowej











1

x

0

x

2

0

. . . x

n
0

1

x

1

x

2

1

. . . x

n
1

..

.

..

.

..

.

..

.

1

x

n

x

2

n

. . . x

n

n





















a

0

a

1

..

.

a

n











=











y

0

y

1

..

.

y

n











.

(3.5)

Rozwia

‘

znie powy˙zszego układu r´owna´n istnieje i jest ono jednoznaczne gdy˙z wyz-

nacznik macierzy gł´ownej, be

‘

da

‘

cy wyznacznikiem Vandermonde’a, jest r´o˙zny od

zera

det

=

∏

(i, j) i> j

(x

i

− x

j

) 6= 0.

(3.6)

Istnieje wie

‘

c dokładnie jeden wielomian interpoluja

‘

cy (3.2) przechodza

‘

cy przez

punkty (3.1). Wielomian ten nazywamy wielomianem Lagrange’a.

Aby znale´z´c jawna

‘

posta´c wielomianu Lagrange’a nale˙zy rozwia

‘

za´c układ r´ow-

na´n (3.5). Dzie

‘

ki warunkowi jednoznaczno´sci alternatywna

‘

metoda

‘

jest poszuki-

wanie wielomianu w postaci

W

n

(x) = y

0

L

0

(x) + y

1

L

1

(x) + ... + y

n

L

n

(x)

(3.7)

gdzie L

i

(x) sa

‘

wielomianami stopnia n, dla kt´orych zachodzi

L

i

(x

j

) =

δ

i j

.

(3.8)

Spełniony jest wtedy warunek (3.3) nało˙zony na wielomian Lagrange’a:

W

n

(x

j

) =

n

∑

i

=0

y

i

L

i

(x

j

) =

n

∑

i

=0

y

i

δ

i j

= y

j

.

(3.9)

Zgodnie z warunkiem (3.8) wielomian L

i

(x) zeruje sie

‘

we wszystkich we

‘

złach

z wyja

‘

tkiem x

= x

i

. Tak wie

‘

c jest on proporcjonalny do iloczynu wszystkich jed-

nomian´ow

(x − x

j

) z wyła

‘

czeniem czynnika

(x − x

i

):

L

i

(x) = a (x − x

0

) ... (x − x

i

−1

) (x − x

i

+1

) ... (x − x

n

) .

(3.10)

Wsp´ołczynnik a wyznaczamy z warunku L

i

(x

i

) = 1, co prowadzi do wzoru

L

i

(x) =

(x − x

0

) ... (x − x

i

−1

) (x − x

i

+1

) ... (x − x

n

)

(x

i

− x

0

) ... (x

i

− x

i

−1

) (x

i

− x

i

+1

) ... (x

i

− x

n

)

.

(3.11)

19

Przyklad

Rozwa˙zmy interpolacje

‘

zale˙zno´sci funkcyjnej okre´slonej w trzech we

‘

złach

x

0

, x

1

, x

2

. Wielomian Lagrange’a przyjmuje posta´c

W

2

(x) = y

0

(x − x

1

)(x − x

2

)

(x

0

− x

1

)(x

0

− x

2

)

+ y

1

(x − x

0

)(x − x

2

)

(x

1

− x

0

)(x

1

− x

2

)

+ y

2

(x − x

0

)(x − x

1

)

(x

2

− x

0

)(x

2

− x

1

)

Podsumowuja

‘

c, interpolacja Lagrange’a pozwala jednoznacznie rozwia

‘

za´c pro-

blem znalezienia funkcji, przechodza

‘

cej przez

(n + 1) zadanych punkt´ow. Ta

‘

funkcja

‘

jest wielomian Lagrange’a stopnia n. Poniewa˙z prawdziwa zale˙zno´s´c fun-

kcyjna nie jest znana, nie mo˙zna okre´sli´c błe

‘

du tej metody.

3.2

Interpolacja Lagrange’a znanej funkcji

Cze

‘

sto w zastosowaniach numerycznych mamy do czynienia z problemem przy-

bli˙zenia znanej funkcji y

= f (x) w przedziale [a, b] przy pomocy wyra˙zenia wyko-

rzystuja

‘

cego znajomo´s´c tej funkcji w sko´nczonej liczbie punkt´ow z tego przedziału.

Wybierzmy w tym celu

(n + 1) we

‘

zł´ow i znajd´zmy odpowiadaja

‘

ce im warto´sci

funkcji

x

0

,

x

1

...

x

n

f

(x

0

)

f

(x

1

)

...

f

(x

n

) .

(3.12)

Przybli˙zmy naste

‘

pnie znana

‘

funkcje

‘

przy pomocy wielomianu interpolacyjnego

(3.7):

W

n

(x) =

n

∑

i

=0

f

(x

i

) L

i

(x) .

(3.13)

Zakładaja

‘

c, ˙ze istnieje

(n + 1) pochodna f mo˙zna pokaza´c (dow´od w podre

‘

czniku

[1]), ˙ze

f

(x) −W

n

(x) =

f

(n+1)

(

ξ

)

(n + 1)!

ω

n

+1

(x)

(3.14)

gdzie

ξ

∈ [a,b], natomiast

ω

n

+1

to wielomian:

ω

n

+1

(x) = (x − x

0

)(x − x

1

) . . . (x − x

n

) .

(3.15)

20

Ze wzoru tego wynika, ˙ze maksymalny bła

‘

d interpolacji Lagrange’a jest ograni-

czony przez

| f (x) −W

n

(x)| ≤

M

n

+1

(n + 1)!

|

ω

n

+1

(x)|

(3.16)

gdzie M

n

+1

jest kresem g´ornym:

M

n

+1

= sup

x

∈[a,b]

| f

(n+1)

(x)|.

(3.17)

Zauwa˙zmy, ˙ze dla wielomian´ow stopnia

≤ n pochodna f

(n+1)

znika. Sta

‘

d M

n

+1

= 0

i bła

‘

d interpolacji Lagrange’a wynosi zero. Tak wie

‘

c prawdziwe jest:

Twierdzenie
Interpolacja Lagrange’a z

(n + 1) we

‘

złami jest dokładna dla ka˙zdego wielomianu

stopnia

≤ n.

3.3

Wielomiany Czebyszewa

Powstaje pytanie, jak dobra´c we

‘

zły interpolacji by prawa strona wyra˙zenia (3.16)

była jak najmniejsza. Nale˙zy w tym celu znale´z´c najmniejsze oszacowanie maksy-
malnej warto´sci

|

ω

n

+1

(x)| w przedziale [a,b]. Odpowied´z na to pytanie otrzymuje

sie

‘

rozwa˙zaja

‘

c wielomiany Czebyszewa.

Wielomian Czebyszewa stopnia n jest zdefiniowany przy pomocy wzoru

T

n

(x) = cos(n arccos x)

n

= 0, 1, 2, . . .

(3.18)

gdzie x

∈ [−1,1]. Z definicji tej wynika relacja

|T

n

(x)| ≤ 1.

(3.19)

Dwa pierwsze wielomiany Czebyszewa to

T

0

(x) = 1

T

1

(x) = x .

(3.20)

Kolejne wielomiany mo˙zna wyliczy´c korzystaja

‘

c z relacji rekurencyjnej.

T

n

+1

(x) = 2x T

n

(x) − T

n

−1

(x) ,

n

≥ 1.

(3.21)

Dow´od:

21

Podstawiaja

‘

c

φ

= arccos x, rozwa˙zmy

T

n

+1

(x) = cos(n + 1)

φ

= cos(n

φ

) cos

φ

− sin(n

φ

) sin

φ

= x T

n

(x) − sin(n

φ

) sin

φ

.

Wykorzystuja

‘

c naste

‘

pnie to˙zsamo´s´c trygonometryczna

‘

sin

α

sin

β

=

1
2

{cos(

α

−

β

) − cos(

α

+

β

)}

otrzymamy

T

n

+1

= x T

n

−

1
2

{cos((n − 1)

φ

) − cos((n + 1)

φ

)} = x T

n

−

1
2

(T

n

−1

− T

n

+1

) .

Sta

‘

d wynika ju˙z relacja (3.21).

Tak wie

‘

c naste

‘

pne wielomiany Czebyszewa to

T

2

(x) = 2x

2

− 1

T

3

(x) = 4x

3

− 3x

T

4

(x) = 8x

4

− 8x

2

+ 1 .

(3.21)

Wida´c sta

‘

d, ˙ze wielomian T

n

jest funkcja

‘

o okre´slonej parzysto´sci, dodatniej dla

parzystych n i ujemna

‘

dla nieparzystych warto´sci stopnia wielomianu. Ponadto,

rozwa˙zaja

‘

c wsp´ołczynnik przy najwy˙zszej pote

‘

dze zauwa˙zamy, ˙ze

T

n

(x) = 2

n

−1

x

n

+ ··· .

(3.22)

Ka˙zdy wielomian Czebyszewa stopnia n ma dokładnie n pierwiastk´ow rzeczy-

wistch. Aby je znale´z´c rozwia

‘

zujemy r´ownanie

T

n

(x) = cos(n arccos x) = 0 ,

(3.23)

otrzymuja

‘

c naste

‘

puja

‘

ce pierwiastki

x

k

= cos

π

(k + 1/2)

n

,

k

= 0, 1, . . . , n − 1

(3.24)

Dowolny wielomian Czebyszewa mo˙zna wie

‘

c zapisa´c w postaci

T

n

(x) = 2

n

−1

(x − x

0

)(x − x

1

) . . . (x − x

n

−1

)

= 2

n

−1

ω

n

(x) ,

(3.25)

gdzie wsp´ołczynnik 2

n

−1

wynika z uwagi (3.22).

22

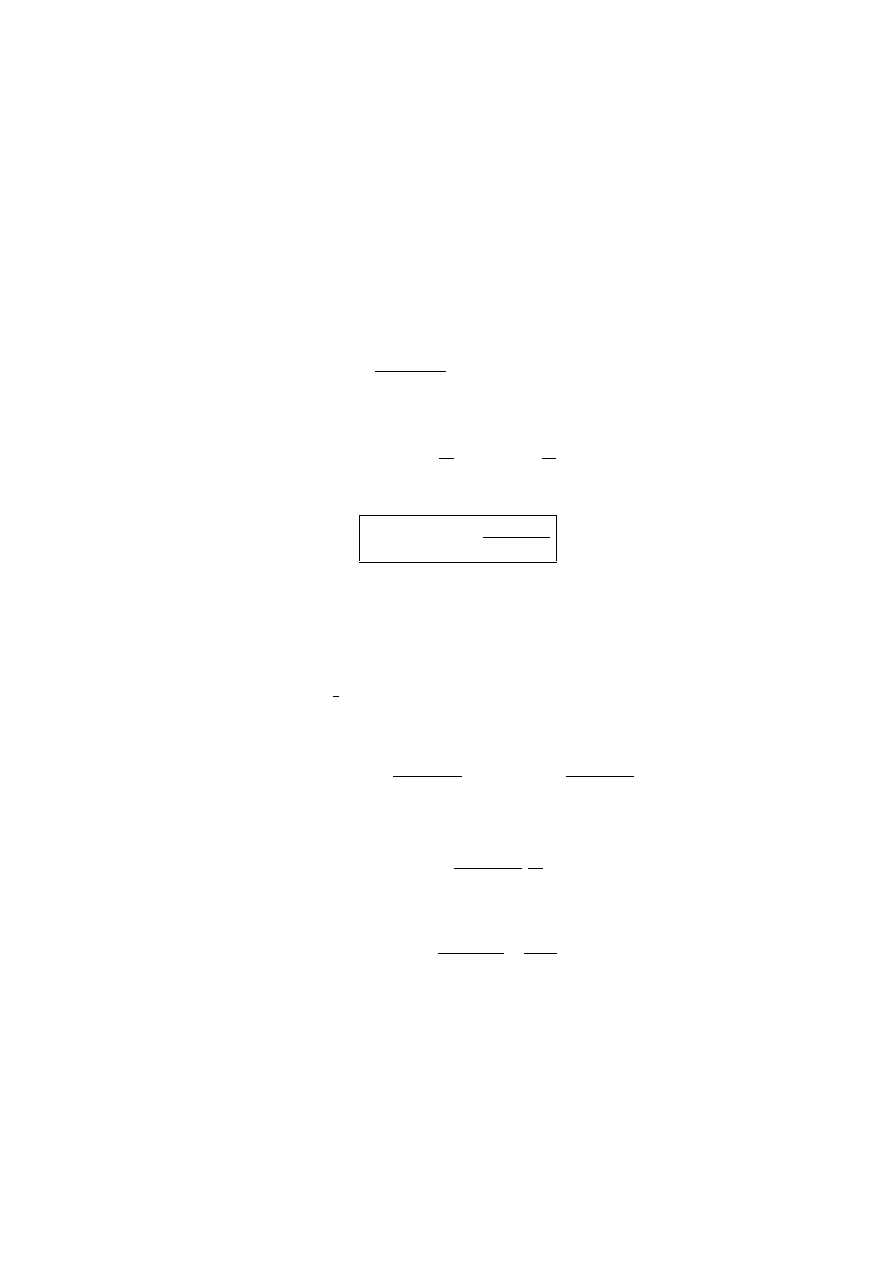
3.4

Optymalny wyb´or we¸zł´ow interpolacji

Powracaja

‘

c do problemu optymalnego wyboru we

‘

zł´ow interpolacji dla dowolnej

funkcji f

(x), rozpatrzymy najpierw funkcje zadane na przedziale [−1,1].

Wybierzmy

(n + 1) we

‘

zł´ow interpolacji

{x

0

, x

1

, . . . , x

n

} jako zera wielomianu

Czebyszewa T

n

+1

, wz´or (3.24):

x

k

= cos

π

(k + 1/2)

(n + 1)

,

k

= 0, 1, . . . n .

(3.26)

Na podstawie relacji (3.25) oraz własno´sci (3.19) otrzymujemy dla tak wybranych
we

‘

zł´ow

|

ω

n

+1

(x)| =

1

2

n

|T

n

+1

(x)| ≤

1

2

n

.

(3.27)

Relacja (3.16) przyjmuje wie

‘

c teraz posta´c

| f (x) −W

n

(x)| ≤

M

n

+1

2

n

(n + 1)!

(3.28)

gdzie M

n

+1

to kres g´orny

| f

(n+1)

(x)| w przedziale [−1,1]. Otrzymali´smy najm-

niejsze oszacowanie maksymalnego błedu interpolacji Lagrange’a.

Dla funkcji f

(y) okre´slonej na przedziale [a, b], optymalnie wybranymi we

‘

złami

sa

‘

obrazy zer (3.26) poprzez transformacje

‘

liniowa

‘

y

=

1
2

{(b − a)x + (a + b)},

x

∈ [−1,1].

(3.29)

Wtedy

ω

n

+1

(y) =

n

∏

k

=0

(y − y

k

) =

(b − a)

n

+1

2

n

+1

n

∏

k

=0

(x − x

k

) =

(b − a)

n

+1

2

n

+1

ω

n

+1

(x) .

Wykorzystuja

‘

c naste

‘

pnie relacje

‘

(3.27) otrzymujemy

|

ω

n

+1

(y)| ≤

(b − a)

n

+1

2

n

+1

1

2

n

.

(3.30)

Sta

‘

d najmniejsze oszacowanie błe

‘

du maksymalnego interpolacji Lagrange’a

| f (y) −W

n

(y)| ≤

M

n

+1

2

n

(n + 1)!

b

− a

2

n

+1

,

(3.31)

gdzie M

n

+1

to kres g´orny warto´sci

| f

n

+1

(y)| w przedziale [a,b].

23

3.5

Interpolacja przy pomocy funkcji sklejanych

Dla ka˙zdego układu

(n + 1) we

‘

zł´ow w przedziale

[a, b] istnieje funkcja cia

‘

gła w

przedziale, dla kt´orej metoda interpolacyjna nie jest zbie˙zna. Dla takiej funkcji
zwie

‘

kszenie liczby we

‘

zł´ow pogarsza jako´s´c interpolacji (zwłaszcza bli˙zej ko´nc´ow

przedziału), zwie

‘

kszaja

‘

c r´o˙znice

‘

| f (x) −W

n

(x)|. Przykładem jest funkcja f (x) =

|x| interpolowana w przedziale [−1,1] przy pomocy r´ownoodległych we

‘

zł´ow.

W takich przypadkach stosuje sie

‘

interpolacje

‘

, w kt´orej nie zwie

‘

ksza sie

‘

liczby

we

‘

zł´ow. Dla

(n + 1) we

‘

zł´ow

{x

0

, x

1

, . . . , x

n

} otrzymujemy n przedział´ow numero-

wanych indeksem lewego ko´nca:

[x

0

, x

1

] ∪ [x

1

, x

2

] ∪ ... ∪ [x

n

−1

, x

n

] .

(3.32)

W ka˙zdym takim przedziale funkcja f

(x) jest interpolowana przy pomocy wielo-

mianu trzeciego stopnia:

P

i

(x) = a

0 i

+ a

1 i

x

+ a

2 i

x

2

+ a

3 i

x

3

.

(3.33)

gdzie i

= 0, 1, . . . , (n − 1). Otrzymujemy n wielomian´ow o 4n wsp´ołczynnikach do

wyznaczenia. Nakładamy na nie 4n warunk´ow prowadza

‘

cych do jednoznacznego

rozwia

‘

zania.

1. Na brzegach ka˙zdego przedziału spełnione jest 2n warunk´ow interpolacji:

P

i

(x

i

) = f (x

i

)

P

i

(x

i

+1

) = f (x

i

+1

) .

(3.34)

2. W punktach wewne

‘

trznych

{x

1

, . . . , x

n

−1

} spełnione jest 2(n − 1) warunk´ow

cia

‘

gło´sci dla pierwszych i drugich pochodnych:

P

′

i

(x

i

+1

) = P

′

i

+1

(x

i

+1

)

P

′′

i

(x

i

+1

) = P

′′

i

+1

(x

i

+1

) ,

(3.35)

gdzie i

= 0, 1, . . . , (n − 2).

3. W punktach zewne

‘

trznych

{x

0

, x

n

} ˙za

‘

damy dla drugich pochodnych:

P

′′

0

(x

0

) = f

′′

(x

0

)

P

′′

n

−1

(x

n

) = f

′′

(x

n

) .

(3.36)

W sumie otrzymujemy wie

‘

c 2n

+ 2(n − 1) + 2 = 4n warunk´ow.

24

Rozdział 4

Aproksymacja

W wielu przypadkach przybli˙zanie zale˙zno´sci funkcyjnej poprzez wielomian prze-
chodza

‘

cy przez wszystkie znane punkty nie jest dobra

‘

metoda

‘

, w szczeg´olno´sci,

gdy punkty sa

‘

obarczone błe

‘

dem lub gdy jest ich bardzo du˙zo. W tym ostat-

nim przypadku stopie´n wielomianu Lagrange’a byłby bardzo wysoki co prowadzi´c
mo˙ze do niestabilno´sci numerycznych. Znacznie lepsza

‘

metoda

‘

jest wtedy aproksy-

macja przy pomocy wzgle

‘

dnie prostej funkcji, tak by była ona jak najmniej “od-

legła” od aproksymowanej funkcji. Metode

‘

te

‘

zilustrujemy na pocza

‘

tek w najprost-

szym przypadku, gdy dobrym przybli˙zeniem jest zało˙zenie o liniowej zale˙zno´sci
funkcyjnej.

4.1

Regresja liniowa

W metodzie tej mamy do czynienia z

(N + 1) we

‘

złami x

k

i odpowiadaja

‘

cymi im

warto´sciami y

k

. Zał´o˙zmy, ˙ze dobra

‘

poszukiwana

‘

zale˙zno´scia

‘

jest funkcja liniowa

y

= ax + b ,

(4.1)

gdzie parametry a i b pozostaja

‘

do wyznaczenia. Utw´orzmy w tym celu funkcje

‘

S

(a, b) =

N

∑

k

=0

(y

k

− (ax

k

+ b))

2

(4.2)

be

‘

da

‘

ca

‘

suma

‘

kwadrat´ow odległo´sci punkt´ow

(x

k

, y

k

) od prostej (4.1), mierzonych

wzdłu˙z osi y. Dobierzmy naste

‘

pnie parametry a i b tak, by warto´s´c tej funkcji była

25

jak najmniejsza. R´o˙zniczkuja

‘

c, otrzymamy

∂

S

∂

a

=

N

∑

k

=0

(−2x

k

)(y

k

− ax

k

− b) = 0

∂

S

∂

b

=

N

∑

k

=0

(−2)(y

k

− ax

k

− b) = 0,

(4.3)

ska

‘

d dostajemy układ r´owna´n na wsp´ołczynniki a i b:

a

(

∑

k

x

2
k

) + b (

∑

k

x

k

) =

∑

k

x

k

y

k

a

(

∑

k

x

k

) + b (

∑

k

1

) =

∑

k

y

k

.

(4.4)

Rozwia

‘

zanie zadane jest poprzez wzory Cramera

a

=

(N + 1)(

∑

x

k

y

k

) − (

∑

x

k

)(

∑

y

k

)

(N + 1)(

∑

x

2
k

) − (

∑

x

k

)

2

b

=

(

∑

x

2
k

)(

∑

y

k

) − (

∑

x

k

y

k

)(

∑

x

k

)

(N + 1)(

∑

x

2
k

) − (

∑

x

k

)

2

.

(4.5)

Uog´olnienie tej metody polega na rozwa˙zeniu zale˙zno´sci wielomianowej

y

= a

0

+ a

1

x

+ . . . + a

n

x

n

(4.6)

i minimalizacje

‘

ze wzgle

‘

du na wsp´ołczynniki tego wielomianu naste

‘

puja

‘

cej r´o˙znicy

S

(a

i

) =

N

∑

k

=0

{y

k

− (a

0

+ a

1

x

+ . . . + a

n

x

n

)}

2

.

(4.7)

Zwr´o´cmy uwage

‘

, ˙ze na og´oł liczba punkt´ow

(N + 1), w kt´orych znamy aproksy-

mowana

‘

funkcje

‘

, jest du˙zo wieksza od stopnia wielomianu aproksymuja

‘

cego n.

4.2

Aproksymacja ´sredniokwadratowa

Przedstawiona w poprzednim rozdziale metoda jest przykładem aproksymacji ´sre-
dniokwadratowej. W og´olno´sci, znaja

‘

c

(N + 1) we

‘

zł´ow x

k

i warto´sci f

(x

k

) niez-

nanej na og´oł funkcji f , chcemy ja

‘

aproksymowa´c przy pomocy wyra˙zenia

F

(x) = c

0

φ

0

(x) + c

1

φ

1

(x) + . . . + c

M

φ

M

(x) ,

(4.8)

26

gdzie

{

φ

0

,

φ

1

. . .

φ

M

} jest układem dogodnie wybranych funkcji bazowych. W

przykładzie (4.7) funkcjami bazowymi sa

‘

jednomiany

φ

i

(x) = x

i

. Zauwa˙zmy, ˙ze

liczba we

‘

zł´ow

(N + 1) jest niezale˙zna od liczby funkcji bazowych (M + 1).

Wsp´ołczynniki c

i

sa

‘

tak dobrane by zminimalizowa´c odległo´s´c pomie

‘

dzy funk-

cja

‘

dokładna

‘

f

(x) i przybli˙zona

‘

F

(x):

S

(c

i

) =

N

∑

k

=0

{ f (x

k

) − (c

0

φ

0

(x

k

) + c

1

φ

1

(x

k

) + . . . + c

M

φ

M

(x

k

))}

2

.

(4.9)

R´o˙zniczkuja

‘

c po parametrach,

∂

S

/

∂

c

i

= 0, otrzymujemy naste

‘

puja

‘

cy układ r´owna´n

(

φ

0

,

φ

0

) c

0

+ (

φ

0

,

φ

1

) c

1

+ ··· + (

φ

0

,

φ

M

) c

M

= (

φ

0

, f )

(

φ

1

,

φ

0

) c

0

+ (

φ

1

,

φ

1

) c

1

+ ··· + (

φ

1

,

φ

M

) c

M

= (

φ

1

, f )

...

(

φ

n

,

φ

0

) c

0

+ (

φ

n

,

φ

1

) c

1

+ ··· + (

φ

n

,

φ

M

) c

M

= (

φ

n

, f ) ,

(4.10)

gdzie

(·, ·) to iloczyn skalarny w przestrzeni funkcji bazowych, zdefiniowany przy

pomocy dyskretnego zbioru we

‘

zł´ow

{x

k

}:

(

φ

i

,

φ

j

) =

N

∑

k

=0

φ

i

(x

k

)

φ

j

(x

k

)

(4.11)

Rozwia

‘

zanie układu (4.10) jest szczeg´olnie proste, gdy układ funkcji bazowych

jest ortogonalny:

(

φ

i

,

φ

j

) ∼

δ

i j

.

(4.12)

W r´ownaniach (4.10) pozostaja

‘

tylko składowe diagonalne i sta

‘

d

c

i

=

(

φ

i

, f )

(

φ

i

,

φ

i

)

,

i

= 0, 1, . . ., M .

(4.13)

Ostatecznie funkcja aproksymuja

‘

ca to

F

(x) =

M

∑

i

=0

(

φ

i

, f )

(

φ

i

,

φ

i

)

φ

i

(x)

(4.14)

W naste

‘

pnych rozdziałach przedstawimy przykłady dw´och szczeg´olnie wa˙znych

realizacji powy˙zszego rozwia

‘

zania. Rozwa˙zymy aproksymacje

‘

przy pomocy wielo-

mian´ow Czebyszewa oraz funkcji trygonometrycznych.

27

4.3

Aproksymacja Czebyszewa

Aproksymacja wielomianami Czebyszewa jest szczeg´olnie efektywna

‘

metoda

‘

przy-

bli˙zania funkcji przy pomocy wielomian´ow ortogonalnych w sensie iloczynu ska-
larnego (4.11).

Wybierzmy

(N + 1) we

‘

zł´ow x

k

be

‘

da

‘

cych zerami wielomianu Czebyszewa

T

N

+1

(x

k

) = 0

(4.15)

Zgodnie ze wzorem (3.24) we

‘

zły

x

k

= cos

π

(2k + 1)

2

(N + 1)

,

k

= 0, 1, . . . N .

(4.16)

Wielomiany Chebyszewa

{T

0

, T

1

, . . . , T

N

} sa

‘

ortogonalne wzgle

‘

dem iloczynu ska-

larnego (4.11) z powy˙zszymi we

‘

złami.

(T

m

, T

n

) =

N

∑

k

=0

T

m

(x

k

) T

n

(x

k

) =






















N

+ 1

dla

m

= n = 0

(N + 1)/2

dla

m

= n 6= 0

0

dla

m

6= n

(4.17)

Dow´od

Policzmy iloczyn skalarny dla 0

≤ n,m ≤ N:

N

∑

k

=0

T

m

(x

k

) T

n

(x

k

) =

N

∑

k

=0

cos

m

π

(2k + 1)

2

(N + 1)

cos

n

π

(2k + 1)

2

(N + 1)

.

Dla m

= n = 0 otrzymujemy sume

‘

r´owna

‘

(N + 1). Rozwa˙zmy naste

‘

pnie

przypadek m

6= n. Korzystaja

‘

c ze wzoru

cos

α

cos

β

=

1

2

{cos(

α

+

β

) + cos(

α

−

β

)}

otrzymujemy

(T

m

, T

n

) =

1

2

N

∑

k

=0

cos

(2k + 1)

π

(m + n)

2

(N + 1)

+ cos

(2k + 1)

π

(m − n)

2

(N + 1)

.

(4.18)

28

Policzmy naste

‘

pnie dla dowolnego ka

‘

ta

φ

6= 0:

N

∑

k

=0

cos

(2k + 1)

φ

= Re

N

∑

k

=0

e

i

(2k+1)

φ

(4.19)

= Re

e

i

φ

(1 + e

2i

φ

+ . . . + e

2Ni

φ

)

= Re

(

e

i

φ

1

− e

2i

φ

(N+1)

1

− e

2i

φ

)

=

sin

(2(N + 1)

φ

)

2 sin

φ

.

Podstawiaja

‘

c

φ

±

=

π

(m ± n)/2(N + 1) 6= 0, otrzymujemy dla wzoru (4.18)

(T

m

, T

n

) =

sin

(

π

(m + n))

4 sin

φ

+

+

sin

(

π

(m − n))

4 sin

φ

−

.

Wyra˙zenie to znika dla m

6= n. Sta

‘

d warunek ortogonalno´sci dla wielo-

mian´ow Czebyszewa. Dla m

= n 6= 0 r´ownanie (4.18) przyjmuje posta´c

(T

m

, T

m

) =

1

2

N

∑

k

=0

{cos(2k + 1)

φ

+ 1}

=

1

2

N

∑

k

=0

cos

(2k + 1)

φ

+

N

+ 1

2

,

gdzie

φ

=

π

m

/(N + 1). Z (4.19) suma cosinus´ow daje zero i sta

‘

d warto´s´c

(N + 1)/2 iloczynu skalarnego.

Mo˙zemy wie

‘

c aproksymowa´c przy pomocy wielomian´ow Czebyszewa funkcje

okre´slone w przedziale

[−1,1]:

f

(x) ≃

1

2

c

0

+

N

∑

j

=1

c

j

T

j

(x)

(4.20)

gdzie wsp´ołczynniki c

j

sa

‘

wyliczone ze wzoru (4.13):

c

j

=

2

N

+ 1

N

∑

k

=0

T

j

(x

k

) f (x

k

) ,

j

= 0, 1, . . . , N .

(4.21)

Wsp´olczynnik 1

/2 we wzorze (4.20) wynika z dwukrotnie wie

‘

kszej warto´sci ilo-

czynu sklaranego

(T

0

, T

0

) w stosunku do (T

m

, T

m

) dla m ≥ 1.

29

Zaleta

‘

aproksymacji Czebyszewa jest fakt, ˙ze w sumie (4.20) mo˙zna zachowa´c

jedynie M

< N składnik´ow przy niezmienionych wsp´ołczynnikach c

j

. W wie

‘

kszo-

´sci przypadk´ow staja

‘

sie

‘

one coraz mniejsze dla rosna

‘

cych warto´sci wska´znika,

natomiast ka˙zdy wielomian Czebyszewa jest ograniczony warunkiem (3.19). Nie
popełniamy w ten spos´ob du˙zego błe

‘

du odrzucaja

‘

c wyrazy z j

> M.

Podsumowuja

‘

c, kluczowym punktem w aproksymacji Czebyszewa jest zna-

jomo´s´c funkcji f w we

‘

złach Chebyszewa. Na tej podstawie konstruuje sie

‘

wsp´oł-

czynniki (4.21), a naste

‘

pnie przybli˙zenie (4.20).

4.3.1

Aproksymacja Czebyszewa w dowolnym przedziale

Rozwa˙zmy aproksymacje

‘

funkcji f

(y) okre´slonej na dowolnym przedziale [a, b].

Niech

y

= y(x) ,

x

∈ [−1,1]

(4.22)

be

‘

dzie dowolna

‘

transformacja

‘

bijektywna

‘

odwzorowuja

‘

ca

‘

[−1,1] → [a,b]. Istnieje

wie

‘

c funkcja odwrotna odwzorowuja

‘

ca

[a, b] → [−1,1]

x

= y

−1

(y) ,

y

∈ [a,b].

(4.23)

Zdefiniujmy przy pomocy transformacji y

= y(x) nowa

‘

funkcje

‘

okre´slona

‘

na

przedziale

[−1,1]:

˜

f

(x) = f (y) ,

(4.24)

a naste

‘

pnie zastosujmy do niej wz´or aproksymacyjny (4.20):

˜

f

(x) ≈

1

2

c

0

+

N

∑

j

=1

c

j

T

j

(x) .

(4.25)

Podstawiaja

‘

c po prawej stronie relacje

‘

odwrotna

‘

x

= y

−1

(y), otrzymujemy apro-

ksymacje

‘

funkcji f

(y):

f

(y) ≈

1

2

c

0

+

M

<N

∑

j

=1

c

j

T

j

(y

−1

(y)) .

(4.26)

Wsp´ołczynniki c

j

sa

‘

zadane przez

c

j

=

2

N

+ 1

N

∑

k

=0

T

j

(x

k

) f (y

k

) .

(4.27)

W powy˙zszym wzorze y

k

= y(x

k

) sa

‘

obrazami we

‘

zł´ow Czebyszewa (4.16) poprzez

transformacje

‘

(4.22).

30

4.4

Aproksymacja trygonometryczna

Aproksymacje

‘

te

‘

stosujemy, gdy mamy do czynienia z funkcja

‘

okresowa

‘

f

(x) o

okresie 2

π

. Wła´sciwym układem funkcji bazowych dla aproksymacji (4.8) sa

‘

wte-

dy funkcje trygonometryczne

{1, sinx , cosx , sin2x , cos2x ... sinkx , coskx ...}

(4.28)

Zał´o˙zmy, ˙ze znamy funkcje

‘

f

(x) w parzystej liczbie 2N r´ownoodległych punkt´ow

z przedziału

[0, 2

π

):

x

k

= k

π

N

,

k

= 0, 1, . . . , (2N − 1)

(4.29)

Zbi´or funkcji (4.28) z maksymalna

‘

warto´scia

‘

k

= (N − 1) jest ortogonalny na tym

zbiorze punkt´ow. Zachodzi bowiem dla 1

≤ m,n ≤ (N − 1):

2N

−1

∑

k

=0

sin

(mx

k

) · sin(nx

k

) =

2N

−1

∑

k

=0

cos

(mx

k

) · cos(nx

k

) = N

δ

mn

2N

−1

∑

k

=0

cos

(mx

k

) · sin(nx

k

) = 0 .

(4.30)

Ponadto

2N

−1

∑

k

=0

sin

(mx

k

) · 1 =

2N

−1

∑

k

=0

cos

(mx

k

) · 1 = 0,

2N

−1

∑

k

=0

1

· 1 = 2N .

(4.31)

Sta

‘

d, aproksymuja

‘

c funkcje

‘

f

(x) przy pomocy funkcji trygonometrycznych,

otrzymujemy

f

(x) ≈

1

2

a

0

+

M

<N

∑

j

=1

a

j

cos

( jx) + b

j

sin

( jx)

.

(4.32)

Wsp´ołczynniki a

j

i b

j

dla j

= 0, 1, . . ., (N − 1) mo˙zna wyliczy´c ze wzoru (4.13):

a

j

=

1

N

2N

−1

∑

k

=0

f

(x

k

) cos( jx

k

)

b

j

=

1

N

2N

−1

∑

k

=0

f

(x

k

) sin( jx

k

) .

(4.33)

31

4.4.1

Wzory dla dowolnego okresu

Zastosujmy powy˙zsza

‘

aproksymacje

‘

do funkcji czasu o okresie T

f

(t) = f (t + T ) .

(4.34)

Zdefiniujmy nowa

‘

funkcje

‘

˜

f

(x) o okresie 2

π

:

˜

f

(x) = f (t)

(4.35)

przy pomocy transformacji:

t

= x

T

2

π

.

(4.36)

Naste

‘

pnie aproksymujemy funkcje

‘

˜

f

(x) za pomoca

‘

wzoru (4.32):

˜

f

(x) ≈

1

2

a

0

+

N

−1

∑

j

=1

a

j

cos

( j x) + b

j

sin

( j x)

(4.37)

Podstawiaja

‘

c po prawej stronie transformacje

‘

odwrotna

‘

x

= 2

π

t

/T , otrzymamy

aproksymacje

‘

funkcji f

(t):

f

(t) ≈

1

2

a

0

+

M

<N

∑

j

=1

a

j

cos

2

π

j

T

t

+ b

j

sin

2

π

j

T

t

.

(4.38)

Wsp´ołczynniki a

j

i b

j

dla j

= 0, 1, . . ., (N − 1) sa

‘

teraz zadane wzorami:

a

j

=

1

N

2N

−1

∑

k

=0

f

(t

k

) cos( j x

k

)

b

j

=

1

N

2N

−1

∑

k

=0

f

(t

k

) sin( j x

k

) ,

(4.39)

w kt´orych t

k

sa

‘

obrazami we

‘

zł´ow (4.29) poprzez transformacje

‘

(4.36):

t

k

= x

k

T

2

π

=

k

2N

T

,

k

= 0, 1, . . ., (2N − 1).

(4.40)

32

Rozdział 5

R´o˙zniczkowanie

5.1

Metody z aproksymacja¸

W metodzie tej najpierw aproksymujemy funkcje

‘

, kt´orej pochodna

‘

chcemy znale´z´c

przy pomocy jednej z metod opisanych w poprzednim rozdziale:

f

(x) ≃

N

∑

i

=0

c

i

φ

i

(x) ,

(5.1)

gdzie

φ

i

to znane i r´o˙zniczkowalne funkcje bazowe, np. jednomiany x

i

lub wielo-

miany Czebyszewa T

i

(x). Przyjmujemy, ˙ze pochodna tej funkcji to

f

′

(x) ≃

N

∑

i

=0

c

i

φ

′

i

(x)

(5.2)

Podobnie poste

‘

pujemy przy obliczniu wy˙zszych pochodnych.

5.2

Metody z rozwinie¸ciem Taylora

Ta metoda r´o˙zniczkowania wykorzystuja

‘

rozwinie

‘

cie Taylora funkcji. Zakladaja

‘

c,

˙ze rozwinie

‘

cie takie istnieje w otoczeniu punktu x, mamy

f

(x + h) = f (x) + f

′

(x) h + f

′′

(x)

h

2

2!

+ f

′′′

(x)

h

3

3!

+

O

(h

4

)

(5.3)

33

gdzie symbol

O

(h

4

) oznacza reszte

‘

rze

‘

du h

4

, tzn

lim

h

→0

O

(h

4

)

h

4

= const .

(5.4)

Aby obliczy´c pierwsza

‘

pochodna

‘

wykorzystujemy wz´or

f

(x + h) = f (x) + f

′

(x) h +

O

(h

2

) ,

ska

‘

d wynika

f

′

(x) =

f

(x + h) − f (x)

h

+

O

(h) .

(5.5)

Aby poprawi´c dokładno´s´c oblicznej w ten spos´ob pochodnej wykorzystujemy dwa
rozwinie

‘

cia Taylora

f

(x + h) = f (x) + f

′

(x) h + f

′′

(x)

h

2

2!

+

O

(h

3

)

f

(x − h) = f (x) − f

′

(x) h + f

′′

(x)

h

2

2!

+

O

(h

3

) .

(5.6)

Po odje

‘

ciu stronami wyra˙zenia z parzystymi potegami h upraszczaja

‘

sie

‘

i sta

‘

d

dostajemy

f

′

(x) =

f

(x + h) − f (x − h)

2h

+

O

(h

2

)

(5.7)

Znaja

‘

c wie

‘

c warto´sc funkcji w punktach sa

‘

siednich

(x − h) oraz (x + h), poprawia-

my dokładno´s´c obliczonej pochodnej.

5.3

Wy˙zsze pochodne

Dodaja

‘

c stronami wyra˙zenia (5.6) otrzymujemy wz´or na druga

‘

pochodna

‘

f

′′

(x) =

f

(x + h) − 2 f (x) + f (x − h)

h

2

+

O

(h

2

)

(5.8)

Rza

‘

d reszty wynika z faktu kasowanie sie

‘

wyra˙ze´n z nieparzystymi pote

‘

gami h

przy dodawaniu stronami.

Lepsza

‘

dokładno´s´c obliczanych pochodnych mo˙zna uzyska´c rozwa˙zaja

‘

c roz-

winie

‘

cia Taylora zapisane z dokładno´scia do pia

‘

tej pote

‘

gi h dla warto´sci funkcji

34

w czterech punktach: f

(x − 2h), f (x − h), f (x + h), f (x + 2h). Jako po˙zyteczne

´cwiczenie nale˙zy udowodni´c, ˙ze w takim przypadku dla pierwszej pochodnej otrzy-

mujemy

f

′

(x) =

f

(x − 2h) − 8 f (x − h) + 8 f (x + h) − f (x + 2h)

12h

+

O

(h

4

) ,

(5.9)

natomiast druga pochodna to

f

′′

(x) =

− f (x − 2h) + 16 f (x − h) − 30 f (x) + 16 f (x + h) − f (x + 2h)

12h

2

+

O

(h

4

) .

(5.10)

W podobny spos´ob mo˙zna wyprowadzi´c wzory na wy˙zsze pochodne, korzys-

taja

‘

c z wyprowadzonych wcze´sniej formuł dla ni˙zszych pochodnych. Na przykład,

aby obliczy´c trzecia

‘

pochodna

‘

odejmujemy od siebie dwa rozwinie

‘

cia

f

(x + h) = f (x) + f

′

(x) h + f

′′

(x)

h

2

2!

+ f

′′′

(x)

h

3

3!

+

O

(h

4

)

f

(x − h) = f (x) − f

′

(x) h + f

′′

(x)

h

2

2!

− f

′′′

(x)

h

3

3!

+

O

(h

4

) ,

(5.11)

otrzymuja

‘

c

f

′′′

(x) = 3

f

(x + h) − f (x − h)

h

3

− 6

f

′

(x)

h

2

+

O

(h

2

) .

(5.12)

Zwr´o´cmy uwage

‘

, ˙ze podstawienie wzoru (5.7) w miejsce pierwszej pochodnej w

powy˙zszym wzorze daje reszte

‘

O

(1), niezale˙zna

‘

od odchylenia h. Jeste´smy wie

‘

c

zmuszeni do u˙zycia dokładniejszego wzoru (5.9), prowadza

‘

cego do

f

′′′

(x) =

− f (x − 2h) + 2 f (x − h) − 2 f (x + h) + f (x + 2h)

2h

3

+

O

(h

2

)

35

Rozdział 6

Całkowanie

6.1

Podstawowe metody

Rozwa˙zmy jednowymiarowa

‘

całke

‘

na przedziale

[a, b ]

I

( f ) =

Z

b

a

f

(x) dx

(6.1)

Podzielmy przedział całkowania na N r´ownych odcink´ow o długo´sci h

= (b−a)/N

i wyznaczonych przez kolejne punkty

x

k

= x

0

+ kh

k

= 0, 1, . . ., N .

(6.2)

Zauwa˙zmy, ˙ze x

0

= a oraz x

N

= b sa

‘

ko´ncami przedziałow. Wtedy

I

( f ) =

N

−1

∑

i

=0

Z

x

i

+1

x

i

f

(x) dx

(6.3)

Nale˙zy wie

‘

c policzy´c całke

‘

w ka˙zdym z przedział´ow

[x

i

, x

i

+1

].

6.1.1

Metoda prostokat´ow

W metodzie prostoka

‘

t´ow

Z

x

i

+1

x

i

f

(x) dx ≃ h f (x

i

)

(6.4)

36

i wtedy, wprowadza

‘

c oznacznie f

i

≡ f (x

i

),

Z

b

a

f

(x) dx ≃ h( f

0

+ f

1

+ . . . + f

N

−1

)

(6.5)

Otrzymany wynik odpowiada przybli˙zeniu funkcji f w ka˙zdym z podprzedziałow
poprzez funkcje

‘

stała

‘

f

(x) = f

i

. Warto´sci funkcji f

i

moga

‘

by´c r´ownie˙z wzie

‘

te w

´srodkach podprzedział´ow

f

i

= f

x

i

+ x

i

+1

2

.

(6.6)

6.1.2

Metoda trapez´ow

W metodzie trapez´ow otrzymujemy

Z

x

i

+1

x

i

f

(x) dx ≃

h

2

{ f

i

+ f

i

+1

}

(6.7)

i wtedy

Z

b

a

f

(x) dx ≃

h

2

{ f

0

+ 2( f

1

+ . . . + f

N

−1

) + f

N

}

(6.8)

W tym przypadku wynik otrzyma´c mo˙zna korzystaja

‘

c z liniowej interpolacji

Lagrange’a w ka˙zdym z podprzedziałow:

f

(x) ≃ f

i

x

− x

i

+1

x

i

− x

i

+1

+ f

i

+1

x

− x

i

x

i

+1

− x

i

.

(6.9)

Całkuja

‘

c bowiem (6.9) i pamie

‘

taja

‘

c, ˙ze x

i

+1

− x

i

= h, otrzymujemy wz´or (6.7):

1

h

Z

x

i

+1

x

i

{ f

i

+1

(x − x

i

) − f

i

(x − x

i

+1

)} dx =

h

2

{ f

i

+ f

i

+1

}.

Łatwo uog´olni´c te

‘

metode

‘

, przybli˙zaja

‘

c funkcje

‘

podcałkowa

‘

przy pomocy wie

‘

kszej

liczby punkt´ow. Przykładem jest metoda Simpsona.

6.1.3

Metoda parabol Simpsona

W metodzie tej dzielimy

[a, b ] na parzysta

‘

liczbe

‘

przedziałow o r´ownej długo´sci:

h

=

(b − a)

2N

.

(6.10)

W ka˙zdej sa

‘

siedniej parze przedział´ow wyznaczonych przez

(x

i

, x

i

+1

, x

i

+2

) stosu-

jemy interpolacje

‘

Lagrange’a:

37

f

(x) ≃ f

i

(x − x

i

+1

)(x − x

i

+2

)

(x

i

− x

i

+1

)(x

i

− x

i

+2

)

+ f

i

+1

(x − x

i

)(x − x

i

+2

)

(x

i

+1

− x

i

)(x

i

+1

− x

i

+2

)

+ f

i

+2

(x − x

i

)(x − x

i

+1

)

(x

i

+2

− x

i

)(x

i

+2

− x

i

+1

)

.

(6.11)

Wykonuja

‘

c całkowanie i pamie

‘

taja

‘

c, ˙ze

(x

i

+1

− x

i

) = (x

i

+2

− x

i

+1

) = h oraz

(x

i

+2

− x

i

) = 2h, otrzymujemy

Z

x

i

+2

x

i

f

(x) dx ≃

h

3

{ f

i

+ 4 f

i

+1

+ f

i

+2

}.

(6.12)

Sta

‘

d wz´or przybli˙zony dla warto´sci całki w przedziale

[a, b]:

Z

b

a

f

(x) dx ≃

h

3

{ f

0

+ 4( f

1

+ . . . + f

2N

−1

) + 2( f

2

+ . . . + f

2N

−2

) + f

2N

}

(6.13)

6.1.4

Bła¸d przybli˙zenia

Zdefiniujmy bła

‘

d obliczenia całki

ε

, rozumiany jako r´o˙znice

‘

pomie

‘

dzy warto´scia

‘

dokładna

‘

a przybli˙zona

‘

. Mo˙zna pokaza´c (podre

‘

cznik [1]), ˙ze bła

‘

d ten jest ograni-

czony od g´ory przez

w metodzie prostoka

‘

t´ow:

|

ε

| < (b − a)

h

2

sup

x

∈[a,b]

| f

′

(x)|

(6.14)

w metodzie trapez´ow:

|

ε

| < (b − a)

h

2

12

sup

x

∈[a,b]

| f

(2)

(x)|

(6.15)

w metodzie parabol:

|

ε

| < (b − a)

h

4

180

sup

x

∈[a,b]

| f

(4)

(x)|

(6.16)

Jak łatwo zauwa˙zy´c, przy tej samej długo´sci podprzedział´ow h

< 1, najlepsza

parametrycznie jest metoda parabol Simpsona.

38

6.2

Kwadratura i jej rza¸d

Naszym celem jest znalezienie og´olnej metody przybli˙zonego obliczania całek

I

( f ) =

Z

b

a

f

(x) w(x) dx

(6.17)

Granice całkowania moga

‘

by´c r´owne

±

∞

. Funkcja w

(x) ≥ 0 jest nazywana waga

‘

.

Mo˙ze ona zawiera´c osobliwo´sci, kt´ore wyła

‘

czyli´smy z funkcji podcałkowej. Przy-

kładowo, dla f

∼ 1/

√

x kładziemy w

(x) = 1/

√

x natomiast f

(x) jest zasta

‘

piona

przez nieosobliwa

‘

funkcje

‘

√

x f

(x)

Kwadratura

‘

nazywamy przybli˙zona

‘

warto´s´c całki (6.17) dana

‘

w postaci

S

( f ) =

N

∑

k

=0

A

k

f

(x

k

)

(6.18)

przy czym wsp´ołczynniki A

k

nie zale˙za

‘

od funkcji f . Punkty x

k

∈ [a,b] nazywamy

we

‘

złami kwadratury. Wszystkie wzory z poprzedniego rozdziału były kwadratura-

mi z r´ownoodległymi od siebie we

‘

złami (kwadratury Newtona-Cotesa).

Bła

‘

d kwadratury to r´o˙znica mie

‘

dzy warto´scia

‘

dokładna

‘

a przybli˙zona

‘

całki

E

( f ) = I( f ) − S( f )

(6.19)

Kryterium dokładno´sci całkowania jest okre´slone poprzez r´owno´s´c I

( f ) = S( f ),

gdy f jest wielomianem. Sta

‘

d definicja rze

‘

du kwadratury:

Rza

‘

d kwadratura wynosi r, gdy:

- istnieje wielomian W stopnia r taki, ˙ze bła

‘

d E

(W ) 6= 0

- dla wszystkich wielomian´ow W stopnia

< r, bła

‘

d E

(W ) = 0 .

Rza

‘

d kwadratury okre´sla najmniejszy stopie ´n wielomianu, dla kt´orego kwadra-

tura nie jest dokładna. Prawdziwe jest naste

‘

puja

‘

ce twierdzenie o maksymalnym

rze

‘

dzie kwadratury.

Twierdzenie
Nie istnieje kwadratura rze

‘

du wy˙zszego ni˙z 2

(N + 1).

39

Dla wielomianu W

(x) = [(x −x

0

) . . . (x −x

N

)]

2

, stopnia 2

(N +1), kwadratura

nie jest dokładna:

I

(W ) =

Z

b

a

w

(x)W (x) dx > 0 ,

S

(W ) =

N

∑

k

=0

A

k

W

(x

k

) = 0 .

Szczeg´olnie wa˙zna

‘

role

‘

odgrywa kwadratura powstała z interpolacji funkcji

f

(x) przy pomocy wielomianu Lagrange’a (3.13):

f

(x) ≃

N

∑

k

=0

f

(x

k

) L

k

(x) .

(6.20)

Podstawiaja

‘

c te

‘

posta´c do (6.17), a naste

‘

pnie zmieniaja

‘

c kolejno´s´c całkowania i

sumowania, otrzymujemy kwadrature

‘

Z

b

a

f

(x) w(x) dx ≈

N

∑

k

=0

f

(x

k

)

Z

b

a

L

k

(x) w(x) dx

|

{z

}

A

k

,

(6.21)

Zauwa˙zmy, ze wsp´ołczynniki kwadratury A

k

zale˙za

‘

od wyboru we

‘

zł´ow poprzez

wielomiany L

k

(x), wz´or (3.11).

Rza

‘

d powy˙zszej kwadratury wynika z naste

‘

puja

‘

cego twierdzenia.

Twierdzenie
Rzad kwadratury (6.18) wynosi co najmniej

(N + 1) wtedy i tylko wtedy gdy ma

ona posta´c (6.21).

Zał´o˙zmy, ˙ze kwadratura ma posta´c (6.21). Dowolny wielomian stopnia

≤ N

mo˙zemy zapisa´c w spos´ob dokładny przy pomocy interpolacji Lagrange’a
(6.20). Tym samym kwadratura (6.21) jest dokładna i jej rza

‘

d jest

≥ (N +1).

Zał´o˙zmy teraz, ˙ze kwadratura jest rze

‘

du co najmniej

(N + 1). Jest wie

‘

c

dokładna dla wszystkich wielomian´ow stopnia

≤ N, w szczeg´ołno´sci dla

wielomian´ow Lagrange’a L

i

(x) stopnia N otrzymujemy

Z

b

a

L

i

(x) w(x) dx =

N

∑

k

=0

A

k

L

i

(x

k

) =

N

∑

k

=0

A

k

δ

ik

= A

i

.

Podsumowuja

‘

c, rza

‘

d r kwadratury (6.21) spełnia warunek

(N + 1) ≤ r ≤ 2(N + 1).

(6.22)

Powstaje pytanie jak skonstruowa´c kwadrature

‘

o maksymalnym rze

‘

dzie r´ow-

nym 2

(N + 1). Odpowiedzia

‘

na to pytanie jest kwadratura Gaussa oparta o kon-

strukcje

‘

wielomian´ow ortogonalnych.

40

6.3

Wielomiany ortogonalne

Wielomiany okre´slone na odcinku

[a, b]

{P

0

(x) , P

1

(x) , . . . P

N

(x) , . . .}

(6.23)

tworza

‘

układ ortogonalny z waga

‘

w

(x) ≥ 0 je´sli zachodzi

P

i

|P

j

≡

Z

b

a

P

i

(x) P

j

(x) w(x) dx = 0

dla

i

6= j .

(6.24)

Wielomiany ortogonalne maja

‘

bardzo wa˙zna

‘

własno´s´c wyra˙zona

‘

w naste

‘

puja

‘

-

cym twierdzeniu.

Twierdzenie
Ka˙zdy wielomian ortogonalny P

n

ma dokładnie n jednokrotnych pierwiastk´ow w

przedziale

[a, b].

Gdyby P

n

miał tylko m

< n r´o˙znych pierwiastk´ow

ξ

i

o nieparzystej krotno´sci

to wielomian W

(x) = (x −

ξ

0

)(x −

ξ

1

) . . . (x −

ξ

m

) mo˙zna by zapisa´c przy

pomocy kombinacji liniowej wielomian´ow P

0

, . . . , P

m

:

W

(x) = a

0

P

0

(x) + . . . + a

m

P

m

(x) .

(6.25)

Wtedy

hW |P

n

i =

m

∑

k

=0

a

k

hP

k

|P

n

i = 0.

(6.26)

Z drugiej strony P

n

(x) = W (x)R(x), gdzie wielomian R(x) ≥ 0 i wtedy

P

n

(x)W (x) ≥ 0 w całym przedziale [a,b]. Tak wie

‘

c

hW |P

n

i > 0, co przeczy

wnioskowi (6.33). Przyje

‘

ta hipoteza co do pierwiastk´ow jest wie

‘

c fałszywa.

W konstrukcji wielomian´ow ortogonalnych wykorzystuje sie

‘

procedure

‘

Grama-

Schmidta. Zdefiniujmy najpierw dwa pierwsze wielomiany

P

0

(x) = 1

P

1

(x) = (x − a)P

0

(x) .

(6.27)

41

Wsp´olczynnik a wyznacza sie

‘

z warunku ortogonalno´sci

hP

0

|P

1

i = 0

=>

a

=

hP

0

|xP

0

i

hP

0

|P

0

i

(6.28)

Naste

‘

pne wielomiany konstruuje sie

‘

posługuja

‘

c sie

‘

relacja

‘

rekurencyjna

‘

P

j

+1

(x) = (x − a

j

) P

j

− b

j

P

j

−1

(6.29)

dla j

= 1, 2, . . ., gdzie wsp´ołczynniki

a

j

=

P

j

|xP

j

P

j

|P

j

b

j

=

P

j

|P

j

P

j

−1

|P

j

−1

.

(6.30)

Udowodnimy, ˙ze P

j

+1

jest ortogonalny do ka˙zdego P

k

dla k

≤ j.

Dow´od

Policzmy dla k

= j:

P

j

|P

j

+1

= −b

j

P

j

|P

j

−1

= −b

j

P

j

−1

|P

j

= (−1)

j

b

j

b

j

−1

. . . b

1

hP

0

|P

1

i = 0.

Dla k

= ( j − 1) mamy

P

j

−1

|P

j

+1

=

xP

j

−1

|P

j

−

P

j

|P

j

=

(P

j

+ a

j

−1

P

j

−1

+ b

j

−1

P

j

−2

) |P

j

−

P

j

|P

j

= 0 ,

gdzie skorzystali´smy z relacji (6.29) zapisanej dla j

→ ( j − 1) oraz z warun-

k´ow ortogonalno´sci.

Z kolei dla k

≤ ( j − 2) otrzymujemy

P

k

|P

j

+1

=

xP

k

|P

j

=

(P

k

+1

+ a

k

P

k

+ b

k

P

k

−1

) |P

j

= 0 .

Przyklad

Wielomiany Czebyszewa (3.18) z iloczynem skalarnym

hT

m

|T

n

i =

Z

1

−1

T

m

(x) T

n

(x)

√

1

− x

2

dx

=






π

dla

m

= n = 0

π

/2

dla

m

= n 6= 0

0

dla

m

6= n.

(6.31)

sa

‘

wielomianami ortogonalnymi.

42

6.4

Kwadratura Gaussa

Kwadratura Gaussa ma posta´c (6.21)

S

( f ) =

N

∑

k

=0

A

k

f

(x

k

) ,

A

k

=

Z

b

a

L

k

(x) w(x) dx ,

(6.32)

gdzie L

k

(x) to wielomiany (3.11). We

‘

zły tej kwadratury wybrano jako pierwiastki

wielomianu ortogonalnego:

P

N

+1

(x

k

) = 0 ,

k

= 0, 1, . . . N .

(6.33)

Zauwa˙zmy, ˙ze wyb´or wielomianu ortogonalnego jest zdeterminowany przez wage

‘

w

(x) w całce (6.18), kt´ora

‘

chcemy obliczy´c przy pomocy kwadratury. Odpowied-

nie wielomiany sa

‘

ortogonalne wzgle

‘

dem tej wagi.

Rza

‘

d kwadratury Gaussa wynosi 2

(N + 1), gdy˙z zachodzi.

Twierdzenie
Kwadratura (6.32) jest rze

‘

du 2

(N + 1) wtedy i tylko wtedy, gdy jej we

‘

zły sa

‘

pier-

wiastkami wielomianu P

N

+1

(x).

Zał´o˙zmy, ˙ze we

‘

zły kwadratury sa

‘

pierwiastkami wielomianu P

N

+1

. Roz-

wa˙zmy dowolny wielomian W

(x) stopnia < 2(N + 1). Mo˙zemy go zapisa´c

W

= a P

N

+1

+ b, gdzie a i b sa

‘

wielomianami stopnia

< (N + 1). Wtedy

(symbolicznie)

Z

W w

=

Z

a P

N

+1

w

|

{z

}

0

+

Z

b w

.

Wielomian a jest liniowa

‘

kombinacja

‘

P

0

, . . . , P

N

, wie

‘

c pierwsza całka znika

z ortogonalno´sci wielomian´ow P. Poniewa˙z kwadratura (6.21) jest dokładna
dla wieloman´ow stopnia

< (N + 1), otrzymujemy

Z

b w

=

N

∑

k

=0

A

k

b

(x

k

) .

gdzie A

k

sa

‘

dane wzorem (6.21). Rozwa˙zmy naste

‘

pnie

N

∑

k

=0

A

k

b

(x

k

) =

N

∑

k

=0

A

k

W

(x

k

) −

N

∑

k

=0

A

k

a

(x

k

) P

N

+1

(x

k

)

|

{z

}

0

.

43

Druga suma znika, gdy˙z dla wybranych we

‘

zł´ow P

N

+1

(x

k

) = 0. Ostatecznie

otrzymujemy kwadrature

‘

postaci (6.21). Dow´od twierdzenia w druga

‘

strone

‘

znale´z´c mo˙zna w podre

‘

czniku [1].

Prawdziwa jest r´ownie˙z naste

‘

puja

‘

ca własno´s´c kwadratury Gaussa.

Twierdzenie
Wsp´ołczynniki A

i

kwadratury Gaussa sa

‘

dodatnie.

Rozwa˙zmy wielomian stopnia 2N be

‘

da

‘

cy kwadratem wielomianu (3.11).

Kwadratura Gaussa jest dokładna dla tego wielomianu i wtedy

Z

b

a

w

(x) [L

i

(x)]

2

dx

=

N

∑

k

=0

A

k

[L

i

(x)]

2

=

N

∑

k

=0

A

k

δ

ik

= A

i

> 0 .

Zauwa˙zmy, ˙ze ła

‘

cza

‘

c og´olnie słuszne r´ownanie (6.21) z powy˙zsza

‘

relacja

‘

dostajemy dla kwadratury Gaussa:

A

i

=

Z

b

a

w

(x) L

i

(x) dx =

Z

b

a

w

(x) [L

i

(x)]

2

dx

.

(6.34)

Zacytujmy bez dowodu, ˙ze wsp´ołczynniki kwadratury Gaussa mo˙zna znale´z´c

ze wzoru [2]

A

k

=

hP

N

|P

N

i

P

N

(x

k

) P

′

N

+1

(x

k

)

,

k

= 0, 1, . . . , N

(6.35)

gdzie x

k

sa

‘

we

‘

złami tej kwadratury P

N

+1

(x

k

) = 0.

6.4.1

Popularne kwadratury Gaussa

Poni˙zej podajemy najbardziej popularne kwadratury Gaussa, specyfikuja

‘

c wage

‘

w

(x), przedział całkowania [a, b] oraz relacje

‘

rekurencyjna

‘

przy pomocy kt´orej

mo˙zna znale´z´c odpowiednie wielomiany ortogonalne. Ich nazwa jest okre´slona
przez drugi człon w nazwie kwadratury.

44

Gaussa-Legendre’a

w

(x) = 1

− 1 ≤ x ≤ 1

( j + 1)P

j

+1

= (2 j + 1) xP

j

− jP

j

−1

(6.36)

Gaussa-Czebyszewa

w

(x) = (1 − x

2

)

−1/2

− 1 ≤ x ≤ 1

T

j

+1

= 2xT

j

− T

j

−1

(6.37)

Gaussa-Laguerre’a

w

(x) = x

α

e

−x

0

≤ x <

∞

( j +

α

)L

α

j

+1

= (−x + 2 j +

α

+ 1)L

α

j

− ( j +

α

)L

α

j

−1

(6.38)

Gaussa-Hermite’a

w

(x) = e

−x

2

−

∞

< x <

∞

H

j

+1

= 2xH

j

− 2 jH

j

−1

(6.39)

Gaussa-Jacobiego

w

(x) = (1 − x)

α

(1 + x)

β

− 1 ≤ x ≤ 1

c

j

P

(

α

,

β

)

j

+1

= (d

j

+ e

j

x

)P

(

α

,

β

)

j

− f

j

P

(

α

,

β

)

j

−1

,

(6.40)

gdzie

α

,

β

> −1, a wsp´ołczynniki sa

‘

zadane wzorami

c

j

= 2( j + 1)( j +

α

+

β

+ 1)(2 j +

α

+

β

)

d

j

= (2 j +

α

+

β

+ 1)(

α

2

−

β

2

)

e

j

= (2 j +

α

+

β

)(2 j +

α

+

β

+ 1)(2 j +

α

+

β

+ 2)

f

j

= 2( j +

α

)( j +

β

)(2 j +

α

+

β

+ 2) .

(6.41)

Zauwa˙zmy, ˙ze dla

α

=

β

= 0 otrzymujemy wielomiany Legendre’a

P

(0,0)
j

= P

j

,

(6.42)

natomiast dla

α

=

β

= −1/2 dostajemy wielomiany Czebyszewa

P

(−1/2,−1/2)
j

= T

j

.

(6.43)

We

‘

zły i wsp´ołczynniki dla podanych kwadratur Gaussa mo˙zna znale´z´c w tabli-

cach lub podre

‘

czniku [1].

45

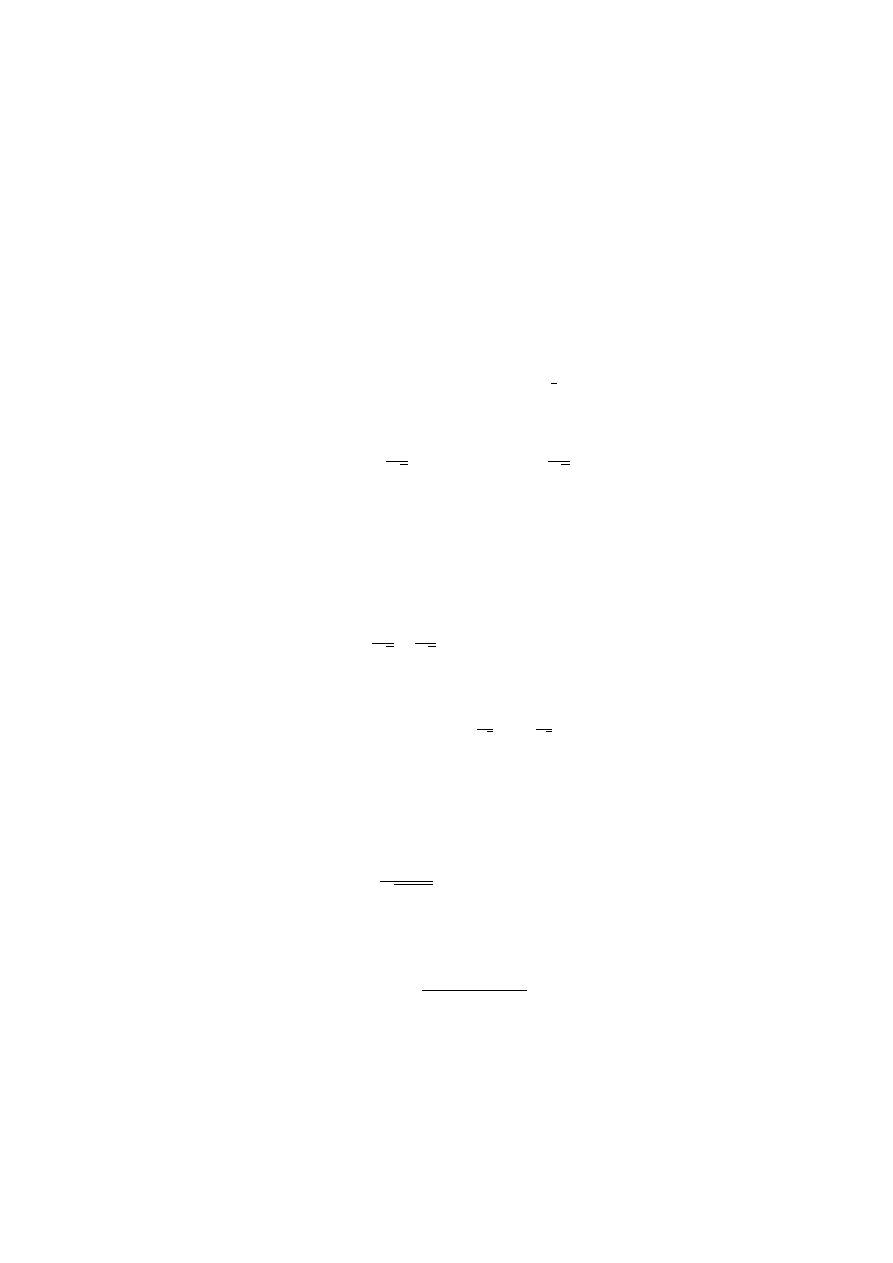
Przyklad 1

Skonstruujemy kwadrature

‘

Gaussa-Legendre’a rze

‘

du 4. Mamy do czynienia z

dwoma we

‘

złami

(x

0

, x

1

) be

‘

da

‘

cych zerami wielomianu Legendre’a P

2

. Wtedy

Z

1

−1

f

(x) dx ≈ A

0

f

(x

0

) + A

1

f

(x

1

) .

(6.44)

Znajd´zmy te we

‘

zły. Kolejne wielomiany Legendre’a to

P

0

(x) = 1 ,

P

1

(x) = x ,

P

2

(x) =

1
2

(3x

2

− 1).

(6.45)

We

‘

zły kwadratury sa

‘

rozwia

‘

zaniami r´ownania P

2

(x) = 0:

x

0

= −

1

√

3

,

x

1

=

1

√

3

.

(6.46)

Wsp´ołczynniki A

i

mo˙zna obliczy´c ze wzoru (6.35). Pro´sciej jest wykorzysta´c fakt,

˙ze kwadratura Gaussa (6.44) jest dokładna dla wielomian´ow stopnia

< 4, w szcze-

g´olno´sci dla f

(x) = 1 oraz f (x) = x. Wtedy

A

0

+ A

1

=

Z

1

−1

dx

= 2

−

A

0

√

3

+

A

1

√

3

=

Z

1

−1

x dx

= 0 .

(6.47)

Sta

‘

d wsp´ołczynniki kwadratury A

1

= A

2

= 1 i ostatecznie

Z

1

−1

f

(x) dx ≈ f (−

1

√

3

) + f (

1

√

3

) .

(6.48)

Przyklad 2

Rozwa˙zmy kwadrature

‘

Gaussa-Chebyszewa

Z

1

−1

f

(x)

√

1

− x

2

dx

≈

N

∑

k

=0

A

k

f

(x

k

) ,

(6.49)

gdzie we

‘

zły x

k

to zera wielomianu Czebyszewa T

N

+1

zadane przez (4.16). Wsp´oł-

czynniki A

k

mo˙zna wyliczy´c ze wzoru (6.35),

A

k

=

hT

N

|T

N

i

T

N

(x

k

) T

′

N

+1

(x

k

)

.

(6.50)

46

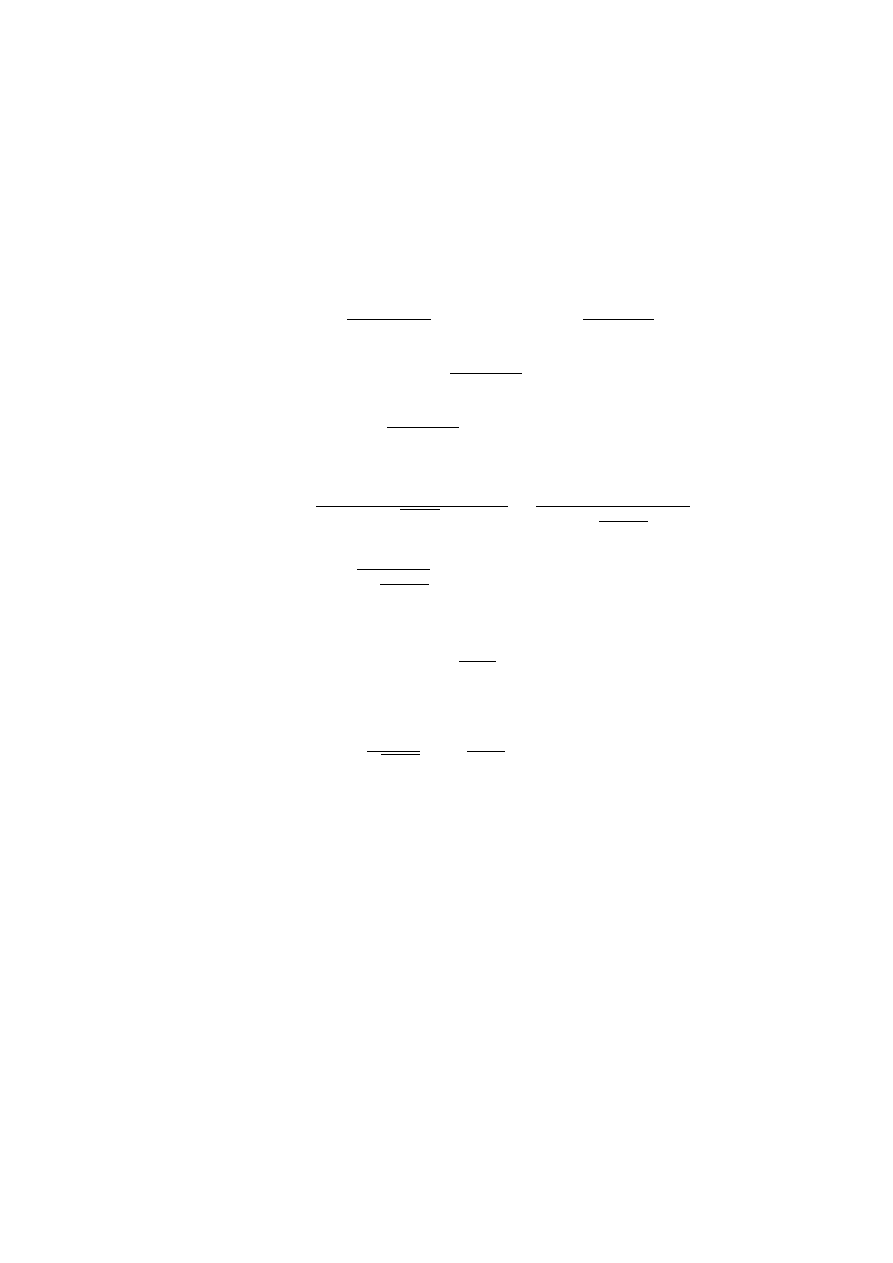
W tym celu wykorzystamy całkowa

‘

relacje

‘

ortogonalno´sci (6.31) dla wielomian´ow

Czebyszewa. Wtedy

hT

N

|T

N

i =

π

/2 ,

(6.51)

natomiast

T

N

(x

k

) = cos

N

π

(k + 1/2)

N

+ 1

= cos

π

(k + 1/2) −

π

(k + 1/2)

N

+ 1

= sin(

π

(k + 1/2)) sin

π

(k + 1/2)

N

+ 1

= (−1)

k

sin

π

(k + 1/2)

N

+ 1

(6.52)

oraz

T

′

N

+1

(x

k

) =

(N + 1) sin((N + 1) arccos x

k

)

q

1

− x

2
k

=

(N + 1) sin(

π

(k + 1/2))

sin

π

(k+1/2)

N

+1

= (−1)

k

(N + 1)

sin

π

(k+1/2)

N

+1

.

(6.53)

Sta

‘

d otrzymujemy wsp´ołczynniki kwadratury Gaussa-Czebyszewa

A

k

=

π

N

+ 1

(6.54)

Jak wida´c, wsp´ołczynniki sa

‘

niezale˙zne od k i ostatecznie

Z

1

−1

f

(x)

√

1

− x

2

dx

≈

π

N

+ 1

N

∑

k

=0

f

(x

k

) .

(6.55)

47

Rozdział 7

Zera funkcji

Nie ka˙zde r´ownanie (lub układ r´owna´n) mo˙zna rozwia

‘

za´c dokładnie. Na przykład,

nie mo˙zna poda´c og´olnych wzor´ow na rozwia

‘

zanie dowolnego r´ownanie alge-

braicznego stopnia wy˙zszego ni˙z cztery.

Rozpatrzmy zagadnienie znajdowania pierwiastka r´ownania

f

( ¯x) = 0

(7.1)

w pewnym przedziale. Prezentowane tutaj metody mo˙zna stosowa´c gdy znamy
przedział, w kt´orym znajduje sie

‘

pierwiastek. Zakładamy, ˙ze jest to pierwiastek

jednokrotny, tzn. f

(x) ∼ (x − ¯x) w jego otoczeniu. Nale˙zy wie

‘

c wcze´sniej okre´sli´c

taki przedział, na przykład wykonuja

‘

c wykres funkcji y

= f (x).

7.1

Metoda połowienia

Zakładamy, ˙ze funkcja f

(x) jest cia

‘

gła w przedziale

[a, b]. Zgodnie z twierdze-

niem Bolzano-Cauchego, je´sli na ko´ncach tego przedziału warto´sci funkcji maja

‘

przeciwne znaki,

f

(a) f (b) < 0

(7.2)

to wewna

‘

trz przedziału znajduje sie

‘

co najmniej jeden pierwiastek r´ownania (7.1).

Zgodnie z uwaga

‘

z poprzedniego rozdziału zakładamy, ˙ze jest to pierwiastek

jednokrotny. W pierwszym kroku dzielimy przedział

[a, b] na połowe

‘

x

1

=

a

+ b

2

.

(7.3)

48

Je˙zeli f

(x

1

) = 0 to x

1

jest poszukiwanym pierwiastkiem, w przeciwnym wypadku

pierwiastek le˙zy w tym z przedział´ow

[a, x

1

] lub [x

1

, b], dla kt´orego funkcja zmienia

znak na jego ko´ncach. Dzielimy ten przedział na połowe

‘

otrzymuja

‘

c x

2

. Za-

uwa˙zmy, ˙ze

|x

2

− x

1

| =

1

4

(b − a).

(7.4)

W wyniku wielokrotnego zastosowania tej procedury otrzymujemy pierwiastek ¯

x

lub cia

‘

g punkt´ow x

i

, dla kt´orych zachodzi

|x

n

− x

n

−1

| =

1

2

n

(b − a)

(7.5)

Po dostatecznie du˙zej liczbie krok´ow r´o˙znica (7.5) jest dowolnie mała. Zadaja

‘

c

wie

‘

c dokładno´s´c

ε

, przerywamy procedure

‘

z chwila

‘

gdy

|x

n

− x

n

−1

| ≤

ε

.

(7.6)

Poszukiwanym pierwiastkiem jest wtedy

¯

x

= x

n

±

ε

,

(7.7)

Przyklad

Rozwia

‘

˙zmy r´ownanie exp

(−x) = x. W tym celu poszukajmy zer funkcji

f

(x) = x − exp(−x).

(7.8)

Zero znajduje sie

‘

przedziale

[0, 1] gdy˙z f (0) = −1 i f (1) ≈ 0.63. Kolejne warto´sci

´srodk´ow przedziałow x

i

wraz z r´o˙znicami (7.5) to

n

x

n

|x

n

− x

n

−1

|

1

0.50000

0.50000

2

0.75000

0.25000

3

0.62500

0.12500

4

0.56250

0.06250

5

0.59375

0.03125

6

0.57812

0.01562

7

0.57031

0.00781

8

0.56641

0.00391

9

0.56836

0.00195

W 18 kroku otrzymujemy liczbe

‘

0.56714, kt´ora ju˙z nie ulega zmianie przy zadanej

liczbie pie

‘

ciu cyfr po przecinku (dokładno´s´c

ε

< 10

−5

).

49

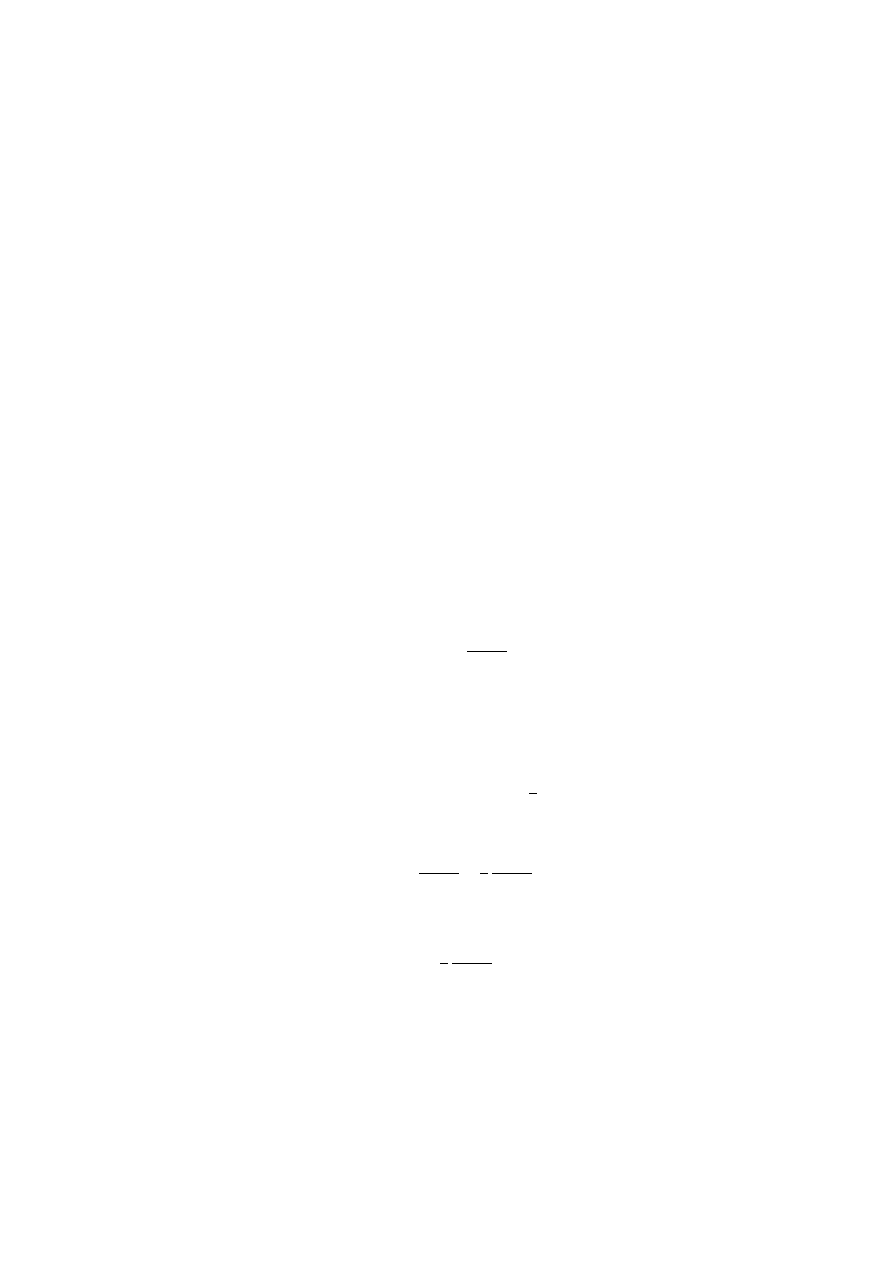
7.2

Metoda Newtona

Zał´o˙zmy, ˙ze f jest klasy C

2

w przedziale

[a, b] na ko´ncach, kt´orego zmienia znak.

Ponadto, niech pochodne f

′

oraz f

′′

maja

‘

stały znak w całym przedziale. Metoda

Newtona obejmuje wie

‘

c cztery przypadki be

‘

da

‘

ce kombinacja

‘

naste

‘

puja

‘

cych wa-

runk´ow: funkcja f jest

• rosna

‘

ca oraz wypukła ku dołowi

( f

′

> 0, f

′′

> 0)

• rosna

‘

ca oraz wypukła ku g´orze

( f

′

> 0), f

′′

< 0)

• maleja

‘

ca oraz wypukła ku dołowi

( f

′

< 0, f

′′

> 0)

• maleja

‘

ca oraz wypukła ku g´orze

( f

′

< 0, f

′′

< 0).

Przyjmuja

‘

c dla ustalenia uwagi, ˙ze obie pochodne sa

‘

dodatnie, wystawmy

styczna

‘

do wykresu funkcji w punkcie x

0

= b, w kt´orym f (x

0

) > 0:

y

− f (x

0

) = f

′

(x

0

)(x − x

0

) .

(7.9)

Kłada

‘

c y

= 0 otrzymujemy punkt przecie

‘

cia stycznej z osia

‘

x:

x

1

= x

0

−

f

(x

0

)

f

′

(x

0

)

.

(7.10)

Sta

‘

d x

1

< x

0

. Je´sli ¯

x jest poszukiwanym pierwiastkiem to tak˙ze zachodzi x

1

> ¯x.

Dow´od tego faktu polega na rozwa˙zeniu rozwinie

‘

cia Taylora wok´oł punktu

x

0

:

f

( ¯x) = f (x

0

) + f

′

(x

0

)( ¯x − x

0

) +

1

2

f

′′

(

ξ

)( ¯x − x

0

)

2

,

gdzie

ξ

∈ ( ¯x,x

0

). Poniewa˙z f ( ¯x) = 0, mamy

¯

x

= x

0

−

f

(x

0

)

f

′

(x

0

)

−

1

2

f

′′

(

ξ

)

f

′

(x

0

)

( ¯x − x

0

)

2

.

Wykorzystuja

‘

c (7.10), otrzymujemy nasza

‘

teze

‘

¯

x

− x

1

= −

1

2

f

′′

(

ξ

)

f

′

(x

0

)

( ¯x − x

0

)

2

< 0 .

50

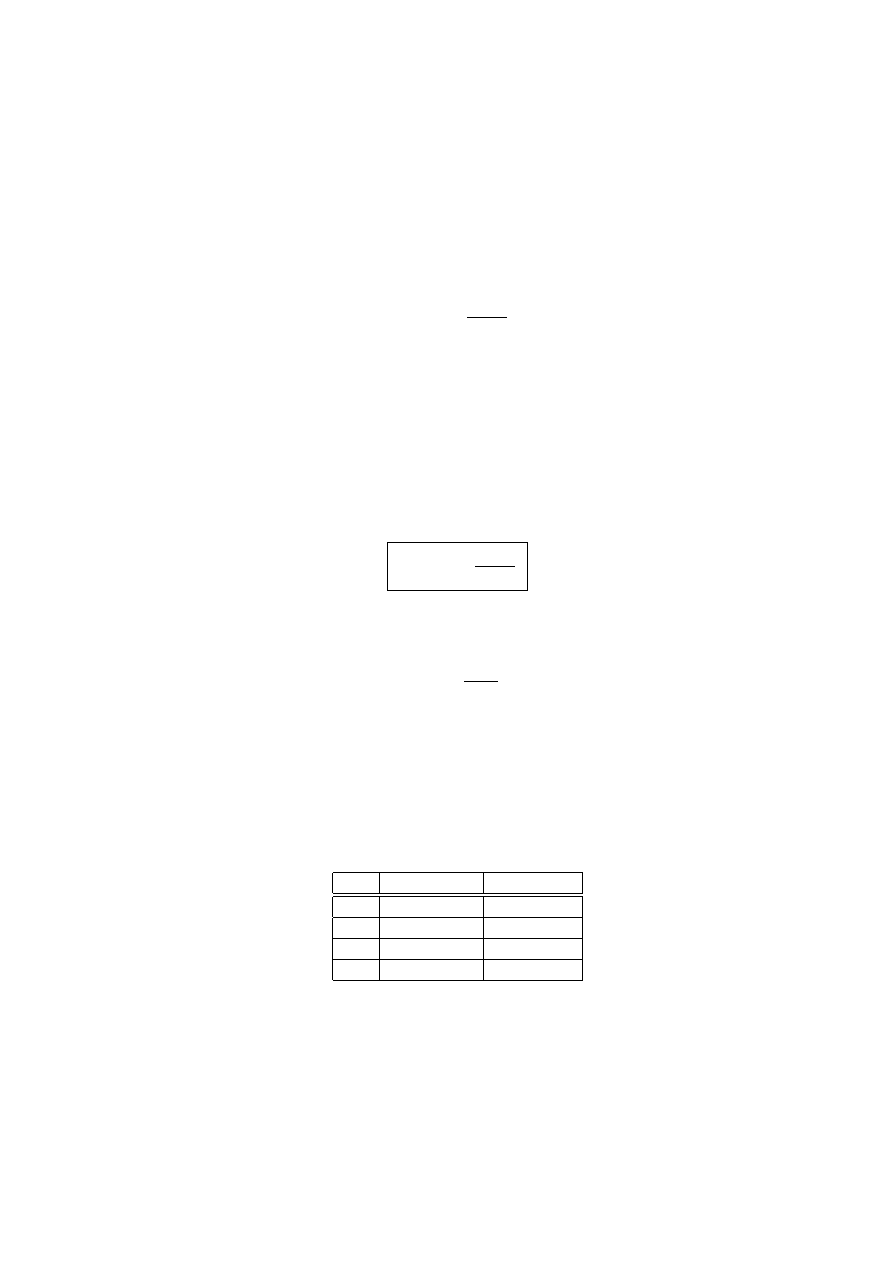
Powt´orzmy procedure

‘

, wystawiaja

‘

c styczna

‘

w punkcie

(x

1

, f (x

1

)):

y

− f (x

1

) = f

′

(x

1

)(x − x

1

) .

(7.11)

Przecina ona o´s x w punkcie x

2

< x

1

:

x

2

= x

1

−

f

(x

1

)

f

′

(x

1

)

,

(7.12)

Dow´od warunku x

2

< x

1

polega na pokazaniu, ˙ze f

(x

1

) > 0. W tym celu

skorzystajmy z twierdzenia Lagrange’a zastosowanego do przedziału

[ ¯x, x

1

]:

f

(x

1

) − f ( ¯x) = f

′

(

ζ

)(x

1

− ¯x),

ζ

∈ ( ¯x,x

1

) .

Ze wzgle

‘

du na f

( ¯x) = 0 i f

′

(

ζ

) > 0 dostajemy: f (x

1

) > 0. Podobnie jak

powy˙zej mo˙zna udowodni´c, ˙ze x

2

> ¯x.

Kolejne kroki procedury prowadza

‘

do relacji

x

n

+1

= x

n

−

f

(x

n

)

f

′

(x

n

)

.

(7.13)

Otrzymany cia

‘

g punkt´ow jest maleja

‘

cy i ograniczony od dołu: ¯

x

< x

n

. Z twierdzenia

Cauchego wynika, ˙ze istnieje granica tego cia

‘

gu g. W granicy otrzymujemy z

(7.13):

g

= g −

f

(g)

f

′

(g)

.

(7.14)

Tak wiec f

(g) = 0 i g = ¯x. Procedura Newtona jest wie

‘

c zbie˙zna do poszukiwanego

zera funkcji. W praktyce procedure

‘

przerywamy gdy

|x

n

+1

− x

n

| <

ε

.

Przyklad

Metoda Newtona jest znacznie szybciej zbie˙zna ni˙z metoda połowienia. Dla

przykładu z poprzedniego rozdziału otrzymujemy wynik po czterech krokach

n

x

n

|x

n

− x

n

−1

|

1

0.53788

0.46212

2

0.56699

0.02910

3

0.56714

0.00016

4

0.56714

0.00000

51

7.3

Metoda siecznych i metoda falsi

W metodzie Newtona konieczna jest znajomo´s´c pierwszej pochodnej funkcji f . W
metodzie siecznych unikamy tego warunku przybli˙zaja

‘

c pochodna

‘

w wyra˙zeniu

(7.13) przez iloraz r´o˙znicowy. W ten spos´ob otrzymujemy

x

n

+1

= x

n

− f (x

n

)

(x

n

− x

n

−1

)

f

(x

n

) − f (x

n

−1

)

.

(7.15)

Zatem do wyznaczenia

(n+1) przybli˙zenia poszukiwanego pierwiastka wykorzys-

tuje sie

‘

punkty

(x

n

, f (x

n

)) i (x

n

−1

, f (x

n

−1

)), przez kt´ore przeprowadza sie

‘

sieczna

‘

przecinaja

‘

ca

‘

o´s x w punkcie x

n

+1

. Aby rozpocza

‘

c procedure

‘

konieczne jest wie

‘

c

wybranie dw´och punkt´ow startowych x

0

i x

1

. W omawianej przez nas przykładzie

wybieramy x

0

= b oraz x

1

= x

0

−

∆

x z mała warto´scia

‘

r´o˙znicy

∆

x

≪ x

0

.

Metoda siecznych mo˙ze nie by´c zbie˙zna, na przykład, gdy pocza

‘

tkowe przy-

bli˙zenia nie le˙za

‘

dostatecznie blisko szukanego pierwiastka. Jako dodatkowe kry-

terium przerwania iteracji, opr´ocz warto´sci r´o˙znic

|x

n

+1

− x

n

|, nale˙zy przyja

‘

´c war-

to´sci

| f (x

n

)|, tak by tworzyły one cia

‘

g maleja

‘

cy w ko´ncowej fazie oblicze´n.

Wracaja

‘

c do przykładu, w metodzie siecznych otrzymujemy wynik 0

.56714 z

błe

‘

dem mniejszym ni˙z 10

−5

po pie

‘

ciu krokach

W metodzie falsi (fałszywej prostej) znajomo´s´c f

′

tak˙ze nie jest potrzebna.

Przy przyje

‘

tych zało˙zeniach co do funkcji ( f

′

, f

′′

> 0) przeprowadzamy kolejno

cie

‘

ciwy przez punkty

(b, f (b)) i (x

n

, f (x

n

)):

y

− f (x

n

) =

f

(b) − f (x

n

)

b

− x

n

(x − x

n

) .

(7.16)

Przecinaja

‘

one o´s x w punkcie:

x

n

+1

= x

n

− f (x

n

)

b

− x

n

f

(b) − f (x

n

)

(7.17)

Punkt

(b, f (b)) jest punktem stałym wszystkich cie

‘

ciw, natomiast pierwszym punk-

tem jest

(x

0

= a, f (a)). Mo˙zna pokaza´c, ˙ze metoda ta prowadzi do cia

‘

gu warto´sci

x

n

zbie˙znych do granicy ¯

x be

‘

da

‘

cej jednokrotnym pierwiastkiem r´ownania f

( ¯x) = 0.

52

Przyklad

W naszym przykładzie otrzymujemy w metodzie falsi:

n

x

n

|x

n

− x

i

−1

|

1

0.61270

0.61270

2

0.56384

0.04886

3

0.56739

0.00355

4

0.56713

0.00026

5

0.56714

0.00002

6

0.56714

0.00000

Jak wida´c metoda falsi jest stosunkowo wolno zbie˙zna.

53

Rozdział 8

Macierze

8.1

Układ r´owna ´n liniowych

Macierze pojawiaja

‘

sie

‘

naturalnie w problemie rozwia

‘

zywania układ´ow r´owna´n

liniowych

a

11

x

1

+ a

12

x

2

+ ... + a

1n

x

n

= y

1

a

21

x

1

+ a

22

x

2

+ ... + a

2n

x

n

= y

2

...

a

n1

x

1

+ a

n2

x

2

+ ... + a

nn

x

n

= y

n

.

(8.1)

Układ ten mo˙zna zapisa´c w postaci macierzowej











a

11

a

12

. . . a

1n

a

21

a

22

. . . a

2n

..

.

..

.

..

.

a

n1

a

n2

. . . a

nn





















x

1

x

2

..

.

x

n











=











y

1

y

2

..

.

y

n











.

(8.2)

lub w skr´oconej formie.

A x

= y .

(8.3)

Tak wie

‘

c A jest macierza

‘

kwadratowa

‘

o wymiarze n

×n. Rozwia

‘

zanie układu (8.1)

istnieje i jest ono jednoznaczne je´sli wyznacznik

det A

6= 0.

(8.4)

54

Istnieje wtedy macierz odwrotna A

−1

i rozwia

‘

zanie jest zadane przez

x

= A

−1

y

.

(8.5)

Metoda ta wymaga wie

‘

c znajomo´sci metod odwracania macierzy A.

Alternatywnie, mo˙zna skorzysta´c ze wzor´ow Cramera

x

1

=

det A

1

det A

,

x

2

=

det A

2

det A

,

. . . x

n

=

det A

n

det A

.

(8.6)

Macierze A

i

w liczniku powstały poprzez zamiane

‘

i-tej kolumny w macierzy A

przez wektor y. Przykładowo

A

1

=











y

1

a

12

. . . a

1n

y

2

a

22

. . . a

2n

..

.

..

.

..

.

y

n

a

n2

. . . a

nn











.

(8.7)

Z punktu widzenia metod numerycznych wzory Cramera mo˙zna zastosowa´c je-
dynie dla macierzy o małych wymiarach. Obliczenie wyznacznika macierzy o
wymiarze n

×n wymaga bowiem wykonanie n! mno˙ze´n oraz n! dodawa´n. We wzo-

rach (8.6) musimy policzy´n

(n + 1) wyznacznik´ow macierzy, sta

‘

d całkowita liczba

działa´n potrzebnych do znalezienia rozwia

‘

zania wynosi 2

(n + 1)!. Korzystaja

‘

c ze

wzoru Stirlinga, słusznego dla du˙zych n,

n!

≈ n

n

e

−n

√

2

π

n

∼ e

n ln n

,

(8.8)

widzimy, ˙ze liczba działa´n w metodzie Cramera ro´snie wykładniczo z n. Metoda
szybko staje sie

‘

wie

‘

c bezu˙zyteczna. Przykładowo, rozwia

‘

zuja

‘

c układ zło˙zony z 15

r´owna´n musimy wykona´c

2

· 16! ≈ 10

13

(8.9)

działa´n.

Przykład ten ilustruje zagadnienie zło˙zono´sci obliczeniowej. Wszystkie algo-

rytmy, w kt´orych liczba działa´n do wykonania ro´snie wykładniczo z wymiarem
problemu szybko staja

‘

sie

‘

bezu˙zyteczne. Aby rozwia

‘

za´c problem musimy znale´z´c

bardziej wydajne algorytmy, w kt´orych liczba działa´n zale˙zy na przykład pote

‘

gowo

od n.

55

8.2

Metoda eliminacji Gaussa

Metoda eliminacji Gaussa pozwala znale´z´c rozwia

‘

zanie układu r´owna´n liniowych

przy pote

‘

gowo zale˙znej od n liczbie wykonanych działa´n. Pozwala ona sprowadzi´c

układ (8.1) do r´ownowa˙znej postaci z macierza

‘

tr´ojka

‘

tna

‘

, w kt´orej wszystkie skła-

dowe poni˙zej (lub powy˙zej) diagonali sa

‘

r´owne zeru

















a

′

11

a

′

12

. . .

a

′

1

(n−1)

a

′

1n

0

a

′

22

. . .

a

′

2

(n−1)

a

′

2n

..

.

..

.

..

.

..

.

0

0

. . . a

′

(n−1)(n−1)

a

′

(n−1)n

0

0

. . .

0

a

′

nn































x

1

x

2

..

.

x

n

−1

x

n















=















y

′

1

y

′

2

..

.

y

′

n

−1

y

′

n















.

(8.10)

Wyznacznik macierzy tr´ojka

‘

tnej jest iloczynem liczb na diagonali

det A

′

=

n

∏

i

=1

a

′

ii

.

(8.11)

Warunkiem istnienia rozwia

‘

zania układu (8.10) jest by det A

′

6= 0. Sta

‘

d wszystkie

wyrazy na diagonali sa

‘

r´ozne od zera. Łatwo ju˙z rowia

‘

za´c taki układ. Zaczynaja

‘

c

od ostatniego r´ownania dostajemy

x

n

=

1

a

′

nn

y

′

n

x

n

−1

=

1

a

′

(n−1)(n−1)

y

′

n

−1

− a

′

(n−1)n

x

n

. . .

x

i

=

1

a

′

ii

y

′

i

−

n

∑

k

=i+1

a

′

ik

x

k

!

.

(8.12)

Rozwa˙zmy r´ownanie (8.1):

A x

= y .

W pierwszym kroku metody eliminacji Gaussa mno˙zymy pierwsze r´ownanie w
tym układzie przez a

i1

/a

11

i odejmujemy kolejno od i-tych r´owna´n, gdzie i

=

2

, 3, . . ., n. W wyniku tego otrzymamy układ r´owna´n:

A

(1)

x

= y

(1)

,

(8.13)

56

lub w jawnej postaci

a

(1)
11

x

1

+ a

(1)
12

x

2

+ ... + a

(1)
1n

x

n

= y

(1)
1

a

(1)
22

x

2

+ ... + a

(1)
2n

x

n

= y

(1)
2

...

a

(1)
n2

x

2

+ ... + a

(1)

nn

x

n

= y

(1)

n

.

(8.14)

Wyeliminowali´smy w ten spos´ob pierwsza

‘

niewiadoma

‘

w r´ownaniach o numerach

i

≥ 2.

Mno˙zymy naste

‘

pnie drugie r´ownanie w układzie (8.14) przez a

(1)
i2

/a

(1)
22

i odej-

mujemy od i-tego r´ownania dla i

= 3, 4, . . ., n. Eliminujemy wie

‘

c druga

‘

niewiado-

ma

‘

x

2

z r´owna´n o numerach i

≥ 3, otrzymuja

‘

c nowy układ:

A

(2)

x

= y

(2)

,

(8.15)

lub

a

(2)
11

x

1

+ a

(2)
12

x

2

+ a

(2)
13

x

3

+ ... + a

(2)
1n

x

n

= y

(2)
1

a

(2)
22

x

2

+ a

(2)
23

x

3

+ ... + a

(2)
2n

x

n

= y

(2)
2

...

a

(2)
n2

x

3

+ ... + a

(2)

nn

x

n

= y

(2)

n

.

(8.16)

Procedure

‘

te

‘

kontynuujemy a˙z do chwili otrzymania układu r´owna´n z macierza

tr´ojka

‘

tna

‘

:

A

(n−1)

x

= y

(n−1)

, ,

(8.17)

lub

a

(n−1)
11

x

1

+ a

(n−1)
12

x

2

+ a

(n−1)
13

x

3

+ ... + a

(n−1)
1n

x

n

= y

(n−1)
1

a

(n−1)
22

x

2

+ a

(n−1)
23

x

3

+ ... + a

(n−1)
2n

x

n

= y

(n−1)
2

...

a

(n−1)

nn

x

n

= y

(n−1)

n

. (8.18)

Naste

‘

pnie rozwia

‘

zujemy ten układ korzystaja

‘

c ze wzor´ow (8.12).

Do wyznaczenia ta

‘

metoda

‘

rozwia

‘

zania wykonujemy, odpowiednio

1
3

n

3

+ n

2

−

1
3

n

,

1
3

n

3

+

1
2

n

2

−

5
6

n

(8.19)

mno˙ze´n i dziele´n oraz dodawa´n. Całkowita liczba działa´n zale˙zy wie

‘

c pote

‘

gowo

od n.

57

8.3

Rozkład LU macierzy

Bardzo po˙zytecznym dla zastosowa´n numerycznych jest rozkład danej macierzy A
na iloczyn dw´och macierzy tr´ojka

‘

tnych L i U:

A

= L U

(8.20)

takich, ˙ze











a

11

a

12

. . . a

1n

a

21

a

22

. . . a

2n

..

.

..

.

..

.

a

n1

a

n2

. . . a

nn











=











1

0

. . . 0

l

21

1

. . . 0

..

.

..

.

..

.

l

n1

l

n2

. . . 1





















u

11

u

12

. . . u

1n

0

u

22

. . . u

2n

..

.

..

.

..

.

0

0

. . . u

nn











. (8.21)

W takim przypadku wyznaczenie rozwia

‘

zania układu r´owna´n

A x

= L(U x) = y

(8.22)

polega na rozwia

‘

zaniu dw´och układ´ow r´owna´n liniowych z macierzami tr´ojka

‘

tny-

mi

L w

= y ,

U x

= w ,

(8.23)

stosuja

‘

c metode

‘

z poprzedniego rozdziału.

Metoda eliminacji Gaussa prowadzi do rozkładu LU, gdy˙z kolejne jej kroki sa

‘

r´ownowa˙zne operacji mno˙zenia przez odpowiednie macierze L

(i)

:

A

(1)

= L

(1)

A

(8.24)

A

(2)

= L

(2)

A

(1)

. . .

A

(n−1)

= L

(n−1)

A

(n−2)

(8.25)

Podobnie dla wektor´ow y

(i)

. Kolejne macierze L to

L

(1)

=















1

0

0

. . . 0

−l

21

1

0

. . . 0

−l

31

0

1

. . . 0

..

.

..

.

..

.

..

.

−l

n1

0

0

. . . 1















l

i1

= a

i1

/a

11

,

i

> 1

(8.26)

58

naste

‘

pnie

L

(2)

=















1

0

0

. . . 0

0

1

0

. . . 0

0

−l

32

1

. . . 0

..

.

..

.

..

.

..

.

0

−l

n2

0

. . . 1















l

i2

= a

(1)

i2

/a

(1)
12

,

i

> 2

(8.27)

a˙z do macierzy L

(n−1)

.

Ostatecznie otrzymujemy

A

(n−1)

= L

(n−1)

L

(n−2)

. . . L

(1)

A

(8.28)

oraz dla wektora y:

y

(n−1)

= L

(n−1)

L

(n−2)

. . . L

(1)

y

,

(8.29)

Ka˙zda z macierzy L

(i)

jest nieosobliwa. Istnieja

‘

wie

‘

c ich macierze odwrotne, kt´ore

powstaja

‘

z L

(i)

poprzez zamiane

‘

wyste

‘

puja

‘

cych w nich minus´ow na plusy. Na

przykład,

(L

(1)

)

−1

=















1

0

0

. . . 0

l

21

1

0

. . . 0

l

31

0

1

. . . 0

..

.

..

.

..

.

..

.

l

n1

0

0

. . . 1















.

(8.30)

Odwracaja

‘

c wz´or (8.28), znajdujemy

A

= (L

(1)

)

−1

(L

(2)

)

−1

. . . (L

(n−1)

)

−1

|

{z

}

L

(A

(n−1)

)

|

{z

}

U

,

(8.31)

Otrzymujemy w ten spos´ob rozkład LU, gdy˙z A

(n−1)

jest macierza

‘

tr´ojka

‘

tna

‘

typu

U, natomiast iloczyn macierzy odwrotnych to macierz typu L,

L

=















1

0

0

. . . 0

l

21

1

0

. . . 0

l

31

l

32

1

. . . 0

..

.

..

.

..

.

..

.

l

n1

l

n2

l

n2

. . . 1















.

(8.32)

59

Wsp´ołczynniki macierzy L i U mo˙zna te˙z znale´z´c bezpo´srednio traktuja

‘

c (8.21)

jako układ n

2

r´owna´n na n

2

poszukiwanych wsp´ołczynnik´ow l

i j

(i > j) oraz u

i j

(i ≤ j). Rozwa˙zmy dla uproszczenia n = 3





a

11

a

12

a

13

a

21

a

22

a

23

a

31

a

32

a

33





=





1

0

0

l

21

1

0

l

31

l

32

1









u

11

u

12

u

13

0

u

22

u

23

0

0

u

33





.

(8.33)

Mno˙za

‘

c pierwszy wiersz macierzy L przez kolumny macierzy U, otrzymujemy

u

11

= a

11

u

12

= a

12

u

13

= a

13

.

(8.34)

Mno˙za

‘

c drugi wiersz macierzy L, znajdujemy

l

21

a

11

= a

21

l

21

a

12

+ u

22

= a

22

l

21

a

13

+ u

23

= a

23

.

Sta

‘

d mo˙zna wyznaczy´c

l

21

= a

21

/a

11

u

22

= a

22

− l

21

a

12

u

23

= a

23

− l

21

a

13

.

(8.35)

Mno˙za

‘

c trzeci wiersz macierzy L, dostajemy

l

31

a

11

= a

31

l

31

a

12

+ l

32

u

22

= a

32

l

31

a

13

+ l

32

u

23

+ u

33

= a

33

,

co prowadzi do

l

31

= a

31

/a

11

l

32

= (a

32

− l

31

a

12

)/u

22

u

33

= a

33

− l

31

a

13

− l

32

u

23

.

(8.36)

Przedstawiona metoda nazywa sie

‘

metoda

‘

Doolittle’a. Rozwia

‘

zuja

‘

c przy jej

pomocy układ r´owna´n (8.1) wykonuje sie

‘

tyle samo dzia

‘

ła´n algebraicznych co w

metodzie eliminacji Gaussa. Zale˙zno´s´c od n jest wie

‘

c pote

‘

gowa.

60

8.3.1

Wyznacznik

Rozkładu LU umo˙zliwia tak˙ze policzenie wyznacznika macierzy A, korzystaja

‘

c z

własno´sci wyznacznika iloczynu macierzy:

det A

= det L · det U

(8.37)

oraz z faktu, ˙ze wyznacznik macierzy tr´ojka

‘

tnej jest iloczynem liczb na diagonali.

Tak wie

‘

c

det A

=

n

∏

i

=1

u

ii

.

(8.38)

61

Rozdział 9

R´ownania r´o˙zniczkowe
zwyczajne

R´ownanie r´o˙zniczkowe zwyczajne rze

‘

du pierwszego ma posta´c

dy

dt

= F(t, y) .

(9.1)

Funkcja y

= y(t) jest rozwia

‘

zaniem je´sli po podstawieniu do (9.1) otrzymujemy

to˙zsamo´s´c. Rozwia

‘

zanie jest wyznaczone jednoznacznie poprzez zadanie warunku

pocza

‘

tkowego:

y

(t

0

) = y

0

.

(9.2)

Układ r´owna´n r´o˙zniczkowych 1. rze

‘

du to

dy

1

dt

= F

1

(t, y

1

, y

2

, . . . y

n

)

dy

2

dt

= F

2

(t, y

1

, y

2

, . . . y

n

)

...

dy

n

dt

= F

n

(t, y

1

, y

2

, . . . y

n

) .

(9.3)

Wprowadzaja

‘

c notacje

‘

wektorowa

‘

y

= (y

1

, y

2

, . . . y

n

) ,

F

= (F

1

, F

2

, . . . F

n

)

(9.4)

układ (9.3) mo˙zemy zapisa´c w formie identycznej z (9.1)

dy

dt

= F(t, y) .

(9.5)

62

Rozwia

‘

zanie y

= y(t) układu (9.3) jest wyznaczone jednoznacznie poprzez warunek

pocza

‘

tkowy

y

(t

0

) = (y

10

, y

20

, . . . , y

n0

) ≡ y

0

.

(9.6)

Przyklad

Rozwia

‘

zaniem r´ownania

dy

dt

= y

z warunkiem pocza

‘

tkowym y

(0) = 2 jest y(t) = 2 exp(t), co łatwo sprawdzi´c poprzez

proste podstawienie.

R´ownanie r´o˙zniczkowe zwyczajne rze

‘

du n ma posta´c

d

n

y

dt

n

= F(t, y, y

(1)

, y

(2)

, . . . y

(n−1)

) ,

(9.7)

gdzie y

(k)

jest k-ta

‘

pochodna

‘

. Rozwia

‘

zanie y

= y(t) jest wyznaczone jednoznacznie

przez warunki pocza

‘

tkowe

y

(t

0

) = y

10

,

y

(1)

(t

0

) = y

20

,

. . .

y

(n−1)

(t

0

) = y

n0

.

(9.8)

Ka˙zde r´ownanie r´o˙zniczkowe zwyczajne rze

‘

du n mo˙zna zapisa´c jako układ n

r´owna´n 1. rze

‘

du. Wprowad´zmy bowiem oznaczenia

y

1

= y ,

y

2

= y

(1)

,

. . .

y

n

= y

(n−1)

.

(9.9)

Wtedy r´ownanie (9.7) mo˙zna zapisa´c w r´ownowa˙znej formie układu r´owna´n 1.
rze

‘

du:

dy

1

dt

= y

2

dy

2

dt

= y

3

...

dy

n

dt

= F(t, y

1

, y

2

, . . . y

n

) .

(9.10)

Z obserwacji tej wynika wniosek, ˙ze r´ownanie (9.1) jest podstawowym obiektem
zainteresowa´n. Rozwinie

‘

cie metod przybli˙zonego rozwia

‘

zywania tego r´ownania

63

pozwala na znalezienie rozwia

‘

za´n dla układu r´owna´n (9.5), a tym samym dla

r´owna´n wy˙zszych rze

‘

d´ow (9.7).

Przyklad

Rozwa˙zmy r´ownanie Newtona (masa m

= 1)

d

2

r

dt

2

= F

t

, r,

dr

dt

.

(9.11)

Definiuja

‘

c v

= dr/dt dostajemu układ r´owna´n 1. rze

‘

du dla funkcji

(r, v):

dr

dt

= v

(9.12)

dv

dt

= F(t, r, v) .

(9.13)

9.1

Metody Eulera

Prezentowane tutaj metody znajdowania przybli˙zonych rozwia

‘

za´n r´ownania (9.1)

bazuja

‘

na dyskretyzacji przedziału czasu

[t

0

, T ], w kt´orym chcemy znale´z´c rozwia

‘

-

zanie

t

0

< t

1

. . . < t

n

−1

< t

n

. . . < T .

(9.14)

Zał´o˙zmy, ˙ze punkty czasowe sa

‘

r´ownoodległe:

t

n

−t

n

−1

=

τ

.,

(9.15)

Omawiane metody dostarczaja

‘

rekurencji wia

‘

˙za

‘

cej warto´s´c rozwia

‘

zania y

n

+1

w

chwili t

n

+1

z warto´sciami rozwia

‘

zania y

n

w chwili wcze´sniejszej t

n

:

y

n

+1

= f (t

n

, y

n

) .

(9.16)

Warto´s´c y

0

= y(t

0

) jest zadana przez warunek pocza

‘

tkowy (9.2). Bardzo wa˙znym

zagadnieniem tak okre´slonych metod jest numeryczna stabilno´s´c rozwia

‘

zania dla

du˙zych czas´ow T .

Punktem wyj´scia metod Eulera jest r´ownanie otrzymane po scałkowaniu po

czasie obu stron r´ownania (9.1) w przedziale

(t

n

, t

n

+1

):

y

n

+1

= y

n

+

Z

t

n

+1

t

n

F

(t, y(t)) dt .

(9.17)

64

Poniewa˙z nie znamy y

(t) w funkcji podcałkowej musimy zastosowa´c metode

‘

przy-

bli˙zona

‘

obliczenia tej całki. Wykorzystuja

‘

c wz´or (6.4) na całkowanie metoda

‘

pros-

toka

‘

t´ow,

Z

t

n

+1

t

n

dt F

(t, y(t)) ≃

τ

F

(t

n

, y

n

) .,

(9.18)

otrzymujemy relacje

‘

rekurencyjna

‘

w metodzie Eulera:

y

n

+1

= y

n

+

τ

F

(t

n

, y

n

)

(9.19)

Zauwa˙zmy, ˙ze mogliby´smy przybli˙zy´c całke

‘

(9.18) przez warto´s´c funkcji dla

g´ornej granicy:

y

n

+1

= y

n

+

τ

F

(t

n

+1

, y

n

+1

) .

(9.20)

Pojawia sie

‘

jednak w tym momencie problem, gdy˙z nieznane y

n

+1

wyste

‘

puje po

obu stronach r´ownania. Nale˙załoby wie

‘

c u˙zy´c dodatkowo metody poszukiwania

zer z rozdziału 7. Jest to do´s´c niepraktyczne, chocia˙z r´ownanie (9.20) mo˙ze by´c
lepsze ze wzgle

‘

du na stabilno´s´c numeryczna

‘

rozwia

‘

zania. Zagadnienie to zostanie

om´owione w naste

‘

pnym rozdziale.

Przybli˙zmy całke

‘

w r´ownaniu (9.17) stosuja

‘

c metoda

‘

trapez´ow (6.7):

Z

t

n

+1

t

n

F

(t, y(t)) dt ≃

τ

2

(F(t

n

, y

n

) + F(t

n

+1

, y

n

+1

)) .

(9.21)

Sta

‘

d

y

n

+1

= y

n

+

τ

2

(F(t

n

, y

n

) + F(t

n

+1

, y

n

+1

)) .

(9.22)

Podobnie jak we wzorze (9.20), nieznana warto´s´c y

n

+1

znajduje sie

‘

po obu stronach

r´ownania rekurencyjnego. Nale˙zy wie

‘

c wykorzysta´c jedna

‘

z metod znajdowania

zer funkcji z rozdziału 7.

Alternatywna

‘

metoda

‘

jest dwustopniowa procedura. Najpierw okre´slamy prze-

widywa

‘

warto´s´c y

n

+1

korzystaja

‘

c z metody Eulera (9.19):

¯

y

n

+1

= y

n

+

τ

F

(t

n

, y

n

) ,

(9.23)

a naste

‘

pnie obliczamy poprawiona

‘

warto´s´c:

y

n

+1

= y

n

+

τ

2

(F(t

n

, y

n

) + F(t

n

+1

, ¯y

n

+1

))

(9.24)

Sta

‘

d nazwa metody przewid´z i popraw.

65

9.2

Stabilno´s´c numeryczna rozwia¸za ´n

Rozwa˙zmy r´ownanie r´o˙zniczkowe

dy

dt

= −

λ

y

,

λ

> 0 .

(9.25)

Rozwia

‘

zanie dokładne to

y

(t) = y

0

e

−

λ

t

,

(9.26)

kt´ore da

‘

˙zy do zera dla t

→

∞

. Szukaja

‘

c rozwia

‘

zania metoda

‘

Eulera (9.19), otrzy-

mujemy

y

n

+1

= y

n

−

λτ

y

n

= (1 −

λτ

) y

n

,

(9.27)

co prowadzi do naste

‘

puja

‘

cej relacji dla kolejnych chwil t

n

= n

τ

:

y

n

= (1 −

λτ

)

n

y

0

.

(9.28)

Powy˙zsze rozwia

‘

znie dobrze przybli˙za rozwia

‘

zanie dokładne (9.26) pod warun-

kiem, ˙ze krok czasowy

τ

jest dostatecznie mały i słuszne jest

|1 −

λτ

| < 1

=>

0

<

τ

<

2

λ

.

(9.29)

Wprzeciwnym przypadku

|y

n

| →

∞

dla rosna

‘

cych n.

Najprostszym rozwia

‘

zaniem dla tego problemu (opr´ocz dobrania

τ

≪ 2/

λ

) jest

skorzystanie ze wzoru Eulera (9.20). Wtedy otrzymujemy dla naszego r´ownania

y

n

+1

= y

n

−

λτ

y

n

+1

,

(9.30)

co prowadzi do

y

n

+1

=

y

n

1

+

λτ

.

(9.31)

Warto´s´c 1

/(1 +

λτ

) < 1 i metoda ta jest stabilna niezale˙znie od kroku

τ

oraz

warto´sci

λ

.

Rozwa˙zmy układ dw´och r´owna´n r´o˙zniczkowych

dy

dt

= −Ay

(9.32)

z macierza

‘

A o dodatnich warto´sciach własnych

λ

1

oraz

λ

2

. Rozwia

‘

zanie jest suma

‘

dw´och rozwia

‘

za´n:

y

(t) = e

−

λ

1

t

y

1

+ e

−

λ

2

t

y

2

.

(9.33)

66

Je˙zeli

λ

2

≫

λ

1

to drugie rozwia

‘

zanie szybko da

‘

zy do zera i przestaje by´c istotne.

W numerycznej realizacji drugie rozwia

‘

zanie mo˙ze jednak odgrywa´c kluczowa

‘

role

‘

, prowadza

‘

c do niestabilnego zachowania całego rozwia

‘

zania. Stosuja

‘

c metode

‘

Eulera (9.19), otrzymujemy

y

n

= (1 −

λ

1

τ

)

n

y

1

+ (1 −

λ

2

τ

)

n

y

2

.

(9.34)

Je´sli krok czasowy

τ

> 2/

λ

2

to wyra˙zenie

|1 −

λ

2

τ

| > 1, co prowadzi do rosna

‘

cych

i oscyluja

‘

cych warto´sci y

n

gdy n

→

∞

. Nawet dla

τ

≤ 2/

λ

2

rozwia

‘

zanie zachowuje

charakter oscylacyjny dla niezbyt długich czas´ow.

Podsumowuja

‘

c, drugie rozwia

‘

zanie okre´sla krok czasowy przy kt´orym rozwia

‘

-

zanie (9.34) jest stabilne numerycznie

τ

≪ 2/

λ

2

.

(9.35)

Cena

‘

jest zwykle

‘

mała warto´s´c

τ

, czyli du˙za liczba krok´ow n

= t/

τ

by osia

‘

gnac

ko´ncowe t.

Przyklad

Je˙zeli

y

(t) = e

−t

y

1

+ e

−1000 t

y

2

,

(9.36)

to krok

τ

≪ 2 · 10

−3

, a całkowita liczba krok´ow n

≫ 10

3

dla t

∼ 1.

9.3

Metoda Rungego-Kutty

Zastosujmy rozwinie

‘

cie Taylora do rozwia

‘

zania r´ownania (9.1):

y

(t

n

+1

) = y(t

n

+

τ

) = y(t

n

) +

τ

dy

(t

n

)

dt

+

τ

2

2

d

2

y

(t

n

)

dt

2

+ . . . .

(9.37)

Korzystaja

‘

c z to˙zsamo´sci

d

2

y

dt

2

=

dF

(t, y)

dt

=

∂

F

∂

t

+

∂

F

∂

y

dy

dt

=

∂

t

F

+ F

∂

y

F

,

(9.38)

w kt´orej wykorzystali´smy r´ownania ruchu (9.1), otrzymujemy

y

n

+1

= y

n

+

τ

F

(t

n

, y

n

) +

τ

2

2

{

∂

t

F

+ F

∂

y

F

}(t

n

, y

n

) +

O

(

τ

3

) ,

(9.39)

67

Jest to wz´or ´scisły i mo˙zmy go wykorzysta´c do znajdowania rozwia

‘

zania. Wada

‘

tej metody jest konieczno´s´c znajomo´sci pochodnych funkcji F.

Zaniedbanie wyraz´ow

O

(

τ

2

) w (9.39) prowadzi do wzoru Eulera (9.19). Meto-

da przewid´z i popraw daje zgodno´s´c ze wzorem (9.39) z dokładno´scia

‘

do wyraz´ow

O

(

τ

3

). Rozwijaja

‘

c bowiem (9.24) z dokładno´scia

‘

do wyraz´ow kwadratowych w

τ

otrzymamy wz´or (9.39).

Metoda Rungego-Kutty pozwala unikna

‘

´c problemu pochodnych po prawej stro-

nie wzoru (9.39) poprzez wzie

‘

cie warto´sci F w odpowiednio dobranych punktach

pomie

‘

dzy t

n

i t

n

+1

. W metodzie drugiego rze

‘

du wybiera sie

‘

dwa takie punkty:

k

1

=

τ

F

(t

n

, y

n

)

k

2

=

τ

F

(t

n

+ a

τ

, y

n

+ a k

1

)

y

n

+1

= y

n

+

α

1

k

1

+

α

2

k

2

,

(9.40)

gdzie wsp´ołczynniki

α

1

,

α

2

i a sa

‘

tak dobrane by spełni´c r´ownanie (9.39) po roz-

winie

‘

ciu (9.40) w szereg w zmiennej

τ

. Rozwijaja

‘

c k

2

otrzymujemy:

k

2

=

τ

{F + a

τ ∂

t

F

+ a k

1

∂

y

F

} =

τ

{F + a

τ ∂

t

F

+ a

τ

F

∂

y

F

}

=

τ

F

+ a

τ

2

(

∂

t

F

+ F

∂

y

F

) ,

(9.41)

gdzie wszystkie funkcje po prawej stronie sa

‘

wzie

‘

te w punkcie

(t

n

, y

n

).

Podstawiaja

‘

c do (9.40), otrzymujemy

y

n

+1

= y

n

+ (

α

1

+

α

2

)

τ

F

+

α

2

a

τ

2

(

∂

t

F

+ F

∂

y

F

) +

O

(

τ

3

) .

Zgodno´s´c z (9.39) wymaga spełnienia warunk´ow

α

1

+

α

2

= 1

α

2

a

=

1
2

.

(9.42)

Jednym z mo˙zliwych wybor´ow jest

α

1

=

α

2

= 1/2

a

= 1 .

(9.43)

68

Otrzymujemy w ten spos´ob wzory dla metody Rungego-Kutty drugiego rze

‘

du:

k

1

=

τ

F

(t

n

, y

n

)

k

2

=

τ

F

(t

n

+

τ

, y

n

+ k

1

)

y

n

+1

= y

n

+

1
2

(k

1

+ k

2

)

(9.44)

Jak łatwo zauwa˙zy´c wzory te sa

‘

identyczne ze wzorami (9.23) i (9.24) w metodzie

przewid´z i popraw. Dla układu r´owna´n r´o˙zniczkowych (9.5) otrzymujemy wzory
analogiczne do powy˙zszych, zapisane w formie wektorowej

k

1

=

τ

F

(t

n

, y

n

)

k

2

=

τ

F

(t

n

+

τ

, y

n

+ k

1

)

y

n

+1

= y

n

+

1
2

(k

1

+ k

2

)

(9.45)

W metodzie czwartego rze

‘

du otrzymuje sie

‘

naste

‘

puja

‘

ce wzory dla układu r´owna´n

r´o˙zniczkowych:

k

1

=

τ

F

(t

n

, y

n

)

k

2

=

τ

F

(t

n

+

1
2

τ

, y

n

+

1
2

k

1

)

k

3

=

τ

F

(t

n

+

1
2

τ

, y

n

+

1
2

k

2

)

k

4

=

τ

F

(t

n

+

τ

, y

n

+ k

3

)

y

n

+1

= y

n

+

1
6

(k

1

+ 2k

2

+ 2k

3

+ k

4

) .

(9.46)

Relacja (9.46) jest zgodna z rozwie

‘

ciem Taylora (9.37) rozwia

‘

zania r´ownania r´o˙z-

niczkowego a˙z do wyraz´ow rze

‘

du

τ

4

.

69

Rozdział 10

Metody Monte Carlo

Podstawowym elementem metod Monte Carlo sa

‘

liczby losowe (zmienne loso-

we), kt´ore sa

‘

generowane z pewnym prawdopodobie´nstwem. Og´olnie, metody te

stosuje sie

‘

w dw´och klasach problem´ow.

• Do symulacji proces´ow o charakterze stochastycznym, w kt´orych wynik po-

jawia sie

‘

z okre´slonym prawdopodobie´nstwem.

• Przy obliczaniu całek jako sum liczb losowych. Zaleta

‘

metod Monte Carlo

jest mo˙zliwo´s´c obliczania wielowymiarowych całek po skomplikowanych
obszarach w wielowymiarowej przestrzeni. Na og´oł inne metody całkowania
zawodza

‘

w takich przypadkach.

10.1

Zmienna losowa i jej rozkład

Zmienna losowa X przyjmuja

‘

ca warto´sci rzeczywiste jest zdefiniowana przez rozkład

prawdopodobie´nstwa p

(x) ≥ 0 o naste

‘

pujacych własno´sciach.

• Niech P(x < X < x + dx) jest prawdopodobie´nstwem, ˙ze zmienna losowa X

przyjmuje warto´sci z infinitezymalnego przedziału:

(x, x + dx). Wtedy

P

(x < X < x + dx) = p(x) dx .

(10.1)

70

• Prawdopodobie´nstwo, ˙ze zmienna losowa przyjmuje warto´sci w sko´nczonym

przedziale jest okre´slone przez całke

‘

P

(a < X < b) =

Z

b

a

p

(x) dx

(10.2)

• Całkowite prawdopodobie´nstwo P(−

∞

< X <

∞

) = 1. Sta

‘

d warunek nor-

malizacji

Z

∞

−

∞

p

(x) dx = 1 .

(10.3)

Zmienna losowa X mo˙ze przyjmowa´c warto´sci dyskretne:

{x

1

, x

2

, . . . , x

N

}. Wte-

dy jej rozkład prawdopodobie´nstwa jest dany przez

p

(x) =

N

∑

i

=1

p

i

δ

(x − x

i

) ,

N

∑

i

=1

p

i

= 1 .

(10.4)

gdzie normalizacja wynika z warunku (10.3).

Funkcja rzeczywista f

(X) zmiennej losowej X jest tak˙ze zmienna

‘

losowa

‘

.

Warto´s´c ´srednia tej zmiennej losowej

h f (X)i jest okre´slona przez

h f (X)i =

Z

∞

−

∞

f

(x) p(x) dx

(10.5)

W szczeg´olno´sci, rozkład prawdopodobie´nstwa p

(x) zmiennej losowej X jest

scharakteryzowany przez momenty rozkładu

hX

n

i =

Z

∞

−

∞

x

n

p

(x) dx ,

n

= 1, 2, . . .

(10.6)

Pierwszy moment

(n = 1) to warto´s´c ´srednia zmiennej losowej X:

hXi =

Z

∞

−

∞

x p

(x) dx .

(10.7)

Wariancja zmiennej losowej X to

σ

2
X

=

Z

∞

−

∞

(x − hXi)

2

p

(x) dx =

(X − hXi)

2

.

(10.8)

Jest ona miara

‘

rozrzutu zmiennej losowej wok´oł jej warto´sci ´sredniej. Łatwo

udowodni´c, ˙ze wariancja wyra˙za sie

‘

poprzez dwa pierwsze momenty

σ

2
X

=

X

2

− hXi

2

(10.9)

Pierwiastek kwadratowy z wariancji nazywa sie

‘

odchyleniem stadardowym.

71

Przyklad

Przedstawmy dwa wa˙zne rozkłady cia

‘

głych zmiennej losowej X .

• Rozkład jednostajny:

p

(x) =

1

x

∈ [0,1]

0

poza

.

(10.10)

Warto´s´c ´srednia

hXi = 1/2, natomiast wariancja

σ

2

X

= 1/12.

• Rozkład normalny Gaussa z parametrami µ oraz

σ

2

:

p

(x) =

1

√

2

πσ

2

e

−

(x−µ)

2

2

σ

2

(10.11)

Warto´s´c ´srednia

hXi = µ, natomiast wariancja

σ

2

X

=

σ

2

.

Przykładami rozkład´ow dyskretnych zmiennych losowych sa

‘

.

• Rozkład dwumianowy. Rozwa˙zmy N niezale˙znych pr´ob (np. rzut moneta

‘

).

Pytamy jakie jest prawdopodobie´nstwo odniesienia n sukces´ow, je´sli praw-
dopodbie´nstwo pojedynczego sukcesu wynosi q. Zmienna losowa X opisuje
liczbe

‘

sukces´ow przyjmuja

‘

c warto´sci n

= 0, 1, . . . N, natomiast jej rozkład to

p

(n) =

N

n

q

n

(1 − q)

N

−n

.

(10.12)

Warto´s´c ´srednia

hXi = Nq, natomiast dyspersja

σ

2

X

= Nq(1 − q).

• Rozkład Poissona. Zmienna losowa X przyjmuje warto´sci n = 0,1,2,....

Jej rozkład jest dany przez

p

(n) =

µ

n

n!

e

−µ

,

µ

> 0 .

(10.13)

Warto´s´c ´srednia

hXi = µ, a dyspersja

σ

2

X

= µ. Rozkład Poissona mo˙zna

otrzyma´c z rozkładu dwumianowego w granicy: N

→

∞

, q → 0 takiej, ˙ze

Nq

= µ = const. Opisuje on wie

‘

c liczbe

‘

sukces´ow w bardzo du˙zej pr´obie,

gdy prawdopodobie´nstwo pojedynczego sukcesu jest małe.

Dla µ

=

λ

t rozkład Poissona opisuje rozpad promieniotw´orczy, odpowiadaja

‘

c

na pytanie jakie jest prawdopodbie´nstwo zaj´scia n rozpad´ow w przedziale
czasowym

[0,t]. Zakłada sie

‘

, ˙ze rozpady sa

‘

niezale˙zne, natomiast

λ

jest

prawdopodobie´nstwem na jednostke

‘

czasu wysta

‘

pienia dokładnie jednego

rozpadu w dowolnej chwili czasu.

72

10.1.1

Rozkład wielu zmiennych losowych

La

‘

czny rozkład prawdopodobie´nstwa p

(x, y) ≥ 0 dw´och zmiennych losowych X i

Y jest zdefiniowany poprzez relacje

‘

p

(x, y) dx dy = P(x < X < x + dx i y < Y < y + dy) ,

(10.14)

gdzie wielko´s´c po prawej stronie to prawdopodobie´nstwo, ˙ze warto´sci zmiennych
losowych le˙za

‘

w zaznaczonych przedziałach. Warunek normalizacji przyjmuje

teraz posta´c

∞

Z

−

∞

∞

Z

−

∞

p

(x, y) dx dy = 1 .

(10.15)

Warto´sci ´srednie zmiennych losowych

hXi oraz hY i to

hXi =

∞

Z

−

∞

∞

Z

−

∞

x p

(x, y) dx dy ,

hY i =

∞

Z

−

∞

∞

Z

−

∞

y p

(x, y) dx dy .

(10.16)

Kowariancja zmiennych losowych cov

(X,Y ) jest zdefiniowana jako

cov

(X,Y ) = h(X − hXi)(Y − hY i)i

(10.17)

=

∞

Z

−

∞

∞

Z

−

∞

(x − hXi)(y − hY i) p(x,y)dx dy = hXY i − hXihY i

Kowariancja jest miara

‘

korelacji zmiennych losowych X i Y .

Rozkłady brzegowe zmiennych losowych definiuje sie

‘

poprzez

p

X

(x) =

∞

Z

−

∞

∞

Z

−

∞

p

(x, y) dy ,

p

Y

(y) =

∞

Z

−

∞

∞

Z

−

∞

p

(x, y) dx .

(10.18)

Sa

‘

to zatem rozkłady jednej zmiennej losowej niezale˙znie od warto´sci pozostałych

zmiennych losowych. Warunek (10.15) prowadzi do wniosku, ˙ze rozkłady brze-
gowe sa

‘

unormowymi do jedynki rozkładami prawdopodobie´nstwa

∞

Z

−

∞

p

X

(x) dx =

∞

Z

−

∞

p

Y

(y) dy = 1 .

(10.19)

73

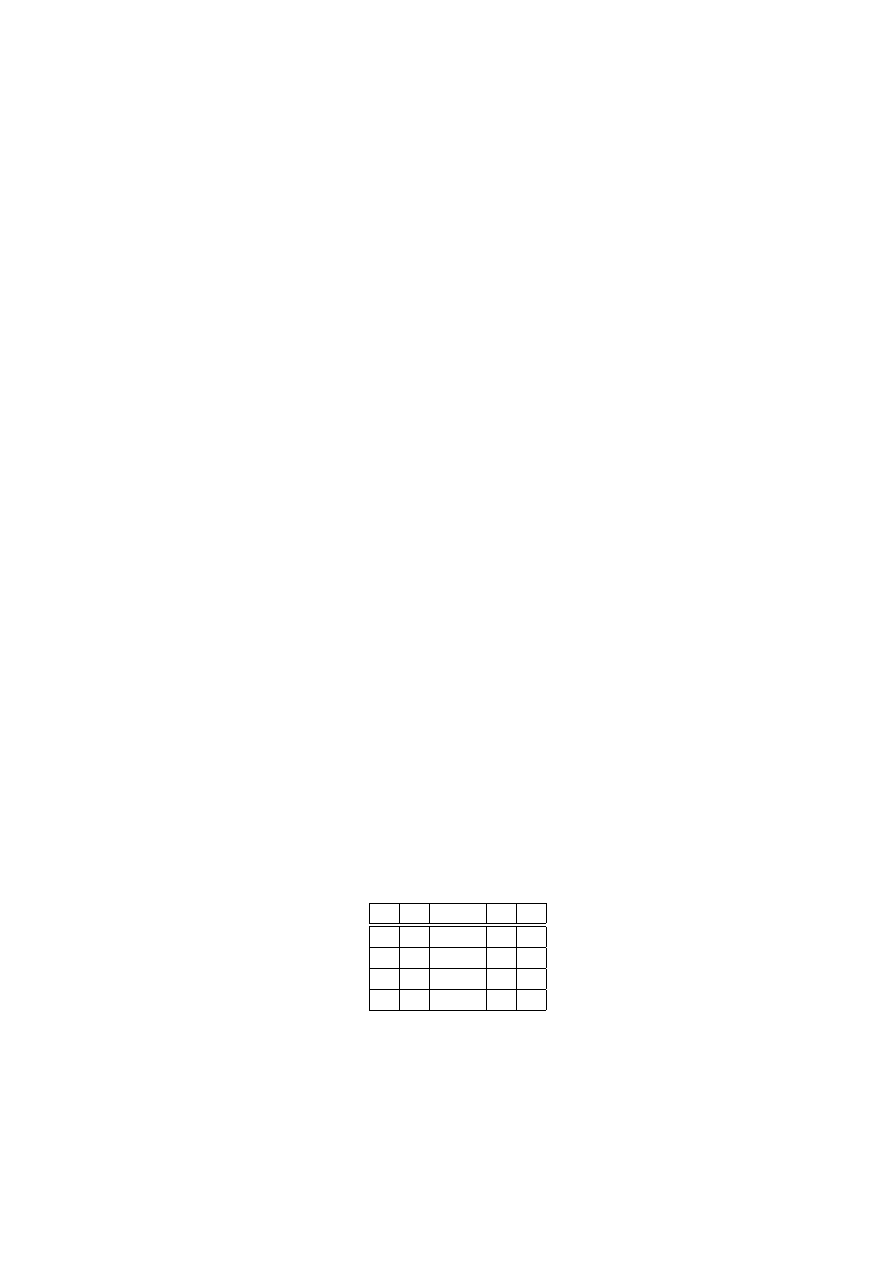
10.1.2

Niezale˙zno´s´c zmiennych losowych

Jednym z najwa˙zniejszych problem´ow dla wielu zmiennych losowych jest pytanie
o ich niezale˙zno´s´c.

Zmienne losowe X i Y sa

‘

niezale˙zne je´sli ich łaczny rozkład prawdopodobie´n-

stwa jest iloczynem rozkład´ow brzegowych:

p

(x, y) = p

X

(x) p

Y

(y) .

(10.20)

Istotnym jest rozr´o˙znienie pomie

‘

dzy niezale˙zno´scia zmiennych losowych a

brakiem korelacji mie

‘

dzy nimi.

Dwie zmienne losowe X i Y sa

‘

nieskorelowane, gdy ich kowariancja znika:

cov

(X,Y ) = hXY i − hXihY i = 0.

(10.21)

Korelacja dotyczy drugich moment´ow zmiennych losowych, jest wie

‘

c poje

‘

ciem

słabszym ni˙z niezale˙zno´s´c, kt´ora odnosi sie

‘

do własno´sci całego rozkładu.

Tak wie

‘

c, niezale˙zne zmienne losowe sa

‘

nieskorelowane, gdy˙z

hXY i − hXihY i =

∞

Z

−

∞

∞

Z

−

∞

x y p

X

(x) p

Y

(y) dx dy −

∞

Z

−

∞

x p

X

(x) dx

∞

Z

−

∞

y p

Y

(y) dy = 0.

Twierdzenie odwrotne nie jest prawdziwe. Jak pokazuje przykład poni˙zej, istnieja

‘

nieskorelowane zmienne losowe, kt´ore nie sa

‘

niezale˙zne. Warunek (10.20) nie jest

zatem dla nich spełniony.

Przyklad

Dwie zmienne losowe X i Y przyjmuja

‘

warto´sci

{0,1}. Ich ła

‘

czny rozkład

prawdopodobie´nstwa jest podany w tabelce. Rozwa˙zmy nowe zmienne losowe:

U

= X +Y przyjmuja

‘

ca

‘

warto´sci

{0,1,2} oraz V = |X −Y | o warto´sciach {0,1}.

X

Y

p(x,y)

U

V

0

0

1/4

0

0

1

0

1/4

1

1

0

1

1/4

1

1

1

1

1/4

2

0

74

Zmienne losowe U i V sa

‘

nieskorelowane gdy˙z

hUV i =

1
4

· 1 · 1 +

1
4

· 1 · 1 =

1
2

hUi =

1
2

· 1 +

1
4

· 2 = 1

=>

hUV i = hUihV i

hV i =

1
2

· 1 =

1
2

.

Ich rozkłady brzegowe to

p

U

(0) =

1
4

p

V

(0) =

1
4

P

U

(1) =

1
2

p

V

(1) =

1
2

P

U

(2) =

1
4

Wynika sta

‘

d, ˙ze U i V nie sa

‘

niezale˙zne, gdy˙z

p

(U = 0,V = 1) = 0 6= p

U

(0) p

V

(1) =

1
4

·

1
2

.

10.2

Generowanie liczb losowych

Generowanie liczb losowych o zadanym rozkładzie prawdopodbie´nstwa to cen-
tralny element metod Monte Carlo. Zwykle wykorzystuje sie

‘

do tego celu genera-

tory liczb losowych o rozkładzie jednostajnym na odcinku

[0, 1]

p

(x) =

1

x

∈ [0,1]

0

poza

[0, 1] .

(10.22)

W praktyce takie generatory sa

‘

oferowane w ramach bibliotek program´ow kompu-

terowych, na przykład CERNLIB. Dysponuja

‘

c liczbami o rozkładzie jednostajnym

mo˙zemy otrzyma´c liczby losowe o dowolnych rozkładach. Poni˙zej om´owimy kilka
metod ich otrzymywania.

10.2.1

Metoda transformacji

Niech X jest zmienna

‘

losowa

‘

o znanym rozkładzie p

X

(x) oraz Y = f (X) jest

inna

‘

zmienna

‘

losowa

‘

, kt´orej rozkład p

Y

(y) chcemy znale´z´c. Zakładamy, ˙ze f jest

funkcja

‘

monotoniczna

‘

75

Zdefiniujmy dystrybuante

‘

dla tych rozkład´ow, be

‘

da

‘

ca

‘

prawdopodobie´nstwem,

˙ze warto´s´c zmiennej losowej jest mniejsza ni˙z zadana liczba:

F

X

(x) = P(X < x) =

Z

x

−

∞

p

X

(t) dt

F

Y

(y) = P(Y < y) =

Z

y

−

∞

p

Y

(t) dt .

(10.23)

Warto´sci dystrybuant zawieraja

‘

sie

‘

w przedziale

[0, 1].

Je˙zeli y

= f (x) oraz f jest funkcja

‘

rosna

‘

ca

‘

to chcemy by zachodziło

F

X

(x) = F

Y

(y) .

(10.24)

R´o˙zniczkuja

‘

c po x, otrzymujemy

p

X

(x) =

dF

X

(x)

dx

=

dF

Y

(y)

dy

d f

dx

= p

Y

(y)

d f

dx

.

(10.25)

Podobnie, je´sli f jest maleja

‘

ca to chcemy by

F

X

(x) = 1 − F

Y

(y) .

(10.26)

R´o˙zniczkowanie po x daje wynik (10.25) z minusem, rekompensuja

‘

cym ujemna

‘

warto´s´c pochodnej d f

/dx. Ostatecznie, znajdujemy

p

X

(x) = p

Y

(y)

d f

dx

.

(10.27)

Jest to wz´or, kt´ory wia

‘

˙ze znany rozkład zmiennej losowej X z poszukiwanym

rozkładem zmiennej losowej Y .

Przyklad

Rozwa˙zmy transformacje

‘

Y

= −ln(X). Je˙zeli X jest zmienna

‘

o rozkładzie

jednostajnym na odcinku

[0, 1] to rozkład Y jest rozkładem eksponencjalnym:

1

= p

Y

(y)/x

=>

p

Y

(y) = e

−y

,

y

∈ [0,

∞

] .

76

10.2.2

Metoda odwracania dystrybunaty

Zał´o˙zmy, ˙ze X

= R jest zmienna

‘

losowa

‘

o rozkładzie jednostajnym (10.22). Od-

wr´o´cmy problem i poszukajmy transformacji Y

= f (R), kt´ora prowadzi do zada-

nego rozkładu p

Y

(y) zmiennej losowej Y .

Je˙zeli 0

≤ r ≤ 1, otrzymujemy

F

Y

(y) = F

R

(r) =

Z

r

0

dt

= r .

(10.28)

Sta

‘

d

y

= F

−1

Y

(r) ,

(10.29)

co oznacza, ˙ze

f

= F

−1

Y

.

(10.30)

Poszukiwana transformacja powstaje z odwr´ocenia dystrybunaty rozkładu p

Y

(y).

Metode

‘

te

‘

ilustruje naste

‘

puja

‘

cy przykład.

Przyklad

Chcemy wygenerowa´c liczby losowe y o rozkładzie eksponencjalnym

p

(y) =

λ

e

−

λ

y

y

≥ 0

0

y

< 0 .

(10.31)

• Obliczymy dystrybuante

‘

dla tego rozkładu

F

(y) =

Z

y

0

λ

e

−

λ

t

dt

= 1 − e

−

λ

y

.

• Zgodnie ze wzorem (10.28), przyr´ownujemy ja

‘

do wylosowanej liczby r z

rozkładu jednostajnego, a naste

‘

pnie odwracamy te

‘

relacje

‘

wyliczaja

‘

c y:

F

(y) = 1 − e

−

λ

y

= r

=>

y

= −

1

λ

ln

(1 − r).

(10.32)

Prezentowana metoda nie mo˙ze by´c zastosowana do rozkładu Gaussa (10.11),

gdy˙z nie potrafimy odwr´oci´c jego dystrybuanty w spos´ob analityczny. Aby wy-
generowa´c liczby losowe o takim rozkładzie, rozwa˙zmy dwie niezale˙zne zmienne

77

losowe Y

1

i Y

2

o rozkładzie Gaussa (dla uproszczenia z µ

= 0 i

σ

2

= 1). Ich rozkład

ła

‘

czny to

p

(y

1

, y

2

) =

1

2

π

e

−(y

2

1

+y

2

2

)/2

.

(10.33)

Zgodnie z metoda

‘

transformacji, przechodza

‘

c do zmiennych biegunowych

(

ρ

,

φ

),

gdzie

y

1

=

ρ

cos

φ

y

2

=

ρ

sin

φ

,

(10.34)

otrzymujemy ła

‘

czny rozkład prawdopodobie´nstwa dla nowych zmiennych

p

(

ρ

,

φ

) = p(y

1

, y

2

)

∂

(y

1

, y

2

)

∂

(

ρ

,

φ

)

=

ρ

e

−

ρ

2

/2

1

2

π

.

Ze wzgle

‘

du na faktoryzacje

‘

rozkładu p

(

ρ

,

φ

) = p(

ρ

) p(

φ

), zmienne (

ρ

,

φ

) sa

‘

nieza-

le˙zne.

Sta

‘

d procedura:

• Zmienna losowa

φ

ma rozkład jednostajny na odcinku

[0, 2

π

]. Generuja

‘

c

liczbe

‘

r

1

o rozkładzie jednostajnym na odcinku

[0, 1] otrzymujemy liczbe

‘

losowa

‘

φ

= 2

π

r

1

.

• Losujemy druga

‘

liczbe

‘

r

2

o rozkładzie jednostajnym na odcinku

[0, 1], a

naste

‘

pnie odwracamy dystrybunate

‘

rozkładu p

(

ρ

),

F

(

ρ

) =

Z

ρ

−

∞

t e

−t

2

/2

dt

= 1 − e

−

ρ

2

/2

= r

2

.

Otrzymujemy w ten spos´ob zmienna

‘

losowa

‘

ρ

=

p

−2ln(1 − r

2

).

• Wykorzystuja

‘

c transformacje

‘

(10.34), otrzymamy dwie niezale˙zne liczby

losowe o rozkładzie Gaussa

y

1

=

p

−2ln(1 − r

2

) cos(2

π

r

1

)

y

2

=

p

−2ln(1 − r

2

) sin(2

π

r

1

) .

(10.35)

10.2.3

Metoda odrzucania

Zaleta

‘

tej metody jest to, ˙ze nie wymaga odwr´ocenia dystrybuanty dla generowa-

nego rozkładu. Jak wiemy w wielu przypadkach nie potrafimy odwr´oci´c dystry-
buanty w spos´ob analityczny. U˙zywanie do tego celu metod przybli˙zonych szalenie
wydłu˙za czas generacji i jest niepraktyczne.

78

Zał´o˙zmy, ˙ze chcemy wygenerowa´c liczby losowe o rozkładzie p

(x), dla kt´orego

nie potrafimy odwr´oci´c dystrybuanty. Niech f

0

(x) be

‘

dzie pomocnicza

‘

funkcja

‘

taka

‘

,

˙ze f

0

(x) ≥ p(x). Funkcja f

0

powinna by´c tak wybrana by łatwo było wygenerowa´c

liczby losowe o unormowanym do jedynki rozkładzie

p

0

(x) =

f

0

(x)

∞

R

−

∞

f

0

(x)dx

.

(10.36)

Metoda odrzucania składa sie

‘

z dw´och zasadniczych krok´ow.

• Generujemy rozkład punkt´ow (x,y) rozło˙zonych r´ownomiernie mie

‘

dzy osia

‘

x a wykresem funkcji f

0

(x). Osiaga sie

‘

to w dw´och krokach:

– generujemy liczbe

‘

x z rozkładu p

0

(x); zwykle korzystamy w tym kroku

z metody odwracania dystrybuanty,

– losujemy liczbe

‘

r z rozkładu jednostajnego na odcinku

[0, 1], a naste

‘

p-

nie definiujemy liczbe

‘

losowa

‘

y

= f

0

(x) r.

• Para (x,y) jest akceptowana je´sli y ≤ p(x), a odrzucana w przeciwnym przy-

padku.

Zaakceptowane punkty sa

‘

rozło˙zone r´ownomiernie pod wykresem funkcji p

(x).

W ten spos´ob otrzymujemy liczby losowe x o rozkładzie p

(x). Efektywno´s´c tej

metody zale˙zy od liczby zaakceptowanych przypadk´ow. Dobrze jest wie

‘

c wybra´c

funkcje

‘

pomocnicza

‘

f

0

(x) tak, by le˙zała jak najbli˙zej rozkładu p(x).

Przyklad

Chcemy wygenerowa´c liczby losowe o rozkładzie

p

(x) =

(

2

1

√

2

π

e

−x

2

/2

x

≥ 0

0

x

< 0 .

(10.37)

Wybierzmy funkcje

‘

pomocnicza

‘

f

0

(x) =

( q

2

π

e

−x+1/2

x

≥ 0

0

x

< 0 .

Jest to dobry wyb´or, gdy˙z

p

(x)

f

0

(x)

= e

−(x−1)

2

/2

≤ 1.

79

Odpowiadaja

‘

cy f

0

unormowany rozkład (10.36) jest eksponencjalny

p

0

(x) =

e

−x

x

≥ 0

0

x

< 0 .

(10.38)

W metodzie odrzucania generujemy najpierw dwie liczby losowe r

1

i r

2

z rozkładu

jednostajnego na odcinku

[0, 1]. Nastepnie definiujemy liczby losowe:

x

= −lnr

1

,

y

= f

0

(x) r

2

.

Zgodnie ze wzorem (10.32) x ma rozkład eksponencjalny p

0

(x). Para (x, y) jest

akceptowana je´sli

y

≤ p(x)

<=>

r

2

≤

p

(x)

f

0

(x)

= e

−(x−1)

2

/2

.

(10.39)

W przeciwnym wypadku para jest odrzucana.

Tak wie

‘

c w praktyce, po wylosowaniu r

1

i r

2

znajdujemy x

= −lnr

1

, kt´ore

akceptujemy jesłi spełniony jest warunek r

2

< exp{−(x − 1)

2

/2}. Efektywno´s´c

generacji jest okre´slona poprzez stosunek p´ol pod wykresami funkcji p

(x) oraz

f

0

(x):

1

p

2e

/

π

≈ 0.76.

Akceptujemy wie

‘

c 76% wygenerowanych przypadk´ow.

10.3

Centralne twierdzenie graniczne

Niech X

1

, X

2

, . . . , X

N

be

‘

da

‘

niezale˙znymi zmiennymi losowymi o dowolnych roz-

kładach prawdopodobie´nstwa scharakteryzowanych ta

‘

sama

‘

warto´scia

‘

´srednia

‘

µ i

wariancja

‘

σ

2

. Centralne twierdzenie graniczne m´owi, ˙ze w granicy N

→

∞

zmienna

losowa

S

N

=

X

1

+ X

2

+ . . . + X

N

N

(10.40)

ma rozkład normalny Gaussa z parametrami µ oraz

σ

2

/N

p

(s) =

1

p

2

πσ

2

/N

e

−

(s−µ)

2

2

σ

2

/N

.

(10.41)

Tak wie

‘

c warto´s´c ´srednia i wariancja zmiennej losowej S

N

to

hS

N

i = µ,

σ

2
S

N

=

σ

2

N

.

(10.42)

80

Jak wida´c,

σ

2

S

N

→ 0 dla N →

∞

co oznacza, ˙ze dla rosna

‘

cych N zmienna losowa S

N

przyjmuje warto´sci bliskie µ z coraz wie

‘

kszym prawdopodobie´nstwem.

Je˙zeli X

1

, X

2

, . . . , X

N

sa

‘

niezale˙znymi zmiennymi losowymi o rozkładzie p

(x)

a f dowolna

‘

funkcja

‘

to f

(X

1

), f (X

2

), . . ., f (X

N

) sa

‘

r´ownie˙z niezale˙znymi zmien-

nymi losowymi. Ich rozkłady posiadaja

‘

takie same warto´sci ´sredniej i wariancji.

Spełnione sa

‘

wie

‘

c zało˙zenia centralnego twierdzenia granicznego, kt´ore prowadzi

do wniosku, ˙ze w granicy N

→

∞

zmienna losowa

I

N

=

1

N

N

∑

i

=1

f

(X

i

)

(10.43)

ma rozkład normalny z warto´scia

‘

´srednia

hI

N

i =

Z

f

(x) p(x) dx

(10.44)

i wariancja

‘

σ

2
I

N

=

σ

2

f

(X)

N

=

f

2

(X)

− h f (X)i

2

N

→ 0.

(10.45)

Twierdzenie to jest podstawa

‘

całkowania metoda

‘

Monte Carlo prowadza

‘

c do wzo-

r´ow dyskutowanych w naste

‘

pnym rozdziale.

10.4

Całkowanie metoda¸ Monte Carlo

Podstawowy wz´or na oblicznie całki w metodzie Monte Carlo to

b

Z

a

f

(x) dx ≈ V h f i ± V

s

h f

2

i − h f i

2

N

,

(10.46)

gdzie V

= b − a oraz

h f i =

1

N

N

∑

i

=1

f

(x

i

) ,

f

2

=

1

N

N

∑

i

=1

f

2

(x

i

) .

(10.47)

W powy˙zszych wzorach x

i

sa

‘

liczbami losowymi o rozkładzie jednostajnym na

odcinku

[a, b], natomiast N jest liczba

‘

wygenerowanych liczb losowych. Stała V

wynika z konieczno´sci normalizacji rozkładu jednostajnego do jedynki, gdy˙z

Z

b

a

dx

= b − a.

81

Drugie wyra˙zenie po prawej stronie (10.46) jest estymacja

‘

błe

‘

du wyniku wynika-

ja

‘

ca

‘

z centralnego twierdzenia granicznego.

Wz´or (10.46) jest słuszny tak˙ze dla całkowania w n-wymiarowej przestrzeni z

punktami x

= (x

1

, x

2

, . . . , x

n

),

Z

W

f

(x) dx ≈ V h f i ± V

s

h f

2

i − h f i

2

N

.

(10.48)

We wzorze tym V jest n-wymiarowa

‘

obje

‘

to´scia

‘

przestrzeni W , po kt´orej całkujemy

V

=

Z

W

dx

1

dx

2

. . . dx

n

,

(10.49)

natomiast

h f i =

1

N

N

∑

i

=1

f

(x

i

) ,

f

2

=

1

N

N

∑

i

=1

f

2

(x

i

) ,

(10.50)

gdzie tym razem x

i

= (x

1i

, x

2i

, . . . , x

ni

) to wielowymiarowe liczby losowe o rozkła-

dzie jednostajnym w obszarze całkowania.

W praktyce obszar W mo˙ze by´c na tyle skomplikowany, ˙ze nie jest łatwo

pr´obkowa´c go przy pomocy rozkładu jednostajnego. Wybieramy wtedy obszar U
zawieraja

‘

cy W , w kt´orym łatwo wygenerowa´c liczby losowe o rozkładzie jedno-

stajnym. Dodatkowo definiujemy nowa

‘

funkcje

‘

˜

f r´owna

‘

funkcji f w obszarze W i

zero poza nim. Wtedy

Z

U

˜

f

(x) dx =

Z

W

f

(x) dx .

(10.51)

Wyb´or obszaru U wpływa na wielko´s´c błedu w metodzie Monte Carlo. Bła

‘

d jest

tym wie

‘

kszy im wie

‘

ksza jest r´o˙znica mie

‘

dzy obszarami U i W . Dobrze jest wie

‘

c

wybra´c U tak, by liczba wylosowanych punkt´ow poza obszarem W była jak naj-
mniejsza.

Przyklad

Opisana

‘

metoda

‘

mo˙zemy policzy´c całke

‘

R

b

a

f

(x) dx z dodatniej funkcji f , defi-

niuja

‘

c funkcje

‘

dw´och zmiennych

F

(x, y) =

1

x

≤ y = f (x)

0

x

> y

(10.52)

82

okre´slona

‘

w kwadracie U

= [a, b] × [0,max( f )]. Wtedy

b

Z

a

f

(x) dx =

Z

U

F

(x, y) dx dy ≈ V

1

N

∑

x

i

≤y

i

1

,

(10.53)

gdzie V jest polem kwadratu U, po kt´orym całkujemy. Warto´s´c całki jest wie

‘

c

proporcjonalna do stosunku liczby punkt´ow le˙zacych pod wykresem funkcji y

=

f

(x) do całkowitej liczby N wygenerowanych punkt´ow o rozkładzie jednostajnym

w obszarze całkowania.

Wz´or (10.46) mo˙zna uog´olni´c dla całek z dodatnia

‘

waga

‘

w

(x):

b

Z

a

f

(x) w(x) dx ≈ V h f i ± V

s

h f

2

i − h f i

2

N

.

(10.54)

gdzie obje

‘

to´s´c V jest zadana wzorem

V

=

b

Z

a

w

(x) dx .

(10.55)

Tym razem liczby losowe we wzorach (10.47) sa

‘

generowane według rozkładu

w

(x) po unormowaniu do jedynki (podzieleniu przez V ). Wz´or (10.46) jest wie

‘

c

szczeg´olnym przypadkiem (10.54) gdy w jest rozkładem jednostajnym.

10.4.1

Metoda importance sampling

Wz´or (10.54) pozwala oblicz´c całke

‘

I

=

Z

b

a

f

(x) dx

(10.56)

z mniejszym błe

‘

dem je´sli z funkcji f

(x) wyła

‘

czymy dodatnia

‘

funkcje

‘

g

(x) zawie-

raja

‘

ca

‘

istotna

‘

cze

‘

´s´c jej zmienno´sci. Wtedy

I

=

b

Z

a

f

(x)

g

(x)

g

(x) dx ≈ V

f

g

± V

s

h( f /g)

2

i − h f /gi

2

N

,

(10.57)

83

gdzie obje

‘

to´s´c

V

=

b

Z

a

g

(x) dx

(10.58)

natomiast

h f /gi =

1

N

N

∑

i

=1

f

(x

i

)

g

(x

i

)

,

( f /g)

2

=

1

N

N

∑

i

=1

f

2

(x

i

)

g

2

(x

i

)

.

(10.59)

Liczby losowe x

i

w powy˙zszych wzorach sa

‘

generowane według unormowanego

rozkładu g

(x)/V .

Wyniki (10.46) oraz (10.57) na warto´s´c całki sa

‘

identyczne w granicy N

→

∞

.

To co rozr´o˙znia te dwa sposoby obliczania całek jest wielko´s´c błe

‘

du, kt´ory mo˙ze

by´c znacznie mniejszy w prezentowanej metodzie. Optymalnym wyborem jest [2]:

g

(x) = | f (x)|.

(10.60)

W praktyce jednak nie stosuje sie

‘

go, gdy˙z zwykle r´ownie trudno jest obliczy´c

obje

‘

to´s´c V dla tego rozkładu jak interesuja

‘

ca

‘

nas całke

‘

. Kluczowa

‘

role

‘

odgrywa

zatem ”ma

‘

dry wyb´or” g

(x).

84

Literatura

[1] Z. Fortuna, B. Macukow, J. Wa

‘

sowski; Metody numeryczne; WNT,

Warszawa, 2005.

[2] W. H. Press, S. A. Teukolski, W. T. Vetterling, B. P. Flannery;

Numerical Recipes; Cambridge University Press, 1992.

[3] Tao Pang; Metody obliczeniowe w fizyce, PWN, Warszawa, 2001.

85