możemy stwierdzić, że wzór różnicowy (5.6) jest dobrą aproksymacją pierwszej pochodnej, gdy liczba falowa k jest mała, a długość fali jest duża. Tak więc metody różnicowe można stosować w zjawiskach długofalowych, a aproksymacja jest tym lepsza im więcej jest punktów dyskretyzacji.

Podobnie dla operatora różnicowego drugiego rzędu (5.15) otrzymujemy

i po rozwinięciu
dla małych mamy

(5.23)

Jeśli porównamy ten rezultat z wyrażeniem dla drugiej pochodnej modu (5.21)

to widzimy, że operator różnicowy drugiego rzędu jest aproksymacją operatora różniczkowego drugiego rzędu z dokładnością do wyrazów drugiego rzędu ze względu na iloczyn liczby falowej i kroku siatki.

5.2. Metody całkowania numerycznego

Zagadnienie przybliżonego obliczania całki oznaczonej danej funkcji ciągłej
w przedziale

(5.24)

często występuje w praktyce obliczeniowej, gdyż wyznaczanie funkcji pierwotnej jest bardzo trudne lub wręcz niemożliwe, gdy funkcja
nie jest funkcją elementarną lub gdy funkcja
jest określona za pomocą tablicy.

Zagadnienie przybliżonego obliczania całek można traktować jako aproksymację funkcjonału I innymi, prostszymi do obliczenia funkcjonałami. W rachunku numerycznym muszą mieć one postać pozwalającą na obliczenie ich wartości za pomocą skończonej liczby działań arytmetycznych. Wzory numeryczne całkowania funkcji jednej zmiennej niezależnej nazywane są kwadraturami, funkcji wielu zmiennych niezależnych - kubaturami.

Istnieją różne rodzaje kwadratur. Najważniejsze z nich to:

- kwadratury interpolacyjne i aproksymacyjne,

- kwadratury Newtona-Cotesa,

- kwadratury Gaussa.

Mianem kwadratur interpolacyjnych lub aproksymacyjnych określamy kwadratury otrzymane przez całkowanie wzorów interpolacyjnych lub aproksymacyjnych funkcji podcałkowej W szczególności mogą to być wzory oparte na całkowaniu wielomianów interpolacyjnych Lagrange'a niskiego stopnia lub też równań funkcji sklejanych.

Po scałkowaniu wielomianu interpolacyjnego Lagrange'a (4.13) - (4.14) otrzymamy kwadraturę postaci

(5.25)

w której są ustalonymi węzłami, a współczynniki są określone wzorem

(5.26)

Dla wyznaczenia współczynników zauważmy, że:

1) współczynniki przy danym wyborze węzłów nie zależą od wyboru postaci funkcji

2) wzór (5.25) jest dokładny dla wielomianu stopnia n.

Podstawiając więc we wzorze (5.25) otrzymamy układ
równań liniowych:

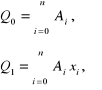
(5.27)

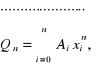
(5.27cd.)

gdzie

z którego można obliczyć współczynniki: Wyznacznik macierzy współczynników układu (5.27) jest wyznacznikiem Vandermonda.

Prostym przykładem kwadratury interpolacyjnej tego rodzaju może być kwadratura postaci

(5.28)

Układ (5.27) dla
oraz:

redukuje się do układu następującego:

Stąd:

i ostatecznie

Dokładność obliczania całki (5.24) za pomocą kwadratur interpolacyjnych lub aproksymacyjnych zależy od oszacowania dokładności przybliżenia funkcji
funkcją

(5.29)

Wynika stąd, że w wielu przypadkach szczególnie przydatne mogą okazać się kwadratury interpolacyjne lub aproksymacyjne oparte na całkowaniu równań funkcji sklejanych. Przy wykorzystaniu równań wielomianowej funkcji sklejanej trzeciego stopnia (4.74) ÷ (4.78) otrzymujemy

(5.30)

W podobny sposób, po scałkowaniu równania hiperbolicznej funkcji sklejanej (4.129) w połączeniu z układem równań (4.132), dostajemy

(5.31)

*

Kwadraturami Newtona-Cotesa nazywamy kwadratury postaci (5.25), otrzymane przez całkowanie wielomianów interpolacyjnych opartych na równoodległych węzłach

(5.32)

Współczynniki kwadratur Newtona-Cotesa można wyznaczyć drogą całkowania wielomianu interpolacyjnego Lagrange'a (4.18) - (4.19) lub też, stosowaną w rozdziale poprzednim, metodą rozwijania funkcji
w szeregi Taylora względem punktu

Dla zastosowania drugiej z tych możliwości rozważymy zależność wynikającą ze wzorów (5.24) i (5.25)

(5.33)

gdzie
jest błędem przybliżenia. Po scałkowaniu rozwinięcia danej funkcji
w szereg Taylora

i podstawieniu rozwinięć

uzyskujemy związek

(5.34)

Z porównania mnożników występujących przy kolejnych potęgach h, z lewej i prawej strony tego związku, otrzymujemy równania, z których wyznaczamy nieznane współczynniki

W przypadku
mamy

skąd wynikają równania:

i ostatecznie po porównaniu dokładnej wartości całki

z jej wartością przybliżoną

jest

(5.35)

Jest to znany wzór trapezów, odznaczający się nadspodziewanie małym błędem
Widzimy więc, że operacja całkowania przybliżonego jest znacznie dokładniejsza od operacji różniczkowania numerycznego.

Zależność (5.34) w przypadku
przyjmuje postać

Stąd otrzymujemy układ równań:

którego rozwiązaniem są liczby:

Podstawiając je do (5.33) uzyskujemy znany wzór parabol, zwany też wzorem Simpsona

(5.36)

Zwraca uwagę bardzo wysoka dokładność tego wzoru, wynikająca z tożsamościowego znikania współczynników przy pochodnej
po podstawieniu wyznaczonych wartości i

Ze względu na trudności związane ze stosowaniem wielomianów interpolacyjnych wysokich stopni, w praktyce raczej nie wykorzystuje się kwadratur Newtona-Cotesa wysokich rzędów. Na ogół bardziej celowe jest podzielenie przedziału całkowania na większą liczbę podprzedziałów i stosowanie dla nich kwadratur New-tona-Cotesa niskiego rzędu. Skonstruowane w ten sposób kwadratury, określone na całym przedziale
, są nazywane złożonymi kwadraturami Newtona-Cotesa.

Złożony wzór trapezów otrzymujemy po podzieleniu przedziału całkowania
na m równych części
i zsumowaniu całek (5.35) dla każdego podprzedziału

(5.37)

Na podstawie oszacowania (5.35) błąd złożonego wzoru trapezów wynosi

(5.38)

gdzie

Analogicznie wyprowadza się złożony wzór parabol przy założeniu, że m jest parzyste. Po zsumowaniu całek (5.36) dla kolejnych podprzedziałów o długości 2 h mamy

(5.39)

gdzie:

Błąd złożonego wzoru parabol jest następujący:

(5.40)

gdzie

*

Rozważane dotąd kwadratury interpolacyjne lub aproksymacyjne, jak i kwadra-tury Newtona-Cotesa są kwadraturami z ustalonymi węzłami. Kwadratury Gaussa są natomiast kwadraturami postaci (5.25), w których dobierane są nie tylko współ-czynniki ale także węzły - w taki sposób, aby kwadratura była dokładna dla możliwie najwyższego stopnia wielomianu.

Przy wyznaczaniu parametrów kwadratur Gaussa wygodnie jest w obliczanej całce (5.24) dokonać liniowej zamiany zmiennej całkowania

(5.41)

pozwalającej na transformację dowolnego przedziału
na przedział znormalizowany

(5.42)

Rozważymy teraz zadanie: jak wybrać węzły: oraz współczynniki: żeby kwadratura postaci

(5.43)

była dokładna dla wielomianu stopnia
, którego liczba współczynników jest równa liczbie nieznanych parametrów i Oznacza to, że równość (5.43) musi być spełniona dla wielomianów:

gdyż dla

mamy

Stąd przy wykorzystaniu związków:

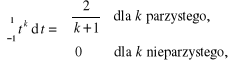
otrzymujemy układ równań:

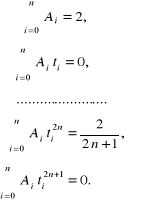
(5.44)

Bezpośrednie rozwiązywanie nieliniowego układu równań (5.44) napotyka na duże trudności matematyczne. Dlatego też najczęściej funkcję
przyjmuje się w postaci

(5.45)

gdzie są wielomianami Legendre'a, zdefiniowanymi wzorami:

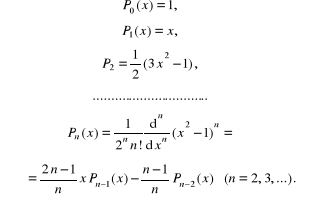
(5.46)

Wielomian Legendre'a jest funkcją parzystą dla n = 2 m i nieparzystą dla n = = 2 m +1, dla n ≥ 1 ma n różnych pierwiastków rzeczywistych, leżących w przedziale otwartym (1, 1).

Wielomiany Legendre'a są ortogonalne do wszystkich wielomianów stopnia mniejszego od n+1. Zatem mamy

i następnie po podstawieniu (5.45) do (5.43) stwierdzamy, że suma

(5.47)

znika dla dowolnych jeśli

(5.48)

Kwadratura (5.43) będzie więc dokładna dla wielomianów stopnia gdy jej węzłami będą zera wielomianu Legendre'a Po obliczeniu wartości węzłów współczynniki
można łatwo wyznaczyć z układu równań liniowych (5.44).

W najprostszym przypadku dla n = 0 jest - co oznacza, że kwadratura Gaussa z jednym węzłem jest równoważna wzorowi prostokątów

W przypadku
obliczając najpierw pierwiastki wielomianu Legendre'a drugiego stopnia

otrzymujemy:

i następnie z układu równań:

dostajemy

Interpretacja geometryczna kwadratury Gaussa z dwoma węzłami

(5.49)

dokładnej dla wielomianów stopnia trzeciego, jest przedstawiona na rysunku 5.3. Funkcja podcałkowa
jest interpolowana funkcją liniową
przechodzącą przez punkty i

Rys. 5.3

Po wyznaczeniu pierwiastków wielomianu Legendre'a trzeciego stopnia

można, w podobny sposób, otrzymać kwadraturę Gaussa z trzema węzłami

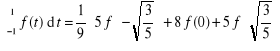
(5.50)

oraz kwadratury z większą liczbą węzłów.

Błąd popełniany przy obliczaniu całki (5.24) za pomocą kwadratur Gaussa dla dowolnej wartości n wynosi [9]

(5.51)

Tak samo jak w przypadku kwadratur Newtona-Cotesa można budować złożone kwadratury Gaussa dzieląc przedział całkowania na mniejsze podprzedziały i stosując w każdym z nich kwadraturę Gaussa ustalonego stopnia

*

Na zakończenie omawiania najważniejszych metod całkowania numerycznego przedstawimy jeszcze kilka uwag dotyczących kwadratury Czebyszewa i ekstrapolacji Richardsona.

Kwadraturą Czebyszewa nazywamy wzór całkowania numerycznego, w którym wszystkie współczynniki są sobie równe

(5.52)

Wartość B znajdujemy przyjmując

,

a wartości współrzędnych węzłów są wyznaczane z warunków, aby kwadratura była dokładna dla wszystkich wielomianów do stopnia
włącz-nie

Ekstrapolacja Richardsona jest metodą przyspieszania szybkości zbieżności ciągu kwadratur o znanym rzędzie błędu

gdzie

pozwalającą na obliczenie całki I z większą dokładnością dla dwóch znanych jej przybliżeń i - odpowiadającym krokom całkowania

Przy założeniu, że

(5.53)

możemy napisać:

(5.54)

Stąd otrzymujemy zależność

z której wyznaczamy

i następnie ze wzoru (5.53) mamy

W szczególnym przypadku dla uzyskujemy oszacowanie błędu

i ostatecznie z (5.54b) jest

(5.55)

*

Program 5.1 jest przeznaczony do całkowania funkcji
w przedziale
dla zadanej liczby podprzedziałów m przy wykorzystaniu czterech rodzajów kwadratur:

1) złożony wzór trapezów,

2) złożony wzór parabol,

3) złożony wzór Gaussa z dwoma węzłami,

4) złożony wzór Gaussa z trzema węzłami.

{Program 5.1}

uses

Crt;

var

m: Integer;

a,b: Real;

zn: Char;

label powt;

function f(x: Real): Real;

begin

f:=Sqrt(1+2*x);

end;

function Calka1(a,b: Real; m: Integer): Real;

{zlozony wzor trapezow}

var

i: Integer;

h,x,s: Real;

begin

h:=(b-a)/m;

s:=(f(a)+f(b))/2;

for i:=1 to m-1 do begin

x:=a+i*h;

s:=s+f(x);

end;

Calka1:=s*h;

end;

function Calka2(a,b: Real; m:Integer): Real;

{zlozony wzor parabol}

var

k,q: Integer;

h,x,s1,s2,x1,x2: Real;

begin

h:=(b-a)/m;

q:=m div 2;

s1:=0; s2:=0;

for k:=1 to q do begin

x1:=a+(2*k-1)*h;

s1:=s1+f(x1);

end;

for k:=1 to q-1 do begin

x2:=a+2*k*h;

s2:=s2+f(x2);

end;

Calka2:=h*(f(a)+f(b)+4*s1+2*s2)/3;

end;

function Calka3(a,b: Real; m: Integer): Real;

{zlozony wzor Gaussa z dwoma wezlami}

var

i: Integer;

h,t0,t1,x0,x1,xp,s: Real;

begin

s:=0;

h:=(b-a)/m;

t0:=-1/Sqrt(3);

t1:=1/Sqrt(3);

for i:=1 to m do begin

xp:=a+(i-1)*h+h/2;

x0:=xp+h*t0/2;

x1:=xp+h*t1/2;

s:=s+(f(x0)+f(x1));

end;

Calka3:=s*h/2;

end;

function Calka4(a,b: Real; m: Integer): Real;

{zlozony wzor Gaussa z trzema wezlami}

var

i: Integer;

h,t0,t1,t2,x0,x1,x2,xp,s: Real;

begin

s:=0;

h:=(b-a)/m;

t0:=-Sqrt(3/5);

t1:=0;

t2:=Sqrt(3/5);

for i:=1 to m do begin

xp:=a+(i-1)*h+h/2;

x0:=xp+h*t0/2;

x1:=xp+h*t1/2;

x2:=xp+h*t2/2;

s:=s+(5*f(x0)+8*f(x1)+5*f(x2));

end;

Calka4:=s*h/18;

end;

begin

powt:

ClrScr;

Writeln('PROGRAM 5.1');

Writeln('Obliczanie calki oznaczonej.');

Writeln;

Writeln('Granice calkowania:');

Write(' a = '); Readln(a);

Write(' b = '); Readln(b);

Write('Liczba podprzedzialow - m = '); Readln(m);

if (m div 2)*2<>m then begin

m:=m+1;

Writeln('Liczba podprzedzialow - m = ',m:3);

end;

Writeln;

Writeln('Obliczone wartosci calki:');

Writeln(' 1) wzor trapezow - I = ',Calka1(a,b,m):16);

Writeln(' 2) wzor parabol - I = ',Calka2(a,b,m):16);

Writeln(' 3) wzor Gaussa(n=2) - I = ',Calka3(a,b,m):16);

Writeln(' 4) wzor Gaussa(n=3) - I = ',Calka4(a,b,m):16);

Writeln;

Write('Nowe obliczenia: (t/n)? ');

zn:=ReadKey;

if zn='t' then goto powt;

end.

Za pomocą programu 5.1, przyjmując m = 10, obliczono trzy całki:

Otrzymano wyniki reprezentowane następującymi wydrukami:

PROGRAM 5.1

Obliczanie calki oznaczonej.

Granice calkowania

a = 0

b = 2

Liczba podprzedzialow - m = 10

Obliczone wartosci calki:

1) wzor trapezow - I = 6.410338768E+00

2) wzor parabol - I = 6.389112621E+00

3) wzor Gaussa(n=2) - I = 6.389053736E+00

4) wzor Gaussa(n=3) - I = 6.389056099E+00

Nowe obliczenia: (t/n)?

PROGRAM 5.1

Obliczanie calki oznaczonej.

Granice calkowania

a = 0

b = 1

Liczba podprzedzialow - m = 10

Obliczone wartosci calki:

1) wzor trapezow - I = 6.937714032E-01

2) wzor parabol - I = 6.931502307E-01

3) wzor Gaussa(n=2) - I = 6.931470512E-01

4) wzor Gaussa(n=3) - I = 6.931471805E-01

Nowe obliczenia: (t/n)?

PROGRAM 5.1

Obliczanie calki oznaczonej.

Granice calkowania

a = 0

b = 1

Liczba podprzedzialow - m = 10

Obliczone wartosci calki:

1) wzor trapezow - I = 1.398365653E+00

2) wzor parabol - I = 1.398715977E+00

3) wzor Gaussa(n=2) - I = 1.398717538E+00

4) wzor Gaussa(n=3) - I = 1.398717474E+00

Nowe obliczenia: (t/n)?

*

Przedstawione kwadratury, przeznaczone do obliczania całek pojedynczych, mogą być uogólniane w rozmaity sposób do numerycznego przybliżenia całek wielokrotnych. W najprostszym przypadku, w którym całka wielokrotna daje się wyrazić jako całka iterowana, zadanie sprowadza się do wielokrotnego zastosowania kwadratur jednowymiarowych. Przy budowaniu kwadratur wielowymiarowych (kubatur) podstawową trudnością jest brak możliwości dowolnego wyboru węzłów, stąd też najczęściej stosowane są wielowymiarowe odpowiedniki kwadratur Gaussa - mające przy ustalonym rzędzie kubatury minimalną liczbę węzłów.

Ograniczymy się do przedstawienia kubatur Gaussa do obliczania całek podwójnych po dowolnym trójkącie i dowolnym czworokącie, gdyż całki tego typu często występują przy rozwiązywaniu różnych zagadnień metodą elementów skończonych oraz metodą elementów brzegowych [24]. Kubatury Simpsona są omówione w monografii [2].

Rys. 5.4

W pierwszym przypadku należy obliczyć całkę podwójną

(5.56)

funkcji w trójkącie o wierzchołkach: - rys. 5.4a.

Dokonując zamiany zmiennych niezależnych:

(5.57)

obszar trójkąta pierwotnego transformujemy do obszaru trójkąta prostokątnego równoramiennego (rys. 5.4b) o wierzchołkach:

oraz
- przy czym wierzchołkowi
odpowiada punkt
wierzchołkowi
- punkt
a wierzchołkowi
- punkt

Przy zmianie układu współrzędnych funkcję podcałkową mnożymy przez jakobian przekształcenia

który jest równy modułowi podwojonego pola A wyjściowego trójkąta (moduł iloczynu wektorowego wektorów zbudowanych na dwóch kolejnych bokach trójkąta). Funkcja podcałkowa dla trójkąta znormalizowanego jest więc następująca

Kubaturę Gaussa dla obszaru trójkąta znormalizowanego przyjmujemy w postaci

(5.58)

gdzie
są współrzędnymi punktów Gaussa, a - wagami.

W najprostszym przypadku liniowej aproksymacji funkcji

mamy

Porównując otrzymaną całkę z kubaturą (5.58)

otrzymujemy

Zatem ostatecznie jest

czyli przybliżona wartość całki podwójnej (5.56) jest iloczynem pola trójkąta i wartości funkcji podcałkowej w środku ciężkości trójkąta.

Przyjęcie aproksymacji kwadratowej (n = 2) daje następujące wartości współrzędnych punktów Gaussa i wag:

Rys. 5.5

Dla wyznaczenia całki podwójnej (5.56) w dowolnym czworokącie (rys. 5.5a) o wierzchołkach: dokonujemy najpierw transfor-macji określonej zależnościami:

280 5. Różniczkowanie, całkowanie i aproksymacja

5.2. Metody całkowania numerycznego 281

---