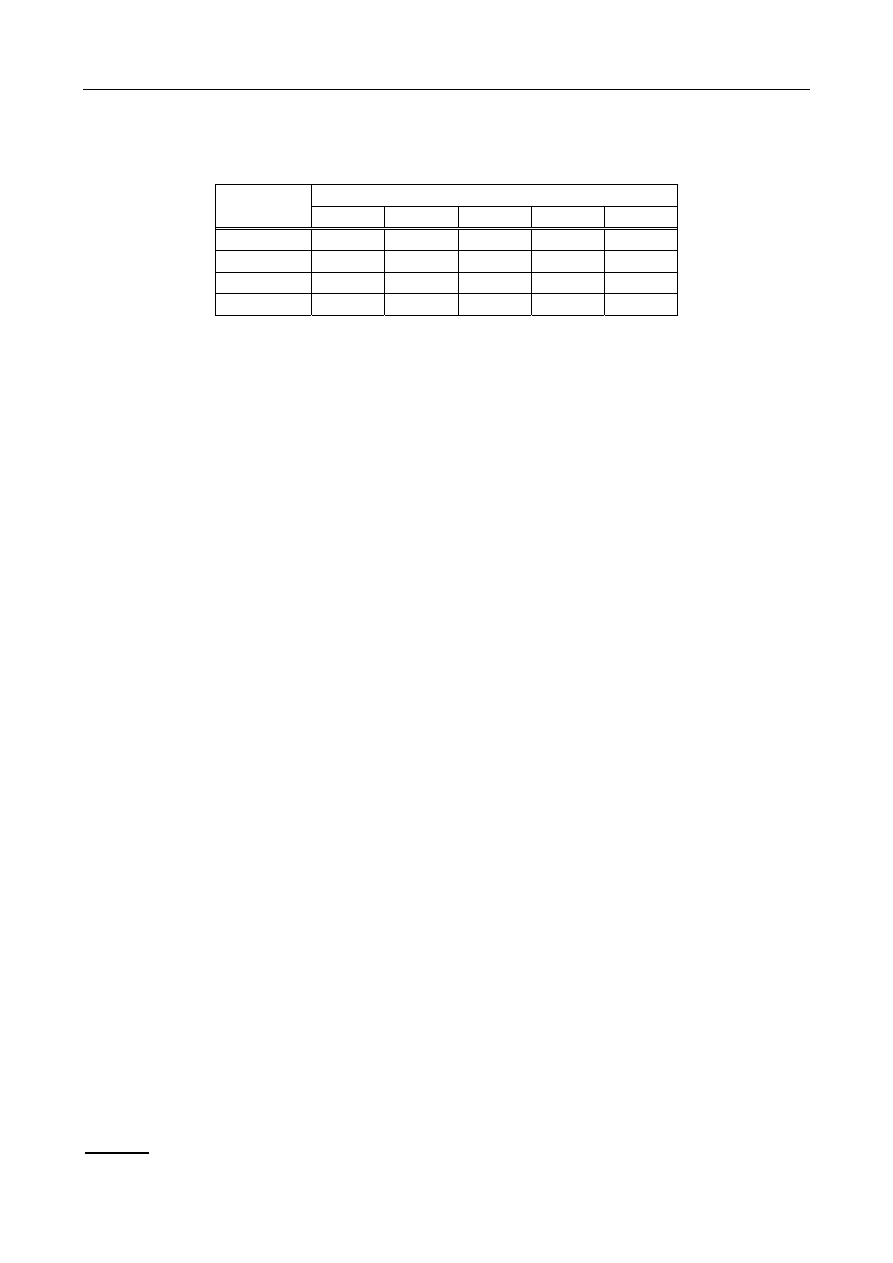
ZADANIE – ESTYMACJA PRZEDZIAŁOWA, NIEZBĘDNA LICZEBNOŚĆ PRÓBY
1
W celu zbadania zależności między liczbą osób w rodzinie a miesięcznymi
wydatkami na cele kulturalne wylosowano w sposób niezależny 230 rodzin
zamieszkujących pewne osiedle i uzyskano następujące wyniki:
Wydatki w
zł
Liczba rodzin wg liczby osób
2 3 4 5 6
10-20
5 - - - -
20-30
14 6 18 40 -
30-40
6 14 22 40 -
40-50
- 5 20 - 40
Na podstawie zebranych wyników obliczono, że średnie wydatki rodzin 2-
osobowych są równe 25,4 zł; rodzin 3-osobowych 34,6 zł, rodzin 4-osobowych 35,33 zł, a
rodzin 5-osobowych 30 zł. Odchylenia standardowe wydatków wynoszą odpowiednio: 6,62
zł; 6,62 zł; 7,97 zł, 5 zł.
1. Z prawdopodobieństwem 0,95 ocenić średnie wydatki na kulturę rodzin 3-osobowych
przyjmując odpowiednie założenie.
2. Oszacować średnie wydatki na kulturę rodzin 5-osobowych, przyjmując poziom ufności
0,99.
3. Ocenić zróżnicowanie wydatków na kulturę rodzin ogółem z wiarygodnością 0,95.
4. Z wiarygodnością 0,90 oszacować zróżnicowanie wydatków na kulturę rodzin 3-
osobowych.
5. Z prawdopodobieństwem 0,95 ocenić odsetek rodzin ogółem wydających na kulturę
powyżej 40 zł.
6. Ile rodzin należy dolosować do próby, aby można było oszacować średnie wydatki
rodzin 3-osobowych z wiarygodnością 0,95 i maksymalnym błędem szacunku równym 2
zł?
7. Ile rodzin należy dolosować do próby, aby ocenić średnie wydatki na kulturę rodzin 5-
osobowych z wiarygodnością 0,99 i maksymalnym błędem szacunku równym 1 zł?
8. Ile rodzin należy dolosować do próby, aby oszacować odsetek rodzin ogółem
wydających na kulturę mniej niż 30 zł z wiarygodnością 0,96 i błędem szacunku
równym 4%, jeżeli wiadomo, że w całej zbiorowości rodzin 3-osobowych około 1/3
wydaje miesięcznie na kulturę do 30 zł?
9. Ile rodzin należy dolosować do próby, aby ocenić odsetek rodzin ogółem wydających na
kulturę powyżej 40 zł z tą samą wiarygodnością i błędem szacunku równym 3%?
Uwaga: Tam, gdzie to konieczne przyjąć stosowne założenia.
ZADANIE – ESTYMACJA PRZEDZIAŁOWA, NIEZBĘDNA LICZEBNOŚĆ PRÓBY
2
Rozwiązanie:
Badana cecha X: wydatki na kulturę w zł.
Badane zbiorowości: 1. rodziny ogółem (n
1
=230;
1
x
=34 zł obliczone z próby; s
1
=8,36 zł);
2. rodziny 2-osobowe (n
2
=25;
2
x
=25,4 zł; s
2
=6,62 zł)
3. rodziny 3-osobowe (n
3
=25;
3
x
=34,6 zł; s
3
=6,62 zł)
4. rodziny 4-osobowe (n
4
=60;
4
x
=35,33 zł; s
4
=7,97 zł)
5. rodziny 5-osobowe (n
5
=80;
5
x
=30,00 zł; s
5
=5,00 zł)
(1)
Z prawdopodobieństwem 0,95 ocenić średnie wydatki na kulturę rodzin 3-osobowych
przyjmując odpowiednie założenie.
Szacowany parametr:
θ=m (średnie wydatki na kulturę rodzin 3-osobowych).
Estymatorem jest średnia arytmetyczna z próby T
n
=
x
.
Ponieważ próba jest mała (n=25 rodzin 3-osobowych) przedział ufności dla
parametru m jest następujący:
α
α
α
−
=
⎭
⎬
⎫
⎩
⎨
⎧
−
+
<
<
−
−
1
1
1
n
s
t
x
m
n
s
t
x
P
,
przy czym przyjmujemy założenie, iż X: N(m,
σ); σ - nieznane.
Dla współczynnika ufności 0,95 i liczby stopni swobody n-1=25-1=24 z tablic
rozkładu Studenta odczytujemy wartość t
α
=2,0639. Podstawiając dane liczbowe
otrzymujemy następujący przedział ufności:
1
25
62
,
6
0639
,
2
6
,
34
1
25
62
,
6
0639
,
2
6
,
34
−
+
<
<
−
−
m
31,81 zł < m < 37,39 zł
Interpretacja: Przedział o krańcach 31,81 i 37,39 zł pokrywa z wiarygodnością 0,95
nieznaną wartość średnich wydatków na kulturę rodzin 3-osobowych.
ZADANIE – ESTYMACJA PRZEDZIAŁOWA, NIEZBĘDNA LICZEBNOŚĆ PRÓBY
3
Badana cecha X: wydatki na kulturę w zł.
Badane zbiorowości: 1. rodziny ogółem (n
1
=230;
1
x
=34 zł obliczone z próby; s
1
=8,36 zł);
2. rodziny 2-osobowe (n
2
=25;
2
x
=25,4 zł; s
2
=6,62 zł)
3. rodziny 3-osobowe (n
3
=25;
3
x
=34,6 zł; s
3
=6,62 zł)
4. rodziny 4-osobowe (n
4
=60;
4
x
=35,33 zł; s
4
=7,97 zł)
5. rodziny 5-osobowe (n
5
=80;
5
x
=30,00 zł; s
5
=5,00 zł)
(2)
Oszacować średnie wydatki na kulturę rodzin 5-osobowych, przyjmując poziom ufności
0,99.
Szacowany parametr:
θ=m
(średnie wydatki na kulturę rodzin 5-osobowych).
Estymatorem jest średnia arytmetyczna z próby
T
n
=
x
.
Ponieważ próba jest duża (n=80 rodzin 5-osobowych) przedział ufności dla parametru m
jest następujący:
α
α
α
−
=
⎭
⎬
⎫
⎩
⎨
⎧
+
<
<
−
1
n
s
u
x
m
n
s
u
x
P
.
Dla współczynnika ufności 0,99 z tablic dystrybuanty rozkładu normalnego
standaryzowanego odczytujemy u
α
, tak aby
2
1
)
(
α
α
−
=
Φ u
=0,995. Zatem u
α
=2,58.
Podstawiając dane liczbowe otrzymujemy następujący przedział ufności:
80
5
58
,
2
30
80
5
58
,
2
30
+
<
<
−
m
28,58 zł < m < 31,44 zł
Interpretacja: Przedział o krańcach 28,58 i 31,44 zł pokrywa z wiarygodnością 0,99
nieznaną wartość średnich wydatków na kulturę rodzin 5-osobowych.
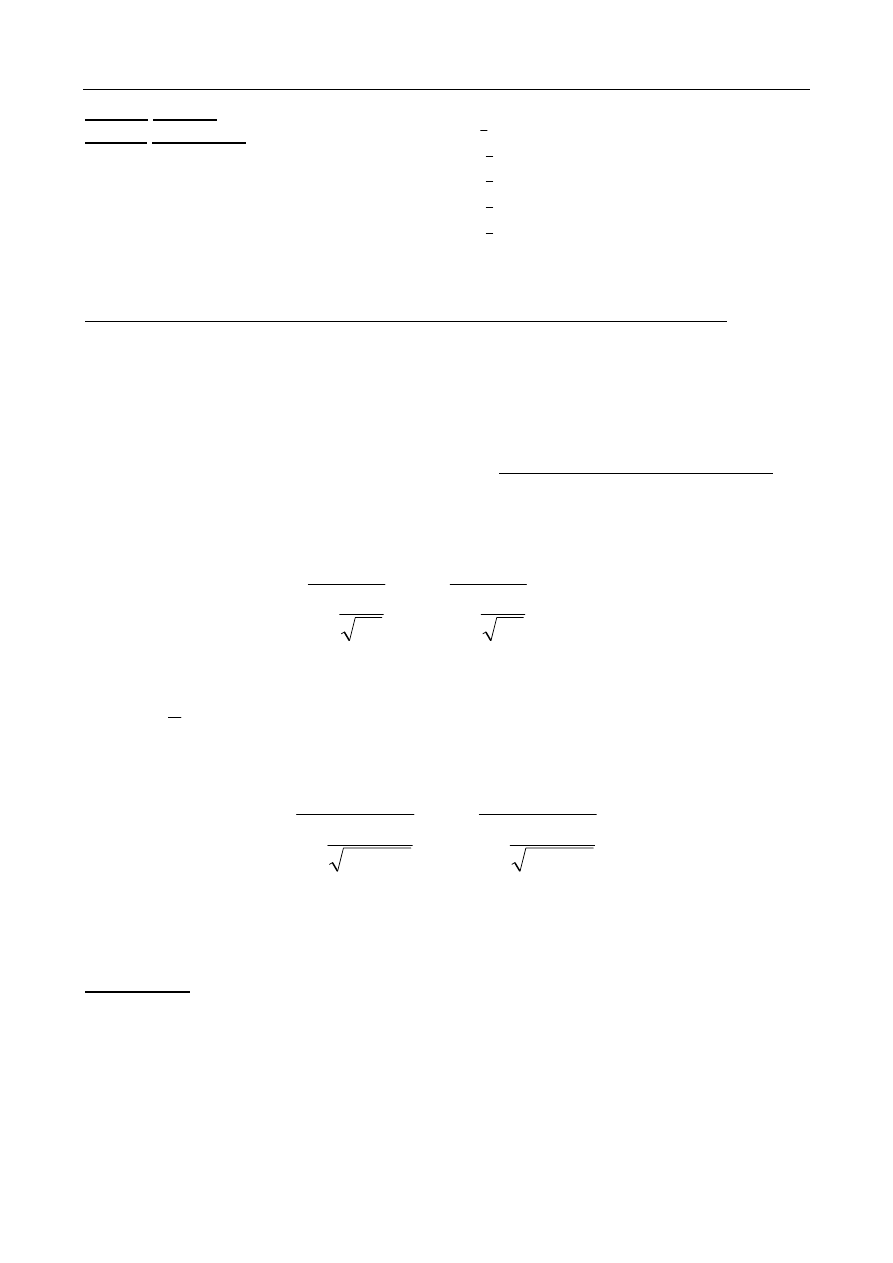
ZADANIE – ESTYMACJA PRZEDZIAŁOWA, NIEZBĘDNA LICZEBNOŚĆ PRÓBY
4
Badana cecha X: wydatki na kulturę w zł.
Badane zbiorowości: 1. rodziny ogółem (n
1
=230;
1
x
=34 zł obliczone z próby; s
1
=8,36 zł);
2. rodziny 2-osobowe (n
2
=25;
2
x
=25,4 zł; s
2
=6,62 zł)
3. rodziny 3-osobowe (n
3
=25;
3
x
=34,6 zł; s
3
=6,62 zł)
4. rodziny 4-osobowe (n
4
=60;
4
x
=35,33 zł; s
4
=7,97 zł)
5. rodziny 5-osobowe (n
5
=80;
5
x
=30,00 zł; s
5
=5,00 zł)
(
3)
Ocenić zróżnicowanie wydatków na kulturę rodzin ogółem z wiarygodnością 0,95
Szacowany parametr:
θ=σ
(zróżnicowanie wydatków na kulturę rodzin ogółem na
osiedlu). Estymatorem jest odchylenie standardowe z próby
T
n
=s.
Ponieważ próba jest duża (n=230 rodzin ogółem), przedział ufności dla parametru
σ jest
następujący:
α
σ
α
α
−
=
⎪
⎪
⎭
⎪⎪
⎬
⎫
⎪
⎪
⎩
⎪⎪
⎨
⎧
−
<
<
+
1
2
1
2
1
n
u
s
n
u
s
P
.
Przy współczynniku 0,95 wartość u
α
odczytujemy z tablic rozkładu normalnego tak, aby
2
1
)
(
α
α
−
=
Φ u
. Zatem u
α
=1,96. Podstawiając do wzoru dane liczbowe otrzymujemy przedział
ufności:
230
*
2
96
,
1
1
36
,
8
230
*
2
96
,
1
1
36
,
8
−
<
<
+
σ
7,69 zł <
σ < 9,23 zł
Interpretacja: Przedział o krańcach 7,69 i 9,23 zł pokrywa z wiarygodnością 0,95 nieznaną
wartość odchylenia standardowego wydatków na kulturę rodzin ogółem.
ZADANIE – ESTYMACJA PRZEDZIAŁOWA, NIEZBĘDNA LICZEBNOŚĆ PRÓBY
5
Badana cecha X: wydatki na kulturę w zł.
Badane zbiorowości: 1. rodziny ogółem (n
1
=230;
1
x
=34 zł obliczone z próby; s
1
=8,36 zł);
2. rodziny 2-osobowe (n
2
=25;
2
x
=25,4 zł; s
2
=6,62 zł)
3. rodziny 3-osobowe (n
3
=25;
3
x
=34,6 zł; s
3
=6,62 zł)
4. rodziny 4-osobowe (n
4
=60;
4
x
=35,33 zł; s
4
=7,97 zł)
5. rodziny 5-osobowe (n
5
=80;
5
x
=30,00 zł; s
5
=5,00 zł)
(4)
Z wiarygodnością 0,90 oszacować zróżnicowanie wydatków na kulturę rodzin 3-
osobowych.
Szacowany parametr:
θ=σ
2
(zróżnicowanie wydatków na kulturę rodzin 3-osobowych).
Estymatorem jest wariancja z próby
T
n
=s
2
.
Ponieważ próba jest mała (n=25 rodzin 3-osobowych), przedział ufności dla parametru
σ
2
,
przy założeniu, że X~N(m,
σ), σ - nie jest znane, jest następujący:
α
σ
−
=
⎭
⎬
⎫
⎩
⎨
⎧
<
<
1
1
2
2
2
2
c
ns
c
ns
P
.
Przy współczynniku ufności 0,90 wartości c
1
i c
2
odczytujemy z tablic wartości krytycznych
rozkładu
χ
2
dla n-1=24 stopni swobody (boczek tablicy) i w główce tablicy dla c
1
:
2
1
α
−
(P{
χ
2
≥c
1
}=0,95) oraz dla c
2:
2
α
(P{
χ
2
≥c
2
}=0,05). Odczytane wartości – c
1
=13,848 oraz
c
2
=36,415. Podstawiając do wzoru dane liczbowe otrzymujemy przedział ufności:
848
,
13
)
62
,
6
(
*
25
415
,
36
)
62
,
6
(
*
25
2
2
2
<
<
σ
30,08 zł
2
<
σ
2
< 79,11 zł
2
oraz wyciągając pierwiastek
5,48 zł <
σ < 8,89 zł
Interpretacja: Przedział o krańcach 5,48 i 8,89 zł pokrywa z wiarygodnością 0,99 nieznaną
wartość odchylenia standardowego wydatków na kulturę rodzin 3-osobowych.
ZADANIE – ESTYMACJA PRZEDZIAŁOWA, NIEZBĘDNA LICZEBNOŚĆ PRÓBY
6
Badana cecha X: wydatki na kulturę w zł.
Badane zbiorowości: 1. rodziny ogółem (n
1
=230;
1
x
=34 zł obliczone z próby; s
1
=8,36 zł);
2. rodziny 2-osobowe (n
2
=25;
2
x
=25,4 zł; s
2
=6,62 zł)
3. rodziny 3-osobowe (n
3
=25;
3
x
=34,6 zł; s
3
=6,62 zł)
4. rodziny 4-osobowe (n
4
=60;
4
x
=35,33 zł; s
4
=7,97 zł)
5. rodziny 5-osobowe (n
5
=80;
5
x
=30,00 zł; s
5
=5,00 zł)
(5)
Z prawdopodobieństwem 0,95 ocenić odsetek rodzin ogółem wydających na kulturę
powyżej 40 zł.
Szacowany parametr:
θ=p
(odsetek rodzin ogółem wydających powyżej 40 zł).
Estymatorem jest wskaźnik struktury z próby
T
n
=
n
k
. Wśród rodzin ogółem 65 wydaje na
kulturę ponad 40 zł miesięcznie. Przedział ufności jest postaci:
α
α
α
−
=
⎪
⎪
⎭
⎪⎪
⎬
⎫
⎪
⎪
⎩
⎪⎪
⎨
⎧
⎟
⎠
⎞
⎜
⎝
⎛ −
+
<
<
⎟
⎠
⎞
⎜
⎝
⎛ −
−
1
1
1
n
n
k
n
k
u
n
k
p
n
n
k
n
k
u
n
k
P
.
Dla 1-
α=0,95 odczytana z tablic wartość u
α
=1,96. Podstawiając wartości liczbowe
uzyskujemy następujący przedział ufności:
230
230
65
1
230
65
96
,
1
230
65
230
230
65
1
230
65
96
,
1
230
65
⎟
⎠
⎞
⎜
⎝
⎛ −
+
<
<
⎟
⎠
⎞
⎜
⎝
⎛ −
−
p
0,22 < p < 0,34
Interpretacja: Przedział o krańcach 0,22 i 0,34 pokrywa z prawdopodobieństwem 0,95
nieznany odsetek rodzin ogółem wydających na kulturę powyżej 40 zł.
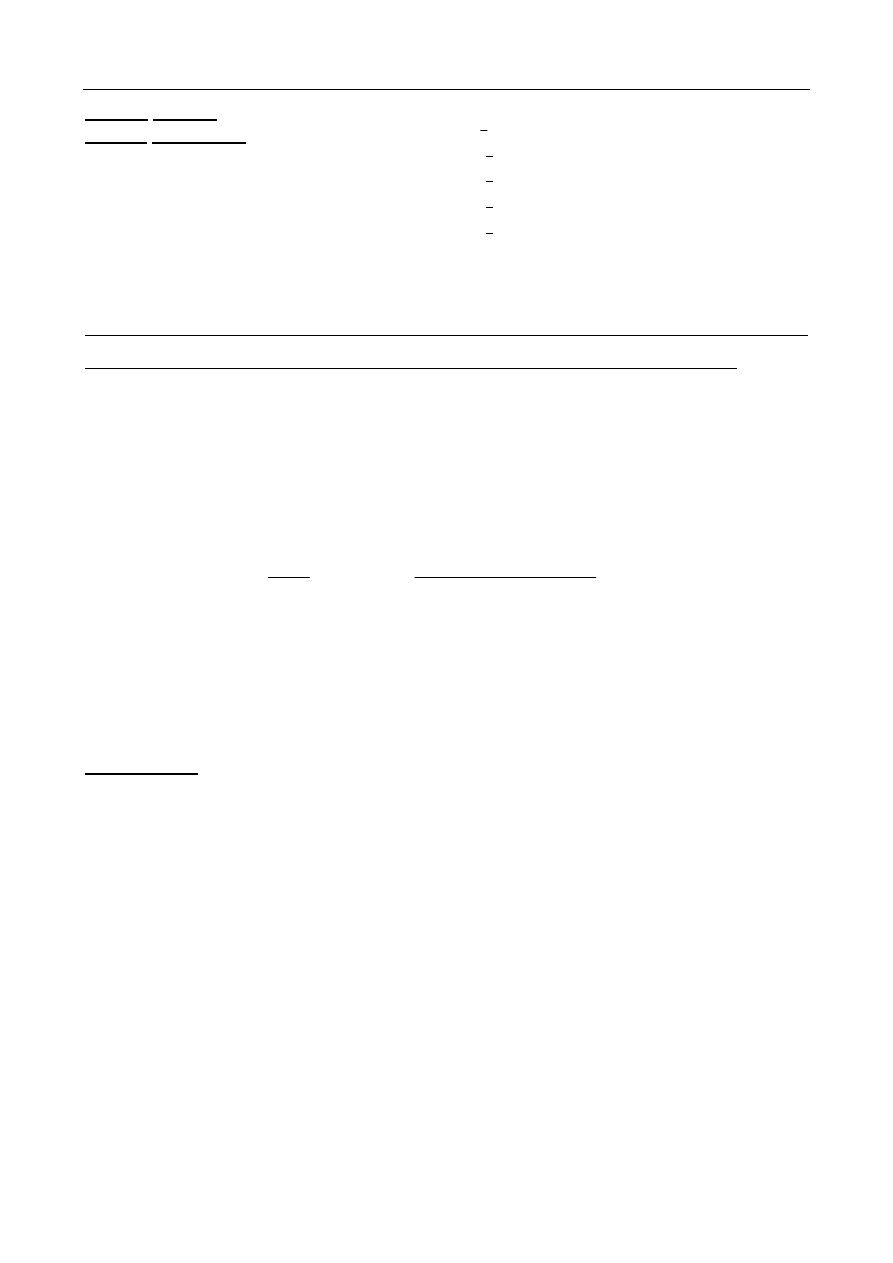
ZADANIE – ESTYMACJA PRZEDZIAŁOWA, NIEZBĘDNA LICZEBNOŚĆ PRÓBY
7
Badana cecha X: wydatki na kulturę w zł.
Badane zbiorowości: 1. rodziny ogółem (n
1
=230;
1
x
=34 zł obliczone z próby; s
1
=8,36 zł);
2. rodziny 2-osobowe (n
2
=25;
2
x
=25,4 zł; s
2
=6,62 zł)
3. rodziny 3-osobowe (n
3
=25;
3
x
=34,6 zł; s
3
=6,62 zł)
4. rodziny 4-osobowe (n
4
=60;
4
x
=35,33 zł; s
4
=7,97 zł)
5. rodziny 5-osobowe (n
5
=80;
5
x
=30,00 zł; s
5
=5,00 zł)
(6)
Ile rodzin należy dolosować do próby, aby można było oszacować średnie wydatki rodzin 3-
osobowych z wiarygodnością 0,95 i maksymalnym błędem szacunku równym 2 zł?
Ponieważ próba jest mała (25 rodzin 3-osobowych), zatem niezbędną liczebność
próby obliczymy ze wzoru:
1
1
)
2
(
)
62
,
6
(
*
)
0639
,
2
(
1
1
2
2
2
2
2
2
+
⎥
⎦
⎤
⎢
⎣
⎡
+
=
+
⎥
⎦
⎤
⎢
⎣
⎡
+
=
d
s
t
n
α
.
1-
α = 0,95; stąd: t
α
=2,0639; d=2 zł, s=6,62 zł.
Podstawiając wartości liczbowe uzyskujemy
n=[46,67+1]+1=48.
Interpretacja: Aby z wiarygodnością 0,95 oszacować średnie wydatki rodzin 3-
osobowych na kulturę z maksymalnym błędem szacunku równym 2 zł, należy do
próby dolosować
48-25=23 osoby.
ZADANIE – ESTYMACJA PRZEDZIAŁOWA, NIEZBĘDNA LICZEBNOŚĆ PRÓBY
8
Badana cecha X: wydatki na kulturę w zł.
Badane zbiorowości: 1. rodziny ogółem (n
1
=230;
1
x
=34 zł obliczone z próby; s
1
=8,36 zł);
2. rodziny 2-osobowe (n
2
=25;
2
x
=25,4 zł; s
2
=6,62 zł)
3. rodziny 3-osobowe (n
3
=25;
3
x
=34,6 zł; s
3
=6,62 zł)
4. rodziny 4-osobowe (n
4
=60;
4
x
=35,33 zł; s
4
=7,97 zł)
5. rodziny 5-osobowe (n
5
=80;
5
x
=30,00 zł; s
5
=5,00 zł)
(7)
Ile rodzin należy dolosować do próby, aby ocenić średnie wydatki na kulturę rodzin 5-
osobowych z wiarygodnością 0,99 i maksymalnym błędem szacunku równym 1 zł?
Ponieważ próba jest duża (80 rodzin 5-osobowych), niezbędną liczebność próby
obliczymy ze wzoru:
1
1
5
*
)
58
,
2
(
1
2
2
2
2
2
2
+
⎥
⎦
⎤
⎢
⎣
⎡
=
+
⎥
⎦
⎤
⎢
⎣
⎡
=
d
s
u
n
α
.
1-
α = 0,99; stąd: u
α
=2,58; d=1 zł, s=5 zł.
Podstawiając wartości liczbowe uzyskujemy
n
=[166,41]+1=167.
Interpretacja: Aby z wiarygodnością 0,99 oszacować średnie wydatki rodzin 5-
osobowych na kulturę z maksymalnym błędem szacunku równym 1 zł, należy do
próby dolosować
167-80=87 osób.
ZADANIE – ESTYMACJA PRZEDZIAŁOWA, NIEZBĘDNA LICZEBNOŚĆ PRÓBY
9
Badana cecha X: wydatki na kulturę w zł.
Badane zbiorowości: 1. rodziny ogółem (n
1
=230;
1
x
=34 zł obliczone z próby; s
1
=8,36 zł);
2. rodziny 2-osobowe (n
2
=25;
2
x
=25,4 zł; s
2
=6,62 zł)
3. rodziny 3-osobowe (n
3
=25;
3
x
=34,6 zł; s
3
=6,62 zł)
4. rodziny 4-osobowe (n
4
=60;
4
x
=35,33 zł; s
4
=7,97 zł)
5. rodziny 5-osobowe (n
5
=80;
5
x
=30,00 zł; s
5
=5,00 zł)
(8)
Ile rodzin należy dolosować do próby, aby oszacować odsetek rodzin ogółem wydających
na kulturę mniej niż 30 zł z wiarygodnością 0,96 i błędem szacunku równym 4%, jeżeli
wiadomo, że w całej zbiorowości rodzin 3-osobowych około 1/3 wydaje miesięcznie na
kulturę do 30 zł?
1-
α = 0,96; stąd: u
α
=2,05; d=0,04.
Z treści zadania wiemy, że odsetek rodzin ogółem wydających na kulturę poniżej 30
zł jest równy p=0,33. Zatem niezbędną liczebność próby obliczymy ze wzoru:
1
)
04
,
0
(
)
33
,
0
1
(
33
,
0
)
05
,
2
(
1
)
1
(
2
2
2
2
+
⎥
⎦
⎤
⎢
⎣
⎡
−
=
+
⎥
⎦
⎤
⎢
⎣
⎡
−
=
d
p
p
u
n
α
.
Podstawiając dane liczbowe otrzymujemy
n=[580,73]+1=581.
Interpretacja: Aby z prawdopodobieństwem 0,96 oszacować odsetek rodzin
wydających na kulturę mniej niż 30 zł z błędem szacunku równym 4% należy
dolosować do próby
581-230=351 osób.
ZADANIE – ESTYMACJA PRZEDZIAŁOWA, NIEZBĘDNA LICZEBNOŚĆ PRÓBY
10
Badana cecha X: wydatki na kulturę w zł.
Badane zbiorowości: 1. rodziny ogółem (n
1
=230;
1
x
=34 zł obliczone z próby; s
1
=8,36 zł);
2. rodziny 2-osobowe (n
2
=25;
2
x
=25,4 zł; s
2
=6,62 zł)
3. rodziny 3-osobowe (n
3
=25;
3
x
=34,6 zł; s
3
=6,62 zł)
4. rodziny 4-osobowe (n
4
=60;
4
x
=35,33 zł; s
4
=7,97 zł)
5. rodziny 5-osobowe (n
5
=80;
5
x
=30,00 zł; s
5
=5,00 zł)
(9)
Ile rodzin należy dolosować do próby, aby ocenić odsetek rodzin ogółem wydających na
kulturę powyżej 40 zł z tą samą wiarygodnością i błędem szacunku równym 3%?
1-
α = 0,95; stąd: u
α
=1,96; d=0,03
Ponieważ nie znamy odsetka p (rodziny ogółem wydające na kulturę ponad 40 zł w
całej zbiorowości) zatem niezbędną liczebność próby obliczymy ze wzoru:
1
)
03
,
0
(
*
4
)
96
,
1
(
1
4
2
2
2
2
+
⎥
⎦
⎤
⎢
⎣
⎡
=
+
⎥
⎦
⎤
⎢
⎣
⎡
=
d
u
n
α
.
Po podstawieniu danych otrzymujemy
n=[1067,11]+1=1068.
Interpretacja: Aby z wiarygodnością 0,95 i błędem szacunku 3% ocenić odsetek
rodzin ogółem wydających na kulturę ponad 40 zł należy dolosować do próby
1068-230=838 rodzin.