Testy parametryczne - rozwiązania

WERYFIKACJA HIPOTEZY O RÓWNOŚCI DWÓCH ŚREDNICH

Niech będą dane dwie próby proste X

1

, X

2

,..., X

n1

oraz Y

1

, Y

2

,..., Y

n2

(gdzie n

1

i n

2

oznaczają liczebności prób). Niech

1

x

i

2

x

oznaczają średnie arytmetyczne (oszacowania

wartości oczekiwanej) w odpowiednio 1 i 2 zbiorowości, a

2

1

s

i

2

2

s

oszacowania wariancji

odpowiednio w 1 i 2 zbiorowości.

Na podstawie wyników prób należy zweryfikować hipotezę o równości wartości

oczekiwanych

H

0

:

µ

1

=

µ

2

wobec H

1

:

µ

1

≠µ

2

(dwustronny obszar odrzucenia)

lub

µ

1

<

µ

2

(lewostronny obszar odrzucenia)

lub

µ

1

>

µ

2

(prawostronny obszar odrzucenia).

1. Gdy nie ma podstaw do przyjęcia założenia, że badane populacje mają rozkłady

normalne ale wylosowano duże próby (n

1

, n

2

> 30), korzystamy ze statystyki postaci:

2

2

2

1

2

1

2

1

n

s

n

s

x

x

U

+

−

=

,

która przy założeniu prawdziwości hipotezy zerowej H

0

ma rozkład N(0,1)

Dla przyjętego poziomu istotności

α wartości krytyczne u

α

odczytujemy tak, by spełnione

były równości:











>

≥

<

≤

≠

≥

=

2

1

1

2

1

1

2

1

1

:

gdy

},

{

:

gdy

},

{

:

gdy

},

{

µ

µ

µ

µ

µ

µ

α

α

α

α

H

u

u

P

H

u

u

P

H

u

u

P

czyli dla obszaru jednostronnego

Φ(u

α

)=1-

α, zaś dla dwustronnego obszaru odrzucenia:

Φ(u

α

)=1-

α/2. Jeżeli:

α

u

u

≥

, to odrzucamy H

0

na rzecz H

1

:

2

1

µ

µ

≠

,

α

u

u

≤

, to odrzucamy H

0

na rzecz H

1

:

2

1

µ

µ

<

,

α

u

u

≥

, to odrzucamy H

0

na rzecz H

1

:

2

1

µ

µ

>

,

w przeciwnym razie nie ma podstaw do odrzucenia hipotezy zerowej.

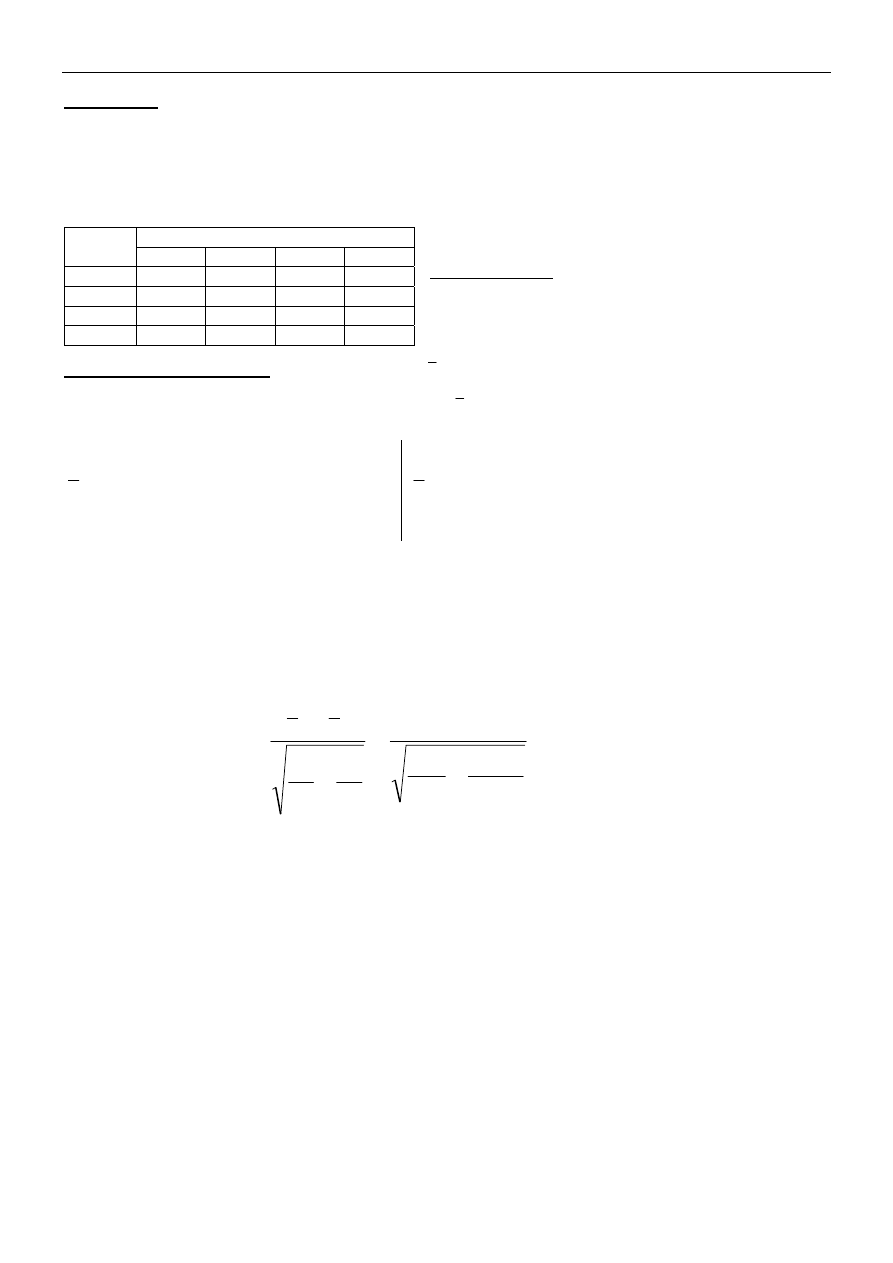
Testy parametryczne - rozwiązania

Zadanie 1.

Zebrano informacje o liczbie osób w rodzinie i miesięcznych wydatkach na

przetwory zbożowe wśród wylosowanych w sposób niezależny 200 rodzin

zamieszkujących pewne osiedle. Uzyskano następujące wyniki:

Liczba rodzin wg liczby osób

Wydatki

w zł

3 4 5 6

5-15

20 20 - -

15-25

- 20 40 -

25-35

- 20 40 -

35-45

- - - 40

Sprawdzić, czy średnie wydatki rodzin ogółem są
istotnie wyższe od średnich wydatków rodzin 4-
osobowych, godząc się na ryzyko popełnienia
błędu I rodzaju równe 0,02.

Obliczenia pomocnicze: rodziny ogółem:

x

=25 zł, s

2

=105 zł

2

;

rodziny 4-osobowe:

x

=20 zł, s

2

=66,67 zł

2

.

200

1

=

n

25

1

=

x

zł

105

2

1

=

S

zł

2

60

2

=

n

20

2

=

x

zł

67

,

66

2

2

=

S

zł

2

2

1

0

:

m

m

H

=

2

1

1

:

m

m

H

>

(prawostronny obszar odrzucenia)

α=0,02

duże próby, czyli jest to trzeci przypadek testu o równości dwóch średnich. Obliczamy
statystykę :

9089

,

3

60

67

,

66

200

105

20

25

2

2

2

1

2

1

2

1

=

+

−

=

+

−

=

n

s

n

s

x

x

U

porównujemy wynik z wartością u

α

odczytaną z tablic dystrybuanty rozkładu normalnego

w oparciu o prawdopodobieństwo 1- α = 0,98 stąd u

α

= 2,06.

U = 3,9089 > u

α

= 2,06 czyli

Odp. Na poziomie istotności

α=0,02 odrzucamy hipotezę zerową na rzecz hipotezy

alternatywnej mówiącej, iż średnie wydatki na przetwory zbożowe rodzin ogółem są

istotnie wyższe od średnich wydatków rodzin 4-osobowych.

Testy parametryczne - rozwiązania

WERYFIKACJA HIPOTEZY O DWÓCH WSKAŹNIKACH STRUKTURY

Niech będą dane dwie populacje mające rozkłady dwupunktowe z parametrami

odpowiednio p

1

i p

2

. Na podstawie wyników dwóch niezależnych prób o liczebnościach n

1

i n

2

(>100) należy zweryfikować hipotezę, że parametry p

1

i p

2

są jednakowe, tzn.

H

0

: p

1

=p

2

wobec alternatywnej

H

1

: p

1

≠p

2

(p

1

>p

2

, p

1

<p

2

).

Jeśli k

1

oraz k

2

oznaczają odpowiednio liczbę elementów z wyróżnioną cechą w populacji

I i II, to wskaźniki struktury z obu prób będą równe odpowiednio

1

1

n

k

i

2

2

n

k

. Statystyka

testu jest postaci:

2

1

2

1

2

1

2

1

2

2

1

1

1

gdzie

*

n

n

n

n

n

p

q

n

n

k

k

p

n

q

p

n

k

n

k

U

+

=

−

=

+

+

=

−

=

i przy założeniu prawdziwości hipotezy zerowej ma rozkład N(0, 1). Wartości krytyczne

odczytujemy z tablic rozkładu N(0, 1) dla przyjętego poziomu

α.

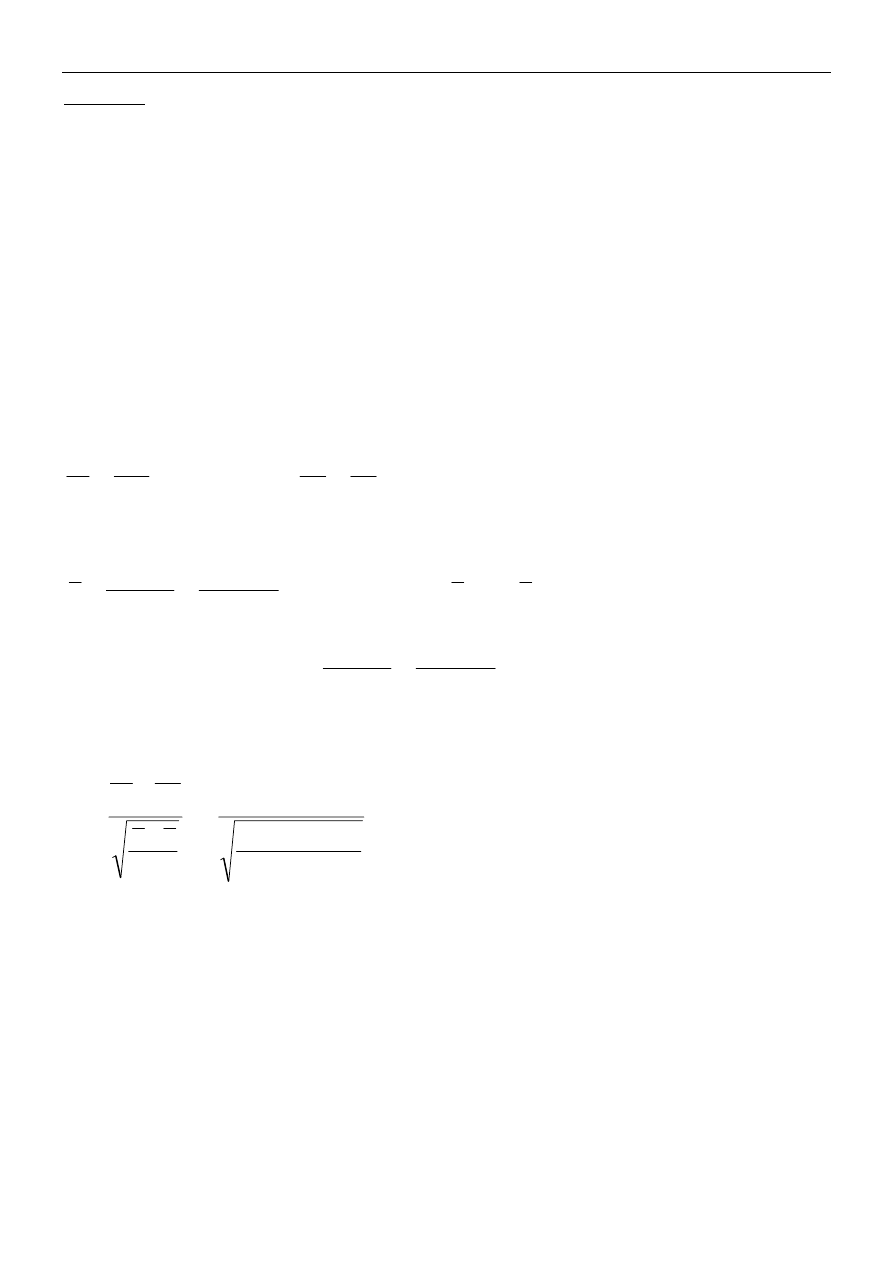
Testy parametryczne - rozwiązania

Zadanie 2.

Panuje przekonanie, że studenci stacjonarni UŁ zdają lepiej egzamin ze statystyki niż

studenci zaoczni. W celu sprawdzenia tej hipotezy wylosowano 100 osób ze studiów

stacjonarnych i okazało się, że wśród nich 40 uzyskało z egzaminu ocenę przynajmniej

dobrą. Wśród 80 osób wylosowanych z grupy studentów zaocznych podobną ocenę

uzyskało 24 osób. Czy rzeczywiście studenci stacjonarni zdają lepiej egzamin ze statystyki

niż studenci zaoczni ?

α=0,05

H

0

: p

1

=p

2

H

1

: p

1

>p

2

Z danych w zadaniu otrzymujemy:

40

,

0

100

40

1

1

=

=

n

k

30

,

0

80

24

2

2

=

=

n

k

356

,

0

80

100

24

40

2

1

2

1

=

+

+

=

+

+

=

n

n

k

k

p

644

,

0

356

,

0

1

1

=

−

=

−

=

p

q

444

,

44

80

100

80

*

100

2

1

2

1

=

+

=

+

=

n

n

n

n

n

a następnie korzystając z wzoru na statystykę testu obliczamy:

3923

,

1

444

,

44

644

,

0

*

356

,

0

0,30

-

0,40

*

2

2

1

1

=

=

−

=

n

q

p

n

k

n

k

U

ponieważ H

1

: p

1

>p

2

, więc zbiór krytyczny jest prawostronny i porównujemy wynik z

wartością u

α

odczytaną z tablic dystrybuanty rozkładu normalnego w oparciu o

prawdopodobieństwo 1- α = 0,95 stąd u

α

= 1,65.

ponieważ

u = 1,1,3923 < u

α

= 1,65

zatem

Odp. Na poziomie istotności

α=0,05 nie mamy podstaw do odrzucenia hipotezy zerowej

mówiącej o takim samym poziomie zdawania egzaminu ze statystyki na studiach

stacjonarnych i zaocznych.