
Zadania z oryginalną numeracją pochodzą z Informatora o egzaminie maturalnym od 2010 roku
z matematyki (zdawanej jako przedmiot obowiązkowy) – Arkusz P2.
Potrzebne wzory oraz inne informacje znajdziesz w
Tydzień 15.
Odp. B
Możemy, zgodnie z własnościami wartości bezwzględnej, zapisać warunki równoważne
Po ich rozwiązaniu otrzymujemy
Odp. A
Odp. C
Możemy np. rozwiązać warunek
. Jego rozwiązaniem jest liczba 100.
Odp. D

Suma miar dwóch sąsiednich kątów równoległoboku jest równa 180
o
. Zatem kąty spełniające warunek
zadania to kąty o miarach 75
o
i 105
o
.
Odp. A
Możemy rozwiązać dwa warunki wynikające z definicji miejsca zerowego funkcji.
Funkcja nie posiada miejsc zerowych.
Odp. A
Wystarczy sprawdzić w tablicy wartości funkcji trygonometrycznych, aby stwierdzić, że
dla
Odp. D
Przy przekształcaniu danego wyrażenia będziemy korzystali z definicji potęgi o wykładniku wymiernym
i z własności potęg.
Odp. B

Zbiór wartości możemy odczytać z wykresu.
Odp. C
Skorzystamy ze wzoru na n-ty wyraz ciągu geometrycznego (a
n
), o pierwszym wyrazie a
1
i ilorazie q.
i
Odp. C
Obliczymy długości boków tego trójkąta.
Boki AB i AC okazały się tej samej długości, a zatem są one ramionami trójkąta równoramiennego.
Ramię tego trójkąta ma długość
.

c
2
4
α
Na początek pogrupujemy wyrazy i wyłączymy wspólny czynnik przed nawias.
Drugi z czynników rozkładamy na iloczyn czynników liniowych.
lub
lub
Rozwiązaniem tego równania jest
Przedstawmy w tabeli wyniki takiego doświadczenia.
Na podstawie tabeli możemy ustalić, że
Na żółto zaznaczono te wyniki. Które sprzyjają zdarzeniu A – liczby oczek otrzymane w obu rzutach
różnią się o 1. Stąd |A| = 16.
1
2
2
3
3
3
1 (1,1) (1,2) (1,2) (1,3) (1,3) (1,3)
2 (2,1) (2,2) (2,2) (2,3) (2,3) (2,3)
2 (2,1) (2,2) (2,2) (2,3) (2,3) (2,3)
3 (3,1) (3,2) (3,2) (3,3) (3,3) (3,3)
3 (3,1) (3,2) (3,2) (3,3) (3,3) (3,3)
3 (3,1) (3,2) (3,2) (3,3) (3,3) (3,3)
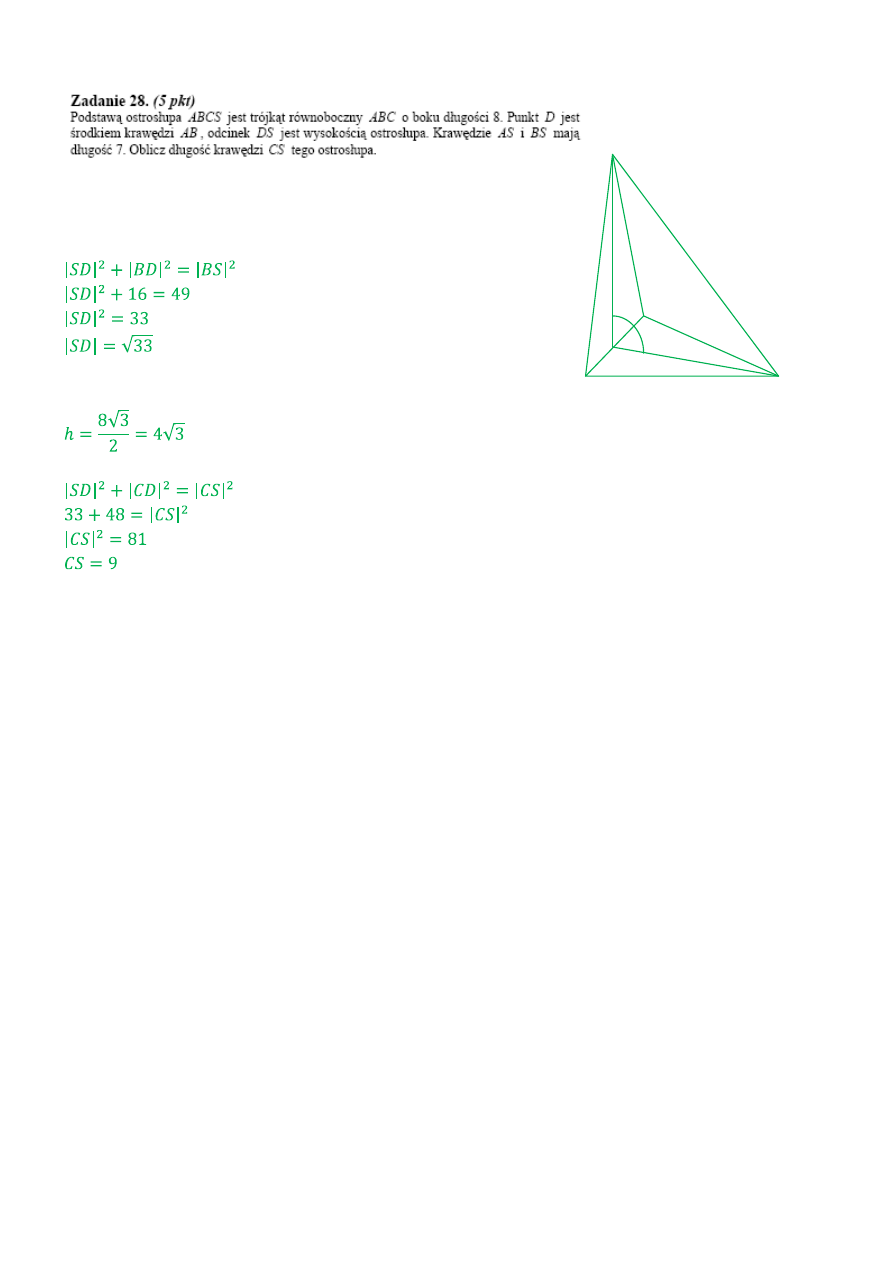
A
B
C
7
D
H
h
•
S
W trójkącie równoramiennym ABS, H jest jego wysokością. Korzystając
z twierdzenia Pitagorasa obliczymy długość SD.
Do obliczenia długości CS potrzebujemy jeszcze długości odcinka
DC , czyli wysokości trójkąta równobocznego.
Teraz obliczymy długość CS znów korzystając z twierdzenia Pitagorasa.
Wyszukiwarka
Podobne podstrony:
Zestaw 15 3 id 587996 Nieznany
Zestaw 15, Opracowane zagadnienia na egzamin
ZESTAW 15 lal, kinezjologia awf wrocław, kinezjologia awf wrocław
ZESTAW 15
zestawy maturalne, ZESTAW 15, ZESTAW 15
Mikrobiologia i parazytologia zestaw 15, Pielęgniarstwo, II rok, Mikrobiologia i parazytologia
Zestaw 15, 4 semestr, matlab, testy
zestaw 15, AiR, Semestr 2, Grafika inżynierska, zadania grafika
zestaw C 15-29, Studia, ZiIP, SEMESTR II, Materiały metalowe, Zestaw C
Zestaw 15
Urządzanie lasu Gołojuch zestawy 15
Zestaw 15 3 id 587996 Nieznany
Zestaw 15
Stymulus Zestaw 15 STP AN Gesundheit und Fitness
zestaw 15 ALzG
Zestaw 15 Bożena Bednarczyk
ZESTAW 15 doc
zestaw 15 teoria
więcej podobnych podstron