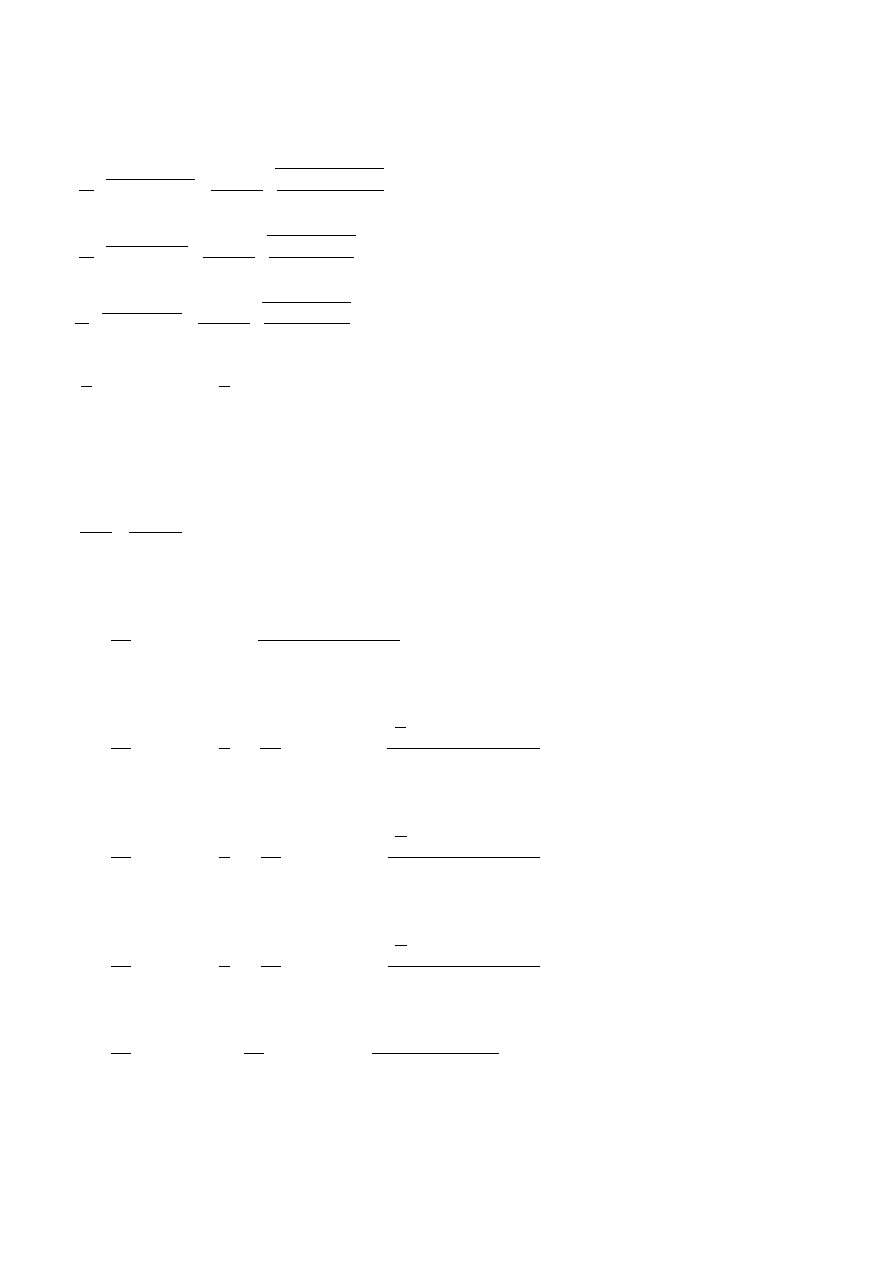
Przykładowe obliczenia – dla pomiaru 1 (oznaczanego dalej jako P1):
z
R
- z
a
= 141,3- 115,8= 25,50 [mm]
z
R
- z
1
= 141,30- 130= 11,30 [mm]
z
1
- z
a
= 130- 115,8= 14,20 [mm]
ω
1
=
1
R
2g Z
R
−
Z
a
=
1
0,0635
2∗9,81∗25,50
1000
=
11,14 [rad / s]
ω
2
=
2
R
g Z
R
−
Z
1
=
2
0,0635
9,81∗11,30
1000
=
10,49 [rad / s ]
ω
3
=
2
R
g Z
1
−
Z
a
=
2
0,0635
9,81∗14,20
1000
=
11,76 [rad / s ]
ω
śr
=
1
3
ω1ω2ω3=
1
3
11,1410,4911,76=11,13 [rad / s]
W obliczeniach ω
1
,ω
2
,ω
3
wykorzystałam wcześniej policzone wartości
z
r
- z
a
,
z
r
-z
1
,
z
1
-z
a
, przy czym podzielone one
zostały przez 1000, ponieważ do ww. wzorów wstawia się wartości w jednostkach układu SI – konieczne było
zamienienie mm na m.
ω
0
=
n
0
30
=
∗
110
30
=
11,52[ rad / s]
dla r=0
p
n
=
ρ [r
2
ω
2
2
gz
a
]=
ρ [ gz
a
]=
1000∗9,81∗115,80
1000
=
1136[ Pa ]
dla r=1/4R
p
n
=
ρ [r
2
ω
2
2
gz
a
]=
ρ [
1
4
R
2
ω
2
2
gz
a
]=
1000[
1
4
∗
0,0635
2
∗
11,13
2
2
9,81∗115,8]=1151,6[ Pa]
dla r=1/2R
p
n
=
ρ [r
2
ω
2
2
gz
a
]=
ρ [
1
2
R
2
ω
2
2
gz
a
]=
1000 [
1
2
∗
0,0635
2
∗
11,13
2
2
9,81∗115,8]=1198,40 [ Pa]
dla 3/4R
p
n
=
ρ [r
2
ω
2
2
gz
a
]=
ρ [
3
4
R
2
ω
2
2
gz
a
]=
1000[
3
4
∗
0,0635
2
∗
11,13
2
2
9,81∗115,8]=1276,41[ Pa]
dla r=R
p
n
=
ρ [r
2
ω
2
2
gz
a
]=
ρ [ R
2
ω
2
2
gz
a
]=
1000[
0,0635
2
∗
11,13
2
2
9,81∗115,8]=1385,61[ Pa]
dla z=0
p
n
=
ρgz
R
=
1000∗9,81∗141,30=1386,15[ Pa ]
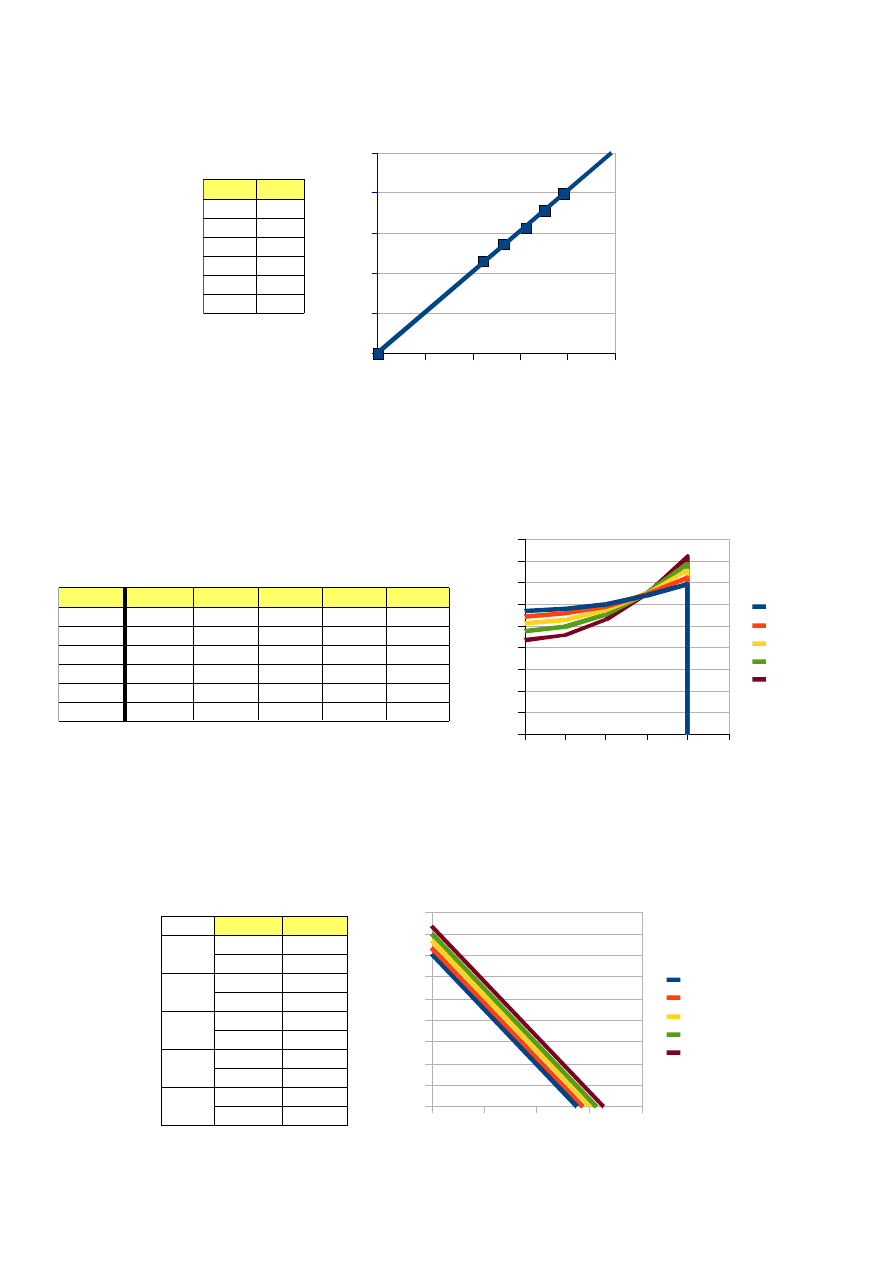
Wykresy i fragmenty tabel służące do ich sporządzenia:
r
P1
P2
P3
P4
P5
0
1136 1085,97 1019,26
946,17
862,79
0,25
1151,6 1108,36
1050
985,31
911,32
0,5
1198,4 1175,56 1142,22
1102,7
1056,9
0,75
1276,41 1287,55 1295,92 1298,35 1299,55
1
1385,61 1444,33 1511,09 1572,27 1639,25
1
0
0
0
0
0
0
0,25
0,5
0,75
1
1,25
0
200
400
600
800
1000
1200
1400
1600
1800
Wykres zaleznosci pn=f(r)
P1
P2
P3
P4
P5
r [m m ]
p
n
[P
a
]
Pn
z
P1
0
141,3
1386,15
0
P2
0
147,25
1444,52
0
P3
0
154,05
1511,23
0
P4
0
160,3
1572,54
0
P5
0
167,15
1639,74
0
0
500
1000
1500
2000
0
20
40
60
80
100
120
140
160
180
Wykres zależności pn=f(z)
P1
P2
P3
P4
P5
pn [Pa]
z
[m
m
]
0
0
11,13 11,52
13,33 13,61
15,62 15,71
17,62
17,8
19,62
19,9
ω
0
ω
śr
0
5
10
15
20
25
0
5
10
15
20
25
Wykres zalezności pn=f(z)
pn [Pa]
z
[m
m
]
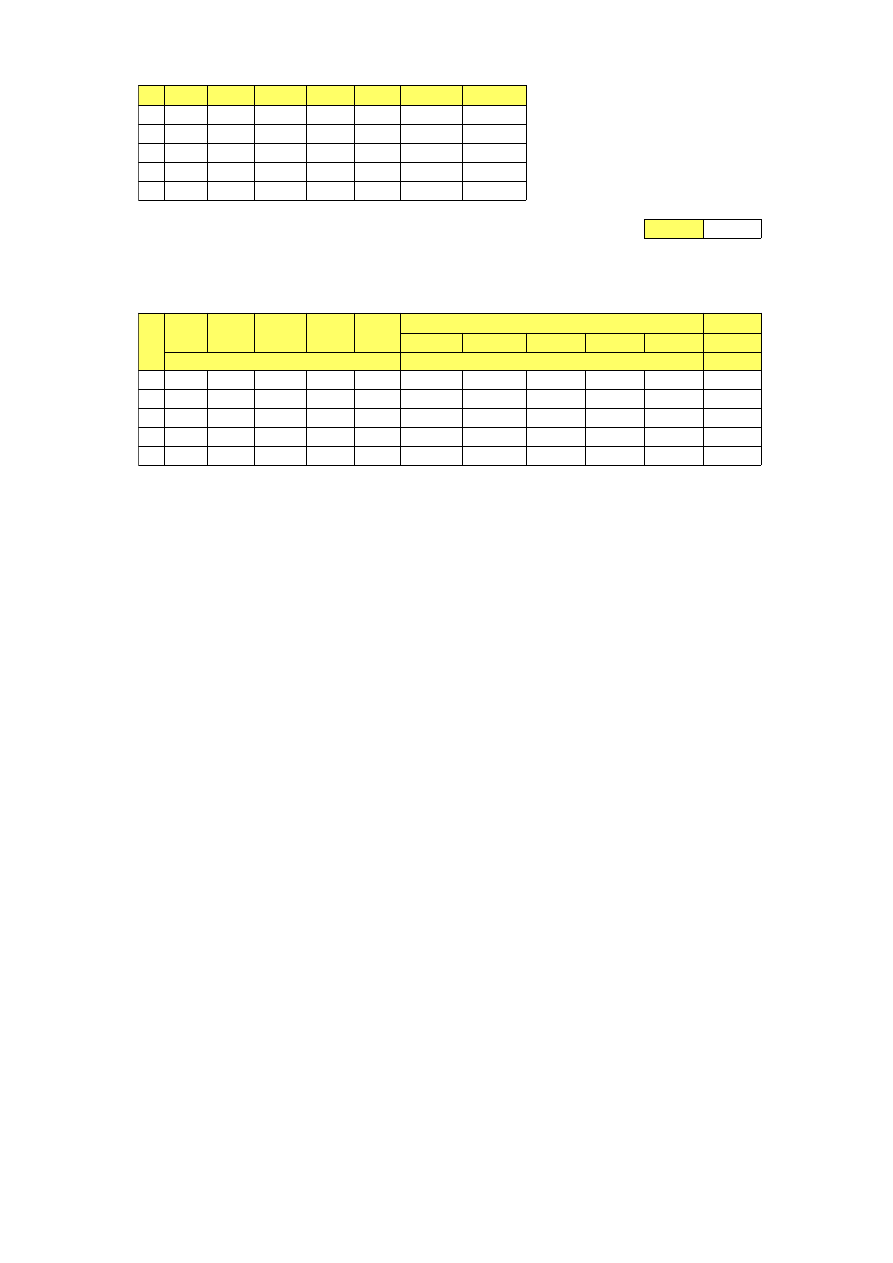
Tabele pomiarów i wyników:
Wnioski:
Na podstawie wykonanego doświadczenia mogę potwierdzić tezę, że powierzchnia swobodna cieczy w
naczyniu wirującym wokół własnej osi jest paraboloidą obrotową.
Rozkład ciśnień na dnie i na ściankach naczynia w stanie równowagi jest następujący: najmniejsze
nadciśnienie występuje w miejscu wierzchołka paraboloidy obrotowej tj. na środku dnia naczynia,
natomiast nadciśnienie jest największe w „rogach” naczynia, czyli w miejscy połączenia dna ze
ściankami naczynia.
Do wyznaczenia wykresu pn=f(z) wystarczy skorzystać z równania 1.13, ponieważ znamy wartość zR.
Lp.
1
110 115,8 141,3
130
25,5
11,3
14,2
2
130 110,7 147,25
130 36,55
17,25
19,3
3
150 103,9 154,05
130 50,15
24,05
26,1
4
170 96,45 160,3
130 63,85
30,3
33,55
5
190 87,95 167,15
130
79,2
37,15
42,05
R= 0,0635
Lp.
r=0
r=1/4R r=1/2R r=3/4R
r=R
z=0
rad/s
Pa
Pa
1 11,14 10,49 11,76 11,13 11,52
1136
1151,6 1198,4 1276,41 1385,61 1386,15
2 13,34 12,96
13,7 13,33 13,61 1085,97 1108,36 1175,56 1287,55 1444,33 1444,52
3 15,62
15,3 15,94 15,62 15,71 1019,26
1050 1142,22 1295,92 1511,09 1511,23
4 17,63 17,17 18,07 17,62
17,8
946,17
985,31 1102,7 1298,35 1572,27 1572,54
5 19,63 19,01 20,23 19,62
19,9
862,79
911,32 1056,9 1299,55 1639,25 1639,74
n
0
z
a
z
r
z
1
Z
r
-z
a
Z
r
-z
1
z
1
-z
a
ω
1
ω
2
ω
3
ω
sr
w
0
p
n
=f(r)
p
n
=f(z)
Wyszukiwarka
Podobne podstrony:
płyny spr 9
płyny spr 11
płyny spr 7
płyny spr 10
płyny spr 4
płyny spr 8
płyny spr 9
płyny spr 8
płyny spr 12
płyny spr 3
płyny spr 2
płyny spr 5
płyny spr 1
płyny spr 6
płyny spr 4
płyny spr 2
płyny spr 3
płyny spr 6
płyny spr 11
więcej podobnych podstron