1

00529 Ruch harmoniczny prosty D

TEORIA

00529

Ruch harmoniczny prosty D

Ogólna charakterystyka drgań prostych.

Wahadło matematyczne i fizyczne.

Drgania własne i wymuszone. Rezonans.

Energia ruchu harmonicznego.

Drgania mechaniczne, a elektryczne.

Instrukcja dla zdającego
1.

Proszę sprawdzić, czy arkusz teoretyczny zawiera 8
stron. Ewentualny brak należy zgłosić.

2.

Do arkusza może być dołączona karta wzorów i sta-
łych fizycznych. Jeśli jest, należy ją dołączyć do od-
dawanej pracy.

3.

Proszę uważnie i ze zrozumieniem przeczytać zawar-
tość arkusza.

4.

Proszę precyzyjnie wykonywać polecenia zawarte w
arkuszu: rozwiązać przykładowe zadania, wyprowa-
dzić wzory, gdy jest takie polecenie.

5.

Proszę analizować wszelkie wykresy i rysunki pod
kątem ich zrozumienia.

6.

W trakcie obliczeń można korzystać z kalkulatora.

7.

Wszelkie fragmenty trudniejsze proszę zaznaczyć w
celu ich późniejszego przedyskutowania.

8.

Uzupełniaj wiadomości zawarte w arkuszu o informa-
cje zawarte w Internecie i dostępnej ci literaturze.

śyczymy powodzenia!

(Wpisuje zdający przed rozpoczęciem pracy)

PESEL ZDAJĄCEGO

Aktualizacja

Listopad

ROK 2008

Dane osobowe właściciela arkusza

2

00529 Ruch harmoniczny prosty D

TEORIA

Temat 140

Ruch harmoniczny prosty.

1.

Dotychczas zajmowaliśmy się ruchami liniowymi i obrotowymi, na ogół o stałym przy-
spieszeniu. Zajmowaliśmy się także ruchem jednowymiarowym i dwuwymiarowym, wy-
nikającym z siły odwrotnie proporcjonalnej do kwadratu odległości (grawitacja). Teraz
zajmiemy się ruchem, w którym ciała przemieszczają się tam i z powrotem sinusoidalnie w
czasie (tzn. tak jak funkcja sinus lub cosinus czasu). Ruch sinusoidalny jest najbardziej
powszechną formą ruchu w życiu codziennym (okresowo zmienia się napięcie na zaci-
skach prądnicy, natężenie prądu w sieci miejskiej, bicie ludzkiego serca, świecenie niektó-
rych gwiazd itp.) i dlatego jest ważnym przedmiotem badań fizyki.

2.

Siła harmoniczna. Działająca na ciało siła, która jest proporcjonalna do przesunięcia ciała
od początku układu i która jest skierowana ku początkowi układu, nazywamy siłą harmo-
niczną. Jeżeli obierzemy oś x wzdłuż przesunięcia, to siła harmoniczna wyrażona równa-
niem:

( )

1

F

kx

= −

gdzie x jest przesunięciem od położenia równowagi jest np. siłą wywierana przez rozcią-
gniętą (lub ściśniętą) sprężynę, o ile sprężyna nie została rozciągnięta poza granicę sprę-
ż

ystości.

Spostrzeżenie, że sprężyna, jeżeli nie jest zbytnio rozciągnięta, wywiera siłę harmoniczną,
nazywa się prawem Hooke’a:

(

)

( )

2

0

F

k x

x

= −

−

,

gdzie x

0

jest położeniem równowagi.

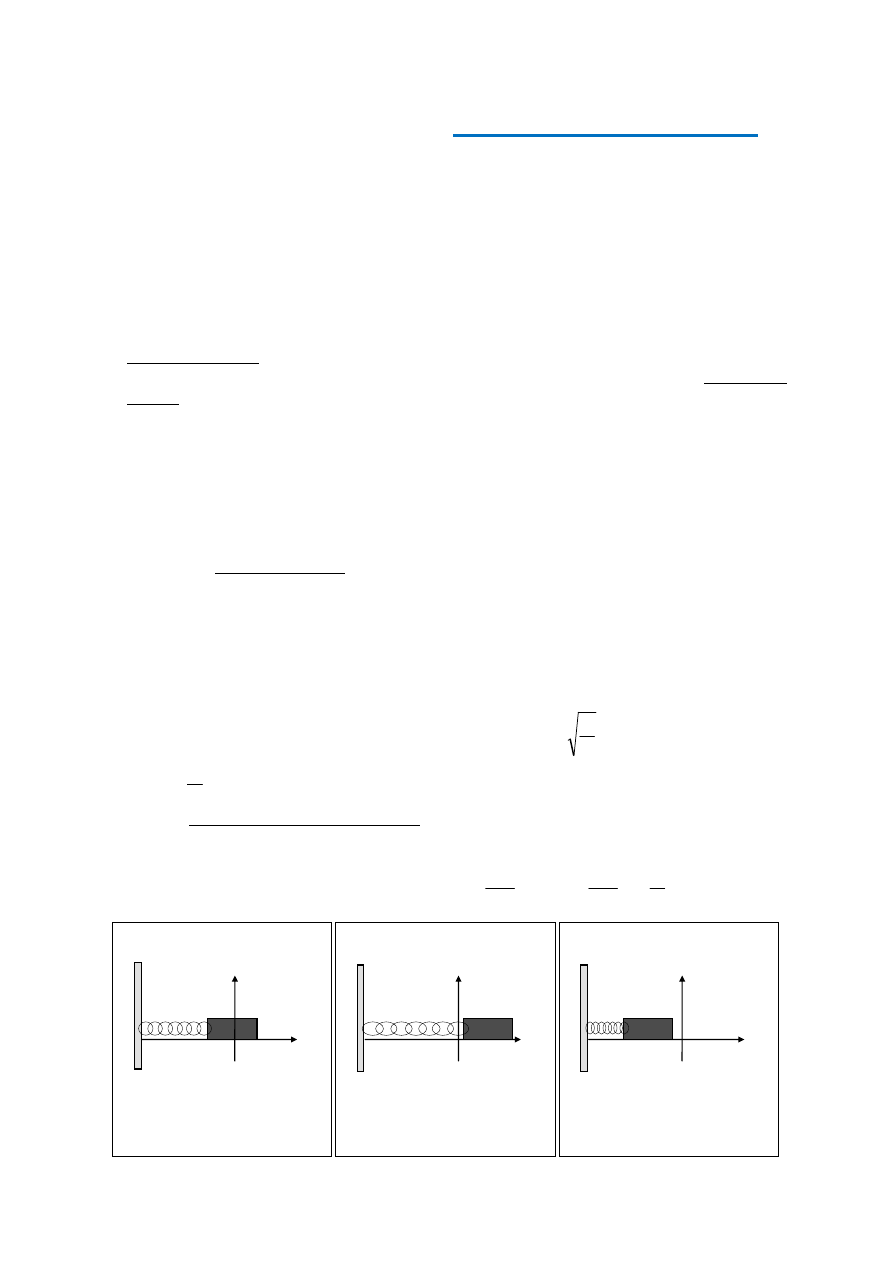
Na rys.1 początek układu współrzędnych obrano w położeniu równowagi (x

0

= 0). Poka-

ż

emy, że jeżeli sprężyna zostanie rozciągnięta tak, aby masa m. znalazła się w położeniu

x

m

, a następnie w chwili t = 0 sprężyna zostanie zwolniona, to położenie masy w funkcji

czasu będzie:

( )

cos

,

3

x

x

t

gdzie

k

m

m

=

⋅

=

ω

ω

i

k

F

x

= −

jest stałą sprężyny (stała sprężystości). Taki ruch sinusoidalny nazywany jest

zwykle ruchem harmonicznym prostym (RHP). Zaczynamy od równania

F

m a

wypadkowa

= ⋅

,

gdzie

F

wypadkowa

jest siłą sprężyny (-kx)

( )

,

,

4

2

2

2

2

−

=

−

=

= − ⋅

kx

ma

czyli

kx

m

d x

dt

czyli

d x

dt

k

m

x

O

Y

X

Rys.1a.

O

Y

X

Rys.1b.

O

Y

X

Rys.1c.

3

00529 Ruch harmoniczny prosty D

TEORIA

Tego typu równanie nazywa się równaniem różniczkowym drugiego rzędu. Zwykłym po-
stępowaniem przy rozwiązywaniu równań różniczkowych jest „odgadnięcie” odpowiedzi i
sprawdzenie czy jest ona rozwiązaniem równania. „Zgadujemy” więc, że x

x

t

= ⋅

cos

ω

i

sprawdzamy:

( )

sin

5

dx

dt

x

t

m

= −

ω

ω

(prędkość w RHP)

( )

cos

6

2

2

2

d x

dt

x

t

m

= −

ω

ω

(przyspieszenie w RHP)

Podstawmy wynik (6) do lewej strony równania (4) oraz zamiast x wyrażenie

x

t

m

cos

ω

do

prawej strony równania (6):

( )

cos

cos

( )

7

8

2

2

−

= − ⋅

=

x

t

k

m

x

t

czyli

k

m

m

m

ω

ω

ω

ω

Widzimy, że x

=

x

t

m

cos

ω

jest rzeczywiście rozwiązaniem, ale tylko w przypadku, gdy

ω

=

k

m

. Funkcja

x

x

t

m

=

sin

ω

jest również pełnoprawnym rozwiązaniem matematycz-

nym, ale nie spełnia warunku początkowego, że gdy t = 0, to x = x

m

. Najbardziej ogólnym

rozwiązaniem jest

x

x

t

m

=

+

cos(

)

ω ϕ

, gdzie

ϕ

jest dowolną stałą fazową. Stałe

x

m

i

ϕ

wyznaczone są przez warunki początkowe.

3.

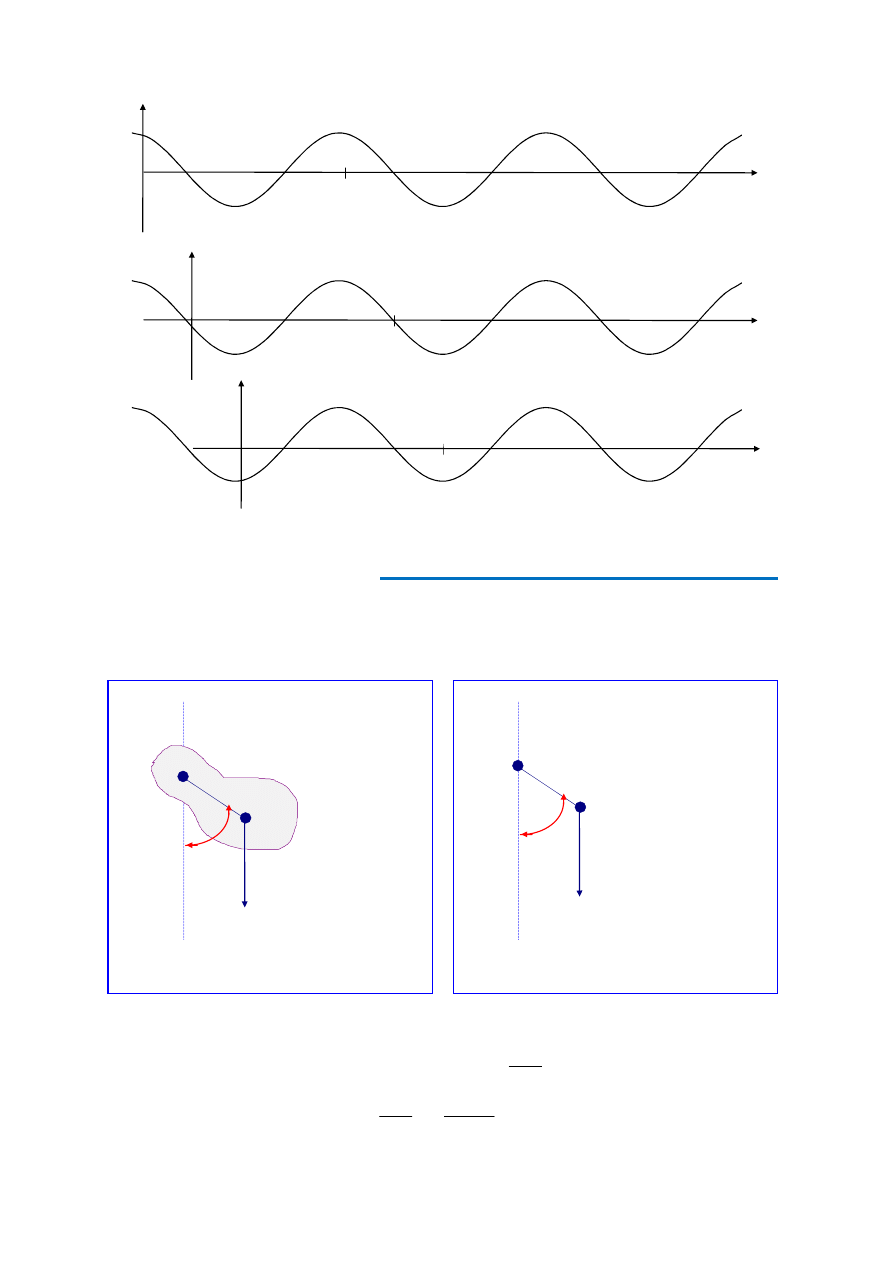
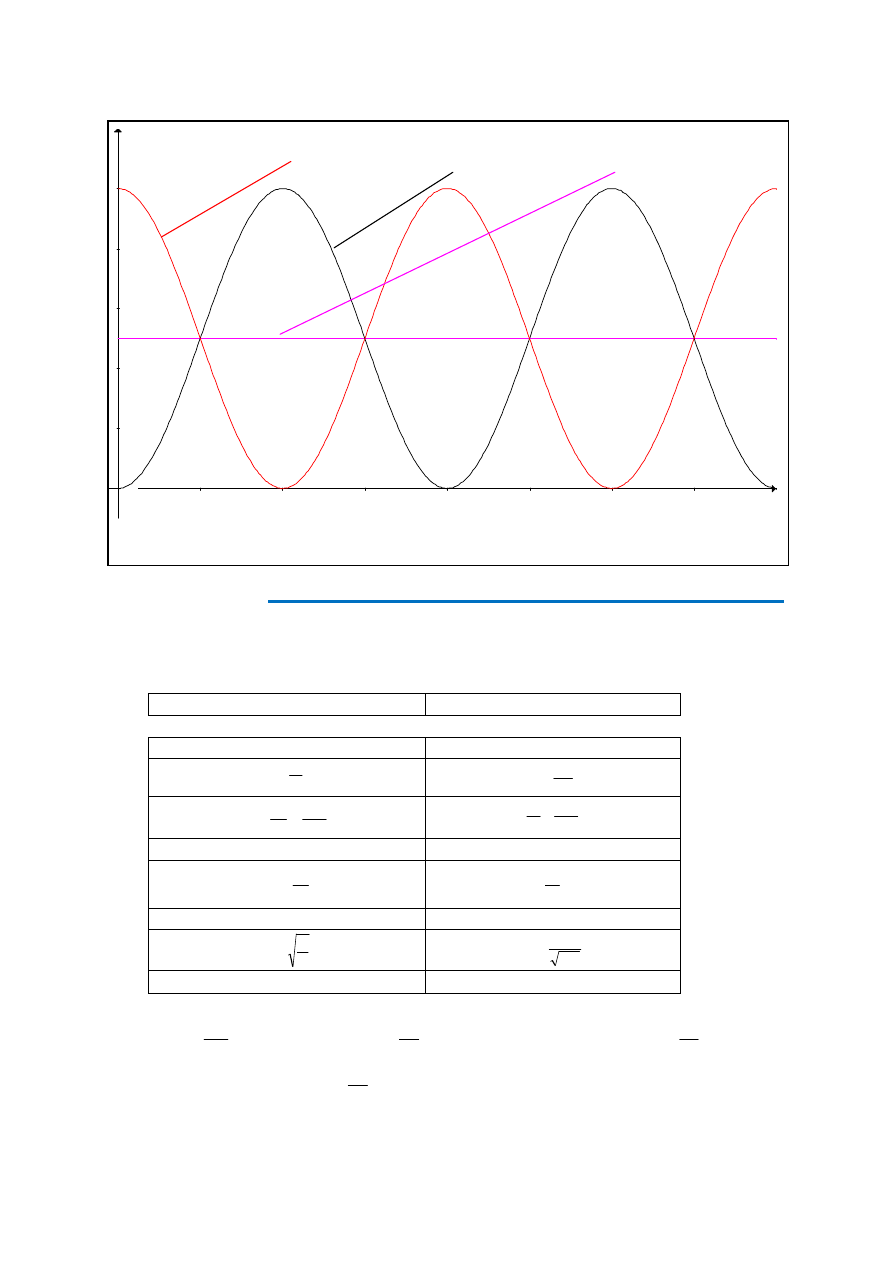
Prędkość jako funkcja czasu dana jest równaniem (5), przyspieszenie - równaniem (6).Te
funkcje zostały wykreślone, jedna nad drugą na rys.2. Z równania (5) wynika, że maksy-
malna prędkość:

( )

m ax

9

v

x

m

=

ω

i występuje , gdy x = 0.

Z równania (4) widać, że przyspieszenie jest zawsze

−

ω

2

razy wychylenie x:

(

)

10

2

2

2

d x

dt

x

= −

ω

To jest bardzo użyteczny związek: jeżeli równanie ruchu ciała możemy zapisać w postaci

d x

dt

Cx

2

2

= −

, gdzie C jest jakąś stałą, to

x

x

t

i

C

m

=

=

cos

ω

ω

, zatem:

Jeżeli: ( )

11

2

2

d u

dt

Cu

= −

to:

( )

12

ω

=

C

oraz

u

u

t

m

=

cos

ω

,

gdzie u jest jakimkolwiek przesunięciem Można to pokazać różniczkując

u

u

t

m

=

cos

ω

.

Wtedy

d u

dt

u

2

2

2

= −

ω

, co również równa się

−

Cu

. Tak więc:

−

= −

ω

2

u

Cu

ω

=

C

4

00529 Ruch harmoniczny prosty D

TEORIA

Temat 141

Wahadło fizyczne i matematyczne.

1.

*Rozważmy dowolną bryłę sztywną zawieszoną w punkcie 0, jak na rys. 1. Jej środek ma-
sy znajduje się w punkcie 0’ w odległości l od punktu zawieszenia. Chcąc obliczyć okres
drgań musimy znać jedynie moment bezwładności I względem punktu 0.

2.

Moment siły działającej na ciało wynosi

M

m g l

= − ⋅ ⋅

sin

Θ

. Korzystając ze związku

M

I

= ⋅

ε

, otrzymujemy:

(1)

− ⋅ ⋅

= ⋅

m g l

I

d

dt

sin

Θ

Θ

2

2

,

(2)

d

dt

m g l

I

2

2

Θ

Θ

= −

⋅ ⋅

sin

,

T

t

x

m

- x

m

T

t

ω

x

m

-

ω

x

m

T

t

ω

2

x

-

ω

2

x

m

Θ

0

l

0'

m

r

g

Rys. 1 Wahadło fizyczne.

Rys. 2 Wahadło matematyczne (proste).

Θ

0

l

m

r

g

m

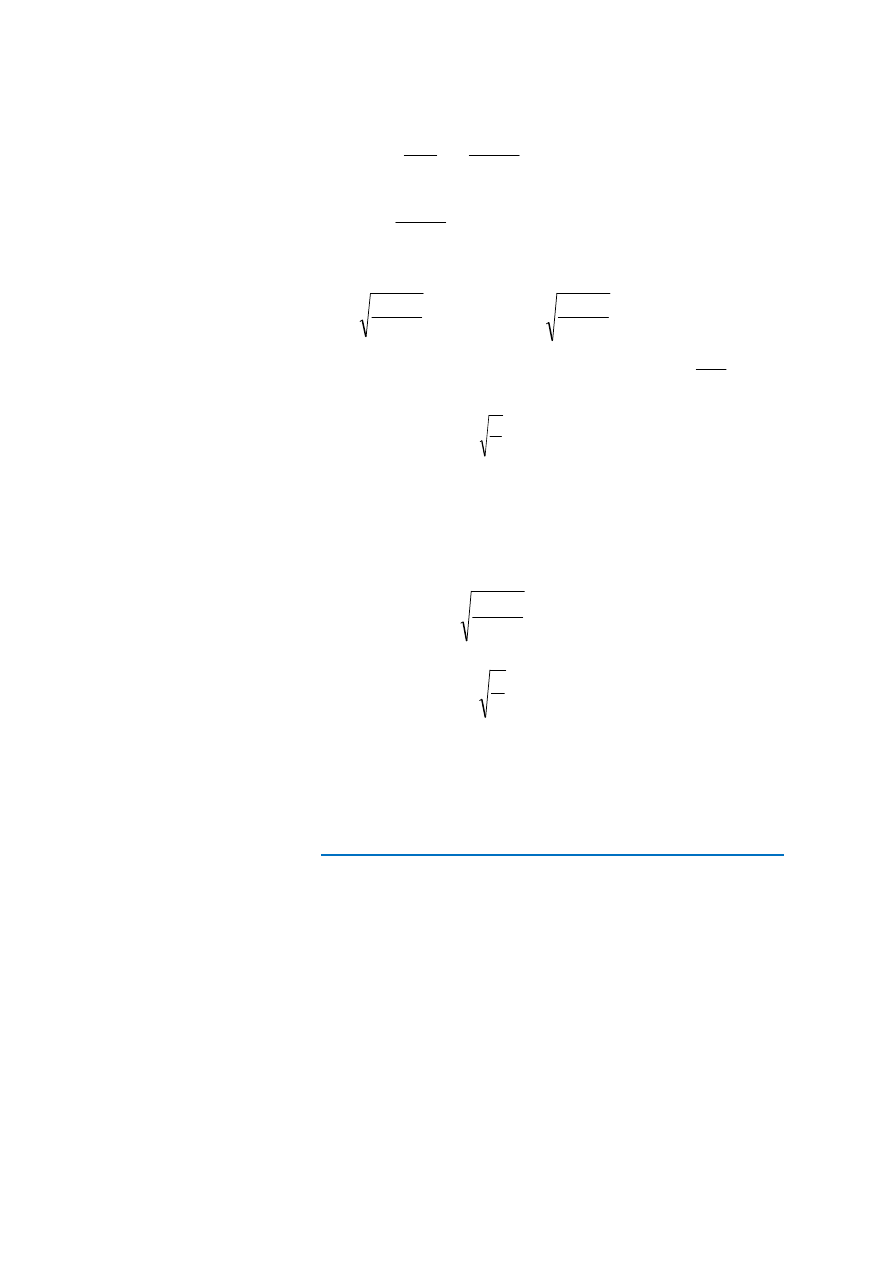
5

00529 Ruch harmoniczny prosty D

TEORIA

Dla małych wychyleń sin

Θ

≈

Θ

i wtedy:

(3)

d

dt

m g l

I

2

2

Θ

Θ

= −

⋅ ⋅

.

Równanie (3) ma tę samą postać co równanie ruchu harmonicznego poznanego wcześniej,

przy czym u odpowiada

Θ

oraz C

m g l

I

=

⋅ ⋅

.

Tak więc

(4)

Θ Θ

=

⋅

0

cos

ω

t

i...

(5)

ω

=

⋅ ⋅

m g l

I

lub (5a)

T

I

m g l

=

⋅ ⋅

2

π

.

Często wprowadza się pojęcie tzw. długości wahadła zredukowanego l

I

m l

0

=

⋅

, wtedy

wzór (5a) będzie miał postać:

(6)

T

l

g

=

2

0

π

.

Równanie (6) jest ostateczną wersją wyrażenia określającego okres drgań wahadła fizycz-
nego.*

2.

W przypadku wahadła prostego (rys. 2) cała masa jest skupiona w odległości l oraz

(7) I

m l

= ⋅

2

.

Podstawmy równanie (7) do równania (5a):

(8) T

m l

m g l

=

⋅

⋅ ⋅

2

2

π

.

Ostatecznie:

(9)

T

l

g

=

2

π

.

Zauważmy, że okres drgań jest niezależny nie tylko od amplitudy (zjawisko to nazywamy
izochronizmem drgań), ale również od masy. Jednak, gdy kąt

Θ

0

jest duży nie można sto-

sować przybliżenia sin

Θ Θ

≈

, ale nawet dla tak dużego kąta jak

Θ

0

= 20

0

równanie (9)

jest poprawne w granicach 1 %.

Temat 142

Drgania wymuszone. Rezonans mechaniczny.

1.

Z doświadczenia wiemy, że wahadło pobudzone jednorazowo do drgań przez wychylenie
go z położenia równowagi waha się w miarę upływu czasu coraz słabiej, czyli amplituda
jego drgań maleje, aż wreszcie wahadło zatrzymuje się. Zjawisko to świadczy o rozprasza-
niu energii wahadła, która jest zużywana na pokonywanie oporów ruchu. Drgania takie na-
zywamy drganiami zanikającymi, tłumionymi lub gasnącymi.

2.

Drgania, które wykonuje ciało wychylone z położenia równowagi i pozostawione samemu
sobie, tj. nie poddane działaniu dodatkowych sił zewnętrznych określamy mianem drgań
własnych

ciała. Drgania te mają zawsze tę samą charakterystyczną dla niego częstotliwość

niezależnie od sposobu ich wzbudzenia, np. częstotliwość drgań własnych struny jest nie-
zależna od tego czy były one wzbudzone przez szarpnięcie, uderzenie, czy pociągnięcie
smyczkiem.

6

00529 Ruch harmoniczny prosty D

TEORIA

3.

Wiemy, że zanikaniu drgań wahadła można zapobiec przez okresowe pobudzanie go do
ruchu, np. za pomocą uderzenia lub wychylenia, jak to ma miejsce w mechanizmie zega-
rowym. Jeżeli energia dostarczana w każdym impulsie pobudzającym zrównoważy energię
rozpraszaną, to drgania wahadła staną się niegasnące. Takie drgania wzbudzone za pomo-
cą zmieniających się okresowo sił zewnętrznych lub przenoszone z innego ciała drgające-
go nazywamy drganiami wymuszonymi. Amplituda drgań wymuszonych zależy od tego,
czy częstotliwość drgań własnych ciała jest równa czy też nie częstotliwości przekazywa-
nych impulsów.

4.

Okazuje się, że największe pobudzenie wahadła do drgań następuje wówczas, gdy często-
tliwość przekazywanych impulsów jest dokładnie równa częstotliwości drgań własnych
pobudzanego wahadła. Zjawisko to nazywa się rezonansem mechanicznym, zaś częstotli-
wość, której odpowiada maksymalna amplituda drgań wymuszonych - częstotliwością re-
zonansową

.

5.

Zjawisko rezonansu jest wykorzystywane w różnorodnych urządzeniach akustycznych
(tzw. rezonatory), w obwodach prądu zmiennego (zwróć uwagę na obwody LC) i w fizyce
atomowej (drgania atomów w kryształach). Niekiedy jednak należy unikać jego skutków.
Drgania maszyn lub urządzeń, albo też powtarzające się okresowo podmuchy wiatru mogą
znaleźć się w rezonansie z drganiami własnymi budynków, mostów itp. i spowodować ich
zniszczenie w wyniku ogromnego wzrostu amplitudy drgań wymuszonych.

Temat 143

Energia ruchu harmonicznego.

Energia potencjalna masy zamocowanej do końca sprężyny była tematem analiz wcześniej-

szych. Jeżeli sprężyna jest rozciągnięta na odległość x, energia potencjalna wynosi:

(1) E

kx

p

=

2

2

.

Jeżeli masę pociągniemy na odległość początkową x

0

, a następnie puścimy, to początkowa

energia układu jest:

(2) E

kx

=

0

2

2

.

Zauważmy teraz, że energia ruchu harmonicznego prostego rośnie jak kwadrat amplitudy
x

0

(niekiedy oznaczanej jako A). Przy założeniu, że nie ma sił tarcia, ani sił oporu, suma

energii kinetycznej i potencjalnej musi równać się (2). W dowolnej chwili mamy:

(3)

mv

kx

kx

2

2

0

2

2

2

2

+

=

.

Obliczymy teraz energię kinetyczną z równania (3):

(4)

(

)

mv

m

dx

dt

m

d

dt

x

t

m

x

t

mx

t

2

2

0

2

0

2

0

2

2

2

2

2

2

2

2

= ⋅











= ⋅











= ⋅ −

=

cos

sin

sin

ω

ω

ω

ω

ω

,

(5) E

kx

t

k

=

0

2

2

2

sin

ω

.

W równaniu (5) wykorzystano tożsamość poznaną wcześniej, a mianowicie

ω

=

k

m

.

Teraz określimy energię potencjalną z równania (3):

(6)

(

)

E

kx

k

x

t

kx

t

p

=

= ⋅

=

2

0

2

0

2

2

2

2

2

cos

cos

ω

ω

.

Sumując równania (5) i (6) widzimy, że rzeczywiście równanie (3) jest spełnione.

7

00529 Ruch harmoniczny prosty D

TEORIA

x

E

0

0.25π

0.5π

0.75π

1π

1.25π

1.5π

1.75π

0

0.2

0.4

0.6

0.8

1

Energia kinetyczna

Energia potencjalna

Energia całkowita

Temat 144

Drgania mechaniczne, s drgania elektryczne.

1.

Dotychczas poznaliśmy elektryczne układy drgające (np. oscylator harmoniczny LC) oraz drgające układy
mechaniczne (np. wahadło fizyczne). Zauważmy, że istnieje formalna analogia między obwodami elektrycz-
nymi a ruchami mechanicznymi:

Drgania mechaniczne

Drgania elektryczne

x

Q

v

dx

dt

=

I

dQ

dt

=

a

dv

dt

d x

dt

=

=

2

2

dI

dt

d Q

dt

=

2

2

m

L

k

E

=

1

1

C

A = x

m

Q

m

ω

=

k

m

ω

=

1

LC

γ

R

2.

Niech ładunek na kondensatorze będzie Q i niech będzie on analogiem x. Wtedy natężenie

prądu I

dQ

dt

=

będzie analogiem v

dx

dt

=

. Wielkość (bez specjalnej nazwy)

dI

dt

jest z kolei

analogiem przyspieszenia a

dv

dt

=

.

Rys. Zależność energii w ruchu harmonicznym od czasu.

8

00529 Ruch harmoniczny prosty D

TEORIA

Zatem równanie:

(1) L

dI

dt

Q

C

= −

jest analogiem równania:

(2) m

dv

dt

kx

= −

,

jeżeli przyrównamy L do m, a k do

1

C

.

Gdy jakieś procesy są scharakteryzowane takimi samymi równaniami, to muszą być opisa-
ne takimi samymi funkcjami. A więc ładunek musi zmieniać się harmonicznie w czasie
zgodnie ze wzorem:

(3)

Q

Q

t

m

=

cos

ω

,

gdzie Q

m

jest amplitudą ładunku analogiczną do amplitudy ruchu A.

Częstość kołową

ω

wyznaczymy ze wzoru

m

k

=

ω

podstawiając L zamiast m, a

C

1

za-

miast k, czyli

(4)

LC

LC

1

1

=

=

ω

.

Wynik (4) jest zgodny z dotychczasowymi wnioskami: zarówno wzrost L jak i wzrost C
powoduje malenie częstości drgań. Poza tym jest naturalne, że jeżeli w obwodzie jest
opór, to obserwujemy drgania tłumione, bo energia jest rozpraszana.
Zwróćmy uwagę, że jeżeli w obwodzie jest opór, to II prawo Kirchhoffa musimy napisać
w postaci (sprawdź to samodzielnie !):

(5)

IR

C

Q

dt

dI

L

=

−

−

, czyli

(6)

IR

Q

C

dt

dI

L

−

−

=

1

,

Podstawiając

dt

dQ

I

=

dostajemy:

(7)

R

dt

dQ

Q

C

dt

Q

d

L

−

−

=

1

2

2

,

jest to równanie analogiczne do:

(8)

dt

dx

kx

dt

x

d

m

γ

−

−

=

2

2

,

w którym ostatni człon oznacza siłę oporu (tłumienia)

v

F

⋅

=

γ

.

Analogiem współczynnika tłumienia

γ

jest opór R. W związku z tym amplituda oscylacji

ładunku na kondensatorze musi znikać wykładniczo w funkcji czasu, podobnie jak ampli-
tuda ruchu tłumionego oscylatora harmonicznego.

3.

Obwód drgający LC jest podstawowym elementem każdego odbiornika radiowego. Drga-
nia elektryczne wzbudzają w nim fale elektromagnetyczne radiowe, przychodzące do nas
z radiostacji (stacji nadawczej). Obwód LC znajduje się także w elektronicznych genera-
torach LC drgań niegasnących, które są bardzo wygodnymi źródłami napięcia przemien-
nego małej mocy.