1. Zerowa zasada termodynamiki:

Jeżeli dwa układy nie graniczące ze sobą znajdują się w równowadze cieplnej z trzecim
układem, z którym graniczą, to są one również w równowadze cieplnej między sobą.

2. Pierwsza zasada termodynamiki:

Zmiana zasobu energii wewnętrznej (EW) w układzie substancjalnym w warunkach
odwracalności procesu termodynamicznego powodowana jest jej wymianą przez
granice układu pod postaciami ciepła oraz pracy bezwzględnej objętościowej
wykonanej przez układ nad otoczeniem.

3. Druga zasada termodynamiki (dla przemian odwracalnych):

We wszystkich przemianach odwracalnych sumaryczny zasób entropii układu i
otoczenia jest stały.

4. Druga

zasada

termodynamiki

(dla

przemian

nieodwracalnych

):

We wszystkich przemianach nieodwracalnych sumaryczny zasób entropii układu i
otoczenia stale rośnie, aż do osiągnięcia stanu równowagi, w którym osiąga wartość
maksymalną.

5. Trzecia zasada termodynamiki:

Zasób entropii każdego układu złożonego z substancji czystej w stanie kryształu
doskonałego w temperaturze zera bezwzględnego równy jest zeru,

S(0)=0

6. Co to są wielkości ekstensywne (WE):

Wielkością ekstensywną (WE) nazywamy wielkość geometryczną lub fizyczną, której
zasób w obszarze złożonym z sumy podobszarów równy jest sumie zasobów we
wszystkich podobszarach. (sumowalne)

7. Co to są wielkości intensywne (WI):

Zbiór wszystkich odpowiednio rozpatrywanych wielkości polowych definiuje klasę
wielkości określaną mianem wielkości intensywnych, nie mają one własności
addywnych = nie tworzą zasobu.



Skalarne:

masowa gęstość zasobu objętości, objętościowa gęstość zasobu

masy,temperatura, ciśnienie.



Wektorowe:

masowa gęstość zasobu pędu( prędkość substancjalna lub

barycentryczna), parcjalna gęstość zasobu pędu( prędkość komponencjalna).

8. Wymień trzy parametry stanu:

Ciśnienie, temperatura, objętościowa gęstość zasobu masy.

9. Osłona adiabatyczna:

Takie ograniczenie układu, które powoduje, że zmiany dokonujące się w ciałach poza
układem mogą mieć wpływ na stan układu jedynie w wyniku zmian objętości układu.

10. Osłona diatermiczna:

Takie ograniczenie układu, które umożliwia dojście faz nie graniczących ze sobą do
równowagi termodynamicznej poprzez fazę pośrednią, zdążającą do równowagi
termodynamicznej ze wszystkimi fazami z nią graniczącymi.

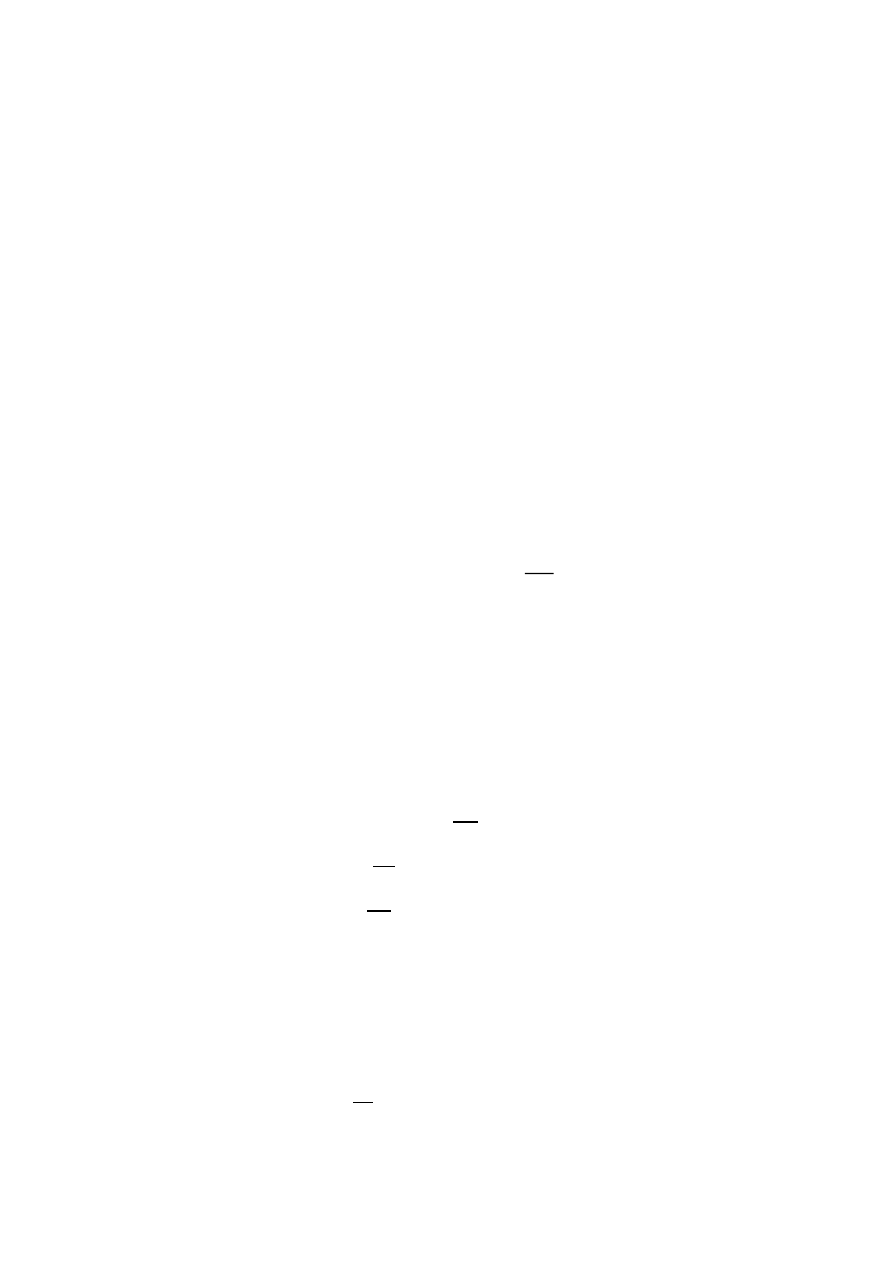
11. Model gazu doskonałego:



Cząsteczki gazu mają rozmiar punktów materialnych,



Objętość zajmowana przez cząsteczki gazu jest pomijalnie mała,



Cząsteczki gazu wykazują cechy doskonale sprężystych kulek znajdujących się
w ciągłym, przypadkowym, chaotycznym ruchu, powodującym zderzenia
cząsteczek między sobą oraz ściankami naczynia,



Między cząsteczkami gazu nie występują żadne inne oddziaływania poza
zderzeniami doskonale sprężystymi,



Bezpośrednią miarą temperatury gazu jest średnia energia kinetyczna jego
cząsteczek.

12. Prawo Avogadra:

W jednakowych objętościach przy tym samym ciśnieniu i temperaturze znajduje się
taka sama ilość cząsteczek (ilość moli) dowolnego gazu doskonałego.

 

mol

A

N

1

23

10

023

,

6





13. Pojemność cieplna substancji:

Pojemnością cieplną lub ciepłem właściwym substancji nazywamy iloraz
elementarnego przyrostu masowej gęstości ilości ciepła do elementarnego przyrostu
temperatury bezwzględnej, wywołanej przyrostem tego ciepła.

Dla gazu doskonałego:

Stąd wynika, że równanie Meyera i wykładnik izentropy:

14. Współczynnik ściśliwości:

W przypadku gazu doskonałego wartość współczynnika ściśliwości z dla wszystkich
ciśnień i temperatur równa jest jedności, niedoskonałość gazu przejawia się różnicą
między obserwowaną wartością współczynnika a jednością

15. Prawo stanów odpowiadających sobie:

Wartości współczynnika ściśliwości będącego funkcją zredukowanych ciśnień i
temperatur jest jednakowa dla wszystkich gazów rzeczywistych

Wniosek:

Jeżeli dwa różne gazy rzeczywiste mają dwa jednakowe zredukowane

parametry stanu, to również trzeci ich zredukowany parametr stanu jest taki sam dla
każdego z tych gazów.

16. Prawo Daltona:

Ciśnienie całkowite p fazy gazowej wieloskładnikowej, będącej mieszaniną gazów

doskonałych, równoważne jest ciśnieniu, jakie wywierałby gaz doskonały
jednoskładnikowy mający następujące parametry stanu:



Temperaturę T , równą temperaturze fazy gazowej wieloskładnikowej,



Objętościową gęstość zasobu ilości moli ρ

n

, równą sumie objętościowych

gęstości zasobu ilości moli składników mieszaniny ρ

ni.

Równanie Clapeyrona zgodne z pr. Daltona:

∑

17. Twierdzenie Joule’a:

Masowa gęstość zasobu energii wewnętrznej dla gazu doskonałego jest funkcją

jedynie temperatury bezwzględnej T gazu.

18. Zjawisko Joule’a-Thomsona

Zjawisko Joul’a-Thomsona opisuje dławienie adiabatyczno-izentalpowe gazu
doskonałego w przepływie otwartym. Po przetłaczaniu gazu przez adiabatycznie
izlowaną rurę, zawierającą porowatą przegrodą:



wartości temperatur przed i za przeponą jest jednakowa i równa T



ciepło wymienione między układem a otoczeniem równa jest zero



ciśnienia i masowe gęstości zasobu objętości mają różne wartości przed i za
przeponą.

19. Aksjomat bilansowy dla wielkości ekstensywnych (WE):

Zmiana zasobu wielkości ekstensywnej (WE) zmagazynowanej w układzie

bilansowania może być dokonana tylko bądź za przyczyną produkcji WE wewnątrz
układu bilansowania, bądź za przyczyną wymiany WE poprzez granice układu
bilansowania lub w wyniku jednoczesnego przebiegu obu tych procesów.

20. Przemiany termodynamiczne:



Izochoryczna



Izobaryczna



izotermiczna



Izentropowa (adiabata odwracalna)



Politropowa

21. Różniczkowy współczynnik efektu zjawiska Joule a-

Thomsona:

Miara temperaturowego efektu dławienia

(

)

(

)

22. Równanie stopnia suchości pary mokrej:

m

p

- masa fazy gazowej (pary nasyconej suchej)

m

c

- masa fazy ciekłej (cieczy nasyconej) w parze mokrej.

( x przyjmuje wartości od 0 do 1 )

23. Sprawność termodynamiczna w obiegach:

prawobieżnym

:

lewobieżnym:

24. Reguła faz Gibbs’a:

Dla zachowania równowagi musi być spełniony warunek:

25. Prawo Charles’a

Opisuje zachowanie rozrzedzonego gazu podczas jego ogrzewania w stałej
objętości:

26. Ciśnienie gazu, działające na powierzchnię padania Ap w

funkcji średniej kwadratów prędkości jego cząsteczek:

̅

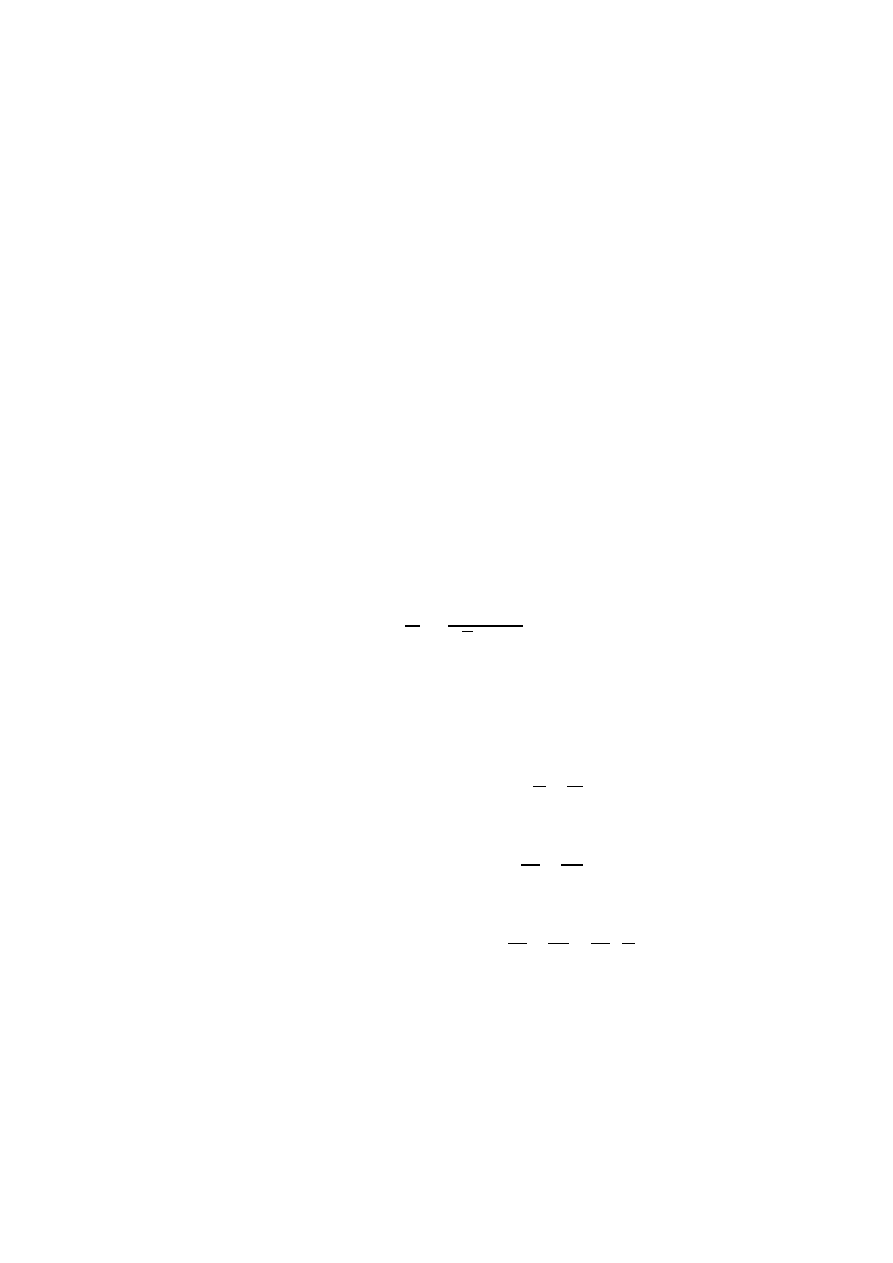
27. Zasada równowagi szczegółowej:

Jeżeli gaz znajduje się w równowadze termodynamicznej, to w ustalonym odstępie
czasu następuje tyle samo zderzeń cząsteczek o zasobach energii kinetycznych E

1

i E

2

prowadzących po zderzeniu do stanów o zasobach energii E

1

’ i E

2

’ , co i zderzeń

cząsteczek realizujących procesy odwrotne.

28. Zasada zachowania energii:

Przy założeniu, iż cząsteczki zachowują się tak jak sprężyste kule suma zasobu energii
kinetycznej cząsteczek przed zderzeniem równa jest sumie zasobu energii kinetycznej
cząsteczek po zderzeniu.

29. Średnia droga swobodna cząsteczki gazu:

Średnia długość drogi cząsteczki gazu do zderzenia z pierwszą
n

apotkaną cząsteczką:

̅

√

30. Sprawności i moce silników spalinowych:

31. Prędkość średniej kwadratów prędkości cząsteczek:

Średnia kwadratów prędkości cząsteczek w gazie doskonałym może być określona z
definicji skali temperatury T tak, że:

̅̅̅

Czyli:

̅̅̅

Stąd prędkość średniej kwadratów prędkości cząsteczek określona jest zależnością

̅

√ ̅

(

)

32. Funkcja rozkładu widmowego objętościowej gęstości zasobu

ilości oscylatorów promieniowania elektromagnetycznego w
polu częstotliwości fal:

[

]

33. Funkcja rozkładu widmowego objętościowej gęstości zasobu

energii promieniowania w ujęciu Plancka:

̅

( (

) )

[

]

34. Prawo promieniowania Plancka:

( (

) )

[

]

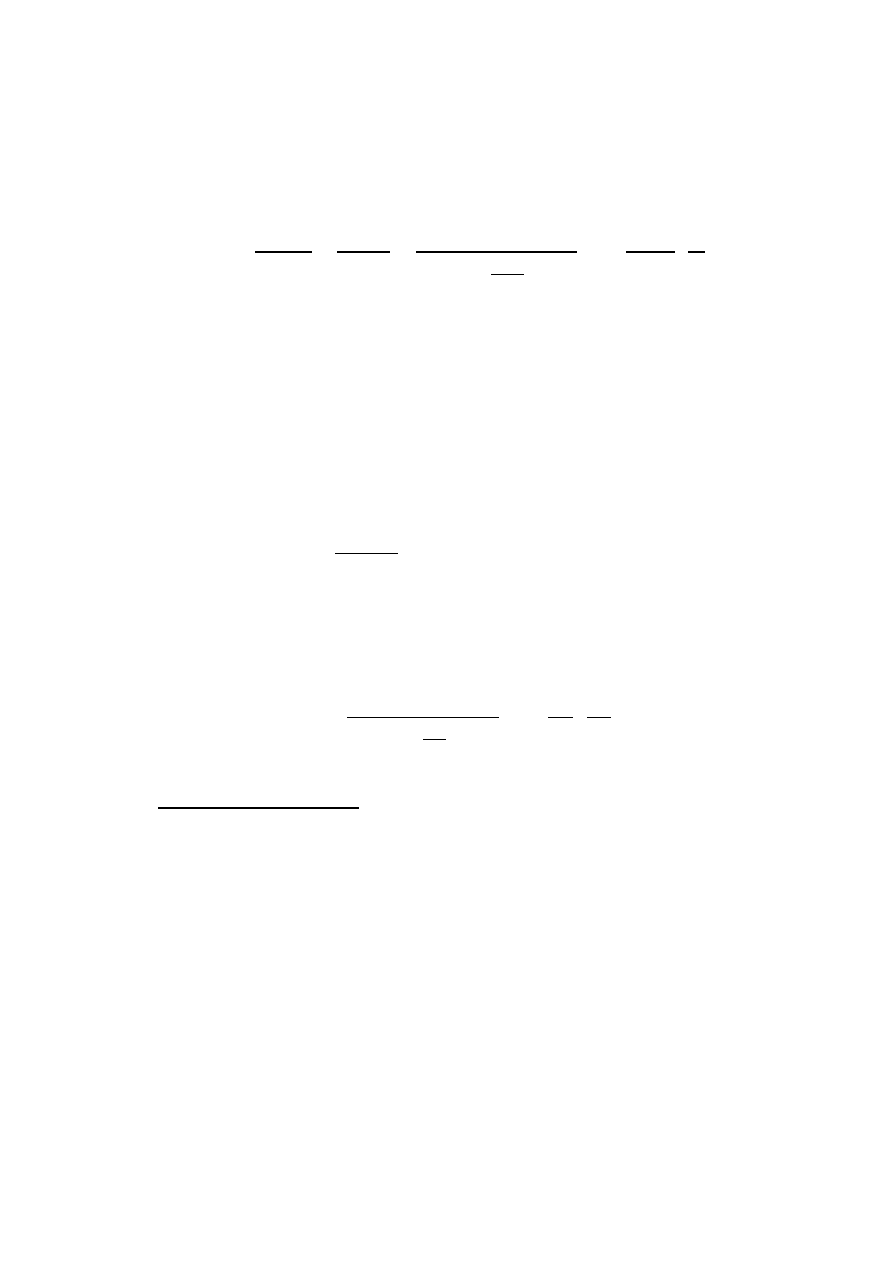
35. Funkcja rozkładu widmowego gęstości strumienia emisji

(wymiany) energii promieniowania elektromagnetycznego w
polu długości fal:

( (

) )

[

]

36. Prawo przesunięć Wiena:

Odwrotnie proporcjonalna zależność długości fal λ

m

od temperatury T opisuje

ilościowo mechanizm przesuwania się maksimum rozkładu widmowego objętościowej
gęstości zasobu energii promieniowania elektromagnetycznego

w miarę

wzrostu temperatury w stronę fal krótszych.

37. Funkcja rozkładu widmowego objętościowej gęstości zasobu

energii promieniowania ciała doskonale czarnego:

( (

) )

[

]

,,Klasyfikacja Energii"

38. Energia zewnętrzna:



Energia kinetyczna makroskopowego ruchu substancji



Energia grawitacji pola grawitacyjnego



Energia elektromagnetyczna pola elektromagnetycznego dalekiego zasięgu.

39. Energia wewnętrzna:



Energia cieplna ruchu cieplnego substancji,



Energia wiązań pól bliskiego zasięgu

40. Energia wiązań:



Energia wiązań między-molekularnych w płynie



Energia wiązań między-atomowych w ciele stałym (energia sprężystości)



Energia wiązań wewnątrz-molekularnych (energia chemiczna)



Energia wiązań wewnątrz-atomowych (energia jonizacyjna)



Energia wiązań jądrowych (energia jądrowa)

Wielkości substancjalne :Energie: kinetyczna, grawitacyjna, wewnętrzna.
Niesubstancjalna-> energia elektromagnetyczna (poza klasyfikacj

ą

)

41. Objętościowa gęstość zasobu energii promieniowania w

ujęciu Plancka:

Całka funkcji rozkładu widmowego objętościowej gęstości zasobu energii
promieniowania określa otrzymaną gęstość zasobu energii promieniowania.

∫

(

)

[

]

Po podstawieniu

(

)

42. Indywidualna translacyjna prędkość cieplna:

̅̅̅

̅̅̅ ̅

43. Fenomenologiczne przedziały czasu i rozmiaru:

Powinny być dostatecznie małe, aby uwzględniały zmiany makroskopowe zjawisk,
lecz również na tyle duże, aby nastąpiło zaniknięcie zmienności mikroskopowej,
wynikającej z ziarnistej budowy struktury materiału.
Jeżeli fenomenologiczny przedział uśredniania czasu oraz przedział liniowo-
przestrzenny spełniają warunki

̅

to analizowana wielkości fizycznych może być opisana makroskopowo przy
zastosowaniu ciągłego pola liniowo-przestrzennego. Przedziały czasowy oraz liniowy
gwartantują w takim przypadku zaniknięcie dyskretnych własności struktury materii
przy zachowaniu zmienności makroskopowej.

44. Wilgotność względna:

Stosunek wilgotności bezwzględnej ρ

p

do maksymalnej wilgotności bezwzględnej

dla danej temperatury.

(

)

W przedziale <0;1>

45. Wewnętrzne ciepło parowania:

Stanowi energię niezbędną do pokonania przyciągania wzajemnego cząsteczek w
fazie ciekłej w celu zmiany przez nie fazy z ciekłej na gazową. Stanowi około 90%
ciepła przemiany parowania ,,r’’

46. Katastrofa ultrafioletowa w pudle izotermicznym:

W funkcji rozkładu widmowego objętościowej gęstości zasobu energii

promieniowania

w polu długości fal zdąża do nieskończoności gdy

→ 0

.

47. Kryterium istnienia skalarnego pola jednorodnego:

Gdy pole nie podlega żadnym zmianom przestrzennym w dowolnej ustalonej chwili
czasu,czyli gdy pochodne referencyjne przyjmują odpowiednie wartości
- dla skalarnej wielkości polowej:

̅

- dla wektorowej wielkości polowej:

̅

̅

̅

To pole nazywa się jednorodnym lub homogenicznym. Pola takie charakteryzują się
tym, że gradienty odpowiednich pól równe są zeru:

̅̅̅̅̅̅̅ ̅

̅̅̅̅̅̅̅ ̅

48. Zasada ekwipartycji Boltzmann’a

Zasadą ekwipartycji energii nazywa się rozdział zasobu energii pomiędzy stopnie
swobody, tak aby średni zasób energii przypadający na każdy stopień swobody był
jednakowy.

̅

Gdzie:
f-ilość stopni swobody
k= 1,3806*10

-23

[J/K] – stała Boltzmann’a)

49. Prędkość substancjalna:

Granica pozorna masowej gęstości zasobu pędu (prędkość substancjalna):

̅ (

∑

̅̅̅

)

̅

*obszar substancjalny jest zamknięty dla przepływu masy, częściowo
niesubstancjalny to układ otwarty.

50. Prędkość komponencjalna:

Granica pozorna parcjalnej gęstości zasobu pędu składnika substancji:

̅ (

∑

̅̅̅̅

)

̅

*obszar komponencjalny (tyle obszarów ile komponentów w mieszaninie)

51. Energia kinetyczna zbioru cząstek

Energia kinetyczna zbioru cząsteczek jest sumą makroskopowej energii kinetycznej i
translacyjnej energii cieplnej mikroruchów o pędzie skompensowanym do zera.

…

52. Jakie składniki ciśnienia składają się na ciśnienie całkowite

w przepływie strumienia cieczy

Na ciśnienie całkowite składa się ciśnienie statyczne p

s

i ciśnienie dynamiczne p

d

53. Równanie stanu gazu fotonu.

54. Teoremat Nersnsta

Dla układów skondensowanych ciepło przemiany równe jest ilości pracy maksymalnej
przemiany w temperaturze zbliżonej do zera bezwzględnego i w samej temperaturze
zera bezwzględnego.