1
Szczególna Teoria Względności
Załó
ż
my,
ż
e pr
ę
dko
ść
ś
wiatła jest stała
wzgl
ę
dem eteru. Jaka jest wi
ę
c pr
ę
dko
ść
Ziemi wzgl
ę
dem eteru ?
Do
ś
wiadczenie Michelsona i Morleya (1881 i 1887)
1) Załó
ż
my,
ż
e na ekranie obserwujemy maksimum
interferencyjne (pr
ąż
ki). Je
ś
li przesuniemy
zwierciadło ruchome o ¼ długo
ś
ci fali ( ¼
λ
) w
prawo, to promie
ń
2 przejdzie dodatkowo drog
ę
½
λ
i oba promienie na ekranie wygasz
ą
si
ę
w miejscach
gdzie si
ę
wzmacniały (maksima przejd
ą
w minima i
odwrotnie).
2) Zakłócenie ustawionego maksimum
interferencyjnego mo
ż
na by tak
ż
e uzyska
ć
, gdyby
pr
ę
dko
ś
ci
ś
wiatła w ramieniu 1 lub 2 ulegały
zmianie.
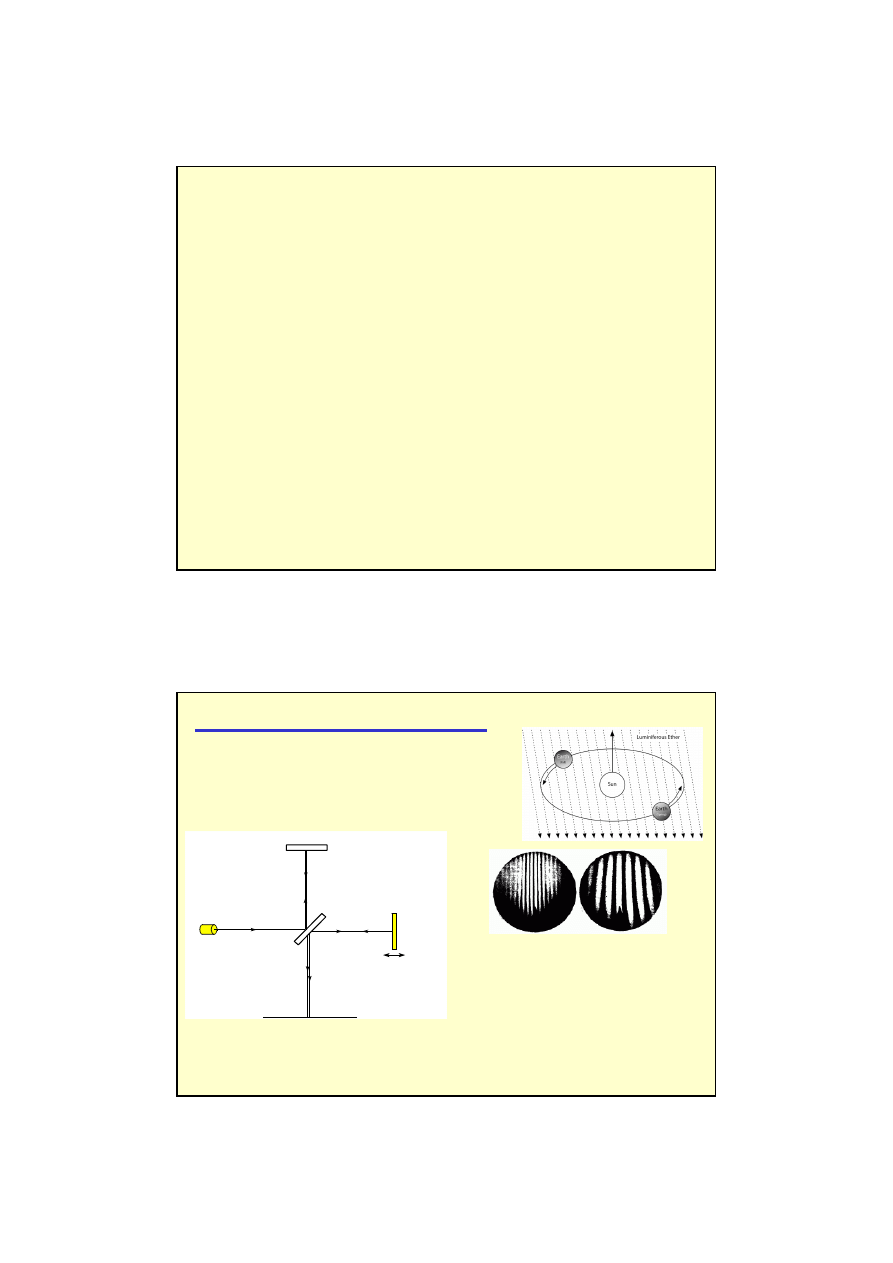
zwierciadło
półprzepuszczalne
zwier ciadło
ź
ródło światła
1
2
zwierciadło
ruchome
ekran
Zasada budowy interferometru Michelsona. Zwierciadło
„2” można przesuwać i w ten sposób doprowadzać do
powstawania kolejnych maksimów i minimów
interferencyjnych.
Kinematyka relatywistyczna
2
-v
Z
c
Z
c
E
c
Z
=
c
E
+
v
Z
c
Z
-v
Z
c
E
-v
Z
c
Z
=
c
E
-
v
Z
B
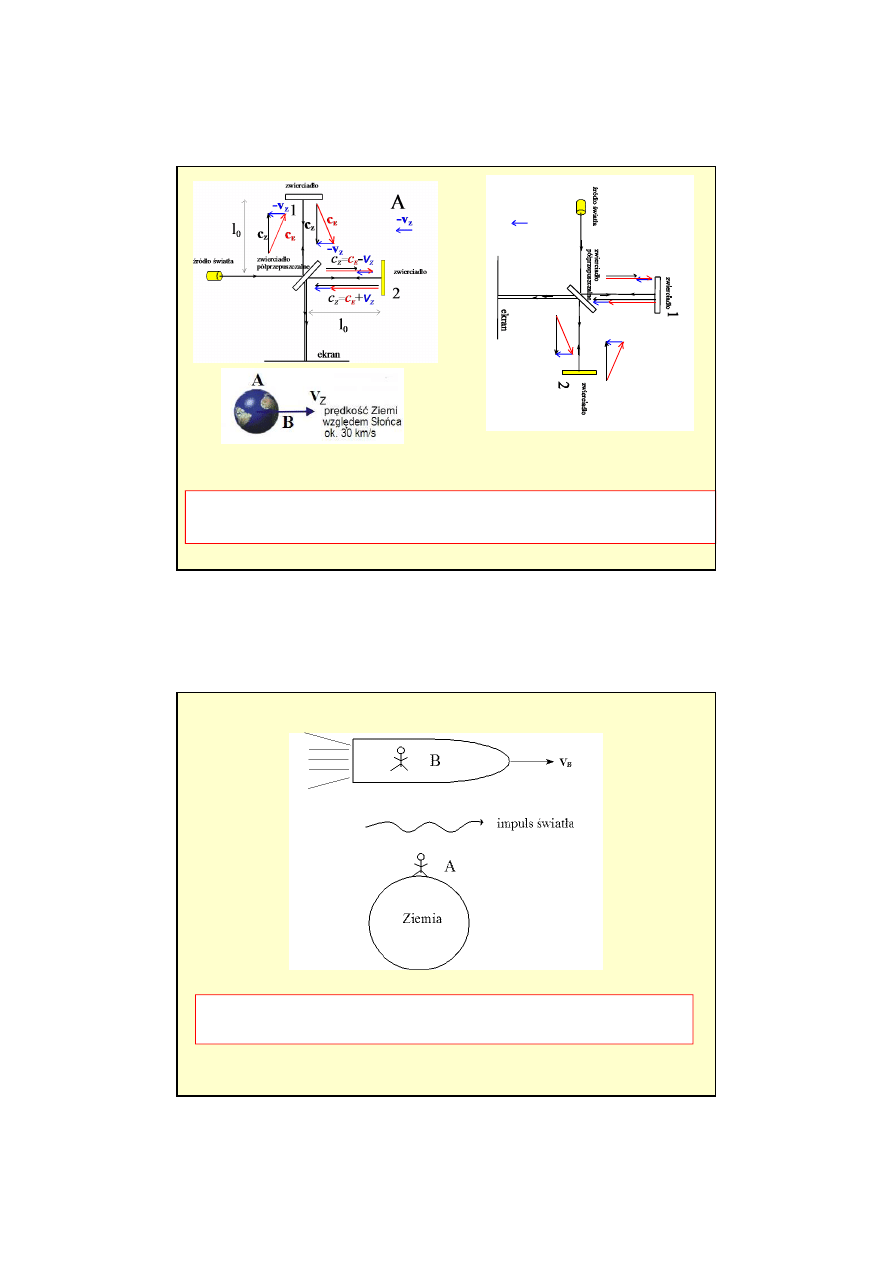
Je
ż
eli obrócimy interferometr o 90
0
,
obydwa lustra S
1
i S
2
zamieni
ą
si
ę
rolami,
a wi
ę
c:
Po obróceniu ramion pr
ąż
ki interferencyjne si
ę
przesun
ą
. Z przesuni
ę
cia tego mo
ż
na
wyznaczy
ć
v
Z
.
Do
ś
wiadczenie pokazało,
ż
e
v
Z
=0
(z dokł. 5 km/s) czyli albo Ziemia si
ę
nie
porusza (wzgl. eteru) albo pr
ę
dko
ść
ś
wiatła jest stała w ka
ż
dym układzie inercjalnym.
Zmierzona pr
ę
dko
ść
ś
wiatła jest taka sama w ka
ż
dym
układzie inercjalnym (np. dla obserwatora A oraz B) !!!
3
Konsekwencje stałej warto
ś
ci pr
ę
dko
ś
ci
ś
wiatła
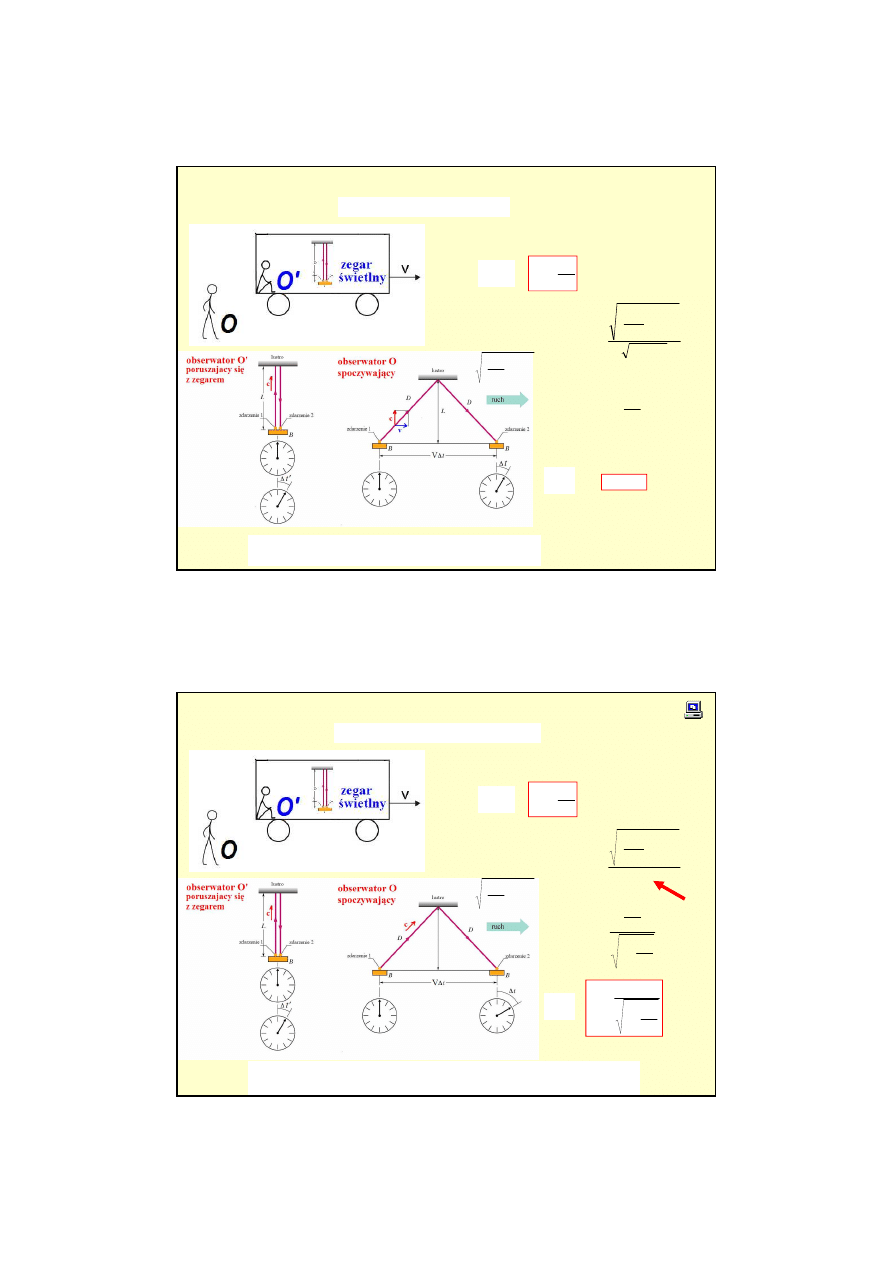
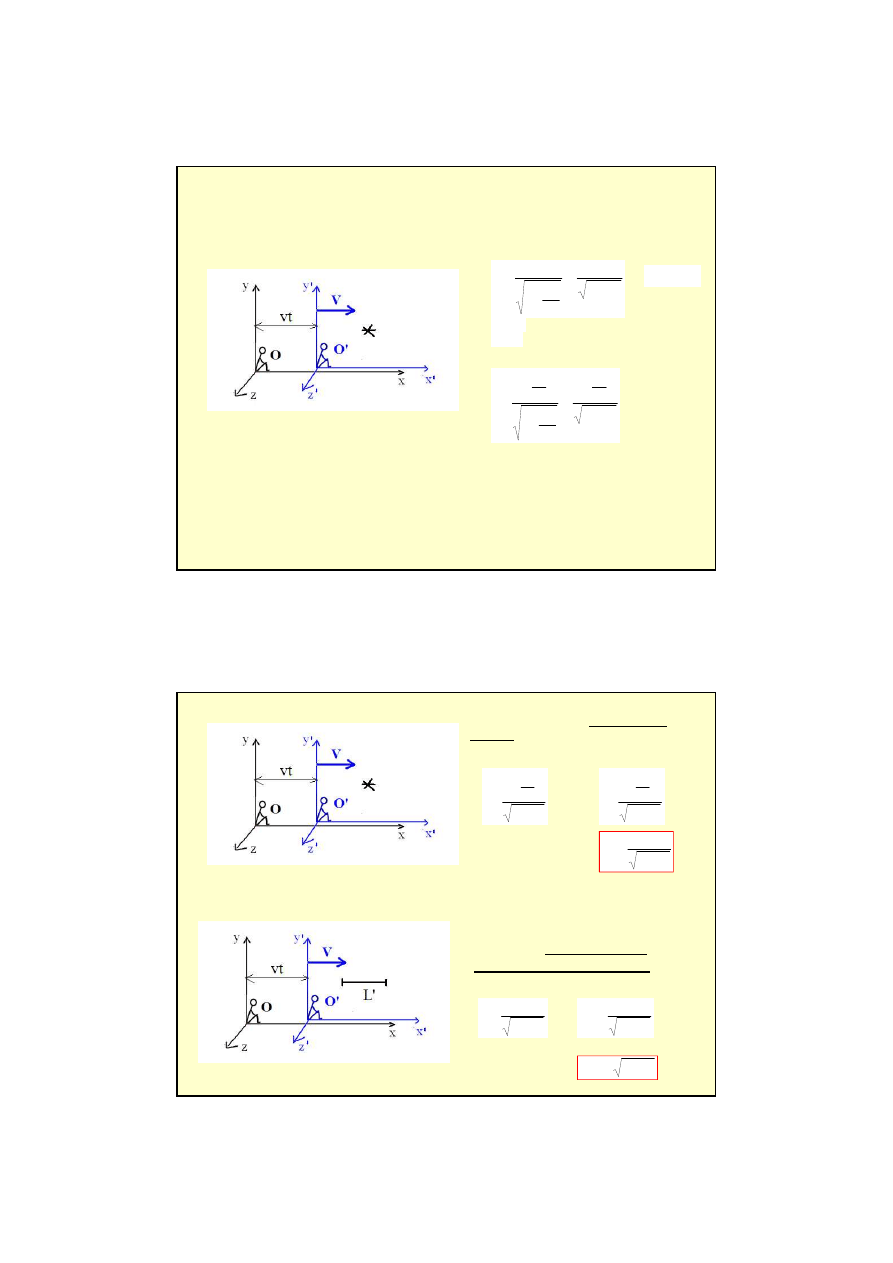
Zakładamy,
ż
e c
≠≠≠≠
const.
Dla
obydwu
obserwatorów zegary
chodz
ą
tak samo
.
c
L
t
2
'
=
∆
O’:
2
2
2
2
2
2
V
c
L
t
V
t
+
+
∆
=
∆
c
L
t
2
=
∆
'
t
t
∆
=
∆
O:
O:
2
2
2
L
t
V
D
+
∆
=
A co si
ę
stanie dla c = const. ?
c
L
t
2
'
=
∆
Ka
ż
dy obserwator stwierdza,
ż
e poruszaj
ą
cy si
ę
zegar
idzie wolniej
ni
ż
identyczny zegar w spoczynku (
dylatacja
czasu).
O’:
2
2
2
L
t
V
D
+
∆
=
c
L
t
V
t
2
2
2
2
+
∆
=
∆
2
2
1
2
c
V
c
L
t
−
=
∆
2
2
1
'
c
V
t
t
−
∆
=
∆
O:
O:
4
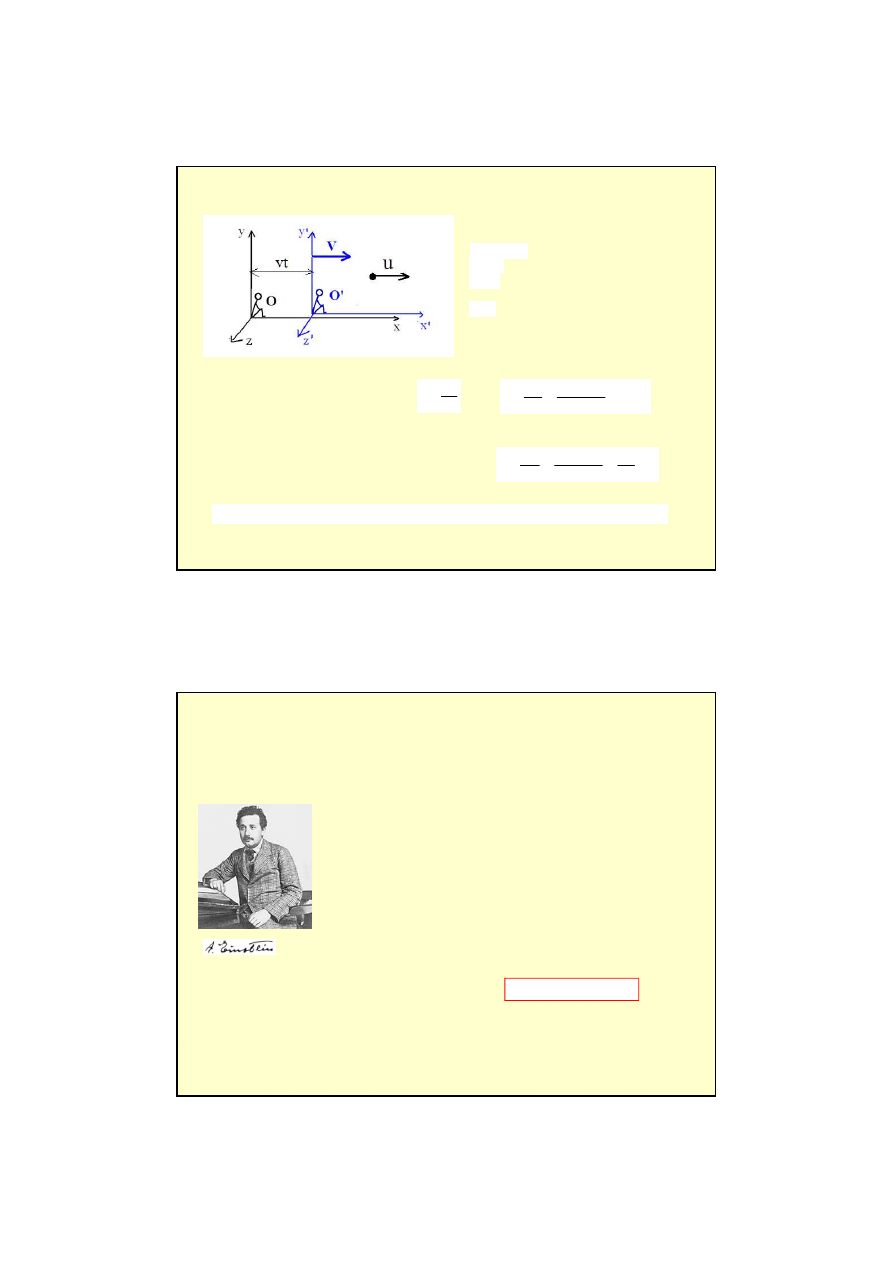
Vt
x
x
−
=
'
y
y
=
'
z
z
=
'
t
t
=
'
t
x
u
∆
∆
=
V
u
t
t
V
x
t
x
u
−
=
∆
∆
−
∆
=
∆
∆
=
'
'
'
składanie pr
ę
dko
ś
ci
a
t
u
t
V
u
t
u
a
=
∆
∆
=
∆
−
∆
=
∆
∆
=
)
(
'
'
'
przyspieszenie w układzie
poruszaj
ą
cym si
ę
Pr
ę
dko
ść
ś
wiatła nie jest stała dla transformacji Galileusza.
Transformacja Galileusza
Postulat II:
Pr
ę
dko
ść
ś
wiatła w pró
ż
ni jest jednakowa we
wszystkich kierunkach i w dowolnym obszarze danego inercjalnego
układu odniesienia i jednakowa dla wszystkich inercjalnych układów
odniesienia.
Postulat I
(zasada wzgl
ę
dno
ś
ci):
Przy identycznych warunkach pocz
ą
tkowych wszystkie to
ż
same
zjawiska fizyczne przebiegaj
ą
jednakowo w inercjalnych układach
odniesienia. Inaczej mówi
ą
c, w
ś
ród inercjalnych układów
odniesienia nie ma układu „uprzywilejowanego„
i stwierdzenie stanu absolutnego ruchu nie jest mo
ż
liwe.
c = 299 792 458 m/s
Postulaty szczególnej teorii wzgl
ę
dno
ś
ci, Albert Einstein 1905.
5
Szukamy transformacji współrz
ę
dnych, która uwzgl
ę
dnia niezale
ż
no
ść
pr
ę
dko
ś
ci
ś
wiatła od układu odniesienia.
2
2
2
1
1
'
β
−
−
=
−
−
=
Vt
x
c
V
Vt
x
x
y
y
=
'
z
z
=
'
2
2
2
2
2
1
1
'
β
−
−
=
−
−
=
x
c
V
t
c
V
x
c
V
t
t
β = V/c
Własno
ś
ci czasoprzestrzeni s
ą
inne ni
ż
przewiduje to transformacja Galileusza.
Dla
β
<< 1
otrzymujemy transformacj
ę
Galileusza.
Transformacja Lorentza
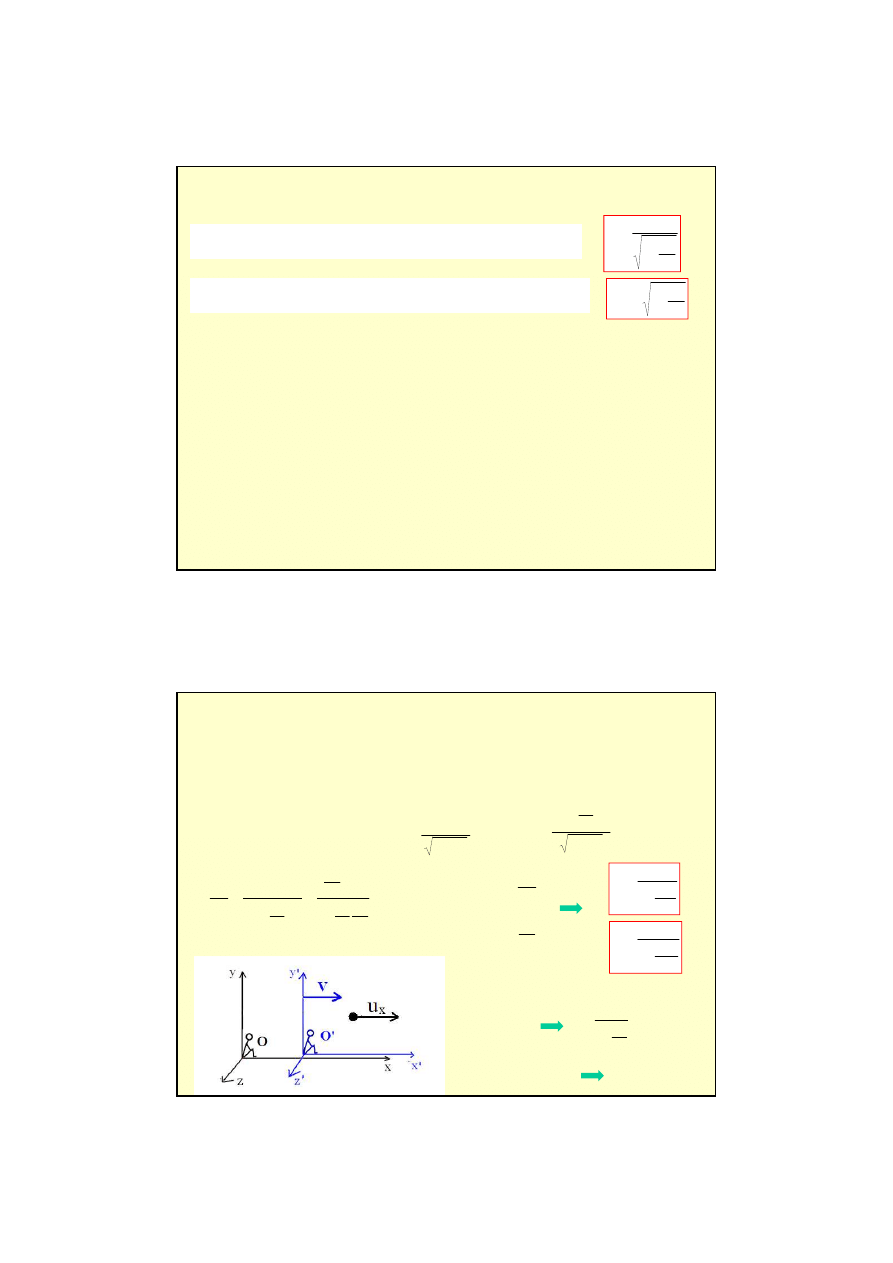
... czy dylatacja czasu wynika z transformacji Lorentza???
Dwa zdarzenia zaszły w tym samym
miejscu
w układzie poruszaj
ą
cym
si
ę
(O’), w odst
ę
pie czasu .
Dylatacja czasu
0
'
=
∆
x
2
1
'
β
−
∆
=
∆
t
t
0
'
=
∆
x
0
'
≠
∆
t
0
'
≠
∆
t
2
2
1
'
β
−
−
=
x
c
V
t
t
2
2
1
'
'
β
−
+
=
x
c
V
t
t
Pr
ę
t o długo
ś
ci (wzgl
ę
dem O’)
porusza si
ę
z pr
ę
dko
ś
ci
ą
V wzgl
ę
dem O.
Mierzymy długo
ść
w układzie O,
wyznaczaj
ą
c w tej samej chwili
współrz
ę
dne ko
ń
ca i pocz
ą
tku.
2
1
'
β
−
∆
=
∆
x
x
Skrócenie długo
ś
ci
2
1
'
β
−
=
L
L
'
'
L
x
=
∆
0
=
∆
t
2
1
'
β
−
−
=
Vt
x
x
L
x
=
∆
0
=
∆
t
6
Potwierdzenie dylatacji czasu i kontrakcji długo
ś
ci
2
2
1
'
c
V
t
t
−
∆
=
∆
1) Ka
ż
dy obserwator stwierdza,
ż
e poruszaj
ą
cy si
ę
zegar idzie wolniej
ni
ż
identyczny zegar w spoczynku (
dylatacja
czasu).
2
2
1
'
c
V
L
L
−
=
2) Ka
ż
dy obserwator stwierdza,
ż
e poruszaj
ą
cy si
ę
przedmiot jest krótszy
ni
ż
identyczny przedmiot w spoczynku (
kontrakcja
długo
ś
ci).
Dowody do
ś
wiadczalne
Miony docieraj
ą
do Ziemi cho
ć
maj
ą
zbyt krótki czas
ż
ycia (2
µ
s ).
W układzie zwi
ą
zanym z Ziemi
ą
jest to spowodowane dylatacj
ą
czasu (ich czas
ż
ycia
w układzie zwiazanym z Ziemi
ą
jest 30 razy dłu
ż
szy poniewa
ż
poruszaj
ą
si
ę
one z
pr
ę
dko
ś
ci
ą
99,3% pr
ę
dko
ś
ci
ś
wiatła).
Patrz
ą
c z układu odniesienia poruszaj
ą
cej si
ę
cz
ą
stki, atmosfera
Ziemi porusza si
ę
z pr
ę
dko
ś
ci
ą
ok. 99,3% pr
ę
dko
ś
ci
ś
wiatła wzgl
ę
dem spoczywaj
ą
cej
cz
ą
stki i tym samym, ze wzgl
ę
du na skrócenie długo
ś
ci, jest 30 razy cie
ń
sz
ą
warstw
ą
.
W ci
ą
gu 2
µ
s (czas
ż
ycia mionu) cała atmosfera zd
ąż
y przesun
ąć
si
ę
wzgl
ę
dem
cz
ą
stki i powierzchnia Ziemi dotrze do mionu.
Obiekt ma pr
ę
dko
ść
u
x
wzl
ę
dem Ziemii (nieruchomego obserwatora O).
Jak
ą
pr
ę
dko
ść
u’
x
zarejestruje obserwator O’ w rakiecie poruszaj
ą
cej si
ę
z pr
ę
dko
ś
ci
ą
V
wzdłu
ż
osi
x
.
Z transformacji Lorentza:
2
1
'
β
−
∆
−
∆
=
∆
t
V
x
x
2
2
1
'
β
−
∆
−
∆
=
∆
x
c
V
t
t
t
x
c
V
V
t
x
x
c
V
t
t
V
x
t
x
∆
∆
−
−
∆
∆
=
∆
−
∆
∆
−
∆
=
∆
∆
2
2
1
'
'
'
'
'
t
x
u
x
∆
∆
=
t
x
u
x
∆
∆
=
Poniewa
ż
:
2
1
'
c
Vu
V
u
u
x
x
x
−
−
=
2
'
1
'
c
Vu
V
u
u
x
x
x
+
+
=
β = V/c
Składanie pr
ę
dko
ś
ci w transformacji Lorentza
dla u
x
= c
c
c
Vc
V
c
c
=
−
−
=
2
1
'
V =0.9c, u
x
’ = 0.9c
u
x
= 0.994c
Przykłady:
1)
2)
7
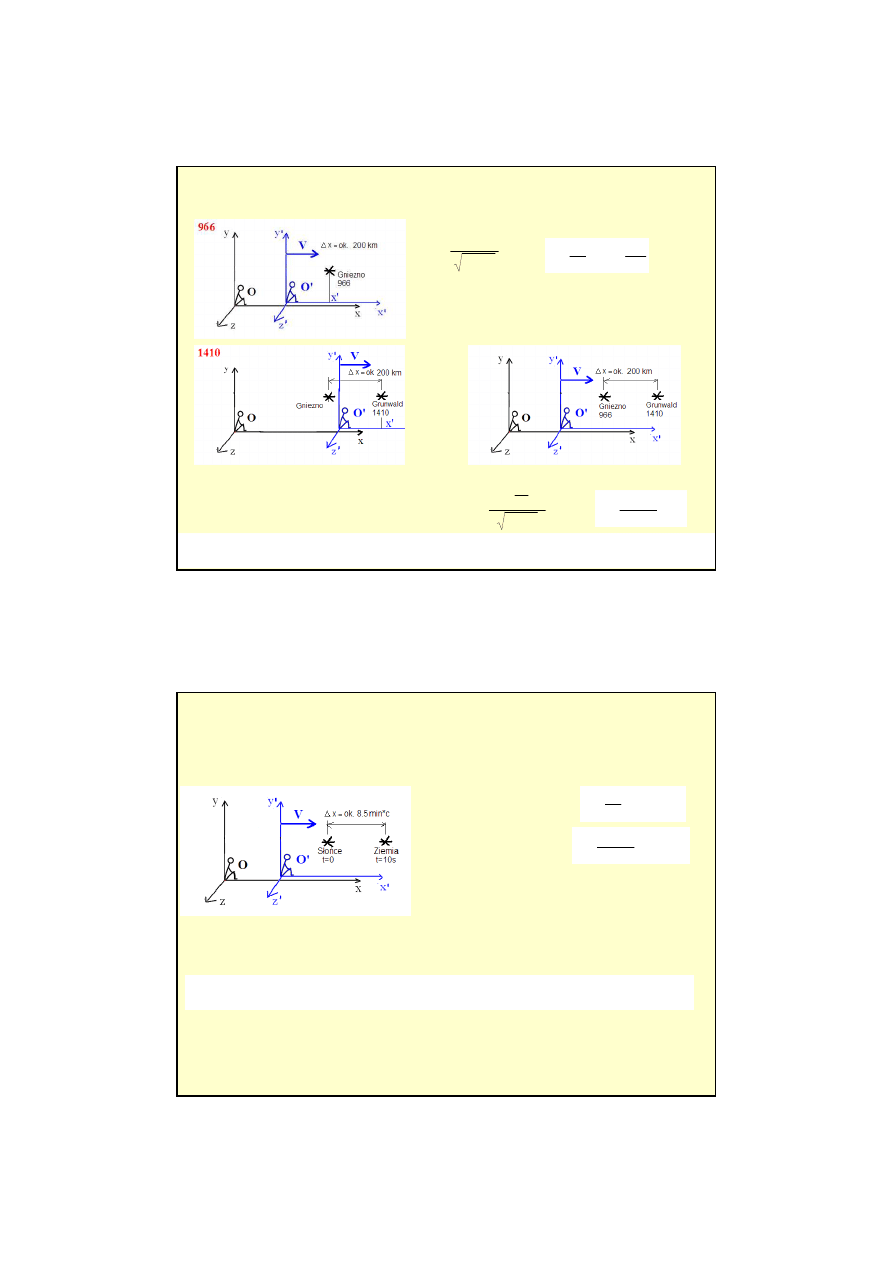
Zwi
ą
zek przyczynowo skutkowy a jednoczesno
ść
1) Czy istnieje układ, w którym bitwa pod Grunwaldem i chrzest Polski zaszły:
a) w tym samym miejscu:
rok
km
t
x
V
45
.
0
≈
∆
∆
=
0
1
'
2
=
−
∆
−
∆
=
∆
β
t
V
x
x
b) tym samym czasie:
0
1
'
2
2
=
−
∆
−
∆
=
∆
β
x
c
V
t
t
c
t
x
c
V
>>
∆
∆
=
/
2
Zdarzenia zajd
ą
w tym samym miejscu w układzie poruszaj
ą
cym si
ę
z pr
ę
dko
ś
ci
ą
ok. 0.45km/rok, z
Gniezna do Grunwaldu. Nie istnieje układ, w którym te zdarzenia s
ą
jednoczesne.
β = V/c
2) Po 10s od zaj
ś
cia protuberancji na Sło
ń
cu, na Ziemi wybuchł wulkan. Czy istnieje układ w
którym te zdarzenia zaszły:
a) w tym samym miejscu:
c
c
t
x
V
>
≈
∆
∆
=
*
51
b) tym samym czasie :
c
t
x
c
V
*
02
.
0
/
2
≈
∆
∆
=
Zdarzenia zajd
ą
w tym samym czasie w układzie poruszaj
ą
cym si
ę
z pr
ę
dko
ś
ci
ą
ok. 0.02*c.
Nie istnieje układ, w którym te zdarzenia zajd
ą
w tym samym miejscu.
8
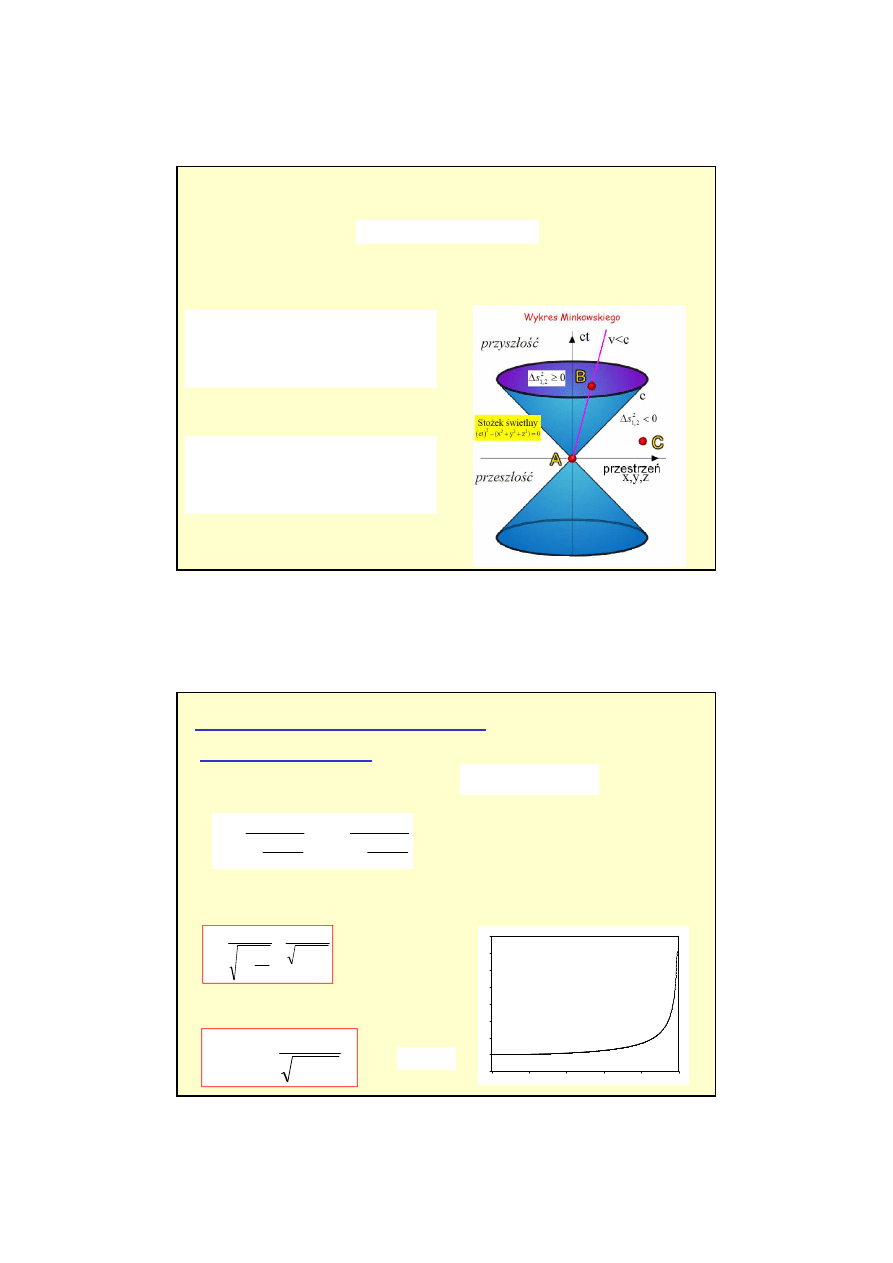
Wielko
ść
fizyczna opisuj
ą
ca odległo
ść
mi
ę
dzy dwoma zdarzeniami nazywa si
ę
interwałem
zdefiniowanym nast
ę
puj
ą
co:
(
)
2
2
2
2
2
2
2
,
1
z
y
x
t
c
s
∆
+
∆
+
∆
−
∆
=
∆
Mo
ż
na wykaza
ć
,
ż
e interwał jest niezmiennikiem wzgl
ę
dem transformacji Lorentza, tzn. ma
tak
ą
sam
ą
warto
ść
w ka
ż
dym inercjalnym układzie odniesienia:
2
2
,
1
2
2
,
1
'
s
s
∆
=
∆
2
,
1
s
∆
1) Je
ś
li istnieje układ, w którym zdarzenia
zajd
ą
w tym samym miejscu to mo
ż
e istnie
ć
miedzy nimi zwi
ą
zek przyczynowy (te
zdarzenia nie mog
ą
by
ć
jednoczesne w
ż
adnym układzie). Wtedy :
0
2
2
,
1
≥
∆
s
2) Je
ś
li istnieje układ, w którym zdarzenia
zajd
ą
w tym samym czasie to nie mo
ż
e
istnie
ć
miedzy nimi zwi
ą
zek przyczynowy
(nie istnieje układ, w którym zdarzenia zajd
ą
w tym samym miejscu ). Wtedy :
0
2
2
,
1
<
∆
s
Geometria czasoprzestrzeni
DYNAMIKA RELATYWISTYCZNA
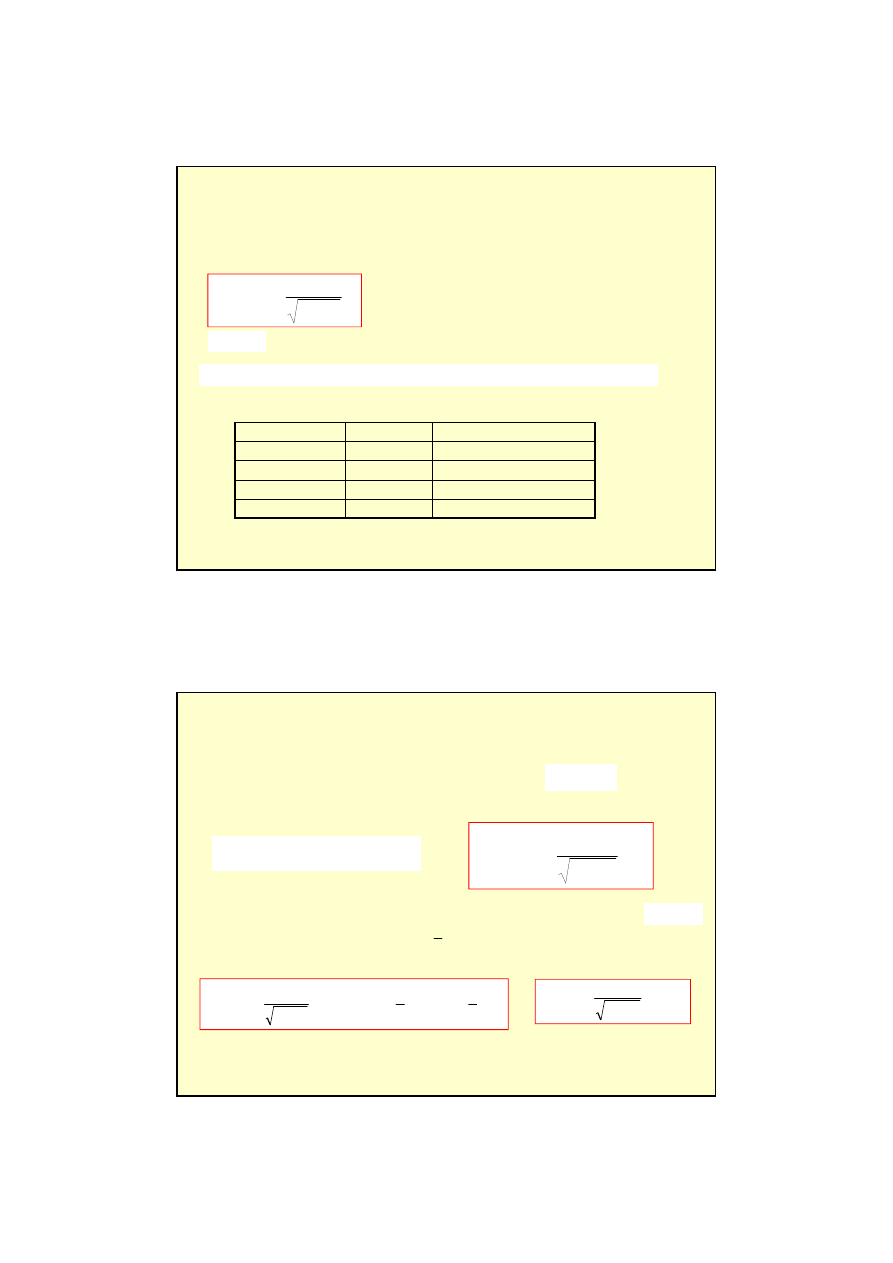
Pęd i masa relatywistyczna
Je
ś
li ma pozosta
ć
słuszna zasada zachowania p
ę
du
, to masa ciała nie mo
ż
e
by
ć
wielko
ś
ci
ą
stał
ą
; musi ona zale
ż
e
ć
od pr
ę
dko
ś
ci wg. wzoru:
γ=
m/m
0
v/c
0.0
0.2
0.4
0.6
0.8
1.0
0
1
2
3
4
5
6
7
8
2
0
2
2
0
1
1
β
−
=
−
=
m
c
u
m
m
Sprawd
ź
my czy zasada zachowania p
ę
du:
∑
∑
=
i
i
xkonc
i
i
i
xpocz
i
u
m
u
m
,
,
obowi
ą
zuje
w układzie poruszaj
ą
cym si
ę
z pr
ę
dko
ś
ci
ą
V:
∑
∑
−
−
≠
−
−
i
i
xkonc
i
xkonc
i
i
i
xpocz
i
xpocz
i
c
Vu
V
u
m
c
Vu
V
u
m
2
,
,
2
,
,
1
1
problem: zas. zach. p
ę
du nie jest spełniona !!!
P
ę
d w mechanice relatywistycznej
definiujemy:
u
m
mu
p
2
0
1
β
−
=
=
β = u/c
9
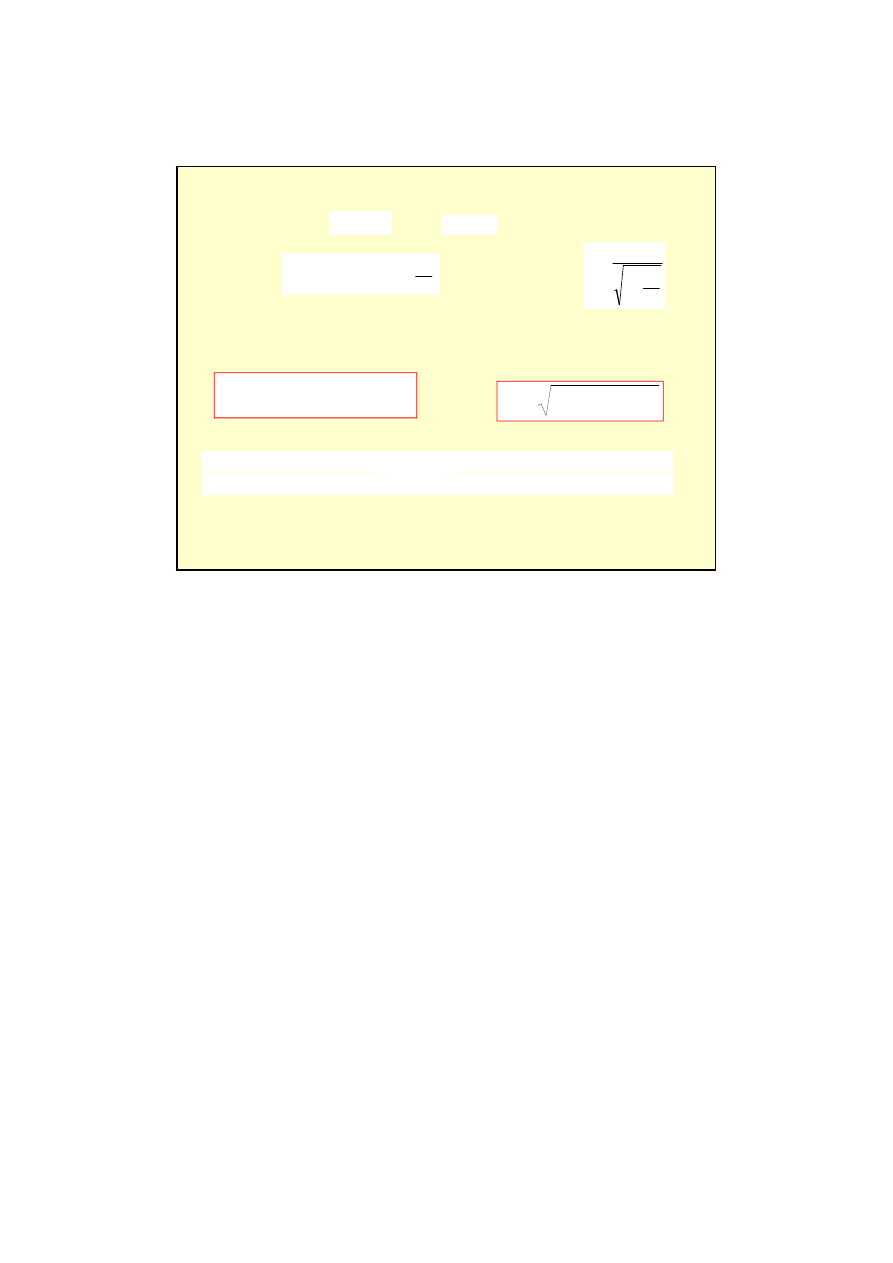
Energia relatywistyczna
Aby utrzyma
ć
w mocy zasad
ę
zachowania energii w mechanice relatywistycznej,
pomi
ę
dzy mas
ą
całkowit
ą
a energi
ą
ciała (zwan
ą
energi
ą
całkowit
ą
) musi
zachodzi
ć
zwi
ą
zek :
2
2
0
2
1
c
m
mc
E
β
−
=
=
Jest to słynne równanie Einsteina
wyra
ż
aj
ą
ce
równowa
ż
no
ść
masy i energii.
Uwaga: Zasada zachowania energii obowi
ą
zuje dla energii całkowitej !!!
masa [kg]
energia
elektron
9.11×10
-31
8.19 ×10
-14
J (= 511 keV)
proton
1.67 ×10
-27
1.5 ×10
-10
J (= 938 MeV)
atom Uranu
3.95 ×10
-25
3.55 ×10
-8
J (= 225 GeV)
cz
ą
steczka kurzu
1 ×10
-13
1 ×10
4
J
β = u/c
Mo
ż
na wykaza
ć
,
ż
e gdy
u<<c
(tj. ) , wzory relatywistyczne przechodz
ą
w klasyczne:
u
m
u
m
mu
p
0
2
0
1
≈
−
=
=
β
2
0
2
2
0
2
2
0
2
1
1
...
2
1
1
1
1
1
u
m
c
m
c
m
E
k
≈
−
+
=
−
−
=
β
β
0
→
=
c
u
β
Załó
ż
my najpierw,
ż
e ciało jest w spoczynku. Wtedy masa tego ciała jest równa
m
0
i jego energia, zwana
energi
ą
spoczynkow
ą
, wynosi:
2
0
0
c
m
E
=
Jaka jest wi
ę
c definicja energii kinetycznej ?
(
)
2
0
0
c
m
m
E
E
E
k
−
=
−
=
−
−
=
1
1
1
2
2
0
β
c
m
E
k
Relatywistyczna energia kinetyczna
jest równa:
β = u/c
10
2
mc
E
=
mu
p
=
oraz
)
1
(
2
2
4
2
2
2
2
c
u
c
m
c
p
E
−
=
−
2
2
0
1
c
u
m
m
−
=
st
ą
d:
podstawiaj
ą
c:
Zwi
ą
zek energii, masy i p
ę
du
4
2
0
2
2
2
c
m
c
p
E
=
−
otrzymamy:
2
2
4
2
0
c
p
c
m
E
+
=
Zauwa
ż
my,
ż
e wyra
ż
enie:
2
2
2
c
p
E
−
jest niezmiennikiem (podobnie jak
interwał ma tak
ą
sam
ą
warto
ść
we wszystkich układach inercjalnych).
lub
Wyszukiwarka
Podobne podstrony:
8 IMIR teoria wzglednosci id 46 Nieznany (2)
Co to jest teoria względności podstawy geometryczne
F3 teoria wzglednosci
II 10 Teoria wzglednosci
Czy ogólna teoria względności dopuszcza perpetuum mobile pierwszego rodzaju
swiat kwantowy a teoria wzglednosci, Przydatne
Szczególna teoria względności Einstaina, Fizyka
szczególna teoria względności, Fizyka - hasło fizyka, Fizyka(1)
P A M Dirac Ogolna teoria wzglednosci id 34
5 5 Teoria względności
pawlikowski, fizyka, szczególna teoria względności
INTYMNA TEORIA WZGLEDNOSCI J L Wisniewski
8 teoria wzglednosci
einstein-teoria-fiza, SZCZEGÓLNA TEORIA WZGLĘDNOŚCI - szybkość światła C w próżni jest jednakowa dla
Teoria Względności
Teoria względności, Odpowiedzi Do Zadań Poziom Podstawowy
teoria wzglednosci r, Przedmioty Szkolne, Fizyka
Ogólna teoria względności
więcej podobnych podstron