1
TESTOWANIE HIPOTEZ
TESTOWANIE HIPOTEZ
STATYSTYCZNYCH
STATYSTYCZNYCH
Dr in
Dr in
ż
ż
. Marek Bauer
. Marek Bauer
0
10
20
30
40
50
60
0
30
60
90
120
150
180
TESTOWANIE HIPOTEZ STATYSTYCZNYCH
TESTOWANIE HIPOTEZ STATYSTYCZNYCH
Cel: obiektywna ocena wielko
Cel: obiektywna ocena wielko
ś
ś
ci r
ci r
ó
ó
ż
ż
nic pomi
nic pomi
ę
ę
dzy
dzy
wybranymi, odpowiadaj
wybranymi, odpowiadaj
ą
ą
cymi sobie parametrami
cymi sobie parametrami
Przyk
Przyk
ł
ł
ady zastosowa
ady zastosowa
ń
ń
praktycznych:
praktycznych:
¾
¾
Por
Por
ó
ó
wnanie pr
wnanie pr
ę
ę
dko
dko
ś
ś
ci chwilowej w przekroju drogi z
ci chwilowej w przekroju drogi z
pr
pr
ę
ę
dko
dko
ś
ś
ci
ci
ą
ą
dopuszczaln
dopuszczaln
ą
ą
(test istotno
(test istotno
ś
ś
ci dla warto
ci dla warto
ś
ś
ci
ci
ś
ś
redniej)
redniej)
¾
¾
Por
Por
ó
ó
wnanie czasu przejazdu odcinka
wnanie czasu przejazdu odcinka
„
„
przed
przed
”
”
i
i
„
„
po
po
”
”
wybudowaniu pasa autobusowego
wybudowaniu pasa autobusowego
(test istotno
(test istotno
ś
ś
ci dla
ci dla
dw
dw
ó
ó
ch
ch
ś
ś
rednich)
rednich)
¾
¾
Por
Por
ó
ó
wnanie zmienno
wnanie zmienno
ś
ś
ci wielko
ci wielko
ś
ś
ci nat
ci nat
ęż
ęż
e
e
ń
ń
ruchu w
ruchu w
szczycie porannym i popo
szczycie porannym i popo
ł
ł
udniowym
udniowym
(test istotno
(test istotno
ś
ś
ci
ci
dla dw
dla dw
ó
ó
ch wariancji)
ch wariancji)
TESTOWANIE HIPOTEZ STATYSTYCZNYCH
TESTOWANIE HIPOTEZ STATYSTYCZNYCH
Przyk
Przyk
ł
ł
ady zastosowa
ady zastosowa
ń
ń
praktycznych (c.d.):
praktycznych (c.d.):
¾
¾
Por
Por
ó
ó
wnanie preferencji komunikacyjnych pasa
wnanie preferencji komunikacyjnych pasa
ż
ż
er
er
ó
ó
w
w
dw
dw
ó
ó
ch miast
ch miast
(test istotno
(test istotno
ś
ś
ci dla dw
ci dla dw
ó
ó
ch wska
ch wska
ź
ź
nik
nik
ó
ó
w
w
struktury)
struktury)
¾
¾
Por
Por
ó
ó
wnanie zmienno
wnanie zmienno
ś
ś
ci potok
ci potok
ó
ó
w pasa
w pasa
ż
ż
erskich w
erskich w
ci
ci
ą
ą
gu trzech okres
gu trzech okres
ó
ó
w dnia
w dnia
(test istotno
(test istotno
ś
ś
ci dla wielu
ci dla wielu
wariancji
wariancji
–
–
np
np
. test
. test
Bartletta
Bartletta
)
)
¾
¾
Por
Por
ó
ó
wnanie pr
wnanie pr
ę
ę
dko
dko
ś
ś
ci pojazd
ci pojazd
ó
ó
w przy r
w przy r
ó
ó
ż
ż
nych
nych
szeroko
szeroko
ś
ś
ciach pasa ruchu (
ciach pasa ruchu (
testy por
testy por
ó
ó
wna
wna
ń
ń
wielokrotnych
wielokrotnych
–
–
np
np
. test
. test
Duncana
Duncana
)
)
TEST ISTOTNO
TEST ISTOTNO
Ś
Ś
CI DLA DW
CI DLA DW
Ó
Ó
CH WARTO
CH WARTO
Ś
Ś
CI
CI
Ś
Ś
REDNICH
REDNICH
Hipotezy statystyczne:
Hipotezy statystyczne:
¾
¾
Hipoteza zerowa (sprawdzana):
Hipoteza zerowa (sprawdzana):
m
m
1
1
=
=
m
m
2
2
¾
¾
Hipoteza alternatywna
Hipoteza alternatywna
:
:
m
m
1
1
≠
≠
m
m
2
2
lub
lub
m
m
1
1
>
>
m
m
2
2
lub
lub
m
m
1
1
<
<
m
m
2
2
Statystyka testu:
Statystyka testu:
2
2
2
1
2
1
2
1
n
s
n
s
x
x
u
+
−
=
2
1
2
,
1
∑
=
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
n
i
i
x
x
S
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
⋅
−
+
+
−
=
−
−
2
1
2
1
2
1
2
1
1
1
2
n
n
n
n
S
S
x
x
t
Obie pr
Obie pr
ó
ó
by du
by du
ż
ż
e
e
Przynajmniej jedna pr
Przynajmniej jedna pr
ó
ó
ba ma
ba ma
ł
ł
a
a
Por
Por
ó
ó
wnanie statystyki testu z
wnanie statystyki testu z
t
t
α
α
(
(
α
α
; n
; n
-
-
2
2
)
)
lub
lub
u
u
α
α
(
(
α
α
)
)
¾
¾
je
je
ś
ś
li
li
u<
u<
u
u
α
α
lub
lub
t<
t<
t
t
α
α
–
–
brak podstaw do odrzucenia H
brak podstaw do odrzucenia H
0
0
¾
¾
je
je
ś
ś
li
li
u>
u>
u
u
α
α
lub
lub
t>
t>
t
t
α
α
–
–
podstawa do odrzucenia H
podstawa do odrzucenia H
0
0
TEST ISTOTNO
TEST ISTOTNO
Ś
Ś
CI DLA WARTO
CI DLA WARTO
Ś
Ś
CI
CI
Ś
Ś
REDNIEJ
REDNIEJ
Hipotezy statystyczne:
Hipotezy statystyczne:
¾
¾
Hipoteza zerowa (sprawdzana):
Hipoteza zerowa (sprawdzana):
m
m
1
1
=
=
m
m
0
0
¾
¾
Hipoteza alternatywna
Hipoteza alternatywna
:
:
m
m
1
1
≠
≠
m
m
0
0
lub
lub
m
m
1
1
>
>
m
m
0
0
lub
lub
m
m
1
1
<
<
m
m
0
0
n
m
x
u
⋅
−
=
σ
0
Statystyka testu:
Statystyka testu:
Pr
Pr
ó
ó
ba du
ba du
ż
ż
a
a
Pr
Pr
ó
ó
ba ma
ba ma
ł
ł
a
a
Por
Por
ó
ó
wnanie statystyki testu z
wnanie statystyki testu z
t
t
α
α
(
(
α
α
; n
; n
-
-
1
1
)
)
lub
lub
u
u
α
α
(
(
α
α
)
)
¾
¾
je
je
ś
ś
li
li
u<
u<
u
u
α
α
lub
lub
t<
t<
t
t
α
α
–
–
brak podstaw do odrzucenia H
brak podstaw do odrzucenia H
0
0
¾
¾
je
je
ś
ś
li
li
u>
u>
u
u
α
α
lub
lub
t>
t>
t
t
α
α
–
–
podstawa do odrzucenia H
podstawa do odrzucenia H
0
0
n
s
m
x
t
⋅
−
=
0
TEST ISTOTNO
TEST ISTOTNO
Ś
Ś
CI DLA DW
CI DLA DW
Ó
Ó
CH WARIANCJI
CH WARIANCJI
Hipotezy statystyczne:
Hipotezy statystyczne:
¾
¾
Hipoteza zerowa (sprawdzana):
Hipoteza zerowa (sprawdzana):
σ
σ
1
1
=
=
σ
σ
2
2
¾
¾
Hipoteza alternatywna
Hipoteza alternatywna
:
:
σ
σ
1
1
≠
≠
σ
σ
2
2
;
;
σ
σ
1
1
>
>
σ
σ
2
2
;
;
σ
σ
1
1
<
<
σ
σ
2
2
Statystyka testu:
Statystyka testu:
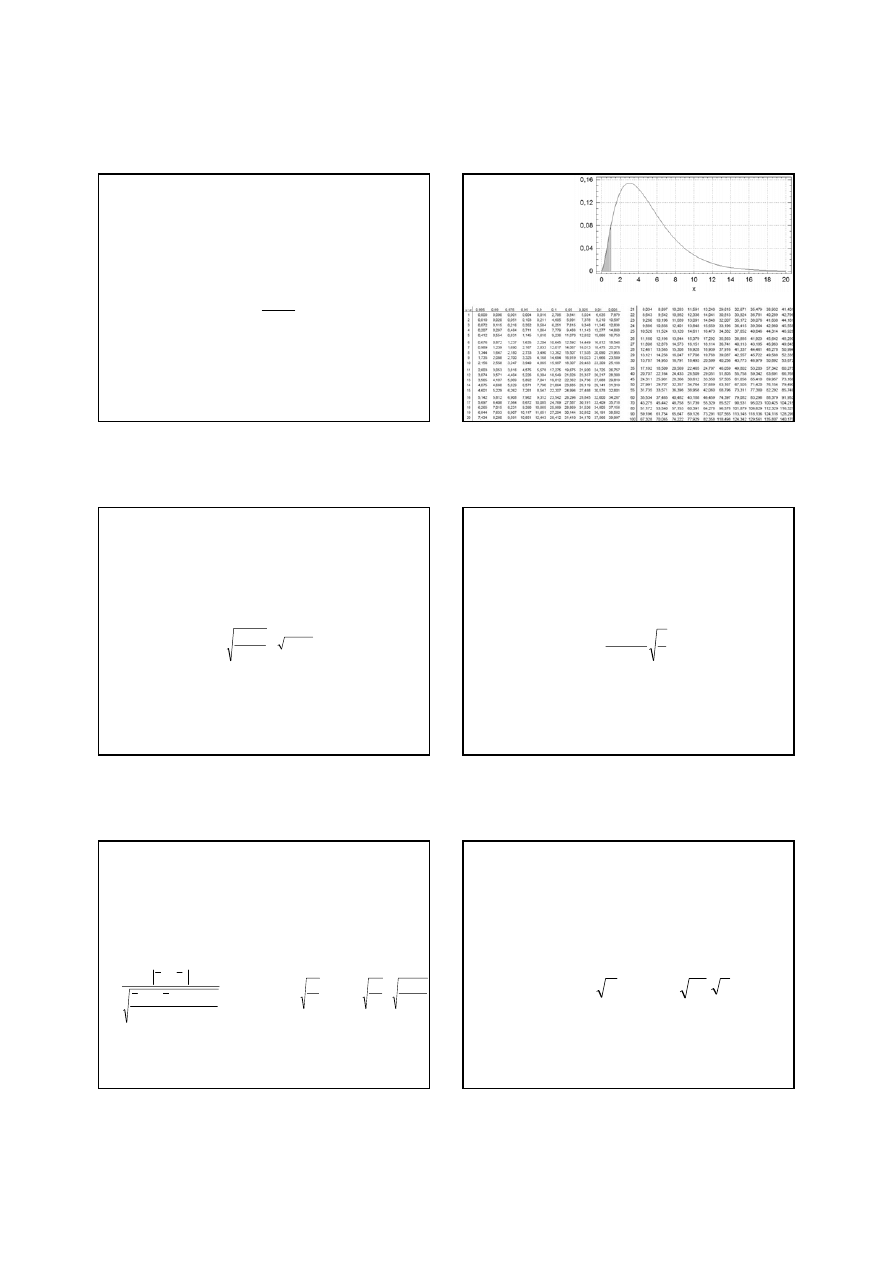
Por
Por
ó
ó
wnanie statystyki testu z
wnanie statystyki testu z
F
F
α
α
(
(
α
α
; n
; n
1
1
; n
; n
2
2
)
)
z rozk
z rozk
ł
ł
adu
adu
Snedecora
Snedecora
¾
¾
je
je
ś
ś
li
li
F
F
<
<
F
F
α
α
–
–
brak podstaw do odrzucenia H
brak podstaw do odrzucenia H
0
0
¾
¾
je
je
ś
ś
li
li
F
F
>
>
F
F
α
α
–
–
podstawa do odrzucenia H
podstawa do odrzucenia H
0
0
2
2
2
1
s
s
F
=
2
TEST ISTOTNO
TEST ISTOTNO
Ś
Ś
CI DLA WARIANCJI (n<50)
CI DLA WARIANCJI (n<50)
Hipotezy statystyczne:
Hipotezy statystyczne:
¾
¾
Hipoteza zerowa (sprawdzana):
Hipoteza zerowa (sprawdzana):
σ
σ
2
2
=
=
σ
σ
0
0
2
2
¾
¾
Hipoteza alternatywna
Hipoteza alternatywna
:
:
σ
σ
2
2
=
=
σ
σ
0
0
2
2
;
;
σ
σ
2
2
>
>
σ
σ
0
0
2
2
;
;
σ
σ
2
2
<
<
σ
σ
0
0
2
2
Statystyka testu:
Statystyka testu:
Por
Por
ó
ó
wnanie statystyki testu z
wnanie statystyki testu z
X
X
α
α
(
(
α
α
/2
/2
;
;
n
n
-
-
1
1
)
)
z rozk
z rozk
ł
ł
adu
adu
Chi
Chi
-
-
kwadrat
kwadrat
¾
¾
je
je
ś
ś
li
li
X
X
2
2
<
<
X
X
α
α
2
2
–
–
brak podstaw do odrzucenia H
brak podstaw do odrzucenia H
0
0
¾
¾
je
je
ś
ś
li
li
X
X
2
2
>
>
X
X
α
α
2
2
–
–
podstawa do odrzucenia H
podstawa do odrzucenia H
0
0
2
0
2
2
σ
χ
S
n
⋅
=
TABLICE
TABLICE
STATYSTYCZNE
STATYSTYCZNE
(3)
(3)
Rozkład Chi-
kwadrat
c
2
=Χ
2
(1-α/2; n-1)
c
1
=Χ
2
(α/2; n-1)
TEST ISTOTNO
TEST ISTOTNO
Ś
Ś
CI DLA WARIANCJI (n>50)
CI DLA WARIANCJI (n>50)
Hipotezy statystyczne:
Hipotezy statystyczne:
¾
¾
Hipoteza zerowa (sprawdzana):
Hipoteza zerowa (sprawdzana):
σ
σ
2
2
=
=
σ
σ
0
0
2
2
¾
¾
Hipoteza alternatywna
Hipoteza alternatywna
:
:
σ
σ
2
2
=
=
σ
σ
0
0
2
2
;
;
σ
σ
2
2
>
>
σ
σ
0
0
2
2
;
;
σ
σ
2
2
<
<
σ
σ
0
0
2
2
Statystyka testu:
Statystyka testu:
Por
Por
ó
ó
wnanie statystyki testu z
wnanie statystyki testu z
u
u
α
α
(
(
α
α
)
)
z rozk
z rozk
ł
ł
adu
adu
Normalnego standaryzowanego
Normalnego standaryzowanego
N[0,1]
N[0,1]
¾
¾
je
je
ś
ś
li
li
u<
u<
u
u
α
α
–
–
brak podstaw do odrzucenia H
brak podstaw do odrzucenia H
0
0
¾
¾
je
je
ś
ś
li
li
u
u
>
>
u
u
α
α
2
2
–
–
podstawa do odrzucenia H
podstawa do odrzucenia H
0
0
3
2
2
2
0
2
−
−
⋅
=
n
S
n
u
σ
TEST ISTOTNO
TEST ISTOTNO
Ś
Ś
CI DLA WARIANCJI (n>100)
CI DLA WARIANCJI (n>100)
Hipotezy statystyczne:
Hipotezy statystyczne:
¾
¾
Hipoteza zerowa (sprawdzana):
Hipoteza zerowa (sprawdzana):
σ
σ
2
2
=
=
σ
σ
0
0
2
2
¾
¾
Hipoteza alternatywna
Hipoteza alternatywna
:
:
σ
σ
2
2
=
=
σ
σ
0
0
2
2
;
;
σ
σ
2
2
>
>
σ
σ
0
0
2
2
;
;
σ
σ
2
2
<
<
σ
σ
0
0
2
2
Statystyka testu:
Statystyka testu:
Por
Por
ó
ó
wnanie statystyki testu z
wnanie statystyki testu z
u
u
α
α
(
(
α
α
)
)
z rozk
z rozk
ł
ł
adu
adu
Normalnego standaryzowanego
Normalnego standaryzowanego
N[0,1]
N[0,1]
¾
¾
je
je
ś
ś
li
li
u<
u<
u
u
α
α
–
–
brak podstaw do odrzucenia H
brak podstaw do odrzucenia H
0
0
¾
¾
je
je
ś
ś
li
li
u
u
>
>
u
u
α
α
2
2
–
–
podstawa do odrzucenia H
podstawa do odrzucenia H
0
0
2
2
2
2
n
S
u
σ
σ
−
=
TEST ISTOTNO
TEST ISTOTNO
Ś
Ś
CI DLA DW
CI DLA DW
Ó
Ó
CH
CH
WSKA
WSKA
Ź
Ź
NIK
NIK
Ó
Ó
W STRUKTURY
W STRUKTURY
Hipotezy statystyczne:
Hipotezy statystyczne:
¾
¾
Hipoteza zerowa (sprawdzana):
Hipoteza zerowa (sprawdzana):
p
p
1
1
=
=
p
p
2
2
¾
¾
Hipoteza alternatywna
Hipoteza alternatywna
:
:
p
p
1
1
≠
≠
p
p
2
2
lub
lub
p
p
1
1
>
>
p
p
2
2
lub
lub
p
p
1
1
<
<
p
p
2
2
Statystyka testu:
Statystyka testu:
Obie pr
Obie pr
ó
ó
by du
by du
ż
ż
e
e
Przynajmniej jedna pr
Przynajmniej jedna pr
ó
ó
ba ma
ba ma
ł
ł
a
a
Por
Por
ó
ó
wnanie statystyki testu z
wnanie statystyki testu z
u
u
α
α
(
(
α
α
)
)
¾
¾
je
je
ś
ś
li
li
u<
u<
u
u
α
α
–
–
brak podstaw do odrzucenia H
brak podstaw do odrzucenia H
0
0
¾
¾
je
je
ś
ś
li
li
u>
u>
u
u
α
α
–
–
podstawa do odrzucenia H
podstawa do odrzucenia H
0
0
2
1
2
1
2
2
1
1
arcsin
2
arcsin
2
n
n
n
n
n
m
n
m
u
+
⋅
⋅
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
−
⋅
=
2
1
2
1
2
1
)
(
)
1
(
n
n
n
n
p
p
p
p
u
⋅
+
⋅
−
⋅
−
=
TEST ISTOTNO
TEST ISTOTNO
Ś
Ś
CI DLA WSKA
CI DLA WSKA
Ź
Ź
NIKA
NIKA
STRUKTURY (n<100)
STRUKTURY (n<100)
Hipotezy statystyczne:
Hipotezy statystyczne:
¾
¾
Hipoteza zerowa (sprawdzana):
Hipoteza zerowa (sprawdzana):
p
p
=
=
p
p
0
0
¾
¾
Hipoteza alternatywna
Hipoteza alternatywna
:
:
p
p
≠
≠
p
p
0
0
lub
lub
p
p
>
>
p
p
0
0
lub
lub
p
p
<
<
p
p
0
0
Statystyka testu:
Statystyka testu:
Por
Por
ó
ó
wnanie statystyki testu z
wnanie statystyki testu z
u
u
α
α
(
(
α
α
)
)
¾
¾
je
je
ś
ś
li
li
u<
u<
u
u
α
α
–
–
brak podstaw do odrzucenia H
brak podstaw do odrzucenia H
0
0
¾
¾
je
je
ś
ś
li
li
u>
u>
u
u
α
α
–
–
podstawa do odrzucenia H
podstawa do odrzucenia H
0
0
(
)
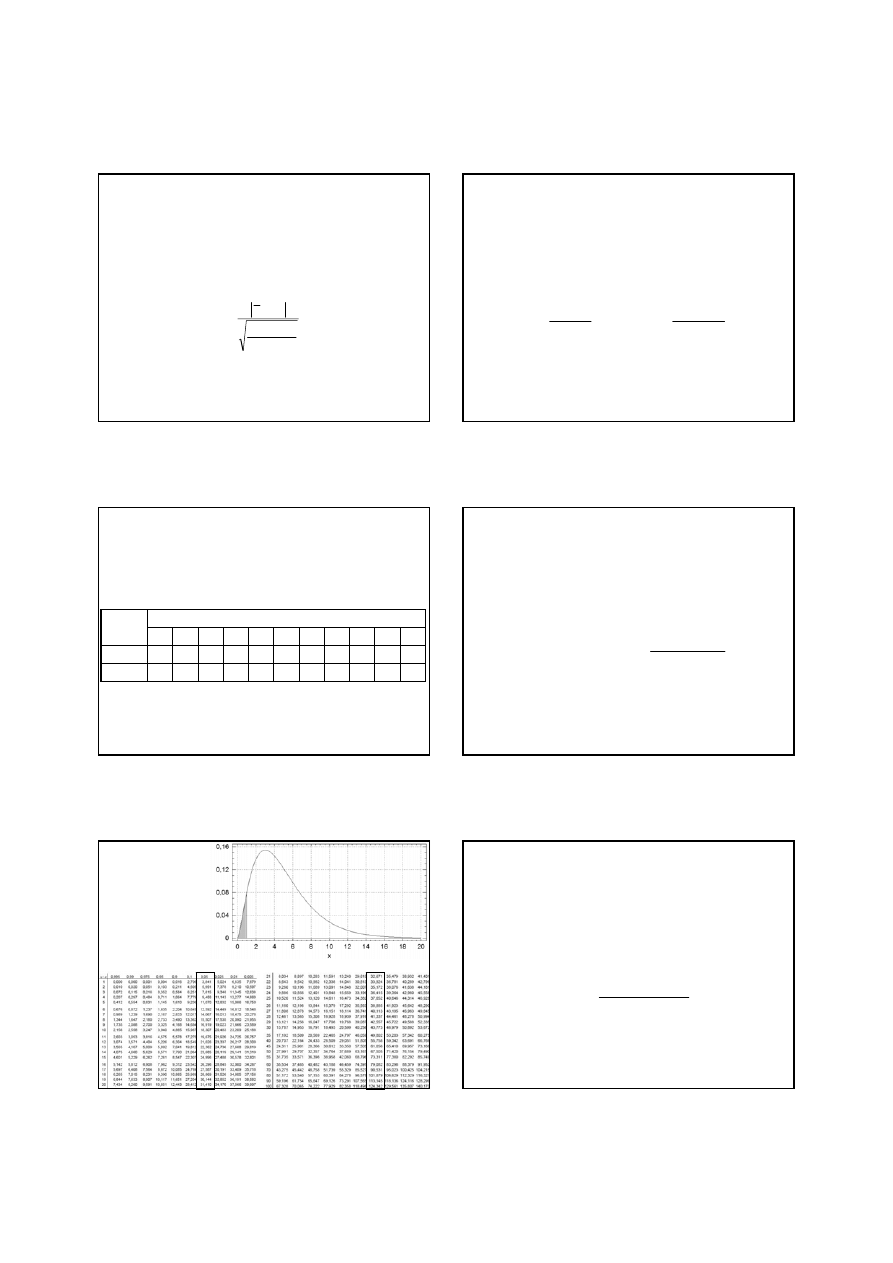
n
p
p
u
0
arcsin
2
arcsin
2
−
=
3
TEST ISTOTNO
TEST ISTOTNO
Ś
Ś
CI DLA WSKA
CI DLA WSKA
Ź
Ź
NIKA
NIKA
STRUKTURY (n>100)
STRUKTURY (n>100)
Hipotezy statystyczne:
Hipotezy statystyczne:
¾
¾
Hipoteza zerowa (sprawdzana):
Hipoteza zerowa (sprawdzana):
p
p
=
=
p
p
0
0
¾
¾
Hipoteza alternatywna
Hipoteza alternatywna
:
:
p
p
≠
≠
p
p
0
0
lub
lub
p
p
>
>
p
p
0
0
lub
lub
p
p
<
<
p
p
0
0
Statystyka testu:
Statystyka testu:
Por
Por
ó
ó
wnanie statystyki testu z
wnanie statystyki testu z
u
u
α
α
(
(
α
α
)
)
¾
¾
je
je
ś
ś
li
li
u<
u<
u
u
α
α
–
–
brak podstaw do odrzucenia H
brak podstaw do odrzucenia H
0
0
¾
¾
je
je
ś
ś
li
li
u>
u>
u
u
α
α
–
–
podstawa do odrzucenia H
podstawa do odrzucenia H
0
0
(
)
n
p
p
p
p
u
0
0
0
1
−
−
=
TEST JEDNORODNO
TEST JEDNORODNO
Ś
Ś
CI DO ELIMINACJI
CI DO ELIMINACJI
B
B
ŁĘ
ŁĘ
D
D
Ó
Ó
W GRUBYCH
W GRUBYCH
Hipotezy statystyczne:
Hipotezy statystyczne:
¾
¾
Hipoteza zerowa
Hipoteza zerowa
:
:
pr
pr
ó
ó
ba jest jednorodna
ba jest jednorodna
¾
¾
Hipoteza alternatywna
Hipoteza alternatywna
:
:
pr
pr
ó
ó
ba nie jest jednorodna
ba nie jest jednorodna
1
1
2
x
x
x
x
B
n
−
−
=
Statystyki testu (dane u
Statystyki testu (dane u
ł
ł
o
o
ż
ż
one rosn
one rosn
ą
ą
co):
co):
Por
Por
ó
ó
wnanie statystyki testu z
wnanie statystyki testu z
B
B
α
α
(
(
α
α
)
)
¾
¾
je
je
ś
ś
li
li
B
B
<
<
B
B
α
α
–
–
brak podstaw do odrzucenia H
brak podstaw do odrzucenia H
0
0
¾
¾
je
je
ś
ś
li
li
B
B
>
>
B
B
α
α
–
–
podstawa do odrzucenia H
podstawa do odrzucenia H
0
0
1
1
x
x
x
x
B
n
n
n
−
−
=
−
TEST JEDNORODNO
TEST JEDNORODNO
Ś
Ś
CI DO ELIMINACJI
CI DO ELIMINACJI
B
B
ŁĘ
ŁĘ
D
D
Ó
Ó
W GRUBYCH
W GRUBYCH
Warto
Warto
ś
ś
ci krytyczne
ci krytyczne
:
:
Liczebność próby
Poziom
istotności α
3 4 5 6 7 8 10 12 15 20 30
0,05
0,94 0,76 0,64 0,56 0,51 0,47 0,41 0,38 0,34 0,30 0,28
0,10
0,89 0,68 0,56 0,48 0,43 0,40 0,35 0,32 0,28 0,25 0,22
TEST ZGODNO
TEST ZGODNO
Ś
Ś
CI CHI
CI CHI
-
-
KWADRAT
KWADRAT
Hipotezy statystyczne:
Hipotezy statystyczne:
¾
¾
Hipoteza zerow
Hipoteza zerow
a: badany
a: badany
rozk
rozk
ł
ł
ad jest zgodny z rozk
ad jest zgodny z rozk
ł
ł
adem
adem
Normalnym
Normalnym
¾
¾
Hipoteza alternatywna
Hipoteza alternatywna
: badany
: badany
rozk
rozk
ł
ł
ad NIE JEST zgodny z
ad NIE JEST zgodny z
rozk
rozk
ł
ł
adem Normalnym
adem Normalnym
Statystyka testu:
Statystyka testu:
Por
Por
ó
ó
wnanie statystyki testu z
wnanie statystyki testu z
X
X
α
α
(
(
α
α
;
;
r
r
-
-
l
l
-
-
1
1
)
)
z rozk
z rozk
ł
ł
adu
adu
Chi
Chi
-
-
kwadrat
kwadrat
(l
(l
–
–
liczba parametr
liczba parametr
ó
ó
w r. hipotetycznego)
w r. hipotetycznego)
¾
¾
je
je
ś
ś
li
li
X
X
2
2
<
<
X
X
α
α
2
2
–
–
brak podstaw do odrzucenia H
brak podstaw do odrzucenia H
0
0
¾
¾
je
je
ś
ś
li
li
X
X
2
2
>
>
X
X
α
α
2
2
–
–
podstawa do odrzucenia H
podstawa do odrzucenia H
0
0
(
)
∑
=
⋅
⋅
−
=
r
j
j
j
j
p
n
p
n
n
1
2
2
χ
TABLICE
TABLICE
STATYSTYCZNE
STATYSTYCZNE
Rozkład Chi-
kwadrat
Χ
2
(α; r-l-1)
POR
POR
Ó
Ó
WNANIE WA
WNANIE WA
Ż
Ż
NO
NO
Ś
Ś
CI CECH
CI CECH
O CHARAKTERZE JAKO
O CHARAKTERZE JAKO
Ś
Ś
CIOWYM
CIOWYM
Wsp
Wsp
ó
ó
ł
ł
czynnik korelacji rang Spearmana :
czynnik korelacji rang Spearmana :
)
1
(
)
(
6
1
2
1
2
−
⋅
−
⋅
−
=
∑
=
n
n
Y
X
r
n
i
i
i
s
4
POR
POR
Ó
Ó
WNANIE PREFERENCJI PASA
WNANIE PREFERENCJI PASA
Ż
Ż
ER
ER
Ó
Ó
W
W
KOMUNIKACJI MIEJSKIEJ W KRAKOWIE
KOMUNIKACJI MIEJSKIEJ W KRAKOWIE
r
r
s
s
= 0,92
= 0,92
Autobusy
Autobusy
10
10
8
8
9
9
6
6
5
5
4
4
7
7
3
3
2
2
1
1
Ranga
Ranga
Tramwaje
Tramwaje
Ranga
Ranga
Kryterium
Kryterium
oceny jako
oceny jako
ś
ś
ci
ci
funkcjonowania komunikacji miejskiej
funkcjonowania komunikacji miejskiej
10
10
Informacja dla pasa
Informacja dla pasa
ż
ż
era
era
9
9
Niezmienno
Niezmienno
ść
ść
czasu przejazdu
czasu przejazdu
8
8
Komfort podr
Komfort podr
ó
ó
ż
ż
y
y
7
7
Bezprzesiadkowo
Bezprzesiadkowo
ść
ść
6
6
Koszt przejazdu
Koszt przejazdu
5
5
Bezpiecze
Bezpiecze
ń
ń
stwo osobiste pasa
stwo osobiste pasa
ż
ż
er
er
ó
ó
w
w
4
4
Regularno
Regularno
ść
ść
3
3
Czas podr
Czas podr
ó
ó
ż
ż
y
y
2
2
Cz
Cz
ę
ę
stotliwo
stotliwo
ść
ść
1
1
Punktualno
Punktualno
ść
ść