

1
1. Układy i procesy termodynamiczne
1.1. Wstęp
Termodynamika zajmuje się badaniem makroskopowych własności układu. Jest
(nauką) teorią fenomenologiczną, opartą na doświadczeniu i dedukcji. Można ją określić
najogólniej jako naukę o metodach badania najbardziej ogólnych makroskopowych własności
ciał materialnych, które ujawniają się w procesach przekształcania energii, z jednego rodzaju
na inny. Podstawą termodynamiki jest najbardziej ogólna zasada zachowania energii,
wyrażająca pełny bilans różnych rodzajów energii. Termodynamika jest w istocie rzeczy
teorią stanów równowagi i właściwiej byłoby nazywać ją termostatyką.
Każdy układ termodynamiczny określa się przez podanie jego podstawowych
charakterystyk fizyko-chemicznych i ograniczeń wydzielających ten układ z otoczenia. Stąd
układ jest charakteryzowany przez parametry zewnętrzne i wewnętrzne. Parametrami
zewnętrznymi są te, które możemy zadawać poprzez działanie ciał zewnętrznych na układ,
np. pole elektryczne, magnetyczne itp. Parametry wewnętrzne są natomiast określane przez
stan układu.
Inny
podział parametrów to: intensywne i ekstensywne. Parametry intensywne to te,
które nie zależą od liczby cząstek układu i charakteryzują stan ogólny cieplnego ruchu cząstek
w układzie, np. ciśnienie p, temperatura T, potencjał chemiczny
µ itp. Parametry ekstensywne
(addytywne), przy tych samych parametrach intensywnych zależą od masy układu lub liczby
cząstek. Same układy termodynamiczne dzielimy na:
1. Układy izolowane adiabatycznie. Są to układy oddzielone od otoczenia ściankami adiabatycznymi,
które nie przewodzą ciepła. Dla tych układów przy stałych parametrach zewnętrznych energia układu
nie może się zmieniać.
2. Układy izolowane diatermicznie. Wyodrębnione są z otoczenia ściankami diatermicznymi. Energia
układu może się zmieniać przez proste oddziaływanie układu z otoczeniem wskutek zderzeń cząstek
układu i otoczenia.
3. Układy otwarte. Są to układy wymieniające cząstki z otoczeniem.
1.2. Zasada zachowania energii w termodynamice.
Weźmy pod uwagę pewien układ wydzielony z otoczenia zwanego dalej termostatem.
(patrz rysunek).
2
Układ
Termostat
Doświadczenie uczy nas, że te dwie części świata oddziaływują ze sobą na wiele
bardzo różnych sposobów. Skutkiem tego oddziaływania jest zmiana energii wewnętrznej
układu.
Najogólniej, konkretny rodzaj oddziaływania układu i
termostatu możemy
scharakteryzować przy pomocy zmiany energii wewnętrznej rozpatrywanego układu. Jeżeli
układ oddziaływuje „na sposób” k-ty, to z tym wiąże się infinitezymalnie mała zmiana energii
dU
k
.
Jeżeli układ oddziaływuje na n różnych sposobów to zmiana energii wewnętrznej
całego układu, jako wielkości ekstensywnej, może być zapisana jako suma po tych różnych
oddziaływaniach.
.
dU
dU
n
k
k
∑
=
Powstaje pytanie:, Jakie rodzaje oddziaływań między układem i termostatem mają
miejsce, oraz ile jest takich oddziaływań?
Odpowiedzi na te pytania uzyskamy posługując się metodą fenomenologiczną
termodynamiki. Podkreślmy, że przyczyną jakiegokolwiek procesu termodynamicznego jest
oddziaływanie z otoczeniem. Procesem termodynamicznym będziemy nazywać każdą zmianę
stanu układu, który jest określony przez odpowiednie parametry termodynamiczne.
Aby
odpowiedzieć na postawione wyżej pytania zwróćmy uwagę na fakt, że jeżeli
jakiś proces termodynamiczny zachodzi to musi istnieć pewna wielkość fizyczna (parametr
termodynamiczny), mierzona bezpośrednio lub pośrednio i ta wielkość musi się zmieniać
tylko wtedy, gdy dany proces zachodzi. w pozostałym przypadku ta wielkość musi być
zachowana. z danym procesem termodynamicznym k możemy więc związać pewną wielkość
fizyczną zwaną dalej współrzędną uogólnioną lub zmienną niezależną, którą oznaczać
będziemy przez x.
Jeżeli zatem k-ty rodzaj oddziaływania między układem i termostatem ma miejsce, to
z nim związany proces (również oznaczony abstrakcyjnie przez k) zachodzi tylko wtedy, gdy
w czasie obserwacji układu istnieje zmiana współrzędnej uogólnionej, to jest zmiana
wielkości dx
k
≠ 0 i z nim związana zmiana energii wewnętrznej dU
k
≠ 0
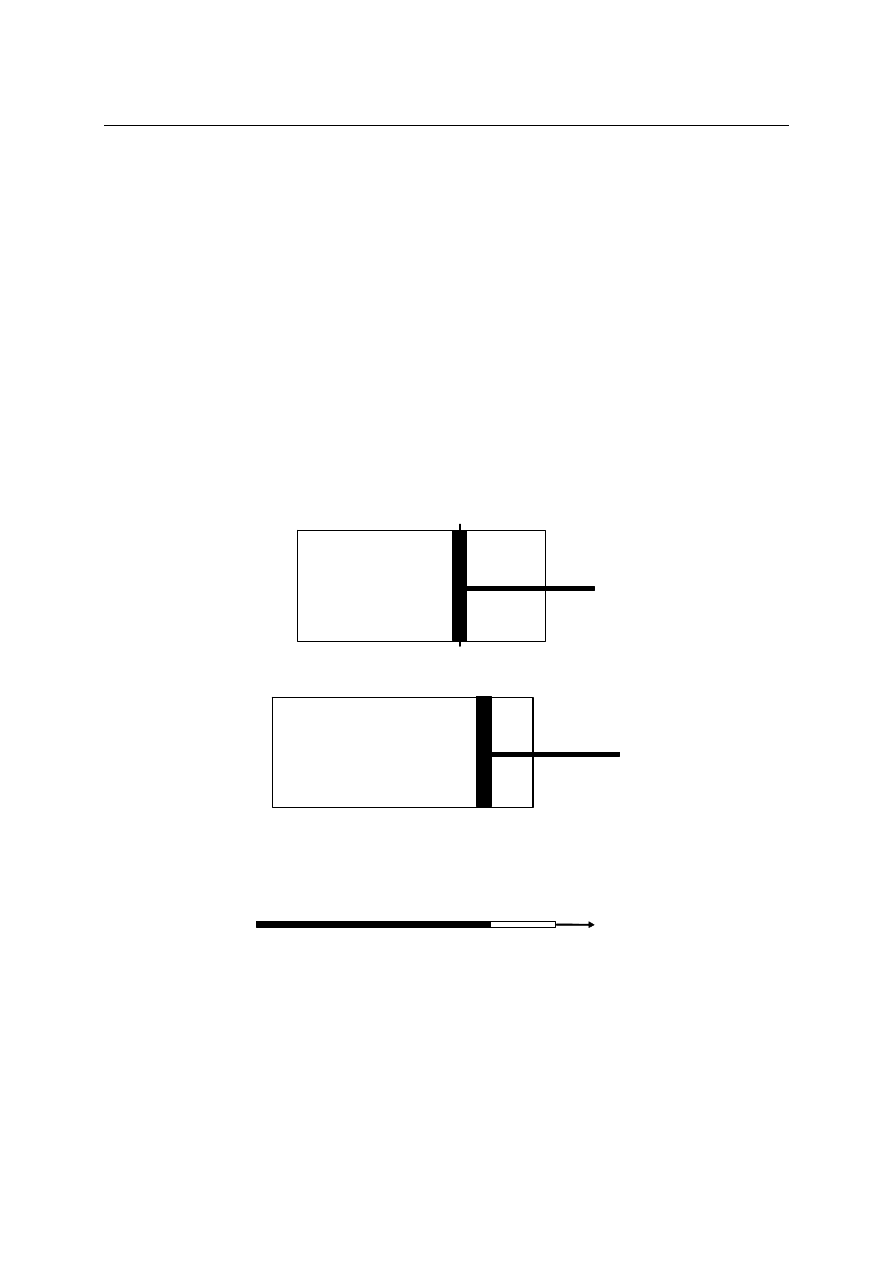
3
W innej, przeciwnej sytuacji, tj. gdy nie zachodzi dany proces (brak k-tego rodzaju
oddziaływania), musi być: dx
k
= 0 i dU
k
= 0.
Jeżeli zdefiniujemy pracę uogólnioną związaną z
danym k-tym procesem
termodynamicznym przez dU
k
, to będzie ona równa:
dU
k
= P
k
dx
k
,
gdzie zmienną zależną P
k
sprzężoną ze zmienną niezależną x
k
nazywać będziemy potencjałem
termodynamicznym k-tego procesu.
1.3. Przykłady oddziaływań układu z termostatem.
1. Deformacja mechaniczna.
Dla tego rodzaju oddziaływania istnieje taka wielkość (objętość), która się nie
zmienia., gdy nie ma deformacji układu. Dla gazu zamkniętego pod tłokiem
unieruchomionym, jak na rysunku:
U k ła d g a z u p o d
t ło k ie m
z a m o c o w a n ym
V = c o n st
dV = 0, V = const i dU
k
= P
k
dx
k
= -pdV = 0.
U k ła d g a z u p o d
t ło k ie m
r u c h o m y m
d V
≠ 0
dV
≠0, dU
k
= P
k
dx
k
= dU
V
≠ 0 (V jest współrzędną uogólnioną)
2.
Odkształcenie długości.
dl
dl
l
F
l
W tym przypadku oddziaływanie ma miejsce, gdy zmienia się długość, tzn. gdy dl
≠ 0.
Współrzędną uogólnioną jest zatem długość l. Potencjałem termodynamicznym w tym
przypadku jest siła F
l
prostopadła do przekroju pręta. Mamy bowiem wyrażenie na pracę
odkształcenia dW = dU = F
l
dl. Siła F
l
pełni zatem rolę potencjału termodynamicznego P
l
.
4
Gdy dl
≠ 0, to dU = F
l
dl ; l jest współrzędną uogólnioną dla odkształcenia długości, a F
l
to
siła prostopadła do przekroju. Siła ta jest w tym przypadku potencjałem termodynamicznym.
3.
Oddziaływanie elektryczne.
Gdy mamy dwa przewodniki o różnych potencjałach elektrycznych, jak to pokazano
na rysunku niżej, wówczas przez cienki drut łączący te przewodniki będzie płynął ładunek dq.
ϕ
1
ϕ
2
dq
Ładunek q możemy przyjąć za współrzędną uogólnioną tego oddziaływania. Zatem gdy
mamy do czynienia z oddziaływaniem tego typu, to:
dq
≠ 0 i dU = ϕ dq.
Ładunek przepływający jest współrzędną uogólnioną, a
potencjał elektryczny jest
potencjałem termodynamicznym dla tego procesu.
4.Magnesowanie
magnetyka.
J
H
M
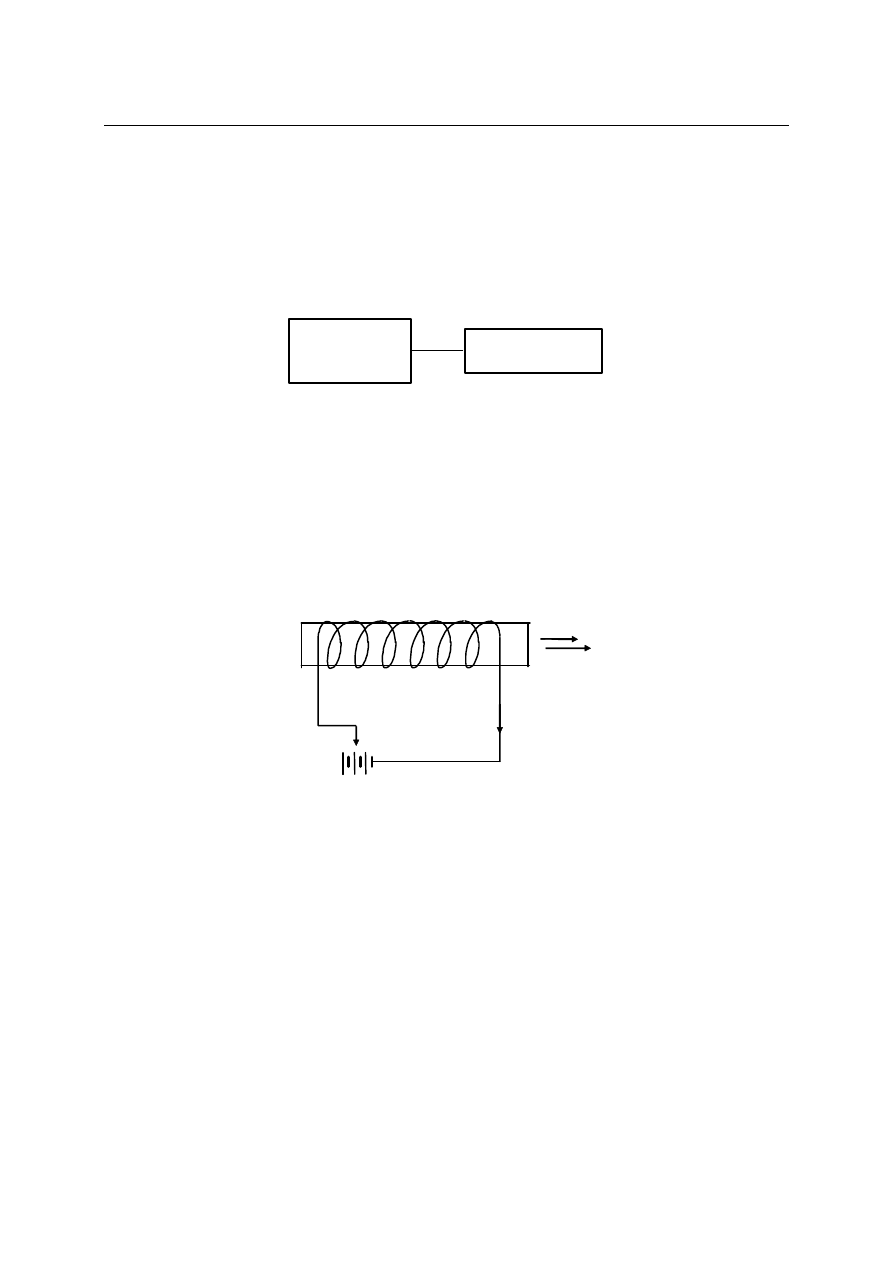
Proces termodynamiczny związany z
oddziaływaniem pola magnetycznego H
wytworzonego przez prąd elektryczny płynący w
solenoidzie sprowadza się do
magnesowania się rdzenia solenoidu. Jeżeli nie ma procesu magnesowania się rdzenia, to
infinitezymalnie mała zmiana jego namagnesowania dM = 0 i dU
M
=0. Gdy proces
magnesowania występuje, to odpowiednia zmiana energii wewnętrznej rdzenia związana
z magnesowaniem jest równa:
HdM
dU
0
M
µ
=
,
µ
0
H oznacza tutaj pełne pole magnetyczne zewnętrzne (indukcję magnetyczną
B
0
)
w solenoidzie bez rdzenia. Pole to pełni zatem rolę potencjału termodynamicznego,
a namagnesowanie M jest współrzędną uogólnioną dla tego rodzaju oddziaływania.
5.
Oddziaływanie cieplne. w tym przypadku, jednym z ważniejszych z punktu
widzenia termodynamiki, zagadnienie jest bardziej skomplikowane. w
doświadczeniu

5
bowiem nie obserwuje się wielkości, którą można by związać z wymianą ciepła. Nie jest nią
temperatura, bo nie spełnia wyżej sformułowanego kryterium, tj. dT
≠ 0, gdy nie ma
transportu ciepła (proces adiabatyczny). Okazuje się jednak, że z przepływem ciepła związana
jest entropia, wielkość fizyczna mierzona pośrednio. Mamy zatem: dS
≠ 0, gdy układ jest
w kontakcie cieplnym. Wtedy zmiana energii wewnętrznej związanej z oddziaływaniem
cieplnym
. Temperatura T w
tym procesie jest więc potencjałem
termodynamicznym, a entropia S jest zmienną niezależną.
TdS
dU
=
Podsumowując, tę opisową (fenomenologiczną) metodę znajdowania współrzędnych
uogólnionych i
potencjałów termodynamicznych dla konkretnych procesów
termodynamicznych możemy zapisać zasadę zachowania energii dla rozważanego układu
termodynamicznego w postaci:
,
dx
P
dx
P
dV
p
dS
T
dU
k
n
k
k
k
2
n
k
k
⋅
=
⋅
+
⋅
−
⋅
=
∑
∑
−
gdzie:
pdV
dx
P
i
TdS
dx
P
2
2
1
1
−
=
=
.
Jeżeli (według ostatniego wzoru) w
układzie zachodzi n różnych procesów
termodynamicznych, tj. zmienia się n zmiennych niezależnych, to mówimy, że układ ma n
stopni swobody termodynamicznej. Z każdym stopniem swobody termodynamicznej
związany jest konkretny rodzaj oddziaływania układu z otoczeniem (termostatem).
Z procesem (oddziaływaniem) wiąże się bezpośrednio pojęcie izolacji. Rozważmy
układ oddzielony pewną powierzchnią od reszty świata. Powierzchnia ta będzie tym
miejscem, w którym prowadzimy pomiary odpowiednich wielkości fizycznych związanych
z wymianą różnych rodzajów energii między układem i otoczeniem. Jeżeli stwierdzimy, że
dV = 0 (tłok nieruchomy) to powiemy, że układ jest izolowany ze względu na oddziaływania
mechaniczne. Układ jest izolowany adiabatycznie, gdy dS = 0 itd.
Układ jest całkowicie izolowany, gdy wszystkie dx
k
(k = 1, 2,..., n) są równe zeru.
w tym układzie nie zachodzi żaden proces termodynamiczny. Ponieważ z każdą zmienną
niezależną układu jest związany odpowiedni potencjał termodynamiczny, to na problem
izolacji możemy popatrzeć trochę inaczej. Korzystając z tego, że jeżeli proces zachodzi, to
potencjał termodynamiczny w rzeczywistości przedstawia różnicę potencjałów termostatu P
k
t
i układu P
k
u
k
u
k
t
k
P
P
P
=
−
.
P
k
jest przyczyną dynamiczną procesu, a dx
k
jest skutkiem tej przyczyny (oddziaływania).

6
Warunek izolacji układu termodynamicznego ze względu na dany proces
termodynamiczny k, może być zapisany przy pomocy potencjałów
i
. Układ jest
izolowany, jeżeli potencjały termodynamiczne układu są odpowiednio równe potencjałom
termostatu:
t
k
P
u
k
P
u
k
t
k
P
P
=
, k = 1, 2,...., n.
Jeżeli, jako przykład weźmiemy gaz pod zamocowanym tłokiem, to warunek ten
oznacza, że ciśnienie zewnętrzne jest równe ciśnieniu gazu pod tłokiem, p
u
= p
t
i to oznacza
dalej, że układ gazu jest układem izolowanym ze względu na deformację objętości.
Temperatura otoczenia równa temperaturze układu, zapewnia izolację układu na
wymianę ciepła, tzn. zapewnia stan równowagi, w którym potencjał termodynamiczny T jest
stały.
Ogólnie
możemy powiedzieć, że warunek równowagi termodynamicznej układu jest
realizowany przez stałość potencjału zewnętrznego i wewnętrznego dla danej zmiennej
termodynamicznej:
u
k
t
k
P
P
=
.
Z
kolei,
jeżeli w układzie zachodzi dany proces termodynamiczny, to musi istnieć
różnica potencjałów na granicy układ-termostat:
0
P
P
u
k
t
k
≠
−
.
Ta różnica potencjałów determinuje również kierunek zachodzenia procesu wymiany energii
z układu do termostatu i odwrotnie.
Różnicę potencjałów na granicy układu i termostatu uważamy za dodatnią:
0
P
P
u
k
t
k
>
−
,
jeżeli powoduje ona dodatnią zmianę zmiennej niezależnej, tj. zmianę parametru stanu x
o wielkość:
0
dx
k
>
.
W tym przypadku układ otrzymuje energię od otoczenia. To z kolei oznacza, że energia
wewnętrzna układu rośnie o wielkość dU
k
>0, i że potencjał termostatu jest większy od
potencjału układu
.
u
k
t
k
P
P
>
Analogicznie
różnicę potencjałów uważamy za ujemną:
0
P
P
u
k
t
k
<
−
,
gdy następuje zmniejszanie się odpowiedniej zmiennej niezależnej:
0
dx
k
<
.

7
W takim przypadku układ traci energię, co oznacza, że energia wewnętrzna U i potencjały
termodynamiczne P
k
t
, P
k
u
spełniają relacje:
0
dU
k
<
i
.
u
k
t
k
P
P
<
Zwróćmy uwagę, że potencjałem termodynamicznym procesu wymiany ciepła jest
temperatura, a zmienną niezależną entropia. Wielkości te spełniają sformułowane wyżej
prawidło znaków. Jeżeli bowiem temperatura termostatu jest wyższa od temperatury układu,
to
0
Q
i
0
dS
,
0
T
T
u
t
>
δ
>
>
−
.
Ten ostatni warunek oznacza, że ciepło przepływa do układu. Powiadamy inaczej, że entropia
układu rośnie w takim procesie, w którym temperatura termostatu jest wyższa od temperatury
układu.
Jeżeli temperatura termostatu jest niższa od temperatury układu,
0
T
T
u
t
<
−
,
to
δQ < 0, a to oznacza, że ciepło wypływa z układu i entropia układu maleje.
1.4. Reakcje chemiczne
Podobną metodą można rozpatrywać reakcje chemiczne. Problem jest podobny do
wymiany ciepła. Zmienną niezależną jest masa. Proces reakcji zachodzi, gdy zmienia się
masa i-tego składnika, tj. gdy dm
i
≠ 0.
Wtedy dU
i
≠ 0. Rolę potencjału termodynamicznego pełni w tym przypadku potencjał
chemiczny i-tego składnika
µ
i
odniesiony do jednostki masy. Możemy zapisać dla takiego
procesu wyrażenie na infinitezymalną zmianę energii wewnętrznej:
i
i
i
dm
dU
µ
=
.
Podczas, gdy w układzie reaguje n składników, to energia wewnętrzna zmienia się
o wielkość:
i
i
i
i
i
i
reakcji
dN
dm
dU
∑
∑
µ
=
µ
=
W ostatnim równaniu dN
i
oznacza liczbę atomów i-tego składnika, zaś
µ
i
jest potencjałem
chemicznym odniesionym do jednego atomu i-tego składnika.
Możemy zatem zapisać ogólną zasadę zachowania energii w postaci:
k
n
k
k
k
n
2
k
k
dx
P
dx
P
dV
p
dS
T
dU
⋅
=
⋅
+
⋅
−
⋅
=
∑
∑
=
dla układu bez reakcji chemicznych lub dla układu z reakcjami chemicznymi w postaci:

8
.
dx
P
dN
dx
P
dN
dx
P
dV
p
dS
T
dU
j
N
j
j
i
i
i
k
n
k
k
i
i
i
k
2
n
k
k
⋅
=
µ
+
⋅
=
µ
+
⋅
+
⋅
−
⋅
=
∑
∑
∑
∑
∑
−
N w granicy ostatniej sumy oznacza teraz pełną liczbę stopni swobody łącznie ze stopniami
swobody związanymi z reakcją chemiczną.
1.5. Termodynamiczny stan układu i równanie stanu
Rozważmy układ o n stopniach swobody bez reakcji chemicznych. Niech z każdym
stopniem swobody x
k
będzie związany potencjał termodynamiczny P
k
. Mamy:
x
1
, x
2
,..., x
n
,
P
1
, P
2
,..., P
n
.
Zbiór zmiennych niezależnych i
zmiennych zależnych nazywa się parametrami
termodynamicznymi. Mówimy, że stan układu jest opisany przez 2n parametrów
termodynamicznych tego układu. Zadając n zmiennych niezależnych (parametrów
termodynamicznych), możemy określić pozostałe n parametrów zależnych. To wystarcza do
pełnego, z termodynamicznego punktu widzenia, określenia dowolnej makroskopowej
wielkości fizycznej charakteryzującej nasz układ. Oznacza to, że dowolna makroskopowa
wielkość, w szczególności potencjały termodynamiczne, mogą być wyrażone przez parametry
niezależne. i tak dowolny z potencjałów termodynamicznych P
k
jest jednoznaczną funkcją
parametrów niezależnych:
P
k
= P
k
(x
1
, x
2
,..., x
n
).
Mamy zatem układ równań:
P
k
= P
k
(x
1
, x
2
,..., x
n
); k = 1, 2,....., n.,
który zawiera 2n parametrów, n potencjałów P
k
i n zmiennych niezależnych x
k
.
Eliminując z tych równań n-1 parametrów można sprowadzić ten układ równań do
jednego równania, które będzie wiązało n+1 pozostałych parametrów, tj. do równania postaci:
F(x
1
, P
1
, Z
2
, Z
3
,.... Z
n
) = 0,
gdzie Z
k
oznacza jeden z parametrów termodynamicznych x
k
lub P
k
w zależności od tego,
który z nich został wyeliminowany w procedurze redukcji układu równań do jednego
równania.
Takie równanie nazywa się równaniem stanu układu. Równanie stanu jest więc
funkcjonalną zależnością między n+1 parametrami termodynamicznymi, przy czym n
oznacza liczbę stopni swobody danego układu.

9
Termodynamika nie wyprowadza równań stanu, bierze je w gotowej postaci dla
danego układu, bazując na doświadczeniu lub fizyce statystycznej.
Jako przykład rozważmy układ gazu doskonałego o dwóch stopniach swobody:
x
1
=S, x
2
= V,
którym odpowiadają odpowiednio potencjały termodynamiczne:
P
1
= T, P
2
= -p.
W tym przypadku, tj. w procesie oddziaływania układu z otoczeniem przez wymianę ciepła
i odkształcenie objętości, z doświadczenia lub fizyki statystycznej mamy następujące związki
na potencjały termodynamiczne:
T = T(S, V),
p = p(S, V).
Eliminując z tych równań entropię jako wielkość fizyczną mierzoną pośrednio, zapisujemy
w tym celu pierwsze równanie w postaci:
S = S(T, V)
i podstawiając tę postać do drugiego z równań, możemy napisać:
p = p(S(T,V),V) = p(T, V).
Równanie to jest równaniem stanu dla gazu doskonałego, znanym jako równanie Clapeyrona.
w jawnej postaci znane ono jest z elementarnego kursu fizyki doświadczalnej:
p
m RT
V
=
⋅
µ
.
Równanie to wyraża związek między trzema parametrami termodynamicznymi, co jest
zgodne z ogólną definicją (2n-1 = 3) dla układu o dwu stopniach swobody.
Przyjmując gotową postać równań stanu dla danego układu, termodynamika podaje
kryterium stabilności stanu układu, niezależnie jaka jest postać tego równania.
Termodynamika twierdzi na podstawie doświadczenia, że w przyrodzie zachodzą tylko takie
procesy, które spełniają kryterium stabilności:
∂
∂
P
x
k
k
≥ 0
.
2. Pierwsza i druga zasada termodynamiki
Wiemy
już, że zmiana energii wewnętrznej układu termodynamicznego o n stopniach
swobody może być zapisana przy pomocy sumy:

10
,
dx
P
dU
n
,
1
k
k
k
∑
=
⋅
=
tj. sumy iloczynów potencjału termodynamicznego k-tego stopnia swobody i różniczki
zupełnej zmiennej niezależnej albo współrzędnej uogólnionej związanej z danym stopniem
termodynamicznej swobody. Każdy z tych składników sumy został przyporządkowany
danemu oddziaływaniu z układem. z mechaniki wiadomo, że praca związana z uogólnionym
przesunięciem dx
k
jest równa:
dA
X dx
k
k
k
=
,
przy czym X
k
pełni rolę siły uogólnionej, tj.
X
H
x
k
k
= −
∂
∂
,
gdzie H oznacza energię całkowitą układu.
Ponieważ siła uogólniona dla oddziaływania potencjalnego jest równa ujemnemu
potencjałowi, to powyższe równanie możemy zapisać inaczej. Niech
δQ będzie ilością ciepła
wymienioną podczas infinitezymalnie małego procesu oddziaływania, a
pozostałe
oddziaływania będą związane z zachowawczymi polami zewnętrznymi działającymi na układ.
Wtedy zasadę zachowania energii, nazywaną pierwszą zasadą termodynamiki, można
zapisać w postaci:
,
A
Q
dU
δ
−
δ
=
przy czym
∑
∑
∑
=
=
=
=
δ
=
−
=
δ
n
2
k
k
k
n
2
k
k
n
2
k
k
k
dx
X
A
dx
P
A
.
Wtedy,
∑
=
−
δ
=
n
2
k
k
k
dx
X
Q
dU
lub inaczej:
δ
δ
Q dU
A
=
+
.
W
powyższych równaniach
δA jest pełną pracą wykonaną przez układ nad ciałami
termostatu łącznie z pracą objętościową. Symbolu
δx (x = a lub Q itp.) używamy do
oznaczenia faktu, że x nie jest funkcją stanu, ale zależy od samego procesu. Ostatnie równanie
przedstawia treść pierwszej zasadą termodynamiki w zwykłej postaci. Zasada ta mówi, że
dostarczana ilość ciepła do układu idzie na zmianę energii wewnętrznej układu i pracę
wykonaną przez układ przeciwko siłom zewnętrznym.

11
Często zapisując tę zasadę, z ogólnego wyrażenia na pracę
δA, wydziela się jeszcze
pracę objętościową, wtedy zasada ta przyjmuje postać:
δ
δ
Q dU pdV
A
=
+
+
,
gdzie
δA oznacza teraz pełną pracę nieobjętościową, która wyraża się ogólnym wzorem:
∑
δ
n
3
=
k
k
k
dx
X
=
A
2.1. Procesy równowagowe i nierównowagowe.
Wiemy
już, że proces termodynamiczny w układzie zachodzi, jeżeli dx
k
≠ 0. Wtedy,
na granicy termostat-układ, istnieje różnica potencjałów:
P
P
P
k
t
k
u
k
−
= ±∆
.
Intensywność oddziaływania układu i termostatu oczywiście zależy od wielkości tej różnicy
potencjałów.
Mamy dwa przypadki skrajne, które musimy rozważać oddzielnie:
1
0
P
P
P
1
2 P
P
P
P
1
k
t
k
u
k
k
k
u
0
k
t
k
u
k
k
k
u
−
= ±
<<
−
= ±
≥
∆ε
∆
∆
∆
ε
P
Przypadek 1
0
, to procesy równowagowe, kiedy oddziaływanie układu i termostatu jest
niewielkie. Przypadek 2
0
, to procesy nierównowagowe, gdy oddziaływanie układu
i termostatu jest silne.
Rozważmy powyższe zagadnienie na kilku konkretnych przykładach.
Przykład 1
. Rozciągania sprężyny:
X
u
= – kx
X
t
= mg
Proces
równowagowy:
P
P
X
X
k
u
k
t
k
u
k
t
=
=
, lub
.
Każda mała zmiana ciężaru mg powoduje niewielką zmianę długości sprężyny. Proces jest
więc równowagowy. Może w każdej chwili być odwrócony. Zmianie siły uogólnionej X
k
odpowiada zmiana współrzędnej uogólnionej dx
k
.
Proces nierównowagowy:

12
∆
∆
P
P
mg
mg
k
k
u
=
≥
(
)
1
.
Gdy
ciężar mg położony na szalkę będzie duży, to oprócz rozciągania obserwujemy
ruch przyspieszony elementów sprężyny, tzn. następuje zmiana pędu sprężyny. z tą zmianą
pędu (nową współrzędną uogólnioną p = mv) d(mv) jest związany potencjał
termodynamiczny -v (minus prędkość), albo równoważna mu siła uogólniona X = v. Iloczyn
tej siły uogólnionej i infinitezymalnie małej zmiany współrzędnej uogólnionej p określa nową
nieobjętościową pracę, związaną z pojawiającym się nowym stopniem swobody. Praca ta jest
równa:
)
mv
(
vd
vdp
dA
p
=
=
.
Proces ten jest procesem nieodwracalnym, układ (sprężyna) w różnych momentach czasu jest
w innym stanie. Oznacza to, że proces ten jest zależny od czasu i układ nie jest w stanie
równowagi z termostatem. Procesu nie da się odwrócić, stąd nazwa procesu nieodwracalnego
lub nierównowagowego.
W procesach nierównowagowych zawsze pojawia się co najmniej jeden nowy proces
termodynamiczny wywołany procesem pierwotnym. w rozważanym przypadku, rozciąganie
sprężyny dużymi siłami (proces pierwotny) powoduje pojawienie się nowego procesu
termodynamicznego, w wyniku którego obserwujemy ruch przyspieszony sprężyny (proces
wtórny).
Przykład 2
. Układ dwóch przewodników naładowanych.
ϕ
1
ϕ
2
dq
Proces
równowagowy:
.
1
,
2
1
<<
ϕ
ϕ
∆
ϕ
≈
ϕ
W tym przypadku popłynie prąd stacjonarny między układem i termostatem. Zmiana różnicy
potencjałów d
ϕ z dodatniej na ujemną powoduje zmianę kierunku prądu na przeciwny. Proces
jest więc odwracalny.
Proces nierównowagowy:
∆ϕ
ϕ
>> 1
.
W przypadku tym, tj. dla dużej różnicy potencjałów, między układem i termostatem następuje
zmiana natężenia prądu, a to powoduje powstanie zmiennego pola elektromagnetycznego.

13
z kolei zmienne pole elektromagnetyczne powoduje ruch przyspieszony płynącego w drucie
ładunku, co powoduje promieniowanie energii w postaci fali elektromagnetycznej. Mamy
znowu nowy efekt, nowy proces termodynamiczny: wymiany energii przez promieniowanie.
Jest to zatem nowy stopień swobody dla rozważanego układu. Układ nie jest w stanie
równowagi z termostatem.
Nasuwa
się zatem następujące pytanie: Czy w każdym procesie oddziaływania
nierównowagowego pojawiają się nowe stopnie swobody (nowe, nieoczekiwane)?
Okazuje
się, że oddziaływanie cieplne nie prowadzi do nowych procesów. Rozważmy
to zagadnienie dokładnie. Weźmy pod uwagę układ składający się z dwóch podukładów
o temperaturach odpowiednio równych T
1
i T
2
jak na rysunku:
T
1
1111111
T
2
2
T
1
1
Niech T
1
> T
2
. Zatem niech różnica temperatur T
1
-T
2
=
∆Τ. Przy elementarnym procesie
wymiany ciepła ciało 1 oddaje, a ciało 2 pobiera ciepło
δQ. w rezultacie zmienia się
współrzędna niezależna-entropia S. Entropia ciała 1 zmaleje o dS
1
a entropia ciała 2 wzrośnie
o dS
2.
Ilość ciepła straconą i uzyskaną można wyrazić przez parametry ciała 1 i 2:
Ciało 1:
−δQ
1
= T
1
dS
1
lub inaczej
δQ = −TdS.
Ciało 2:
δQ
2
= T
2
dS
2
.
Ponieważ jednak
δQ
1
=
δQ
2
, to stąd T
1
dS
1
=
−T
2
dS
2
lub inaczej:
2
2
1
1
dS
T
|
dS
|
T
=
.
Mamy zatem związek między wartościami entropii przekazanej i pobranej:
dS
T
T
dS
2
1
2
1
=
.
Ponieważ jednak zgodnie z założeniem T
1
> T
2
, to stąd wynika wniosek:
1
2
dS
dS
>
.
Całkowita zmiana entropii układu 1 i 2 jako całości jest więc równa:
0
dS
dS
dS
2
1
>
+
=
W procesach nierównowagowych entropia układu izolowanego zawsze rośnie:

14
0
dS
>
.
W procesie równowagowym zaś mamy:
0.
=
dS
czyli
,
dS
dS
T
T
dS
1
1
1
1
2
=
=
Podsumowując, formułujemy drugą zasadę termodynamiki: w
dowolnym procesie
termodynamicznym entropia układu pozostaje stała (proces równowagowy) lub rośnie (proces
nierównowagowy), co zapisujemy w postaci:
0
dS
≥
.
2.2. Procesy quasi statyczne i niestateczne
Zmiana energii wewnętrznej układu o n stopniach swobody może być zawsze
wyrażona związkiem:
,
dQ
dU
n
1
k
k
∑
=
=
gdzie đQ
k
jest miarą oddziaływania układu z
otoczeniem w
k-tym procesie
termodynamicznym i może być zapisane jako:
.
dx
P
=
dQ
k
k
k
k
∑
Rolę potencjałów termodynamicznych P
k
pełnią tutaj potencjały otoczenia
P
k
= P .
k
t
Zatem, w jawnej postaci, pierwsze równanie winno mieć postać:
dU =
P dx .
k
t
k
k
∑
Jeżeli oddziaływanie otoczenia na układ jest równowagowe, tzn.
P
P
k
t
k
u
k
=
± ε
i
,
ε
k
k
u
P
<<
wtedy zmiana energii wewnętrznej układu musi być wyrażona przez potencjały układu
:
P
k
u
dU
P
dx
P dx
dx
k
t
k
k
k
k
t
k
k
k
k
k
=
±
=
±
∑
∑
∑
(
)
ε
ε
.
Drugi
składnik jest bardzo mały w porównaniu z pierwszym ze względu na to, że
ε
κ
dx
k
z definicji jest bardzo małe i może być pominięte. Stąd widać, że w procesach
równowagowych potencjały zewnętrzne można wymieniać, tzn. zastępować potencjałami
układu. Nie musimy zatem ich rozróżniać:
. Dla tych procesów mamy więc:
P
P
P
k
u
k
t
k
=
=
dU
P dx
k
k
n
k
=
=
∑
1
.
Porównanie
potencjałów zewnętrznego i wewnętrznego, ściślej występowanie małej
ich różnicy powoduje tylko tyle, że dany k-ty proces zachodzi, ale nie wpływa na wielkość

15
k
zmiany energii wewnętrznej. Znak tej różnicy charakteryzuje kierunek procesu
termodynamicznego. Niewielka zmiana potencjału może spowodować zmianę kierunku
zachodzącego procesu. Ponieważ różnica potencjałów jest niewielka, proces jest bardzo
powolny tak, że w dowolnej chwili możemy uważać, że układ jest w stanie równowagi.
Dowolny tak powstały proces można traktować jako kolejne stany równowagowe.
Procesy tego typu nazywa się quasi statycznymi. Procesy quasi statyczne posiadają
własność odwracalności. Rzeczywiście wielkość
ε
k
nie wpływa na ilościowe zmiany energii
wewnętrznej, stąd kierunek procesu nie wpływa na wielkość zmian energii wewnętrznej.
z własności quasi-statyczności procesów równowagowych wynika, że gdy na układ nałożymy
izolację, to proces natychmiast przestaje zachodzić i układ znajduje się w stanie równowagi.
Inna sytuacja jest w przypadku, gdy różnica potencjałów na granicy układ i termostat
jest duża dla danego stopnia swobody. Wtedy ilościowo, wymieniona energia
δQ musi być
zapisana równaniem:
dQ
P dx
P dx
P
k
k
u
k
k
k
k
u
=
+
≥
∆
∆
, przy czym P
.
Zauważmy, że drugi składnik jest zawsze dodatni, chociaż sama różnica
∆P
k
może być
dodatnia lub ujemna. Rzeczywiście:
gdy
∆P
k
> 0, to dx
k
> 0 i
∆P
k
dx
k
> 0,
gdy
∆P
k
< 0, to dx
k
< 0 i
∆P
k
dx
k
> 0.
Podstawiając tak określone ilości wymienionej energii między układem i otoczeniem
do wyrażenia na zmianę energii wewnętrznej układu, mamy:
dU
P
P dx
P dx
P dx
k
u
k
k
k
k
u
k
k
k
k
k
=
+
=
+
∑
∑
∑
(
)
∆
∆
.
Widzimy,
że zmiana energii wewnętrznej jest zawsze większa niż wyliczona przy
pomocy potencjałów termodynamicznych układu:
k
k
u
k
dx
P
dU
∑
>
.
Druga suma w przedostatnim wyrażeniu, tj. wielkość:
∆P dx
k
k
k
∑
,
może być bardzo duża w porównaniu z sumą
P dx
k
k
k
∑
. Na podstawie jej wartości można
sądzić o stopniu nierównowagi zachodzących procesów. Ta dodatkowa część energii,
związana jest z dodatkowymi procesami, które pojawiają się wskutek nierównowagi
oddziaływania między układem i termostatem.

16
W takich nierównowagowych procesach możemy jedynie stwierdzić, że wśród
składników nierównowagowej zmiany energii, znajdzie się zawsze składnik odpowiadający
procesowi cieplnemu. Proces cieplny ma zawsze miejsce w procesach nierównowagowych.
Zauważmy jeszcze, że w układzie, gdy na granicy istnieje duży skok k-tego potencjału P
k
, to
istnieje pewien rozkład tego potencjału w układzie. Tak więc układ nie może już być
charakteryzowany jednym potencjałem dla danego procesu. Mówimy, że układ jest w tym
przypadku układem niejednorodnym. Procesy tego typu nie są już niezależne od czasu.
Nazywamy je niestatycznymi albo dynamicznymi.
Procesy dynamiczne charakteryzują się tym, że:
1
0
Nie występuje jednoznaczna relacja między liczbą zmiennych niezależnych i liczbą
procesów termodynamicznych. w układzie obserwuje się dodatkowe stopnie swobody,
w których zawsze występuje stopień swobody związany z oddziaływaniem cieplnym.
2
0
Ponieważ procesy zachodzą pod wpływem dużej różnicy potencjałów, to układ jest
niejednorodny ze względu na wielkości intensywne.
W przyrodzie nie występują procesy ściśle quasi statyczne. Przybliżenie to jest jednak
użyteczną idealizacją rzeczywistego procesu prawie równowagowego. Procesami
niestatycznymi, dynamicznymi zajmuje się termodynamika stanów nierównowagowych.
2.3. Energia wewnętrzna, ciepło i praca.
Rozważajmy dla uproszczenia układ termodynamiczny o dwu stopniach swobody
(S,V), tj. układ, który wymienia ciepło z otoczeniem i doznaje odkształcenia objętości. Pisząc
pierwszą zasadę termodynamiki w postaci:
dU =
δQ – δΑ, gdzie
δΑ = pdV
pokażemy, że przekazane ciepło
δQ i wykonana praca δΑ w elementarnym procesie
termodynamicznym nie są różniczkami zupełnymi, natomiast odpowiednia zmiana energii
wewnętrznej dU jest różniczką zupełną. To oznacza, że energia wewnętrzna jest funkcją
stanu, a ciepło i praca nie są funkcjami stanu, zależą bowiem od procesu w wyniku, którego
układ znalazł się w danym stanie.
Dowolną funkcję wielu zmiennych (parametrów termodynamicznych) używaną
w termodynamice do opisu stanu układu nazywa się funkcją stanu, jeżeli dla takiej funkcji
całka po dowolnej zamkniętej drodze całkowania jest równa zeru:
∫
= 0
)
x
,...
x
,
x
(
dF
n
2
1
.

17
Z matematyki wiemy, iż dla funkcji dwóch zmiennych F(x
1
, x
2
) warunek wymagany
na to, aby forma różniczkowa dF(x
1
, x
2
) = Mdx
1
+ Ndx
2
była różniczką zupełną, jest
następujący warunek:
.
x
N
x
M
2
1
x
1
x
2
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
Biorąc pod uwagę, że
δQ = dU + pdV
oraz fakt, że dla rozważanego układu (dwa stopnie swobody) energia wewnętrzna z definicji
jest funkcją entropii i objętości,
U = U(S, V),
możemy wyrażenie na ciepło
δQ zapisać w postaci:
.
dV
N
p
V
U
dS
M
S
U
pdV
dV
V
U
dS
S
U
pdV
dU
Q
S
V
S
V
4
43
4
42
1
3
2
1
⎥⎦
⎤
⎢⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
+
=
δ
Na pochodne cząstkowe funkcji M i N otrzymujemy zatem wyrażenia:
∂
∂
∂
∂ ∂
∂
∂
∂
∂ ∂
∂
∂
M
V
U
V S
N
S
U
S V
p
S
S
V
V
⎛
⎝⎜
⎞
⎠⎟ =
⎛
⎝⎜
⎞
⎠⎟ =
+
⎛
⎝⎜
⎞
⎠⎟
2
2
i
,
skąd widać, że:
∂
∂
∂
∂
M
V
N
S
S
V
⎛
⎝⎜
⎞
⎠⎟ ≠
⎛
⎝⎜
⎞
⎠⎟ .
Widzimy więc, że wyrażenie różniczkowe na ciepło elementarne pobrane lub oddane
w elementarnym procesie termodynamicznym nie jest różniczką zupełną, a zatem ciepło jako
wielkość termodynamiczna nie jest funkcją stanu i
zależy od rodzaju procesu
termodynamicznego jaki doprowadził układ do danego stanu.
Można dalej pokazać, że energia wewnętrzna jest funkcją stanu, co jest równoważne
ze stwierdzeniem, że wyrażenie różniczkowe na energię wewnętrzną spełnia wyżej podane
kryterium. To twierdzenie bezpośrednio wynika z postaci różniczki dla energii wewnętrznej:
dU =
∂
∂
∂
∂
U
S
dS
U
V
dV
V
S
⎛
⎝⎜
⎞
⎠⎟
+ ⎛
⎝⎜
⎞
⎠⎟
= M dS + N dV.
Odpowiednie pochodne cząstkowe M i N są równe:
∂
∂
∂
∂ ∂
∂
∂
∂
∂ ∂
M
V
U
V S
N
S
U
S V
S
V
⎛
⎝⎜
⎞
⎠⎟ =
⎛
⎝⎜
⎞
⎠⎟ =
2
2
i
,

18
zatem:
∂
∂
∂
∂
M
V
N
S
S
V
⎛
⎝⎜
⎞
⎠⎟ =
⎛
⎝⎜
⎞
⎠⎟ .
Energia wewnętrzna jest więc rzeczywiście funkcją stanu i nie zależy od procesu, w wyniku
którego układ znalazł się w danym stanie.
Z ostatnich dwóch stwierdzeń wynika natychmiast stwierdzenie, że praca podobnie jak
ciepło nie jest funkcją stanu i zależy od procesu lub jak mówimy inaczej od drogi, po której
układ zbliżał się do danego stanu. w przypadku pracy, mamy mianowicie:
δ
δ
A
Q dU
=
−
.
Ponieważ wyrażenie różniczkowe na ciepło nie jest różniczką zupełną, a odpowiednie
wyrażenie różniczkowe dla energii wewnętrznej jest różniczką zupełną, to stąd wynika, że
wyrażenia różniczkowe dla pracy nie jest różniczką zupełną.
Mamy zatem trzy podstawowe stwierdzenia, które na zakończenie zapiszemy
symbolicznie w postaci całkowej:
⎪
⎪
⎩
⎪⎪
⎨
⎧
≠
≠
=
∫
∫
∫
0
dA
0,
dQ
0,
dU
i w postaci różniczkowej:
⎪⎩
⎪
⎨
⎧
≠
δ
≠
δ
=
.
0
A
,
0
Q
,
0
dU
Niżej na rysunku przedstawiono schematycznie pracę elementarną przy zmianie
objętości układu o
wielkość dV (obszar zaczerniony) i
pracę całkowitą w
procesie
termodynamicznym przebiegającym po drodze zamkniętej: 1-a-2-b-1.
dV
V
p
dA = pdV
2
1
b
a
Praca ta nie jest równa zeru (obszar ograniczony łukami 1-a-2 i 1-b-2). Układ
współrzędnych, którego użyto tutaj, tj. układ p i V, nazywa się układem współrzędnych pracy,

19
bo pole pod dowolną krzywą, np. pod krzywą 1-b-2 jest pracą objętościową wykonaną
w procesie opisanym tą krzywą.
3. Funkcje charakterystyczne
3.1. Sprzężenie przez zmienne niezależne
Weźmy pod uwagę układ o n stopniach swobody. Pełna liczba parametrów
termodynamicznych tego układu wynosi wtedy 2n:
x
1
, x
2
,..., x
n
-zmienne niezależne,
P
1
, P
2
,..., P
n
-zmienne zależne (potencjały).
W
wyniku
oddziaływania układu z termostatem, energia wewnętrzna układu zmienia
się o różniczkę zupełną dU. Ponieważ z definicji energia wewnętrzna
U = U(x
1
, x
2
,..., x
n
),
to jej różniczka jest dana przez wyrażenie:
∑
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
=
k
k
inv
k
n
inv
n
1
inv
1
dx
x
U
dx
x
U
+
........
dx
x
U
dU
Indeks „inv” oznacza, że pozostałe parametry (
k
inv
≠
) w stosunku do tych po których
wykonuje się różniczkowanie są stałe. Dla dwóch stopni swobody, gdy np. inv = S, mamy
proces adiabatyczny, bo entropia jest stała, gdy zaś inv = T, mamy proces izotermiczny itd.
Z drugiej strony wiemy, że infinitezymalnie mała zmiana energii wewnętrznej układu,
jest zawsze dla procesów quasi statycznych dana przez równanie:
k
k
k
dx
P
dU
∑
=
.
Porównując te równania otrzymujemy związek:
.
dx
x
U
dx
P
k
k
inv
k
k
k
k
∑
∑
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
=
Ten
związek można jeszcze zapisać jak następuje:
.
0
dx
x
U
P
k
k
inv
k
k
=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
∑
Ponieważ współrzędne uogólnione x
k
są zmiennymi niezależnymi, to dla dowolnego
stopnia swobody, jeżeli dany proces zachodzi mamy: dx
k
≠ 0. Dlatego też aby ostatnie
równanie było spełnione, potencjały termodynamiczne dla danego stopnia swobody muszą
wiązać się ze zmiennymi niezależnymi w następujący sposób:

20
n.
.......,
2,
1,
=
k
x
U
P
inv
k
k
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
=
Otrzymaliśmy ważny rezultat: potencjał termodynamiczny P
k
, związany ze
współrzędną uogólnioną x
k
, jest równy pochodnej cząstkowej energii wewnętrznej układu po
tej współrzędnej, przy pozostałych zmiennych stałych.
Stałość pozostałych zmiennych niezależnych, tj. różnych od x
k
, oznacza pewne
warunki zewnętrzne przy jakich zachodzi k-ty proces. Te warunki, przy jakich zachodzi dany
proces, nazywa się sprzężeniami układu z otoczeniem.
W
rozważanym przypadku ustalonymi parametrami (inwariantami) są zmienne
niezależne, zatem mamy sprzężenia przez zmienne niezależne. w tym przypadku potencjały
można obliczać przez różniczkowanie energii wewnętrznej, gdy ta ostatnia dana jest jako
funkcja zmiennych niezależnych lub inaczej współrzędnych stanu. Samą funkcję nazywa się
funkcją charakterystyczną
(x
Ψ
1
, x
2
,..., x
n
). Charakteryzuje ona sprzężenie przez zmienne
niezależne.
Ψ
(x
1
, x
2
,..., x
n
) = U(x
1
, x
2
,..., x
n
).
Mamy zatem drugie niezależne określenie energii wewnętrznej.
Oprócz
sprzężenia układu z termostatem przez zmienne niezależne, mamy również
sprzężenie przez potencjały i sprzężenie mieszane. Każdemu z nich odpowiada pewna funkcja
charakterystyczna odpowiednio
Ψ
(P
1
, P
2
,...., P
n
)
i
Ψ(x
1
, x
2
,..., x
r
, P
r+1
, P
r+2
,..., P
n
).
3.2. Sprzężenie przez potencjały
Zgodnie
z
określeniem funkcji charakterystycznej, rozważajmy nową funkcję, tym
razem zależną tylko od potencjałów:
Ψ
=
Ψ
(P
1
,P
2
,..., P
n
). Bierzemy pod uwagę, podobnie jak
w przypadku energii wewnętrznej, układ o n stopniach swobody. Różniczka zupełna tej
funkcji charakterystycznej jest dana przez wyrażenie:
∑
⎟
⎠
⎞
⎜
⎝
⎛
∂
Ψ
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
Ψ
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
Ψ
∂
=
Ψ
k
k
inv
k
n
inv
n
1
inv
1
.
dP
P
dP
P
+
........
dP
P
d
Zapiszmy
teraz
różniczkę zupełną iloczynu d(P
k
⋅x
k
). Mamy:
(
)
k
k
k
k
k
k
dP
x
dx
P
x
P
d
+
=
,
stąd:
(
)
k
k
k
k
k
k
x
P
d
dx
P
dP
x
−
=
−
.
Sumując po wszystkich stopniach swobody obie strony tego równania, mamy:
.
d
)
x
P
(
d
dU
)
x
P
(
d
dx
P
dP
x
k
k
k
k
k
k
k
k
k
k
k
k
Ψ
=
⋅
−
=
⋅
−
=
−
∑
∑
∑
∑

21
Otrzymaliśmy więc drugie równanie na różniczkę funkcji charakterystycznej
Ψ
=
(P
Ψ
1
,P
2,
..., P
n
):
d
x
k
k
k
Ψ = −
dP
∑
.
Porównując zatem odpowiednie strony tych równań otrzymujemy związek:
.
)
x
P
(
U
d
dP
P
dP
x
k
k
k
k
k
inv
k
k
k
k
⎟
⎠
⎞
⎜
⎝
⎛
⋅
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
Ψ
∂
=
−
∑
∑
∑
Po prawej stronie tego równania pod znakiem różniczki zupełnej stoi funkcja zależna
od potencjałów P
k
(k = 1,2...n), co pokazuje lewa strona tego równania i to właśnie uzasadnia
fakt, że jest to funkcja
Ψ
. Mamy zatem jeszcze jedno określenie funkcji charakterystycznej
dla tego sprzężenia Zapisując bowiem ostatnie równanie w postaci:
⎟
⎠
⎞
⎜
⎝
⎛
⋅
−
=
−
=
Ψ
∑
∑
k
k
k
k
k
k
x
P
U
d
dP
x
d
,
widzimy, że różniczka funkcji charakterystycznej jest równa ujemnej sumie po wszystkich
stopniach swobody iloczynów zmiennej niezależnej przez różniczkę potencjału
termodynamicznego sprzężonego z
danym stopniem swobody. Sama zaś funkcja
charakterystyczna dla tego sprzężenia jest zdefiniowana przez związek:
,
)
x
P
(
U
k
k
k
⎟
⎠
⎞
⎜
⎝
⎛
⋅
−
=
Ψ
∑
tzn. jest równa energii wewnętrznej, pomniejszonej o sumę po wszystkich stopniach swobody
iloczynów zmiennych niezależnych i potencjałów odnoszących się do danego stopnia
swobody.
Podobnie jak w przypadku energii wewnętrznej, poprzednie równanie można jeszcze
zapisać jak następuje:
.
0
dP
P
+
x
k
k
inv
k
k
∑
=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
∂
Ψ
∂
Ponieważ rozważamy układ o n stopniach swobody, to znaczy układ, w którym
zachodzi n procesów termodynamicznych, wtedy różniczki potencjałów dP
k
nie są równe
zeru. Dlatego też, aby ostatnie równanie było spełnione, każdy wyraz w nawiasie
kwadratowym musi być równy zero. To zaś daje następujące związki:
n.
....,
2,
1,
=
k
P
x
inv
k
k
⎟
⎠
⎞
⎜
⎝
⎛
∂
Ψ
∂
−
=
Mamy zatem drugi ważny rezultat, współrzędne uogólnione (zmienne niezależne) są
równe pochodnym cząstkowym funkcji charakterystycznej opisującej sprzężenie układu

22
z otoczeniem przez potencjały, tj. funkcji
Ψ
(P
1
,P
2,
..., P
n
), po odpowiednich potencjałach P
k
.
Ustalone wartości potencjałów (P
inv
= inv), przy obliczaniu pochodnych cząstkowych dla
danego stopnia swobody, określają warunki zewnętrzne (sprzężenie z termostatem) dla
danego procesu, stąd też bierze się nazwa „sprzężenie przez potencjały”. Funkcję
charakterystyczną tego sprzężenia, tj. funkcję:
)
P
,....
P
,
P
(
G
)
x
P
(
U
)
P
,....
P
,
P
(
n
2
1
k
k
k
n
2
1
=
⋅
−
=
Ψ
=
Ψ
∑
nazywa się potencjałem Gibsa lub wielkim potencjałem termodynamicznym.
3.3. Sprzężenie mieszane.
Rozważać będziemy w
tym punkcie w
dalszym ciągu dowolny układ
termodynamiczny o
n stopniach swobody, ale znajdujący się w
innych warunkach
zewnętrznych. Założymy, że układ jest sprzężony przez r zmiennych niezależnych i przez (n-
r) potencjałów. Funkcja charakterystyczna, którą również oznaczymy przez
, zależy w tym
przypadku od r zmiennych niezależnych x
Ψ
k i
od (n-r) potencjałów P
k
:
(
)
)
r
n
P
,.......
P
,
P
,
r
x
,....
x
,
x
(
n
2
r
1
r
r
2
1
4
4 3
4
4 2
1
43
42
1
−
Ψ
=
Ψ
+
+
.
Różniczka zupełna funkcji charakterystycznej w tym przypadku, rozbija się na dwie sumy:
.
dP
P
dx
x
d
k
inv
n
1
r
k
k
i
inv
r
1
k
k
∑
∑
+
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
Ψ
∂
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
Ψ
∂
=
Ψ
Z
drugiej
strony
mamy
związek na zmianę energii wewnętrznej:
k
k
k
dx
P
dU
∑
=
,
w którym wszystkie wyrazy są tego samego typu (iloczyn potencjału razy różniczka dx) dla
każdego stopnia swobody. Zaś w poprzednim równaniu w pierwszej sumie mamy wyrazy
podobne, ale suma dotyczy tylko r pierwszych stopni swobody. Aby zatem wykorzystać
ostatni wzór przekształcimy równanie na różniczkę d
Ψ
jak następuje. Najpierw weźmy
różniczkę iloczynu zmiennej x i potencjału P dla k-tego stopnia swobody:
(
)
k
k
k
k
k
k
dP
x
dx
P
x
P
d
+
=
,
stąd
(
)
k
k
k
k
k
k
x
P
d
dx
P
dP
x
−
=
−
.
Sumując obie strony tego ostatniego równania od k = r+1 do n mamy:
−
=
−
= +
= +
= +
∑
∑
∑
x dP
P dx
d x P
k
k
k
k
k r
n
k r
n
k k
k r
n
1
1
1
(
)
.
Aby mieć po prawej stronie energię wewnętrzną, dodamy brakującą część energii
wewnętrznej do obu stron tego równania, mamy wtedy:
23
∑
∑
∑
∑
∑
+
=
+
=
+
=
=
=
−
+
−
n
1
r
k
k
k
n
1
r
k
n
1
r
k
k
k
r
1
k
k
k
k
k
r
1
k
k
k
)
P
x
(
d
dU
dx
P
dx
P
=
dP
x
dx
P
4
4
4
3
4
4
4
2
1
).
P
,....
P
,
x
,....
x
(
d
)
P
x
(
U
d
)
P
x
(
d
dU
n
1
r
r
1
n
1
r
k
k
k
n
1
r
k
k
k
+
+
=
+
=
Ψ
=
Ψ
⎥⎦
⎤
⎢⎣
⎡ −
=
−
=
∑
∑
4
4 3
4
4 2
1
Ostatnia równość wynika stąd, że po lewej stronie stoją pod sumami różniczki
zmiennych x
k
dla (k = 1, ..., r) oraz różniczki potencjałów P
k
dla (k = r + 1,....,n) Zatem
różniczka funkcji:
U
x P
k
k
k r
n
−
= +
∑
(
)
1
,
musi być różniczką funkcji zależnej od zmiennych (x
1
,..., x
r
, P
r+1
,..., P
n
), a zatem jest to
funkcja charakterystyczna
.
Ψ
Możemy teraz porównać różniczkę zupełną tej funkcji z lewą stroną ostatniego
równania. Mamy:
∑
∑
∑
∑
+
=
=
+
=
=
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
Ψ
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
Ψ
∂
n
1
r
k
k
k
r
1
k
k
k
k
inv
n
1
r
k
k
k
inv
r
1
k
k
.
dP
x
dx
P
dP
P
dx
x
Przenosząc na jedną stronę i grupując wyrazy z tego samego typu różniczkami, otrzymujemy:
.
0
dP
x
P
dx
P
x
k
n
1
r
k
k
inv
k
k
r
1
k
k
inv
k
=
⎥
⎦
⎤
⎢
⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
Ψ
∂
+
⎥
⎦
⎤
⎢
⎣
⎡
−
⎟
⎠
⎞
⎜
⎝
⎛
∂
Ψ
∂
∑
∑
+
=
=
Ponieważ dla k = 1 aż do k = r, dx
k
≠
0 i dla k = r+1 aż do n, dP
k
≠ 0, to wyrażenia
w nawiasach kwadratowych muszą być każde oddzielnie równe zeru. Otrzymujemy więc
następujące związki:
n.
,
2,..
+
r
1,
+
r
=
k
,
P
x
r,
2,...,
1,
=
k
,
x
P
inv
k
k
inv
k
k
⎟
⎠
⎞
⎜
⎝
⎛
∂
Ψ
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
Ψ
∂
=
Dodatkowa, otrzymana po drodze jawna zależność funkcji charakterystycznej dla
sprzężenia mieszanego od energii wewnętrznej U jest następująca:
Ψ =
−
= +
∑
U
d x P
k
k
k r
n
(
)
1
.
W odróżnieniu od poprzednich sprzężeń funkcja ta, dla układu o n stopniach swobody, nie ma
specjalnej nazwy poza wymienioną wyżej nazwą funkcji charakterystycznej sprzężenia
mieszanego. Funkcji tego typu z definicji jest wiele, ogólnie n!.

24
Podsumowując ogólne zagadnienie funkcji charakterystycznych, wypiszemy jawnie
trzy funkcje charakterystyczne, dla trzech różnych sprzężeń:
Sprzężenie przez zmienne niezależne
Ψ = Ψ(x
1
, x
2
,..., x
n
) =U(x
1
, x
2
,..., x
n
) = energia wewnętrzna.
Sprzężenie przez potencjały
Ψ = Ψ(P
1
, P
2
,..., P
n
) = G(P
1
, P
2
,..., P
n
)
= potencjał Gibsa.
∑
=
⋅
−
=
n
1
k
k
k
n
3
2
1
x
P
)
x
,...,
x
,
x
,
x
(
U
Sprzężenie mieszane
Ψ = Ψ(
)
(
)
x x
x
r
P
P
P
n r
r
r
r
n
1
2
1
2
,
,.... ,
,
,.......
1 2
4
4
3
44 1
2
44
4
3
444
+
+
−
.
∑
+
=
⋅
−
=
n
1
r
k
k
k
n
3
2
1
x
P
)
x
,...,
x
,
x
,
x
(
U
Przykład 1. Funkcje charakterystyczne dla dwóch stopni swobody (S, V).
1
0
Sprzężenie przez zmienne (S,V)
U = U(S, V) = energia wewnętrzna.
2
0
Sprzężenie przez zmienne (T, p)
pV
TS
U
G
+
−
=
= potencjał Gibsa.
3
0
Sprzężenie mieszane:
przez zmienne (S, p)
H
pV
U
)
p
,
S
(
=
+
=
Ψ
=
Ψ
= entalpia.
przez zmienne (T, V)
F
TS
U
)
V
,
T
(
=
−
=
Ψ
=
Ψ
= energia swobodna.
Przykład 2. Funkcje charakterystyczne oraz parametry termodynamiczne dla dwóch stopni
swobody.
Energia wewnętrzna: U = U(S, V).
Różniczka zupełna:
pdV
TdS
dV
V
U
dS
S
U
dU
S
V
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
.
Definicje
potencjałów:
n.
2,.......,
1,
=
k
x
U
P
inv
k
k
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎪
⎪
⎩
⎪⎪
⎨
⎧
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
.
p
P
V,
=
x
2,
=
k
V
U
p
,
T
P
S,
=
x
1,
=
k
S
U
T
2
2
S
1
1
V

25
Potencjał Gibsa: G = G(T, p) = U
− T S + pV.
Różniczka zupełna:
.
Vdp
SdT
dG
,
Vdp
pdV
SdT
TdS
dU
dV
p
G
dS
T
G
dG
T
p
+
−
=
+
+
−
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
Definicje zmiennych niezależnych:
n.
2,...,
1,
=
k
P
x
inv
k
k
⎟
⎠
⎞
⎜
⎝
⎛
∂
Ψ
∂
−
=
⎪
⎪
⎩
⎪⎪
⎨
⎧
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
.
p
P
V,
=
x
:
2
=
k
,
p
G
V
,
T
P
S,
=
x
:
1
=
k
,
T
G
S
2
2
S
1
1
p
Entalpia: H = H(S, p) = U +pV.
Różniczka zupełna:
.
Vdp
TdS
Vdp
pdV
pdV
TdS
=
)
pV
U
(
d
dp
p
H
dS
S
H
dH
S
p
+
=
+
+
−
+
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
Definicje parametrów termodynamicznych:
n.
2,......,
+
r
1,
+
r
=
k
,
P
x
r,
2,......,
1,
=
k
,
x
P
inv
k
k
inv
k
k
⎟
⎠
⎞
⎜
⎝
⎛
∂
Ψ
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
Ψ
∂
=
⎪
⎪
⎩
⎪⎪
⎨
⎧
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
.
p
P
V,
=
x
:
2
=
k
,
p
H
V
,
T
P
S,
=
x
:
1
=
k
,
S
H
T
2
2
S
1
1
p
Energia
swobodna:
TS
U
)
V
,
T
(
F
F
−
=
=
.
Różniczka zupełna:
.
pdV
SdT
)
TS
(
d
)
SdT
TdS
(
dU
pdV
TdS
=
)
TS
U
(
d
dV
V
F
dT
T
F
dF
T
V
−
−
=
+
−
−
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
43
42
1
43
42
1
Definicje parametrów termodynamicznych:
n.
2,...,
+
r
1,
+
r
=
k
,
P
x
r,
1,2,..,
=
k
,
x
P
inv
k
k
inv
k
k
⎟
⎠
⎞
⎜
⎝
⎛
∂
Ψ
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
Ψ
∂
=

26
⎪
⎪
⎩
⎪⎪
⎨
⎧
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
.
p
P
V,
=
x
:
2
=
k
V
F
p
,
T
P
S,
=
x
:
1
=
k
T
F
S
2
2
T
1
1
V
3.4. Sens fizyczny funkcji charakterystycznych
Rozważmy jeszcze jedną własność funkcji charakterystycznych. Załóżmy w dalszym
ciągu dla ogólności, że mamy układ o n stopniach swobody, przy czym o niektórych z nich
będziemy zakładać, że znane są dla nich warunki sprzężenia, tj. niektóre z parametrów P
k
i x
k
są stałe, a niektóre się zmieniają. Będziemy używać pojęcia zamocowany stopień swobody,
przez analogię do zamocowanego (nieruchomego) tłoka (V = const, dV = 0).
Niech m pierwszych stopni swobody będzie zamocowanych, tzn. x
k
= const i dx
k
= 0
dla k = 1,..., m. Pozostałe zaś stopnie swobody dla k = m+1,..., n., będziemy nazywać nie
zamocowanymi. Dla tych ostatnich stopni swobody,
dx
k
≠ 0, k = m+1,..., n.. Rozłożymy energię wewnętrzną (jej infinitezymalnie małą zmianę) na
części po zamocowanych i nie zamocowanych stopniach swobody:
∑
∑
+
=
=
+
=
n
1
m
k
k
k
m
1
k
k
k
dx
P
dx
P
dU
.
Wystarczy rozważyć sprzężenie mieszane, tj. funkcję
charakterystyczną:
. Funkcja ta jest zdefiniowana
równaniem:
(
)
n
1
m
m
2
r
1
r
r
2
1
x
,...,
x
,
x
...,
,
x
,
x
,
P
...,
,
P
,
P
+
+
+
Ψ
(
)
∑
=
+
+
+
−
=
Ψ
r
1
k
k
k
n
2
1
n
1
m
m
2
r
1
r
r
2
1
P
x
)
x
...,
,
x
,
x
(
U
x
,...,
x
,
x
...,
,
x
,
x
,
P
...,
,
P
,
P
Jej różniczka zupełna jest równa:
k
r
1
k
k
r
1
k
k
k
dx
P
dP
x
dU
d
∑
∑
=
=
−
−
=
Ψ
.
Wstawiając za dU wyrażenie jak wyżej, mamy:
,
dx
P
dx
P
dx
P
dx
P
dP
x
dx
P
dx
P
d
k
r
1
k
k
m
1
r
k
n
1
m
k
k
k
k
k
k
r
1
k
k
r
1
k
k
k
n
1
m
k
k
k
m
1
k
k
k
∑
∑
∑
∑
∑
∑
∑
=
+
=
+
=
=
=
+
=
=
−
+
=
−
−
+
=
Ψ
ale dx
k
= 0 dla k = r+1, ..., m, oraz dP
k
= 0 dla k = 1,..., r. Stąd otrzymujemy:
d
P d
k
k
k m
n
Ψ =
= +
∑
1
x
.

27
Widzimy,
więc, że różniczka zupełna tej funkcji charakterystycznej, jest równa sumie
oddziaływań cząstkowych po nie zamocowanych stopniach swobody. Jeżeli uwzględnić, że
suma oddziaływań cząstkowych ze znakiem minus jest równa pracy dA:
dA
P dx
k
k
= −
∑
,
to d
Ψ przyjmie postać:
dA
d
−
=
Ψ
.
Oznacza to, że różniczka zupełna funkcji charakterystycznej jest równa pracy po nie
zamocowanych stopniach swobody. Stwierdzenie to jest prawdziwe dla dowolnego
sprzężenia układu z termostatem ponieważ wyprowadziliśmy je posługując się sprzężeniem
mieszanym, a to sprzężenie daje wszystkie znane nam rodzaje sprzężeń jako przypadki
szczególne.
4. Warunki równowagi układów termodynamicznych
Wiemy
już, że dla układu izolowanego druga zasada termodynamiki ustala ważne
kryterium równowagi. Zaczniemy od jednego stopnia swobody (S). Mamy:
x
S
P
T
1
1
=
=
⎧
⎨
⎩
⎫
⎬
⎭
zmienna niezależna
potencjał termodynamiczny
-proces wymiany ciepła.
W tym przypadku mamy:
dU
TdS
lub
dU
TdS
≥
=
.
Jeżeli układ jest całkowicie izolowany od otoczenia, to dU = 0 i T = const. Mamy więc
równanie:
dS
≥ 0,
które mówi nam, że w układzie izolowanym mogą zachodzić tylko takie procesy, które
powodują wzrost entropii. w
stanie równowagi natomiast entropia osiąga wartość
maksymalną S
max
.
4.1. Układy termodynamiczne proste
Układem termodynamicznym prostym nazywa się układ, który może wymienić tylko
jeden rodzaj pracy z termostatem: pracę rozprężania dA = pdV. Dla takich układów jest
spełniona relacja:
pdV
dU
TdS
+
≥
.

28
Odpowiednio do rodzaju sprzężenia dla układów termodynamicznych mamy cztery
podstawowe procesy termodynamiczne pokazane schematycznie przy pomocy grafu
rzymskiej dziesiątki:
V
p
T
S
3
4
2
1
Sprzężenie przez zmienne niezależne (S, V) = const,
(funkcja
charakterystyczna
U),
proces izochoryczno-adiabatyczny.
Sprzężenie przez potencjały (T, p) = const,
(funkcja charakterystyczna G), proces
izobaryczno-izotermiczny.
Sprzężenie mieszane (T, V) = const,
(funkcja charakterystyczna F), proces izochoryczno-izotermiczny.
Sprzężenie mieszane (S, p) = const,
(funkcja
charakterystyczna
H), proces adiabatyczno-izobaryczny.
Dla tych procesów (sprzężeń) odpowiednie funkcje charakterystyczne są następujące:
)
V
,
S
(
U
)
V
,
S
(
=
Ψ
=
Ψ
,
)
pV
TS
)
V
,
S
(
U
)
p
,
T
(
G
)
p
,
T
(
+
−
=
=
Ψ
=
Ψ
,
TS
)
V
,
S
(
U
)
V
,
T
(
F
)
V
,
T
(
−
=
=
Ψ
=
Ψ
,
pV
)
V
,
S
(
U
)
p
,
S
(
H
)
p
,
S
(
+
=
=
Ψ
=
Ψ
.
Biorąc pod uwagę pierwszą zasadę termodynamiki, dla każdego z tych procesów
można podać odpowiednie kryterium równowagi termodynamicznej.
Sprzężenie przez zmienne (S, V)
Dla procesu izochoryczno-adiabatycznego zasada termodynamiki ma postać:
pdV
dU
TdS
+
≥
,
gdy S = const i V = const, to
0
dU
≤
.
W procesie izochoryczno-adiabatycznym zmiana energii wewnętrznej jest mniejsza lub równa
od zera. Oznacza to, że zbliżając się do stanu równowagi energia wewnętrzna maleje i osiąga
minimum w stanie równowagi U
min
Sprzężenie przez potencjały (T, p)

29
W przemianach prostych izobaryczno-izotermicznych pierwsza zasada
termodynamiki,
, może być przekształcona następująco
pdV
dU
TdS
+
≥
Vdp
)
Vdp
pdV
(
dU
SdT
)
SdT
TdS
(
−
+
+
≥
−
+
.
W nawiasach znajdują się różniczki iloczynów, zatem
Vdp
)
pV
U
(
d
SdT
)
TS
(
d
−
+
≥
−
.
Łącząc różniczki razem i uwzględniając warunki sprzężenia mamy relację:
0
dG
,
0
)
pV
TS
U
(
d
≤
≤
+
−
.
Widzimy,
że w procesie izotermiczno-izobarycznym (T = const, p = const), potencjał
termodynamiczny izobaryczno-izotermiczny:
pV
TS
U
G
+
−
=
, zbliżając się do stanu
równowagi, maleje i osiąga minimum G
min
w stanie równowagi.
Sprzężenie mieszane (T, V)
Dla procesów izochoryczno-izotermicznych uogólniona pierwsza zasada
termodynamiki:
, może być przekształcona podobnie jak poprzednio.
Mianowicie, dodając do lewej strony i odejmując ten sam iloczyn SdT, a następnie
odpowiednio grupując składniki, mamy:
pdV
dU
TdS
+
≥
pdV
SdT
)
TS
U
(
d
0
+
+
−
≤
.
Po uwzględnieniu warunków tego sprzężenia (T = const i V =const), dostajemy:
0
)
TS
U
(
d
≤
−
.
W tym przypadku widać, że dla procesów izotermiczno-izochorycznych
energia swobodna
TS
U
F
−
=
spełnia relację:
0
dF
≤
.
Układ zbliżając się do stanu równowagi zmniejsza swoją energię swobodną tak, że w stanie
równowagi osiąga ona minimum F
min
.
Sprzężenie mieszane (S, p)
W tym przypadku, tj. dla procesów izochoryczno-adiabatycznych, startujemy jak
zawsze z zasady termodynamiki:
pdV
dU
TdS
+
≥
.
Tym razem, dodając i odejmując ten sam wyraz Vdp po prawej stronie tego wyrażenia,
mamy:
Vdp
Vdp
pdV
dU
TdS
−
+
+
≥
.
Grupując wyrazy tak, aby pod różniczką mieć entalpię, otrzymujemy:
Vdp
)
pV
U
(
d
TdS
−
+
≥
.
Dla tego sprzężenia p = const i S. = const, stąd
(
)
0
dH
,
0
pV
U
d
≤
≤
+
.

30
W procesie izobaryczno-adiabatycznym entalpia maleje i
osiąga minimum w
stanie
równowagi H
min
.
4.2. Układy termodynamiczne złożone
Układem złożonym będziemy nazywać taki układ termodynamiczny, w którym
zachodzą procesy związane z wykonaniem oprócz pracy rozprężania dodatkowo pracy
nieobjętościowej Xdx. Jeżeli układ nie jest układem prostym, tzn. jeżeli oprócz pracy
rozprężenia układ może wykonywać inny rodzaj pracy nieobjętościowej, to kryteria
równowagi będą nieco inne. Metoda otrzymywania odpowiednich kryteriów równowagi, jest
taka sama jak poprzednio, i
polega na zastąpieniu we wszystkich wzorach pracy
objętościowej pdV przez (pdV + Xdx), gdzie X jak już wiemy jest siłą uogólnioną, a x
współrzędną uogólnioną związaną z tą siłą. Ograniczamy się zatem do tylko jednego stopnia
swobody dla pracy elementarnej nieobjętościowej a więc do układów o trzech stopniach
swobody
.
)
x
,
V
,
S
(
Sprzężenie przez zmienne (S, V)
Dla procesu izochoryczno-adiabatycznego dla układu o trzech stopniach swobody
zasada termodynamiki ma postać:
Xdx
pdV
dU
TdS
+
+
≥
.
Ponieważ dla tego sprzężenia S = const i V= const, to
0
Xdx
dU
≤
+
.
W procesie izochoryczno-adiabatycznym zmiana energii wewnętrznej i
pracy
nieobjętościowej jest mniejsza od zera.
Sprzężenie przez potencjały (T, p)
W przemianach izobaryczno-izotermicznych dla układu o trzech stopniach swobody
pierwsza zasada termodynamiki: T
⋅dS ≥ dU + p⋅dV + X⋅dx, może być przekształcona do
postaci:
Xdx
Vdp
)
Vdp
pdV
(
dU
SdT
)
SdT
TdS
(
+
−
+
+
≥
−
+
.
W nawiasach znajdują się różniczki odpowiednich iloczynów. Łącząc zatem różniczki razem,
mamy relację:
Xdx
Vdp
)
pV
TS
U
(
d
SdT
+
−
+
−
≥
−
.
Uwzględniając warunki sprzężenia T=const i p=const, otrzymujemy warunek równowagi:
.
0
dG
,
0
Xdx
)
pV
TS
U
(
d
≤
≤
+
+
−
.
Widzimy, że w procesie izotermiczno-izobarycznym (T = const, p. = const), potencjał
termodynamiczny G = U - T + p
⋅dV spełnia następującą relację:
dG + X
⋅dx ≤ 0.

31
Sprzężenie mieszane (V, T)
Dla procesów izochoryczno-izotermicznych zachodzących w
układach o
trzech
stopniach swobody, uogólniona pierwsza zasada termodynamiki:
T
⋅dS ≥ dU + p⋅dV + X⋅dx,
przez dodanie do lewej strony i odjęcie tego samego iloczynu SdT, a następnie odpowiednie
pogrupowanie, prowadzi do relacji:
Xdx
pdV
)
TS
U
(
d
SdT
+
+
−
≥
−
.
Dla procesów izobaryczno-izotermicznych powyższa relacja przyjmuje postać:
0
Xdx
dF
,
0
Xdx
)
TS
U
(
d
≤
+
≤
+
−
.
Układ zbliżając się do stanu równowagi w procesie izochoryczno-izotermicznym zmniejsza
swoją energię swobodną tak, że suma energii swobodnej i pracy nieobjętościowej jest
mniejsza od zera (w procesach nierównowagowych) lub równa zeru (w procesach
równowagowych).
Sprzężenie mieszane (S, p)
W tym przypadku, tj. dla procesów izochoryczno-adiabatycznych zachodzących
w układzie o
trzech stopniach swobody, zasada termodynamiki:
TdS
≥ dU + pdV +Xdx, po dodaniu i odjęciu wyrazu Vdp, przyjmuje postać:
Xdx
Vdp
)
Vdp
pdV
(
dU
TdS
+
−
+
+
≥
.
Grupując wyrazy tak, aby pod różniczką mieć entalpię, otrzymujemy:
Xdx
Vdp
)
pV
U
(
d
TdS
+
−
+
≥
.
Gdy p = const i S = const, to powyższy warunek równowagi redukuje się relacji:
0
Xdx
dH
,
0
Xdx
)
pV
U
(
d
≤
+
≤
+
+
.
W procesie izobaryczno-adiabatycznym entalpia maleje i spełnia nierówność:
dH +Xdx
≤ 0.
Ostatecznie
mamy
więc cztery relacje wyznaczające warunki równowagi dla procesów
termodynamicznych zachodzących w układzie o trzech stopniach swobody (S, V, x):
1. dU + X dx
≤ 0
(S, V) = const, -proces adiabatyczno-izochoryczny.
2. dG + X dx
≤ 0
(T, p) = const, -proces izotermiczno-izobaryczny.
3. dF + X dx
≤ 0
(V, T) = const, -proces izochoryczno-izotermiczny.
4. dH + X dx
≤ 0
(p, S) = const, -proces izobaryczno-adiabatyczny.
Z
powyższych związków widać, że przy odpowiednim sprzężeniu (w każdym
przypadku) praca, która może być wykonana w stanie równowagi, jest równa zmniejszeniu

32
się odpowiedniej funkcji charakterystycznej. Stąd też przez analogię z
mechaniką,
odpowiednie funkcje charakterystyczne nazywa się potencjałami termodynamicznymi.
Zwróćmy jeszcze uwagę na analogie między G i F oraz H i U. Mamy:
⎩
⎨
⎧
−
=
−
=
,
TS
H
G
,
TS
U
F
stąd:
⎩
⎨
⎧
−
=
−
=
.
TS
G
H
,
TS
F
U
Z pierwszego równania ostatniego układu równań wynika, że w warunkach (V,
T)=const, praca wykonana jest kosztem zmiany energii swobodnej. Stąd F jest tą częścią
energii wewnętrznej, którą można zamienić na pracę. Pozostała zaś część energii wewnętrznej
TS jest energią związaną. Podobnie w warunkach (T, p) = const, praca jest związana ze
zmianą G, tj. zmianą swobodnej entalpii. Stąd TS jest nazywane entalpią związaną.
5. Związki termodynamiczne Maxwella
Przejdźmy teraz do rozważań ogólnych nad układem o n stopniach swobody.
Pokażemy jakie związki termodynamiczne wynikają z faktu trzech różnych sprzężeń.
Rozważmy te sprzężenia w tej samej kolejności w jakiej je wprowadzono wyżej.
5.1. Sprzężenie przez zmienne niezależne
Funkcją charakterystyczną jest w tym przypadku energia wewnętrzna:
Ψ (x
1
,..., x
2
) = U(x
1
,..., x
2
).
Jeżeli dana jest ta funkcja, to potencjały mogą być otrzymane jako cząstkowe pochodne
energii wewnętrznej po odpowiedniej zmiennej niezależnej. Możemy więc napisać dla
dowolnych stopni swobody k i l:
inv
l
l
inv
k
k
x
U
P
i
x
U
P
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
,
.
n
,...,
2
,
1
l
,
k
∈
Różniczkując P
k
po x
l
, a P
l
po x
k
otrzymujemy:
.
x
x
U
x
P
,
x
x
U
x
P
inv
l
k
2
inv
k
l
inv
k
l
2
inv
l
k
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
.
Prawe strony tych równań są równe, to i lewe strony muszą być równe. Stąd otrzymujemy
pierwszy typ równań (związków) Maxwella:
inv
k
l
inv
l
k
x
P
x
P
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
Związek Maxwella (Z.M.) prosty.
Oczywiście równanie odwrotne jest również prawdziwe:
33
inv
l
k
inv
k
l
P
x
P
x
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
Z.M. odwrotny.
Przykład.
Dwa stopnie swobody (S, V)
,
p
P
V,
=
x
:
2
=
k
,
T
P
S,
=
x
:
1
=
k
2
2
1
1
⎩
⎨
⎧
−
=
=
⎪
⎪
⎩
⎪
⎪
⎨
⎧
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
,
p
S
T
V
,
S
p
V
T
V
S
V
S
Wielkość
∂
∂
V
T
S
⎛
⎝⎜
⎞
⎠⎟
określa rozszerzalność cieplną układu w procesie adiabatycznym,
podczas gdy
∂
∂
p
S
V
⎛
⎝⎜
⎞
⎠⎟
jest sprężystością układu przy stałej objętości.
5.2. Sprzężenie przez potencjały
Funkcją charakterystyczną jest w tym przypadku potencjał Gibsa:
k
n
1
k
k
n
2
1
P
x
U
)
P
,...,
P
,
P
(
∑
−
−
=
Ψ
=
Ψ
.
W tym przypadku możemy wyliczyć zmienne niezależne x
k
, jako pochodne cząstkowe
funkcji charakterystycznej, po potencjałach. Mamy więc dla dowolnych stopni swobody k i l
następujące związki:
,
P
x
,
P
x
inv
l
l
inv
k
k
⎟
⎠
⎞
⎜
⎝
⎛
∂
Ψ
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
Ψ
∂
−
=
.
n
...,
,
2
,
1
l
,
k
∈
.
Różniczkując x
k
po P
l
i x
l
po P
k
otrzymujemy:
.
P
P
P
x
,
P
P
P
x
inv
l
k
2
inv
k
l
inv
k
l
2
inv
l
k
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
Ψ
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
Ψ
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
Porównując lewe strony tych równań, mamy drugi typ równań Maxwella:
inv
k
l
inv
l
k
P
x
P
x
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
Z.M. prosty
oraz równanie odwrotne:
inv
l
k
inv
k
l
x
P
x
P
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
Z.M odwrotny.
Przykład.
Dwa stopnie swobody(S, V).
,
p
P
V,
=
x
2,
=
k
,
T
P
S,
=
x
1,
=
k
2
2
1
1
⎩
⎨
⎧
−
=
=
⎪
⎪
⎩
⎪⎪
⎨
⎧
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
=
=
=
odwrotny.
.
M
.
Z
V
T
S
p
prosty,
.
M
.
Z
T
V
p
S
const
p
const
T
const
p
const
T

34
5.3. Sprzężenia mieszane
W tym przypadku
Ψ = Ψ(P
1
,..., P
r
, x
r+1
,..., x
n
) i możemy wyliczyć x
k
dla dowolnego
stopnia swobody z przedziału k = 1, 2,..., r, oraz P
l
dla dowolnego stopnia swobody l
z przedziału l = r+1,..., n., korzystając z wyprowadzonych wcześniej związków:
n
2,...,
+
r
1,
r
l
,
x
P
r,
2,...,
1,
k
,
P
x
inv
l
l
inv
k
k
+
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
Ψ
∂
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
Ψ
∂
−
=
.
Różniczkując te równania odpowiednio po x
l
(pierwsze równanie) i po P
k
(drugie
równanie),:
∂
∂
∂
∂ ∂
∂
∂
∂
∂ ∂
x
x
x P
P
P
x
k
l
P
l
k
l
k
P
l
k
k
l
⎛
⎝
⎜
⎞
⎠
⎟ = −
⎛
⎝
⎜
⎞
⎠
⎟ = −
2
2
Ψ
Ψ
i
P
.
Prawe strony tych równości są równe, to i lewe muszą być równe. Stad dostajemy równania
Maxwella (związki Maxwella) dla sprzężenia mieszanego:
odwrotny.
Z.M.
P
P
x
x
i
prosty
Z.M.
P
P
x
x
l
k
l
k
x
l
k
P
k
l
x
k
l
P
l
k
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
Ostatnie równanie otrzymuje się jako odwrotność poprzedniego.
Przykład.
Dwa stopnie swobody(S, V):
Mamy ogólne równania Maxwella dla tego sprzężenia, z których odczytujemy związki dla dwóch
stopni swobody:
odwrotny.
Z.M.
P
P
x
x
i
prosty
Z.M.
P
P
x
x
l
k
l
k
x
l
k
P
k
l
x
k
l
P
l
k
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
,
p
P
V,
=
x
:
2
=
k
,
T
P
S,
=
x
:
1
=
k
2
2
1
1
⎩
⎨
⎧
−
=
=
⎪
⎪
⎩
⎪⎪
⎨
⎧
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
odwrotny.
Z.M.
T
p
V
S
prosty,
Z.M.
p
T
S
V
S
p
S
p
5.4. Związki Maxwella dla dwóch stopni swobody (S, V)
W tym punkcie wypiszemy razem otrzymane wcześnie związki Maxwella.
1. Sprzężenie przez zmienne niezależne: S, V.
⎪
⎪
⎩
⎪⎪
⎨
⎧
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
.
odwrotny
.
M
.
Z
p
S
T
V
,
prosty
.
M
.
Z
S
p
V
T
V
S
V
S
2. Sprzężenie przez zmienne zależne: T, p.

35
⎪
⎪
⎩
⎪⎪
⎨
⎧
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
=
=
=
.
V
T
S
p
,
T
V
p
S
const
p
const
T
const
p
const
T
3. Sprzężenie przez zmienną niezależną S i zmienną zależną p.
⎪
⎪
⎩
⎪⎪
⎨
⎧
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
=
=
=
.
T
p
V
S
,
p
T
S
V
const
S
const
p
const
S
const
p
4. Sprzężenie przez zmienną niezależną V i zmienną zależną T.
⎪
⎪
⎩
⎪⎪
⎨
⎧
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
=
=
=
.
p
T
S
V
,
T
p
V
S
const
V
const
T
const
V
const
T
6. Pojemność cieplna układu termodynamicznego
6.1. Pojemność cieplna układu (dwa stopnie swobody: S i V)
Układem termodynamicznym jednorodnym nazywamy układ, który w warunkach
równowagi, kiedy zachodzą procesy quasi statyczne, jest scharakteryzowany przez parametry
termodynamiczne, które nie zależą od współrzędnych przestrzennych. Innymi słowy cały
układ jest opisany tylko jednym parametrem danego typu (dla każdego stopnia swobody).
w przypadku układów niejednorodnych, np. ze względu na ciśnienie, w różnych częściach
układu mamy inne ciśnienia. Taka sytuacja ma miejsce w stanach nierównowagowych.
Teorię pojemności cieplnej lub ciepła właściwego będziemy budować na przykładzie
układu z dwoma stopniami swobody, tj. dla układu prostego, w którym zachodzą procesy
deformacji i wymiany ciepła z termostatem. Wybór takiego układu jest uzasadniony jego
szerokim występowaniem, a uogólnienie na dowolny układ nie stanowi problemu.
Taki
układ, jak już dobrze wiemy z poprzednich wykładów, jest opisany przez cztery
parametry termodynamiczne, dwie zmienne niezależne x
1
= S i x
2
= V, oraz dwa potencjały
(zmienne zależne)
p
P
i
T
P
2
1
−
=
=
.
Ciepło właściwe odniesione do całego układu lub inaczej, pojemność cieplną układu
C, definiujemy związkiem kalorymetrycznym:

36
.
T
Q
C
δ
δ
=
Dalej będziemy pisać tę ostatnią formułę również w postaci:
C
dQ
dT
=
,
pamiętając o tym, że wyrażenie różniczkowe na ciepło nie jest różniczką zupełną. Już z tego
faktu, że postać różniczkowa ciepła nie jest różniczką zupełną, wynika fakt, że pojemność
cieplna układu zależy od rodzaju procesu, dla którego tę wielkość określamy. Wiemy dalej, że
đQ = dU + đA, przy czym dla termomechanicznego procesu deformacji: đA = pdV i U = U(S,
V).
Z drugiej jednak strony energia wewnętrzna zależy od entropii, tj. wielkości
bezpośrednio niemierzalnej. Wygodnie będzie tę zależność wyrazić przez mierzalną wielkość
jaką jest temperatura.
Przekształcając potencjał termodynamiczny dla stopnia swobody związanego
z wymianą ciepła, tj. równanie:
T = T(S, V), do postaci: S = S(T, V) i podstawiając wynik do równania definiującego energię
wewnętrzną, mamy: U = U(S, V) = U(S(T, V), V) = U(T, V).
Różniczka zupełna tej ostatniej funkcji, jako funkcji stanu jest równa:
dU
U
T
dT
U
V
dV
V
T
= ⎛
⎝⎜
⎞
⎠⎟
+ ⎛
⎝⎜
⎞
⎠⎟
∂
∂
∂
∂
.
Podstawiając ten związek do definicji pojemności cieplnej układu, mamy kolejno:
.
dT
dV
p
V
U
T
U
dT
dV
p
dT
dV
V
U
T
U
dT
dV
p
dT
dU
dT
dQ
C
T
V
T
V
⎥⎦
⎤
⎢⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
+
=
=
Ponieważ U jest wielkością ekstensywną, to można odnieść ją do układu lub dowolnej
jego części, np. do jednostki masy. Wówczas pojemność cieplna jednostki masy c przyjmie
postać:
c
u
T
u
v
p
dv
dT
V
T
=
⎛
⎝⎜
⎞
⎠⎟ +
⎛
⎝⎜
⎞
⎠⎟ +
⎡
⎣
⎢
⎤
⎦
⎥
∂
∂
∂
∂
,
gdzie równania: U = mu i V = mv, definiują energię wewnętrzną u jednostki masy i objętość v
tej samej jednostki masy.
37
Widzimy,
że ciepło właściwe jest skomplikowaną wielkością fizyczną zależną,
zarówno od stanu układu, który jednoznacznie opisuje energia wewnętrzna U, jak i od
procesu, który doprowadził układ do tego stanu.
Zależność ciepła właściwego od procesu, można zilustrować na przykładach różnych
procesów termodynamicznych.
Weźmy pod uwagę proces izochoryczny. Mamy w tym przypadku v = const i dv = 0.
Wtedy ciepło właściwe masowe dane jest wyrażeniem:
c
u
T
v
v const
= ⎛
⎝⎜
⎞
⎠⎟
=
∂
∂
.
Wielkość tę można wyliczyć, gdy znamy energię wewnętrzną jako funkcję parametrów
termodynamicznych.
W
procesie
izotermicznym
T = const i stąd dT = 0. Mamy zatem: c
T
=
∝.
Równość ta oznacza, że ciepło dostarczane do układu nie idzie na podwyższenie temperatury.
W
procesie
adiabatycznym
đQ
≡ δQ = 0 bo wtedy: S = const i dS = 0.
Mamy, zatem: c
S
= 0
Już z tych trzech procesów termodynamicznych widać, że ciepło właściwe może się
zmieniać od zera do nieskończoności.
Analizując otrzymany wzór ogólny na politropowe ciepło właściwe
c, zauważmy, że
możemy go zapisać jeszcze w postaci:
c c
u
v
p
dv
dT
v
T
=
+
⎛
⎝⎜
⎞
⎠⎟ +
⎡
⎣
⎢
⎤
⎦
⎥
∂
∂
.
Wyrażenie w nawiasach kwadratowych zawiera pochodną cząstkową energii wewnętrznej
jednostki objętości po objętości jednostki masy. Pochodna ta jest różna od zera tylko wtedy,
gdy u zależy od objętości v, tj. gdy u = u(v). Wielkość:
∂
∂
u
v
T
⎛
⎝⎜
⎞
⎠⎟
,
ma wymiar ciśnienia i opisuje dodatkowe ciśnienie wynikające z wzajemnego oddziaływania
cząstek układu między sobą. To ciśnienie nazywa się ciśnieniem wewnętrznym.
Przekształćmy jeszcze pochodną
∂
∂
u
v
T
⎛
⎝⎜
⎞
⎠⎟
. Uogólniona pierwsza zasada termodynamiki dla
rozważanej jednostki objętości ma postać:
pdv
Tds
du
−
=
.
Podstawiając ten związek do rozważanej pochodnej, otrzymujemy:
38
∂
∂
∂
∂
u
v
T
s
v
p
T
T
⎛
⎝⎜
⎞
⎠⎟
= ⎛
⎝⎜
⎞
⎠⎟
−
.
Z drugiej strony z ogólnego równania Maxwella dla sprzężenia mieszanego:
j
k
x
k
j
P
j
k
P
P
x
x
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
,
mamy dla x
k
= s i x
j
= v:
v
T
T
p
v
s
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
.
Dlatego też przekształcana pochodna przyjmuje postać:
p
T
p
T
v
u
v
T
−
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
i formuła, na ciepło właściwe masowe, może być przedstawiona równaniem:
c c
T
p
T
dv
dT
v
v
=
+ ⎛
⎝⎜
⎞
⎠⎟
∂
∂
.
Analogiczna formuła dla politropowej pojemności cieplnej całego układu C:
C C
T
p
T
dV
dT
v
V
=
+
⎛
⎝⎜
⎞
⎠⎟
∂
∂
ma taką samą postać i może być otrzymana przez zastąpienie w poprzedniej, wielkości
ekstensywnych odnoszących się do jednostki masy przez odpowiednie wielkości odnoszące
się do całego układu.
Są to ogólne wyrażenie na ciepło właściwe masowe i pojemność cieplną rozważanego
układu. Ze wzorów tych można wyliczyć ciepła właściwe lub pojemność cieplną układu przy
ustalonych parametrach. i tak widzimy, że ciepło właściwe masowe przy stałym ciśnieniu jest
równe:
c
p
v
v
p
c
T
p
T
dv
dT
=
+ ⎛
⎝⎜
⎞
⎠⎟
⎛
⎝⎜
⎞
⎠⎟
∂
∂
.
Równanie to będziemy nazywać ogólnym równaniem Mayera.
6.2. Pojemność cieplna układu (dwa stopnie swobody: S i x)
Przedstawione
w
poprzednim
punkcie wyprowadzenie formuły, na ciepło właściwe
lub pojemność cieplną układu, można uogólnić na układy o dwóch dowolnych stopniach
swobody zakładając, że pierwszym z nich jest stopień związany z wymianą ciepła a drugi
stopień jest dowolny. Oznaczając drugi stopień swobody, dokładniej zmienną niezależną
związaną z tym drugim dowolnym procesem przez x, a siłę uogólnioną przez X, pierwszą
zasadę termodynamiki dla takiego układu możemy zapisać w postaci:
39
Xdx
dU
Q
+
=
δ
,
przy czym energia wewnętrzna tego układu jest opisana funkcją:
U = U(S, x) = U(T, x).
Różniczka zupełna tej ostatniej funkcji, jako funkcji stanu jest równa:
dU
U
T
dT
U
x
dx
x
T
= ⎛
⎝⎜
⎞
⎠⎟
+ ⎛
⎝⎜
⎞
⎠⎟
∂
∂
∂
∂
.
Podstawiając ten związek do definicji pojemności cieplnej układu mamy kolejno:
.
dT
dx
X
x
U
T
U
dT
dx
X
dT
dx
x
U
T
U
dT
dx
X
dT
dU
dT
dQ
C
T
x
T
x
⎥⎦
⎤
⎢⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
+
=
=
Pojemność cieplną, przy stałej wartości zmiennej niezależnej x, oznaczymy przez C
x
.
Wtedy:
.
T
U
=
C
gdzie
,
dT
dx
X
x
U
C
C
x
x
T
x
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎥⎦
⎤
⎢⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
=
Ponieważ w tym przypadku
Xdx
TdS
dU
−
=
, to
dU
dx
T
S
x
X
T
T
⎛
⎝⎜
⎞
⎠⎟
= ⎛
⎝⎜
⎞
⎠⎟
−
∂
∂
.
Zatem wzór na pojemność cieplną upraszcza się do postaci:
C C
T
S
x
dx
dT
x
T
=
+ ⎛
⎝⎜
⎞
⎠⎟
∂
∂
.
Przy pomocy związku Maxwella,
∂
∂
∂
∂
S
x
X
T
T
x
⎛
⎝⎜
⎞
⎠⎟
= ⎛
⎝⎜
⎞
⎠⎟
,
możemy wyrażenie na pojemność cieplną C przekształcić do postaci:
C C
T
X
T
dx
dT
x
x
=
+ ⎛
⎝⎜
⎞
⎠⎟
∂
∂
.
Jeżeli pochodną zupełną występującą po prawej stronie obliczymy dla warunków,
w których siła uogólniona związana z drugim stopniem swobody
X = const,
to otrzymamy formułę:
C
C
T
X
T
x
T
X
x
x
X
=
+
⎛
⎝⎜
⎞
⎠⎟
⎛
⎝⎜
⎞
⎠⎟
∂
∂
∂
∂
lub w postaci ogólnego prawa Mayera:

40
C
C
T
X
T
x
T
X
x
x
X
−
=
⎛
⎝⎜
⎞
⎠⎟
⎛
⎝⎜
⎞
⎠⎟
∂
∂
∂
∂
.
Jest to trochę ogólniejsza niż poprzednio otrzymana formuła Mayera i dotyczy ona
układu w którym zachodzą dwa procesy termodynamiczne. Pierwszym z nich jest wymiana
ciepła a drugi jest dowolnym procesem.
Przykład.
Magnesowanie magnetyka.
Dla procesu magnesowania zmienną niezależna jest namagnesowanie M,
a potencjałem termodynamicznym tego procesu jest indukcja magnetyczna pola
magnesującego B. w związku z tym otrzymujemy formułę Mayera:
C
C
T
X
T
x
T
X
x
x
X
−
=
⎛
⎝⎜
⎞
⎠⎟
⎛
⎝⎜
⎞
⎠⎟
∂
∂
∂
∂
==>
C
C
T
B
T
M
T
B
M
M
B
−
=
⎛
⎝⎜
⎞
⎠⎟
⎛
⎝⎜
⎞
⎠⎟
∂
∂
∂
∂
.
6.3. Zależność pojemności cieplnej od objętości i ciśnienia
Badając ciepło właściwe lub pojemność cieplną układu musimy odpowiedzieć na dwa
zasadnicze pytania:
1. Czy pojemność cieplna, ogólnie C
x,
zależy od zmiennej niezależnej x?
2. Czy pojemność cieplna, ogólnie C
X
, zależy od zmiennej zależnej X?
Aby
odpowiedzieć na postawione pytania musimy obliczyć pochodne cząstkowe
pojemności cieplnych C
x i
C
X
odpowiednio względem x i X. Dla pierwszej z nich mamy:
.
T
X
T
T
X
T
T
x
S
T
T
T
S
T
x
T
Q
x
)
C
(
x
x
2
2
x
x
x
T
T
x
T
x
T
x
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
Dla drugiej z wymienionych pochodnych otrzymujemy analogicznie:
.
T
x
T
T
x
T
T
x
S
T
T
T
S
T
X
T
Q
X
)
C
(
X
X
2
2
X
X
T
T
T
X
T
X
T
X
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
Mamy zatem dwa równania:
.
T
x
T
)
C
(
X
,
T
X
T
)
C
(
x
X
2
2
T
X
x
2
2
T
x
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
Dla ustalenia uwagi rozważmy konkretny proces termodynamiczny. Niech x = V, a X = p,
wtedy nasz układ równań przyjmie postać:
41
.
T
V
T
)
C
(
p
,
T
p
T
)
C
(
V
p
2
2
T
p
v
2
2
T
V
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
Pierwsze z otrzymanych równań mówi nam, że ciepło właściwe w stałej objętości
zależy od tej objętości, jeżeli ciśnienie jest nieliniową funkcją temperatury. Dla układów,
w których zależność ciśnienia od temperatury jest liniowa, C
V
nie zależy od objętości.
Analogicznie drugie równanie mówi nam, że ciepło właściwe przy stałym ciśnieniu
zależy od tego ciśnienia, jeżeli objętość jest nieliniową funkcją temperatury. Dla układów,
w których zależność objętości od temperatury jest liniowa, C
p
nie zależy od ciśnienia..
6.4. Temperaturowe zależności pojemności cieplnej C
V
i C
p
Spróbujmy
zastosować poprzednią metodę do określenia zależności temperaturowej
pojemności cieplnej. w tym przypadku wyliczamy pochodne cząstkowe wymienionych
w temacie pojemności cieplnych względem temperatury. Mamy:
.
T
S
T
T
T
Q
T
)
C
(
T
,
T
S
T
T
T
Q
T
)
C
(
T
p
p
p
p
p
p
V
V
V
V
V
V
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
W
wewnętrznych nawiasach po prawej stronie tych równań stoją pochodne entropii po
temperaturze, tj. pochodne zmiennej niezależnej po potencjale z nią związanym. Dla takich
pochodnych nie ma związku termodynamicznego Maxwella, który pozwoliłby na zastąpienie
tych pochodnych przez inne. Dochodzimy zatem do wniosku, że w ramach termodynamiki
fenomenologicznej nie da się sprowadzić badania temperaturowej zależności pojemności
cieplnej, do badania innych własności termodynamicznych tego układu. Stąd też
w
termodynamice, badanie temperaturowych zależności tych wielkości fizycznych,
sprowadza się do badań czysto eksperymentalnych lub korzysta się z wyników fizyki
statystycznej.
7. Pojemność cieplna gazu doskonałego
W tym rozdziale zastosujemy wszystkie otrzymane wyniki termodynamicznej teorii ciepła,
dla układu gazu doskonałego w przypadku dwóch stopni swobody, reprezentujących proces
wymiany ciepła (zmienna S) i proces deformacji objętości (zmienna V). z tymi zmiennymi
niezależnymi są związane odpowiednio, potencjały termodynamiczne temperatura T i ujemne
ciśnienie p. Dla takiego układu dodatkowo znamy równanie stanu:

42
pV =
m
RT
µ
,
gdzie n =
m
µ
jest liczbą moli tego gazu w układzie. Ograniczymy się do układu jednego mola
dowolnego gazu.
Obliczając różniczkę zupełną obu stron równania stanu, otrzymujemy związek:
pdV Vdp
RdT
+
=
.
Przy pomocy tego związku wyliczamy wszystkie pochodne zupełne i pochodne cząstkowe wg
następującego algorytmu:
:
R
dT
dp
V
dT
V
d
p
=
+
.
V
p
V
p
,
T
p
V
R
T
p
,
T
V
p
R
T
V
T
V
p
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
7.1. Energia wewnętrzna gazu doskonałego
Energia
wewnętrzna dla układu gazu doskonałego jest nam już znana razem z jej
różniczką zupełną oraz jej pochodnymi zupełną i cząstkową po objętości:
.
V
U
dV
dS
S
U
dV
dU
dV
V
U
dS
S
U
dU
)
V
,
S
(
U
U
S
V
S
V
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⇒
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⇒
=
Dalej ostatnie równanie można przekształcić w następujący sposób:
dU
dV
T
dS
dV
p
U
V
T
S
V
p T
p
T
p
T
T
V
=
−
⇒ ⎛
⎝⎜
⎞
⎠⎟
= ⎛
⎝⎜
⎞
⎠⎟
− = ⎛
⎝⎜
⎞
⎠⎟
−
∂
∂
∂
∂
∂
∂
.
Wykorzystując otrzymany z
równania stanu związek dla pochodnej
cząstkowej
∂
∂
p
T
V
⎛
⎝⎜
⎞
⎠⎟
, otrzymujemy bardzo ważne twierdzenie:
∂
∂
∂
∂
U
V
T
p
T
p T
p
T
p
T
V
⎛
⎝⎜
⎞
⎠⎟ =
⎛
⎝⎜
⎞
⎠⎟ − =
− =
⇒
0
U(V) = const
,
tj.: energia wewnętrzna U gazu doskonałego nie zależy od objętości.
Policzymy teraz pochodną cząstkową energii wewnętrznej po ciśnieniu przy ustalonej
temperaturze. Mamy:
const
=
U(p)
0
p
V
0
p
V
V
U
p
U
T
T
T
T
⇒
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
⋅
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
.
Ostatnie z równań mówi nam, że energia wewnętrzna U gazu doskonałego nie zależy od
ciśnienia.

43
Z
powyższych dwóch wniosków i równania stanu wynika kolejne twierdzenie, że:
U = U(T),
tj.: energia wewnętrzna gazu doskonałego zależy tylko od temperatury,
7.2. Równanie Mayera dla gazu doskonałego
Wykorzystamy tutaj otrzymane ogólne równanie Mayera:
C
C
T
p
T
V
T
p
v
V
p
−
=
⎛
⎝⎜
⎞
⎠⎟
⎛
⎝⎜
⎞
⎠⎟
∂
∂
∂
∂
i zastosujemy je do jednego mola gazu. Mamy:
.
R
T
V
V
R
T
dT
dV
T
p
T
C
C
p
V
V
p
=
⋅
=
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
−
Tak otrzymujemy prawo Mayera dla gazu doskonałego. Prawo to mówi, że różnica molowych
pojemności cieplnych C
p
i C
V
dla gazu doskonałego jest równa stałej gazowej R:
.
R
C
C
V
p
=
−
7.3. Temperaturowe zależności pojemności cieplnej
Zauważmy w tym miejscu, że z równania stanu dla gazu doskonałego wynika liniowa
zależność objętości i ciśnienia od temperatury:
.
T
V
R
p
,
T
p
R
V
⋅
=
⋅
=
To oznacza jak pamiętamy, że C
V
i C
p
nie zależą odpowiednio od V i p. Mamy zatem dwa
związki:
.
0
p
C
i
0
V
C
T
p
T
V
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
7.4. Obliczanie energii wewnętrznej gazu doskonałego
Ponieważ energia wewnętrzna gazu doskonałego zależy tylko od temperatury, to jej
różniczka zupełna dana jest wyrażeniem:
dla jedneg
dU
U
T
dT C dT
C dT
V
V
V
o mola gazu: dla n moli gazu:
dU =
m
=
⎛
⎝⎜
⎞
⎠⎟
=
∂
∂
µ
,
.
Całkując to ostatnie (ogólniejsze) równanie, otrzymujemy całkową postać wyrażenia
na energię wewnętrzną gazu doskonałego:
∫
U
U
m
C T dT
V
=
+
0
µ
( )
.
Energia wewnętrzna gazu doskonałego jest więc określona z dokładnością do stałej
całkowania U
0
.

44
8. Obliczanie funkcji charakterystycznych
Każda funkcja charakterystyczna
Ψ
, jak już wiemy z poprzednich rozdziałów, jest
funkcją stanu tzn. charakteryzuje odpowiedni stan układu w warunkach odpowiedniego
sprzężenia układu z termostatem i nie zależy od procesu, który doprowadził układ do danego
stanu. Dla dowolnej z tych funkcji jest zatem spełnione równanie:
d
Ψ =
∫
0
.
Całka krzywoliniowa po dowolnej krzywej zamkniętej jest równa zeru.
Dalej ograniczymy się do funkcji charakterystycznych układu o dwóch stopniach
swobody S i V. w tym przypadku mamy cztery funkcje charakterystyczne, których definicje
i związki między nimi zestawimy razem.
)
V
,
S
(
U
)
V
,
S
(
=
Ψ
=
Ψ
,
)
pV
TS
)
V
,
S
(
U
)
p
,
T
(
G
)
p
,
T
(
+
−
=
=
Ψ
=
Ψ
,
TS
)
V
,
S
(
U
)
V
,
T
(
F
)
V
,
T
(
−
=
=
Ψ
=
Ψ
,
pV
)
V
,
S
(
U
)
p
,
S
(
H
)
p
,
S
(
+
=
=
Ψ
=
Ψ
.
Z przytoczonych związków między tymi funkcjami widać, że zagadnienie obliczania
funkcji charakterystycznych lub inaczej funkcji stanu. sprowadza się do określenia metody
obliczania energii wewnętrznej i metody obliczania entropii, ponieważ pozostałe funkcje
charakterystyczne wyrażają się przez te dwie funkcje stanu.
Metodę obliczania energii wewnętrznej dla dowolnego układu już znamy
z poprzednich wykładów. Przystąpimy zatem do przedstawienia sposobu obliczania entropii
dla dowolnego układu o dwóch stopniach swobody. Zagadnienie rozważymy na przykładzie
układu o dwu stopniach swobody.
8.1. Obliczanie entropii
Obliczanie entropii dla układu o dwu stopniach swobody
Ograniczymy
się w tym zagadnieniu do układów o dwóch stopniach swobody S i V.
Wiemy już, że potencjały
odpowiadające zmiennym S i V są jednoznacznymi
funkcjami tych zmiennych (patrz równanie stanu w postaci parametrycznej):
p
i
T
−
p).
S(T,
=
S
2.
),
V
,
S
(
p
p
V),
S(T,
=
S
1.
),
V
,
S
(
T
T
⎩
⎨
⎧
⇒
=
⇒
=
Mamy zatem dwa równania wyrażające entropię jako funkcję parametrów (T,V) oraz
parametrów (T, p). Dlatego też otrzymujemy dwie postaci różniczki zupełnej dla entropii:
45
.
dp
T
V
dT
T
S
dp
p
S
dT
T
S
dS
2.
,
dV
T
p
dT
T
S
=
dV
V
S
dT
T
S
dS
1.
p
p
T
p
V
V
T
V
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
Wykorzystując wcześniej znalezione wyrażenia na pojemności cieplne C
V
i C
p
, możemy
wyznaczyć pochodne cząstkowe entropii względem temperatury przy pomocy następującego
algorytmu:
1. C
=
C
T
,
2. C
=
Cp
T
V
V
V
V
p
p
p
T
S
T
S
T
T
S
T
S
T
=
⎛
⎝⎜
⎞
⎠⎟
⇒
⎛
⎝⎜
⎞
⎠⎟
=
⎛
⎝⎜
⎞
⎠⎟
⇒
⎛
⎝⎜
⎞
⎠⎟
∂
∂
∂
∂
∂
∂
∂
∂
.
Stąd wyrażenia na różniczki entropii przyjmują następującą postać:
.
dp
T
V
dT
T
C
dS
2.
,
dV
T
p
+
dT
T
C
dS
1.
p
p
V
V
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
Po scałkowaniu tych równań otrzymujemy również dwie całkowe formuły dla obliczania
entropii w rozważanym przypadku:
.
dp
T
V
dT
T
C
S
S
2.
,
dV
T
p
+
dT
T
C
S
S
1.
p
p
0
V
V
0
⎮
⌡
⌠
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
⎮
⌡
⌠
+
=
⎮
⌡
⌠
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎮
⌡
⌠
+
=
Obliczanie entropii dla gazu doskonałego
Aby
obliczyć entropię dla układu jednego mola gazu doskonałego, wychodzimy
z otrzymanych wyżej równań w postaci całkowej i podstawiamy wyrażeń podcałkowych
odpowiednie pochodne cząstkowe wyliczone dla gazu doskonałego. Mamy:
⎮
⌡
⌠
+
+
=
⎮
⌡
⌠
+
⎮
⌡
⌠
+
⎮
⌡
⌠
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎮
⌡
⌠
+
=
.
dT
T
C
V
ln
R
S
dV
V
R
dT
T
C
S
dV
T
p
+
dT
T
C
S
S
1.
V
0
V
0
V
V
0
.
dT
T
C
p
ln
R
S
dp
p
R
dT
T
C
S
dp
T
V
dT
T
C
S
S
2.
p
0
p
0
p
p
0
⎮
⌡
⌠
+
−
=
⎮
⌡
⌠
−
⎮
⌡
⌠
+
=
⎮
⌡
⌠
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
⎮
⌡
⌠
+
=

46
Jeżeli założymy dalej, że C
V i
C
p
nie zależą od temperatury, co jest prawdziwe dla
wysokich temperatur, to ostatnie wyrażenia na entropię znacznie się uproszczą, mianowicie,
dla pierwszego wyrażenia mamy:
).
V
T
ln(
C
S
)
V
T
ln(
S
)
V
T
ln(
S
T
ln
C
V
ln
R
S
dT
T
C
V
ln
R
S
S
1.
V
V
V
V
C
R
V
0
C
C
R
0
R
C
0
V
0
V
0
⋅
+
=
⋅
+
=
⋅
+
=
+
+
=
⎮
⌡
⌠
+
+
=
Drugie wyrażenie na entropię przyjmuje postać:
).
V
T
ln(
C
S
)
p
T
ln(
S
)
p
T
ln(
S
T
ln
C
p
ln
R
S
dT
T
C
p
ln
R
S
S
2.
p
p
p
p
C
R
p
0
C
C
R
0
R
C
0
p
0
p
0
−
−
−
⋅
+
=
⋅
+
=
⋅
+
=
+
−
=
⎮
⌡
⌠
+
−
=
Biorąc pod uwagę wzór Mayera dla gazu doskonałego mamy:
.
C
C
=
gdzie
,
1
-
1
1
C
C
C
C
R
,
1
C
C
C
C
R
V
p
p
V
p
p
V
V
p
V
χ
χ
χ
=
χ
−
=
−
=
−
χ
=
−
=
Przy pomocy tych związków wzory na entropię przyjmują ostatecznie postać:
).
p
T
ln(
C
S
)
p
T
ln(
C
S
S
.
2
),
V
T
ln(
C
S
)
V
T
ln(
C
S
S
.
1
1
p
0
C
R
p
0
1
V
0
C
R
V
0
p
V
χ
χ
−
−
−
χ
⋅
+
=
⋅
+
=
⋅
+
=
⋅
+
=
Jeżeli wykorzystamy jeszcze równanie Clapeyrona, to otrzymamy drugą postać tych
równań:
).
p
V
ln(
C
'
S
)
p
T
ln(
C
S
S
),
V
p
ln(
C
'
S
)
V
T
ln(
C
S
S
1
p
0
1
p
0
V
0
1
V
0
χ
χ
χ
−
χ
−
χ
⋅
+
=
⋅
+
=
⋅
+
=
⋅
+
=
W równaniach tych stałe S
0
’
wyrażają się przez poprzednie stałe S
0
. Odpowiednie związki
mają postać:
).
R
ln(
C
S
'
S
i
R
ln
C
S
'
S
p
0
V
0
−
=
−
=
9. Procesy adiabatyczne, ogólne równanie adiabaty
Mamy dwie formuły na entropię dla dowolnego układu o dwu stopniach swobody:

47
.
dp
T
V
T
dT
C
dS
,
dV
T
p
T
dT
C
dS
p
p
V
V
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
=
W warunkach adiabatycznych, dS = 0 i równania te przyjmują postać:
.
dp
T
V
C
1
T
dT
0
dp
T
V
T
dT
C
,
dV
T
p
C
1
T
dT
0
dV
T
p
T
dT
C
p
p
p
p
V
v
V
V
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⇒
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⇒
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
9.1. Związek między izotermiczną i adiabatyczną ściśliwością
Porównując stronami względne zmiany temperatury mamy:
.
p
T
T
V
C
C
p
V
dV
T
p
C
1
dp
T
V
C
1
V
p
p
V
S
V
v
p
p
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⇒
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
W ostatnim równaniu wielkość stojąca po lewej stronie jest adiabatyczną ściśliwością.
Wielkość ta jest miarą zmiany objętości na jednostkę ciśnienia w warunkach stałej entropii.
Aby określić tę wielkość, przekształcimy prawą stronę, korzystając z równania stanu
w postaci ogólnej dla dwu stopni swobody:
F(p, V, T) = 0.
Równanie to można rozwiązać względem każdego z trzech parametrów wchodzących do tego
równania. Rozwiązania te zapiszemy w następujący sposób:
p).
T(V,
=
T
3.
p),
V(T,
=
V
2.
V),
p(T,
=
p
.
1
Dla każdego z nich można napisać wyrażenie na różniczkę zupełną. w celu określenia adiabatycznej
ściśliwości skorzystamy z równania na ciśnienie, dla którego różniczka zupełna ma postać:
dp
p
T
dT
p
V
dV
V
T
= ⎛
⎝⎜
⎞
⎠⎟
+ ⎛
⎝⎜
⎞
⎠⎟
∂
∂
∂
∂
.
Jeśli ustalimy p = const, wtedy dp = 0 i poprzednie równanie można przekształcić do postaci:
.
1
V
p
p
T
T
V
p
V
T
p
T
V
T
V
p
T
V
p
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⇒
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
Wyrażenie w nawiasach prostokątnych, w otrzymanej tożsamości, jest dokładnie tym, co stoi po
prawej stronie równania dla adiabatycznej ściśliwości. Mamy zatem ostatecznie wyrażenie na
adiabatyczną ściśliwość:
.
C
C
=
,
p
V
1
p
V
p
V
C
C
p
V
V
p
T
S
T
p
V
S
χ
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
χ
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⇒
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
Po prawej stronie stoi wielkość
,
p
V
T
T
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
=
β
która jest miarą zmiany objętości
układu na jednostkę ciśnienia w warunkach izotermicznych. Wielkość ta nazywa się

48
izotermiczną ściśliwością. Jeżeli adiabatyczną ściśliwość oznaczymy przez
,
p
V
S
S
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
α
to
związek między tymi ściśliwościami można krótko zapisać równaniem:
β
χ α
T
S
= ⋅
,
β
α
T
S
≥
.
Widzimy, że izotermiczna ściśliwość jest wprost proporcjonalna do adiabatycznej ściśliwości.
Ściśliwość izotermiczna jest więc większa od ściśliwości adiabatycznej. Oznacza to,
że przy tej samej zmianie ciśnienia, zmiana objętości w warunkach izotermicznych, jest
większa, od odpowiedniej zmiany objętości w warunkach adiabatycznych.
Równanie:
,
p
V
1
p
V
T
S
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
χ
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
jest równaniem adiabaty w ogólnej różniczkowej postaci.
9.2. Równanie adiabaty dla gazu doskonałego.
Dla gazu doskonałego mamy równanie stanu
RT
pV
=
i stąd równanie różniczkowe
adiabaty przekształca się w następujący sposób:
⇒
⎪⎭
⎪
⎬
⎫
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
p
V
=
p
V
,
p
V
χ
1
p
V
T
T
S
.
p
V
1
p
V
S
χ
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
Z drugiej strony, ponieważ równanie stanu można napisać w postaci
V = V(S, p), to różniczka zupełna tej funkcji jest:
.
dp
p
V
dS
S
V
dV
S
p
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
Stąd pochodna zupełna objętości po ciśnieniu jest równa:
.
p
V
dp
dV
p
V
dp
dS
S
V
dp
dV
S
S
p
const
=
S
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
=
⎯
⎯
⎯
⎯
→
⎯
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
Podstawiając ten związek do równania:
V
p
V
p
S
∂
∂
χ
⎛
⎝
⎜
⎞
⎠
⎟ = −
1
,
otrzymujemy równanie adiabaty dla gazu doskonałego w postaci różniczkowej:
V
p
dV
dp
= −
1
χ
.
To równanie wraz z równaniem Clapeyrona, pV = RT, całkowicie opisuje każdy proces
adiabatyczny w gazie doskonałym. Jest to równanie o rozdzielonych zmiennych, zatem łatwo
je całkować. Rozdzielając zmienne mamy:

49
dV
V
dp
p
= −
1
χ
.
Całkując stronami otrzymujemy równanie:
const
)
pV
ln(
const
+
lnp
1
=
lnV
p
dp
1
V
dV
=
⇒
χ
−
⇒
⎮
⌡
⌠
χ
−
=
⎮
⌡
⌠
χ
.
Po opuszczeniu logarytmu dostajemy jawną postać rozwiązania równania adiabaty dla gazu
doskonałego:
p V
const
⋅
=
χ
.
Równanie to wiąże nam ciśnienie i objętość w przemianie adiabatycznej i często
nazywane jest równaniem Poissone’a. Eliminując z tego równania ciśnienie p przy pomocy
równania stanu:
pV = RT,
mamy zależność:
T V
const
⋅
=
−
χ 1
,
która wyraża związek temperatury i objętości w tej samej przemianie.
10. Równanie politropy dla gazu doskonałego
Wychodzimy z pierwszej zasady termodynamiki dla układu jednego mola gazu doskonałego,
który wymienia z termostatem ciepło đQ i wykonuje pracę objętościową pdV:
pdV
dU
ðQ
+
=
.
Definiując pojemność cieplną politropową lub inaczej molowe ciepło właściwe równaniem:
dT
dQ
C
=
i korzystając z wyrażenia na energię wewnętrzną dU = C
V
dT, poprzednie równanie można zapisać
w postaci:
pdV
dT
C
dT
C
V
+
=
C .
Występujące w tym równaniu ciśnienie, można wyeliminować przy pomocy równania stanu, co
prowadzi do równania o rozdzielonych zmiennych:
CdT C dT RT
dV
V
V
=
+
.
Rozdzielamy zatem zmienne i otrzymujemy równanie:
dT
T
R
C C
dV
V
V
=
−
.
Wykorzystując równanie Mayera:
C
C
R
p
−
=
,

50
mamy kolejne postaci tego równania:
.
C
C
;
V
dV
1
1
V
dV
1
C
C
1
C
C
V
dV
C
C
C
C
T
dT
v
v
V
p
V
V
p
≡
γ
−
γ
−
χ
=
−
−
=
−
−
=
Całkując to równanie stronami, dostajemy związki:
⎮
⌡
⌠
−
γ
−
χ
=
⎮
⌡
⌠
V
dV
1
1
T
dT
,
const,
+
V
ln
1
1
=
lnT
−
γ
−
χ
const
TV
const
V
T
ln
1
1
1
1
=
⇒
=
γ
−
−
χ
−
γ
−
χ
.
Jest to jedna z postaci równania politropy, która wiąże temperaturę z objętością. Eliminując
temperaturę z tego równania, przy pomocy równania stanu, otrzymujemy drugą postać tego równania,
jako związek ciśnienia i objętości:
.
-
1
-
=
n
,
const
V
p
V
p
V
p
n
1
1
-
1
1
-
γ
γ
χ
=
⋅
=
⋅
=
⋅
γ
−
γ
−
χ
+
γ
χ
Współczynnik n zdefiniowany wyżej będziemy nazywać wskaźnikiem politropy. Jest to równanie
opisujące najbardziej ogólny proces termodynamiczny w gazie doskonałym.
Z otrzymanego poprzednio równania politropy:
p V
const
n
⋅
=
można otrzymać, jako szczególne przypadki, równania opisujące wszystkie znane nam przemiany
gazowe, tj. kolejno:
1. przemiany izobarycznej,
2. przemiany izochorycznej,
3. przemiany izotermicznej,
4. przemiany adiabatycznej
według następujących algorytmów:
adiabata.
const
=
V
p
=
n
4.
izoterma,
const
=
V
p
1
=
n
.
3
izochora,
const
V
V
p
V
p
=
n
.
2
izobara,
const
p
pV
0
=
n
.
1
1
0
⇒
⋅
⇒
χ
⇒
⋅
⇒
⇒
=
=
⋅
=
⋅
⇒
∝
±
⇒
=
=
⇒
χ
∝
±
∝
±
11. Układy termodynamiczne otwarte
Na
zakończenie rozważań procesów termodynamicznych równowagowych, opiszemy
procesy zachodzące w układach otwartych, tj. układach wymieniających cząstki (materię)

51
z termostatem. Weźmy zatem pod uwagę układ o dwu stopniach swobody (S, V). Dla takiego
układu mamy drugą zasadę termodynamiki:
pdV
dU
TdS
+
=
.
Ponieważ entropia S, energia wewnętrzna U i
objętość V są wielkościami
ekstensywnymi, zależnymi od ilości materii w układzie, to możemy zdefiniować odpowiednie
wielkości odniesione do dowolnej części układu, w szczególności do jednej cząstki:
.
itd
....
,
N
V
=
v
,
N
U
=
u
,
N
S
s
=
Wtedy druga zasada termodynamiki może być zapisana dla jednej cząstki układu.
Mianowicie:
,
pdv
du
Tds
+
=
gdzie
.
itp
........,
,
N
dV
dV
,
N
dU
du
,
N
dS
ds
=
=
=
W jawnej postaci równanie to jest dane przez związek:
.
N
V
pd
N
U
d
N
S
Td
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
Wykonując operacje różniczek z zaznaczonych nawiasów, mamy:
T
NdS SdN
N
NdU UdN
N
p
NdV VdN
N
−
=
−
+
−
2
2
.
Po
uporządkowaniu mamy równanie:
.
dN
N
TS
pV
U
pdV
dU
TdS
−
+
−
+
=
W liczniku po prawej stronie stoi znana nam wielkość potencjału termodynamicznego
Gibsa G. w mianowniku zaś mamy liczbę cząstek N. Definiując potencjał chemiczny
µ jako
potencjał Gibsa na jedną cząstkę układu, tj. przez równanie:
µ =
G
N
,
otrzymujemy uogólnioną pierwszą zasadę termodynamiki dla układów otwartych:
TdS dU pdV
dN
=
+
− µ
.
Widzimy,
że jeżeli układ jest otwarty, to wymiana cząstek z termostatem sprowadza
się do pojawienia się dodatkowego stopnia swobody, scharakteryzowanego zmienną
niezależną N (liczba cząstek w układzie) i potencjałem chemicznym
µ, jako zmienną zależną.
W ten sposób układ zamknięty, przechodząc w otwarty, staje się układem o trzech
stopniach swobody.

52
Energia
wewnętrzna takiego układu, U = U(S, V, N), tzn. energia wewnętrzna zależy
od liczby cząstek w układzie. Potencjał termodynamiczny Gibsa jest funkcją potencjałów, tzn.
G = G(T, p,
µ).
Sens fizyczny potencjału chemicznego można łatwo określić z zapisanej wyżej zasady
termodynamiki, mianowicie dla procesu adiabatyczno - izochorycznego, gdy dS = dV = 0,
mamy:
.
N
U
dN
dU
V
,
S
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
µ
⇒
µ
=
Potencjał chemiczny jest to wielkość energii wewnętrznej przynoszonej lub wynoszonej
z układu przez jedną cząstkę.
12. Termodynamika procesów nieodwracalnych
Pamiętamy, że procesy nieodwracalne charakteryzują się tym, iż nie ma
odpowiedniości między liczbą stopni swobody układu a liczbą zachodzących procesów. Jeden
rodzaj oddziaływania układu z otoczeniem może powodować kilka procesów. Wiemy
również, że w tym przypadku różnica potencjałów na granicy układu z otoczeniem jest duża:
.
1
P
P
,
P
P
P
u
k
k
k
u
k
t
k
≥
∆
∆
±
=
−
Jeżeli przypomnimy sobie wyrażenie na zmianę energii wewnętrznej:
dU
P dx
k
u
k
k
n
=
=
∑
1
,
gdzie
P
P
P
k
u
k
t
k
=
+ ∆
,
to widać, że dla procesów nieodwracalnych zawsze zmiana energii wewnętrznej jest większa
od równowagowej zmiany tej wielkości:
.
dx
P
dU
n
1
k
k
u
k
∑
=
≥
Na
ogół procesy nierównowagowe nie dają się opisać w ramach fenomenologicznej
teorii termodynamiki. Istnieje jednak pewna grupa procesów nierównowagowych, które mogą
być opisane metodami termodynamiki. Do tej grupy należą reakcje chemiczne i przejścia
fazowe. Procesy te są interesujące dlatego, że nie są wynikiem oddziaływania układu
z otoczeniem (termostatem), mogą zatem zachodzić w układach całkowicie izolowanych.

53
Przyczyną procesów nierównowagowych w
układach izolowanych jest
niejednorodność układu. w
tym przypadku w
układzie istnieją gradienty wielkości
termodynamicznych, tj. gradienty wielkości intensywnych, takich jak temperatura T, ciśnienie
p, potencjał chemiczny i tak dalej. Układ jest wtedy silnie niejednorodny. Ta silna
niejednorodność wielkości termodynamicznych (parametrów termodynamicznych) jest
podstawową przyczyną trudności opisu procesów nieodwracalnych. w przypadku układów
niejednorodnych nie wystarcza już jeden parametr intensywny na każdy stopień swobody. Do
opisu układu trzeba użyć, zamiast tego parametru, funkcji ogólnie zależnej od położenia
i czasu. Dlatego też w termodynamice procesów nierównowagowych wprowadza się opis
lokalny, co oznacza, że parametry termodynamiczne odnosimy do poszczególnych punktów
przestrzennych układu. Cały układ dzielimy na małe części (ale dostatecznie duże aby
zawierały dużą liczbę cząstek). Każdą część układu traktujemy jako układ jednorodny, tj.
scharakteryzowany jednym potencjałem termodynamicznym i jedną zmienną niezależną dla
każdego stopnia swobody. Dla wielkości ekstensywnych wprowadzamy odpowiednie gęstości
odniesione do jednostki objętości układu, np.:
u
U
V
s
S
V
=
=
,
…itd.
Zarówno
potencjały, jak i
gęstości odpowiednich wielkości ekstensywnych,
w układach niejednorodnych, zależą od położenia w układzie i czasu. Powyższe równości dla
tych układów należy rozumieć w sensie ogólnych funkcji zależnych od położenia
rr
punktu
w układzie i chwili czasu t:
u u r t
s s r t
=
=
( , )
( , )
r
r
,
.
12.1. Pierwsza zasada termodynamiki w sformułowaniu lokalnym
Podamy teraz lokalne sformułowanie pierwszej i drugiej zasady termodynamiki dla
procesów nieodwracalnych. w tym celu zdefiniujemy wektor gęstości energii wewnętrznej
r
j
u
oraz strumień energii wewnętrznej I
u
, przepływającej przez element powierzchni
,
A
d
u
r
ograniczającej układ:
dI
d
j dA
u
u
u
=
=
⋅
φ
r
r
.
Weźmy pewien obszar (objętość) układu otoczony powierzchnią A. Całkowita energia
wewnętrzna zawarta w tym układzie jest:
( )
∫
( )
∫
V
3
V
dV
'
r
u
r
d
r
u
U
r
r
=
′
′
=
.
Zasada zachowania energii wymaga, aby zmiana energii wewnętrznej w rozważanym
obszarze była wywołana odpływem lub przypływem energii do otoczenia lub z otoczenia, tzn.

54
aby pełny strumień energii wewnętrznej (zwany również natężeniem przepływu energii lub
krótko przepływem) był równy:
∫
∫
V
3
u
A
u
V
3
3
u
r
d
j
div
A
d
j
r
d
t
u
r
d
)
t
,
r
(
u
t
t
U
I
⋅
−
=
⋅
−
=
⎮
⌡
⌠
⎮
⌡
⌠
∂
∂
=
⋅
∂
∂
=
∂
∂
=
r
r
r
r
.
Objętość została tutaj wybrana dowolnie jako część układu. Przejścia od całki po
powierzchni ograniczającej nasz podukład, do całki po objętości tego podukładu dokonujemy
na podstawie twierdzenia Gaussa:
∫
∫
r
r
r
j dA
div d r
u
A
V
⋅
=
⋅
j
u
3
,
całka po dowolnej powierzchni zamkniętej z dowolnego wektora
r
j
, jest równa całce po
objętości ograniczonej tą powierzchnią z dywergencji tego wektora.
Przepisując poprzednie równanie w postaci:
∂
∂
u
t
div j
= −
r
u
,
mamy równanie, które nazywa się równaniem ciągłości lub inaczej zasadą zachowania energii
w ujęciu lokalnym, ponieważ dotyczy ono dowolnego obszaru układu otaczającego punkt
przestrzenny określony w układzie przez współrzędne wektora położenia. Będziemy zatem to
ostatnie równanie nazywać lokalnym sformułowaniem zasady zachowania energii lub
pierwszą zasadą termodynamiki dla procesów nierównowagowych.
12.2. Druga zasada termodynamiki w sformułowaniu lokalnym
W
odróżnieniu od pędu, momentu pędu i energii, entropia S, nie spełnia zasady
zachowania w zwykłym sensie. Wiemy bowiem, że w procesach odwracalnych (quasi-
statycznych) entropia jest stała dla układu izolowanego. w
przypadku procesów
nieodwracalnych entropia rośnie nawet dla układów izolowanych, tj. układów do których nie
może dopływać z zewnątrz. Entropia może być zatem produkowana w układzie. Ogólnie, dla
układów otwartych, zmianę entropii dS układu można przedstawić jako sumę entropii
dopływającej (wypływającej) do układu dS
exc
i entropii produkowanej w układzie dS
inc
:
dS dS
dS
exc
inc
=
+
.
Z drugiej strony wiemy, że druga zasada termodynamiki nakłada na entropię warunek:
dS
inc
≥ 0
,
przy czym znak ”=” odnosi się do procesów równowagowych. w
procesach
nierównowagowych, czyli nieodwracalnych entropia jest zawsze wytwarzana (produkowana):
dS
inc
> 0
.

55
Weźmy teraz pod uwagę dowolny układ termodynamiczny wydzielony z otoczenia za
pomocą powierzchni A. Dla takiego układu entropia wpływająca do układu lub wypływająca
z
niego przez elementarną powierzchnię
A
d
r
, dla infinitezymalnie małego procesu
termodynamicznego zachodzącego w tym układzie, jest równa
A
d
j
S
r
r
, gdzie jest gęstością
prądu (strumienia) entropii. Stąd zmiana entropii w układzie wywołana wymianą entropii
z termostatem może być zapisana jak następuje:
S
j
r
∂
∂
S
t
j dA
exc
s
A
= −
∫
r r
.
Oznaczmy
przez
σ entropię produkowaną w procesie nieodwracalnym w jednostce
czasu przez jednostkę objętości. Wówczas:
∫
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
∂
∂
σ
σ
=
∂
∂
V
S
t
t
s
=
,
r
d
t
S
V
3
inc
.
Zatem:
∫
∂
∂
∂
∂
∂
∂
σ
∂
∂
S
t
S
t
S
t
r
j dA
s
t
dV
inc
exc
V
S
A
V
=
+
=
−
= ⌠
⌡
⎮
∫
d
3
r r
.
Stosując twierdzenie Gaussa-Ostrogradzkiego do całki powierzchniowej z wektora
gęstości strumienia entropii mamy:
r r
j dA
S
A
∫
=
∫
div d r
V
r
j
s
3
.
Wtedy równanie, na pełną zmianę entropii w układzie posiada, po obu stronach całki
objętościowe po objętości układu i może być zapisane w postaci:
∫
∫
V
3
3
V
s
3
V
r
d
r
d
j
div
r
d
t
s
σ
+
−
=
⎮
⌡
⌠
∂
∂
r
.
Opuszczając całki tego samego typu, po lewej i prawej stronie ostatniego równania,
otrzymujemy równanie ciągłości dla entropii:
,
j
div
t
s
s
σ
+
−
=
∂
∂
r
przy czym wielkość gęstości źródła entropii
σ i wielkość gęstości strumienia entropii są
zdefiniowane wyrażeniami:
=
1
V
, s =
S
V
σ
∂
∂
∂
∂
s
t
s
t
inc
=
.
Wzory te wyrażają lokalne sformułowaniem drugiej zasady termodynamiki. Podkreślmy
jeszcze na zakończenie, że gęstość źródła entropii
σ wyraża ilość entropii produkowanej
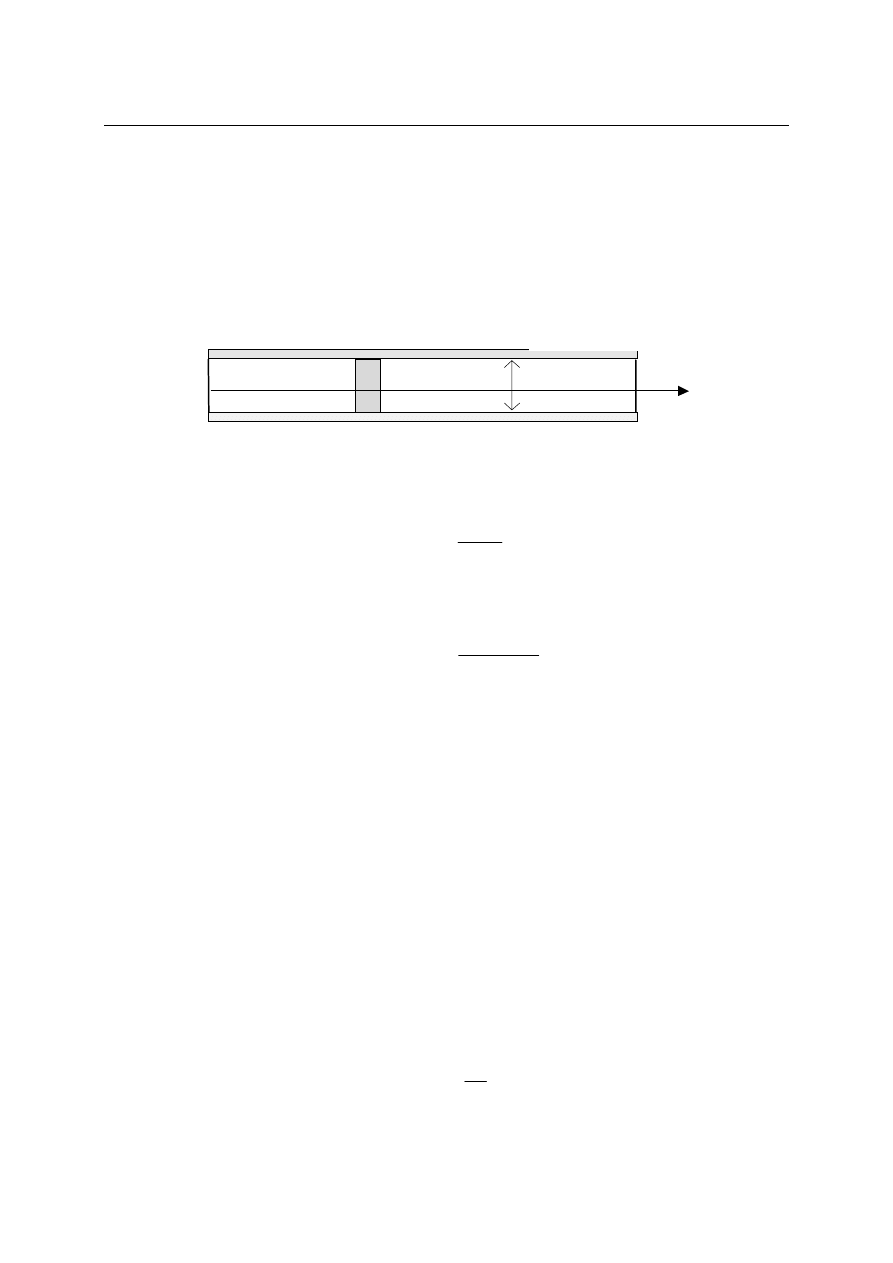
56
w jednostce czasu przez jednostkę objętości układu. Wielkość ta jest miarą odchylenia
procesu nierównowagowego od procesu równowagowego.
12.3. Zagadnienie transportu ciepła
Rozważmy przepływ ciepła (energii) w pręcie o przekroju poprzecznym a jak na
rysunku:
0
x x+dx
dQ(x) dQ(x+dx)
T(x)
T(x+dx)
x
l
T T+dT
osłona adiabatyczna
A
Przez przekrój poprzeczny pręta w punkcie o współrzędnej x z lewej strony pręta na prawą
przepływa w elementarnym procesie (trwającym w czasie dt) ilość ciepła:
đQ
( )
( )
dt
x
x
T
A
x
⋅
∂
∂
χ
−
=
.
Analogicznie z lewej strony na prawą w punkcie o współrzędnej x + dx przez przekrój
poprzeczny przepływa ciepło w ilości:
đQ
(
)
(
)
.
dt
x
dx
x
T
A
dx
x
⋅
∂
+
∂
χ
−
=
+
W tych równaniach
χ jest przewodnictwem właściwym ciepła. Z drugiej strony zgodnie
z określeniem, đQ(x) jest ciepłem wpływającym do elementarnej objętości dV = Adx
przewodnika, đQ(x + dx) jest ciepłem wypływającym z tej objętości. Różnica:
đQ(x) - đQ(x + dx),
jest więc tym ciepłem, które idzie na ogrzanie elementu pręta Adx.
Jeżeli założymy, że ten element nie wykonuje pracy przeciw siłom zewnętrznym, đW
= 0, to ciepło to w całości pójdzie na zmianę energii wewnętrznej tego elementu układu.
Mamy wtedy:
đQ =
AdxdT
c
dT
dm
c
dU
V
V
ρ
=
=
.
Biorąc pod uwagę, że wybrane przekroje pręta x i (x + dx) leżą bardzo blisko siebie, to
zmiana funkcji T(x) przy przejściu z jednego przekroju pręta na drugi może być wyznaczona
z rozwinięcia w szereg względem dx jak następuje:
L
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
=
+
=
dx
x
T
)
x
(
T
)
dx
x
(
T
0
dx
;
Stąd ciepło, które idzie na zmianę energii wewnętrznej daje się przedstawić w postaci:

57
đQ
( )
( )
( )
⎥⎦
⎤
⎢⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
+
∂
∂
−
∂
∂
−
∂
∂
χ
−
=
L
dx
x
x
T
x
x
T
x
x
T
Adt
2
2
,
đQ
( )
.
AdxdT
c
dt
x
x
T
Adx
V
2
2
ρ
=
∂
∂
χ
=
Mamy zatem dwa ważne związki na wielkości đQ i dU w zagadnieniu transportu
ciepła w pręcie:
đQ
s
1
dt
2
2
x
T
Adx
=
∂
∂
χ
=
,
dU c
AdxdT
V
dt
s
=
=
ρ
1
.
Porównując prawe strony tych równań otrzymujemy:
χ
∂
∂
ρ
Adx
T
x
c AdxdT
dt
s
V
dt
s
2
2
1
1
=
=
=
.
Definiując wielkość:
ρ
χ
=
κ
V
2
c
,
zwaną współczynnikiem przewodnictwa temperaturowego, poprzednie równanie przyjmuje
ostateczną postać:
2
2
2
x
T
t
T
∂
∂
κ
=
∂
∂
.
Równanie to znane jest w
teorii transportu jako jednowymiarowe równanie
przewodnictwa cieplnego lub drugie równanie Fouriera. Równanie to łatwo uogólnić na
przypadek transportu ciepła w
ośrodku trójwymiarowym izotropowym. Zagadnienie
sprowadza się do zamiany po prawej stronie tego równania, jednowymiarowego gradientu
temperatury, trójwymiarowym. Wtedy równanie przewodnictwa cieplnego w
ośrodku
izotropowym przyjmuje postać:
∂
∂
κ
T r t
t
T r t
( , )
( , )
r
r
=
∇
2
2
lub równoważną postać (
∇ ≡
):
2
∆
∂
∂
κ
T r t
t
T r t
( , )
( , )
r
r
=
2
∆
.
Dalsze uogólnienie tego ostatniego równania na przypadek ośrodka anizotropowego,
wymaga wprowadzenia tensora drugiego rzędu dla wielkości współczynnika
temperaturowego przewodnictwa cieplnego, w miejsce skalarnej wielkości
κ stojącej
w równaniu dla ośrodka izotropowego.
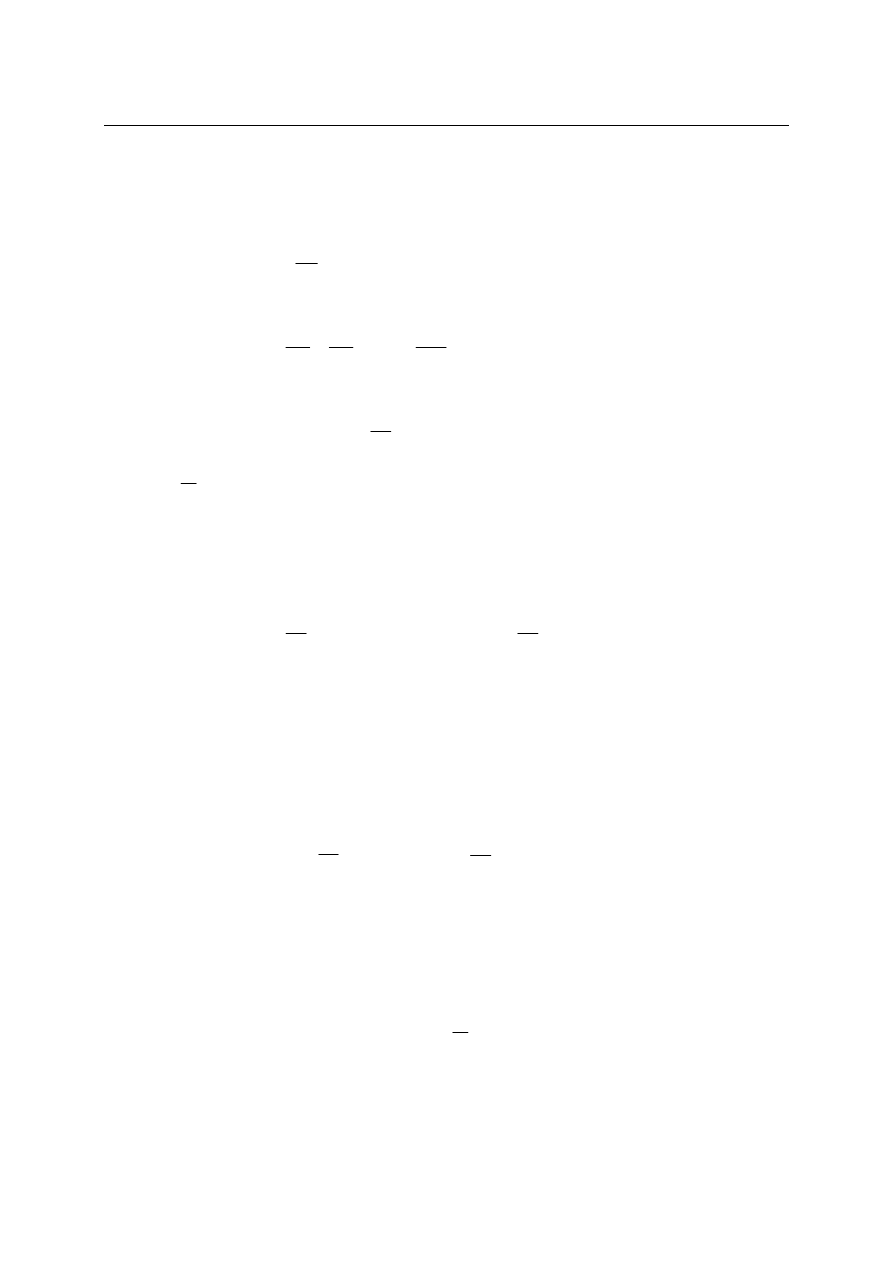
58
Szybkość zmiany gęstości energii wewnętrznej
Przeanalizujmy równanie przewodnictwa cieplnego. Zauważmy, że prawą stronę tego
równania można przedstawić przy pomocy, niezależnych od wyboru układu współrzędnych,
operatorów gradientu i dywergencji jak następuje:
∂
∂
κ
κ
κ
T
t
T
T
div gradT
=
∇
=
∇ ∇
=
2
2
2
2
(
)
(
)
.
Z drugiej strony wiemy, że w przypadku jednowymiarowym mamy:
∂
∂
∂
∂
χ
∂
∂
χ
U
t
Q
t
Adx
T
x
Adx div grad T
x
=
=
=
⋅
2
2
(
)
lub po podzieleniu przez objętość dV = Adx, rozważanego elementu pręta otrzymujemy:
),
T
grad
(
div
t
u
x
⋅
χ
=
∂
∂
gdzie u =
U
V
oznacza energię wewnętrzną na jednostkę objętości.
W zagadnieniu transportu ciepła w trzech wymiarach, odpowiednie równanie dla
zmiany energii wewnętrznej na jednostkę objętości w czasie, czyli szybkości zmiany gęstości
objętościowej energii wewnętrznej, przyjmuje postać:
.
T
t
u
lub
)
gradT
(
div
t
u
∆
⋅
χ
=
∂
∂
⋅
χ
=
∂
∂
.
Jeżeli skorzystamy z elementarnego pierwszego prawa Fouriera, które mówi, iż
gęstość strumienia ciepła
jest proporcjonalna do gradientu temperatury:
r
j
Q
(
)
r
j
gradT
Q
= − ⋅
≡ − ⋅ ∇ ⋅
χ
χ
T
,
to dla przewodnictwa ciepła otrzymujemy równanie wyrażające lokalną postać pierwszej
zasady termodynamiki:
∂
∂
u
t
div j
Q
= −
(
r
)
lub
).
j
(
div
t
u
u
r
−
=
∂
∂
Szybkość zmiany gęstości energii wewnętrznej jest równa ze znakiem minus dywergencji
gęstości strumienia prądu ciepła.
Równanie to bardzo łatwo uogólnić na przypadek procesu transportu dowolnej
wielkości fizycznej. Definiując, gęstość dowolnej wielkości ekstensywnej X wzorem:
x
X
V
=
oraz oznaczając odpowiednią gęstość strumienia przepływu tej wielości przez
,
j
x
r
ogólne
równanie transportu można zapisać w postaci:

59
).
j
(
div
t
x
x
r
−
=
∂
∂
Równanie w tej postaci jest uogólnionym równaniem transportu i w szczególności
wyraża:
1. Przepływ ciepła w stałej objętości układu, gdy x = u oznacza gęstość energii wewnętrznej.
Wtedy równanie:
)
j
(
div
t
u
Q
r
−
=
∂
∂
jest równaniem Fouriera (
- pierwsze prawo Fouriera).
r
j
gra
Q
= −χ
dT
2. Przepływ masy lub proces dyfuzji, gdy x = n oznacza koncentrację. Wtedy równanie:
∂
∂
n
t
div j
n
= −
(
r
)
jest równaniem dyfuzji (
)
n
(
grad
D
j
n
⋅
−
=
r
- pierwsze prawo Ficka).
3. Przepływ pędu, gdy x = p oznacza gęstość objętościową pędu. Wtedy równanie:
)
j
(
div
t
p
p
r
−
=
∂
∂
jest równaniem Newtona (
- prawo Newtona), przy czym v oznacza wartość
prędkość prędkości.
gradv
j
p
η
−
=
r
4. Przepływ prądu, gdy x =
ρ oznacza gęstość ładunku elektrycznego. Wtedy równanie:
)
j
(
div
t
q
r
−
=
∂
∂ρ
jest prawem Ohma (
- pierwsze prawo Ohma).
r
j
gra
q
= − ⋅
σ
d
ϕ
Szybkość zmiany gęstości entropii
Załóżmy teraz, że element pręta w którym badamy transport ciepła, w każdej chwili
jest w równowadze, tj. wymiana ciepła z otoczeniem tego elementu jest odwracalna. Wtedy:
du = Tds,
gdzie s jest gęstością entropii. Zatem równanie wyrażające treść pierwszej zasady
termodynamiki:
),
j
(
div
t
u
u
r
−
=
∂
∂
dla szybkości zmiany gęstości entropii w rozważanym elemencie pręta, przyjmie postać:
T
s
t
div j
Q
∂
∂
= −
(
r
)
lub po podzieleniu przez T:

60
).
j
(
div
T
1
t
s
Q
r
−
=
∂
∂
Równanie to wyraża szybkość zmiany gęstości entropii w funkcji temperatury
i dywergencji z wektora gęstości ciepła lub dywergencji z gęstości strumienia ciepła.
Ponieważ w tym przypadku obowiązuje pierwsze prawo Fouriera:
r
j
gra
Q
= −χ
dT
,
to poprzednie równanie można zapisać w jawnej postaci:
)
T
(
T
1
=
)
gradT
(
div
T
1
t
s
∇
χ
∇
χ
−
−
=
∂
∂
.
Z
matematyki
wiadomo,
że dywergencja z iloczynu skalara przez wektor jest równa:
∇ ⋅
= ⋅ ∇ + ∇ϕ
(
)
ϕ
ϕ
r
r r
a
a a
.
Stosując ten wzór do
div
T
j
q
(
1
r
)
mamy:
∇
⋅
= ⋅ ∇ + ∇
(
)
(
1
1
T
j
T
j
j
T
q
q
q
)
1
r
r
r
.
Zatem szybkość zmiany gęstości entropii jest równa:
T
T
j
)
j
T
1
(
) =
T
1
(
j
)
j
T
1
(
)=
j
div(
T
1
t
s
2
q
q
q
q
u
∇
−
⋅
∇
−
∇
+
⋅
∇
−
−
=
∂
∂
r
r
r
r
r
,
T
T
j
)
j
T
1
(
t
s
2
q
q
∇
−
⋅
−∇
=
∂
∂
r
r
.
Pod znakiem dywergencji, w pierwszym wyrazie po prawej stronie, stoi wyrażenie
definiujące gęstość objętościową strumienia entropii
S
j
r
. Zatem ostatnie równanie można
przedstawić również w postaci:
σ
+
−
=
∇
−
−∇
=
∂
∂
S
2
q
S
j
div
T
T
j
)
j
(
t
s
r
r
r
.
Równanie to definiuje dodatkowo źródło entropii:
{
σ = −
∇ = −
⎛
⎝
⎜⎜
⎞
⎠
⎟⎟ ∇ = − ∇
r
r
r
r
j
T
T
j
T
j
T
T
j
T
T
q
q
S
S
2
1
.
To równanie można jeszcze zapisać inaczej, wykorzystując pierwsze prawo Fouriera. Wtedy
źródło entropii przyjmie drugą postać:
σ
χ∇
χ
= −
∇ = −
−
∇ =
∇
⎛
⎝⎜
⎞
⎠⎟
r
j
T
T
T
T
T
T
T
q
2
2
2
.

61
W ten sposób szybkość zmiany gęstości entropii w procesie transportu ciepła,
sprowadza się do znalezienia rozwiązania równania wyrażającego treść drugiej zasady
termodynamiki dla procesów nierównowagowych, tj. równania:
∂
∂
σ
s
t
divj
S
= −
+
r
,
przy czym źródło entropii dane jest przez dwie możliwe formuły, które przepiszemy tutaj
jeszcze raz w zwartej formie:
.
T
T
,
T
T
j
2
S
⎟
⎠
⎞
⎜
⎝
⎛ ∇
χ
=
σ
∇
−
=
σ
r
Widzimy, że źródło entropii występuje zawsze, gdy w układzie istnieje gradient temperatury.
Oznaczając za Onsagerem przez X
Q
wielkość:
T
T
X
Q
∇
−
=
r
,
którą będziemy dalej nazywać siłą termodynamiczną lub bodźcem termodynamicznym
powodującym proces przepływu ciepła. Wtedy, skutkiem działania takiego bodźca
termodynamicznego jest gęstość strumienia przepływu ciepła, która daje się zapisać
wyrażeniem:
Q
Q
X
T
gradT
j
r
r
χ
−
=
χ
−
=
.
Gęstość strumienia entropii natomiast wyraża się przez X
Q
, jak następuje:
Q
S
X
gradT
T
j
r
r
χ
=
χ
−
=
.
Dla źródła entropii wyrażonego przez siłę termodynamiczną otrzymujemy wyrażenia:
( )
2
Q
2
Q
Q
Q
S
S
X
T
T
,
X
T
j
X
j
T
T
j
χ
=
⎟
⎠
⎞
⎜
⎝
⎛ ∇
χ
=
σ
=
−
=
∇
−
=
σ
r
r
r
r
r
.
Ten pierwszy związek, dla źródła entropii, zapisywany bywa często w postaci:
Q
Q
X
j
T
r
r
⋅
=
σ
⋅
,
jest podstawowym związkiem termodynamiki procesu nieodwracalnego, jakim jest w naszym
przypadku proces wymiany (przepływu) ciepła.
W ogólnym przypadku układy termodynamiczne mogą być trójwymiarowe i
w dodatku anizotropowe. Wtedy prawo Fouriera przyjmuje postać:
( )
,
r
j
T
Q i
i k
k
i
=
∇
∑
χ
.
W takim układzie gradienty: temperatury, potencjału chemicznego lub dowolnego
potencjału P
k
związanego z k-tym procesem, powodują procesy nieodwracalne przewodzenia

62
ciepła, energii, ładunku, itd. Procesy te są scharakteryzowane strumieniami
r
j
x
i bodźcami
termodynamicznymi, które je wywołują X
x
, gdzie symbolu x (małe) w indeksach używa się
do oznaczenia ogólnego dowolnej wielkości fizycznej, która jest transportowana
w rozważanym procesie termodynamicznym.
Przyczyny, albo bodźce termodynamiczne są odchyleniami parametrów
termodynamicznych od stanu równowagi. w
pierwszym przybliżeniu zakładamy, że
strumienie są liniowymi funkcjami sił termodynamicznych X
k
:
k
k
ik
i
X
L
j
∑
=
.
Współczynniki L
ik
są nazywane współczynnikami kinetycznymi. Siły
termodynamiczne X
k
spełniają związek analogiczny jaki otrzymaliśmy wcześniej dla
transportu ciepła:
.
X
j
T
k
k
k
∑
=
σ
⋅
Jest to podstawowy związek termodynamiki procesów nierównowagowych, uogólniony w
stosunku do poprzedniego, na przypadek dowolnych procesów termodynamicznych, w
układach trójwymiarowych i anizotropowych. Widzimy, że źródło entropii w procesach
nierównowagowych zachodzących w układzie jest sumą wszystkich źródeł cząstkowych
entropii pochodzących od różnych przepływów.
Document Outline
- Układy i procesy termodynamiczne
- Pierwsza i druga zasada termodynamiki
- Funkcje charakterystyczne
- Warunki równowagi układów termodynamicznych
- Związki termodynamiczne Maxwella
- Pojemność cieplna układu termodynamicznego
- Pojemność cieplna gazu doskonałego
- Obliczanie funkcji charakterystycznych
- Procesy adiabatyczne, ogólne równanie adiabaty
- Równanie politropy dla gazu doskonałego
- Układy termodynamiczne otwarte
- Termodynamika procesów nieodwracalnych
Wyszukiwarka
Podobne podstrony:
Podstawy termodynamiki wykad
podstawy termodynamiki(1)
Wzory do teorii z podstaw termodynamiki
Podstawy termodynamiki
biologiczne podstawy zachowań, wykad 8
fiza, rozdz.7-Podstawy termodynamiki, 7
Podstawy termodynamiki chemicznej
PODSTAWY TERMODYNAMIKI przepisane wykłady, PODSTAWY TERMODYNAMIKI
termodynamika Wzory do teorii z wymiany ciepla dla USM, Wzory do teorii z podstaw termodynamiki
podstawy termodynamiki(1)
Leble S Podstawy termodynamiki i fizyki statystycznej
6 PODSTAWY TERMODYNAMICZNEGO OPISU UKŁADÓW WIELOSKŁADNIKOWYCH
Wykad Podstawy Prawa Farmaceutycznego Farmakoepidemiologia
6i8 Badanie podstawowych przemian termodynamicznych Wyznaczanie wielkości kappa Wyznaczanie ciepła p
Sawiński, ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Lista z I zasady Termodyna
Estymacja termodynamicznych właściwości biomasy na podstawie zawartości elementarnej
więcej podobnych podstron