Metody systemowe i decyzyjne w informatyce

Kolokwium nr 1 – 4.04.2011

Systemy dynamiczne – równania różniczkowe – równanie stanu

Zadadanie 1 (10pkt)

Na polu bitwy spotkały się dwie armie – Polan, o liczności P

0

, i German, o liczności G

0

. Przez

P (t) oraz G(t) oznaczmy wielkość armii w chwili t Polan i German, odpowiednio. Prędkość zmiany

liczności armii Polan jest proporcjonalna do wielkości armii German z dokładnością do parametru

λ

G

ze znakiem minus. Podobnie, prędkość zmiany liczności armii German jest proporocjonalna do

wielkości armii Polan z dokładnością do parametru λ

P

ze znakiem minus. Oba parametry λ

G

i λ

P

odpowiadają za efektywność obu armii. a) (2pkt) Zapisać równanie stanu oraz podać warunki po-

czątkowe (tj. P (0), G(0), ˙

P (0), ˙

G(0)). b) (4pkt) Przekształcić równanie stanu do postaci równania

różniczkowego drugiego rzędu dla P (t). c) (4pkt) Wyznaczyć transformatę Laplace’a dla P (t).

Rozwiązanie:

a)

dP (t)

dt

= −λ

G

G(t)

dG(t)

dt

= −λ

P

P (t)

oraz warunki początkowe:

P (0) = P

0

G(0) = G

0

˙

P (0) = −λ

G

G

0

˙

G(0) = −λ

P

P

0

b) Biorąc:

G(t) = −

1

λ

G

dP (t)

dt

i wstawiając do drugiego równania mamy

−

1

λ

G

d

2

P (t)

dt

2

= −λ

P

P (t).

Porządkując ostatecznie otrzymujemy

d

2

P (t)

dt

2

− λ

P

λ

G

P (t) = 0.

1

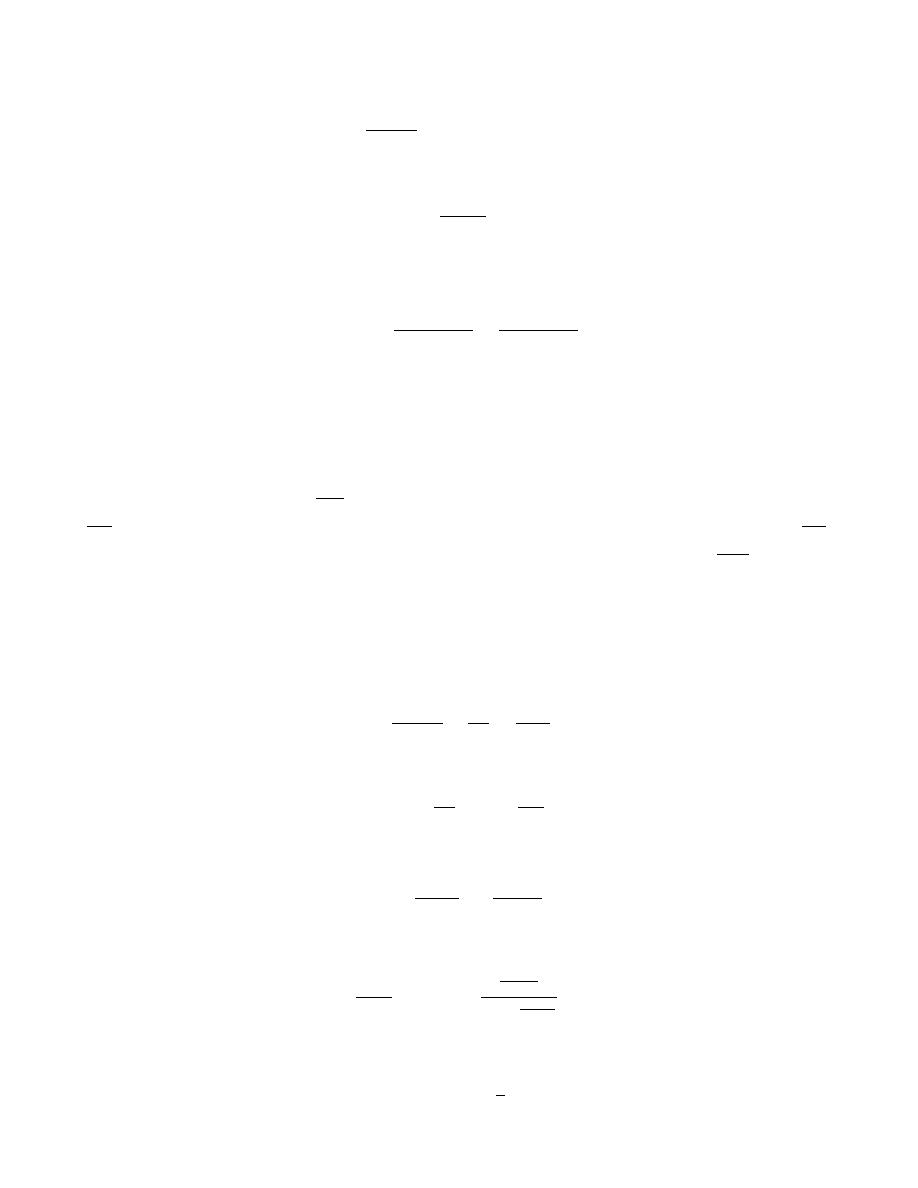
Analogicznie:

d

2

G(t)

dt

2

− λ

P

λ

G

G(t) = 0.

c) Licząc transformatę Laplace’a mamy

s

2

P (s) − sP (0) −

dP (0)

dt

− λ

P

λ

G

P (s) = 0

i porządkując

P (s)(s

2

− λ

P

λ

G

) − sP

0

+ λ

G

G

0

= 0

P (s) =

sP

0

s

2

− λ

P

λ

G

−

λ

G

G

0

s

2

− λ

P

λ

G

.

Zadanie 2 (10pkt)

W sztywnym przewodzie hydraulicznym o kształcie walca i promieniu r pomiędzy dwoma zbior-

nikami przepływa ściśliwy płyn doskonały. Przewód taki modelujemy jako sumę spadku ciśnienia

związanego z masą, tzn. m

h

dI(t)

dt

, oraz spadku ciśnienia związanego ze ściśliwością płynu, tzn.

V (t)

C

h

. Suma spadków równa jest sile tłoczącej płyn działającej na przekrój przewodu, tzn.

F (t)

πr

2

.

Zależność natężenia przepływu od objętości przepływu wyraża się wzorem I(t) =

dV (t)

dt

. a) (2pkt)

Sformułować równanie różniczkowe drugiego rzędu dla V (t). b) (3pkt) Wyznaczyć transmitan-

cję układu. c) (5pkt) Korzystając z tranformaty Laplace’a wyznaczyć odpowiedź układu na siłę

tłoczącą F (t) = m

h

1(t). Przyjąć zerowe warunki początkowe.

Rozwiązanie:

a)

m

h

d

2

V (t)

dt

2

+

V

C

h

=

F (t)

πr

2

b) Licząc transformatę Laplace’a

m

h

s

2

V (s) +

1

C

h

V (s) =

1

πr

2

F (s)

i porządkując otrzymujemy

V (s)(s

2

+

1

m

h

C

h

) =

1

m

h

πr

2

F (s).

Ostatecznie transmitancja układu wynosi

V (s)

F (s)

= K(s) =

1

m

h

πr

2

s

2

+

1

m

h

C

h

.

c) Licząc transformatę Laplace’a wejścia mamy

F (s) = m

h

1

s

2

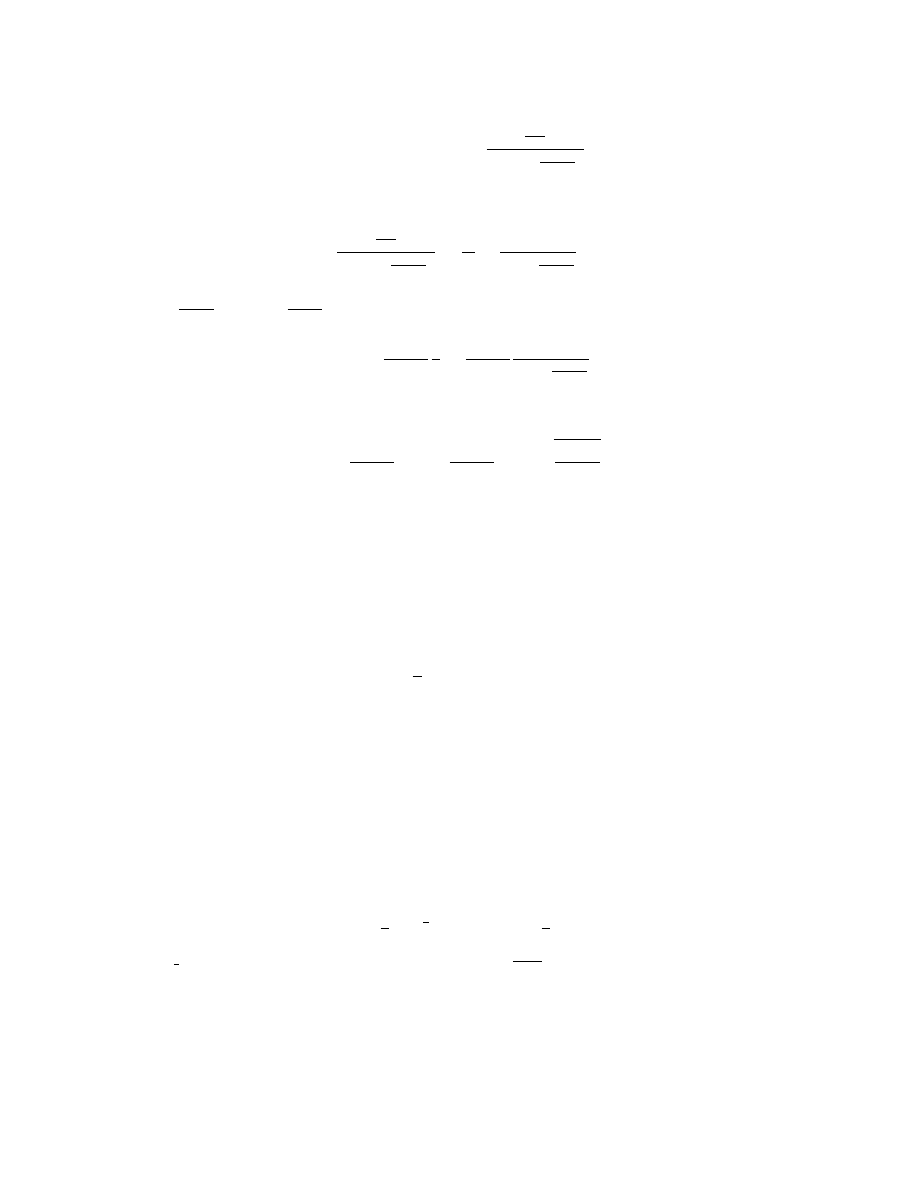
i wstawiając ją do transmitancji otrzymujemy

V (s) = K(s)F (s) =

1

πr

2

s(s

2

+

1

m

h

C

h

)

.

Dalej rozbijamy na ułamki proste

1

πr

2

s(s

2

+

1

m

h

C

h

)

=

A

s

+

Bs + C

s

2

+

1

m

h

C

h

,

gdzie A =

m

h

C

h

πr

2

, B = −

m

h

C

h

πr

2

, C = 0.

Zatem

V (s) =

m

h

C

h

πr

2

1

s

−

m

h

C

h

πr

2

s

s

2

+

1

m

h

C

h

.

Ostatecznie, stosując transformatę odwrotną, mamy

V (t) =

m

h

C

h

πr

2

1(t) −

m

h

C

h

πr

2

cos

r

1

m

h

C

h

t

.

Liniowe zadanie najmniejszych kwadratów

Zadanie 3 (10pkt)

Dany jest model

y = φ(u)

T

a,

gdzie a =

a

0

a

1

. . . a

M −1

T

jest wektorem parametrów, a φ(u) =

φ

0

(u) φ

1

(u) . . . φ

M −1

(u)

T

jest

wektorem funkcji bazowych. Dysponujemy następującymi obserwacjami y =

y

1

y

2

. . . y

N

T

oraz

U = [u

1

u

2

. . . u

N

]. Oznaczmy przez Φ = [φ(u

1

) φ(u

2

) . . . φ(u

N

)]

T

. Ponadto dane są diagonalne

macierze W i V o wymiarach N × N oraz M × M odpowiednio. Zakładamy, że wartości na

diagonaliach macierzy W i V są dodatnie, tj. w

nn

> 0 i v

mm

> 0 dla n = 1, . . . , N i m =

0, . . . , M − 1. Zakładając, że rząd r(Φ) = M , wyznaczyć a minimalizujące następujące kryterium

jakości:

Q(a) =

1

2

kW

1
2

(y − Φa)k

2
2

+

1

2

a

T

Va.

Macierz W

1
2

oznacza macierz diagonalną o wyrazach

√

w

nn

na diagonali, dla n = 1, . . . , N .

Rozwiązanie:

Liczymy gradient z kryterium jakości Q i przyrównujemy do zera:

∇

a

Q(a) = −Φ

T

W(y − Φa) + Va = 0,

3

dalej przekształcając otrzymujemy postać:

(Φ

T

WΦ + V)a = Φ

T

Wy,

i ostatecznie wyznaczamy wartość a:

a = (Φ

T

WΦ + V)

−1

Φ

T

Wy.

Zadanie 4

Dla następujących punktów z płaszczyzny XY :

x

-1

0

1

y

0

2

1

dopasować elipsę (wyznaczyć wektor parametrów a) o następującym równaniu:

y

2

= a

1

x

2

+ a

0

,

korzystając z kwadratowego kryterium jakości. Wskazać wektor funkcji bazowych φ(x).

Rozwiązanie:

Wektor funkcji bazowych φ(x) =

1

x

2

T

macierz danych wejściowych i wektor wyjściowych

mają postać:

Φ =







1 1

1 0

1 1







,

y =







0

4

1







.

Następnie wyznaczamy następujące macierze:

Φ

T

=

"

1 1 1

1 0 1

#

,

Φ

T

Φ =

"

3 2

2 2

#

,

(Φ

T

Φ)

−1

=

"

1

−1

−1

3
2

#

,

(Φ

T

Φ)

−1

Φ

T

=

"

0

1

0

1
2

−1

1
2

#

.

Ostatecznie wyznaczamy parametry elipsy:

a = (Φ

T

Φ)

−1

Φ

T

y =

"

4

−

7
2

#

Elipsa ma zatem równanie:

y

2

= −

7

2

x

2

+ 4,

które możemy przekształcić do bardziej naturalnej postaci:

7

8

x

2

+

1

4

y

2

= 1.

4