Modele rynku kapitałowego

dr M. Kowerski

Ekonometria finansowa

Wykład III

Opracowano na podstawie:

K. Jajuga, T. Jajuga. Inwestycje, instrumenty finansowe, inżynieria
finansowa. PWN, 2000.
W. Tarczyński. Rynki kapitałowe. Metody ilościowe. T. 1, wyd. 2,
Agencja Wydawnicza Placet, Warszawa 2001.
W. Tarczyński. Rynki kapitałowe. Metody ilościowe. T. 1, wyd. 2,
Agencja Wydawnicza Placet, Warszawa 1997.

Indeksy rynku

Najważniejsze funkcje indeksu rynku:

!

w sposób syntetyczny informuje o sytuacji na rynku,

!

jest instrumentem pierwotnym dla instrumentów

pochodnych (opcji, kontraktów futures, kontraktów

forward),

!

stanowi punkt odniesienia przy ocenie efektywności

inwestowania,

!

jest substytutem portfela rynkowego, co ma

znaczenie w teorii portfela i modelach rynku

kapitałowego.

Indeksy rynku

(cd.)

Podstawowe cechy, ze względu na które różnią się

indeksy rynku:

!

liczba spółek, których akcje są uwzględniane przy

konstrukcji indeksu,

!

konstrukcja wag przydzielanych akcjom

poszczególnych spółek,

!

metoda uśredniania stosowana przy konstrukcji

indeksu.

Dow Jones Industrial Average (DJIA)

Charakteryzuje nowojorską giełdę akcji, New York
Stock Exchange. Jest to również najstarszy indeks
giełdowy. Jego początki datują się na rok 1884.
Regularnie DJIA jest obliczany od maja 1886 r.
Wtedy opierał się na 12 spółkach. W 1916 r.
rozszerzono liczbę uwzględnianych spółek do 20,
a w 1928 r. do 30. Ta liczba spółek pozostała do dziś,
z tym że co pewien czas akcje niektórych spółek są
zastępowane akcjami innych spółek.

Dow Jones Industrial Average

(cd.)

Indeks Dow Jones Industrial Average oblicza się

według następującego wzoru:

!

!

wartość wskaźnika DJIA w okresie t,

!

cena akcji i -tej spółki w okresie t,

!

dzielnik przyjęty w okresie t.











 ∑

=

=

N

i

t

it

t

d

P

DJIA

1

/

30

=

N

−

t

DJIA

−

it

P

−

t

d

Inne indeksy Dowa-Jonesa

!

Dow Jones Transportation Average (DJTA), będący

skorygowaną (za pomocą dzielnika) sumą cen akcji

20 spółek transportowych,

!

Dow Jones Utilities Average (DJUA), będący

skorygowaną (za pomocą dzielnika) sumą cen akcji

15 spółek użyteczności publicznej,

!

Dow Jones Composite Average, będący

skorygowaną (za pomocą dzielnika) sumą cen akcji

65 spółek uwzględnianych przy obliczaniu DJIA,

DJTA, DJUA.

Indeks Standard & Poor's 500

Również ten indeks charakteryzuje giełdę
nowojorską. Jego historia rozpoczyna się w 1923 r.,
gdy Standard & Poor's Corporation opublikowała
indeks akcji 233 spółek. W lutym 1957 r. lista ta
została powiększona do 500 spółek.

Indeks Standard & Poor's 500

(cd.)

Indeks Standard & Poor's 500 (S&P 500) określa się

według następującego wzoru:

!

!

wartość indeksu Standard & Poor's 500 w okresie t,

!

liczba akcji i -tej spółki znajdujących się na rynku w okresie t,

!

cena akcji i -tej spółki w okresie t,

!

liczba akcji i -tej spółki znajdujących się na rynku w okresie

podstawowym;

!

cena akcji i -tej spółki w okresie podstawowym.

10

)

(

/

)

(

1

1

⋅













∑

∑

=

=

=

N

i

N

i

iB

iB

it

it

t

P

w

P

w

SP

500

=

N

−

t

SP

−

it

w

−

it

P

−

iB

w

−

iB

P

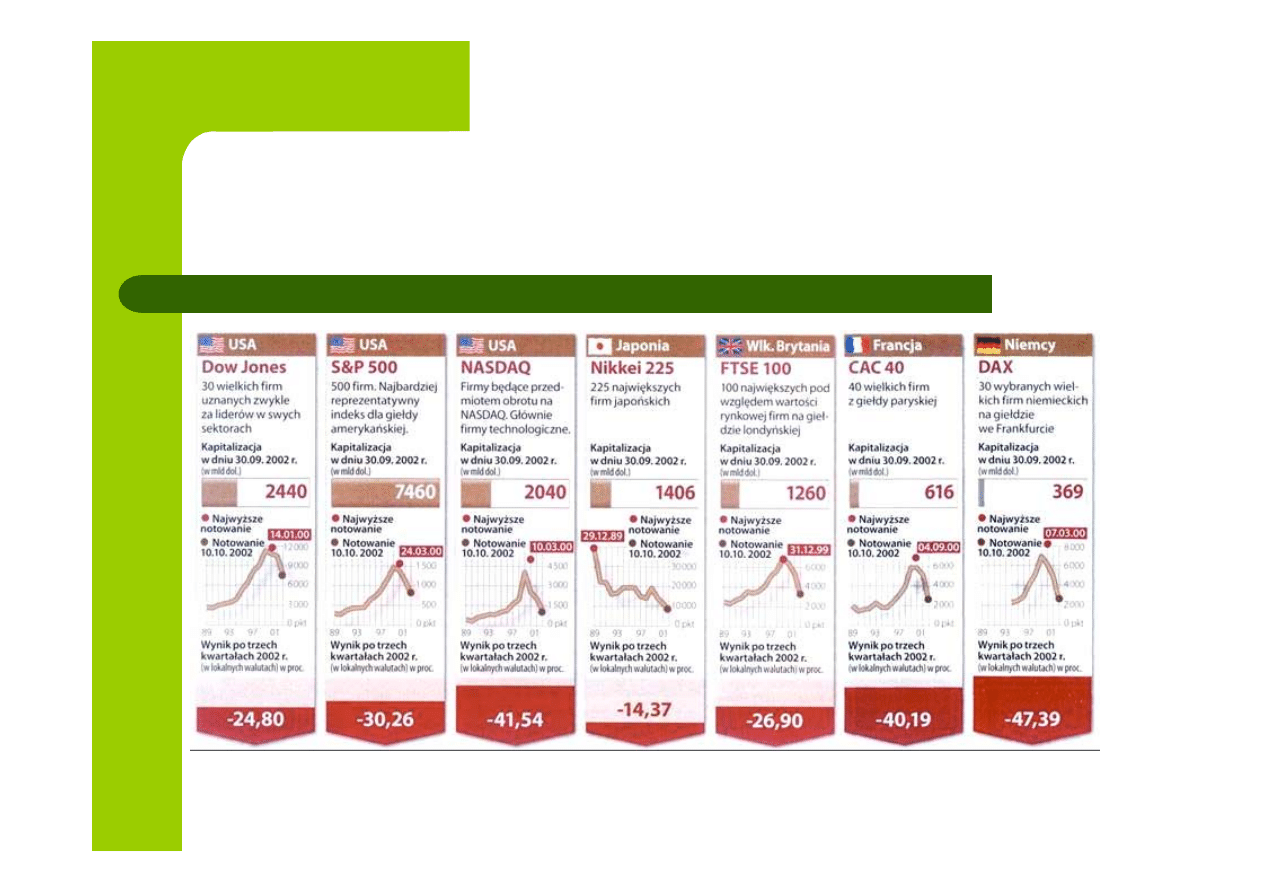
Wielkie giełdy światowe i ich

notowania w latach 1989 - 2002

Źródło: CBS MarketWatch, Polityka nr 42, 19 października 2002

Krach na Wall Street

10,0

-

-

42

-

420

-

Dow Jones
Industrial
Average

4,9

53,7

151,2

6 1/4

59

127 1/2

50 3/4

National
Cash
Register

0,8

89,4

251,4

3 1/2

49 1/4

466 1/2

132 3/4

Montgomery
Ward

2,1

57,6

207,8

8 1/2

168 1/8

396 1/4

128 3/4

General
Electric

4,9

47,3

146,8

7 1/4

78 1/4

148 3/8

56 7/8

Bethlehem
Steel

20,9

41,2

87,0

70 1/4

197 1/4

335 5/8

179 1/2

American
Telephone &
Telegraph

Cena min.
w 1932 do
maksymalnej
z 03.09.1929

Strata
procentowa
03.09.1929
13.11.1929

Zysk
procentowy
03.03.1928
03.09.1929

Minimalna
cena w
1932

Cena
minimalna
13.11.1929

Cena
maksym.
03.09.1929

Cena
otwarcia
03.03.1928

Spółka

Źródło : B. G. Malkiel, Błądząc po Wall Street. Dlaczego nie można wygrać z rynkiem, WIG-Press,
Warszawa 2003, s. 23 – 27.

Warszawski Indeks Giełdowy (WIG)

!

Indeks WIG obliczany jest (z dokładnością do przeprowadzanych co pewien

czas drobnych modyfikacji) według nowej formuły, zgodnie ze wzorem:

!

liczba spółek uwzględnionych w indeksie (wszystkie spółki rynku

podstawowego,

!

wartość WIG w okresie t,

!

liczba akcji i -tej spółki znajdujących się na rynku (dopuszczonych do

obrotu giełdowego) w okresie t,

!

cena akcji i -tej spółki w okresie t,

!

liczba akcji i -tej spółki znajdujących się na rynku w okresie

podstawowym (wtedy na giełdzie było 5 spółek),

!

cena akcji i -tej spółki w okresie podstawowym,

!

współczynnik korygujący w okresie t.

1000

)

(

/

)

(

1

5

1

⋅











 ∑

∑

=

=

=

t

N

i

i

iB

iB

it

it

t

K

P

w

P

w

WIG

−

N

−

t

WIG

−

it

w

−

it

P

−

iB

w

−

iB

P

−

t

K

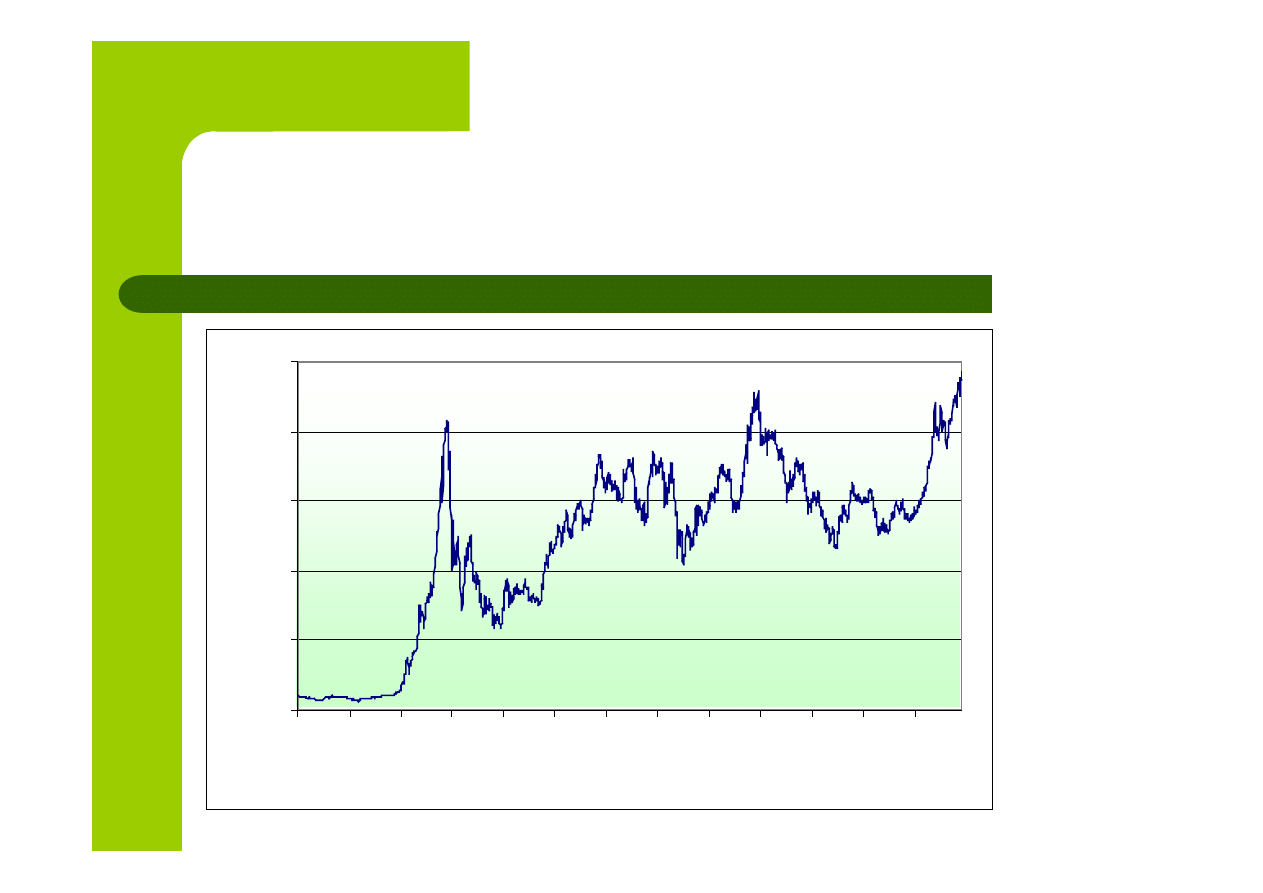
Notowania WIG w latach 1991 - 2004

0

5000

10000

15000

20000

25000

kw

i 9

1

kw

i 9

2

kw

i 9

3

kw

i 9

4

kw

i 9

5

kw

i 9

6

kw

i 9

7

kw

i 9

8

kw

i 9

9

kw

i 0

0

kw

i 0

1

kw

i 0

2

kw

i 0

3

Warszawski Indeks Giełdowy (WIG20)

WIG20 również charakteryzuje rynek podstawowy
Giełdy Papierów Wartościowych w Warszawie.
Jest on notowany od 16 kwietnia 1994 r.

Indeks ten obliczany jest na podstawie portfela
składającego się z akcji 20 spółek o największej
wartości rynkowej i największym obrocie.

Portfel indeksu WIG20

stan na 9 marca 2004 r.

KGHM

KETY

DEBICA

COMPLAND

COMARCH

BZWBK

BUDIMEX

BRE

BPHPBK

AGORA

TPSA

20

10

SWIECIE

19

9

SOFTBANK

18

8

PROKOM

17

7

PKNORLEN

16

6

PGF

15

5

PEKAO

14

4

ORBIS

13

3

NETIA

12

2

MILLENNIUM

11

1

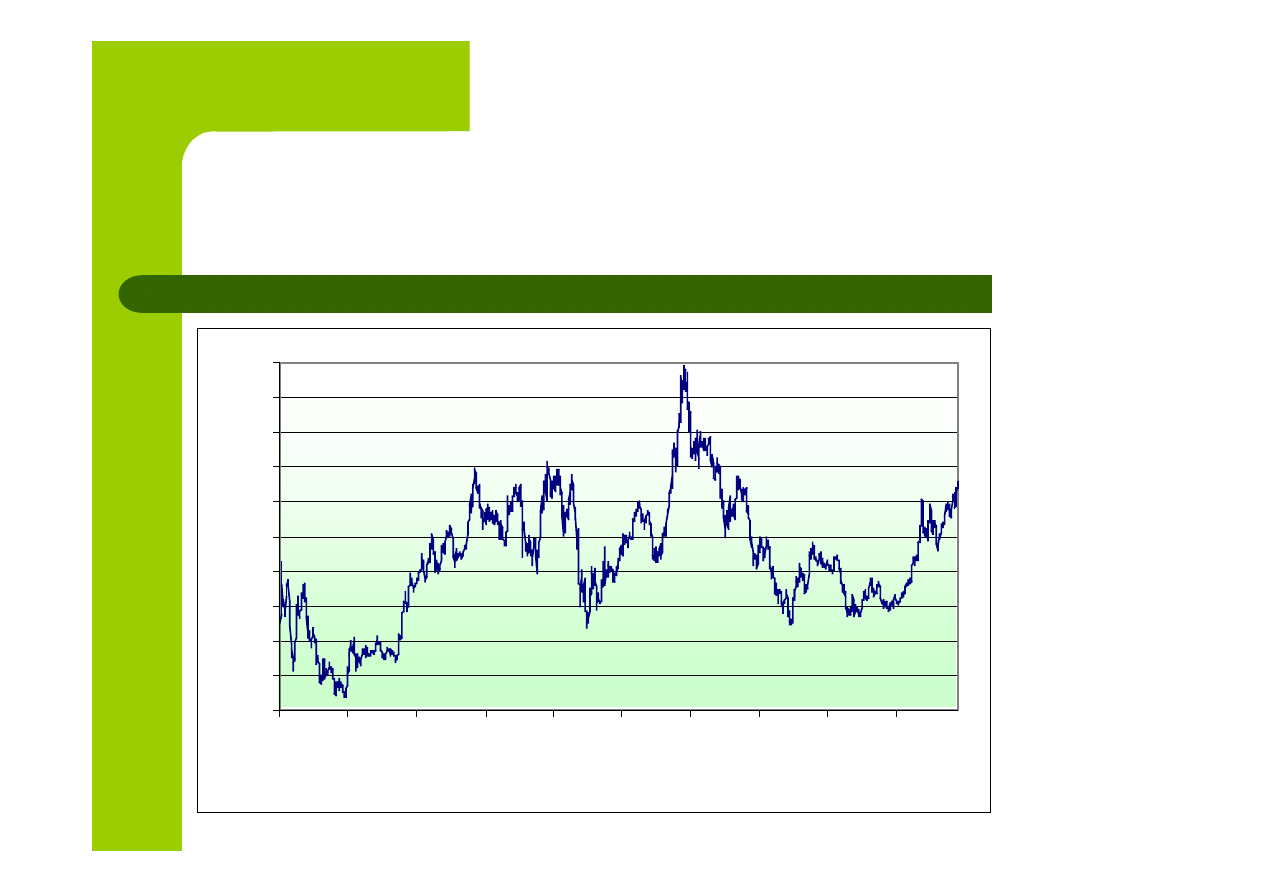
Notowania WIG20 w latach 1994 - 2004

500

700

900

1100

1300

1500

1700

1900

2100

2300

2500

kw

i 9

4

kw

i 9

5

kw

i 9

6

kw

i 9

7

kw

i 9

8

kw

i 9

9

kw

i 0

0

kw

i 0

1

kw

i 0

2

kw

i 0

3

Liczba spółek tworzących indeksy

(1 marca 2004)

14

NIF

75

WIRR

40

MIDWIG

21

TECHWIG

20

WIG20

85

WIG

Liczba spółek

Indeks

Sytuacja finansowa na WGPW

(za rok 2003)

Sytuacja finansowa spółek notowanych na
WGPW w 2003 roku:

!

liczba spółek z zyskiem:

133

!

liczba spółek ze stratą:

84

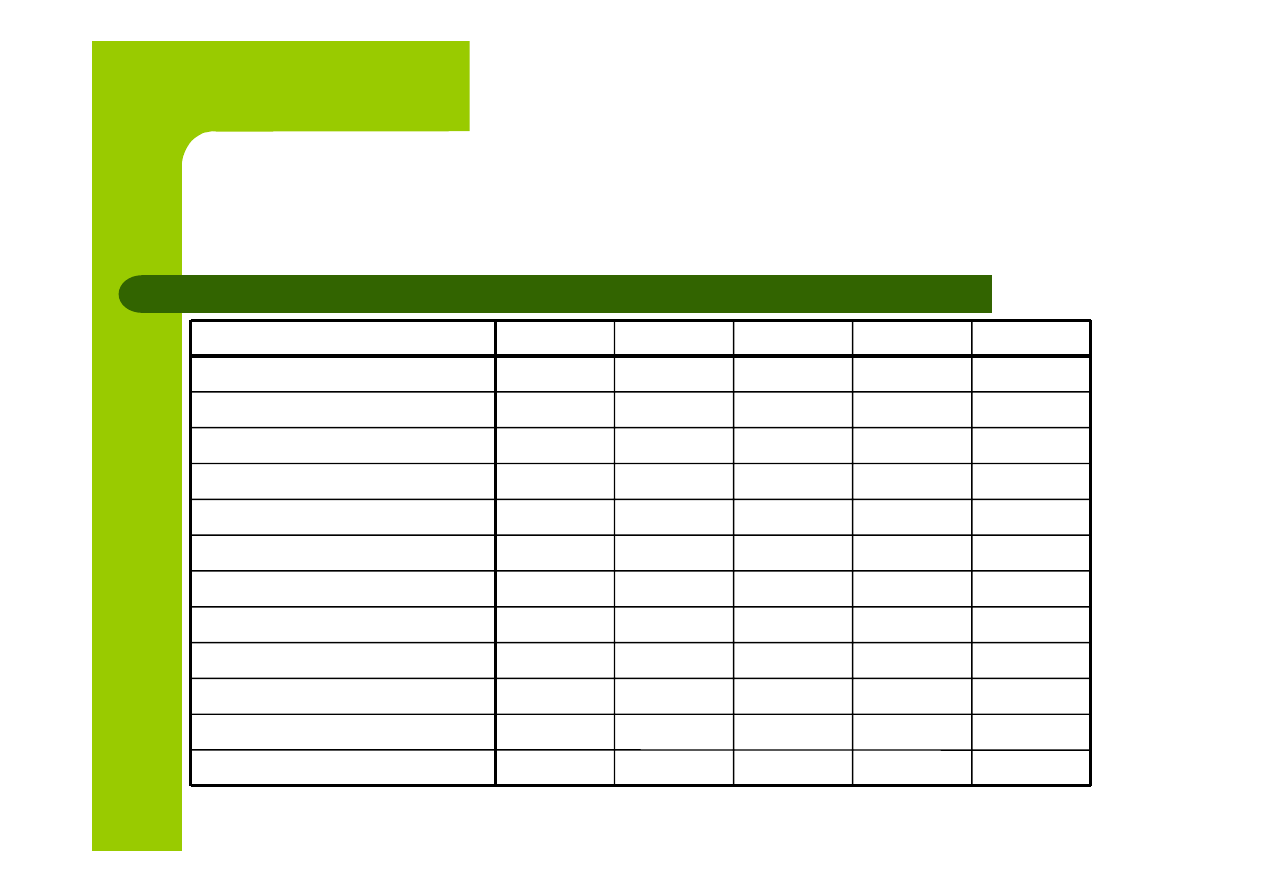
Podstawowe wskaźniki giełdowe

w latach 1999 - 2003

24,6

31,8

-35,8

-22,6

100,7

Stopa zwrotu z WIRR (%)

-7,6

-2,1

-1,3

1,3

-1,8

Stopa zwrotu z NIF (%)

---

45,7

-59,5

-39,7

60,6

Stopa zwrotu z TechWIG (%)

41,3

-1,3

-22

3,2

44,9

Stopa zwrotu z WIG (%)

41,4

-9,9

1,6

-6,9

33,6

Stopa zwrotu z MIDWIG (%)

43,8

1,5

-33,5

-2,7

33,9

Stopa zwrotu z WIG20 (%)

2 085,90

2 748,60

1 763,70

1 365,60

2 740,70

WIRR na koniec roku

60,6

59,8

59

59,8

58,7

NIF na koniec roku

1 000,00

1 456,90

590,2

356,1

571,9

TechWIG na koniec roku

18 083,60

17 847,60

13 922,20

14 366,70

20 820,10

WIG na koniec roku

1 098,70

1 004,70

1 020,50

950,2

1 269,30

MIDWIG na koniec roku

1 755,80

1 816,20

1 208,30

1 175,60

1 574,00

WIG20 na koniec roku

1999

2000

2001

2002

2003

Indeksy

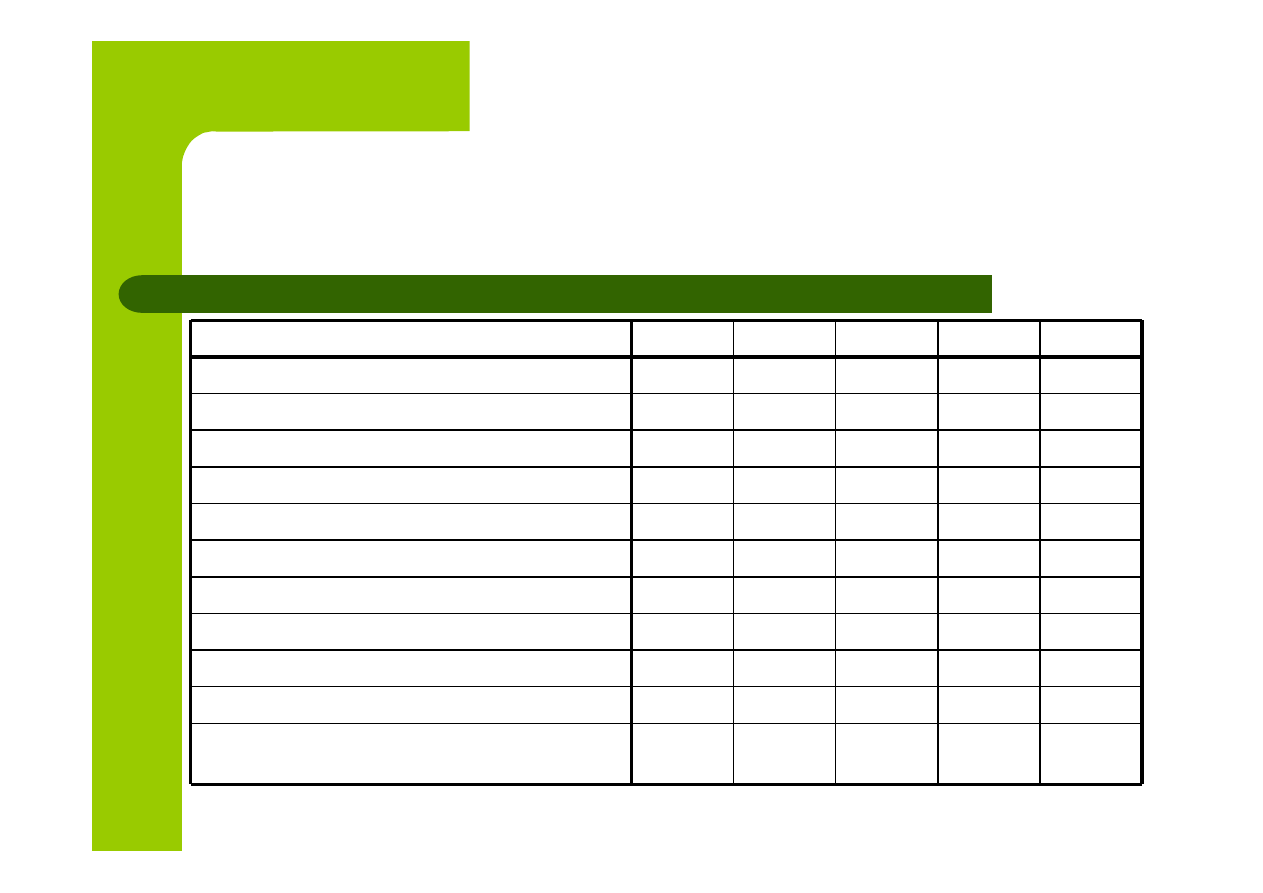
Podstawowe wskaźniki giełdowe

w latach 1999 - 2003

1 158

1 236

1 085

1 016

947

Liczba rachunków inwestycyjnych na koniec
roku (tys.)

249

250

250

249

251

Liczba sesji w roku

10 257

22 668

12 859

11 255

12 996

Średnia wartość transakcji (zł)

17 417

14 919

12 512

11 358

12 228

Liczba transakcji na sesję

357,3

676,4

321,8

255,7

317,8

Średnie obroty na sesji (mln zł)

88 974

169 096

80 443

63 662

79 774

Wartość obrotów w całym roku (mln zł)

0,6

0,8

1,3

1,3

1,6

Stopa dywidendy na koniec roku (%)

1,91

1,98

1,34

1,35

1,42

Średni wskaźnik C/WK

36,2

28,5

31,3

70,3

146,2

Średni wskaźnik C/Z

123 411

130 085

103 370

110 565

167 717

Kapitalizacja na koniec roku (mln zł)

221

225

230

216

203

Liczba notowanych spółek na koniec roku

1999

2000

2001

2002

2003

Spółki

System notowań giełdowych WARSET

System WARSET został wdrożony na Giełdzie Papierów

Wartościowych w Warszawie 17 listopada 2000 roku.
Podstawowym elementem systemu WARSET jest centralny

system notujący, który jest programem komputerowym

zainstalowanym w głównym komputerze giełdowym.
Program realizuje najważniejsze zadania, którymi są:

!

przyjmowanie i weryfikacja zleceń z domów maklerskich,

!

przekazywanie do domów maklerskich informacji o przyjęciu lub

odrzuceniu zlecenia,

!

dystrybuowanie informacji o złożonych zleceniach na zewnątrz

systemu,

!

kojarzenie zleceń w celu zawarcia transakcji,

!

po zawarciu transakcji wysyłanie informacji do domów

maklerskich i odbiorców zewnętrznych.

WARSET

(cd.)

Wszystkie informacje dotyczące sytuacji na rynku giełdowym
trafiają do Satelitarnego Systemu Dystrybucji Informacji
Giełdowej (SSDIG). Za pośrednictwem SSDIG informacje
docierają do wszystkich odbiorców jednocześnie.

Notowania z jednokrotnym fixingiem

Przed otwarciem

zlecenia na kolejny dzien

11:45-16:30

Dogrywka

11:15-11:45

Fixing

11:15

Interwencja

11:00-11:15

Przed otwarciem

8:30-11:00

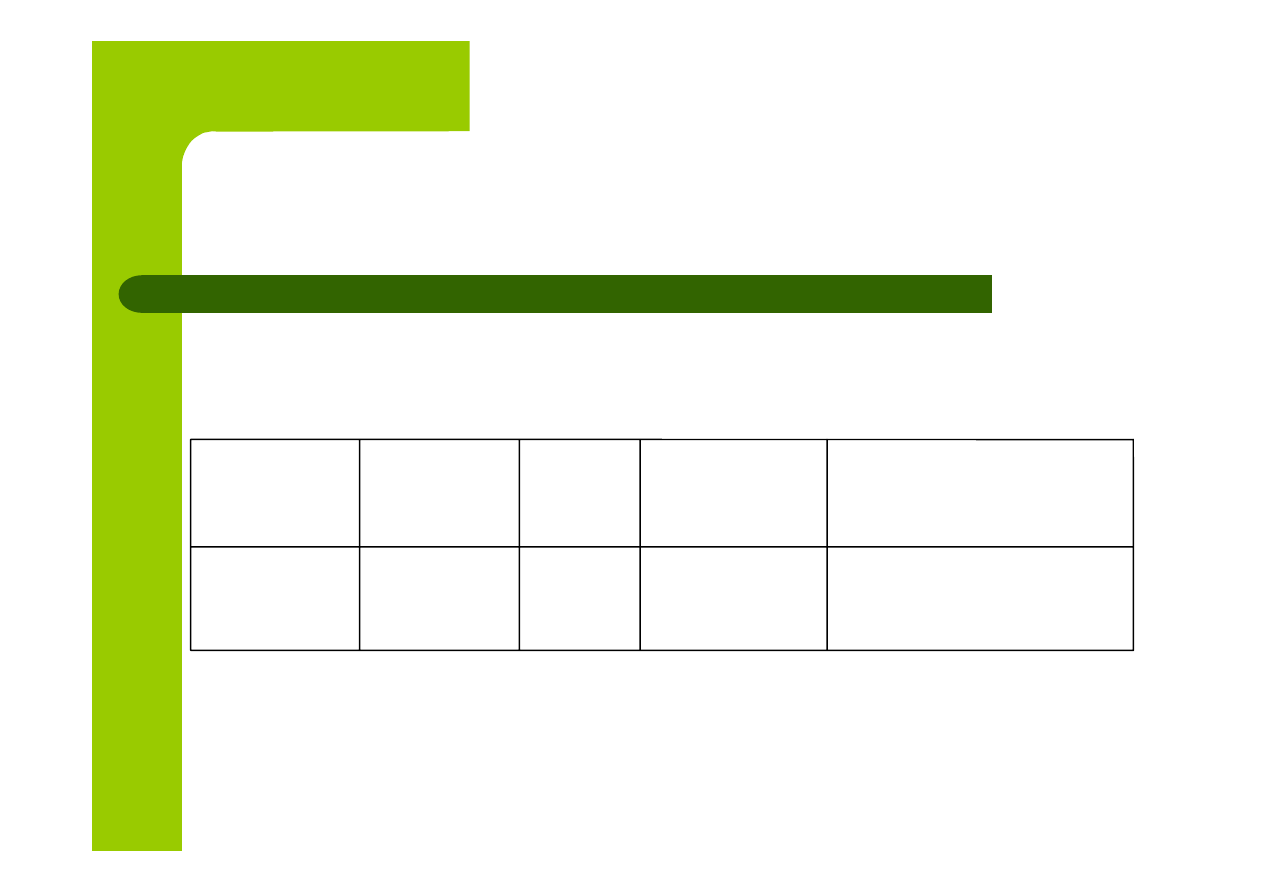
WARSET

(cd.)

Notowania z dwukrotnym fixingiem

Przed otwarciem zlecenia

na kolejny dzien

15:30-16:30

Dogrywka

15:00-15:30

Fixing

15:00

Interwencja

14:45-15:00

Przed otwarciem

11:45-14:45

Dogrywka

11:15-11:45

Fixing

11:15

Interwencja

11:00-11:15

Przed

otwarciem

8:30-11:00

WARSET

(cd.)

Notowania ciągłe

Przed

otwarciem

16:10-16:30

Zamkniecie

Fixing

16:10

Przed

zamknieciem

(zlecenie na

zamkniecie)

16:00-16:10

Notowania

ciagle

10:00-16:00

Otwarcie

Fixing

10:00

Przed

otwarciem

8:30-10:00

Model jednowskaźnikowy Sharpe'a

Model jednowskaźnikowy (single-index model)

opracowany przez Williama Sharpe'a powstał jako

model upraszczający klasyczną teorię portfela:

!

stopa zwrotu i -tej akcji;

!

stopa zwrotu indeksu rynku;

!

współczynniki równania;

!

składnik losowy równania.

i

M

i

i

i

R

R

ε

β

α

+

+

=

−

i

R

−

M

R

−

i

i

β

α

,

−

i

ε

Linia charakterystyczna akcji

W praktyce równanie regresji jest szacowane

i w rezultacie otrzymuje się postać:

Równanie to nazywa się linią charakterystyczną

akcji, a ogólniej - linią charakterystyczną papieru

wartościowego (security characteristic line).

M

i

i

i

R

R

β

α

+

=

ˆ

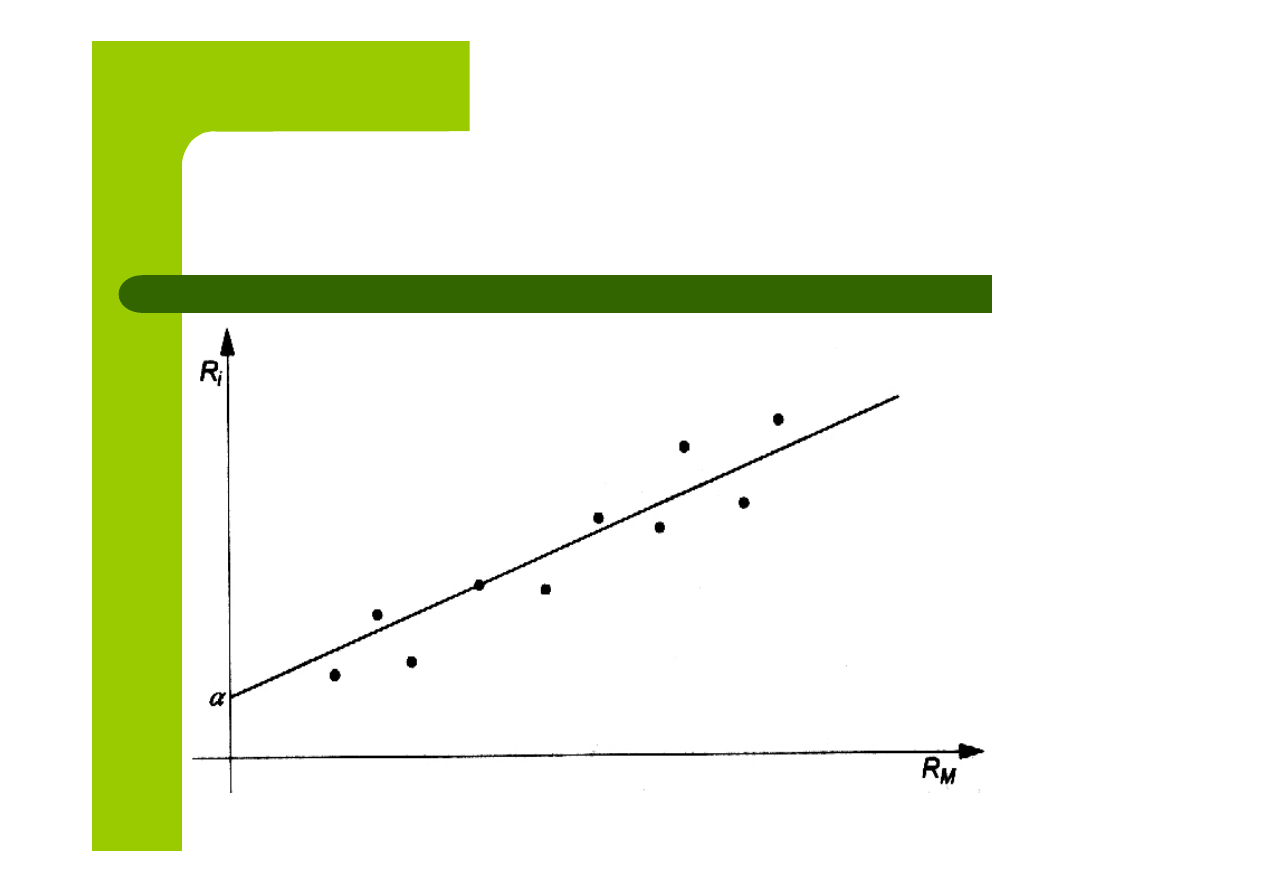
Linia charakterystyczna akcji

Współczynnik Beta

!

0<

ββββ

<1 oznacza, że stopa zwrotu akcji w małym stopniu reaguje

na zmiany zachodzące na rynku - taka akcja nazywana jest

akcją defensywną;

!

ββββ

> 1 oznacza, że stopa zwrotu akcji w dużym stopniu reaguje na

zmiany zachodzące na rynku - taka akcja nazywana jest

akcją agresywną;

!

ββββ

= 1 oznacza, że stopa zwrotu akcji zmienia się w takim samym

stopniu jak stopa zwrotu rynku - w szczególności, portfel rynkowy

ma współczynnik beta równy 1;

!

ββββ

= 0 oznacza, że stopa zwrotu akcji nie reaguje na zmiany rynku;

wobec tego akcja wolna jest od ryzyka rynku - w szczególności

instrument wolny od ryzyka, taki jak bon skarbowy, ma

współczynnik beta równy 0;

!

ββββ

< 0 oznacza, że stopa zwrotu akcji reaguje na zmiany odwrotnie

niż rynek; jest to stosunkowo rzadki przypadek, choć bardzo

pożądany, jeśli spodziewany jest spadek stóp zwrotu większości

akcji na rynku.

Oceny parametrów linii charakterystycznej

Wzory na oceny parametrów linii charakterystycznej
otrzymane metodą najmniejszych kwadratów są
następujące:











 ∑

−











 ∑

−

−

=

=

=

n

t

M

Mt

n

i

M

Mt

i

it

i

R

R

R

R

R

R

1

2

1

)

(

/

)(

(

β

M

i

i

i

R

R

β

α

−

=

Oceny parametrów linii charakterystycznej

(cd.)

!

liczba okresów, z których pochodzą informacje,

!

stopa zwrotu i -tej akcji w t -tym okresie,

!

stopa zwrotu indeksu rynku w t -tym okresie,

!

średnia arytmetyczna stóp zwrotu i -tej akcji,

!

średnia arytmetyczna stóp zwrotu indeksu

rynku.

−

n

−

it

R

−

Mt

R

−

i

R

−

M

R

Zależności w modelu jednowskaźnikowym

!

wariancja stopy zwrotu indeksu rynku;

!

wariancja składnika losowego.

M

i

i

i

R

R

β

α

+

=

2

2

2

2

ei

M

i

i

S

s

s

+

⋅

=

β

)

/(

)

(

2

j

i

M

j

i

ij

s

s

s

r

⋅

⋅

⋅

=

β

β

−

2

M

s

−

2

ei

S

Wariancje w modelu jednowskaźnikowym

Wariancje te określone są na podstawie linii
charakterystycznej akcji, według wzorów:

)

1

/(

)

(

1

2

2

−













∑

−

=

=

n

R

R

s

n

t

M

Mt

M

)

1

/(

)

(

1

2

2

−











 ∑

⋅

−

−

=

=

n

R

R

S

n

t

Mt

i

i

it

ei

β

α

Ryzyko akcji a ryzyko portfela

Współczynnik beta wiąże ryzyko całkowite akcji
z ryzykiem portfela rynkowego w sposób następujący:

!

współczynnik korelacji stopy zwrotu akcji

i stopy zwrotu portfela rynkowego.

M

iM

i

i

s

r

s

/

)

(

⋅

=

β

−

iM

r

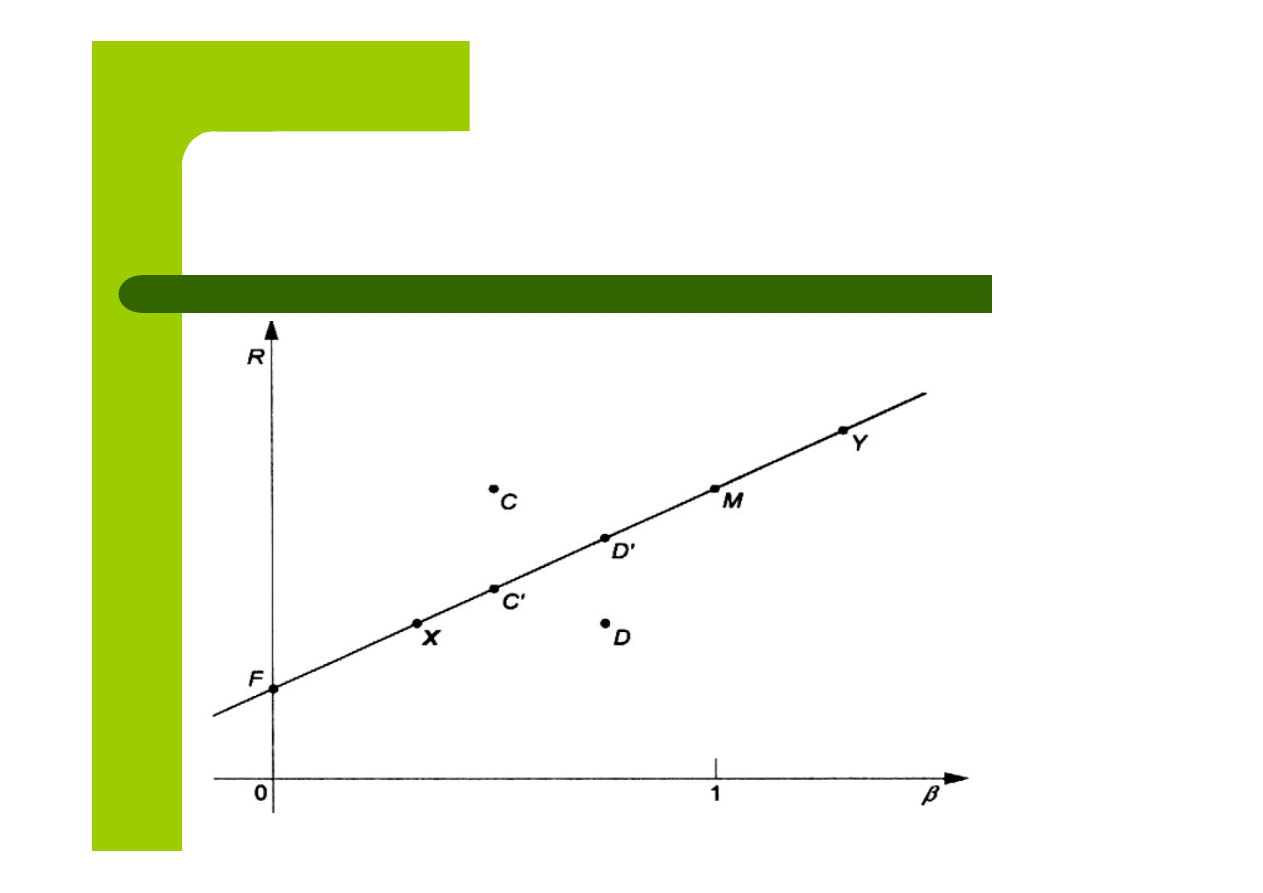
Dywersyfikacja portfela

Współczynnik Beta dla portfela akcji

∑

=

=

n

i

i

i

p

w

1

β

β

CAPM

Model równowagi rynku kapitałowego

Powstanie tego modelu jest zasługą trzech
badaczy: Williama Sharpe'a, Johna Lintnera
i Jana Mossina, którzy opracowali go niemal
niezależnie.

Założenia klasycznej wersji CAPM

!

nie ma kosztów transakcji,

!

jest doskonała podzielność instrumentów
finansowych,

!

nie ma podatków od dochodów osobistych,

!

transakcje pojedynczego inwestora nie mogą mieć
wpływu na cenę instrumentu finansowego,

!

przy podejmowaniu decyzji inwestorzy biorą pod
uwagę tylko oczekiwaną stopę zwrotu i ryzyko
instrumentów finansowych,

Założenia klasycznej wersji CAPM

(cd.)

!

występuje krótka sprzedaż akcji,

!

istnieje nieograniczona możliwość udzielania bądź

zaciągania kredytu przy stopie wolnej od ryzyka,

!

wszyscy inwestorzy podejmują decyzje na jeden

okres,

!

wszyscy inwestorzy mają te same oczekiwania co do

charakterystyk instrumentów finansowych

(oczekiwanych stóp zwrotu, ryzyka, współczynników

korelacji); nazywa się to jednorodnością oczekiwań

(homogeneous expectations) inwestorów,

!

wszystkie instrumenty mogą być bez przeszkód

kupowane lub sprzedawane na rynku.

SML

Linia rynku papierów wartościowych

Security market line:

!

oczekiwana stopa zwrotu portfela (na rynku

znajdującym się w równowadze),

!

współczynnik beta tego portfela.

)

(

f

M

f

R

R

R

R

−

⋅

+

=

β

−

R

−

β

SML – współczynnik Beta

!

gdy

β

= 1 (portfel rynkowy), wówczas R = R

M

(czyli

na SML leży również portfel rynkowy);

!

gdy

β

= 0 (instrumenty wolne od ryzyka), wówczas

R = R

f

(czyli na SML leży też portfel zawierający

instrumenty wolne od ryzyka);

!

gdy

β

> l (portfel agresywny), wówczas R > R

M

;

!

gdy 0<

β

<1 (portfel defensywny), wówczas

R

f

< R < R

M

;

!

gdy

β

< 0, wówczas R < R

f

.

SML – współczynnik Alfa

!

R - oczekiwana stopa zwrotu portfela
(np. oszacowana za pomocą analizy fundamentalnej).

Współczynnik alfa wyznacza się nie tylko dla
pojedynczych akcji, ale również dla portfeli akcji:

))

(

(

f

M

f

R

R

R

R

−

+

−

=

β

α

∑

=

=

n

i

i

i

p

w

1

α

α

Linia rynku papierów wartościowych

Portfel leżący na SML

Po podstawieniu do SML równania określającego
współczynnik beta, otrzymujemy w odniesieniu do
portfela leżącego na SML:

iM

i

M

f

M

f

i

r

s

s

R

R

R

R

⋅

−

+

=

]

/

]

[(

APT - teoria arbitrażu cenowego

Autorem APT (arbitrage pricing theory) jest Stephen

Ross. Model ten zaliczany jest do tzw. modeli

czynnikowych (factor models), w których zakłada się,

że stopy zwrotu akcji generowane są według wzoru:

!

stopa zwrotu i -tej akcji,

!

j -ty czynnik,

!

wyraz wolny,

!

współczynnik wrażliwości (sensitivity factor )

i -tej akcji względem j -tego czynnika.

i

m

im

i

i

i

i

F

b

F

b

F

b

a

R

ε

+

⋅

+

+

⋅

+

⋅

+

=

...

2

2

1

1

−

i

R

−

j

F

−

j

a

−

ij

b

Dwuczynnikowy model APT

Dowodzi się, że oczekiwana stopa zwrotu portfeli
dostępnych na rynku określona jest następującym
równaniem:

2

2

1

1

0

β

λ

β

λ

λ

⋅

+

⋅

+

=

R

Wieloczynnikowy model APT

!

Prowadząc podobne rozważania dla ogólnego
przypadku modelu wieloczynnikowego
(m czynników), otrzymujemy model APT, określający
oczekiwaną stopę zwrotu portfela:

!

oczekiwana stopa zwrotu portfela,

!

współczynniki wrażliwości portfela

względem czynników ryzyka,

!

współczynniki równania.

m

m

b

b

b

R

⋅

+

+

⋅

+

⋅

+

=

λ

λ

λ

λ

...

2

2

1

1

0

−

R

−

m

b

b

b

,......,

,

2

1

−

m

λ

λ

λ

λ

,.....,

,

,

2

1

0

Wieloczynnikowy model APT

(cd.)

Można również dowieść, że współczynniki modelu

dane są jako:

!

stopa wolna od ryzyka,

!

oczekiwana stopa zwrotu portfela, który jest

niewrażliwy na wszystkie czynniki oprócz j -tego,

a którego wrażliwość na j -ty czynnik jest

jednostkowa

Współczynnik jest to premia za

ryzyko wywołane czynnikiem .

i

λ

f

R

=

0

λ

(

)

m

,

1,2,......

j

,

=

−

=

f

pj

i

R

R

λ

−

f

R

−

pj

R

(

)

m

,

1,2,......

j

=

j

λ

j

F

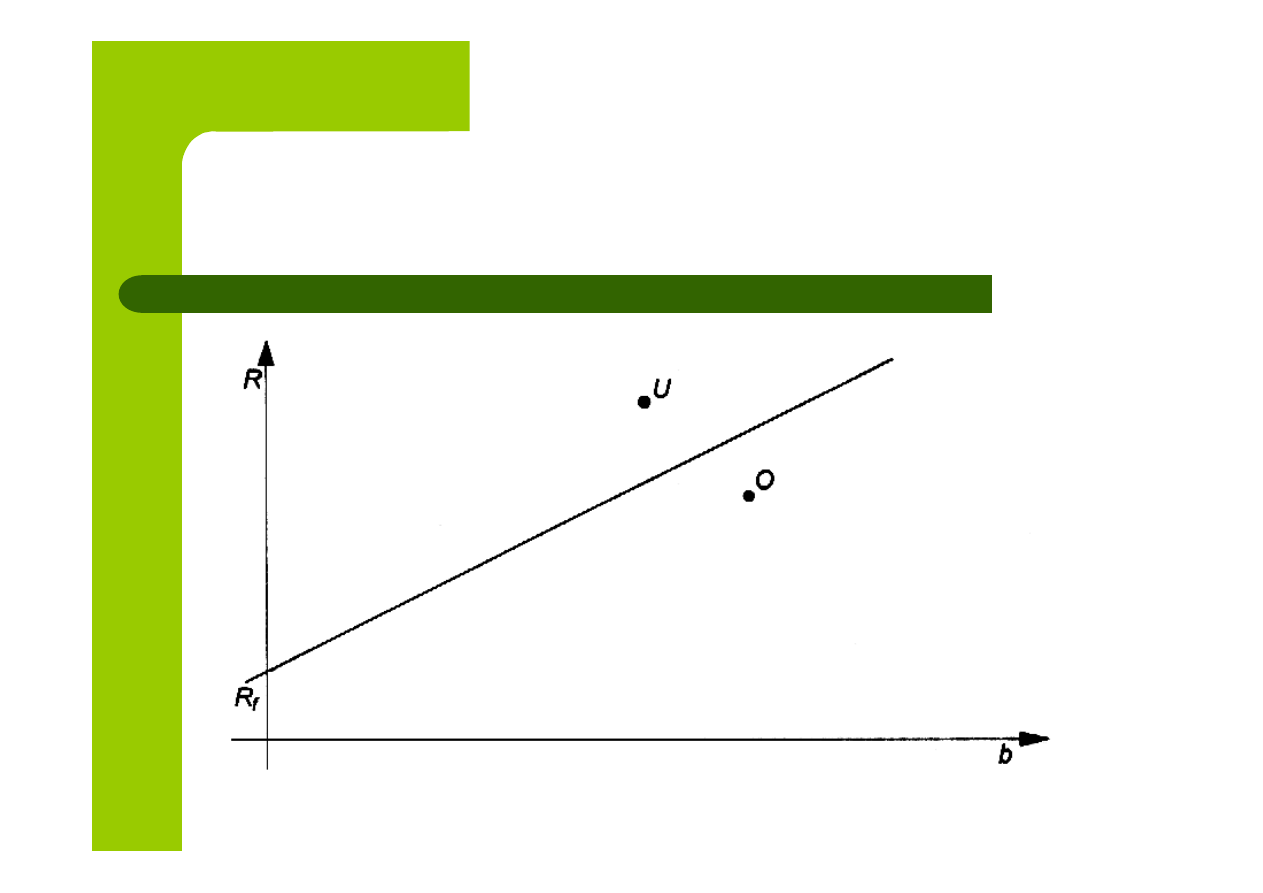
Linia arbitrażu cenowego wyrażonego

wzorem:

λ

⋅

+

=

b

R

R

f

Model APT Model CAPM

Jeśli w modelu jednoczynnikowym APT:

przyjmiemy, że czynnikiem ryzyka jest stopa zwrotu
portfela rynkowego, to otrzymamy model CAPM.
Wtedy współczynnik wrażliwości b jest to po prostu
współczynnik beta, a

λ

, jest to premia za ryzyko

z CAPM, równa

λ

⋅

+

=

b

R

R

f

f

M

R

R

−

Taksonomiczna miara atrakcyjności

inwestycji w papiery wartościowe

Jest to metoda opracowana przez W.Tarczyńskiego,

która może być zaliczona do grupy metod z pogranicza

analizy portfelowej i fundamentalnej z przewagą tej

drugiej. Podstawą rozważań jest dwuwymiarowa

macierz obserwacji:

!

n - liczba obiektów – notowanych na giełdzie spółek,

!

m - liczba zmiennych – wskaźników ekonomiczno-

-finansowych charakteryzujących analizowane spółki.

!

Macierz X dotyczy określonego momentu czasu.

[ ]

(

)

m

j

n

i

x

ij

,.....,

2

,

1

;

,.....,

2

,

1

X

=

=

=

Wskaźniki charakteryzujące spółki

!

wskaźniki płynności (liquidity ratios)
np. wskaźnik bieżącej płynności, wskaźnik szybkiej
płynności,

!

wskaźniki zadłużenia (debt ratios)
np. wskaźnik ogólnego poziomu zadłużenia,
wskaźnik zadłużenia długoterminowego,

!

wskaźniki sprawności – aktywności (activity ratios)
np. wskaźnik rotacji zapasów, okres spływu
należności, wskaźnik rotacji aktywów ogółem,

Wskaźniki charakteryzujące spółki

(cd.)

!

wskaźniki zyskowności (profitability ratios)

np. wskaźnik zyskowności netto, wskaźnik zwrotu

z inwestycji,

!

wskaźniki rynkowe (market based ratios)

np. zysk przypadający na jedną akcję, wskaźnik

cena do zysku, wskaźnik dynamiki zysku firmy,

wskaźnik ryzyka rynkowego beta.

Taksonomiczna miara atrakcyjności

algorytm postępowania

Spośród m potencjalnych zmiennych objaśniających

należy wybrać k zmiennych diagnostycznych.

Przy czym ze zbioru potencjalnych zmiennych

objaśniających należy usunąć zmienne silnie

skorelowane ze sobą. Proces eliminacji zmiennych

kontrolowany będzie miarą słabego uwarunkowania

macierzy. Niech R będzie macierzą korelacji

pomiędzy potencjalnymi zmiennymi objaśniającymi a

liczba N miarą uwarunkowania macierzy R:

Im liczba ta jest mniejsza tym macierz jest lepiej uwarunkowana

numerycznie.

( )

( )

1

R

R

1

−

=

N

N

n

N

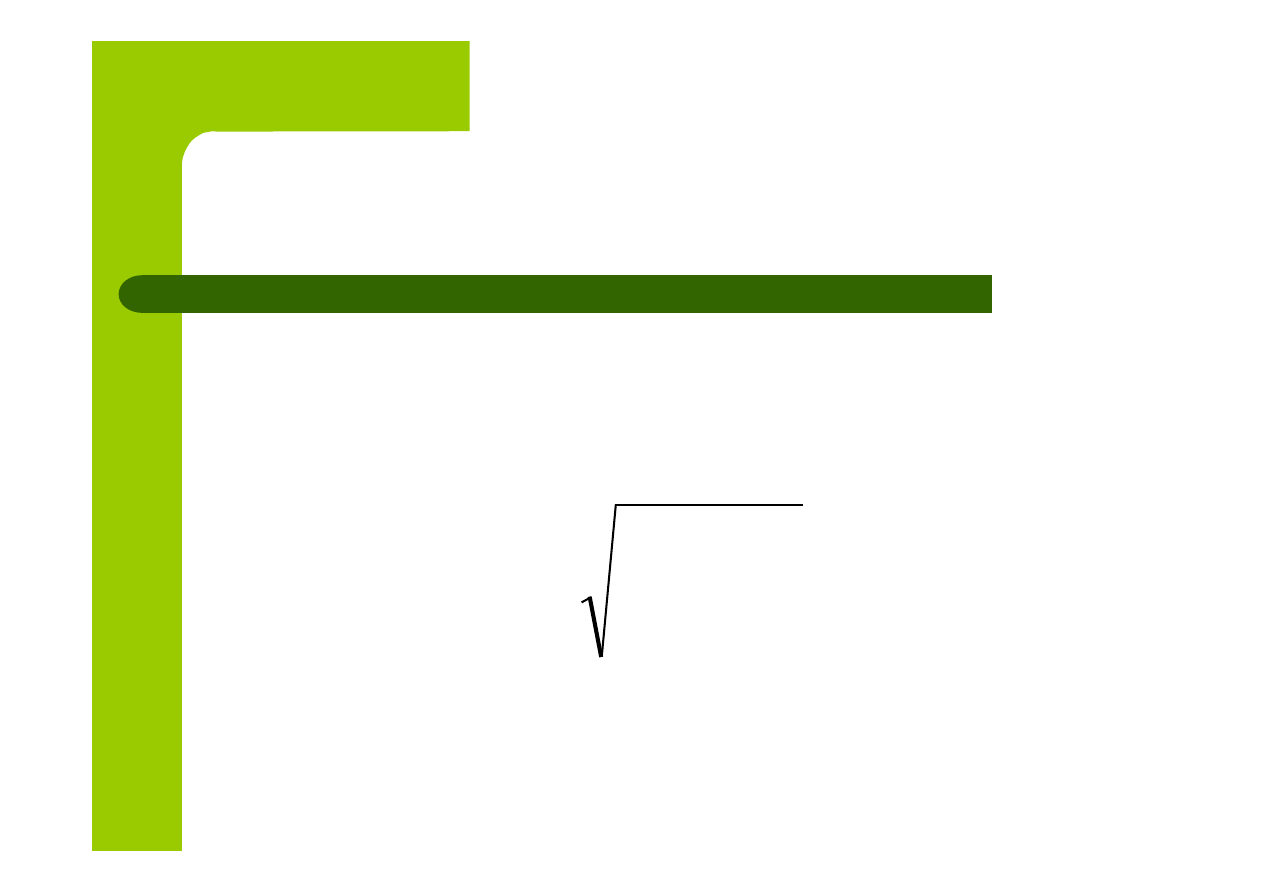
Taksonomiczna miara atrakcyjności

algorytm postępowania

(cd.)

N(R) definiujemy jako średnią kwadratową
elementów macierzy stanowiącą jej normę:

( )

∑ ∑

=

= =

n

i

n

j

ij

r

N

1

1

2

R

1

→

N

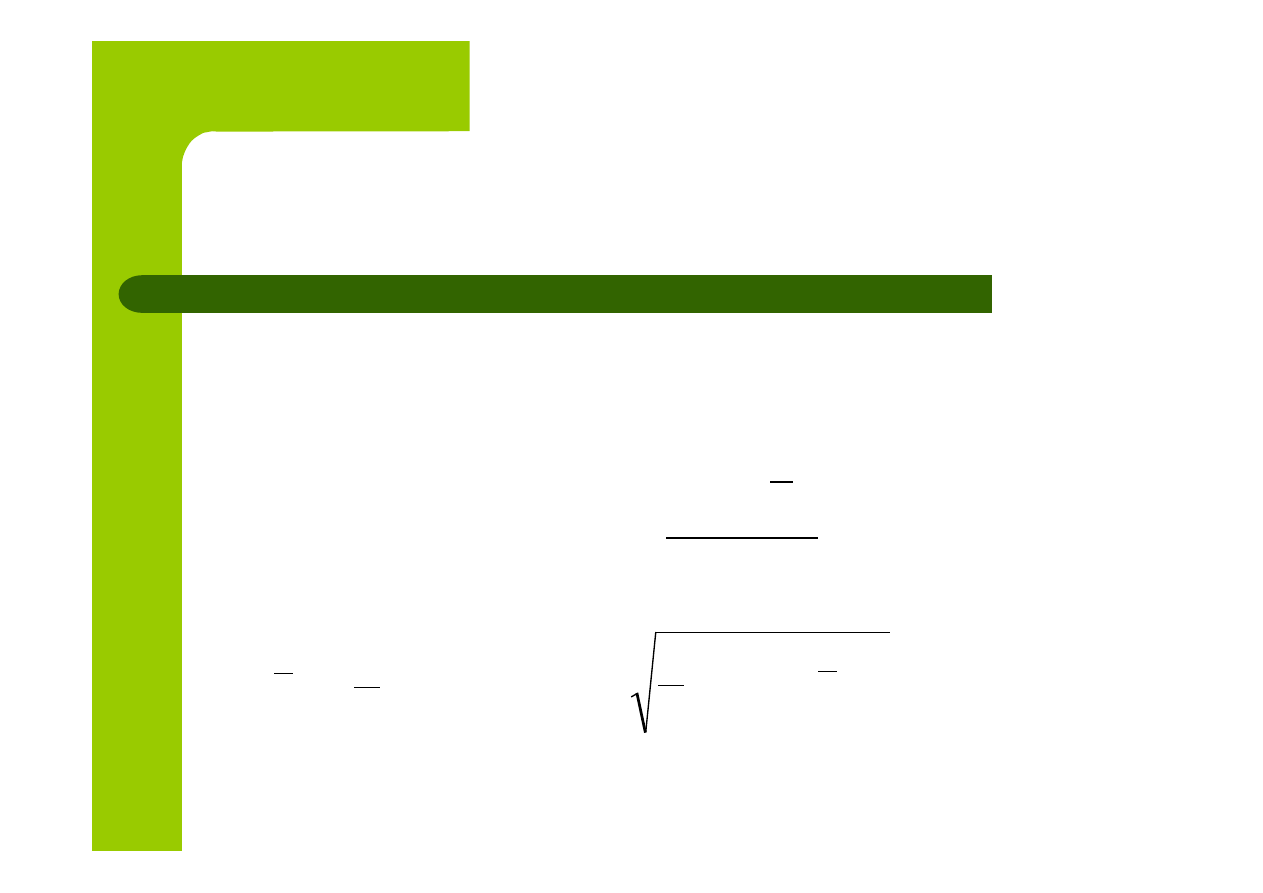
Taksonomiczna miara atrakcyjności

algorytm postępowania

(cd.)

W celu sprowadzenia poszczególnych zmiennych
do porównywalności należy uwolnić je od miana.
W metodzie Hellwiga uzyskuje się to przez ich
standaryzację:

!

m

ij

– zestandaryzowana wartość zmiennej diagnostycznej X

j

w i -tym obiekcie.

j

j

ij

ij

s

x

x

m

−

=

∑

=

=

n

i

ij

j

x

n

x

1

1

(

)

∑

−

=

=

n

i

j

ij

j

x

x

n

s

1

2

1

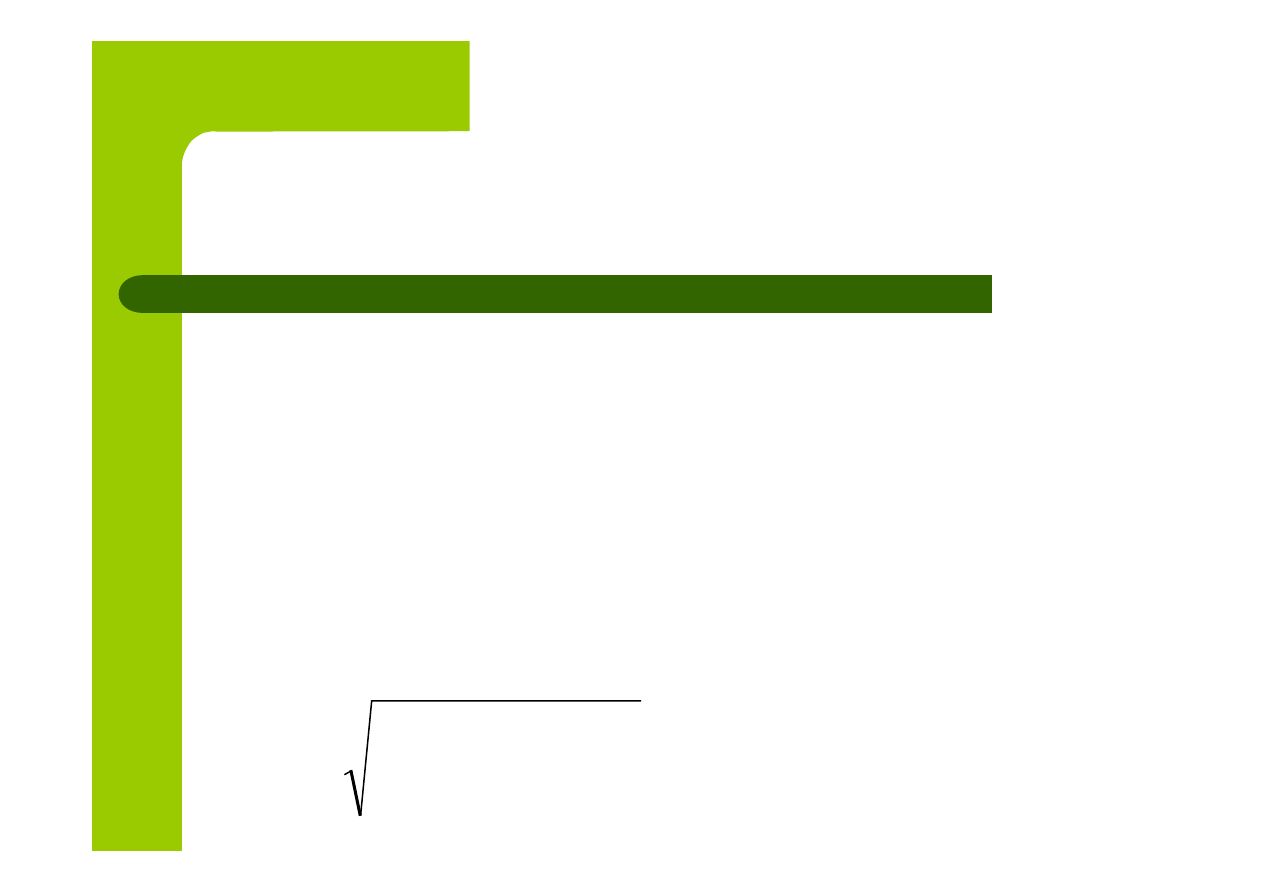
Taksonomiczna miara atrakcyjności

algorytm postępowania

(cd.)

Następnie tworzy się abstrakcyjny obiekt tzw.
wzorzec rozwoju, opisany przez maksymalne
realizacje zmiennych diagnostycznych:

Dla każdego obiektu badania wyznacza się
odległość od wzorca rozwoju o postaci:

ij

i

j

m

m

max

0

=

k

j

,....,

2

,

1

=

(

)

∑

−

=

=

k

j

j

ij

i

m

m

d

1

2

0

n

i

,....,

2

,

1

=

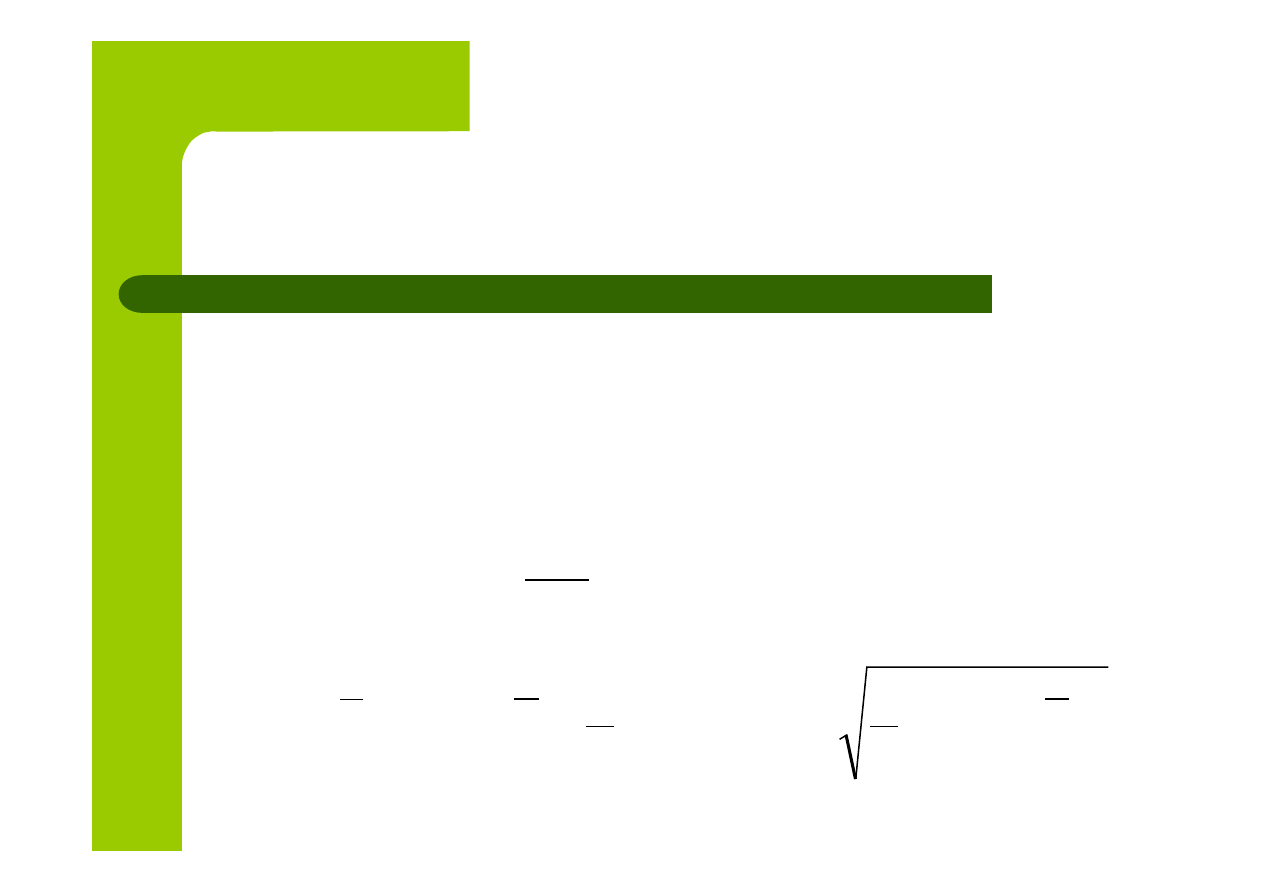
Taksonomiczna miara atrakcyjności

algorytm postępowania

(cd.)

Utworzona w ten sposób miara syntetyczna d

i

nie jest

unormowana. W celu jej unormowania konstruuje tzw.
względną miarę syntetyczną (względny miernik rozwoju)
o postaci:

0

1

d

d

TMAI

i

i

−

=

n

i

,....,

2

,

1

=

d

s

d

d

2

0

+

=

∑

=

=

n

i

i

d

n

d

1

1

(

)

∑

−

=

=

n

i

i

d

d

d

n

s

1

2

1

Taksonomiczna miara atrakcyjności

algorytm postępowania

(cd.)

Utworzona w powyższy sposób miara syntetyczna
TMAI

i

z prawdopodobieństwem bliskim jedności

przyjmuje wartości z przedziału [0;1]. Im wartość
TMAI

i

jest bliższa akcja analizowanej spółki mniej

różni się od modelowej opisanej za pomocą

maksymalnych realizacji zmiennych

diagnostycznych.

Miara TMAI

i

może przyjąć wartości ujemne (w

praktyce bardzo rzadko), co oznacza że

analizowana akcja jest zdecydowanie gorsza od

pozostałych.

Dziękuję za uwagę