Hanna Bogucka

Politechnika Poznańska

unikacji

e-mail: [e-mail]

Warszawa, 16-18 czerwca 2004

ZAKŁÓCENIA IMPULSOWE W TRANSMISJI Z MODULACJĄ

Instytut Elektroniki i Telekom

WIELOTONOWĄ I POSZERZONYM WIDMEM

Streszczenie: W niniejszej pracy rozważono wpływ zakłóceń
impulsowych na transmisję radiową z modulacją wieloto-
nową i poszerzonym widmem w przypadku zastosowania
sekwencji Walsha jako kodów rozpraszających energię
symboli danych. Pokazano, iż w przypadku występowania
szumu impulsowego w rozważanym systemie, można spo-
dziewać się zróżnicowanego wpływu tego szumu na po-
szczególne symbole danych. W pracy przedstawiono meto-
dę eliminacji szumu impulsowego dostosowaną indywidu-
alnie do każdego symbolu w odbieranym bloku danych.

1. WSTĘP

W ostatnich latach techniki modulacji wielotono-

wej cieszą się sporym zainteresowaniem jeśli chodzi o
ich zastosowanie w systemach transmisji radiowej. Jedną
z istotnych własności tych technik, w tym modulacji z
nośnymi ortogonalnymi OFDM (ang. Orthogonal
Frequency Division Multiplexing) jest ich stosunkowo
dobra odporność na szumy impulsowe w porównaniu z
modulacją pojedynczej nośnej. Źródłem szumu impul-
sowego mogą być urządzenia elektryczne i elektroniczne
(np. komputery, monitory, drukarki, kopiarki, windy,
kuchenki mikrofalowe, przełączniki elektryczne, aparat
zapłonowy w samochodzie itp.) a także zjawiska natu-
ralne (np. wyładowania atmosferyczne). Szum ten obja-
wia się jako ciąg impulsów o stosunkowo krótkim czasie
trwania i dużej energii, często przekraczającej energię
sygnału użytecznego mierzoną w czasie występowania
impulsu szumu [1,2].

Pomimo wspomnianej względnej odporności na

zniekształcenia impulsowe, wymagania stawiane syste-
mom wielotonowym dotyczące jakości transmisji są
często bardzo wysokie, co wymaga zastosowania odpo-
wiednich metod usuwania skutków tych zniekształceń w
sygnale odebranym. W literaturze zaproponowano kilka
takich metod dla transmisji OFDM, np. w [2-4].

W niniejszej pracy rozważono koncepcję bezprze-

wodowej transmisji wielotonowej z poszerzonym wid-
mem MC-SS (ang. Multicarrier Spread-Spectrum) w
obecności addytywnego szumu gaussowskiego AWGN
(ang. Additive White Gaussian Noise) oraz szumu impul-
sowego w kanale idealnym. Przyjęto zastosowanie funk-
cji Walsha jako kodów rozpraszających energię symboli
danych. Dobre własności takiej transmisji w różnych
kanałach radiowych pokazano w pracach [5-7] zarówno
w przypadku jednego jak i wielu użytkowników. Zgod-
nie z wiedzą autora nie zaproponowano dotąd żadnych
metod eliminacji skutków szumu impulsowego w trans-
misji MC-SS. Ponieważ wpływ szumu impulsowego na

poszczególne symbole danych w takiej transmisji może
być niezwykle zróżnicowany w zależności od konkret-
nych funkcji Walsha wykorzystywanych przez symbole,
stąd technika eliminacji szumu powinna być odpowied-
nio dopasowana do każdego symbolu i sekwencji Wals-
ha.

2. MODEL MATEMATYCZNY SYSTEMU

W nadajniku rozważanego systemu MC-SS symbo-

le danych QPSK są mnożone przez odpowiednie wza-
jemnie ortogonalne sekwencje Walsha składające się z N
chipów. Powstałe ciągi są następnie sumowane, w wyni-
ku czego powstaje zbiorczy sygnał z poszerzonym wid-
mem. Poszczególne symbole mogą być uważane za dane
generowane synchronicznie dla wielu użytkowników w
tym samym odstępie modulacji lub też za dane poje-
dynczego użytkownika generowane w ciągu N odstępów
modulacji. Zwielokrotnienie symboli danych przy wyko-
rzystaniu ortogonalnych sekwencji Walsha może być w
sposób efektywny zrealizowane za pomocą szybkiej
transformacji Walsha-Hadamarda WHT (ang. Walsh-
Hadamard Transform) [5-7]. W dalszym etapie przetwa-
rzania w nadajniku poszczególne elementy sygnału
zbiorczego modulują N ortogonalnych nośnych, co może
zostać w sposób efektywny zrealizowane za pomocą
szybkiej odwrotnej transformacji Fouriera IFFT (ang.
Inverse Fast Fourier Transform). W odbiorniku zasto-
sowane jest przetwarzanie odwrotne, tj. szybka trans-
formacja Fouriera FFT (ang. Fast Fourier Transform)
oraz odwrotna WHT (IWHT) [6].

Ciąg N próbek

(k = 0,..., N

T

)

(

)

(

}

{

n

k

n

r

=

r

– 1) gene-

rowanych w nadajniku w chwili n-tej jest więc postaci:

)

(

1

)

(

n

N

N

n

a

W

F

r

⋅

⋅

=

−

,

(1)

gdzie

(i

T

)

(

)

(

}

{

n

i

n

a

=

a

1

−

N

F

N

W

= 0,..., N – 1) stanowi wejściowy

wektor równolegle nadawanych symboli danych w chwi-
li n-tej,

jest macierzą o wymiarze N

×N zawierającą

wartości ortogonalnych funkcji harmonicznych używa-
nych w odwrotnym dyskretnym przekształceniu Fourie-
ra, natomiast

jest macierzą Walsha-Hadamarda o

wymiarze N

×N. W rozpatrywanym modelu systemu N-

elementowy wektor odebrany

jest równy:

T

)

(

)

(

}

{

n

k

n

y

=

y

)

(

)

(

)

(

)

(

n

I

n

A

n

n

n

n

r

y

+

+

=

,

(2)

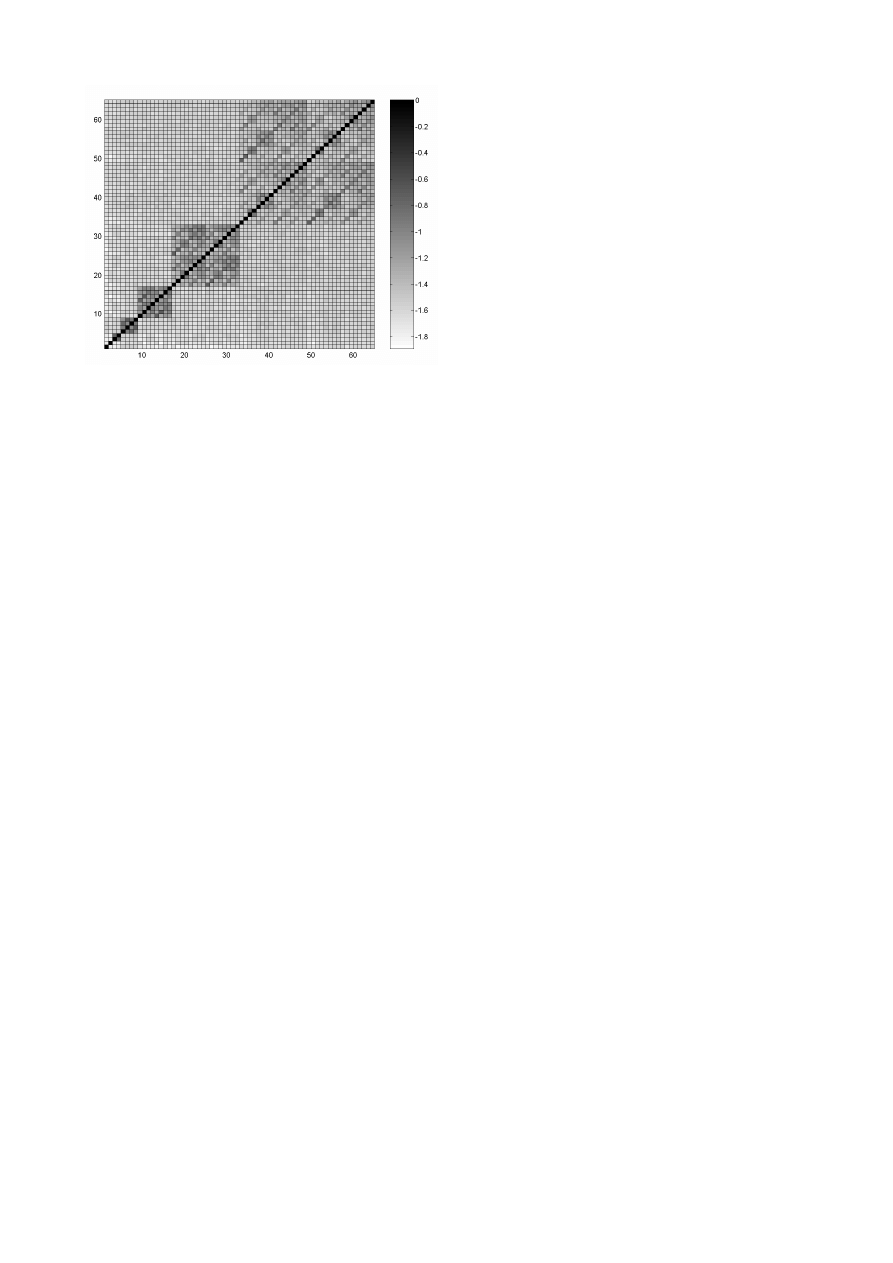
Rys. 1. Moduł znormalizowanej macierzy korelacji po-

między wyjściami transformaty FFT/IWHT w od-
biorniku (skala logarytmiczna)

gdzie

oraz

są N

)

(n

A

n

)

(n

I

n

-elementowymi ciągami zawie-

rającymi zespolone próbki szumu, odpowiednio AWGN
oraz impulsowego.

Po demodulacji i dekorelacji ciągu odebranego, wek-

tor

T

)

(

)

(

}

~

{

~

n

i

n

a

=

a

(i = 0,..., N – 1), na podstawie którego

podejmowana jest decyzja

jest równy:

)

(n

a

)

(

1

)

(

1

)

(

)

(

~

n

I

N

N

n

A

N

N

n

n

n

F

W

n

F

W

a

a

⋅

⋅

+

⋅

⋅

+

=

−

−

. (3)

Zauważmy, że oba składniki szumu:

oraz

są w

odbiorniku przetwarzane przez FFT i IWHT. Można
pokazać, że charakterystyki czasowe i częstotliwościowe
szumu AWGN nie ulegają wyraźnej zmianie w wyniku
tego przetwarzania. Jednakże w przypadku szumu im-
pulsowego możemy zaobserwować wzrost korelacji
pomiędzy niektórymi wyjściami połączonych transfor-
mat FFT/IWHT. Na rysunku 1 przedstawiono macierz
modułu kowariancji (w skali logarytmicznej) pomiędzy
wyjściami FFT/IWHT w przypadku występowania na
wejściu odbiornika nie skorelowanych próbek szumu
impulsowego. W tym przypadku zastosowano model
szumu impulsowego opisanego w pracach [3, 8], w
którym zakłada się rozkład prawdopodobieństwa Pois-
sona momentów występowania zespolonych impulsów
szumu, rozkład Rayleigha wartości modułu tych impul-
sów oraz rozkład jednostajny ich faz. W przeprowadzo-
nych symulacjach wariancja zarówno składowej rze-
czywistej, jak i urojonej impulsu wynosi

, a in-

tensywność występowania impulsów Poissona jest rów-
na

)

(n

A

n

)

(n

I

n

1

=

2

I

σ

N

/

1

=

λ

(w każdym bloku N symboli danych ode-

branych występuje przeciętnie jeden impuls szumu). Jak
pokazano w pracy [2], charakterystyczną cechą modula-
cji OFDM jest “wybielenie” szumu impulsowego po
przejściu przez demodulator FFT w odbiorniku. A zatem
impulsy szumu na wyjściu FFT nie są skorelowane.
Jednakże na rys. 1 możemy już zaobserwować regularny
wzór wskazujący na to, iż niektóre, wybrane próbki
wyjściowe IWHT (w dalszym etapie podawane na układ
decyzyjny) są ze sobą skorelowane. W konsekwencji

tego faktu możemy spodziewać się iż symbole wyjścio-
we będą w różny sposób wrażliwe na szum impulsowy.

Analiza operacji typu “motylek” (ang. „butterfly”)

w szybkich algorytmach FFT oraz IWHT daje wyjaśnie-
nie opisanej wyżej korelacji pomiędzy niektórymi wyj-
ściami połączonych transformat FFT/IWHT oraz braku
tej korelacji pomiędzy innymi wyjściami. Jak pokazano
w pracy [6], połączenie transformat FFT oraz szybkiej
IWHT daje rezultat w postaci redukcji operacji “motyl-
kowych”, które realizują operacje odwrotne w obu algo-
rytmach. W konsekwencji różne próbki wejściowe pod-
legają różnej liczbie operacji typu „motylek” i w związ-
ku z tym są skorelowane ze sobą w różnym stopniu.

3. DOPASOWANIE MARGINESU

DECYZYJNEGO

Jednym ze znanych sposobów łagodzenia skutków

szumu impulsowego jest wykrywanie zniekształconych
tym szumem próbek, wymazywanie ich z ciągu odebra-
nego oraz zastosowanie odpowiedniego kodu korekcyj-
nego ze zdolnością poprawiania wymazanych bitów lub
grupy bitów, np. odpowiedniego kodu Reeda-Solomona
(RS). Dla wykrycia zakłóconych próbek monitoruje się
układ automatycznej regulacji wzmocnienia (ARW) pod
kątem nagłych spadków wartości wzmocnienia, a także
znajdujący się za układem ARW przetwornik A/C pod
kątem obcinania wartości próbek przekraczających za-
kres przetwornika [2]. Wspomniane techniki nie nadają
się do zastosowania w systemach transmisji sygnałów z
modulacją wielotonową, gdyż sygnały te charakteryzują
się dużym stosunkiem mocy szczytowej do średniej. W
związku z tym zakres wzmocnienia ARW musi być
stosunkowo mały, aby zapobiec częstemu obcinaniu
sygnału wielotonowego [2].

W pracy [2] dla systemu z modulacją OFDM za-

proponowano metodę monitorowania błędu średniokwa-
dratowego MSE (ang. mean squared error) pomiędzy
wejściem i wyjściem układu decyzyjnego. W metodzie
tej symbol danych zostaje uznany za niewiarygodny,
jeżeli wartość kwadratu błędu dla tego symbolu przekro-
czy pewną dozwoloną wartość R

2

. Oznacza to, że orygi-

nalne obszary decyzyjne wokół zespolonych symboli
danych (będące kwadratami dla modulacji QAM) zostają
zastąpione okręgami o promieniu R. Dodatkowo zapro-
ponowano zastosowanie odpowiedniego kodu RS. Praw-
dopodobieństwo błędnego odrzucenia symbolu w
przypadku nie wystąpienia impulsu zakłócającego poda-
no również w pracy [2].

W przypadku transmisji MC-SS z wykorzystaniem

rozpraszania Walsha spodziewamy się, iż wrażliwość
symboli na szum impulsowy jest różna dla różnych
symboli, tj. indeksów odpowiednich wyjść transformacji
FFT/IWHT. Stąd też związane z nowymi obszarami
decyzyjnymi wartości promieni R

i

powinny być odpo-

wiednio dopasowane do spodziewanych wartości modu-
łów sygnału błędu dla każdego z wyjść FFT/IWHT i
związanej z nim funkcji Walsha.

Przeprowadzono symulację komputerową opisane-

go w poprzednim rozdziale systemu MC-SS, w czasie
której obserwowano wartości MSE pomiędzy odebra-

nymi symbolami

na każdym (i

)

(

~

n

i

a

-ty

)

(n

m) wyjściu

FFT/IWHT a oryginalnymi symbolami nadawanymi

. Przyjęto stosunek mocy sygnału do szumu białego

SWNR (ang. Signal to White Noise Ratio) równy 30dB,
natomiast stosunek mocy sygnału do szumu impulsowe-
go SINR (ang. Signal to Impulse Noise Ratio) zmieniano
w zakresie od -4 do 4 dB (SINR mierzony jest w zakre-
sie czasu występowania impulsu szumu pod warunkiem
pojawienia się impulsu). W wyniku wspomnianych
obserwacji okazało się, iż wartość kwadratu modułu
błędu uśredniona po liczbie symboli odebranych jest
taka sama dla każdego i

i

a

. Jednakże, jeżeli MSE uśrednio-

ny zostanie po liczbie impulsów szumu przenoszonych
na dane wyjście, zauważymy wyraźnie zróżnicowane
wartości MSE dla poszczególnych wyjść. Wartość MSE
w takim przypadku maleje dla kolejnych podzbiorów
wartości indeksu wyjścia i, tj. dla tych wyjść transfor-
macji FFT/IWHT, dla których występuje znacząca kore-
lacja (porównaj rys. 1). To zjawisko również jest rezul-
tatem opisanego wcześniej połączenia algorytmów FFT i
IWHT. Kiedy pojawia się impuls szumu na jednym z
wejść o indeksie k = N/2,...,N – 1, jest on przenoszony
na wszystkie wyjścia o indeksie i = N/2,...,N – 1. Energia
szumu na pojedynczym wyjściu stanowi tylko część
(2/N) energii impulsu jaki pojawił się na odpowiednim
wejściu. Ponieważ impulsy pojawiają się na każdym z
wejść z tą samą intensywnością, pojawienie się skutków
szumu impulsowego na wyjściach o indeksach i =
N/2,...,N – 1 jest bardziej prawdopodobne niż występo-
wanie skutków tego szumu na dowolnym innym wyj-
ściu. W związku z tym spodziewana wartość MSE
uśredniona po liczbie impulsów przenoszonych na roz-
patrywane wyjścia (tj. dla i = N/2,...,N – 1) jest mniejsza
niż dla dowolnego innego wyjścia. Fakt ten powinien
także przełożyć się na niższą stopę błędów na tych wyj-
ściach. Podobne rozważania można przeprowadzić dla
dowolnego podzbioru indeksów skorelowanych ze sobą
wyjść.

Wobec powyższych rozważań potwierdzonych

wynikami symulacji jest rzeczą oczywistą, iż konieczne
jest dostosowanie wspomnianych wartości promieni R

i

ograniczonych obszarów decyzyjnych do poszczegól-
nych symboli, tj. indeksu wyjścia i. W celu określenia
wartości R

i

należy wyznaczyć wartość odchylenia stan-

dardowego błędu na każdym wyjściu przy założeniu, iż
co najmniej jeden impuls szumu pojawia się na wej-
ściach, które przenoszą ten impuls na dane rozpatrywane
wyjście i:

1/2

2

)

(

)

(

'

'

~

E

'

'





























−

=

n

i

n

i

cond

i

a

a

cond

σ

,

(4)

( )

x

'cond'

E

gdzie

oznacza wartość oczekiwaną zmiennej

losowej x pod warunkiem oznaczonym jako ‘cond.’. W
naszym przypadku warunek ‘cond.’ zdefiniowany jest
jak powyżej, tj. fakt, iż część energii impulsu szumu
pojawiającego się na wejściu przenoszona jest na wyj-
ście o indeksie i Zauważmy, że wartość

zależy

od poziomu SWNR, SINR, a także intensywności szumu

impulsowego

λ . Naturalnie, istnieje możliwość wypro-

wadzenia wzoru na

w sposób analityczny, prze-

prowadziwszy analizę wartości macierzy transformacji
realizowanej w odbiorniku:

. Jednakże

przewidywana złożoność obliczeniowa takiej analizy
jest bardzo duża, gdyż konieczne jest rozpatrzenie różnej
liczby impulsów szumu m pojawiających się w bloku N

'

'cond

i

σ

⋅

=

N

N

F

H

1

−

N

W













m

N

64

=

odebranych próbek oraz możliwości przeniesienia części
ich energii na konkretne (i-te) wyjście. Liczba m może
przyjąć wartości od 0 do N z różnym prawdopodobień-
stwem. Liczba możliwych kombinacji wejść, na których
pojawić się może m impulsów szumu występujących w

bloku N

'

'cond

i

σ

odebranych próbek wynosi:

, i dla N >

32 jest ona bardzo duża. Np. już dla

wartość L

może być rzędu 10

=

L

N

i

8

dla niektórych wartości m. Dlatego

też w celu oszacowania odpowiednich wartości

przeprowadzono symulację komputerową prostego sys-
temu MC-SS przy założeniu występowania warunku
‘cond.’ Wartość estymaty odchylenia standardowego
błędu dla każdego wyjścia

σ

ˆ

została obliczona w wy-

niku uśrednienia kwadratu modułu błędu po liczbie
impulsów szumu przeniesionych na konkretne (i-te)
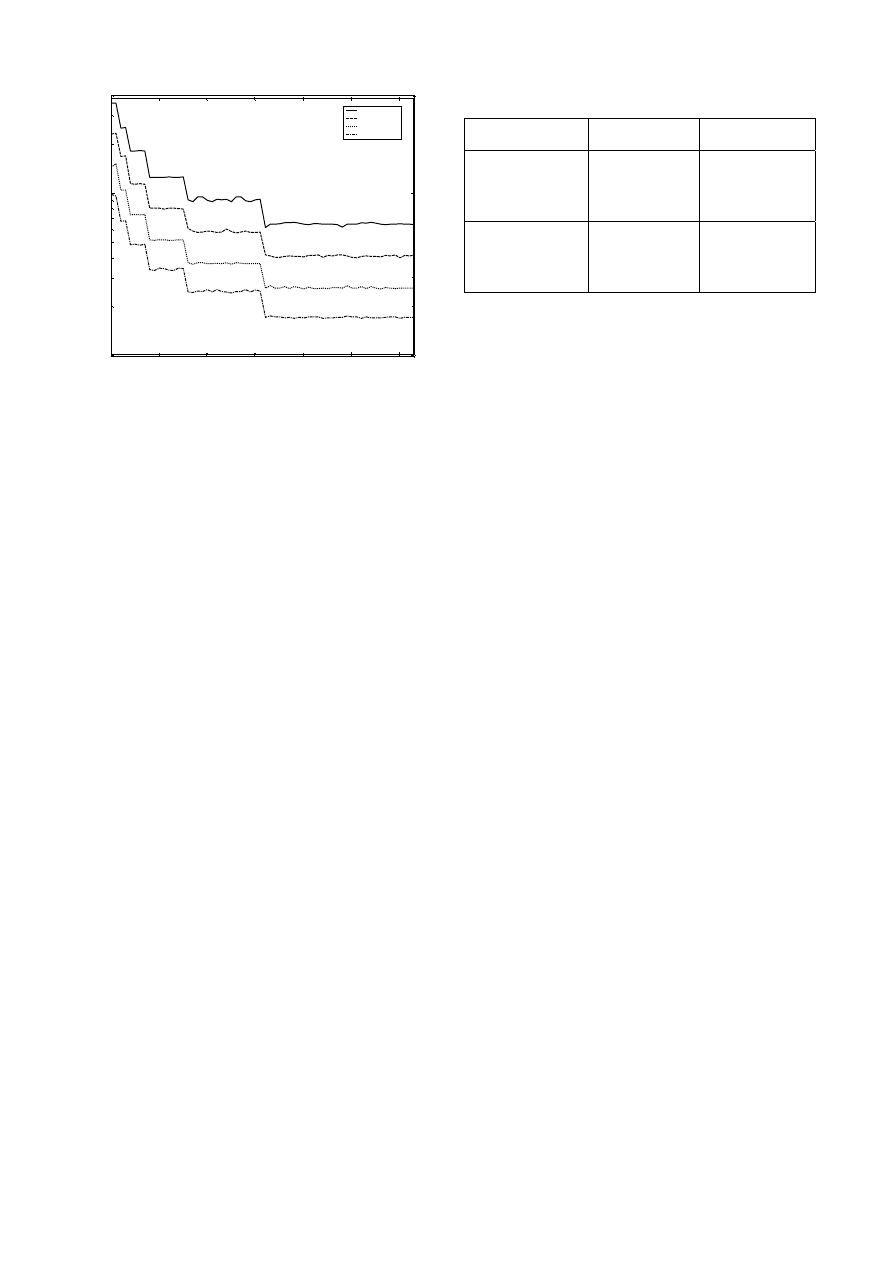
wyjścia transformacji FFT/IWHT. Jak pokazano na rys.
2 wartość

i

różni się dla różnych indeksów wyjść.

Zależy ona również od wartości SINR oraz intensywno-
ści impulsów

λ . Promień ograniczonego obszaru decy-

zyjnego R

i

z pewnością nie powinien przekraczać warto-

ści

(a raczej pewnego ułamka tej wartości) jak rów-

nież połowy odległości minimalnej d pomiędzy nadawa-
nymi symbolami QPSK.

λ



<

2

ˆ

75

.

0

d

i

σ

gdy

75

.

0

σ

ˆ

i

σ

ˆ

4. WYNIKI SYMULACJI KOMPUTEROWEJ

Przeprowadzono symulację komputerową rozwa-

żanego systemu MC-SS bazującego na rozpraszaniu
widma symboli QPSK za pomocą transformacji WHT.
W systemie obecny jest szum AWGN oraz szum impul-
sowy. Liczba nośnych wynosi N = 256, jednakże w
wyniku testów symulacyjnych okazało się, że uzyskane
rezultaty nie zależą od konkretnej wartości N. Ponadto,
przyjęto SWNR równy 30dB, a także zmieniano warto-
ści SINR w zakresie od -4 do 4 dB (mierzone wyłącznie
w czasie trwania impulsu). Odległość minimalna d po-
między nadawanymi symbolami QPSK była równa 2.
Dwa modele szumu impulsowego były testowane:
wspomniany wcześniej model Poissona [3, 8] z inten-
sywnością = 1/N oraz model Middleton’a klasy A [4,
9]. Współczynnik impulsowości w modelu Middleton’a
wyniósł A = 0. Jak opisano w poprzednim paragrafie,
obszary decyzyjne zostały ograniczone do okręgów o
promieniu R

i

, przy czym R

i

wybrano w następujący

sposób:





≥

=

2

2

ˆ

75

.

0

gdy

ˆ

d

i

d

i

i

R

σ

σ

(5)

.

'

'cond

i

σ

0

10

20

30

40

50

60

10

-1

10

0

indeks wyjscia

SINR = -4dB
SINR = -2dB
SINR = 0 dB
SINR = 4 dB

Rys. 2. Estymata odchylenia standardowego sygnału

błędu uśredniona po liczbie impulsów szumu na
poszczególnych wyjściach odbiornika; SWNR=30
dB,

64

/

1

/

1

=

=

N

λ

Jak można było oczekiwać, niektóre z symboli zostały
niesłusznie uznane za niewiarygodne i odrzucone. W
szczególności miało to miejsce w przypadku umiarko-
wanej wartości SINR (tj. 0dB), kiedy to odebrane sym-
bole znajdowały się poza wyznaczonym okręgiem, ale
nadal wewnątrz oryginalnego prostokątnego obszaru
decyzyjnego. Podobnie w niektórych przypadkach ode-
brane symbole były błędnie akceptowane, gdy na skutek
występowania impulsu szumu o umiarkowanej amplitu-
dzie “wpadały” one do sąsiedniego obszaru decyzyjne-
go.

Zaobserwowany procent błędnych odrzuceń oraz

błędnych akceptacji w symulowanym systemie przed-
stawiono w tabeli 1. Zauważmy, że nie przekracza on
11%. Największy procent takich błędów został zaobser-
wowany w przypadku umiarkowanej wartości SINR tj.
dla SINR=0dB, z powodów przedstawionych powyżej.

5. PODSUMOWANIE

W niniejszej pracy pokazano, iż w systemie MC-SS

wykorzystującym funkcje Walsha szum impulsowy ma
nierównomierny wpływ na poszczególne symbole w
odebranym bloku danych. Dlatego też zaproponowano
metodę dopasowania obszaru decyzyjnego indywidual-
nie dla każdego symbolu. Metoda ta wymaga znajomo-
ści wartości odchylenia standardowego sygnału błędu
występującego na każdym z wyjść odbiornika. Wartości
te mogą być wyznaczone analitycznie lub też dopasowa-
ne adaptacyjnie. Jest to możliwe przy założeniu, że
charakterystyki głównych źródeł szumu impulsowego w
rozpatrywanym środowisku nie zmieniają się znacząco.
Takie założenie można przyjąć np. dla systemu działają-
cego wewnątrz budynku. Wówczas jakość zapropono-
wanej metody jest akceptowalna (procent błędnych od-
rzuceń symboli nie przekracza 11%). Dodatkowo można
zastosować odpowiedni kod kanałowy z możliwością
poprawiania wymazanych symboli np. odpowiedni kod
RS, co przyczyniłoby się do obniżenia stopy błędów.

Tab.1. Jakość działania metody ograniczonych

obszarów decyzyjnych

Model szumu

Procent błędnych

odrzuceń

Procent błędnych

akceptacji

Middletona kl. A

SINR=-4 dB

SINR=0 dB
SINR=4 dB

2.5

10.5

1.1

2.0
9.0
1.5

Poissona

SINR=-4 dB

SINR=0 dB
SINR=4 dB

2.1

10.8

2.0

2.7
9.5
1.7

Dalsze badania będą koncentrowały się na imple-

mentacji opisanej metody w kanale radiowym z zanika-
mi oraz jej ocenie pod kątem stopy błędów.

LITERATURA

[1] K. L. Blackard, T. S. Rappaport, C. W. Bostian,

Measurements and Models of Radio Frequency
Impulsive Noise for Indoor Wireless Communica-
tions, IEEE JSAC, Vol. 11, No. 7, Sept. 1993, pp.
991-1001

[2] T. N. Zogakis, P. S. Chow, J. T. Aslanis, J. M.

Cioffi, Impulse Noise Mitigation Strategies for
Multicarrier Modulation, ICC’93, Vol. 2, May
1993, pp.784-788

[3] G. Pay, M. Safak, Performance of OFDM Systems

in Impulsive Noise Channels, Int. OFDM Works-
hop 2001, Hamburg, Germany, Sept. 18-19, 2001,
pp. 36-1--36-4

[4] H. A. Suraweera, C.Chai, J. Shentu, J. Armstrong,

Analysis of Impulse Noise Mitigation Techniques
for Digital Television Systems, Int. OFDM Works-
hop 2003, Hamburg, Germany, Sept. 24-25 2003,
pp. 172-176

[5] L. Hanzo, M. Munster, B.J. Choi, T. Keller,

OFDM and MC-CDMA for Broadband Multi-user
Communications, WLANs and Broadcasting, John
Wiley &Sons, July 2003

[6] H. Bogucka, Application of the Joint Discrete

Complex Hadamard - Inverse Fourier Transform
in a MC-CDMA Wireless Communication System.
Performance and Complexity Studies, accepted for
IEEE Trans. Wireless Commun. (July 2004)

[7] Z. Długaszewski, K. Wesołowski, WHT/OFDM –

an improved OFDM Transmission Method for Se-
lective Fading Channels, Proceedings of IEEE
SCVT 2000, Leuven, Belgium, pp. 71-74, Oct. 19,
2000

[8] M. C. Jeruchim, P. Balaban, K.S. Shanmugan,

Simulation of Communication Systems, 1999 Ple-
num Press, New York

[9] D. Middleton, D., Statistical-Physical Models of

Electromagnetic Interference, IEEE Trans. Elec-
tromagnetic Compatibility, Vo. 19, No. 3, Aug.
1977, pp. 106-127