1

1

Agata Nawrocka

Agata Nawrocka

Katedra Automatyzacji Proces

Katedra Automatyzacji Proces

ó

ó

w

w

Akademia G

Akademia G

ó

ó

rniczo

rniczo

-

-

Hutnicza

Hutnicza

Automatyka i Robotyka

Automatyka i Robotyka

2

2

Plan wyk

Plan wyk

ł

ł

adu

adu

9

Wprowadzenie

9

Synteza metodami klasycznymi

9

Dobór parametrów regulatora

ƒ

metoda Zieglera – Nicholsa

ƒ

metoda charakterystyk częstotliwościowych

ƒ

metoda linii pierwiastkowych

9

Synteza układów sterowania z uwzględnieniem

wskaźników jakości. Metoda przestrzeni stanów.

Automatyka i Robotyka

Wykład nr 10

3

3

Synteza układów sterowania, polega na doborze takiej
struktury układu i parametrów regulatora, by układ
mógł wykonać postawione przed nim zadania.

Postępowanie jest dwuetapowe:

9

Pierwszy etap

: określenie struktury układu regulacji i

typu regulatora (członu korekcyjnego). Zadania tego
etapu są najtrudniejszymi zagadnieniami zarówno teorii,
jak i praktyki sterowania.

9

Drugi etap

: dobór wartości parametrów regulatora.

Wprowadzenie

Automatyka i Robotyka

Wykład nr 10

4

4

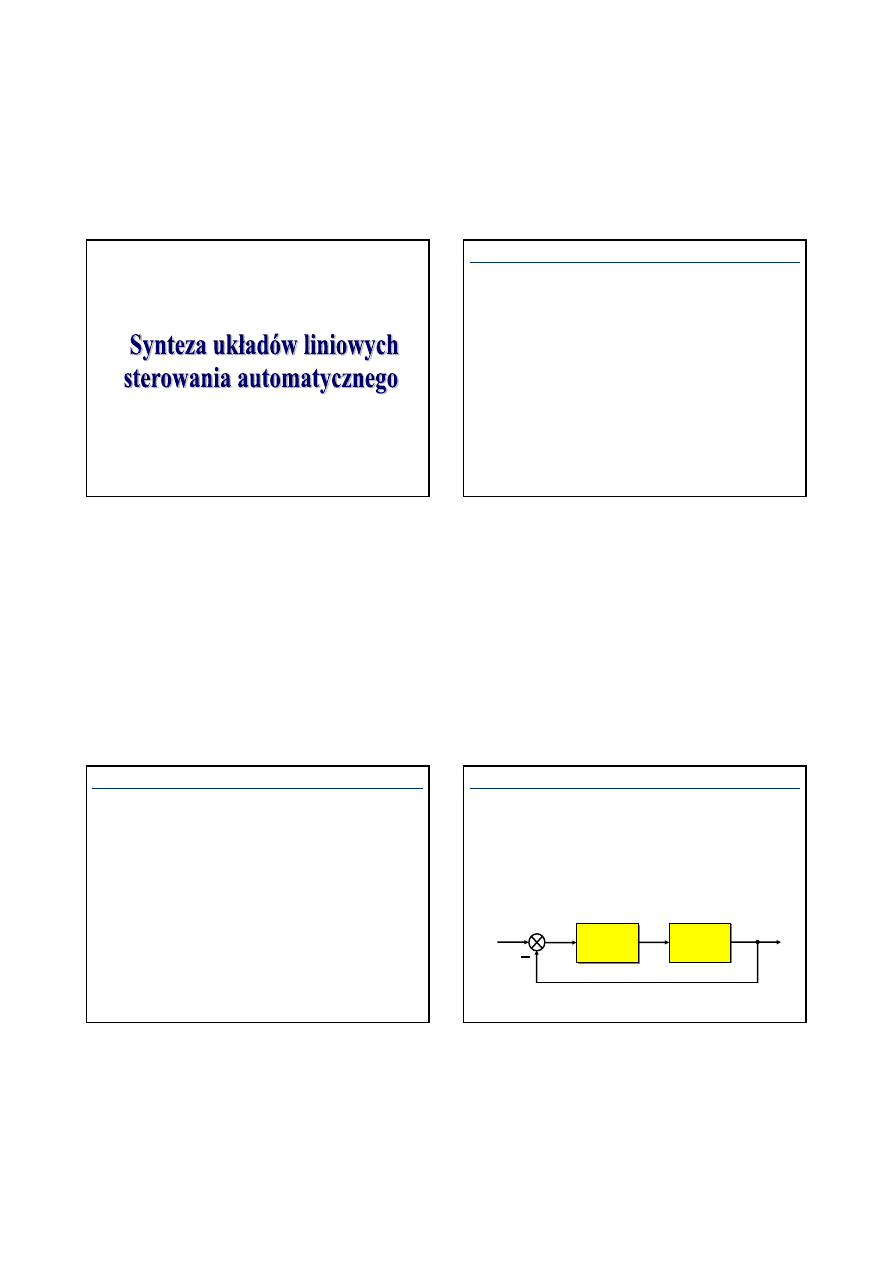
Najczęściej stosowana jest struktura szeregowa, w której

regulator jest włączony w tor główny układu regulacji czyli

szeregowo z obiektem.

Struktura szeregowa układu regulacji

Sygnałem wejściowym regulatora jest sygnał uchybu

e(t

e(t

)

)

,

,

sygnałem wyjściowym - sterowanie obiektu

u(t)

u(t)

.

.

w

w

e

e

u

u

y

y

R

R

O

O

Automatyka i Robotyka

Wykład nr 10

5

5

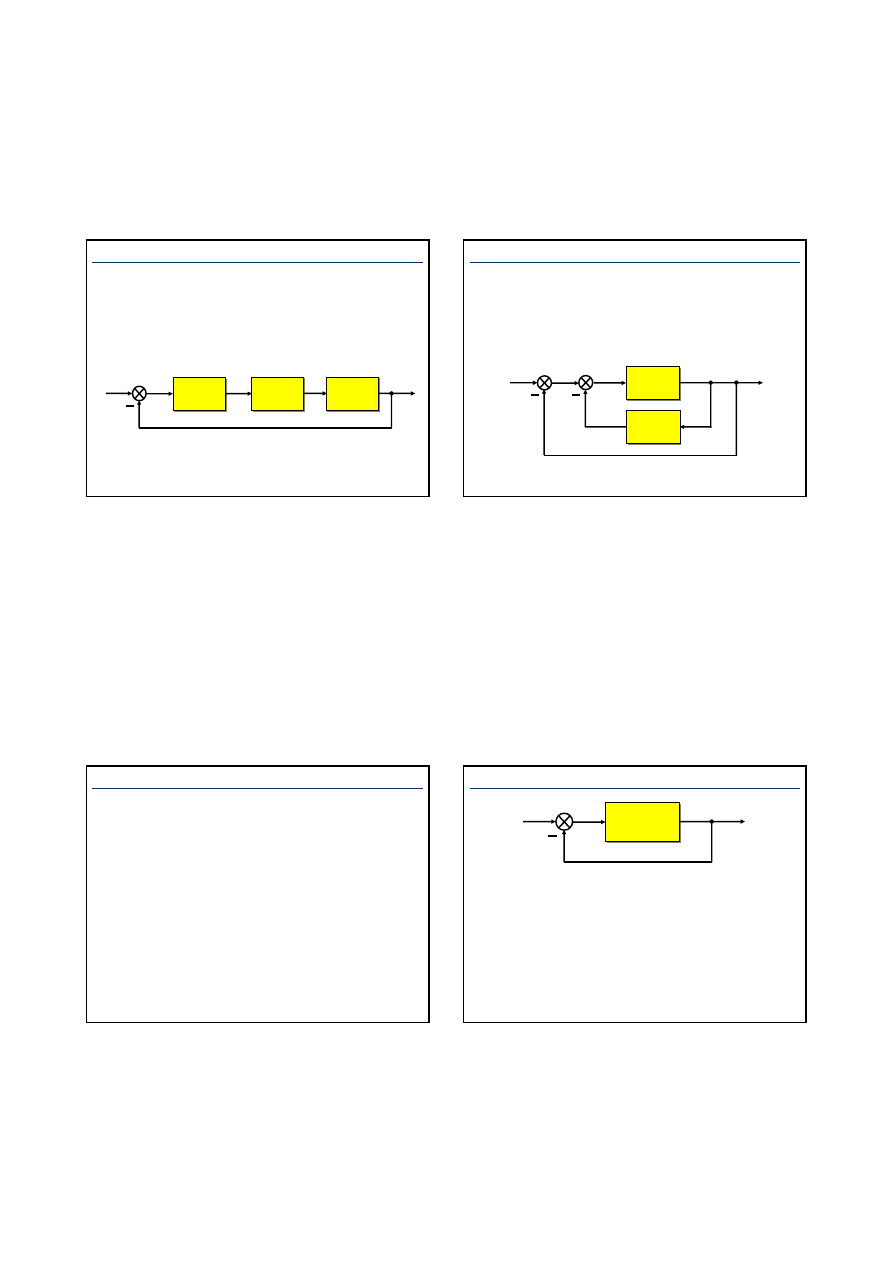
Niekiedy przed regulatorem włączany jest dodatkowo

element (człon) korekcyjny, którego zadaniem jest wstępne

uformowanie sygnału uchybu.

Włączanie członu korekcyjnego przed regulatorem

w

e

u

Człon

korekcyjny

Człon

korekcyjny

Regulator

Regulator

Obiekt

Obiekt

y

Automatyka i Robotyka

Wykład nr 10

6

6

Inną, często stosowaną - zwłaszcza w automatyce napędu -
strukturą układu regulacji jest struktura z dodatkowym
sprzężeniem zwrotnym, w którym człon korekcyjny jest
włączany w tor dodatkowego sprzężenia zwrotnego wokół
obiektu.

Struktura układu regulacji z dodatkowym sprzężeniem

zwrotnym

w

e

u

Człon

korekcyjny

Człon

korekcyjny

Obiekt

Obiekt

y

Automatyka i Robotyka

Wykład nr 10

7

7

W obu powyższych przypadkach regulator i człon

korekcyjny mają za zadanie taką modyfikację właściwości

obiektu, by działanie skorygowanego układu zamkniętego

było zadowalające z punktu widzenia przyjętego kryterium

jakości.

Kryterium to łączy zwykle wiele elementów – takich jak:

9

uzyskanie odpowiednich parametrów odpowiedzi

skokowej na wymuszenie zewnętrzne w(t),

9

odporność na zakłócenia, zwłaszcza oddziałujące na

wejście obiektu.

Automatyka i Robotyka

Wykład nr 10

8

8

Podstawowymi wymaganiami stawianymi
jednowymiarowym układom regulacji automatycznej są:

Skorygowany układ zamknięty regulacji

9

dokładność statyczna,

9

zakres regulacji wielkości wyjściowej,

9

pasmo robocze (pasmo przenoszonych częstotliwości),

9

zapas stabilności.

w

e

y

Układ

zmodyfikowany

Układ

zmodyfikowany

Automatyka i Robotyka

Wykład nr 10

9

9

Synteza metodami klasycznymi

Synteza metodami klasycznymi

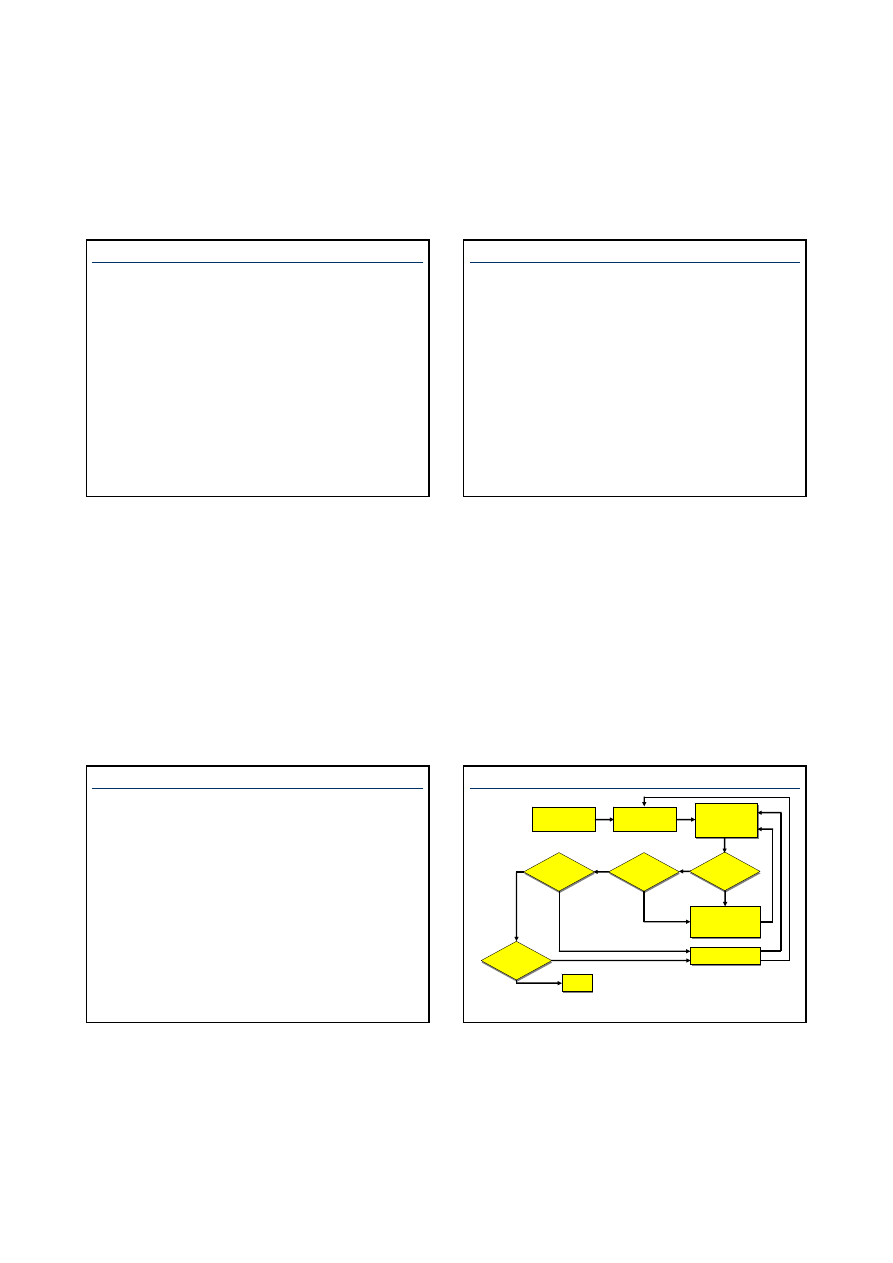
Przy klasycznej metodzie syntezy układów sterowania
najpierw zestawia się dane wyjściowe obejmujące zadanie
stawiane układowi, model matematyczny obiektu,
ograniczenia i warunki pracy. Na tej podstawia określa się
wymagania i ustala założenia.

Do podstawowych wymagań należą:

9

dokładność w stanach ustalonych,

9

zakres, w jakim wielkość

wyjściowa ma być

regulowana, stabilność i odpowiedni jej zapas,

9

charakter przebiegu procesów przejściowych (pasmo
przenoszonych częstotliwości).

Automatyka i Robotyka

Wykład nr 10

10

10

9

wyboru struktury układu,

9

dobiera wstępnie elementy i podzespoły,

9

sprawdza dokładność w stanie ustalonym,

9

sprawdza zakres regulacji.

Jeżeli nie odpowiadają one założonym, wprowadza się

odpowiednią korekcję właściwości statycznych przez

zmiany parametrów lub nastaw niektórych elementów.

Po przyjęciu założeń dokonuje się:

Automatyka i Robotyka

Wykład nr 10

11

11

9

Jeżeli uda się uzyskać wymaganą dokładność w stanie
ustalonym i zakres regulacji, należy z kolei zbadać
stabilność tego układu.

9

Ponieważ parametry układu mogą ulegać zmianie (np.
zależnie od warunków otoczenia oraz przebiegu procesu
technologicznego w obiekcie sterowania) należy
zapewnić

stabilność

w najbardziej niekorzystnym

przypadku.

9

Uzyskuje się to przez zaprojektowanie układu z
odpowiednim marginesem bezpieczeństwa, biorąc pod
uwagę stabilność i jakość regulacji. Dogodnie jest to
wyrazić np. przez zapas amplitudy i zapas fazy.

Automatyka i Robotyka

Wykład nr 10

12

12

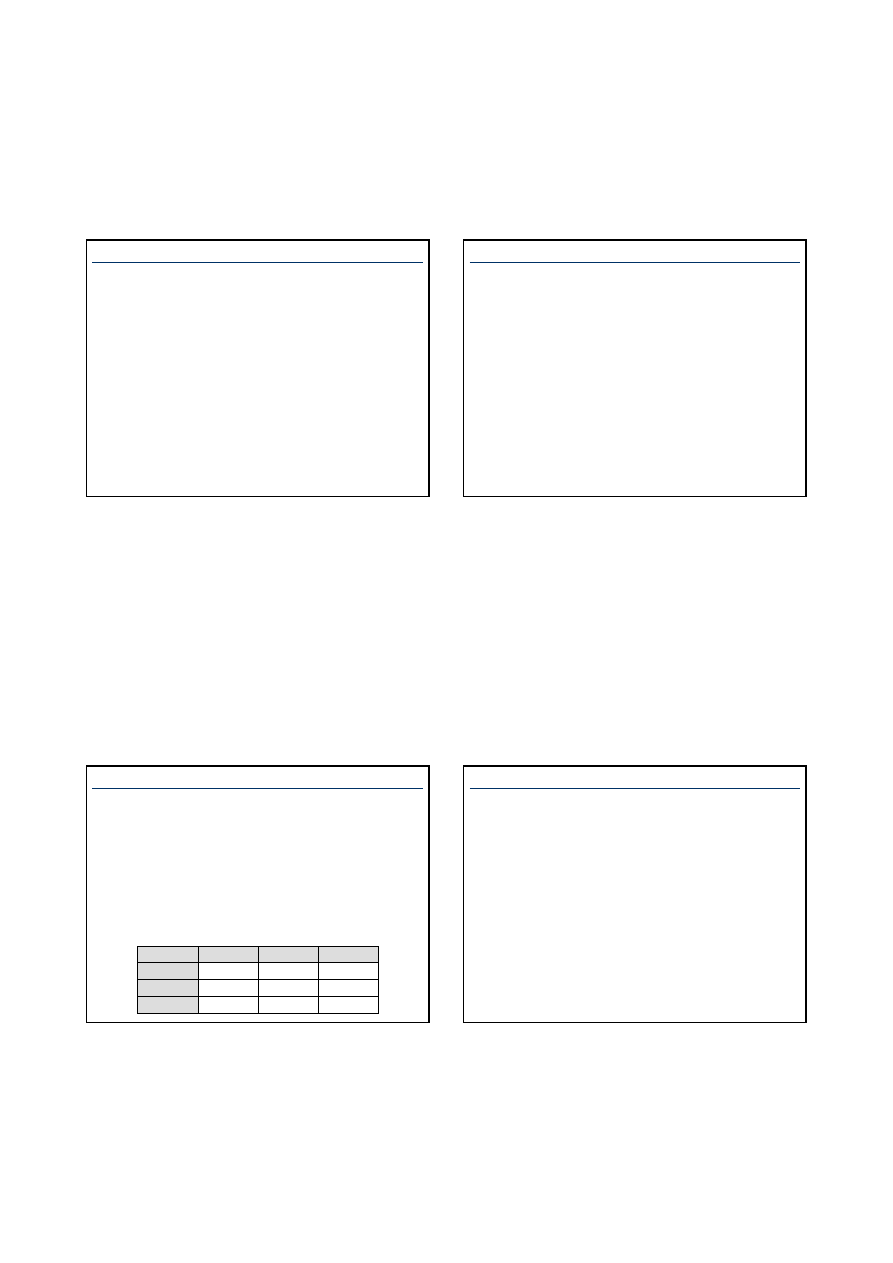
Schemat postępowania przy syntezie układu sterowania metodami

klasycznymi

Ustalenie

założeń

Ustalenie

założeń

Dokładność

w stanie

ustalonym

Stabilność i

jej zapas

tak

tak

tak

tak

nie

nie

nie

Korekcja

właściwości w

stanie ustalonym

Korekcja

właściwości w

stanie ustalonym

Korekcja

dynamiczna

Korekcja

dynamiczna

STOP

STOP

Właściwości

dynamiczne

Wybór struktury

Wybór struktury

Dobór

elementów i

podzespołów

Dobór

elementów i

podzespołów

Wymagania

dodatkowe

nie

Automatyka i Robotyka

Wykład nr 10

13

13

Dob

Dob

ó

ó

r parametr

r parametr

ó

ó

w regulatora

w regulatora

9

Metoda Zieglera

Metoda Zieglera

-

-

Nicholsa

Nicholsa

Są to najbardziej znane i najprostsze w zastosowaniu
reguły, sformułowane na początku lat czterdziestych w
wyniku prowadzonych badań doświadczalnych.

Jak wykazano znacznie później, reguły te prowadzą do
minimalizacji całki z modułu uchybu (kryterium całkowe I).

Korzystanie z tych reguł wymaga wstępnego wprowadzenia
dwóch pojęć:

9

wzmocnienia krytycznego

wzmocnienia krytycznego

K

K

kr

kr

9

okresu drga

okresu drga

ń

ń

krytycznych

krytycznych

T

T

os

os

Automatyka i Robotyka

Wykład nr 10

14

14

Wzmocnienie krytyczne

Wzmocnienie krytyczne

to wzmocnienie regulatora

proporcjonalnego, który połączony szeregowo z obiektem
spowoduje znalezienie się układu zamkniętego na granicy
stabilności (pojawiają się niegasnące drgania okresowe).

Okres tych drgań

nazywany jest

okresem drga

okresem drga

ń

ń

krytycznych

krytycznych

T

T

os

os

.

Ponieważ bezpośrednie doświadczalne wyznaczenie tych
parametrów ze względów bezpieczeństwa jest trudne
stosuje się metody pośrednie.

Automatyka i Robotyka

Wykład nr 10

15

15

Automatyka i Robotyka

Wykład nr 10

Wariant 1

Wariant 1

Kroki eksperymentu Z-N:

9

Ustawić regulator na działanie proporcjonalne P

9

Stopniowo zwiększając doprowadzić układ zamknięty do

granicy stabilności

9

Zapisać wzmocnienie krytyczne

K

K

kr

kr

i okres oscylacji

T

T

os

os

9

Określić nastawy według reguł podanych w tabeli dla

wybranego typu regulatora

0.125T

os

0.5T

os

0.6K

gr

PID

PID

-

0.83T

os

0.45K

gr

PI

PI

-

-

0.5K

gr

P

P

T

d

T

i

K

r

Regulator

16

16

Automatyka i Robotyka

Wykład nr 10

Ograniczenia tej metody:

9

nie zawsze można przeprowadzić eksperyment

9

zakres współczynnika k

p

może być zbyt mały, aby

wzbudzić drgania

9

obiekt nie może być wzbudzony, bo jest stabilny

Nastawy bezpieczne:

9

zaczynamy od małego k

p

i stopniowo go zwiększamy

9

zaczynamy od dużego T

p

i stopniowo ja zmniejszajmy

9

zaczynamy od małego T

d

i stopniowo ja zwiększamy

17

17

Automatyka i Robotyka

Wykład nr 10

Dobrać nastawy regulatora P, PI, PID metoda Zieglera-
Nicholsa dla obiektu

Przyk

Przyk

ł

ł

ad

ad

( )

(

)

2

1

5

1

+

=

s

s

G

o

K

K

p

p

=10

=10

K

K

p

p

=8.2

=8.2

K

K

p

p

=1

=1

K

K

p

p

=5

=5

K

K

pkr

pkr

=8.2

=8.2

T

T

osc

osc

=17.8s

=17.8s

18

18

Automatyka i Robotyka

Wykład nr 10

2.14

8.9

4.92

PID

PID

-

15.18

3.69

PI

PI

-

-

4.1

P

P

T

d

T

i

K

r

Regulator

19

19

t

h(t)

T

τ

1 – charakterystyka

rzeczywista

2 – charakterystyka

przybliżona

1

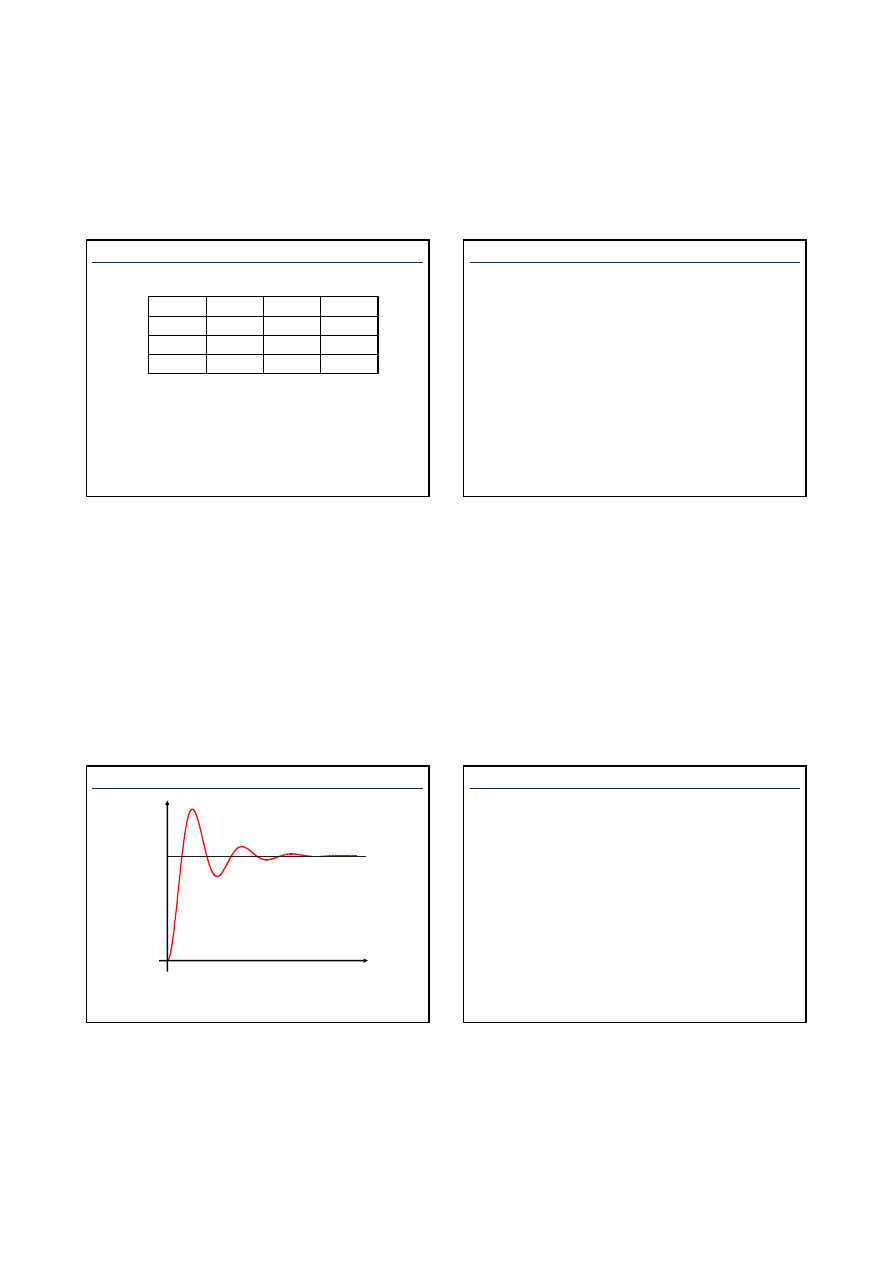
Przybliżenie odpowiedzi skokowej obiektu statycznego

T

2

Automatyka i Robotyka

Wykład nr 10

Wariant 2

Wariant 2

20

20

Metody te oparte są na przybliżeniu odpowiedzi skokowej

obiektu statycznego (krzywa 1) - charakterystyką skokową

członu inercyjnego pierwszego rzędu z opóźnieniem

(krzywa 2) o transmitancji operatorowej

τ

s

e

Ts

s

G

−

+

=

1

1

)

(

0

τ

−

=

2

T

T

;

Według Zieglera i Nicholsa parametry K

kr

i T

os

wyrażone są

wzorami:

τ

τ

−

=

2

T

K

kr

τ

4

=

os

T

;

Automatyka i Robotyka

Wykład nr 10

21

21

Nastawy regulatorów według Zieglera i Nicholsa

0,125

0,5

0,6

PID

PID

-

0,83

0,45

PI

PI

-

-

0,5

P

P

T

d

T

os

T

i/

T

os

K/K

kr

Regulator

Przyjęcie nastaw regulatorów z powyższej tabeli, pozwala
uzyskać przebiegi przejściowe o charakterze zbliżonym do
przedstawionego na następnym rysunku. Przeregulowanie
jest rzędu 15 - 20%, a liczba oscylacji nie przekracza
dwóch.

o

r

K

K

K

=

- iloczyn wzmocnień regulatora i obiektu

Automatyka i Robotyka

Wykład nr 10

22

22

Automatyka i Robotyka

Wykład nr 10

Cechy tej metody:

9

szybka metoda doboru nastaw na podstawie modelu

obiektu

9

prostota, wymagany jest skok jednostkowy

9

układ regulacji jest stabilny

9

jakość regulacji nie jest wysoka

9

nie można jej stosować dla

τ >T

2

, wrażliwa przy

τ = T

2

9

do zastosowania do obiektów z wyrównaniem

9

duży skok może ujawnić istotne nieliniowości

9

wrażliwa na zakłócenia

23

23

Odpowiedź skokowa układu regulacji przy nastawach

regulatora według Zieglera i Nicholsa

h(t)

1

0

t

Automatyka i Robotyka

Wykład nr 10

24

24

9

przebiegu aperiodycznego o najkrótszym czasie

regulacji,

9

minimum całki z kwadratu uchybu,

9

przebiegu o 20% przeregulowaniu i najkrótszym

czasie regulacji.

Bardziej szczegółową analizę doboru nastaw regulatorów

przeprowadził zespół pracujący pod kierunkiem Cypkina.

Opublikował on zestaw nomogramów, umożliwiający dobór

nastaw regulatorów dla trzech zasadniczych kryteriów

jakości:

Automatyka i Robotyka

Wykład nr 10

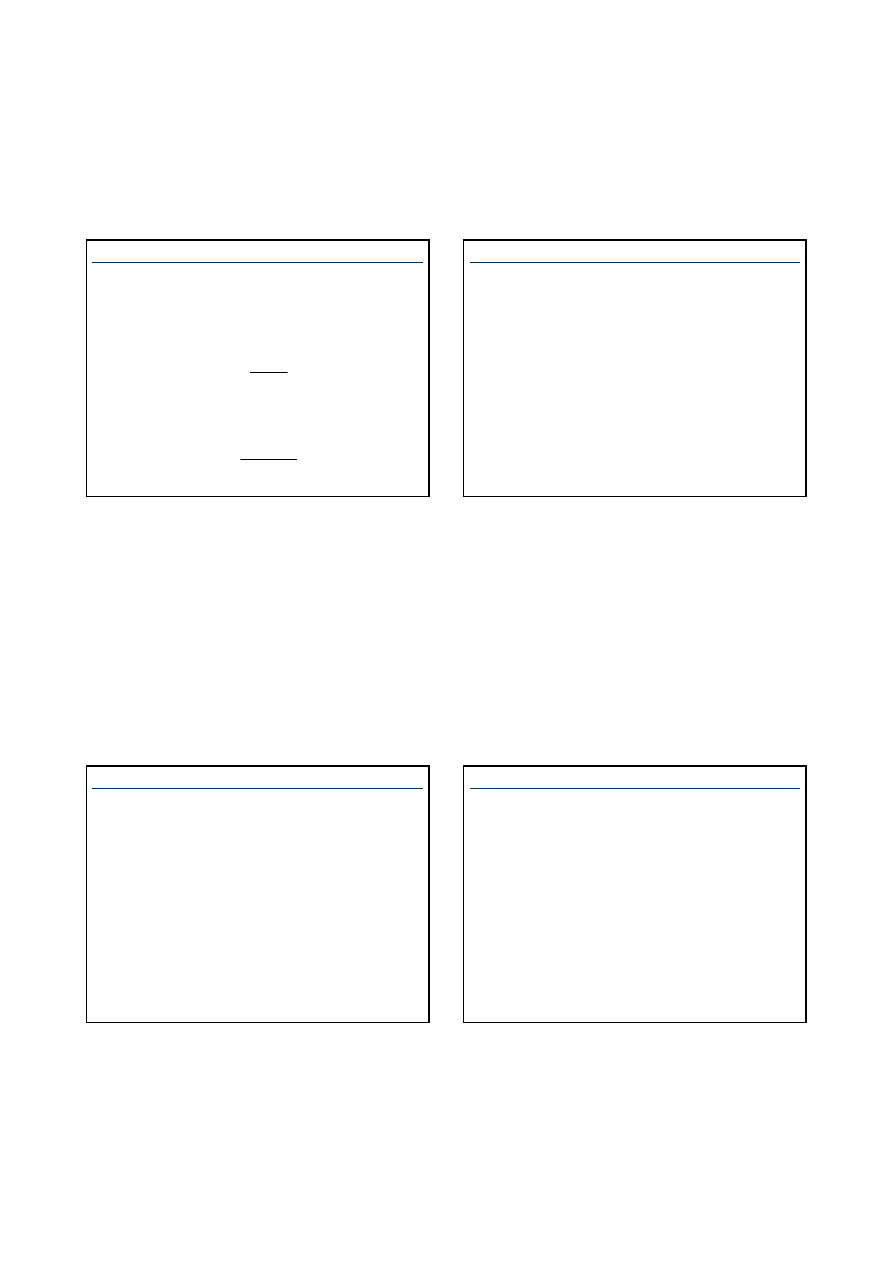
25

25

Nomogramy te opracowano dla regulatorów

P

,

I

,

PI

i

PID

,

przy czym uwzględniano zarówno:

9

obiekty statyczne opisane transmitancją operatorową

9

jak i obiekty astatyczne o transmitancji operatorowej

τ

s

e

Ts

s

G

−

+

=

1

1

)

(

0

τ

s

e

Ts

s

K

s

G

−

+

=

)

1

(

)

(

0

0

Automatyka i Robotyka

Wykład nr 10

26

26

Metoda charakterystyk

Metoda charakterystyk

cz

cz

ę

ę

stotliwo

stotliwo

ś

ś

ciowych

ciowych

Dobór regulatora lub członu korekcyjnego możemy również

przeprowadzić

na podstawie analizy charakterystyk

częstotliwościowych układu.

Określić z nich można przede wszystkim:

9

zapas stabilności,

9

czas regulacji (oceniany na podstawie pulsacji

przecięcia),

9

przeregulowanie (oceniane na podstawie zapasu fazy).

Automatyka i Robotyka

Wykład nr 10

27

27

1.

wykreślić charakterystyki częstotliwościowe obiektu,

2.

wyznaczyć

minimalną

wartość

wzmocnienia,

konieczną

ze względu na ograniczenie uchybu

ustalonego,

3.

wyznaczyć minimalne wartości zapasu modułu i

zapasu fazy, konieczne ze względu na ograniczenie

przeregulowania oraz obszar zabroniony dla

charakterystyki częstotliwościowej układu otwartego,

Tok postępowania jest następujący:

Automatyka i Robotyka

Wykład nr 10

28

28

4.

wyznaczyć minimalną wartość pulsacji przecięcia

(powyżej której moduł transmitancji układu otwartego

jest mniejszy od jedności) układu skorygowanego,

konieczną ze względu na ograniczenie czasu regulacji,

5.

wybrać typ regulatora i naszkicować charakterystykę

układu z regulatorem,

6.

sprawdzić, czy warunki 2-4 są spełnione,

7.

jeśli wybrany typ regulatora nie spełnia postawionych

warunków bez względu na dobór nastaw, wybrać inny

regulator i powtórzyć postępowanie.

Automatyka i Robotyka

Wykład nr 10

29

29

Metoda linii pierwiastkowych

Metoda linii pierwiastkowych

Metoda linii pierwiastkowych (metoda miejsc
geometrycznych pierwiastków) - umożliwia wyznaczenie
położenia pierwiastków równania charakterystycznego
układu zamkniętego na podstawie rozmieszczenia zer
i biegunów transmitancji układu otwartego.

Ze zmianą wzmocnienia układu otwartego pierwiastki te
poruszają się po liniach pierwiastkowych, będących
miejscem geometrycznym pierwiastków.

Automatyka i Robotyka

Wykład nr 10

30

30

Rozpatrzymy układ ze sprzężeniem zwrotnym

Transmitancja układu zamkniętego wynosi

)

(

1

)

(

)

(

)

(

)

(

0

0

0

0

s

G

K

K

s

G

K

K

s

W

s

Y

s

G

p

p

Z

+

=

=

Regulator

K

p

Regulator

K

p

Obiekt

K

o

G

o

(s)

Obiekt

K

o

G

o

(s)

–

W(s)

W(s)

E(s)

E(s)

U(s)

U(s)

Y(s)

Y(s)

Automatyka i Robotyka

Wykład nr 10

31

31

Równanie charakterystyczne, którego pierwiastki są
biegunami transmitancji ma postać

0

)

(

1

0

0

=

+

s

G

K

K

p

Pierwiastki układu zamkniętego zależą od współczynnika
wzmocnienia

K

K

p

p

, tym samym możemy mieć wpływ na

odpowiedź dynamiczną układu zamkniętego przez dobór
odpowiedniej wartości

K

K

p

p

.

Rozważmy mechanizm konstruowania wykresu
pierwiastków przy wykorzystaniu wzmocnienia jako
zmiennego parametru.

Automatyka i Robotyka

Wykład nr 10

32

32

Założymy, że transmitancja układu otwartego K

p

K

0

G

0

(s)

jest funkcją wymierną, licznik ma postać K

p

K

0

b(s)

, gdzie

b(s)

jest wielomianem stopnia m

∏

=

−

−

=

−

−

−

=

=

+

+

+

=

m

i

i

m

m

m

m

z

s

z

s

z

s

z

s

b

s

b

s

s

b

1

2

1

1

1

)

(

)

)...(

)(

(

...

)

(

∏

=

−

−

=

+

+

+

=

n

i

i

n

n

n

p

s

a

s

a

s

s

a

1

1

1

)

(

...

)

(

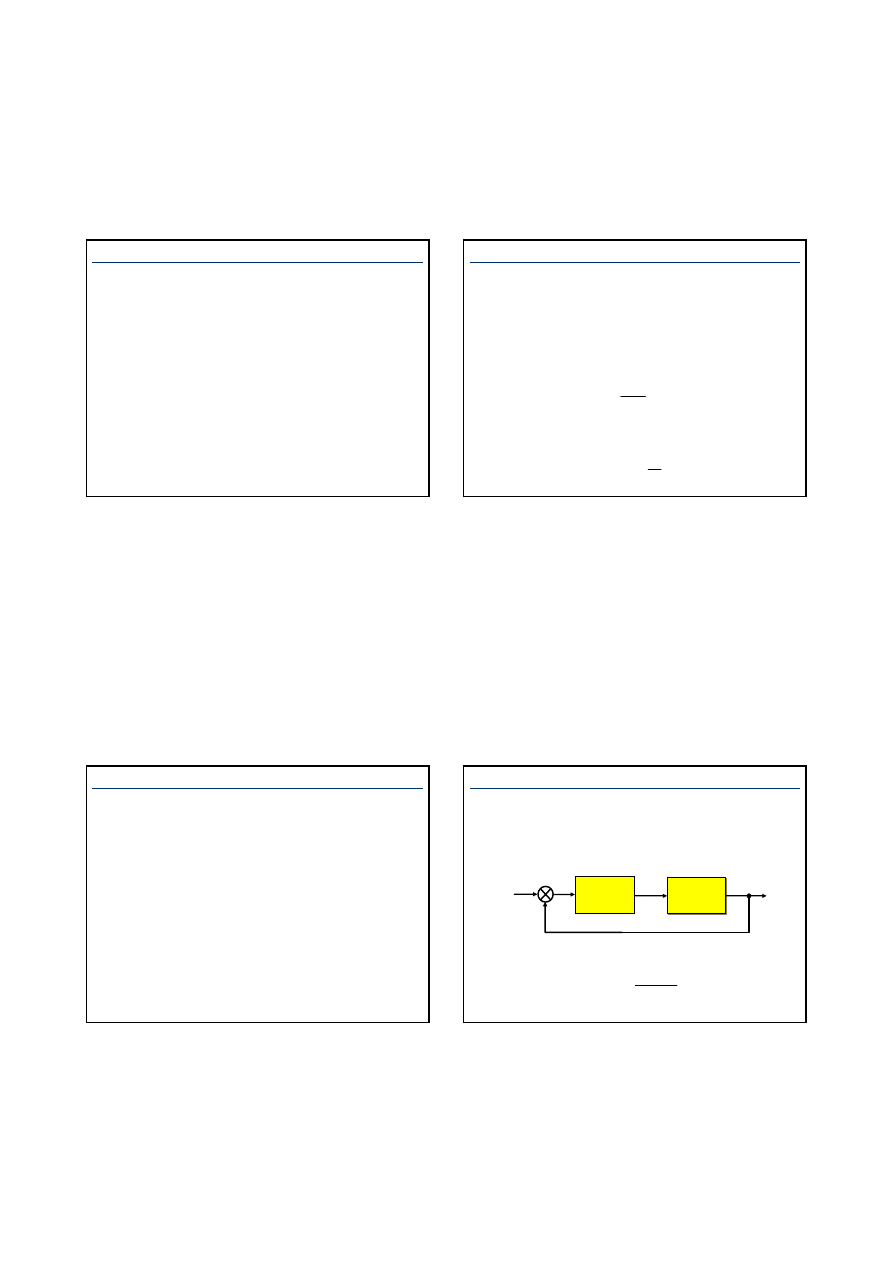
Mianownik jest wielomianem a(s) n-tego stopnia, a n

≥

m

Automatyka i Robotyka

Wykład nr 10

33

33

Dla potrzeb analizy załóżmy, że wzmocnienie obiektu K

0

jest dodatnie, oraz zdefiniujmy parametr miejsca
geometrycznego jako

0

K

K

K

p

=

Miejsca zerowe (pierwiastki) b(s) = 0 są

zerami

zerami

transmitancji

transmitancji

G

Z

(s)

i oznaczamy je jako

z

z

i

i

, podobnie

miejsca zerowe (pierwiastki) a(s) = 0

są

biegunami

biegunami

transmitancji

transmitancji

G

Z

(s)

i oznaczamy je jako

p

p

i

i

.

Automatyka i Robotyka

Wykład nr 10

34

34

Możemy teraz przedstawić

położenie pierwiastków

równania na kilka możliwych sposobów. Każde z

poniższych równań ma te same pierwiastki

0

)

(

1

0

=

+

s

KG

0

)

(

)

(

1

=

+

s

a

s

b

K

0

)

(

)

(

=

+

s

Kb

s

a

K

s

G

1

)

(

0

−

=

Automatyka i Robotyka

Wykład nr 10

35

35

9

Równania te określa się często jako formuły pierwiastków
równania charakterystycznego.

9

Linia pierwiastkowa jest zbiorem wartości s, dla których
w powyższych równaniach zachowana jest dodatnia
wartość K (oraz K

p

).

9

Rozwiązaniami równań

są

pierwiastki układu

zamkniętego, więc można powiedzieć, że metoda linii
pierwiastkowych jest sposobem wnioskowania o
własnościach układu zamkniętego na podstawie
transmitancji układu otwartego KG

0

(s).

Automatyka i Robotyka

Wykład nr 10

36

36

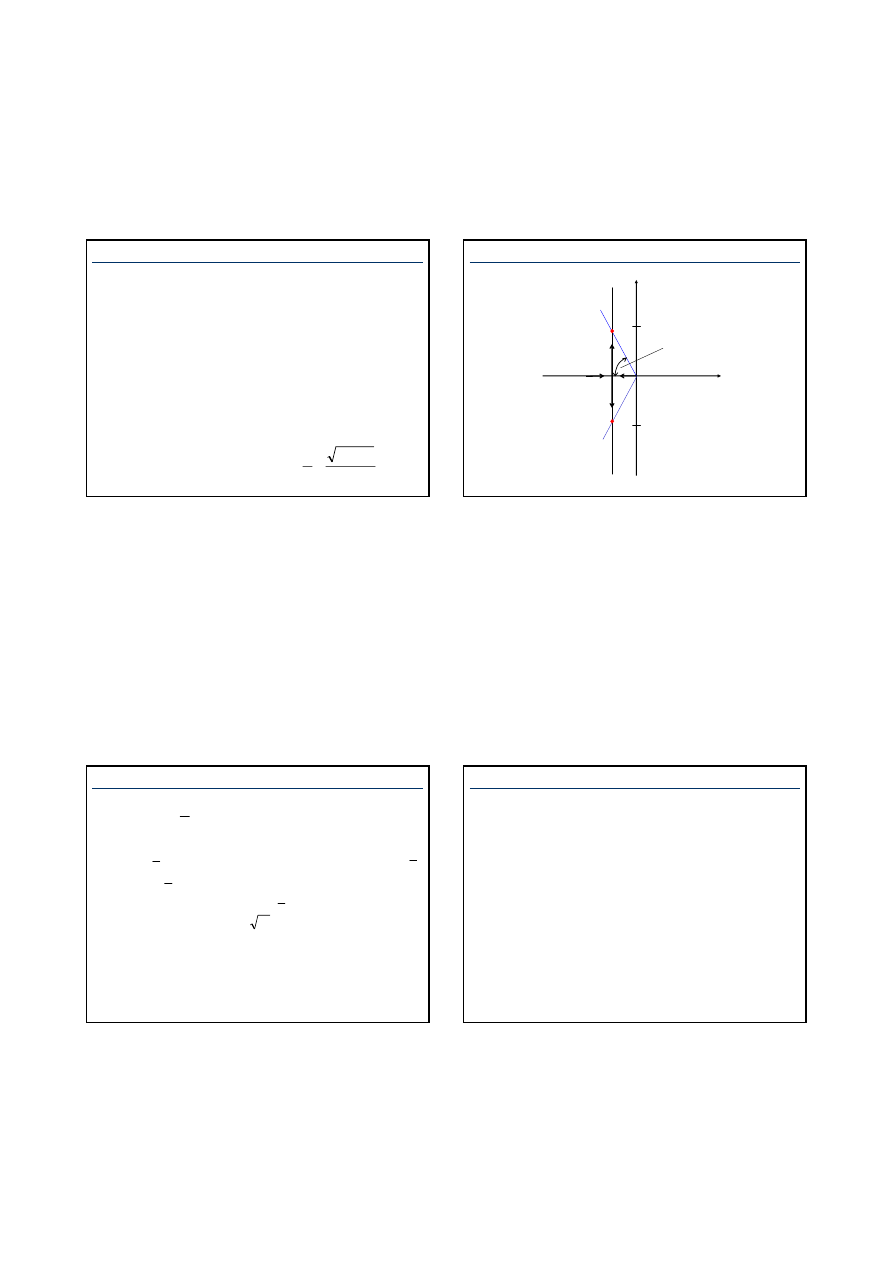
Przykład

Transmitancja obiektu ma postać

)

1

(

)

(

0

0

+

=

s

s

K

s

G

Wyznaczyć położenie pierwiastków układu zamkniętego ze
względu na K

p

.

Regulator

K

p

Regulator

K

p

Obiekt

G

o

(s)

Obiekt

G

o

(s)

–

W(s)

W(s)

E(s)

E(s)

U(s)

U(s)

Y(s)

Y(s)

Automatyka i Robotyka

Wykład nr 10

37

37

Charakterystyka położenia pierwiastków jest graficznym
przedstawieniem pierwiastków równania:

0

2

=

+

+

K

s

s

2

4

1

2

1

,

2

1

K

s

s

−

±

−

=

Rozwiązania mają postać:

czyli

0

)

(

)

(

=

+

s

Kb

s

a

m=

0

n=

2

K

0

=

1

a

(s)=s

2

+s

b

(s)=1

K = K

p

p

i

=

0, -1

Wykorzystując przyjęte wcześniej formy zapisu

Automatyka i Robotyka

Wykład nr 10

38

38

Re

Im

1

-1

-1

Szkic położenia pierwiastków

x

x

°

=

=

30

ξ

cos

θ

-1

Automatyka i Robotyka

Wykład nr 10

39

39

Zmieniając wartość K możemy umiejscowić bieguny układu

zamkniętego w dowolnych punktach należących do

charakterystyki pierwiastków.

9

Dla

pierwiastki przyjmują wartości rzeczywiste z

przedziału (-1,0).

4

1

0

≤

≤ K

9

Dla

istnieją dwa pierwiastki o wartościach równych

4

1

=

K

2

1

−

9

Dla

pierwiastki są liczbami zespolonymi, których

część rzeczywista ma wartość

, natomiast część urojona

wzrasta proporcjonalnie do

.

4

1

>

K

2

1

−

K

Automatyka i Robotyka

Wykład nr 10

40

40

Metoda klasyczna syntezy układu sterowania umożliwia
przyjęcie jednego z rozwiązań, natomiast nie daje podstawy
dla ustalenia, które z nich jest optymalne.

Ograniczeń takich nie mają np.

metody wykorzystujące

wskaźniki jakości

. Umożliwiają

one wyznaczenie

rozwiązań optymalnych tzn. takich, które zapewniają
minimalizację

przyjętego wskaźnika jakości -

przy

spełnieniu warunków wynikających z narzuconych
ograniczeń.

Synteza układów sterowania z uwzględnieniem
wskaźników jakości. Metoda przestrzeni stanów

Automatyka i Robotyka

Wykład nr 10

41

41

Automatyka i Robotyka

Wykład nr 10

Można wyróżnić następujące kryteria:

9

całki z wartości bezwzględnej odchyłki (ang. IAE)

9

całki z kwadratu odchyłki (ang. ISE)

9

całki z czasu pomnożonego przez wartość bezwzględną

odchyłki (ang. ITAE)

9

całki z kwadratu czasu pomnożonego przez odchyłkę,

wyrażenie całkowane i podniesione do kwadratu (ang. ISTES)

9

całki z kwadratu czasu pomnożonej przez kwadrat odchyłki

(ang. ISTSE)

( )

∫

∞

=

0

dt

t

e

I

( )

∫

∞

=

0

2

dt

t

e

I

( )

∫

∞

⋅

=

0

dt

t

t

e

I

( )

(

)

∫

∞

⋅

=

0

2

2

dt

t

t

e

I

( )

∫

∞

⋅

=

0

2

2

dt

t

t

e

I

42

42

Wskaźniki jakości bywają różne w zależności od rodzaju

układu, warunków jego pracy i postawionych mu wymagań.

Najczęściej formułuje się je jako funkcjonały całkowe, które

dla jednowymiarowych ciągłych i stacjonarnych układów

sterowania mają postać:

1

)]

(

,)

(

,...,

)

(

),

(

[

0

−

≤

=

∫

•

n

k

dt

t

u

t

y

t

y

t

y

f

I

k

t

t

r

gdzie: n - rząd równania opisującego układ sterowania.

Automatyka i Robotyka

Wykład nr 10

43

43

Przy takim sformułowaniu problemu sterowania występują
dwa zagadnienia:

9

znalezienie struktury i parametrów układu, przy
których dla danych ograniczeń i zadanych typowych
przebiegów sygnału sterującego, wskaźnik jakości
osiąga minimalną wartość - jest to zagadnienie
syntezy układu sterowania.

9

wyznaczanie takiego sterowania u(t), które
przeprowadza dany układ z pewnego stanu
początkowego do pewnego stanu końcowego w
sposób zapewniający minimalizację wskaźnika jakości
przy zachowaniu narzuconych ograniczeń.

Automatyka i Robotyka

Wykład nr 10

44

44

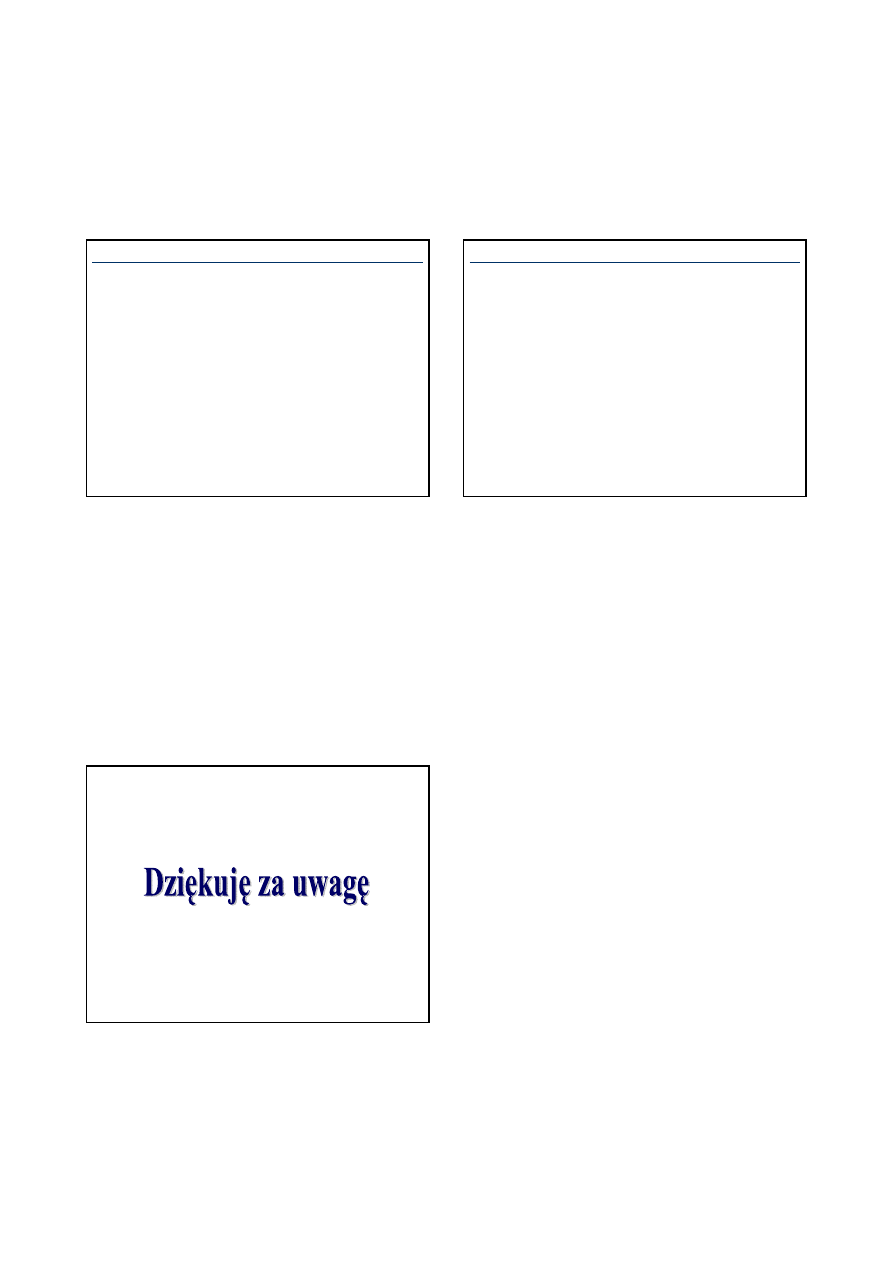
Ponieważ

całkowe kryteria jakości stosuje się

w

przypadkach, gdy głównym celem staje się ocena jakości
pracy układu, w wybranym przedziale czasowym często
stosuje się kryterium całki kwadratu uchybu w postaci:

(

)

∫

+

=

s

t

T

T

dt

Ru

u

Qx

x

J

0

gdzie:

Q

i R - dodatnio określone macierze wagowe,

x

i u - odpowiednio wektory stanu i wektor sterowań.

Automatyka i Robotyka

Wykład nr 10

45

45

Kryterium jakości w formie kwadratowej zawiera odchylenia

zarówno zmiennych stanu x, jak i zmiennych sterujących u,

od ich wartości optymalnych dla stanu ustalonego w

zakresie rozpatrywanego przedziału czasu sterowania t

s

.

Jeżeli układ sterowania opisany jest równaniem stanu:

)

(

)

(

)

(

t

Bu

t

Ax

t

x

+

=

i czas sterowania t

s

jest zadany, zadanie polega na

wyznaczeniu sterowania spełniającego powyższe równanie,
oraz minimalizującego funkcjonał (wskaźnik jakości).

Automatyka i Robotyka

Wykład nr 10

46

46

W zagadnieniach związanych z syntezą często spotykany
jest wskaźnik jakości będący całką kwadratu uchybu w
postaci:

∫

+∞

=

0

2

)

( dt

t

E

J

d

E

którą wyznacza się dla typowych stanów przejściowych w
rozważanym układzie.

Gdy układ jest stabilny asymptotycznie, a jego parametry są
tak dobrane, że odpowiedź jednostkowa ma przebieg
aperiodyczny, to wtedy przy zmniejszeniu wskaźnika jakości
zmniejszają

się

czasy t

m

, t

r

oraz maksymalne

przeregulowanie.

Automatyka i Robotyka

Wykład nr 10

47

47