Algorytm obliczeń konstukcyjnych podnośnika

śrubowego

1

Wysokość podnoszenia

Wysokość podnoszenia oblicza się na podstawie empirycznej zależności:

H

pod

[

mm]=1,6⋅

√

Q[ N ]

lub

H

pod

[

cm]=0,5⋅

√

Q [kG]

1.1

Podnośnik jednostopniowy

W podnośniku jednostopniowym długość śruby roboczej wynosi w przybliżeniu:

l

śr

≃

H

pod

+

50÷70 [mm]

1.2

Podnośnik dwustopniowy

W podnośniku dwu stopniowym wysokość podnoszenia rozdziela się na dwie śruby robocze. Ich
długości w przybliżeniu są równe:

l

śr wew

≃

H

pod

2

+

50÷70 [mm]

l

śr zew

≃

H

pod

2

+

50÷70[mm ]

2

Dobór gwintu wewnętrznej śruby roboczej

2.1

Podnośnik jednostopniowy

Długość wyboczeniowa jedynej śruby wynosi:

l

w

=

2⋅l

śr

2.2

Podnośnik dwustopniowy

Długość wyboczeniowa wewnętrznej śruby wynosi:

l

w

=

2⋅l

śr wew

Na podstawie obciążenia oblicza się wartość siły krytycznej:

P

kr

=

Q⋅X

wew

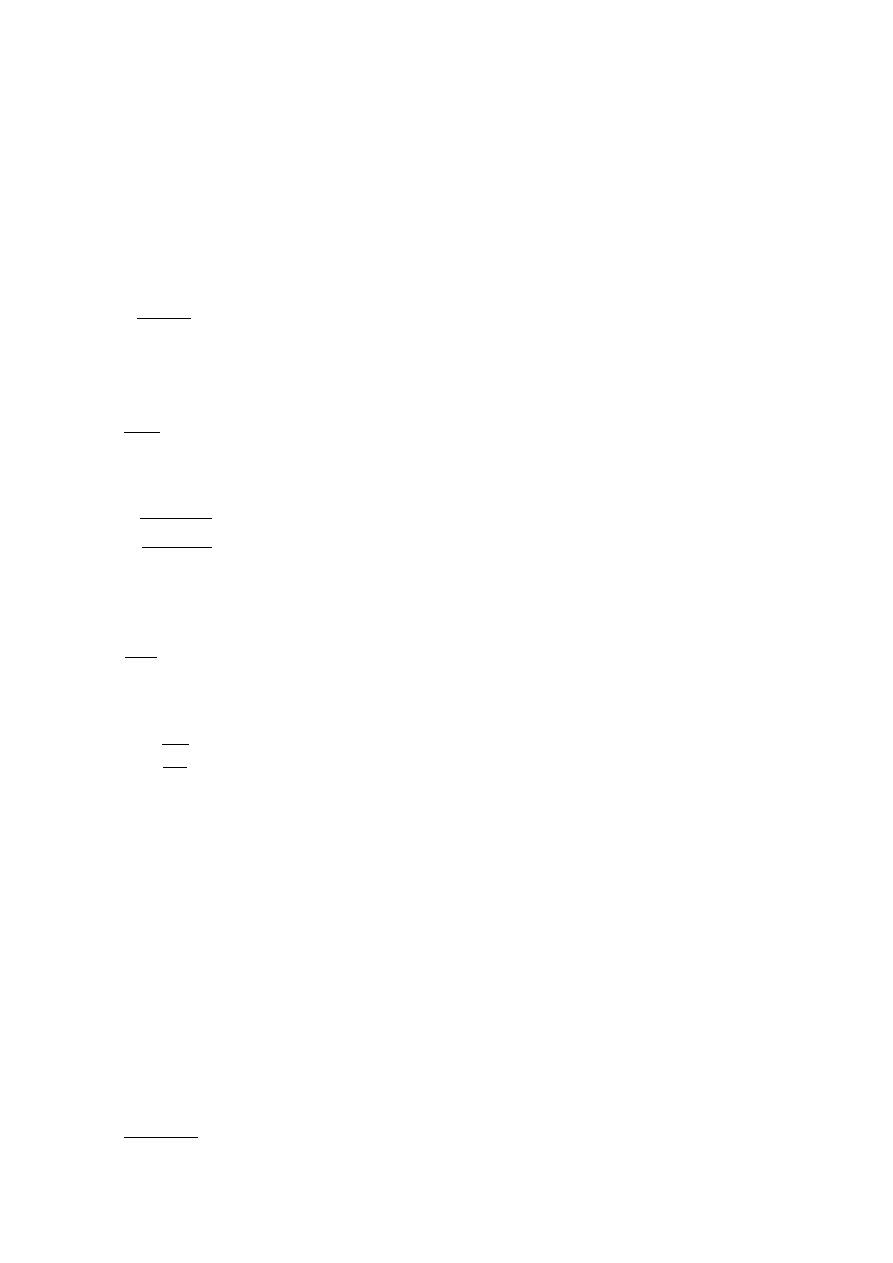
gdzie:

X

wew

=

6÷10

W celu dalszych obliczeń należy wybrać materiał, z którego zostanie wykonana śruba. Powinna być
to stal konstrukcyjna.
Na podstawie wzoru Eulera oblicza się średnicę rdzenie śruby wewnętrznej (wstępnie zakłada się,
że wyboczenie jest spreżyste):

P

kr

=

π

2

⋅

E⋅I

l

w

2

,

gdzie:

I =

π⋅

d

r

4

64

Stąd wzór na średnicę rdzenia ma postać:

d

r

=

4

√

64⋅l

w

2

⋅

P

kr

π

3

⋅

E

Dodatkowo oblicza się smukłość:

λ=

4⋅l

w

d

r

Następnie należy określić smukłość graniczną z zależności:

λ

gr

=π⋅

√

E

σ

H

Jeśli obliczona smukłość jest mniejsza od smukłości granicznej tzn.

λ <λ

gr

,

wtedy zależność na siłę krytyczną jest nieprawdziwa (wyboczenie nie jest sprężyste jak zostało to
założone na początku). W takiej sytuację stosuje się hipotezę T-J lub J-O.

Hipoteza T-J

σ

kr

=

a⋅λ +b

gdzie:

b=σ

plast

a=

σ

H

−σ

plast

λ

gr

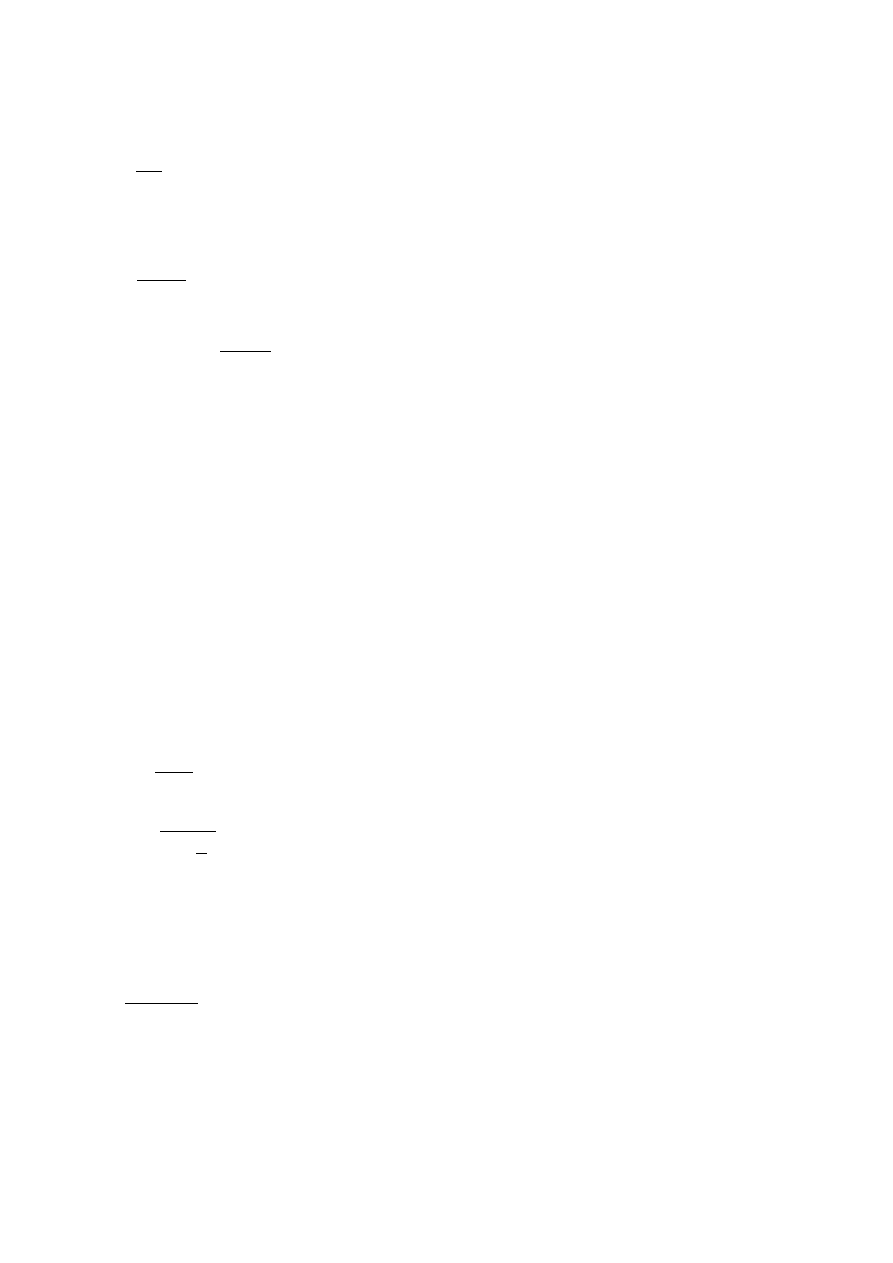
Na podstawie hipotezy T-J, oblicza się się średnicę rdzenia śruby:

σ

kr

=

P

kr

A

=

a⋅λ+b

P

kr

=(

a⋅λ +b)⋅A

P

kr

=

a⋅4⋅l

w

d

r

⋅

A+b⋅A

P

kr

=

a⋅π⋅l

w

⋅

d

r

+

b⋅π⋅d

r

2

4

Wykorzystując dowolną technikę rozwiązywania rownań drugiego stopnia, należy znaleźć
pierwiastki rozpatrywanej równości.

d

r

=

?

Ostatnim krokiem jest dobór gwintu trapezowego symetrycznego z normy, dla którego, średnica
wewnętrzna gwintu jest pierwszą większą od średnicy rdzenia d

r

.

Tr

❑

x

❑

3

Sprawdzenie samohamowności dobranego gwintu

Warunek samohamowności:

γ⩽ρ

'

gdzie:

tg (γ)=

P

π⋅

d

p

tg (ρ ')=

μ

cos

(

β
2

)

4

Sprawność dobranego gwintu

Sprawność gwintu wynosi:

η=

tg(γ)

tg(γ+ρ ')

5

Dobór wysokości nakrętki śruby wewnętrznej

Nakrętkę wykonuje się z brązu lub mosiądzu. Wysokokość nakrętki określa się na podstawie
warunku na naciski powieszchniowe:

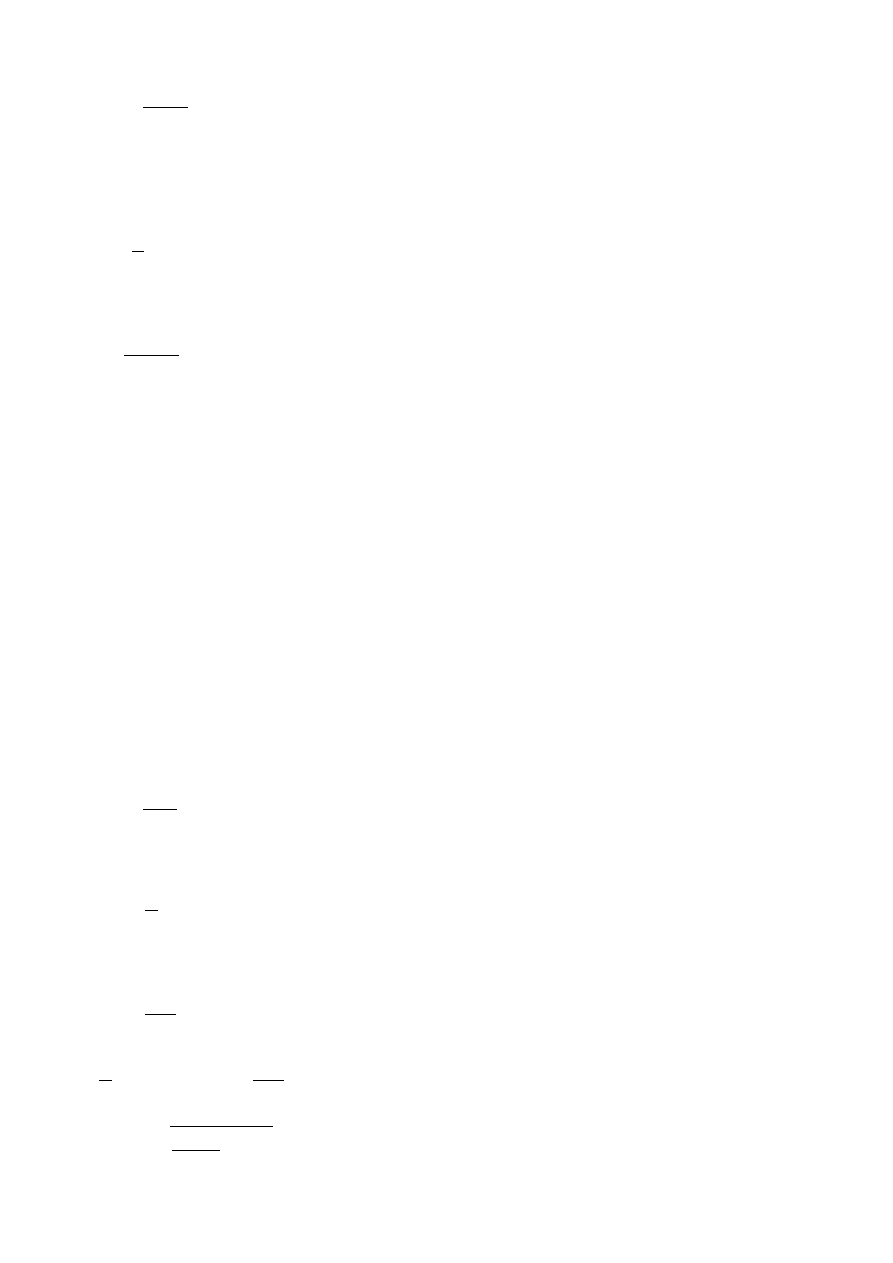
p

dop

⩾

Q

A

n zwoi

gdzie:

A

n zwoi

=

n⋅A

z

A

z

= π

4

⋅

(

d

śr

2

−

D

o nak

2

)

Do obliczenia jest minimalana liczba zwojów czynnych, wymagana do przeniesienia zadanego
obciążenia.

n⩾

Q

A

z

⋅

p

dop

Obliczoną liczbę zwojów zaokrągla się do góry do całkowitej liczby n

z

.

Ponieważ w nakrętce jest 3/4 zwoja wejściowego i 3/4 zwoja wyjściowego nie współpracujacego w
pełni, liczbę zwojów czynnych należy odpowiednio powiększyć.

n

cał

=

n

z

+

1,5

Dodatkowo, minimalna liczba współpracujących zwojów, ze względu niedogładności wykonania
wynosi n=3 .
Ostatecznie całkowita liczba zwojów wynosi:

n

cał

=

max (n

z

+

1,5 ; 4,5)

6

Dobór średnicy zewnętrznej nakrętki śruby wewnętrznej

Średnicę zewnętrzną nakrętki określa się na podstawie warunku na nacisku powieszchniowe lub z
warunku na równość odkształceń:

6.1

Warunek na naciski powieszchniowe

p

dop

⩾

Q

A

pod

gdzie:

A

pod

= π

4

⋅

(

d

zew obl

'

2

−

D

r nak

2

)

Stąd:

A

pod

⩾

Q

p

dop

π

4

⋅

(

d

zew obl

'

2

−

D

r nak

2

)

⩾

Q

p

dop

d

zew obl

'

⩾

√

4⋅Q

π⋅

p

dop

+

D

r nak

2

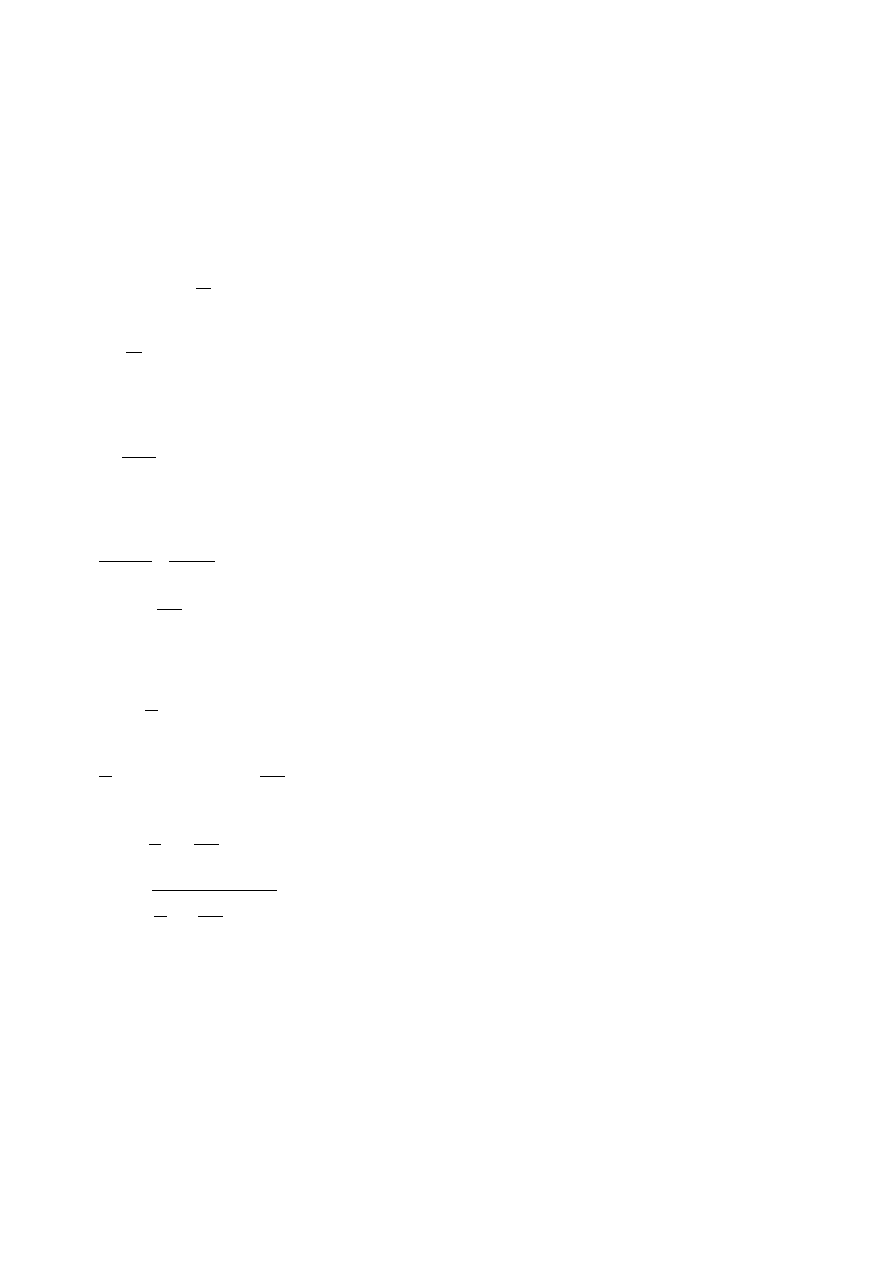
Tak obliczoną średnicę należy powiększyć o około 1÷2 mm, aby możliwe było wykonanie fazy
ułatwiającej wciśnięcie nakrętki w gniazdo

d

zew

'

=

d

zew obl

'

+

1÷2[mm]

6.2

Warunek na równość odkształceń:

ε

śr

=ε

n

σ=

E⋅ε⇔ε= σ

E

σ=

Q

A

Wynika stąd, że:

ε=

Q

E⋅A

Z warunku na równość otrzymuje się:

Q

E

śr

⋅

A

śr

=

Q

E

n

⋅

A

n

A

n

=

A

śr

E

śr

E

n

Pole przekroju nakrętki wynosi:

A

pod

= π

4

⋅

(

d

zew

' ' 2

−

D

r nak

2

)

π
4

⋅

(

d

zew

' ' 2

−

D

r nak

2

)

=

A

śr

E

śr

E

n

d

zew

' ' 2

=

4

π⋅A

śr

E

śr

E

n

+

D

r nak

2

d

zew

' '

=

√

4

π⋅A

śr

E

śr

E

n

+

D

r nak

2

Ostatecznie dobiera się średnicę zewnętrzną nakrętki jako:

d

zew

=

max(d

zew

'

; d

zew

''

)

7

Dobór gwintu zewnętrznej śruby roboczej

7.1

Podnośnik jednostopniowy

W przypadku podnośnika jednostopniowego, zewnętrzna śruba robocza nie istnieje, krok się
pomija.

7.2

Podnośnik dwustopniowy

Długość wyboczeniowa wewnętrznej śruby wynosi:

l

w

=

2⋅l

śr zew

Na podstawie wzoru Eulera oblicza się średnicę rdzenie śruby wewnętrznej (wstępnie zakłada się,
że wyboczenie jest spreżyste):

P

kr

=

π

2

⋅

E⋅I

l

w

2

,

gdzie:

I =

π⋅(

d

r

4

−

D

w

4

)

64

Stąd wzór na średnicę rdzenia ma postać:

d

r

=

4

√

64⋅l

w

2

⋅

P

kr

π

3

⋅

E

+

D

w

4

Dodatkowo oblicza się smukłość:

λ=

l

w

√

I

A

=

l

w

√

π⋅(

d

r

4

−

D

w

4

)

64

⋅

4

π⋅(

d

r

2

−

D

w

2

)

=

4⋅l

w

√

d

r

4

−

D

w

4

d

r

2

−

D

w

2

=

4⋅l

w

√

(

d

r

2

−

D

w

2

)⋅(

d

r

2

+

D

w

2

)

d

r

2

−

D

w

2

gdzie:

A=

π⋅(

d

r

2

−

D

w

2

)

4

λ=

4⋅l

w

√

d

r

2

+

D

w

2

Następnie należy określić smukłość graniczną z zależności:

λ

gr

=π⋅

√

E

σ

H

Jeśli obliczona smukłość jest mniejsza od smukłości granicznej tzn.

λ <λ

gr

,

wtedy zależność na siłę krytyczną jest nieprawdziwa (wyboczenie nie jest sprężyste jak zostało to
założone na początku). W takiej sytuację stosuje się hipotezę T-J lub J-O.

Hipoteza T-J

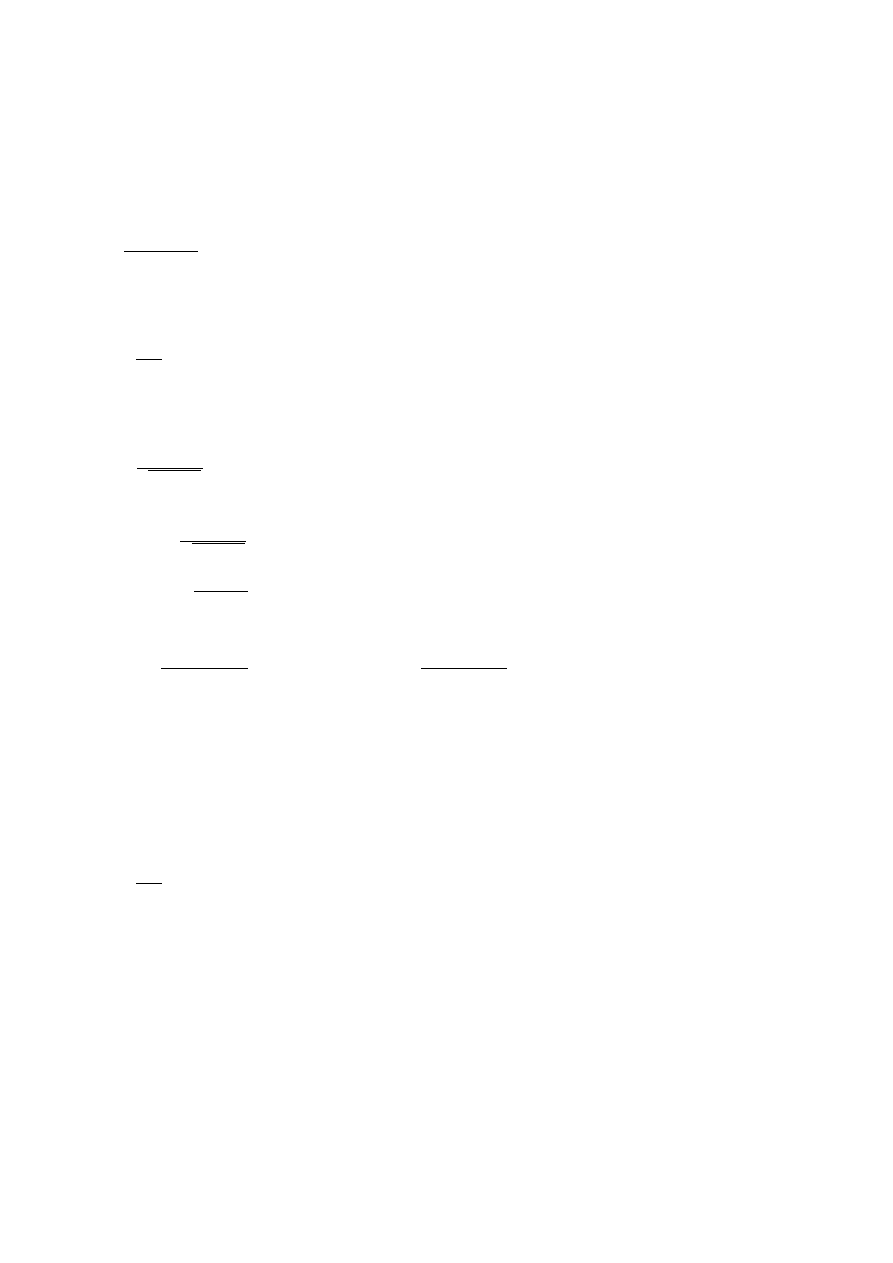
σ

kr

=

a⋅λ +b

gdzie:

b=σ

plast

a=

σ

H

−σ

plast

λ

gr

Na podstawie hipotezy T-J, oblicza się się średnicę rdzenia śruby:

σ

kr

=

P

kr

A

=

a⋅λ+b

P

kr

=(

a⋅λ +b)⋅A

P

kr

=

a⋅4⋅l

w

√

d

r

2

+

D

w

2

⋅

A+b⋅A

P

kr

−

b⋅A=

a⋅4⋅l

w

√

d

r

2

+

D

w

2

⋅

A

(

P

kr

−

b⋅A)⋅

√

d

r

2

+

D

w

2

=

a⋅4⋅l

w

⋅

A

(

P

kr

−

b⋅

π⋅(

d

r

2

−

D

w

2

)

4

)

2

⋅(

d

r

2

+

D

w

2

)=

a

2

⋅

4

2

⋅

l

w

2

⋅

(

π⋅(

d

r

2

−

D

w

2

)

4

)

2

Wykorzystując dowolną technikę rozwiązywania rownań 8 stopnia, należy znaleźć pierwiastki
rozpatrywanej równości.

d

r

=

?

Znalezione pierwiastki, należy podstawić do równania wyjśćiowego:

σ

kr

=

P

kr

A

=

a⋅λ+b

i sprawdzić czy równanie jest spełnione, w celu wyeliminowania rozwiązań nieprawdziwych.

Ostatnim krokiem jest dobór gwintu trapezowego symetrycznego z normy, dla którego, średnica
wewnętrzna gwintu jest pierwszą większą od średnicy rdzenia d

r

.

Tr

❑

x

❑

8

Sprawdzenie samohamowności dobranego gwintu

Warunek samohamowności:

γ⩽ρ

'

gdzie:

tg (γ)=

P

π⋅

d

p

tg (ρ ')=

μ

cos

(

β
2

)

9

Sprawność dobranego gwintu

Sprawność gwintu wynosi:

η=

tg(γ)

tg(γ+ρ ')

10 Dobór wysokości nakrętki śruby zewnętrznej

Nakrętkę wykonuje się z brązu lub mosiądzu. Wysokokość nakrętki określa się na podstawie
warunku na naciski powieszchniowe:

p

dop

⩾

Q

A

n zwoi

gdzie:

A

n zwoi

=

n⋅A

z

A

z

= π

4

⋅

(

d

śr

2

−

D

o nak

2

)

Do obliczenia jest minimalana liczba zwojów czynnych, wymagana do przeniesienia zadanego
obciążenia.

n⩾

Q

A

z

⋅

p

dop

Obliczoną liczbę zwojów zaokrągla się do góry do całkowitej liczby n

z

.

Ponieważ w nakrętce jest 3/4 zwoja wejściowego i 3/4 zwoja wyjściowego nie współpracujacego w
pełni, liczbę zwojów czynnych należy odpowiednio powiększyć.

n

cał

=

n

z

+

1,5

Dodatkowo, minimalna liczba współpracujących zwojów, ze względu niedogładności wykonania
wynosi n=3 .
Ostatecznie całkowita liczba zwojów wynosi:

n

cał

=

max (n

z

+

1,5 ; 4,5)

11 Dobór średnicy zewnętrznej nakrętki śruby zewnętrznej

Średnicę zewnętrzną nakrętki określa się na podstawie warunku na nacisku powieszchniowe lub z

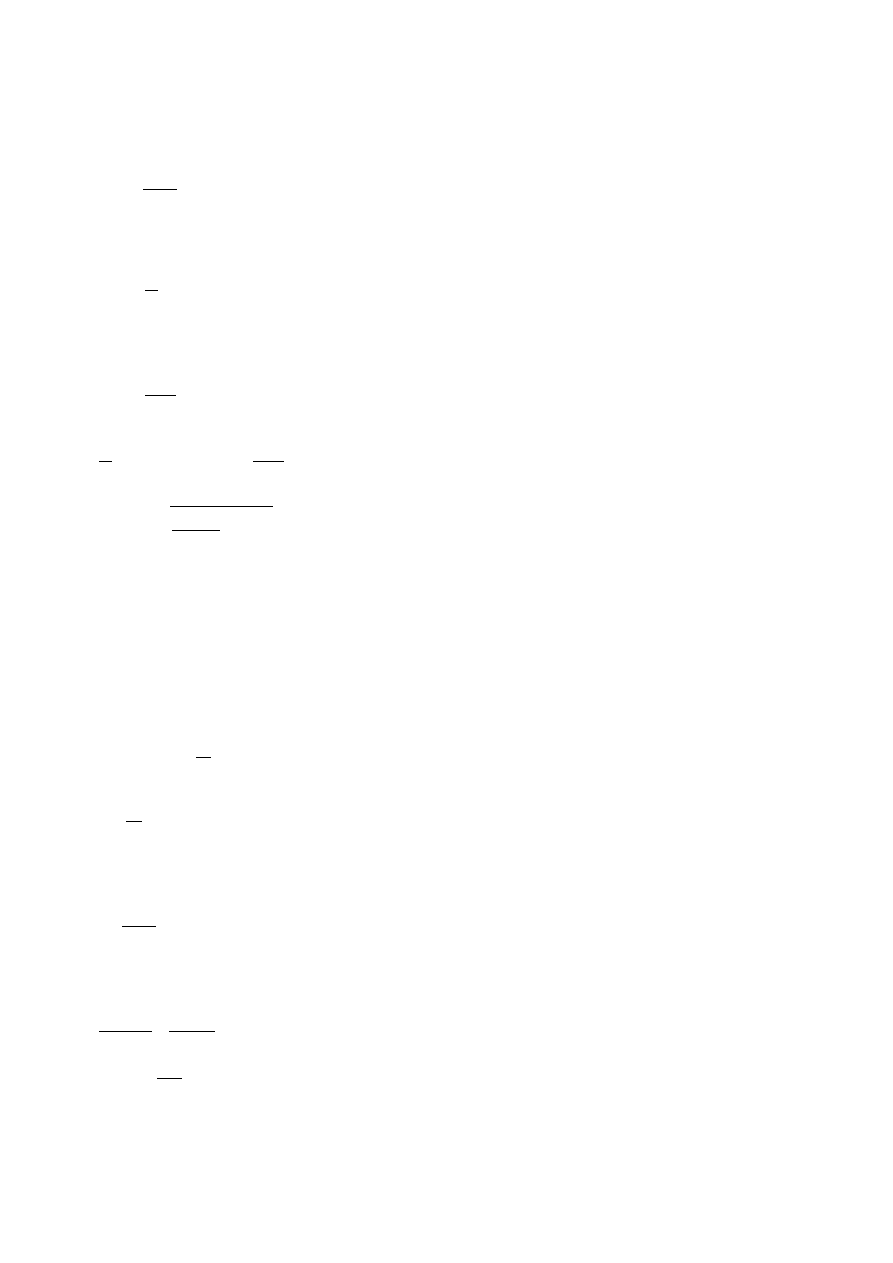
warunku na równość odkształceń:

11.1 Warunek na naciski powieszchniowe

p

dop

⩾

Q

A

pod

gdzie:

A

pod

= π

4

⋅

(

d

zew obl

'

2

−

D

r nak

2

)

Stąd:

A

pod

⩾

Q

p

dop

π

4

⋅

(

d

zew obl

'

2

−

D

r nak

2

)

⩾

Q

p

dop

d

zew obl

'

⩾

√

4⋅Q

π⋅

p

dop

+

D

r nak

2

Tak obliczoną średnicę należy powiększyć o około 1÷2 mm, aby możliwe było wykonanie fazy
ułatwiającej wciśnięcie nakrętki w gniazdo

d

zew

'

=

d

zew obl

'

+

1÷2[mm]

11.2 Warunek na równość odkształceń:

ε

śr

=ε

n

σ=

E⋅ε⇔ε= σ

E

σ=

Q

A

Wynika stąd, że:

ε=

Q

E⋅A

Z warunku na równość otrzymuje się:

Q

E

śr

⋅

A

śr

=

Q

E

n

⋅

A

n

A

n

=

A

śr

E

śr

E

n

Pole przekroju nakrętki wynosi:

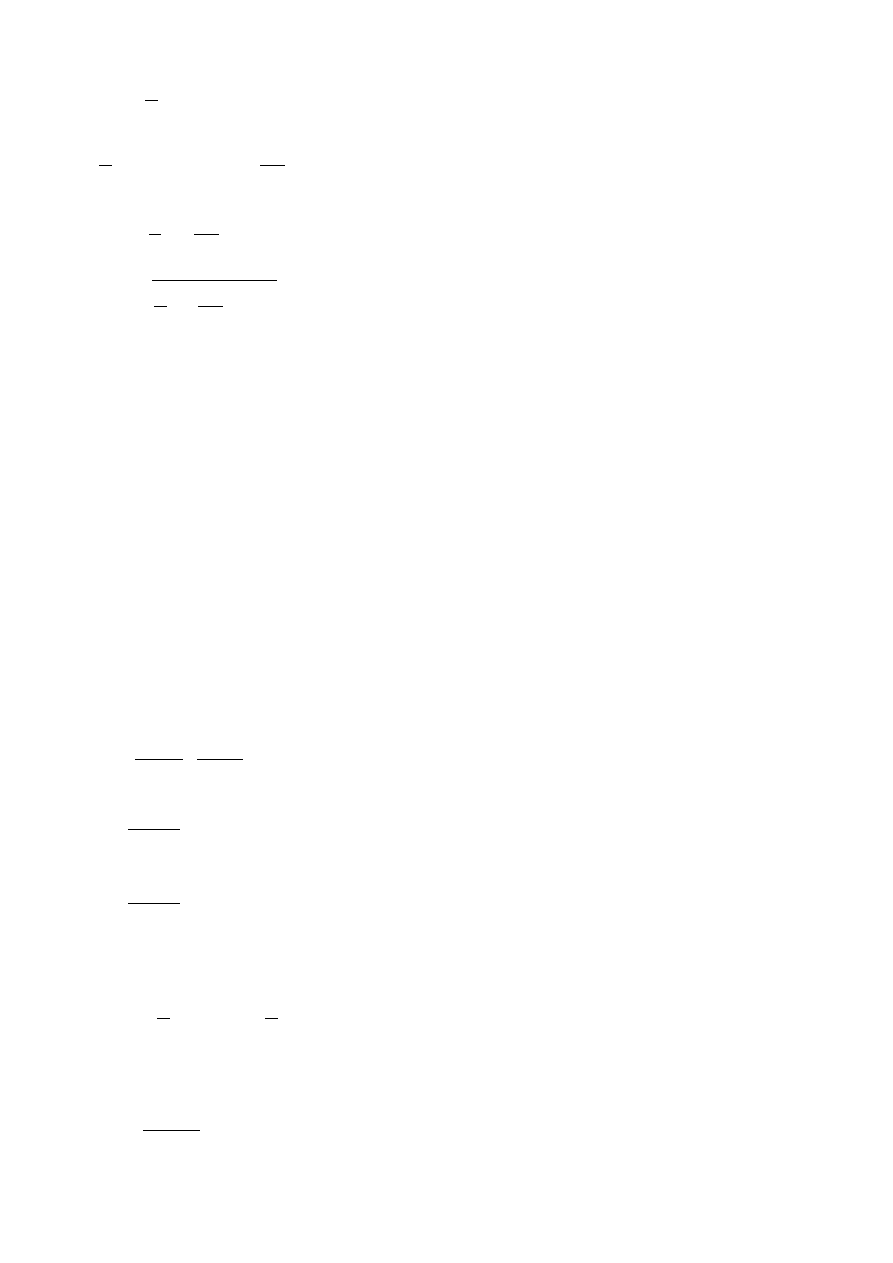
A

pod

= π

4

⋅

(

d

zew

' ' 2

−

D

r nak

2

)

π
4

⋅

(

d

zew

' ' 2

−

D

r nak

2

)

=

A

śr

E

śr

E

n

d

zew

' ' 2

=

4

π⋅A

śr

E

śr

E

n

+

D

r nak

2

d

zew

' '

=

√

4

π⋅A

śr

E

śr

E

n

+

D

r nak

2

Ostatecznie dobiera się średnicę zewnętrzną nakrętki jako:

d

zew

=

max(d

zew

'

; d

zew

''

)

12 Dobór parametrów połączenia wciskowego

Parametry połączenia określa się dla założonej pary ciernej. Obliczenia prowadzi się na podstawie
wyników rozwiązania zagadnienia Lamego.

Wcisk rzeczywisty w połączeniu wciskowym można ustalić na podstawie zależności:

w=d⋅C

w

⋅

p

min

gdzie:

d – średnica połączenia

C

w

=

δ

1

−ν

1

E

1

+

δ

2

+ ν

2

E

2

δ

1

=

d

2

+

d

1

2

d

2

−

d

1

2

δ

2

=

d

2

2

+

d

2

d

2

2

−

d

2

Do ustalenia jest ciśnienie w połączeniu p

min

. Na podstawie statyki układu, otrzymuje się

M

w

=

∫

A

w

d

2

⋅μ⋅

p

min

⋅

dA=

d

2

⋅μ⋅

p

min

⋅

A

w

Stąd:

p

min

=

2⋅M

w

d⋅μ⋅A

w

Moment M

w

wynosi:

M

w

=

X

w

⋅

M

o

gdzie:

X

w

=

2÷3 .

Po obliczeniu wcisku należy określić wpły wtłaczanie czopa w piatę na wcisk rzeczywisty. Podczas
wtłaczania następuje uplastycznienie a⋅R

z

profilu chropowatości. Związki pomiędzy średnicami

przed i po połączeniu są następujęce:

d

m 1

=

d

1

+

2⋅a⋅R

z1

d

m 2

=

d

2

−

2⋅a⋅R

z2

Wcisk wynosi:

w

m

=

d

m 1

−

d

m 1

=

d

1

+

2⋅a⋅R

z1

−

d

2

+

2⋅a⋅R

dz2

=

d

1

−

d

2

+

2⋅a⋅( R

z1

+

R

z2

)

w

m

=

w+2⋅a⋅(R

z1

+

R

z2

)

13 Obliczenia sprawdzające przeguba kulistego

Parametry przegubu określa się na podstawie średnicy śruby, a następnie spradza się naciski ze
wzoru Hertza.

Mając srednicę czopa końcowego śruby wewnętrznej d

cz

(średnica ta jest nie mniejsza niż

średnica rdzenia śruby), promień zaokrąglenia określa się jako:

R

k

=

2÷3⋅d

cz

Dla tak określonego promienia przegubu kulistego, należy sprawdzić naciski powieszchniowe
według wzorów Hertza:

p

H dop

⩾

p

H

=

1

π⋅

3

√

6⋅

(

R−r)

2

R

2

⋅

r

2

⋅

k

2

⋅

Q

gdzie:

k =

1−ν

1

E

1

+

1−ν

2

E

2

p

H dop

=

450 [MPa ]

Aby naciski powieszchniowe były możliwie najmniejsze należy promienie krzywizny przegubu
oraz elementu współpracującego wykonać tak, aby były sobie równe lub różniły się co najwyżej o

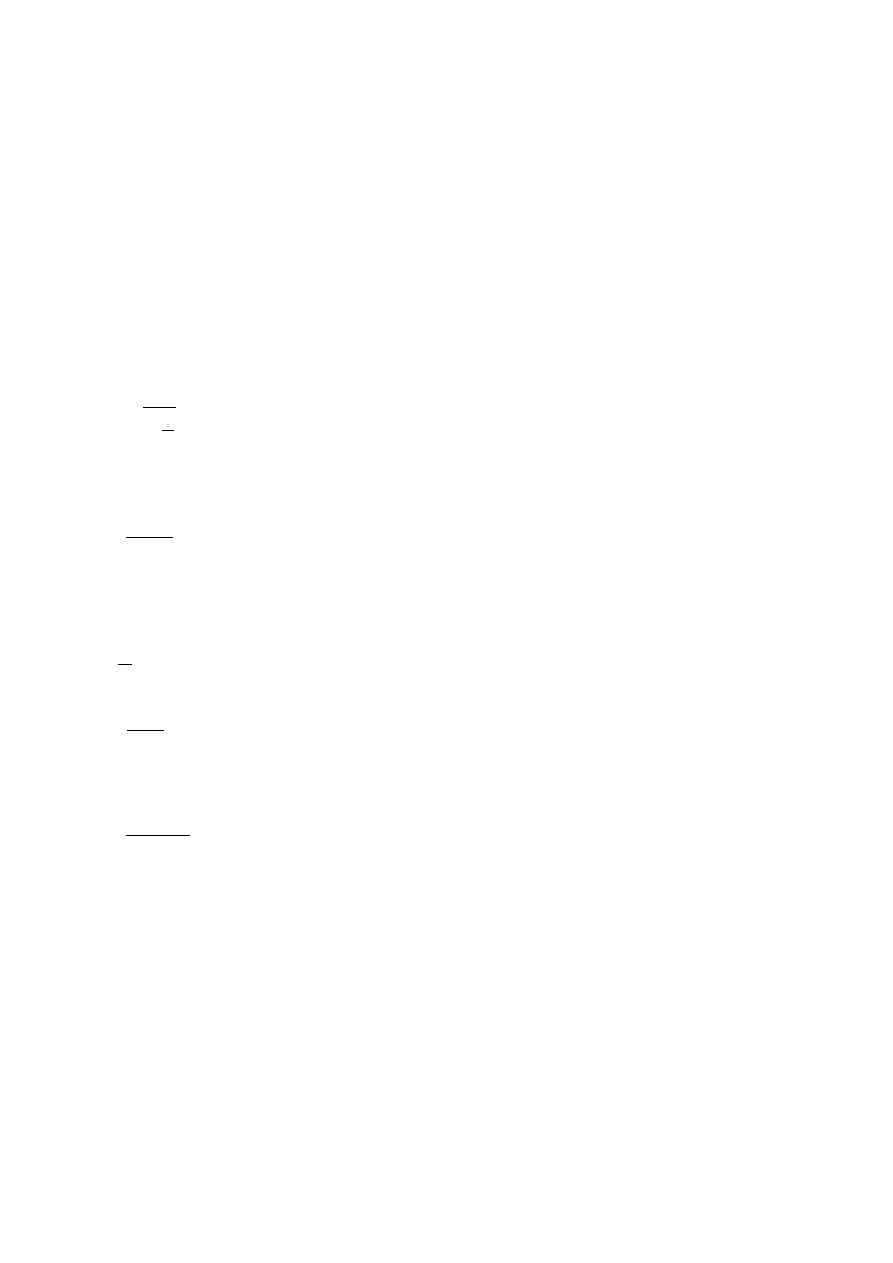
tolerancję wykonania. Przykładowe pasowania, w których spełniony jest taki warunek to:

R

k

H10 /h9 , R

k

H12/ h10 , R

k

H11/h11

14 Dobór parametrów połączenia wpustowego

Dobór parametrów połączenia wpustowego prowadzi się na podstawie normy. Danymi
wejściowymi są: średnica czopa oraz moment skręcający.

Na podstawie średnicy czopa d

cz

z normy dobiera się wymiary przekroju poprzecznego wpustu

b x h . Następnie z warunku na naciski powieszchniowe oblicza się długość czynną wpustu

l

0

(zakłada się przy tym, że rozkład nacisków powieszchniowych jest jednorodny):

p

dop

⩾

P

l

0

⋅

h
2

stąd:

l

0

⩾

2⋅P

p

dop

⋅

h

Siłę w połączeniu wpustowym określa się ze wzoru (równanie statyki momentów):

P⋅

d

2

=

M

P=

2⋅M

d

Ostatecznie długość czynna wpustu wynosi:

l

0

⩾

4⋅M

p

dop

⋅

h⋅d

W zależności od typu wpustu oraz na podstawie jego długości czynnej l

0

wyznacza się długość

minamalną wpustu l

min

:

•

wpust typu A

l

min

=

l

0

+

b

•

wpust typu B

l

min

=

l

0

•

wpust typu AB

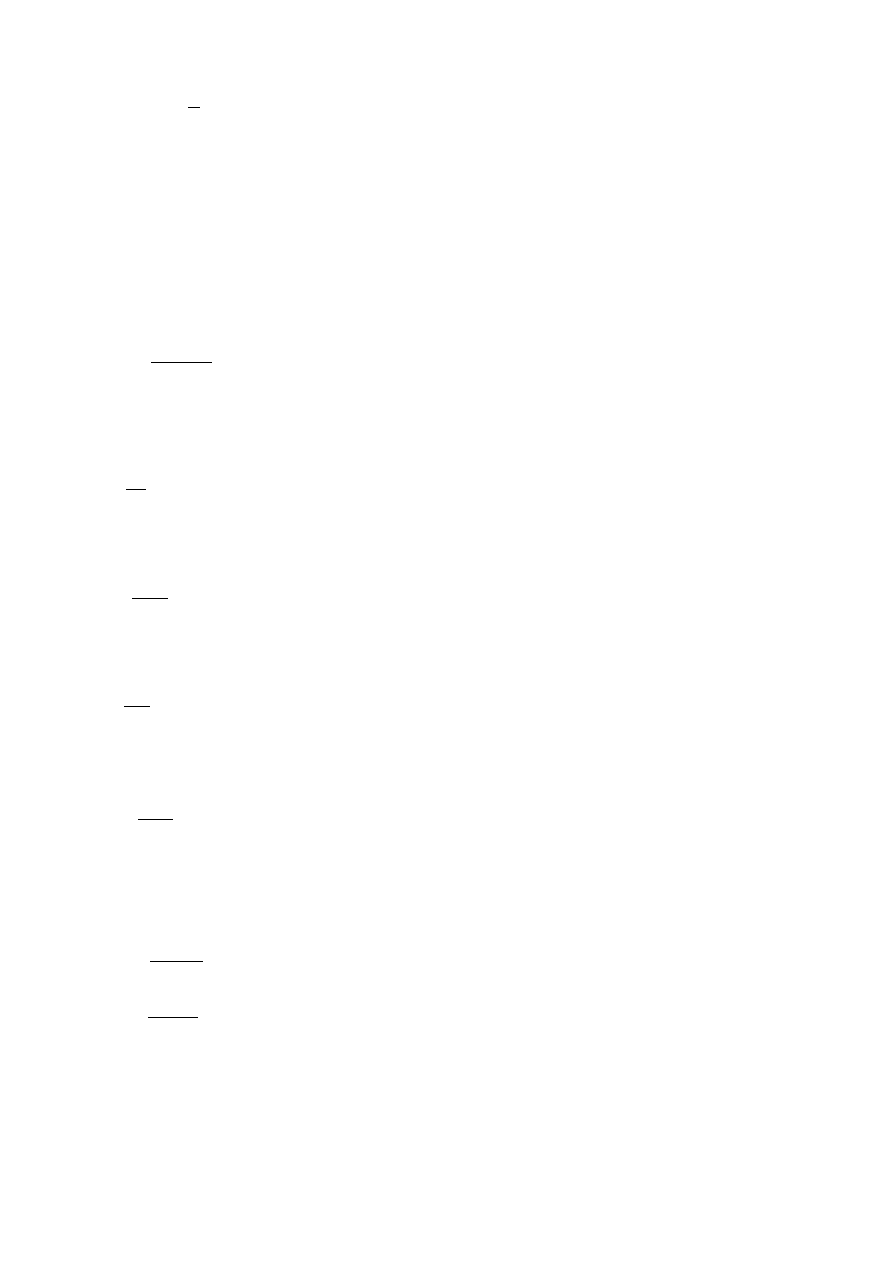
l

min

=

l

0

+

b

2

Ostatecznie z normy dobiera się znormalizowaną długość wpustu: l⩾l

min

. W przypadku, gdy

minimalna długość wpustu jest większa niż długości przewidziane dla danej średnicy w normie,
należy zastosować dwa wpusty. Jeśli długość dwóch wpustów, także zbyt mała, należy zmienić typ
połączenia.

15 Obliczenie naprężeń rzeczywistych w śrubach roboczych i wyznaczenie

rzeczywistych współczynników bezpieczeństwa

Naprężenia zredukowane według hipotezy Hubera:

σ

red

=

√

σ

2

+

3⋅τ

2

Naprężenia normalne pochodzą od ściskania i wynoszą:

σ=

Q
A

r

gdzie:

A

r

=

π⋅

d

r

4

Naprężenia styczne pochodzą od śkręcania i wynoszą:

τ=

M

s

W

o

gdzie:

W

o

=

π⋅

d

r

3

32

Naprężenia zredukowane należy obliczyć dla obu śrub roboczych, z uwzględnieniem wszystkich
momentów skręcających występujących podczas pracy podnośnika. Po ustaleniu naprężeń
zredukowanych σ

red wew

i σ

red zew

określa się rzeczywiste współczynniki bezpieczeństwa:

X

wew

=

σ

kr wew

σ

red wew

X

zew

=

σ

kr zew

σ

red zew