1

Ocena rentowności portfela inwestycji

Jednym z najważniejszych zagadnień w zarządzaniu portfelem inwestycji jest ocena

jego rentowności, czyli odpowiedź na pytanie czy opłacało się dany portfel zbudować i go

utrzymywać, a także czy opłaca się go dalej utrzymywać. Podstawową wielkością poddawaną

tutaj analizie jest stopa zwrotu z portfela, oczywiście w kontekście jego ryzyka

inwestycyjnego. Przeprowadzając taką ocenę należy także uwzględnić koszty poniesione na

analizę i dobór papierów wartościowych w momencie jego formułowania. Ocenę rentowności

portfela inwestycji przeprowadzają zarówno inwestorzy indywidualni, jak i instytucjonalni, a

także powinni ją robić ci, którzy swój portfel oddają do zarządzania profesjonalnym

menedżerom. W tym ostatnim przypadku w ocenie rentowności należy jeszcze uwzględnić

koszty zarządzania portfelem.

W przypadku oddania portfela do zarządzania menedżerowi zarządzającemu stawia

się dwa podstawowe wymagania, którymi są:

1. Uzyskanie wyższych średnich stóp zwrotu przy danym poziomie ryzyka.

2. Zdywersyfikowanie portfela w celu zupełnego usunięcia ryzyka niesystematycznego.

Pierwszy wymóg według współczesnej teorii portfelowej może być spełniony poprzez

efektywną alokację papierów wartościowych na rynku i/lub właściwy dobór inwestycji do

portfela. Zarządzający portfelem prognozując wzrost lub spadek cen walorów powinien

dostosowywać skład portfela do przewidywanych tendencji na rynku , utrzymując np.

całkowicie zdywersyfikowany portfel akcji o wysokim ryzyku systematycznym

(współczynniku beta) na rynku hossy (byka) oraz dobierać akcje o niskim współczynniku beta

oraz instrumenty rynku pieniężnego na rynku bessy (niedźwiedzia). Wyższe zyski na rynku

byka i mniejsze straty na rynku niedźwiedzia pozwalają uzyskać wyższe średnie stopy zwrotu

przy danym poziomie ryzyka. Zarządzający portfelem papierów wartościowych o stałych

dochodach (obligacji) powinien umiejętnie zmieniać czas trwania portfela (durację) na

podstawie przewidywanych zmian stóp procentowych, czyli wydłużać ten czas w przypadku

oczekiwania spadku tych stóp i skracać go w przypadku oczekiwania ich wzrostu. Tak więc

poprawnie zrealizowana strategia zarządzania portfelem obligacji również powinna dać

wyższe stopy zwrotu przy określonym poziomie ryzyka. Inna strategia może polegać na tym,

że zarządzający portfelem oraz jego analitycy będą konsekwentnie dobierać do portfela

niedowartościowane akcje lub obligacje przy danym poziomie ryzyka, co pozwoli im

zrealizować ponadprzeciętne zyski w przyszłości.

2

Z kolei drugi wymóg sprowadza się do umiejętnej dywersyfikacji portfela. Jak wynika

z teorii portfelowej rynek „nagradza” inwestora za ponoszenie ryzyka systematycznego

(rynkowego). Ryzyka niesystematyczne nie jest brane pod uwagę przy określaniu

oczekiwanych zwrotów, gdyż w dobrze zdywersyfikowanym portfelu można je

wyeliminować. Ponieważ za ponoszenie tego ryzyka nie otrzymuje się „nagrody”, stąd też

inwestorzy pragną mieć portfele w pełni zdywersyfikowane, co oznacza, że oczekują oni od

swojego menedżera redukcji znacznej części lub całości ryzyka niesystematycznego. Poziom

dywersyfikacji portfela można ocenić na podstawie analizy współczynników korelacji stóp

zwrotu z tego portfela i stóp zwrotu z rynku. Zupełnie zdywersyfikowany portfel jest idealnie

skorelowany ze zdywersyfikowanym portfelem rynkowym.

Wracając obecnie do głównego problemu rozważań, jakim jest ocena rentowności

portfela inwestycji, zaczniemy od przedstawienia poniżej trzech najważniejszych wskaźników

wykorzystywanych do oceny tej rentowności uwzględniających jednocześnie stopę zwrotu i

stopień ryzyka. Są to syntetyczne mierniki efektywności inwestycji.

Wskaźniki oceny rentowności

Jednym z nich jest wskaźnik efektywności Sharpe’a. Jego konstrukcja oparta jest na

równaniu linii rynku kapitałowego (CML). Jej równanie można również zapisać jako:

(1)

(

)

(

)

R

R

R

R

i

F

i

M

F

M

−

=

−

/

/

σ

σ

gdzie:

R

i

- stopa zysku i-tej akcji (portfela),

R

F

- stopa zysku wolna od ryzyka,

R

M

- stopa zysku portfela rynkowego,

σ

i

- ryzyko i-tej akcji (portfela),

σ

M

- ryzyko portfela rynkowego.

Konstruując swój wskaźnik Sharpe założył, iż inwestor na ogół zwiększa swoje

ryzyko, jeżeli w zamian otrzymuje relatywnie wyższy zysk niż z papierów, które z założenia

przynoszą mu określony zysk, czyli ponad stopę wolna od ryzyka. Tak więc inwestycje o

zwiększającym się ryzyku będą akceptowane, jeżeli jego wzrost będzie łączył się z

odpowiednio wysokim zyskiem. Za taką miarę efektywności inwestycji Sharpe przyjął lewą

stronę wzoru 1, czyli wyrażenie:

(2)

(

)

WES

R

R

i

i

F

i

=

−

/

σ

3

gdzie:

WES

i

- wskaźnik Sharpe’a efektywności inwestycji w i-tą akcję (i-ty portfel).

Według zaproponowanego wzoru bardziej korzystnymi są te inwestycje, które

przynoszą większe wskaźniki efektywności. Wskaźnik wyraża wielkość zysku z inwestycji

zrealizowaną ponad stopę wolną od ryzyka przypadającą na jednostkę ryzyka (całkowitego)

przypisaną tej inwestycji.

Przedstawiony powyżej wskaźnik Sharpe’a można również odnieść do prawej strony

analizowanego równania 1, czyli wyrażenia:

(

)

R

R

M

F

M

−

/

σ

. Interpretowane ono może

być jako zysk z portfela rynkowego (indeksu giełdy) uzyskany ponad stopę wolną od ryzyka

przypadającą na jednostkę ryzyka portfela rynkowego. Jeżeli

(

)

WES

R

R

i

M

F

M

>

−

/

σ

, to

utworzony portfel inwestora przynosi większy zysk niż portfel rynkowy (jest lepszy od

rynku), czyli opłaca się w niego inwestować. W przypadku odwrotnym efektywność portfela

jest niższa od efektywności rynku, co oznacza, iż nie opłaca się w niego angażować środków.

Chcąc zilustrować to na przykładzie przyjmijmy, że stopa zwrotu portfela rynkowego

R

M

= 0,14, stopa wolna od ryzyka R

F

= 0,08, oraz że odchylenie standardowe rocznego

zwrotu z portfela rynku w okresie ostatnich 10 lat wyniosło

σ

M

= 0,20. Do oceny mamy trzy

portfele, których stopy zwrotu i poziom ryzyka są następujące:

Portfel Średni roczny zwrot Odchylenie standardowe zwrotu

D 0,13 0,18

E 0,17 0,22

F 0,16 0,23

Wskaźnik Sharpe’a dla tych portfeli jest następujący:

WES

M

= (0,14 – 0,08) / 0,20 = 0,300

WES

D

= (0,13 – 0,08) / 0,18 = 0,278

WES

E

= (0,17 – 0,08) / 0,22 = 0,409

WES

F

= (0,16 – 0,08) / 0,23 = 0,348

Jak wynika z przyjętych danych portfel D przyniósł najniższy zwrot z tytułu premii za

ryzyko w przeliczeniu na jednostkę całkowitego ryzyka. Z kolei portfele E i F przyniosły

rentowność wyższą niż portfel rynkowy, przy czym portfel E był lepszy od portfela F. Mając

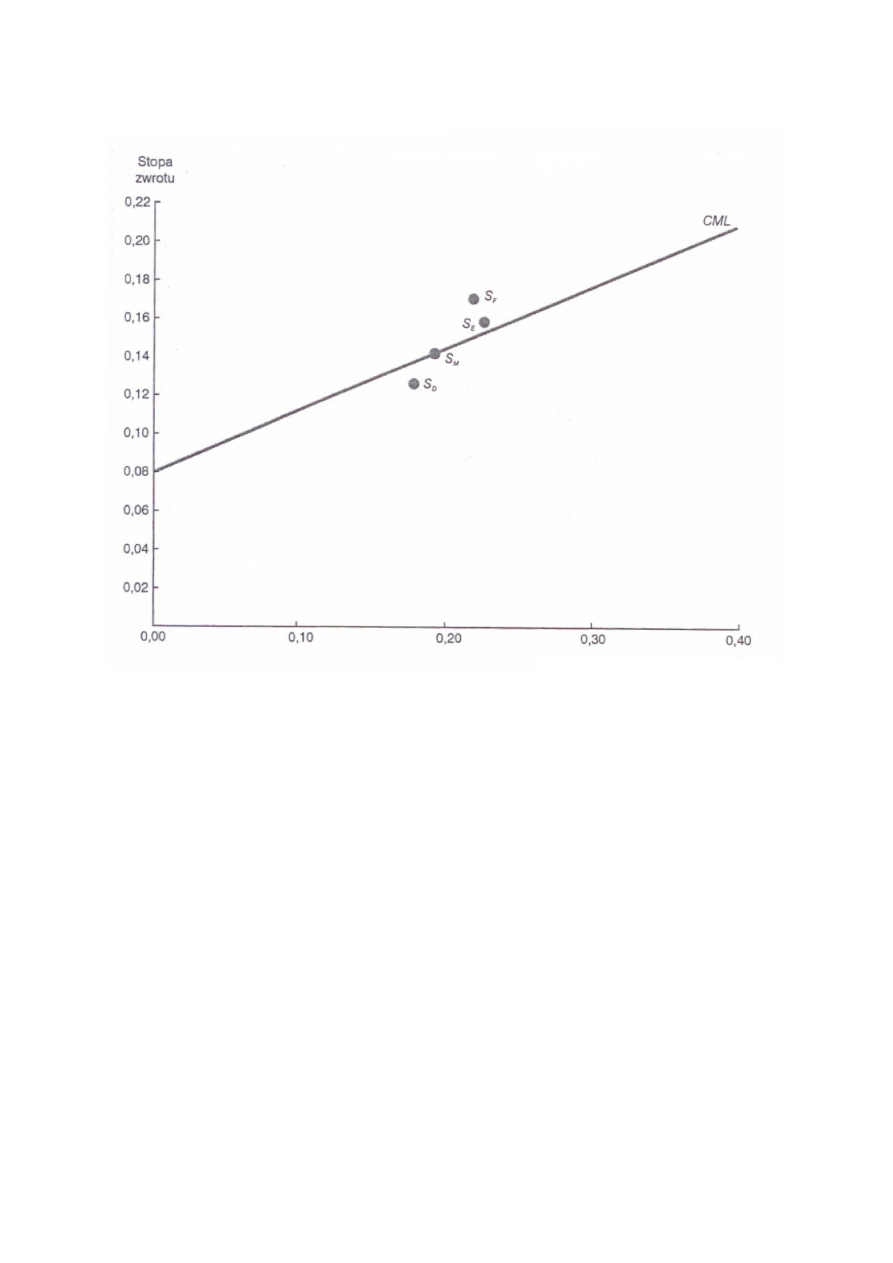
rentowność portfela rynkowego możemy wykreślić linię CML, co pokazuje rys. 1. Nanosząc

na niego także wyniki pozostałych portfeli widzimy, iż portfel D leży poniżej linii CML a

portfele E i F powyżej.

4

Rysunek 1. Rentowno

ść

portfeli na CML (wska

ź

nik WES)

Inną miarą efektywności inwestycji jest, wprowadzony w 1965 r., wskaźnik Treynora,

bazujący na równaniu rynku papierów wartościowych - SML (security market line). Po jego

prostym przekształceniu można go zapisać jako:

(3)

(

)

R

R

R

R

p

F

p

M

F

−

=

−

/

β

gdzie:

R

p

- stopa zysku portfela,

β

p

- współczynnik beta portfela.

Wskaźnikiem efektywności Treynora jest lewa strona równania 3, czyli wyrażenie:

(4)

(

)

WET

R

R

p

p

F

p

=

−

/

β

gdzie:

WET

p

- wskaźnik Treynora efektywności portfela.

Odchylenie standardowe zwrotu

5

W stosunku do wskaźnika efektywności Sharpe’a, wskaźnik Treynora różni się tym, iż

w mianowniku posiada on współczynnik

β

, reprezentujący ryzyko systematyczne portfela,

podczas gdy w mianowniku wskaźnika Sharpe’a jest ryzyko całkowite. Większe ryzyko

systematyczne charakteryzuje portfel, który jest bardziej wrażliwy na zwroty i ryzyko rynku.

Wskaźnik Treynora interpretuje się jako miarę dodatkowego zysku zrealizowanego ponad

stopę wolną od ryzyka przypadającego na jednostkę ryzyka systematycznego. Tak więc im

będzie przyjmował on wyższe wartości, tym dana inwestycja będzie bardziej zyskowniejsza,

czyli wszyscy inwestorzy niechętni ryzyku powinni maksymalizować wartość tego

wskaźnika.

Podobnie jak w przypadku wskaźnika Sharpe’a, wskaźnik efektywności Treynora

można również odnieść do pewnego wzorca, którym będzie wyrażenie zapisane po prawej

stronie wzoru 3, czyli

(

)

R

R

M

F

M

−

/

β

, gdzie, jak wiadomo,

β

M

jest współczynnikiem beta

portfela rynkowego przyjmującym wartość 1. Mówi ono o dodatkowej premii rynku ponad

stopę wolną od ryzyka. Tak więc można porównywać wskaźnik efektywności Treynora z tak

zdefiniowanym wzorcem i oceniać jak zyskowna jest dana inwestycja w porównaniu z

rentownością inwestowania w portfel rynkowy.

Chcąc pokazać jak obliczać wskaźnik Treynora załóżmy, że średni roczny zwrot z

portfela rynkowego (za okres ostatnich 10 lat) wyniósł 14% (R

M

= 0,14) a stopa wolna od

ryzyka 8% (R

F

= 0,08). Interesuje nas ocena efektywności trzech portfeli zarządzanych przez

różnych menedżerów, którzy osiągnęli następujące wyniki:

Zarządzający portfelem Średni roczny zwrot Współczynnik beta

W 0,12 0,90

X 0,16 1,05

Y 0,18 1,20

Wartość wskaźnika WET dla przedstawionych portfeli przedstawia się następująco:

WET

M

= (0,14 – 0,08) / 1,00 = 0,060

WET

W

= (0,12 – 0,08) / 0,90 = 0,044

WET

X

= (0,16 – 0,08) / 1,05 = 0,076

WET

Y

= (0,18 – 0,08) / 1,20 = 0,083

Wyniki te wskazują, że zarządzający portfelem W osiągnął najgorsze wyniki, zwrot z

jego portfela był nawet niższy od portfela rynkowego. Pozostali zarządzający osiągnęli

wyniki lepsze od portfela rynkowego, przy czym najlepszy portfel zbudował zarządzający

6

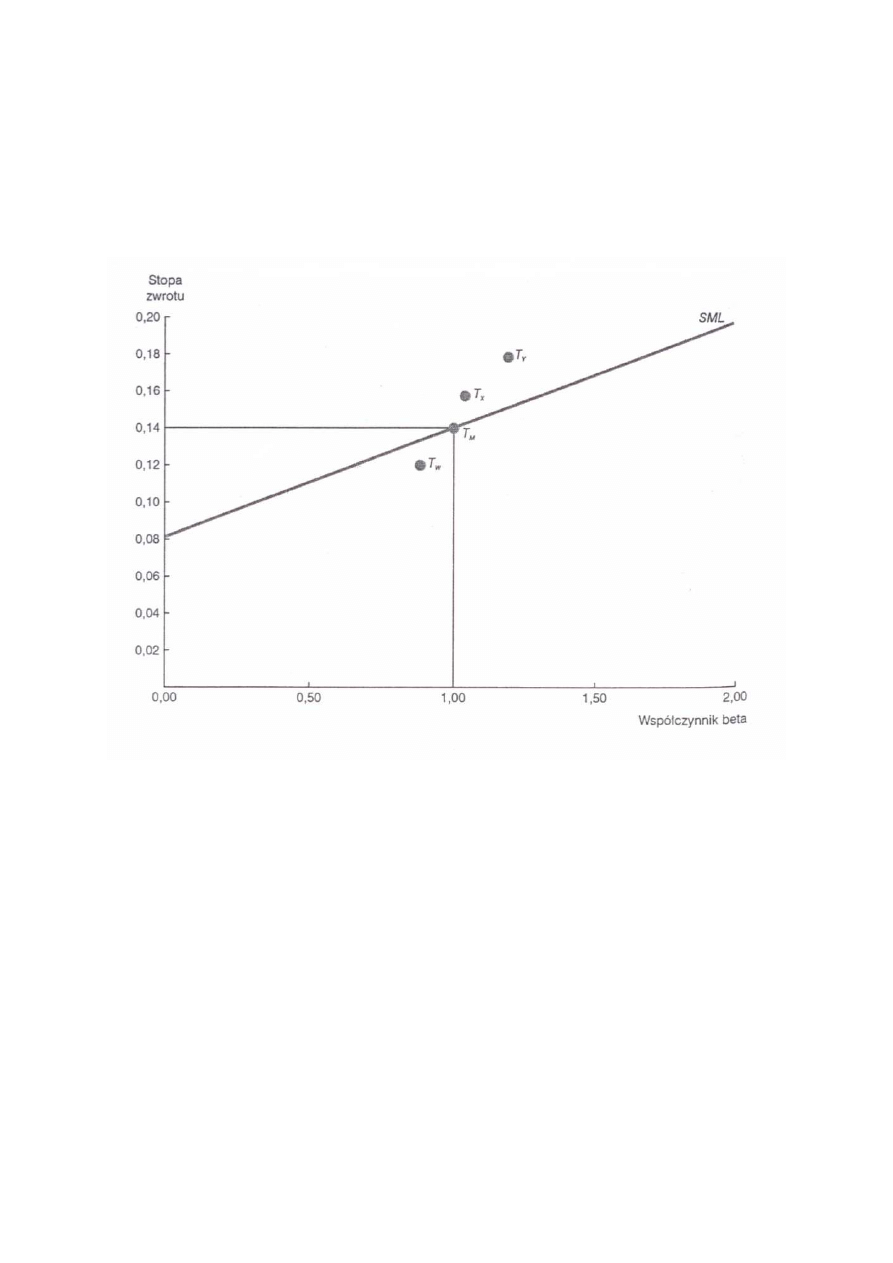
portfelem Y. Osiągnięte wyniki można zaprezentować graficznie wykreślając prostą SML, co

pokazano poniżej na rysunku 2.

Rysunek 2. Rentowno

ść

portfeli na SML (wska

ź

nik WET)

Osiągnięcie bardzo niskiej rentowności portfela może spowodować ujemną wartość

wskaźnika WET. Przykładem takiego wyniku jest portfel przynoszący zwrot niższy od

poziomu stopy wolnej od ryzyka. Zakładając w naszym przykładzie, że zarządzający

portfelem Z osiągnął 7% średnią stopę zwrotu przy poziomie ryzyka 0,50 wskaźnik WET

ukształtowałby się na poziomie: WET

Z

= (0,07 – 0,08) / 0,50 = -0,02, co oznacza, że taki

portfel również znalazłby się poniżej prostej SML.

Także w sytuacji ujemnej wartości współczynnika beta i średniego zwrotu wyższego

od stopy wolnej od ryzyka wskaźnik WET miałby ujemną wartość. Dla przykładu jeżeli

zarządzający portfelem G osiągnąłby średni zwrot na poziomie 10% przy współczynniku beta

równym -0,20, to wówczas wskaźnik WET wyniósłby: WET

G

= (0,10 – 0,08) / (-0,20) =

-0,100. W takiej sytuacji zaleca się korzystanie ze wzoru na prostą SML. Dla naszego

7

przypadku oczekiwany zwrot wyniesie: E(R

G

) = R

F

+ β

G

(R

M

– R

F

) = 0,08 + (-0,20) (0,14 –

0,08) = 0,08 – 0,012 = 0,068, co oznacza pozytywny wynik.

Porównując ze sobą przedstawiony powyżej wskaźnik Sharpe’a i wskaźnik Treynora

trzeba stwierdzić, iż dla w pełni zdywersyfikowanego portfela, czyli pozbawionego ryzyka

niesystematycznego, oba wskaźniki dają identyczne rankingi ze względu na wariancję.

Natomiast słabo zdywersyfikowany portfel może mieć wysoki ranking według wskaźnika

Treynora, ale będzie on dużo niższy według wskaźnika Sharpe’a. Z kolei wadą obu

wskaźników jest to, że są to miary względne a nie absolutne. Można wobec tego stwierdzić, iż

jeden portfel jest bardziej efektywny niż drugi, jednakże nie można stwierdzić czy różnica

pomiędzy nimi jest statystycznie istotna.

Trzecim wskaźnikiem oceny efektywności inwestycji, który zaprezentujemy jest

wskaźnik Jensena, zaproponowany w 1968 r. Jest on skonstruowany na bazie modelu

równowagi rynku kapitałowego CAPM. Wykorzystując jego formułę i używając danych

rzeczywistych z przeszłości, Jensen za pomocą klasycznej metody najmniejszych kwadratów

otrzymał oszacowanie równania regresji postaci:

(4)

(

)

R

R

R

R

u

it

Ft

i

i

Mt

Ft

it

−

=

+

−

+

∧

α β

gdzie:

α β

i

i

,

- oceny parametrów równania, z tym że

β

i

ma interpretację współczynnika beta,

u

it

∧

- ocena składnika losowego,

t

- okres wykorzystany do estymacji równania,

(pozostałe oznaczenia są takie same jak poprzednio).

Do oceny efektywności inwestycji Jensen wykorzystał z przedstawionego równania

ocenę parametru

α

. Utworzony wskaźnik wyraził wzorem:

(5)

(

)

(

)

α

β

i

i

F

i

M

F

R

R

R

R

=

−

−

−

Ocena efektywności inwestycji na podstawie wskaźnika Jensena odbywa się poprzez

przyrównanie parametru

α

i

do zera. Jego wartość dodatnia oznacza sygnał do

zainteresowania się daną inwestycją, natomiast wartość ujemna, iż nie warto się nią

interesować. Wynika stąd, iż im większa wartość

α

i

, tym inwestycja bardziej korzystniejsza,

bowiem w większym stopniu zachodzące w niej zmiany nie są zdeterminowane bezpośrednio

przez zmiany zachodzące na giełdzie. Największą wartość poznawczą wskaźnik Jensena ma

w przypadku porównania dwóch inwestycji o takich samych lub zbliżonych wartościach

współczynnika beta. W przypadku obliczania wskaźnika Jensena należałoby uwzględniać

8

różne wartości stopy wolnej od ryzyka dla każdego przedziału czasowego z badanego okresu.

Dla przykładu oceniając rentowność portfela za okres 10 lat z rocznymi przedziałami należy

najpierw ustalić roczne zwroty z portfela minus roczne zwroty z aktywów wolnych od ryzyka

a następnie odnieść je do rocznych zwrotów z portfela rynkowego pomniejszonych o roczne

zwroty z aktywów wolnych od ryzyka.

Analiza atrybutowa

Jak wskazano zarządzający portfelem inwestycji mogą powiększać jego wartość

poprzez właściwy dobór papierów wartościowych do portfela (efekt doboru) i/lub właściwą

alokację zasobów na rynku (efekt alokacji). Analiza atrybutowa rentowności portfela jest

próbą rozróżnienia, który z tych dwóch efektów stanowi źródło całkowitej rentowności

portfela. Szczególną cechą tej metody jest to, że za jej pomocą porównuje się całkowity zwrot

z bieżących inwestycji ze zwrotem z portfela wzorcowego. Różnica pomiędzy tymi

wielkościami stanowi wpływ obu wyżej wymienionych efektów. Najprostszy sposób pomiaru

obu tych efektów jest następujący:

a) efekt alokacji = Σ

i

[(w

ai

– w

pi

) x (R

pi

– R

p

)],

b) efekt doboru = Σ

i

[w

ai

x (R

ai

– R

pi

)],

gdzie:

w

ai

, w

pi

– wagi inwestycji i w alokacji na rynku i/lub w doborze do portfela inwestora i w

portfelu wzorcowym,

R

ai

, R

pi

– zwrot z inwestycji i dokonanych w wyniku alokacji na rynku i/lub doboru do

portfela inwestora i w portfelu wzorcowym,

R

p

– całkowity zwrot z portfela wzorcowego.

Efekt alokacji mierzy przeinwestowanie lub niedoinwestowanie w określony

segment rynku (w

ai

– w

pi

), odnosząc zwroty z portfela inwestycji dokonanych w tym

segmencie do całkowitego zwrotu z portfela wzorcowego (R

pi

– R

p

). Efektywna alokacja na

rynku jest więc kwestią inwestowania większych środków w te jego segmenty, które

przynoszą wyższe stopy zwrotu. Natomiast poprzez efekt doboru można określić rentowność

portfela inwestora z inwestycjami dokonanymi w takie segmenty rynku, które generują

wyższe zwroty niż zwroty z portfela wzorcowego (R

pi

– R

p

). Wynika stąd, że całkowita

wartość dodana rentowności portfela inwestora stanowi sumę efektów alokacji i doboru.

Jako przykład analizy atrybutowej rozważymy postępowanie inwestora, który

konstruuje portfel w dwóch etapach. W pierwszym etapie decyduje się na wybór trzech

rodzajów papierów wartościowych: (1) akcji, (2) obligacji długoterminowych i (3)

9

instrumentów rynku pieniężnego. W drugim etapie inwestor wybiera już konkretne papiery

wartościowe spośród tych rodzajów, które zakupi. Jako portfel wzorcowy inwestor przyjął

hipotetyczny portfel z alokacją 60-procentową w indeks S&P 500, 30-procentową w Lehman

Corporate Long Bond i 10-procentową w trzymiesięczne weksle skarbowe.

Przypuśćmy, że na początku swojej inwestycji inwestor sadzi, iż wartości akcji na

rynku są nieco przeszacowane. Decyduje się więc dobrać nieco mniej akcji do swego portfela

w porównaniu z portfelem wzorcowym a więcej obligacji i instrumentów rynku pieniężnego.

A zatem wybrał portfel z następującymi udziałami: 50% akcji, 38% obligacji i 12%

instrumentów rynku pieniężnego. Następnie inwestor koncentruje swoją uwagę na sektorach

wrażliwych na zmiany stóp procentowych, takich jak przedsiębiorstwa użyteczności

publicznej czy spółki finansowe a pomija branże technologiczne i produkujące trwałe dobra

konsumpcyjne. Ostatecznie postanawia kupić zarówno obligacje o krótkim terminie

zapadalności, mające wyższy rating niż te, które są w składzie portfela wzorcowego, jak i

weksle handlowe (kupieckie) zamiast weksli skarbowych.

Widzimy więc, że inwestor zdecydował się zarówno na alokację aktywów na rynku,

jak i dobór poszczególnych papierów wartościowych do swojego portfela. Aby stwierdzić,

która z tych decyzji była bardziej trafna powinno się obliczyć całkowitą rentowność własnego

portfela i portfela wzorcowego. Poniżej w tabeli 1 przedstawiamy hipotetyczne zwroty z obu

portfeli wraz z udziałami w nich poszczególnych papierów wartościowych.

Tabela 1. Analiza atrybutowa papierów wartościowych

Udziały

Zwroty w %

Rodzaj
papierów
wartościowych

portfel

inwestora

portfel
wzorcowy

nadwyżka portfel

inwestora

portfel
wzorcowy

nadwyżka

Akcje

0,50

0,60

-0,10

9,70

8,60

1,10

Obligacje

0,38

0,30

0,08

9,10

9,20

-0,10

Instrumenty rynku
pieniężnego

0,12

0,10

0,02

5,60

5,40

0,20

Całkowite stopy zwrotu z portfela inwestora oraz portfela wzorcowego są następujące:

całkowity zwrot z portfela inwestora = (0,50 x 0,097) + (0,38 x 0,091) + (0,12 x 0,056) =

8,98%,

całkowity zwrot z portfela wzorcowego = (0,60 x 0,086) + (0,30 x 0,092) + (0,10 x 0,054) =

8,46%,

10

a zatem inwestor osiągnął rentowność wyższą o 52 punkty bazowe (0,0898 – 0,0846) w

stosunku do portfela wzorcowego. Jest to zarazem jego całkowita wartość dodana

rentowności, która, jak wskazywaliśmy, składa się z efektu alokacji i efektu doboru.

Efekt alokacji można obliczyć jako iloczyn nadwyżki udziału danego papieru

wartościowego w portfelu przez jego względną rentowność (w stosunku do portfela

wzorcowego). W naszym przypadku jest on następujący:

efekt alokacji = [(-010) x (0,086 – 0,0846)] + [0,08 x (0,092 – 0,0846)] + [0,02 x (0,054 –

0,0846)] = -0,02%.

Wynik ten wskazuje, że jeżeli inwestor zdecydowałby się na alokację na rynku i nie wybrałby

innych papierów wartościowych do swojego portfela niż te, które znajdowały się w portfelu

wzorcowym, to jego zwrot byłby niższy o dwa punkty bazowe od zwrotu oczekiwanego.

Wyrażenia w nawiasach kwadratowych informują o efekcie alokacji w dany rodzaj papieru

wartościowego.

Z kolei efekt doboru można obliczyć następująco:

efekt doboru = [0,50 x (0,097 – 0,086)] + [0,38 x (0,091 – 0,092)] + [0,12 x (0,056 – 0,054)]

= 0,54%,

co oznacza, że inwestor osiągnął dodatni efekt w rentowności swojego portfela w wysokości

54 punktów bazowych.

W sumie całkowita wartość dodana rentowności portfela inwestora w stosunku do

rentowności portfela wzorcowego wyniosła:

całkowita wartość dodana = efekt alokacji + efekt doboru = -0,02% + 0,54% = 0,52% (52

punkty bazowe).

Podstawową wadą analizy atrybutowej jest jednak to, że nie uwzględnia ona ryzyka.

Możliwe jest więc, że w wyniku procesu alokacji i doboru papierów wartościowych do

portfela inwestora znajdą się w nim bardziej ryzykowne papiery wartościowe niż w portfelu

wzorcowym. Tak było w analizowanym przez nas przypadku, gdyż w portfelu inwestora

zamiast weksli skarbowych znalazły się weksle handlowe, które mają wyższe ryzyko i można

było oczekiwać z nich wyższej stopy rentowności.

Analizę atrybutową rentowności portfela inwestycji można wykorzystać również do

podejmowania innych decyzji związanych z alokacją aktywów do portfela. Dla przykładu

analizę efektu alokacji na rynku można zastąpić analizą efektu rotacji gałęzi. Może ją

przeprowadzać menedżer zarządzający dużym portfelem, który pragnie ustalić, jakie spółki,

np. surowców podstawowych, produkujące nietrwałe dobra konsumpcyjne czy transportowe

11

mają większe lub mniejsze znaczenie w gałęzi zanim określi, którym z nich nada określone

preferencje.

Ocena rentowności portfela akcji

Używając przedstawionych wyżej wskaźników oceny rentowności portfela

inwestycyjnego należy pamiętać o tym, że ich dokładność obliczeniowa zależy od

dokładności danych (zmiennych) przyjętych do ich obliczania. W ocenie tej trzeba być

również cierpliwym i rozsądnym, co oznacza, że trzeba wiedzieć w jakich okresach

dokonywać takiej oceny. Ogólna zasada mówi, że taka analiza powinna być dokonywana w

odpowiednio długim okresie, co oznacza, że nie jest ona możliwa w okresie kwartału czy

nawet roku. Powinna ona obejmować okres kilku lat a najlepiej pełny cykl koniunkturalny.

Pozwala ona wówczas na ocenę rentowności portfela w różnych okresach tego cyklu, np.

ekspansji czy recesji na rynku. Wykorzystanie przedstawianych wskaźników wiąże się z

przyjęciem określonych portfeli rynku, czyli pewnego hipotetycznego czy teoretycznego

portfela. Bardzo często do tego celu są używane określone portfele znanych indeksów

giełdowych, S&P 500 czy WIG lub WIG20 z rynku polskiego. Problem polega jednakże na

tym, że portfel taki nie zawsze jest dobrym reprezentantem rynku, czyli nie reprezentuje

prawdziwego składu portfela rynku. Problem ten staje się większy gdy inwestor korzysta z

globalnego rynku kapitałowego. Ponadto biorąc pod uwagę znany nawet indeks giełdowy

uwzględnia on jedynie akcje spółek notowanych na giełdzie a nie uwzględnia akcji

notowanych na rynku pozagiełdowym czy innych aktywów (możliwości inwestycyjnych), np.

nieruchomości, metali szlachetnych, dzieł sztuki, numizmatyków itd.

Problem wyboru dobrego portfela rynku do oceny rentowności portfela nazywa się

problemem błędu wzorca. Problem ten narasta przy globalnym inwestowaniu. Badania

empiryczne wskazują, że uwzględnienie w inwestowaniu zagranicznych papierów

wartościowych przesuwa w lewo granicę efektywności, gdyż na skutek zwiększonej

dywersyfikacji portfela zmniejsza się ryzyko inwestycyjne. Czasami granica ta przesuwa się

też w górę ponieważ niektóre z aktywów zagranicznych mogą mieć wyższy oczekiwany

wzrost. Może być również tak, że granica efektywności przesuwa się jednocześnie w lewo i w

górę. Generalnie stopień zmiany położenia granicy efektywności zależy od stopnia powiązań

(korelacji) gospodarczych pomiędzy krajami lub powiązań pomiędzy rynkami finansowymi

tych krajów.

Chcąc uwzględnić w ocenie rentowności portfela problem błędu wzorca należałoby

albo przyjąć bardziej reprezentatywny odpowiednik portfela rynku albo znaleźć jakąś miarę

12

błędu wzorca. Przykładem rozwiązania tego problemu jest konstrukcja odpowiednich

indeksów, tzn. takich, które uwzględniałyby akcje oraz obligacje z różnych rynków

międzynarodowych, a także innego rodzaju aktywa, np. aktywa rzeczowe. Innymi słowy

potrzebny byłby jakiś indeks odzwierciedlający portfel światowego rynku. Innym

rozwiązaniem byłoby nadanie większej wagi wskaźnikowi Sharpe’a, gdyż odnosi on

nadwyżkę zwrotu do całkowitego ryzyka.

Ocena rentowności portfela obligacji

Podstawowym problemem do rozwiązania przy ocenie rentowności portfela obligacji

jest znalezienie odpowiedniej miary ryzyka. Powinna to być miara porównywalna do

współczynnika beta z rynku akcji. Trudność w konstrukcji takiej miary wynika stąd, że

terminy płatności kuponów odsetkowych oraz ich wysokość mają istotny wpływ na

zmienność cen obligacji. Dla rozwiązania tego problemu W. Wagner i D. Tito wprowadzili

linię rynku obligacji (bond market line), podobnie jak linię rynku papierów wartościowych

(SML) stosowaną do oceny rentowności akcji, zastępując współczynnik beta czasem trwania

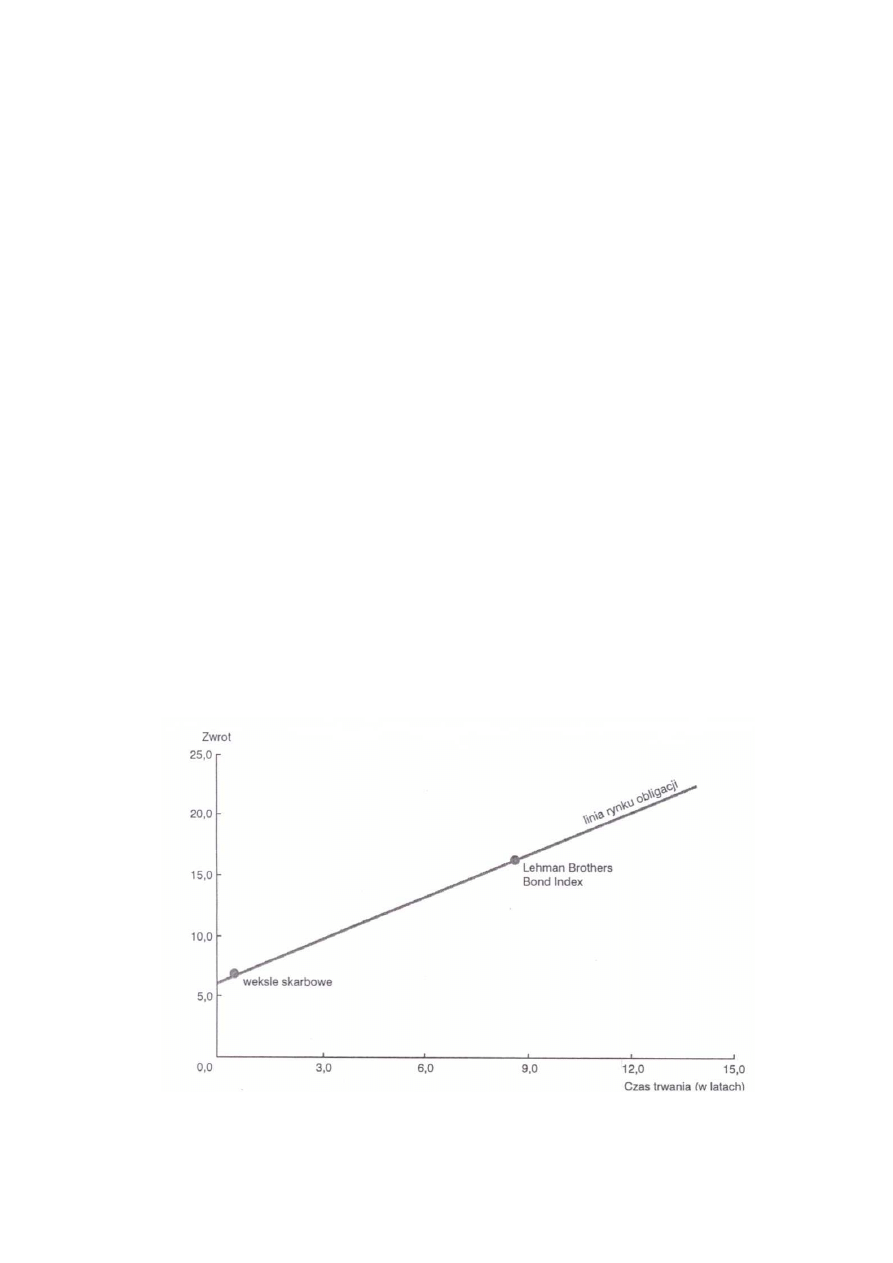
obligacji (duracją). Linia rynku obligacji jest prostą przedstawiającą współrzędne stóp zwrotu

i czasu trwania poszczególnych rodzajów (portfeli) obligacji. Linię rynku obligacji

zobrazowano na rys.3.

Rysunek 3. Linia rynku obligacji przy wykorzystaniu Lehman Brothers Bond Index

Ź

ródło: W.H. Wagner, D.A. Tito, Definitive New Measures of Bond Performance and Risk, “Pension World” 1977

13

Z rysunku wynika, że linia rynku obligacji przebiega od punktu rentowności weksli

skarbowych do punktu Lehman Brothers Government Corporate Bond Index, a nie indeksu

S&P 500, który jest indeksem dla akcji. Lehman Brothers Index (pełniący funkcję portfela

rynku) daje średnią roczną stopę zwrotu dla pewnego wspólnego okresu, a czas trwania tego

indeksu jest ważony długością czasu trwania jego indywidualnych obligacji.

Linia rynku obligacji uzależnia stopy zwrotu obligacji portfela od czasu ich trwania.

Służy więc do mierzenia nadwyżki stopy zwrotu pomiędzy danym portfelem obligacji

(portfelem inwestora) a portfelem rynkowym, czyli inaczej mierzy odchylenie pomiędzy

stopami zwrotu tych portfeli. Jej autorzy wymieniają cztery podstawowe przyczyny, które

różnią stopę zwrotu z portfela inwestora (portfela ocenianego) od stopy zwrotu z portfela

rynku, którym jest portfel indeksu Lehman Brothers Index. Są to:

1. Efekt polityki. Wynika on z różnej długości czasu trwania obligacji długookresowych

wchodzących w skład portfela inwestora, które wybrał on zgodnie z przyjętą długookresową

polityką inwestycyjną. Efekt ten jest mierzony poprzez różnicę pomiędzy zwrotem z obligacji

o średnim czasie trwania dla obligacji długoterminowych a zwrotem z Lehman Brothers

Index (portfela rynkowego).

2. Efekt przewidywania stopy oprocentowania. Wynika on ze zmian czasu trwania portfela

inwestora wiążącego się z chęcią uzyskania korzyści ze zmian zachodzących na rynku

obligacji. Jest on mierzony poprzez różnicę pomiędzy oczekiwaną stopą zwrotu z portfela

inwestora a oczekiwaną stopą zwrotu z portfela obligacji długookresowych. Poznanie tego

efektu jest ważne ponieważ dla przykładu w okresie obniżania się stóp procentowych

inwestor (zarządzający portfelem) może wydłużać czas trwania portfela obligacji dla

aprecjacji ich ceny oraz w okresie wzrostu stóp procentowych może skracać czas trwania dla

minimalizacji obniżki ceny.

3. Efekt analizy. Wynika on z doboru do portfela obligacji niedowartościowanych na rynku

w stosunku do poziomu swojego ryzyka, a więc takich, w stosunku do których inwestor

oczekuje wyższych stóp zwrotu niż średni zwrot z obligacji długookresowych. Miarą tego

efektu jest różnica pomiędzy oczekiwaną stopą zwrotu z portfela na początku okresu, np.

kwartału (obliczonego na podstawie linii rynku obligacji) a jego bieżącą stopą zwrotu. Jeżeli

bieżący zwrot z portfela inwestora przewyższa zwrot oczekiwany, oznacza to, że inwestor

(zarządzający portfelem) nabył niedowartościowane walory, których cena wzrosła (nabyły

właściwej wartości), co w rezultacie przyniosło nadwyżkę stopy zwrotu w badanym okresie.

Dla przykładu przyjmijmy, że wynikająca z linii rynku obligacji oczekiwana stopa zwrotu z

obligacji o 10-letnim czasie trwania wynosi 9% (założenie przyjęte na początku badanego

14

okresu). Jeżeli z kolei bieżąca stopa zwrotu z utworzonego portfela w wyniku doboru

niedowartościowanych na rynku obligacji, a więc zastosowania strategii „kupuj i trzymaj”

wynosi 9,4%, to efekt analizy jest na poziomie 0,4% (40 punktów bazowych).

4. Efekt obrotu. Wynika on z krótkookresowych zmian w portfelu w danym czasie, a więc

efektywnych transakcji dokonywanych na parkiecie giełdowym lub dobór na krótki okres

niedowartościowanych obligacji. Stanowi on różnicę pomiędzy całkowitą nadwyżką stopy

zwrotu wynikającą z czasu trwania portfela inwestora a sumą wymienionych powyżej

efektów, czyli efektu polityki, efektu przewidywania stopy oprocentowania i efektu analizy.

Dla przykładu załóżmy, że bieżąca stopa zwrotu z portfela inwestora wynosi 10,50% a stopa

zwrotu z Lehman Brothers Index wynosi 8,25%, co oznacza, że całkowita nadwyżka

osiągnięta przez inwestora lub zarządzającego portfelem wyniosła 2,25%. Zakładając dalej, że

efekt polityki wyniósł 0,35%, efekt przewidywania stopy oprocentowania 0,40% oraz efekt

analizy 0,40% efekt obrotu wynosi 1,10% (2,25 – 0,35 – 0,40 – 0,40).

Połączenie efektu przewidywania stopy oprocentowania, efektu analizy i efektu obrotu

określane jest mianem efektu zarządzania.

Podsumowując przedstawioną wyżej metodę oceny rentowności portfela obligacji

należy zwrócić uwagę, iż miarą ryzyka obligacji jest czas jej trwania (duracja). Pomija się

jednakże różnice w poziomach ryzyka wynikające ze stopnia wypłacalności ich emitenta. Dla

przykładu obligacje o tym samym czasie trwania posiadające różny rating, np. Aaa i Baa mają

różny stopień wypłacalności ich emitenta. A zatem inwestor, który zdecydował się na wybór

do swojego portfela obligacje o ratingu Baa może osiągnąć istotny efekt analizy, ponieważ

papiery te mają niższą jakość niż średnia jakość papierów tworzących Lehman Brothers

Index. Jednym ze sposobów uwzględnienia ryzyka niewypłacalności emitenta obligacji w

ocenie rentowności portfela jest budowanie linii rynku obligacji dla ich poszczególnych

kategorii ratingowych.