
POLITECHNIKA BIAŁOSTOCKA
WYDZIAŁ ELEKTRYCZNY
___________________________________________________________
Laboratorium Miernictwa Elektrycznego
Galwanometr magnetoelektryczny statyczny
ć
wiczenie nr 4
Białystok 1998
Ć
wiczenie nr 4 Galwanometr magnetoelektryczny
1
1. Wprowadzenie
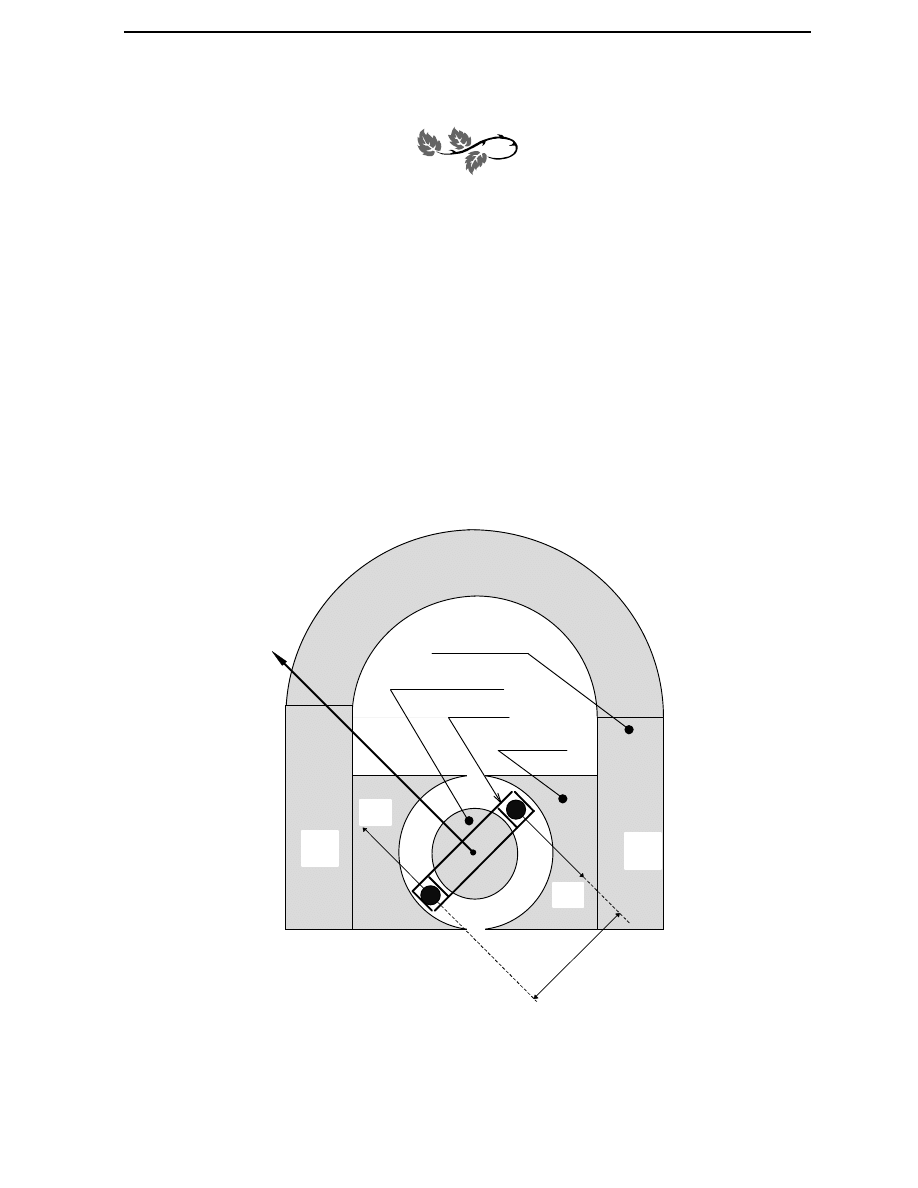
1.1. Ustrój magnetoelektryczny
alwanometr jest szczególn
ą
odmian
ą
ustroju magnetoelektrycznego,
dlatego na wst
ę
pie zostan
ą
omówione podstawowe wła
ś
ciwo
ś
ci tego
ustroju pomiarowego. Zasadniczymi elementami konstrukcyjnymi
ustroju s
ą
, silny magnes trwały oraz delikatna ceweczka stanowi
ą
ca jego organ
ruchomy. Szkic ustroju przedstawiony jest na rysunku 1. W klasycznym ustroju
magnetoelektrycznym wraz z ceweczk
ą
obraca si
ę
wskazówka w postaci
delikatnej cienko
ś
ciennej rurki aluminiowej spłaszczonej na ko
ń
cu. W gal
galwanometrze wskazówka materialna została zast
ą
piona wskazówk
ą
ś
wietln
ą
(rys.2).
a
F
S
F
N
NABIEGUNNIK
CEWKA
RDZE
Ń
Ś
RODKOWY
MAGNES TRWAŁY
Rys. 1. Szkic ustroju magnetoelektrycznego
G

Ć
wiczenie nr 4 Galwanometr magnetoelektryczny
2
Boki cewki zanurzone s
ą
w szczelinie powietrznej utworzonej przez
nabiegunniki magnesu i rdze
ń
ś
rodkowy w kształcie walca. Podkowiasty
element jest magnesem trwałym, natomiast nabiegunniki i rdze
ń
ś
rodkowy s
ą
wykonane ze stali magnetycznie mi
ę
kkiej, to znaczy takiej, która traci swoje
wła
ś
ciwo
ś
ci magnetyczne po ust
ą
pieniu zewn
ę
trznego pola magnesuj
ą
cego.
Elementy takie maj
ą
za zadanie ułatwienie przepływu strumienia magnetycznego
w zamkni
ę
tym obwodzie magnetycznym. W szczelinie powietrznej wyst
ę
puje
jednorodne pole magnetyczne, którego linie sił s
ą
prostopadłe do powierzchni
walcowej rdzenia
ś
rodkowego. Sprawia to,
ż
e boki cewki, w szerokim zakresie
k
ą
ta obrotu znajduj
ą
si
ę
w polu o jednakowej indukcji. Je
ż
eli przez cewk
ę
płynie
pr
ą
d stały na jej boki działaj
ą
siły elektrodynamiczne F. Zwrot tych sił,
przedstawiony na rysunku 1, wyznaczony w oparciu o „reguł
ę
lewej dłoni” przy
zało
ż
eniu,
ż
e pr
ą
d wpływa do prawego (na szkicu wy
ż
szego) boku cewki, a
wypływa z lewego, przy czym mamy tu na my
ś
li umowny kierunek pr
ą
du.
Na pojedynczy zwój cewki działa suma momentów pary sił,
Fa
a
F
a
F
M
N
=
+
=
2
2
Dla
z
zwojów moment ten jest
z
razy wi
ę
kszy,
zFa
M
N
=
Jak wiadomo, siła elektrodynamiczna działaj
ą
ca na przewodnik z pr
ą
dem
(pojedynczy zwój) wyra
ż
a si
ę
wzorem,
BIb
F
=
gdzie:
B - indukcja w szczelinie powietrznej
I - nat
ę ż
enie pr
ą
du w przewodniku
b - długo
ś ć
przewodnika (patrz rys.2)
Podstawiaj
ą
c ostatni wzór do wyra
ż
enia na moment M
N
, otrzymamy
ostatecznie równanie
momentu nap
ę
dowego
ustroju magnetoelektrycznego,
BIzab
M
N
=
(1)
Jedyn
ą
wielko
ś
ci
ą
zmienn
ą
w równaniu (1) jest nat
ę ż
enie pr
ą
du I, mo
ż
na
wi
ę
c je zapisa
ć
nast
ę
puj
ą
co,
M
BIzab
c I
N
m
=
=
(2)
gdzie:
Bzab
c
m
=
Moment nap
ę
dowy jest wi
ę
c liniow
ą
funkcj
ą
nat
ę ż
enia pr
ą
du płyn
ą
cego przez
cewk
ę
.

Ć
wiczenie nr 4 Galwanometr magnetoelektryczny
3
Istnienie samego momentu nap
ę
dowego nie wystarcza do funkcjonowania
przyrz
ą
du pomiarowego. Gdyby istniał tylko ten moment, cewka zachowywałaby
si
ę
jak wirnik silnika, to znaczy obracałaby si
ę
ruchem ci
ą
głym. do ko
ń
ca swego
zakresu ruchu.
Konieczne wi
ę
c jest istnienie drugiego momentu, momentu zwrotnego,
przeciwdziałaj
ą
cego momentowi nap
ę
dowemu w taki sposób, aby ka
ż
dej
warto
ś
ci pr
ą
du płyn
ą
cego przez cewk
ę
odpowiadała jedna i tylko jedna warto
ś ć
k
ą
ta obrotu. Ten bardzo wa
ż
ny moment wytwarzaj
ą
w zwykłym ustroju dwie
płaskie spr
ę ż
yny w kształcie spirali Archimedesa. W galwanometrze moment
zwrotny wytwarzaj
ą
dwie spr
ę ż
yste nitki wykonane z br
ą
zu fosforowego lub
berylowego, które stanowi
ą
jednocze
ś
nie zawieszenie cewki (rys. 2). Podczas
obrotu cewki ulegaj
ą
one skr
ę
ceniu, przeciwdziałaj
ą
c momentowi nap
ę
dowemu.
W obydwu wypadkach moment zwrotny wyra
ż
a si
ę
tym samym zwi
ą
zkiem (3).
α
z
Z
k
M
=
(3)
gdzie:
k
Z
- stała zwracania
α
- k
ą
t obrotu cewki
Moment zwrotny jest wi
ę
c liniow
ą
funkcj
ą
k
ą
ta obrotu organu ruchomego
(patrz rys. 4).
W stanie ustalonym, gdy przeciwnie skierowane momenty sił: nap
ę
dowy i
zwrotny s
ą
sobie równe, mo
ż
emy napisa
ć
,
α
z
k
BIzab
=
,
sk
ą
d
I
k
Bzab
z
=
α
(4)
Zwi
ą
zek
(4)
nazywa
si
ę
funkcj
ą
przetwarzania
ustroju
magnetoelektrycznego. Przedstawia ona zale
ż
no
ś ć
odpowiedzi ustroju (
α
) od
wymuszenia (I)
Wobec tego,
ż
e wszystkie wielko
ś
ci wyst
ę
puj
ą
ce w równaniu (4), z
wyj
ą
tkiem nat
ę ż
enia pr
ą
du, maj
ą
warto
ś
ci stałe, mo
ż
na je zapisa
ć
nast
ę
puj
ą
co,
I
c
I
k
Bzab
z
α
α
=
=
(5)
gdzie:
z
k
Bzab
c
=
α
Ć
wiczenie nr 4 Galwanometr magnetoelektryczny
4
1.2. Galwanometr magnetoelektryczny statyczny
Mianem galwanometru okre
ś
la si
ę
elektryczny miernik wskazówkowy
składaj
ą
cy si
ę
tylko z ustroju , co oznacza,
ż
e jest on pozbawiony układu, bloku
funkcjonalnego charakterystycznego dla znakomitej wi
ę
kszo
ś
ci mierników
wskazówkowych. Mierzona wielko
ść
elektryczna jest tu bez jakiegokolwiek
przetworzenia doprowadzana bezpo
ś
rednio do ustroju. St
ą
d galwanometry maj
ą
niewielkie zakresy pomiarowe napi
ę
cia i pr
ą
du. Wa
ż
nym ich zastosowaniem,
oprócz pomiaru niewielkich napi
ę ć
i pr
ą
dów, jest rola detektorów zera
(wska
ź
ników równowagi) w układach pomiarowych takich jak mostki i
kompensatory napi
ę
cia stałego. W tym
ć
wiczeniu galwanometr rozpatrywany
b
ę
dzie wył
ą
cznie jako mikroamperomierz.
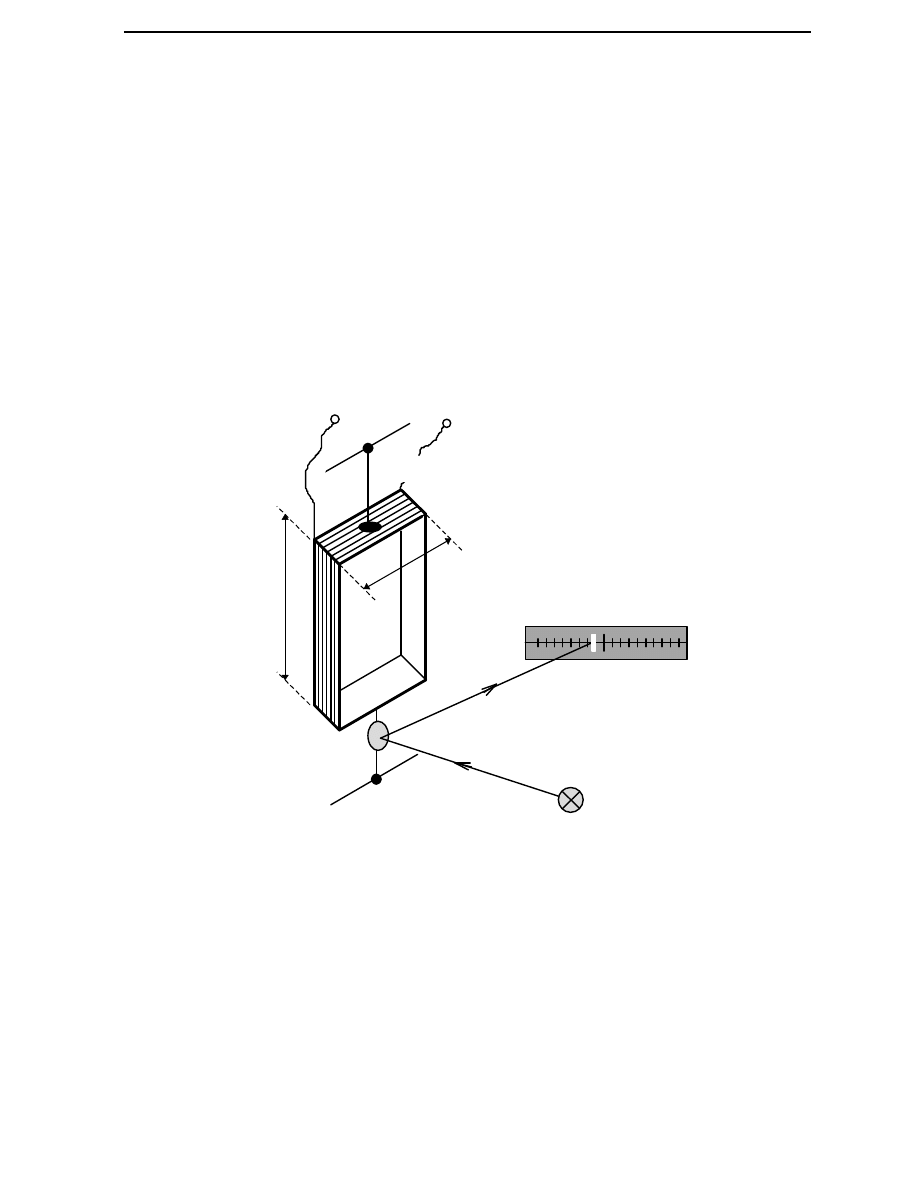
PROMIE
Ń
Ś
WIETLNY
Ż
ARÓWECZKA
LUSTERECZKO
MATÓWKA
DOPROWADZENIEPR
Ą
DU
NITKA SPR
Ę Ż
YSTA
b
a
Rys. 2. Zawieszenie nitkowe cewki i zasada wskazówki
ś
wietlnej
Omawiany galwanometr nazywa si
ę
statycznym, gdy
ż
pełni on swoj
ą
funkcj
ę
w statycznym (ustalonym) stanie pracy. Ni
ż
ej opiszemy jednak jego
prac
ę
tak
ż
e w stanie przej
ś
ciowym, gdy
ż
jest on charakterystyczny dla
wszystkich mierników wskazówkowych, w galwanometrze za
ś
daje si
ę
obserwowa
ć
i analizowa
ć
w sposób najbardziej wyrazisty.

Ć
wiczenie nr 4 Galwanometr magnetoelektryczny
5
Oprócz galwanometrów statycznych wyst
ę
puj
ą
tak
ż
e galwanometry
balistyczne, wibracyjne, pełzne. W tych przyrz
ą
dach wykorzystuje si
ę
ich
wskazania w stanach przej
ś
ciowych pracy. Obecnie jednak s
ą
ju
ż
one w zaniku.
Ni
ż
ej przedstawimy wielko
ś
ci charakteryzuj
ą
ce galwanometr magneto-
elektryczny statyczny, opisuj
ą
c jednocze
ś
nie jego charakterystyczne elementy
konstrukcyjne
Czuło
ść
pr
ą
dowa S
I
. Jest to pochodna odpowiedzi ustroju wzgl
ę
dem
wymuszenia. Wyznaczamy j
ą
, obliczaj
ą
c pochodn
ą
funkcji (5) wzgl
ę
dem pr
ą
du I.
z
I
k
Bzab
dI
d
S
=
=
α
(6)
Wysiłek konstruktorów od pocz
ą
tku zmierzał w kierunku maksymalnego
zwi
ę
kszenia czuło
ś
ci pr
ą
dowej galwanometru. Przyjrzymy si
ę
najwa
ż
niejszym
zabiegom konstrukcyjnym prowadz
ą
cym do zwi
ę
kszenia czuło
ś ć
ustroju
magnetoelektrycznego.
Z zale
ż
no
ś
ci (6) wynika,
ż
e zwi
ę
kszenie czuło
ś
ci mo
ż
liwe jest przez
wzrost indukcji B, zwi
ę
kszenie liczby zwojów cewki z, a tak
ż
e jej wymiarów a,
b. Jednak zwi
ę
kszenie parametrów z, a, b prowadzi do wzrostu ci
ęż
aru
ceweczki, co poci
ą
ga za sob
ą
konieczno
ś ć
zawieszenia jej na grubszych nitkach,
a to powi
ę
ksza stał
ą
zwracania k
z
, zmniejszaj
ą
c, zgodnie z zale
ż
no
ś
ci
ą
(6),
czuło
ś ć
pr
ą
dow
ą
. W praktyce wykorzystuje si
ę
jedynie mo
ż
liwo
ś ć
powi
ę
kszenia
indukcji B poprzez zmniejszenie szeroko
ś
ci szczeliny powietrznej obwodu
magnetycznego. Wymaga to zmniejszenia grubo
ś
ci boków ceweczki zanurzonych
w tej szczelinie. Ceweczk
ę
nawija si
ę
w tym celu na sztywnym korpusie, który
zostaje usuni
ę
ty po wyschni
ę
ciu lakieru spajaj
ą
cego poszczególne zwoje. Dzi
ę
ki
temu jest ona lekka i ma cienkie boki. Mo
ż
na j
ą
zawiesi
ć
(rys. 2) na delikatnych
nitkach spr
ęż
ystych (
ś
rednicy ok. 0,02 mm), wykonanych z br
ą
zu fosforowego
lub berylowego o bardzo małej stałej zwracania k
z
, co zgodnie z zale
ż
no
ś
ci
ą
(6)
sprzyja zwi
ę
kszeniu czuło
ś
ci pr
ą
dowej.
Kolejnym wa
ż
nym zabiegiem zwi
ę
kszaj
ą
cym czuło
ś ć
galwanometru jest
zast
ą
pienie wskazówki materialnej wskazówk
ą
ś
wietln
ą
. Zasada tej wskazówki
jest przedstawiona na rysunku 2. Promie
ń
ś
wietlny przychodz
ą
cy od
ź
ródła
(układu optycznego nie pokazanego na szkicu), pada na miniaturowe lustereczko
przymocowane sztywno do cewki i wykonuj
ą
ce te same ruchy co ona. Promie
ń
odbity zmienia swój kierunek w zale
ż
no
ś
ci od k
ą
ta obrotu cewki. Padaj
ą
c na
szkło matowe, zaznacza si
ę
na nim
ś
wietlistym prostok
ą
tem (plamk
ą
ś
wietln
ą
).
W rzeczywisto
ś
ci budowa tej wskazówki jest bardziej zło
ż
ona, promie
ń
ś
wietlny,
nim padnie na matówk
ę
odbija si
ę
jeszcze od kilku innych lusterek, co daje efekt

Ć
wiczenie nr 4 Galwanometr magnetoelektryczny
6
równowa
ż
ny wydłu
ż
eniu wskazówki, zwi
ę
kszaj
ą
c tym jeszcze bardziej czuło
ś ć
przyrz
ą
du
(niewielkiemu
k
ą
towi
obrotu
ceweczki
odpowiada
du
ż
e
przemieszczenie plamki
ś
wietlnej na matówce).
Ć
wicz
ą
cy b
ę
d
ą
mogli obejrze
ć
jej praktyczn
ą
realizacj
ę
, ogl
ą
daj
ą
c w trakcie
ć
wiczenia eksponat galwanometru.
U
ż
ywaj
ą
c galwanometru jako mikroamperomierza, u
ż
ytkownik korzysta z
zale
ż
no
ś
ci (7).
a
C
I
I
⋅
=
(7)
gdzie:
I - nat
ę ż
enie mierzonego pr
ą
du [A]
C
I
- stała pr
ą
dowa galwanometru [A/dz]
a - przemieszczenie wskazówki na tle płaskiej podziałki mierzone
w działkach (długo
ś ć
jednej działki wynosi 1 mm)
Podziałka galwanometru ma charakter płaskiej milimetrowej linii z ze-
rem po
ś
rodku i jest naniesiona na szkle matowym. Wobec faktu,
ż
e zerowa
kreska działowa umieszczona jest na
ś
rodku podziałki, mniejsz
ą
uwag
ę
przykłada
ć
mo
ż
na do biegunowo
ś
ci napi
ę
cia przył
ą
czanego do zacisków
wej
ś
ciowych tego przyrz
ą
du.
Jak wynika z zale
ż
no
ś
ci (7), do obliczenia pr
ą
du mierzonego przez
galwanometr trzeba zna
ć
nie tylko przemieszczenie wskazówki, ale tak
ż
e
stał
ą
pr
ą
dow
ą
C
I
, a ta mo
ż
e by
ć
zmieniana przez u
ż
ytkownika w pewnych
granicach.
Stała pr
ą
dowa C
I
jest to przyrost nat
ę ż
enia pr
ą
du płyn
ą
cego przez
cewk
ę
, powoduj
ą
cy przemieszczenie wskazówki galwanometru o jedna działk
ę
(1 mm). Stała pr
ą
dowa galwanometrów wyra
ż
a si
ę
zwykle bardzo mał
ą
liczb
ą
ułamkow
ą
rz
ę
du 10
-9
A/dz.
Stała C
I
mo
ż
e by
ć
regulowana przez u
ż
ytkownika w pewnym zakresie,
(podanym na płycie czołowej przyrz
ą
du) za pomoc
ą
pokr
ę
tła oznaczonego „C
I
”,
umieszczonego na jego tylnej
ś
ciance. Pokr
ę
tło to słu
ż
y do regulacji poło
ż
enia
bocznika magnetycznego. Pomiar pr
ą
du musi by
ć
wi
ę
c poprzedzony okre
ś
leniem
warto
ś
ci stałej pr
ą
dowej, zwłaszcza gdy nie wiadomo, w jakim poło
ż
eniu
pozostawili bocznik poprzedni u
ż
ytkownicy. Do
ś
wiadczalne wyznaczenie tej
stałej jest przedmiotem niniejszego
ć
wiczenia.
Nasuwa si
ę
naturalne pytanie, w jakim celu pozostawia si
ę
u
ż
ytkownikowi
mo
ż
liwo
ś ć
regulowania stałej pr
ą
dowej? Mo
ż
liwo
ś ć
ta wykorzystywana jest do
ograniczenia
czuło
ś
ci
galwanometru
w
przypadkach
gdy wysoka czuło
ś ć
nie jest konieczna w danych pomiarach, po
żą
dane jest
natomiast skrócenie czasu ustalania si
ę
wskaza
ń
i skrócenie czasu trwania
pomiarów.
Ć
wiczenie nr 4 Galwanometr magnetoelektryczny
7
Wspomnianej regulacji dokonuje si
ę
przy pomocy pokr
ę
tła oznaczonego
„C
I
”, jako
ż
e parametry S
I
oraz C
I
pozostaj
ą
wzgl
ę
dem siebie w
ś
cisłym zwi
ą
zku,
I
I
C
S
1
=
Jak wynika z powy
ż
szej zale
ż
no
ś
ci, w celu zmniejszenia czuło
ś
ci pr
ą
dowej,
nale
ż
y zwi
ę
kszy
ć
stał
ą
pr
ą
dow
ą
.
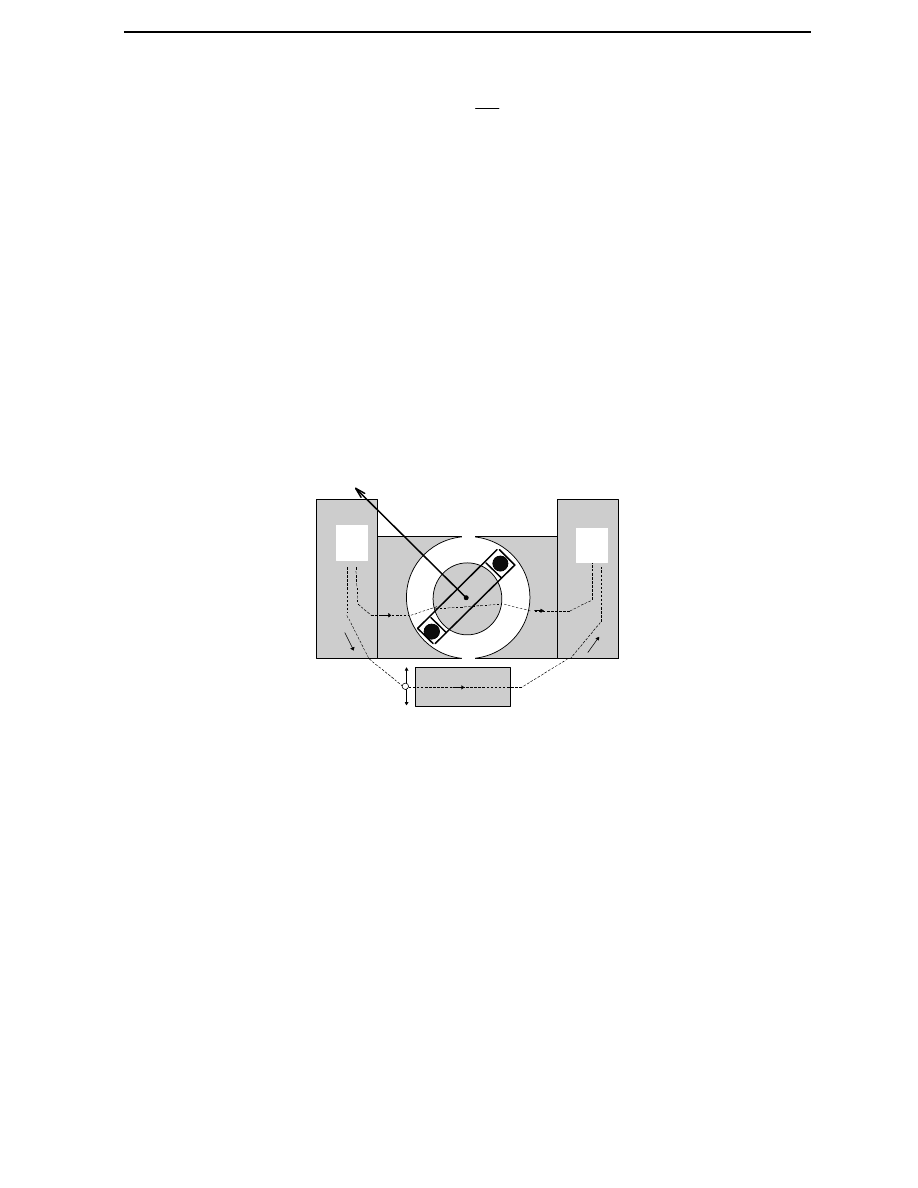
Bocznik magnetyczny
(rys. 3)
jest kawałkiem stali magnetycznie
mi
ę
kkiej, który w zale
ż
no
ś
ci od swego poło
ż
enia wzgl
ę
dem szczeliny
powietrznej w ró
ż
nym stopniu bocznikuje strumie
ń
magnetyczny zmierzaj
ą
cy od
bieguna N do bieguna S poprzez obszar, w którym znajduje si
ę
cewka,
wpływaj
ą
c tym na warto
ś ć
strumienia z ni
ą
skojarzonego (indukcji magnetycznej
B), a tym samym na warto
ś ć
sił elektrodynamicznych i momentu nap
ę
dowego
(patrz zale
ż
no
ś ć
(1)).
Poprzez regulacj
ę
indukcji B, u
ż
ytkownik wpływa na warto
ś ć
momentu
tłumi
ą
cego M
T
(wzór (8)) oraz rezystancji krytycznej R
kr
galwanometru (wzór
(10)).
BOCZNIK
S
N
Rys.3. Zasada bocznika magnetycznego
Moment tłumi
ą
cy M
T
Rola momentu tłumi
ą
cego polega na tłumieniu oscylacji ceweczki wokół
nowego poło
ż
enia ustalonego, w którym powinna si
ę
ona znale
ź ć
po zmianie
nat
ęż
enia pr
ą
du w niej płyn
ą
cego.
Kiedy pr
ą
d cewki wzrasta od zera do pewnej warto
ś
ci, moment nap
ę
dowy
praktycznie bezzwłocznie osi
ą
ga warto
ś ć
M
N1
, co pokazuje rysunek 4, natomiast
moment zwrotny ma warto
ś ć
zerow
ą
. W pierwszej chwili przewa
ż
a wi
ę
c moment
Ć
wiczenie nr 4 Galwanometr magnetoelektryczny
8
nap
ę
dowy, w rezultacie czego cewka zaczyna obraca
ć
si
ę
, za
ś
nitki spr
ęż
yste
zawieszenia ulegaj
ą
stopniowemu skr
ę
ceniu, wytwarzaj
ą
c narastaj
ą
cy liniowo
moment zwrotny.
B
M
0
M
N
M
Z
M
N1
C
A
α
2
α
1
α
1
Rys. 4. Współpraca momentu nap
ę
dowego (M
N
) i zwrotnego (M
Z
) w ustroju
magnetoelektrycznym
Oba momenty staj
ą
si
ę
sobie równe, gdy cewka obróci si
ę
o k
ą
t
α
1
, jednak jej
ruch nie ustaje w tym miejscu. Mo
ż
na wykaza
ć
,
ż
e osi
ą
gnie ona k
ą
t obrotu 2
α
1
(przy zało
ż
eniu braku jakichkolwiek strat energii). W cewce zostanie bowiem
nagromadzona energia kinetyczna ruchu obrotowego, wi
ę
ksza od pracy
potrzebnej do skr
ę
cenia nitek spr
ęż
ystych o k
ą
t
α
1
.
Moment nap
ę
dowy M
N
o warto
ś
ci M
N1
(rys.4) wykonuje na drodze
k
ą
towej (0 -
α
1
) prac
ę
,
1
1
α
N
N
M
W
=
,
proporcjonaln
ą
do pola powierzchni prostok
ą
ta (0,
α
1
, A, M
N1
).
Praca momentu zwrotnego M
Z
, liniowo zale
ż
nego od k
ą
ta obrotu cewki,
wyniesie natomiast,
( )
∫
∫
=
⋅
=
=
1
0
2
1
0
2
1
α
α
α
α
α
α
α
z
z
Z
Z
k
d
k
d
M
W
Stała zwracania k
z
równa jest współczynnikowi nachylenia prostej momentu
zwrotnego i, jak wynika z rysunku 4, mo
ż
e by
ć
wyra
ż
ona jako tangens k
ą
ta
nachylenia tej prostej,
1
1
α
N
z
M
k
=
Podstawiaj
ą
c to wra
ż
enie do ostatniej zale
ż
no
ś
ci, dostaniemy ostatecznie,
1
1
2
1
α
N
Z
M
W
=

Ć
wiczenie nr 4 Galwanometr magnetoelektryczny
9
Jak wida
ć
, praca momentu nap
ę
dowego W
N
jest dwukrotnie wi
ę
ksza od
pracy W
Z
momentu zwrotnego. Nadwy
ż
ka pracy momentu nap
ę
dowego,
proporcjonalna do pola trójk
ą
ta zakreskowanego na rysunku 4, zostaje zu
ż
yta na
nadanie energii kinetycznej ruchu obrotowego ceweczki. Gdy ta ostatnia „mija”
k
ą
t
α
1
, energia kinetyczna zaczyna zamienia
ć
si
ę
na energi
ę
potencjaln
ą
spr
ę ż
ysto
ś
ci, skr
ę
caj
ą
c nitki zawieszenia cewki o k
ą
t 2
α
1
. Energia potencjalna
spr
ę ż
ysto
ś
ci jest proporcjonalna do pola powierzchni trójk
ą
ta (A, B, C)
dokładnie równego polu trójk
ą
ta zakreskowanego. W punkcie 2
α
1
cewka
zatrzyma si
ę
, za
ś
przewa
ż
aj
ą
cy w tym miejscu moment zwrotny zapocz
ą
tkuje jej
ruch powrotny oraz towarzysz
ą
cy mu odwrotny proces zamiany energii
potencjalnej spr
ę ż
ysto
ś
ci na energi
ę
kinetyczn
ą
ruchu obrotowego. W idealnym
stanie rzeczy (brak strat energii) cewka mo
ż
e dotrze
ć
do poło
ż
enia wyj
ś
ciowego
(
α
= 0) i ponownie rozpocz
ą ć
opisany ju
ż
ruch w kierunku przeciwnym.
Oznaczałoby to niegasn
ą
ce oscylacje ceweczki o amplitudzie
|α
1
|
wokół
poło
ż
enia ustalonego
α
1
.
W rzeczywisto
ś
ci, wyst
ę
puj
ą
ce podczas ruchu straty energii na tarcie (o
powietrze i tarcie wewn
ę
trzne w nitkach spr
ę ż
ystych zawieszenia) powoduj
ą
malenie amplitudy oscylacji, stopniowy zanik ruchu cewki i ustalenie si
ę
jej
poło
ż
enia
α
1
odpowiadaj
ą
cego nowej warto
ś
ci pr
ą
du.
Gdyby istniały tylko momenty tarciowe, ustalenie si
ę
wskaza
ń
galwanometru trwałoby zbyt długo i nadmiernie wydłu
ż
ało pomiary. Miałoby to
miejsce tylko wtedy, gdy obwód elektryczny cewki pozostawałby otwarty i nie
istniałby moment tłumi
ą
cy. Istotnie, z zale
ż
no
ś
ci (8) okre
ś
laj
ą
cej moment
tłumi
ą
cy wynika,
ż
e dla rezystancji zewn
ę
trznej R
Z
przył
ą
czonej do zacisków
galwanometru d
ą ż ą
cej do niesko
ń
czono
ś
ci (przypadek rozwarcia obwodu),
moment tłumi
ą
cy M
T
staje si
ę
równy zeru.
(
)
dt
d
R
R
Bzab
M
Z
G
T
α
⋅
+
=
2
(8)
M
T
- moment tłumi
ą
cy
B - indukcja w szczelinie powietrznej
z - liczba zwojów cewki
a, b - wymiary cewki
R
G
- rezystancja wewn
ę
trzna galwanometru
R
Z
- rezystancja zast
ę
pcza obwodu przył
ą
czonego do galwanometru
d
dt
α
- pr
ę
dko
ś ć
k
ą
towa cewki
Z równania (8) wynika,
ż
e moment tłumi
ą
cy zale
ż
y on szeregu wielko
ś
ci,
w tym m. in. od indukcji B, rezystancji całkowitej obwodu cewki (R
G
+R
Z
) i jej
pr
ę
dko
ś
ci k
ą
towej (d
α
/dt). Skupimy si
ę
głównie na wymienionych wielko
ś
ciach.
Ć
wiczenie nr 4 Galwanometr magnetoelektryczny
10
Jak wida
ć
u
ż
ytkownik ma mo
ż
liwo
ś ć
wpływania na warto
ś ć
momentu M
T
poprzez zmian
ę
rezystancji zast
ę
pczej obwodu przył
ą
czonego do zacisków
galwanometru, a tak
ż
e poprzez zmian
ę
indukcji B przy pomocy bocznika
magnetycznego.
Maksymalny moment tłumi
ą
cy uzyskuje si
ę
przy zwartych zaciskach
galwanometru (R
Z
= 0). Producent wyposa
ż
a ten przyrz
ą
d w specjaln
ą
zwor
ę
,
któr
ą
nale
ż
y zakłada
ć
po zako
ń
czonej pracy, zwłaszcza wtedy, gdy galwanometr
ma by
ć
przenoszony na inne miejsce.
Pozostawienie rozwartych zacisków przyrz
ą
du grozi powstaniem
silnych, słabo tłumionych oscylacji ceweczki (po wpływem przechyłów
i drga
ń
), mog
ą
cych prowadzi
ć
do ukr
ę
cenia niezwykle delikatnych nitek, na
których jest ona zawieszona.
Zale
ż
no
ś ć
momentu tłumi
ą
cego od pr
ę
dko
ś
ci k
ą
towej jest zrozumiały.
Szybszy ruch ceweczki w polu magnetycznym magnesu trwałego powoduje
indukowanie si
ę
w niej wi
ę
kszej siły elektromotorycznej i wzrost hamuj
ą
cego
oddziaływania elektrodynamicznego wynikaj
ą
cego z reguły Lenza.
Wpływ momentu tłumi
ą
cego na charakter ruchu cewki galwanometru w
stanie przej
ś
ciowym ilustruj
ą
przebiegi na rysunku 4.
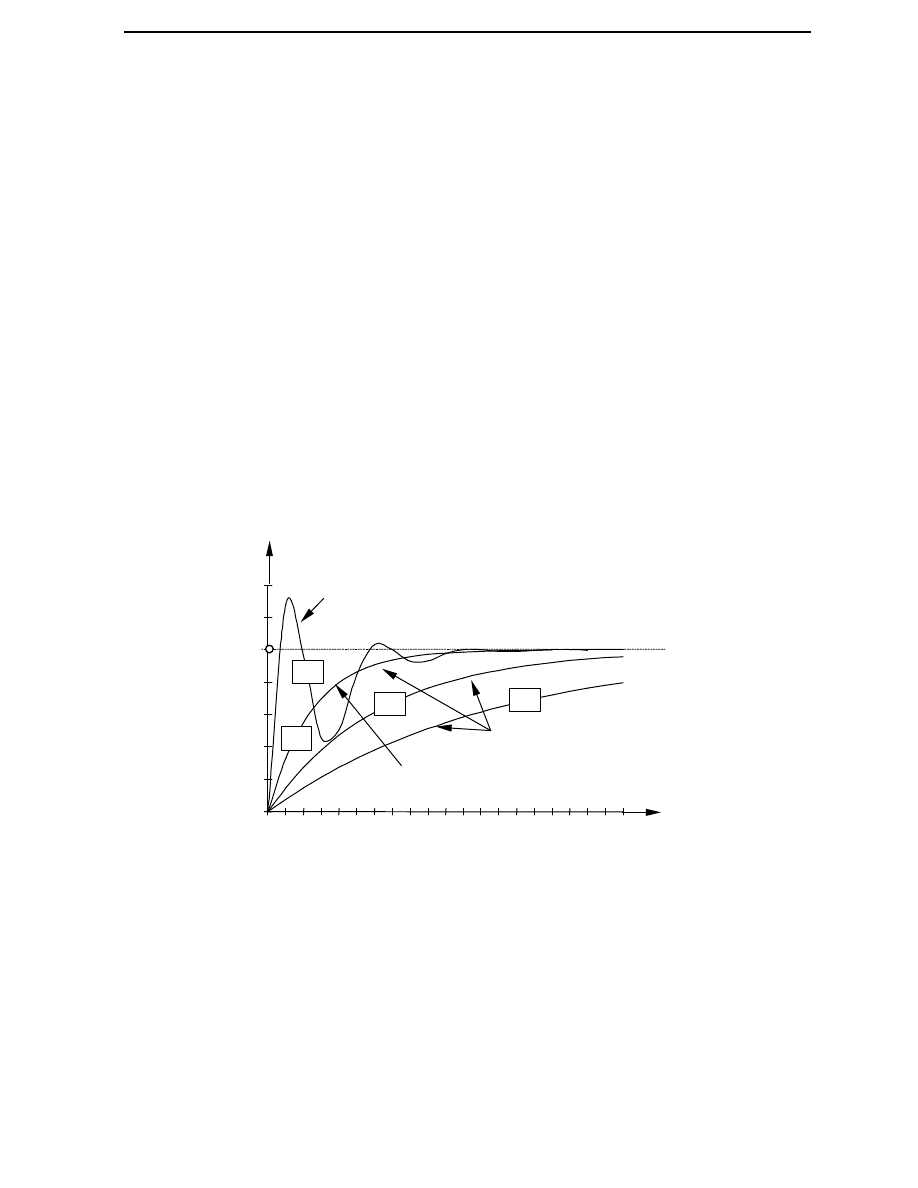
a
u
a
t
rodzina ruchów aperiodycznych
ruch aperiodyczny krytyczny
ruch oscylacyjny tłumiony
M
T1
M
T3
M
T2
M
T4
M
T1
>
M
T2
>
M
T3
>
M
T4
a
u
- poło
ż
enie ustalone
Rys. 4. Rodzaje ruchów cewki galwanometru w stanie przej
ś
ciowym
w zale
ż
no
ś
ci od momentu tłumi
ą
cego M
T
Najkorzystniejszy, z punktu widzenia czasu trwania pomiarów, jest ruch
aperiodyczny krytyczny, to znaczy najszybszy z ruchów nieokresowych.
Wskazówka bowiem dociera wtedy do poło
ż
enia ustalonego najszybciej, bez
zb
ę
dnych oscylacji.

Ć
wiczenie nr 4 Galwanometr magnetoelektryczny
11
Ruch aperiodyczny krytyczny mo
ż
na te
ż
okre
ś
li
ć
jako ruch graniczny
mi
ę
dzy rodzin
ą
ruchów okresowych (oscylacyjnych) i rodzin
ą
ruchów
nieokresowych (aperiodycznych).
Rezystancja zewn
ę
trzna krytyczna R
zkr
.
Jest to taka warto
ś ć
rezystancji zast
ę
pczej obwodu zewn
ę
trznego
przył
ą
czonego do zacisków galwanometru, przy której (za spraw
ą
momentu
tłumi
ą
cego) organ ruchomy pod
ą ż
a do nowego poło
ż
enia ustalonego ruchem
aperiodycznym krytycznym.
Rezystancja zewn
ę
trzna krytyczna dana jest wzorem (9).
(
)
G
z
zkr
R
Jk
Bzab
R
−
=
2
2
(9)
gdzie:
B - indukcja w szczelinie powietrznej
z - liczba zwojów cewki
a, b - wymiary cewki (patrz rys.2)
J - moment bezwładno
ś
ci cewki
k
z
- stała zwracania nitek spr
ę ż
ystych
R
G
- rezystancja wewn
ę
trzna galwanometru
Rezystancja krytyczna R
kr
. Producent podaje dla galwanometru warto
ś ć
rezystancji krytycznej R
kr
. Jest to suma rezystancji wewn
ę
trznej galwanometru
R
G
i rezystancji zewn
ę
trznej krytycznej R
zkr
.
zkr
G
kr
R
R
R
+
=
Rezystancja krytyczna dana jest wzorem (10).
(
)
z
kr
Jk
Bzab
R
2
2
=
,
(10)
w którym znaczenie symboli jest takie same jak w równaniu (9).
Ć
wiczenie nr 4 Galwanometr magnetoelektryczny
12
2. Ogl
ę
dziny galwanometru
Nale
ż
y przyjrze
ć
si
ę
badanemu podczas
ć
wiczenia galwanometrowi,
zanotowa
ć
w Tablicy 1 jego parametry i dokona
ć
wskazanych ni
ż
ej oblicze
ń
.
1. Wska
ż
zaciski wej
ś
ciowe galwanometru
2. Wska
ż
gniazdo zasilania
ż
aróweczki galwanometru
3. Wska
ż
pokr
ę
tło do zerowania galwanometru
4. Wska
ż
pokr
ę
tło do regulacji stałej pr
ą
dowej galwanometru
5. Zanotuj w Tablicy 1 parametry galwanometru podane na podziałce:
•
Rezystancj
ę
wewn
ę
trzn
ą
R
G
•
Rezystancj
ę
krytyczn
ą
R
kr
(przedział liczbowy)
•
Stał
ą
pr
ą
dow
ą
C
I
(przedział liczbowy)
We
ź
mniejsz
ą
z dwóch skrajnych warto
ś
ci stałej pr
ą
dowej C
I
podanej na
podziałce badanego galwanometru i oblicz według formuły (11) warto
ś ć
pr
ą
du,
jaki spowoduje przemieszczenie wskazówki galwanometru o 70 działek. B
ę
dzie
to najwi
ę
ksza dopuszczalna warto
ś ć
pr
ą
du I
G
, jak
ą
mo
ż
e mierzy
ć
galwanometr,
w przypadku, gdy ustawiona jest najwi
ę
ksza czuło
ś ć
tego przyrz
ą
du.
I
G MAX
= 70 C
I
(11)
Znaj
ą
c warto
ś ć
pr
ą
du I
GMAX
oraz warto
ś ć
rezystancji wewn
ę
trznej galwa-
nometru R
G
, oblicz według wzoru (12) maksymalne napi
ę
cie U
max
, jakie mo
ż
na
przykłada
ć
do zacisków wej
ś
ciowych galwanometru.
U
MAX
= R
G
I
G MAX
(12)
Wyniki oblicze
ń
wpisz do Tablicy 1.
Tablica 1
R
G
Ω
R
kr
Ω
C
I
A/dz
I
G MAX
A
U
G MAX
V
Ć
wiczenie nr 4 Galwanometr magnetoelektryczny
13
3. Przebieg pomiarów
Wyznaczanie stałej pr
ą
dowej galwanometru
Schemat układu pomiarowego, w którym wyznaczana jest stał
ą
pr
ą
dow
ą
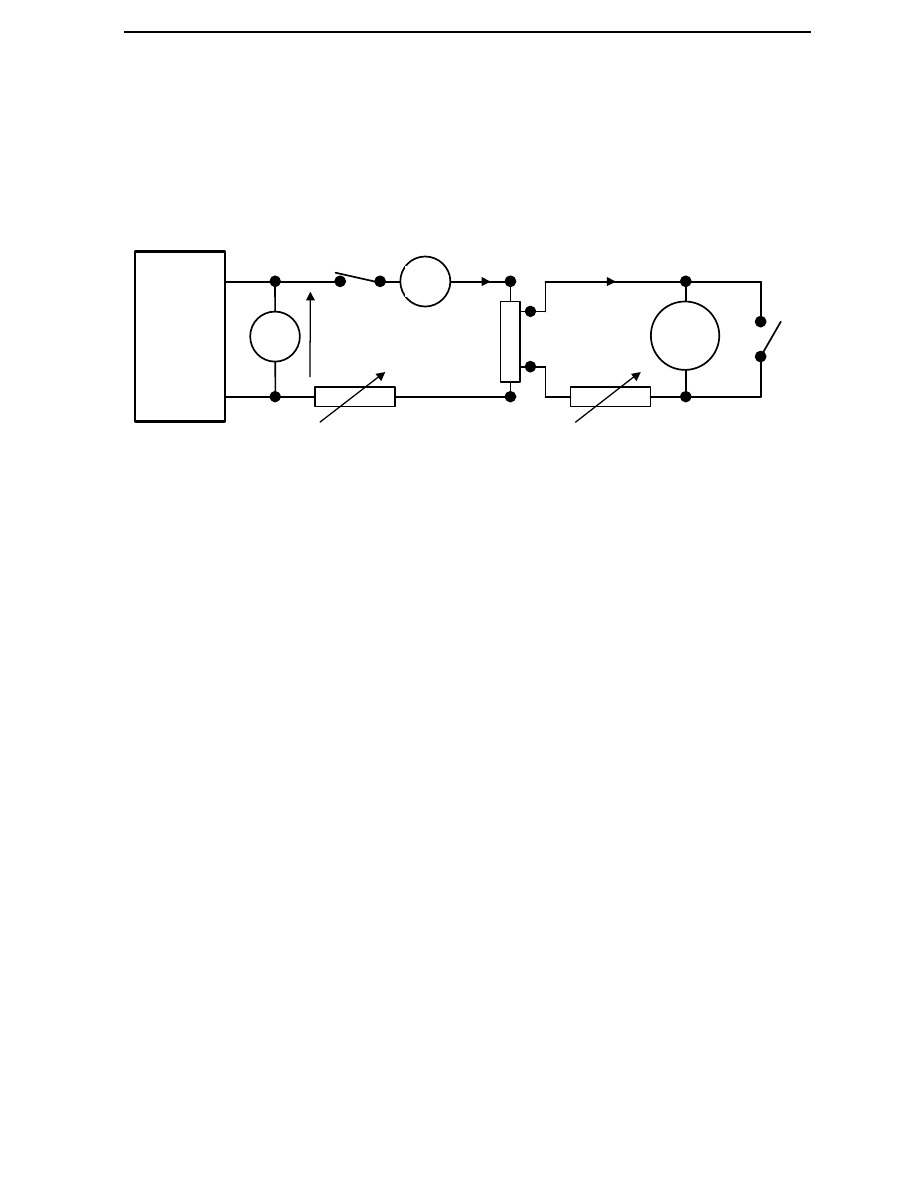
galwanometru, przedstawiony jest na rysunku 5.
V
W
I
G
I
1
U
Z
Z
R
3
R
2
R
1
mA
ZS
G
Rys 5. Schemat układu pomiarowego
G - badany galwanometr
ZS - zasilacz stabilizowany
V - woltomierz magnetoelektryczny typu LM-3
(nastawi
ć
zakres 15 V)
mA - miliamperomierz magnetoelektryczny typu LM-3
(nastawi
ć
zakres 15 mA)
R
2
= 0,1
Ω
rezystor wzorcowy czterozaciskowy
R
1
- rezystor pi
ę
ciodekadowy (nastawi
ć
1000
Ω
)
R
3
- rezystor sze
ś
ciodekadowy (nastawi
ć
wst
ę
pnie 99 999
Ω
)
W - wył
ą
cznik jednobiegunowy
Z - specjalny zwieracz galwanometru
Kolejno
ść
czynno
ś
ci
1. Przed pomiarem nale
ż
y przył
ą
czy
ć
napi
ę
cie do
ż
aróweczki galwanometru za
po
ś
rednictwem specjalnego transformatorka zewn
ę
trznego o przekładni
220V/6V (niektóre galwanometry maj
ą
wbudowany ten transformatorek do
ś
rodka). W rezultacie na matówce galwanometru powinien pojawi
ć
si
ę
ś
wiec
ą
cy prostok
ą
cik. Jest to wskazówka
ś
wietlna galwanometru.
2. Przy otwartym zwieraczu Z nale
ż
y wyzerowa
ć
galwanometr przy pomocy
specjalnego pokr
ę
tła. Je
ż
eli wyst
ą
pi
ą
trudno
ś
ci z ustabilizowaniem wskazówki
(najcz
ę ś
ciej
oscyluje
ona
wokół
pewnego
poło
ż
enia),
Ć
wiczenie nr 4 Galwanometr magnetoelektryczny
14
galwanometr uznajemy za wyzerowany, gdy lewa amplituda oscylacji
wskazówki wokół poło
ż
enia zerowego jest równa prawej. Po wyzerowaniu,
nie mo
ż
na zmienia
ć
poło
ż
enia galwanometru na stole.
3. Przy otwartym wył
ą
czniku W nale
ż
y wł
ą
czy
ć
napi
ę
cie zasilaj
ą
ce zasilacza ZS
i przy pomocy odpowiedniego regulatora nastawi
ć
napi
ę
cie U
Z
= 10 V.
4. Zamkn
ą ć
wył
ą
cznik W. Miliamperomierz powinien wskaza
ć
pr
ą
d bliski
10 mA. Przy pomocy rezystora R
1
nastawi
ć
dokładn
ą
warto
ś ć
pr
ą
du I
1
= 10
mA
5. Reguluj
ą
c rezystancj
ę
R
3
, nale
ż
y ustawia
ć
warto
ś
ci wskaza
ń
a galwanome-
tru podane w Tablicy 2, notuj
ą
c warto
ś
ci rezystancji R
3
oraz pr
ą
du I
1
(ten
ostatni praktycznie pozostanie na poziomie 10 mA).
Uwaga: Je
ż
eli w jakiejkolwiek fazie pomiarów plamka
ś
wietlna zniknie z
pola widzenia, nale
ż
y bezzwłocznie otworzy
ć
wył
ą
cznik W i zamkn
ą ć
zwieracz
Z, a nast
ę
pnie sprawdzi
ć
układ poł
ą
cze
ń
.
Tablica 2
a
dz
20
40
60
R
3
Ω
I
1
mA
I
G
A
C
I
A/dz
Obliczenia
Obliczy
ć
pr
ą
d galwanometru I
G
według wzoru (13)
G
G
R
R
R
R
I
I
+
+
=
3
2
2
1
(13)
Oblicz stał
ą
pr
ą
dow
ą
C
I
według wzoru (14)
a
I
C
G
I
=
(14)
Warto
ś
ci C
I
obliczone dla poszczególnych przemieszcze
ń
wskazówki a
powinny by
ć
bardzo bliskie sobie. W wypadku znacznych ró
ż
nic nale
ż
y
powtórzy
ć
pomiary i obliczenia.

Ć
wiczenie nr 4 Galwanometr magnetoelektryczny
15
4. Pytania i zadania kontrolne
1. Wymie
ń
najwa
ż
niejsze elementy konstrukcyjne ustroju magnetoelektrycz-
nego
2. Napisz zale
ż
no
ś
ci okre
ś
laj
ą
ce moment nap
ę
dowy ustroju i moment zwrotny
3. Które elementy obwodu magnetycznego wykonane s
ą
ze stali magnetycznie
mi
ę
kkiej i jak
ą
rol
ę
one pełni
ą
?
4. Opisz budow
ę
i zasad
ę
działania bocznika magnetycznego
5. Jakie parametry galwanometru reguluje si
ę
przy pomocy bocznika
magnetycznego?
6. Jak
ą
rol
ę
w ustroju pomiarowym pełni moment zwrotny?
7. Jak wytwarzany jest moment zwrotny w klasycznym mierniku, a jak w gal-
wanometrze?
8. Co nazywamy funkcj
ą
przetwarzania ustroju magnetoelektrycznego?
9. Podaj okre
ś
lenie czuło
ś
ci pr
ą
dowej S
I
galwanometru
10. Podaj okre
ś
lenie stałej pr
ą
dowej C
I
galwanometru
11. Podaj zwi
ą
zek mi
ę
dzy parametrami S
I
i C
I
12. Dlaczego stała pr
ą
dowa C
I
(patrz podziałka galwanometru) podana jest
w postaci przedziału liczbowego?
13. Podaj okre
ś
lenie rezystancji zewn
ę
trznej krytycznej galwanometru R
zkr
14. Podaj okre
ś
lenie rezystancji krytycznej galwanometru R
kr
15. Dlaczego rezystancja ta (patrz podziałka galwanometru) podana jest w po-
staci przedziału liczbowego?
16. Jaki ruch nazywamy ruchem aperiodycznym krytycznym galwanometru?
17. Opisz mechanizm powstawania momentu tłumi
ą
cego w galwanometrze
18. Dlaczego nale
ż
y zwiera
ć
zaciski wej
ś
ciowe galwanometru odnosz
ą
c go do
szafy?
19. Jakiego rodzaju uszkodzenie mo
ż
e mie
ć
miejsce przy transporcie
galwanometru bez zwartych zacisków wej
ś
ciowych?
5. Literatura
1. Lebson S. Podstawy miernictwa elektrycznego WNT, Warszawa 1970
2. Łapi
ń
ski M. Miernictwo elektryczne WKiŁ, Warszawa 1967
3. Chwaleba A. i inni Metrologia elektryczna WNT, Warszawa 1994
Wyszukiwarka
Podobne podstrony:
Galwanometr magnetoelektryczny statyczny
Galwanometr magnetoelektryczny statyczny
Galwometr magnetoelektryczny, 1.Celem ˙wiczenia jest poznanie zasady dzia˙ania, budowy oraz podstawo
04 Galwanometr magnetoelektryczny
04 Galwanometr magnetoelektryczny
Budowa i zasada działania galwanometru statycznego
Pomiar galwanometru statycznego v4
Wyznaczenie składowej poziomej indukcji pola magnetycznego Ziemi przy pomocy busoli statycznych, Num
Pomiar galwanometru statycznego v3
37, REAL 37, Galwanometr jest elektrycznym przyrz˙dem pomiarowym, najcz˙˙ciej magnetoelektrycznym,
Badanie galwanometru statycznego v8
Badanie galwanometru statycznego v10
Badanie galwanometru statycznego, AGH IMIR Mechanika i budowa maszyn, II ROK, Metrologia Tyka Haduch
Badanie galwanometru statycznego, I. Cel ˙wiczenia.
Badanie galwanometru statycznego4
Badanie galwanometru statycznego v7
cw 9 badanie własności statycznych materiałów magnetycznie miekkich
Badanie galwanometru statycznego v9
Badanie galwanometru statycznego v2
więcej podobnych podstron