Projekt „Informatyka – inwestycją w przyszłość”
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
Biuro Projektu:
Politechnika Radomska im. Kazimierza Pułaskiego
26-600 Radom, ul. Chrobrego 27, pok. nr 44, tel. 48 361 78 50, 48 361 70 81
www.zamawiane.pr.radom.pl; e-mail: informatyka@pr.radom.pl
Zajęcia wyrównawcze z fizyki -Zestaw 6 -Teoria
Ruch obrotowy bryły sztywnej. Prędkość liniowa i prędkość kątowa, moment bezwładności, moment
siły, przyspieszenie kątowe, moment pędu.
Bryła sztywna –jest to obiekt nie zmieniający swojego kształtu w trakcie, gdy rozpatrujemy jej ruch,
czyli dla każdych dwóch dowolnie wybranych punktów tej bryły ich odległość pozostaje stała.
Bryła sztywna może wykonywać zarówno ruch postępowy, jak również ruch obrotowy. Opis ruchu
postępowego bryły sztywnej jest podobny do opisu ruchu punktu materialnego. ( Z ruchem
postępowym bryły mamy do czynienia wtedy, gdy każdy punkt tej bryły porusza się w identyczny
sposób, czyli po takiej samej trajektorii w tym samym czasie). W rozdziale tym będziemy rozważać
przede wszystkim ruch obrotowy
bryły sztywnej. Z ruchem obrotowym bryły mamy do czynienia, gdy
każdy punkt bryły porusza się z taką samą prędkością kątową po okręgu, a środki tych okręgów leżą
na jednej linii, k
tórą jest oś obrotu bryły. Natomiast okręgi, po których poruszają się poszczególne
punkty bryły mają na ogół różne promienie.
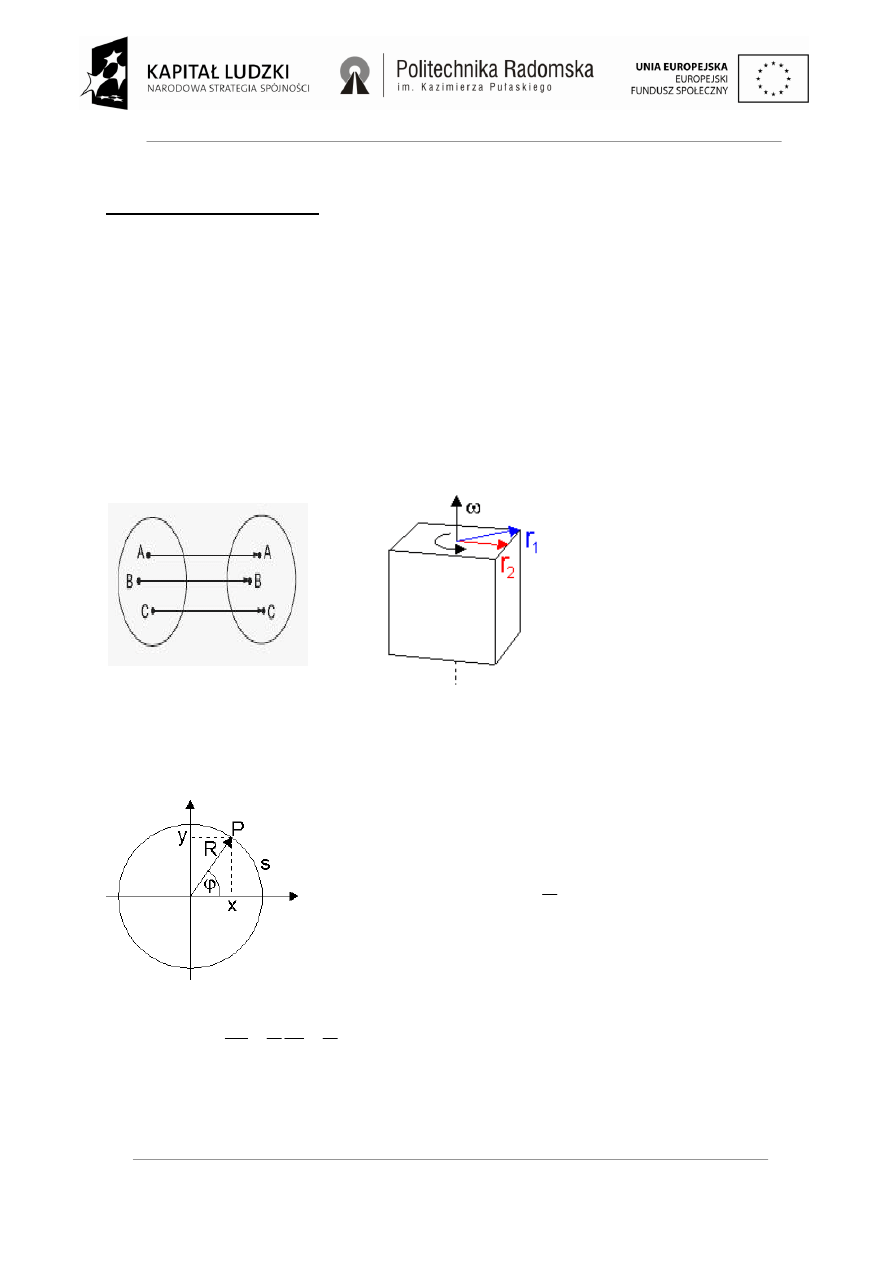
Ruch obrotowy bryły sztywnej.
Ruch postępowy bryły sztywnej.
Kinematyka ruchu obrotowego:
Kąt
φ
określa położenie kątowe punktu P .
Związek między drogą liniową s, a przesunięciem kątowym
:
W ruchu obrotowym wielkością analogiczną chwilowej prędkości
liniowej v jest chwilowa
prędkość kątowa
ω:
W ruchu obrotowym ze stałą prędkością kątową mamy następujące zależności:
(T jest okresem ruchu obrotowego, f -
częstotliwością.)
R
v
dt
ds
R
dt
d
1
f
2
R
s
Projekt „Informatyka – inwestycją w przyszłość”
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
Biuro Projektu:
Politechnika Radomska im. Kazimierza Pułaskiego
26-600 Radom, ul. Chrobrego 27, pok. nr 44, tel. 48 361 78 50, 48 361 70 81
www.zamawiane.pr.radom.pl; e-mail: informatyka@pr.radom.pl
Podobnie jak chwilowe przyspieszenie liniowe
a
zostało zdefiniowane chwilowe
przyspieszenie
kątowe
:
Opis ruchu obrotowego ze stałym przyspieszeniem kątowym
poprzez analogię do ruchu
postępowego jednostajnie zmiennego:
Ruch postępowy
Ruch obrotowy
a=const.
= const.
Dynamika ruchu obrotowego.
Dla ruchu obrotowego wielkością, która odgrywa rolę analogiczną do siły w ruchu postępowym jest
moment siły
(tzw. moment obrotowy)
M
F
.
Moment siły jest wielkością wektorową, której wartość bezwzględna wynosi (
iloczyn wektorowy
)
a
zwrot określamy zgodnie z regułą śruby prawoskrętnej.
Moment pędu: jest to wielkość, która w ruchu obrotowym odgrywa rolę analogiczną do pędu w ruchu
postępowym:
-dla punktu materialnego
-
dla bryły sztywnej
Moment
bezwładności bryły sztywnej: Jest to wielkość pełniąca w ruchu obrotowym rolę analogiczną
do masy w ruchu postępowym, zależna jest od masy bryły i od sposobu, w jaki masa jest rozłożona
względem osi obrotu.
T
R
t
s
v
2
T
f
1
T
f
2
2
R
a
dt
dv
R
dt
d
1
at
v
v
o
2
2
at
t
v
s
s
o
o
t
o
2
2
t
t
o
o
F
r
M
F
sin
rF
M
F
p
r
L
J
L
i
N
i
i
m
r
J
1
2
Projekt „Informatyka – inwestycją w przyszłość”
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
Biuro Projektu:
Politechnika Radomska im. Kazimierza Pułaskiego
26-600 Radom, ul. Chrobrego 27, pok. nr 44, tel. 48 361 78 50, 48 361 70 81
www.zamawiane.pr.radom.pl; e-mail: informatyka@pr.radom.pl
Dla ciągłego rozkładu mas:
Tabela momentów bezwładności brył.
Ciało
moment bezwładności J
Obręcz, pierścień o promieniu R, względem osi obręczy
Krążek, walec względem osi walca
Pręt o długości d, względem osi symetrii prostopadłej do pręta
Pełna kula o promieniu R, względem średnicy
Czasza kulista o promieniu R
, względem średnicy
Często do obliczania momentu bezwładności wygodnie jest posłużyć się twierdzeniem Steinera.
Podaje ono zależność pomiędzy momentem bezwładności I ciała względem danej osi, a momentem
bezwładności I
śr.m.
te
go ciała względem osi przechodzącej przez jego środek masy i równoległej do
danej. Związek ten wyraża się zależnością
:
gdzie d
jest odległością między osiami, a M jest masą ciała.
Zasady dynamiki w ruchu obrotowym
I.
Zasada dynamiki w ruchu obrotowym
Bryła sztywna, na którą nie działa moment siły, pozostaje w spoczynku lub porusza się ruchem
obrotowym jednostajnym.
II.
Zasada dynamiki w ruchu obrotowym
Wypadkowy moment siły działający na punkt materialny jest równy prędkości zmian momentu pędu.
dm
r
J
2
2
.
.
Md
J
J
m
sr
I
dt
L
d
M
wyp
Projekt „Informatyka – inwestycją w przyszłość”
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
Biuro Projektu:
Politechnika Radomska im. Kazimierza Pułaskiego
26-600 Radom, ul. Chrobrego 27, pok. nr 44, tel. 48 361 78 50, 48 361 70 81
www.zamawiane.pr.radom.pl; e-mail: informatyka@pr.radom.pl
III.
Zasada dynamiki w ruchu obrotowym
Jeżeli dwa ciała oddziałują wzajemnie, to moment siły z jakim działa ciało drugie na ciało pierwsze jest
równy i przeciwnie skierowany do momentu siły, z jakim ciało pierwsze działa na drugie.
Zasada zachowania momentu pędu.
Jeżeli na układ nie działa zewnętrzny moment siły (lub wypadkowy moment sił zewnętrznych jest
równy zeru) to całkowity moment pędu układu pozostaje stały.
Energia kinetyczna
bryły.
Energia kinetyczna bryły składa się z energii kinetycznej ruchu postępowego i z energii kinetycznej
ruchu obrotowego.
2
2
.
.
Mv
E
post
K
2
2
.
.
I
E
obr
K