www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
P
RÓBNY
E
GZAMIN
M
ATURALNY
Z
M
ATEMATYKI
Z
ESTAW PRZYGOTOWANY PRZEZ SERWIS
WWW
.
ZADANIA
.
INFO
POZIOM ROZSZERZONY
26
MARCA
2011
C
ZAS PRACY
: 180
MINUT
Z
ADANIE
1
(5
PKT
.)
Rozwi ˛
a ˙z nierówno´s´c
|
2x
2
+
28x
+
89
| >
9.
R
OZWI ˛
AZANIE
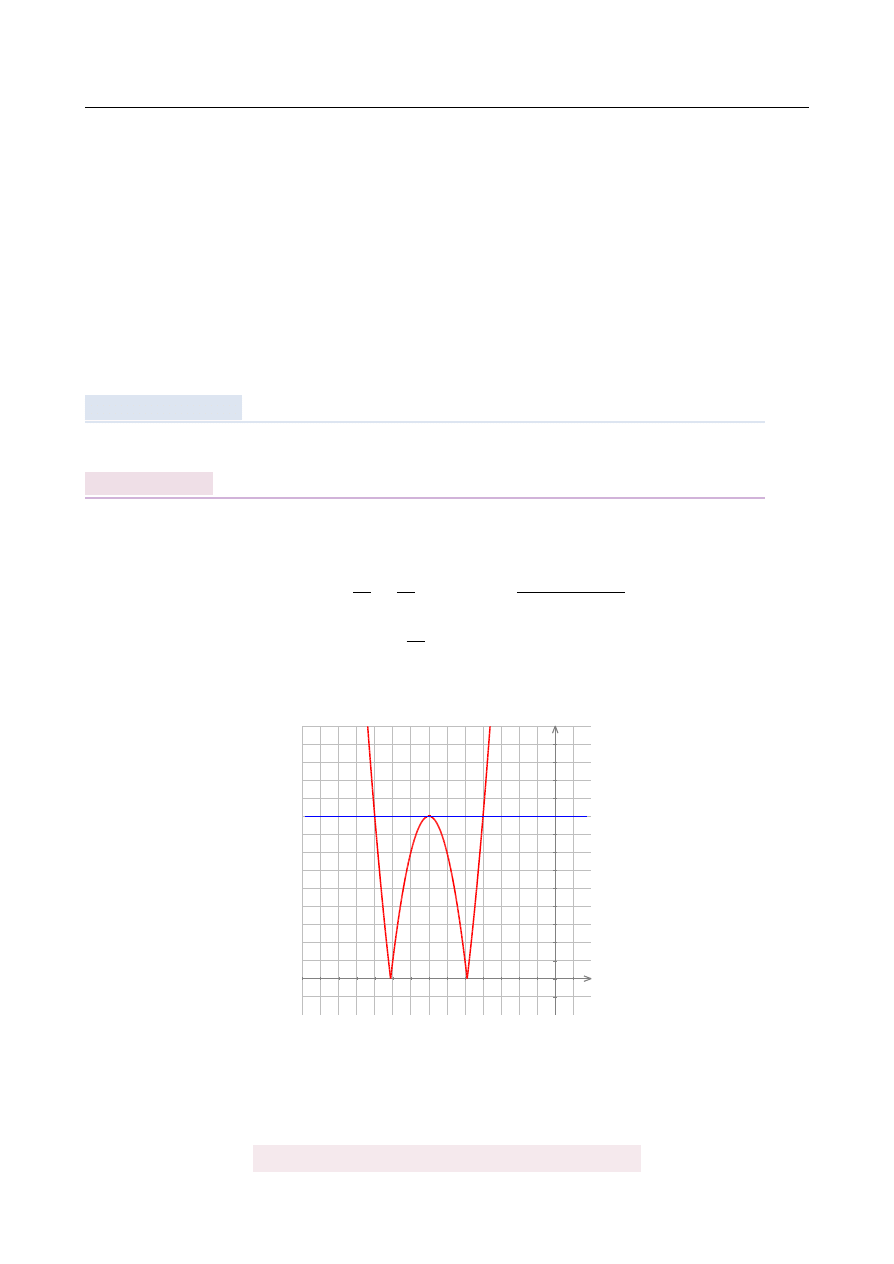
Aby zobaczy´c co jest grane, naszkicujemy wykres lewej strony. Wykresem b˛edzie parabola
o ramionach skierowanych w gór˛e i wierzchołku w punkcie
(
x
w
, y
w
) =
−
b
2a
,
−
∆
4a
=
−
7,
−
28
2
−
4
·
2
·
89
8
=
=
−
7,
−
72
8
= (−
7,
−
9
)
.
Szkicujemy wykres y
= |
2x
2
+
28x
+
89
|
– pami˛etamy o odbiciu cz˛e´sci pod osi ˛
a Ox do góry.
-10
-5
-1
x
-1
+1
+5
+10
y
y=9
Z obrazka wida´c ju ˙z jak b˛edzie wygl ˛
ada´c rozwi ˛
azanie nierówno´sci, musimy jeszcze jed-
Materiał pobrany z serwisu
1

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
nak wyznaczy´c punkty przeci˛ecia paraboli y
=
2x
2
+
28x
+
89 z prost ˛
a y
=
9.
2x
2
+
28x
+
89
=
9
2x
2
+
28x
+
80
=
0
/ : 4
1
2
x
2
+
7x
+
20
=
0
∆
=
49
−
40
=
9
x
= −
7
−
3
= −
10
∨
x
= −
7
+
3
= −
4.
Zatem rozwi ˛
azaniem nierówno´sci jest zbiór
(−
∞,
−
10
i ∪ {−
7
} ∪ h−
4,
+
∞
)
.
Odpowied´z: x
∈ (−
∞,
−
10
i ∪ {−
7
} ∪ h−
4,
+
∞
)
Z
ADANIE
2
(5
PKT
.)
Ci ˛
ag
(
a
1
, a
2
, . . . , a
100
)
jest ci ˛
agiem geometrycznym o ilorazie q
=
1
2
i pierwszym wyrazie
równym a
1
=
√
3. Oblicz sum˛e
a
1
a
2
+
a
2
a
3
+ · · · +
a
99
a
100
.
R
OZWI ˛
AZANIE
Korzystamy ze wzoru a
n
=
a
1
q
n
−
1
na n-ty wyraz ci ˛
agu geometrycznego.
a
1
a
2
+
a
2
a
3
+ · · · +
a
99
a
100
=
=
a
1
·
a
1
q
+
a
1
q
·
a
1
q
2
+
a
1
q
2
·
a
1
q
3
+ · · · +
a
1
q
98
·
a
1
q
99
=
=
a
2
1
q
(
1
+
q
2
+
q
4
+ · · · +
q
196
)
=
a
2
1
q
1
+ (
q
2
)
1
+ (
q
2
)
2
+ · · · + (
q
2
)
98
.
W nawiasie mamy sum˛e 99 wyrazów ci ˛
agu geometrycznego o ilorazie q
2
. Zatem ze wzoru
na sum˛e kolejnych wyrazów ci ˛
agu geometrycznego mamy
a
2
1
q
1
+ (
q
2
)
1
+ (
q
2
)
2
+ · · · + (
q
2
)
98
=
=
a
2
1
q
·
1
− (
q
2
)
99
1
−
q
2
=
3
·
1
2
·
1
−
1
2
198
1
−
1
4
=
=
3
·
1
2
·
4
3
1
−
1
2
198
=
2
1
−
1
2
198
=
=
2
−
1
2
197
.
Odpowied´z: 2
−
1
2
197
Materiał pobrany z serwisu
2

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
3
(5
PKT
.)
Wyznacz wszystkie warto´sci parametru m, dla których równanie x
2
+
mx
+
3
=
0 ma dwa
ró ˙zne pierwiastki rzeczywiste, takie, ˙ze suma ich czwartych pot˛eg jest równa 82.
R
OZWI ˛
AZANIE
Sprawd´zmy kiedy równanie ma dwa pierwiastki rzeczywiste.
0
<
∆
=
m
2
−
12
0
< (
m
−
2
√
3
)(
m
+
2
√
3
)
m
∈ (−
∞,
−
2
√
3
) ∪ (
2
√
3,
+
∞
)
.
Spróbujmy teraz zapisa´c sum˛e czwartych pot˛eg przy pomocy sumy i iloczyny tak, aby móc
skorzysta´c ze wzorów Viète’a.
x
4
1
+
x
4
2
= (
x
2
1
+
x
2
2
)
2
−
2x
2
1
x
2
2
=
(
x
1
+
x
2
)
2
−
2x
1
x
2
2
−
2
(
x
1
x
2
)
2
.
Teraz korzystamy ze wzorów Viète’a.
82
=
m
2
−
6
2
−
2
·
9
0
= (
m
2
−
6
)
2
−
10
2
= (
m
2
−
6
−
10
)(
m
2
−
6
+
10
)
0
= (
m
2
−
16
)(
m
2
+
4
)
m
2
=
16
m
= −
4
∨
m
=
4.
Łatwo sprawdzi´c, ˙ze obie te liczby spełniaj ˛
a warunek z
∆- ˛a.
Odpowied´z: m
= −
4 lub m
=
4
Zadania
.info
Podobają Ci się nasze rozwiązania?
Pokaż je koleżankom i kolegom ze szkoły!
Z
ADANIE
4
(5
PKT
.)
Długo´sci boków prostok ˛
ata ABCD s ˛
a równe:
|
AB
| =
12
√
2 i
|
AD
| =
6. Na odcinku BD
wybrano punkt E w ten sposób, ˙ze
|
AE
| =
4
√
3. Oblicz długo´s´c odcinka DE.
R
OZWI ˛
AZANIE
Sposób I
Materiał pobrany z serwisu
3
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
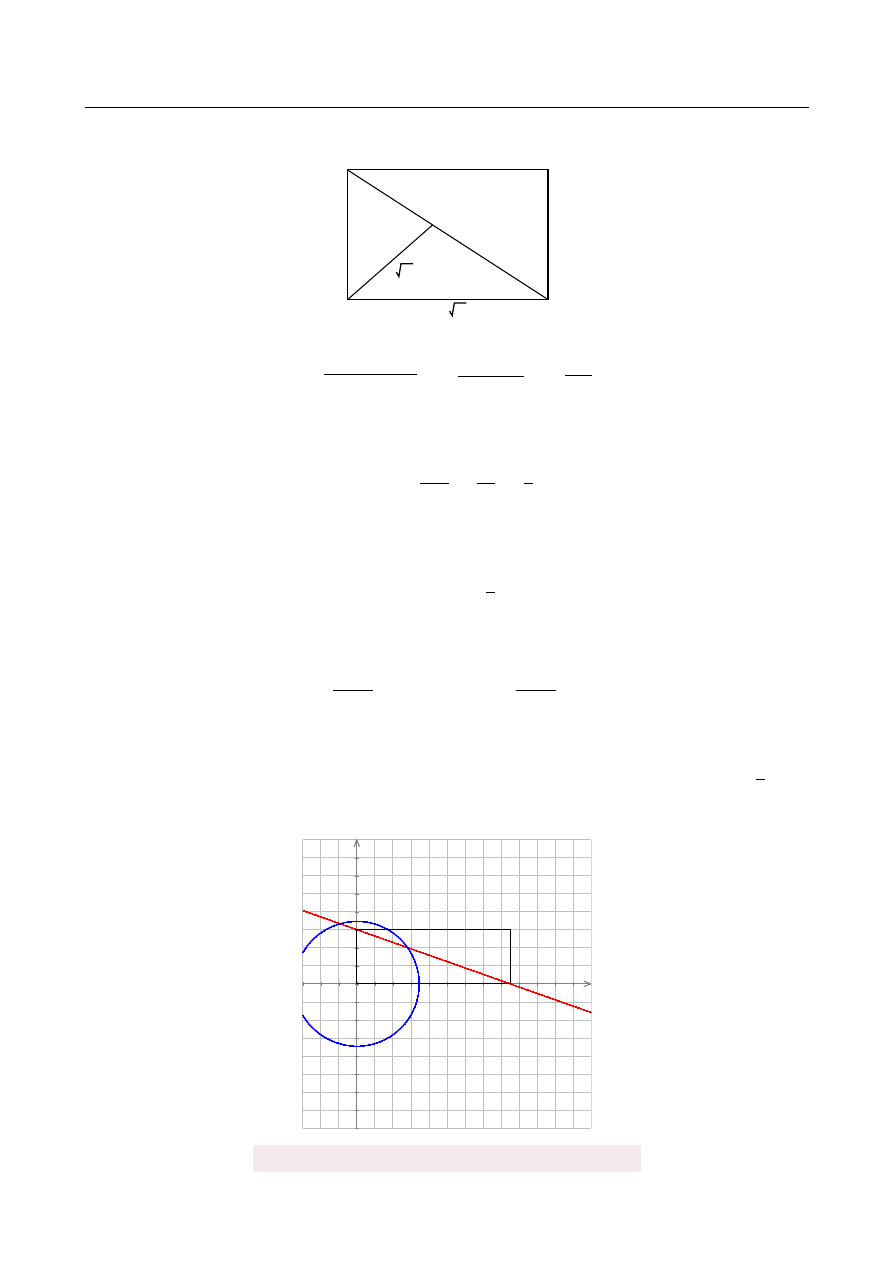
Rozpoczynamy od rysunku.
α
A
B
C
6
D
E
12 2
4 3
x
Obliczmy na pocz ˛
atek długo´s´c przek ˛
atnej.
BD
=
p
AB
2
+
AD
2
=
√
288
+
36
=
√
324
=
18.
Długo´s´c odcinka DE
=
x obliczymy pisz ˛
ac twierdzenie cosinusów w trójk ˛
acie AED. Zanim
to jednak zrobimy zauwa ˙zmy, ˙ze je ˙zeli
]
ADE
=
α
to
cos α
=
AD
BD
=
6
18
=
1
3
.
Piszemy teraz twierdzenie cosinusów w trójk ˛
acie AED.
AE
2
=
AD
2
+
DE
2
−
2
·
AD
·
DE cos α
48
=
36
+
x
2
−
2
·
6
·
x
·
1
3
0
=
x
2
−
4x
−
12
∆
=
16
+
48
=
64
x
=
4
−
8
2
= −
2
∨
x
=
4
+
8
2
=
6.
Zatem DE
=
6.
Sposób II
Umie´s´cmy prostok ˛
at ABCD w układzie współrz˛ednych tak, aby A
= (
0, 0
)
, B
= (
12
√
2, 0
)
, D
=
(
0, 6
)
.
-2
+6
+10
+20
x
-10
-2
+2
+10
y
A
B
C
D
E
Materiał pobrany z serwisu
4

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Co wiemy o punkcie E? – wiemy, ˙ze le ˙zy jednocze´snie na prostej BD i okr˛egu o ´srodku
w A
= (
0, 0
)
i promieniu 4
√
3. Napiszemy wi˛ec równania prostej i okr˛egu i znajdziemy ich
punkty wspólne.
Z okr˛egiem jest łatwo:
x
2
+
y
2
= (
4
√
3
)
2
=
48.
Teraz prosta BD. Szukamy jej w postaci y
=
ax
+
b i podstawiamy współrz˛edne punktów B
i D.
(
0
=
12
√
2a
+
b
6
=
b.
Z pierwszego równania wyliczamy a
12
√
2a
= −
b
= −
6
⇒
a
= −
6
12
√
2
= −
√
2
4
.
Prosta BD ma wi˛ec równanie y
= −
√
2
4
x
+
6. Podstawiamy to wyra ˙zenie do równania okr˛e-
gu.
x
2
+
−
√
2
4
x
+
6
!
2
=
48
x
2
+
1
8
x
2
−
3
√
2x
+
36
=
48
/
·
8
9x
2
−
24
√
2x
−
96
=
0
/ : 3
3x
2
−
8
√
2x
−
32
=
0
∆
=
128
+
384
=
512
= (
16
√
2
)
2
x
=
8
√
2
−
16
√
2
6
<
0
∨
x
=
8
√
2
+
16
√
2
6
=
4
√
2.
Pierwszy pierwiastek odpowiada punktowi, który nie le ˙zy na odcinku BD, wi˛ec x
=
4
√
2 i
y
= −
√
2
4
·
4
√
2
+
6
=
4.
Tak wi˛ec E
= (
4
√
2, 4
)
i
DE
=
q
(
4
√
2
)
2
+ (
4
−
6
)
2
=
√
32
+
4
=
6.
Odpowied´z:
|
DE
| =
6
Z
ADANIE
5
(6
PKT
.)
Rozwi ˛
a ˙z równanie 4 sin 2x
+
9 tg x
=
10 cos x dla x
∈ h
0, 2π
i
.
Materiał pobrany z serwisu
5
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Ze wzgl˛edu na tangens musi oczywi´scie by´c cos x
6=
0. Przekształcamy równanie.
4 sin 2x
+
9 tg x
=
10 cos x
8 sin x cos x
+
9 sin x
cos x
=
10 cos x
/
·
cos x
8 sin x cos
2
x
+
9 sin x
=
10 cos
2
x
8 sin x
(
1
−
sin
2
x
) +
9 sin x
=
10
(
1
−
sin
2
x
)
.
Wida´c, ˙ze mo ˙zemy podstawi´c t
=
sin x.
8t
(
1
−
t
2
) +
9t
=
10
(
1
−
t
2
)
8t
−
8t
3
+
9t
=
10
−
10t
2
8t
3
−
10t
2
−
17t
+
10
=
0.
Teraz trudny moment, bo musimy znale´z´c pierwiastek wymierny tego równania. Najpierw
szukamy w´sród dzielników wyrazu wolnego. Sprawdzaj ˛
ac po kolei mo ˙zna znale´z´c pierwia-
stek t
=
2. Dzielimy teraz równanie przez t
−
2 – my zrobimy to
8t
3
−
10t
2
−
17t
+
10
=
8
(
t
3
−
2t
2
) +
6
(
t
2
−
2t
) −
5t
+
10
=
=
8t
2
(
t
−
2
) +
6t
(
t
−
2
) −
5
(
t
−
2
) =
= (
8t
2
+
6t
−
5
)(
t
−
2
)
.
Rozwi ˛
azanie t
=
2 odpada, bo sin x
6
1, wi˛ec pozostaje równanie
8t
2
+
6t
−
5
=
0
∆
=
36
+
160
=
196
=
14
2
t
=
−
6
−
14
16
= −
20
16
= −
5
4
∨
t
=
−
6
+
14
16
=
8
16
=
1
2
.
Pierwsze rozwi ˛
azanie odpada i otrzymujemy
sin x
=
t
=
1
2
.
W przedziale
h
0, 2π
i
s ˛
a dwa k ˛
aty spełniaj ˛
ace ten warunek: x
=
π
6
i x
=
5π
6
.
Odpowied´z: x
=
π
6
lub x
=
5π
6
Z
ADANIE
6
(5
PKT
.)
Ko ´nce ci˛eciwy AB okr˛egu o równaniu
(
x
+
2
)
2
+ (
y
−
4
)
2
=
25 le ˙z ˛
a na prostej x
−
3y
+
9
=
0.
Oblicz sinus k ˛
ata wypukłego ASB, gdzie S jest ´srodkiem danego okr˛egu.
Materiał pobrany z serwisu
6
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
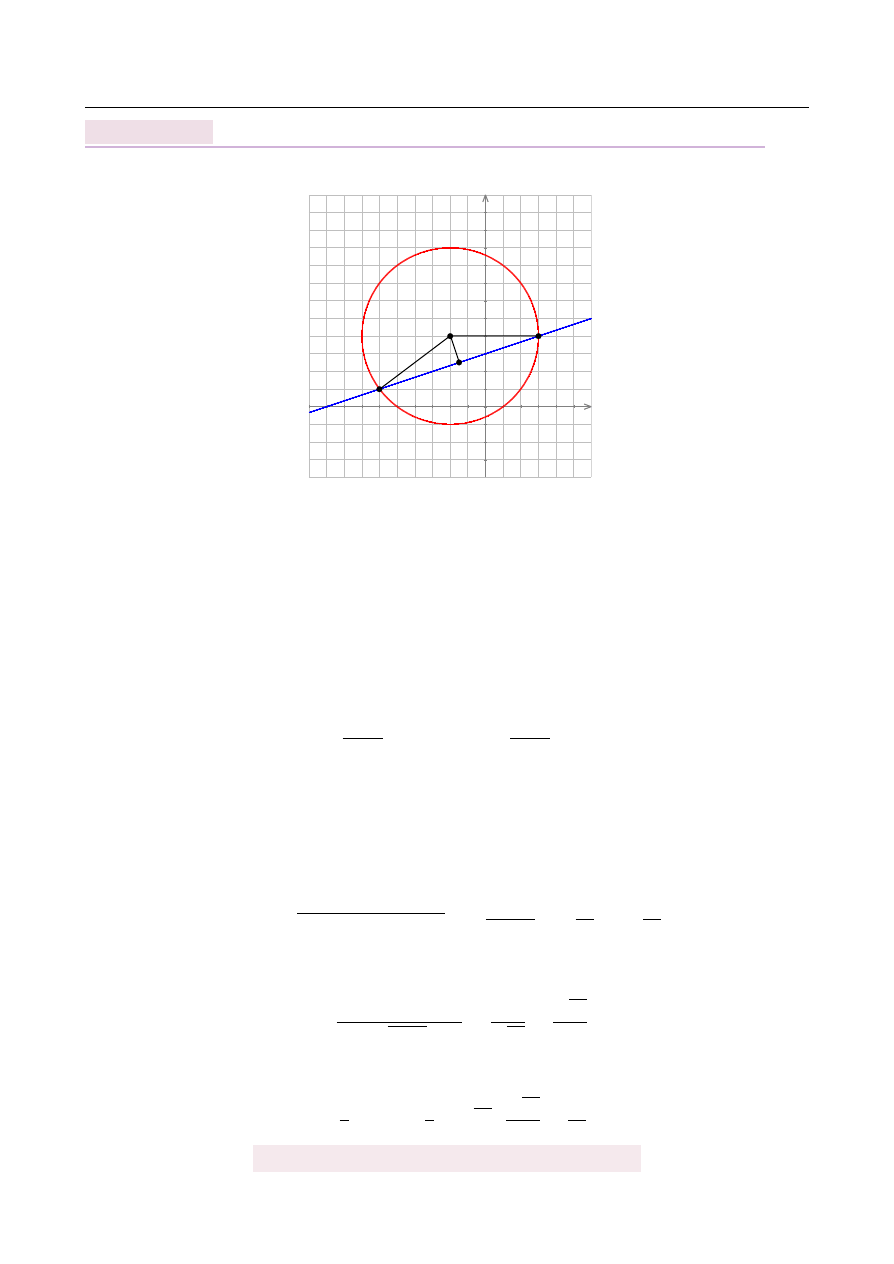
Rozpoczynamy od szkicowego rysunku.
-10
-5
-1
+1
x
-1
+1
+5
+10
y
S
A
B
M
α α
h
5
5
Na pocz ˛
atek wyznaczmy współrz˛edne punktów A i B – podstawiamy x
=
3y
−
9 do
równania okr˛egu.
(
3y
−
9
+
2
)
2
+ (
y
−
4
)
2
=
25
(
3y
−
7
)
2
+ (
y
−
4
)
2
=
25
9y
2
−
42y
+
49
+
y
2
−
8y
+
16
=
25
10y
2
−
50y
+
40
=
0
/ : 10
y
2
−
5y
+
4
=
0
∆
=
25
−
16
=
9
y
=
5
−
3
2
=
1
∨
y
=
5
+
3
2
=
4.
Mamy wtedy odpowiednio x
=
3y
−
9
=
3
−
9
= −
6 i x
=
3y
−
9
=
3. Zatem A
= (−
6, 1
)
i
B
= (
3, 4
)
.
Sposób I
Obliczmy pole trójk ˛
ata ASB ( ˙zeby ze wzoru na pole z sinusem wyliczy´c sin
]
ASB). Jego
podstawa ma długo´s´c
AB
=
q
(
3
+
6
)
2
+ (
4
−
1
)
2
=
√
81
+
9
=
√
90
=
3
√
10.
Wysoko´s´c opuszczona na t˛e podstaw˛e to odległo´s´c punktu S
= (−
2, 4
)
od prostej AB, czyli
h
=
| −
2
−
3
·
4
+
9
|
√
1
+
9
=
5
√
10
=
√
10
2
.
Zatem pole trójk ˛
ata jest równe
P
=
1
2
AB
·
h
=
1
2
·
3
√
10
·
√
10
2
=
15
2
.
Materiał pobrany z serwisu
7
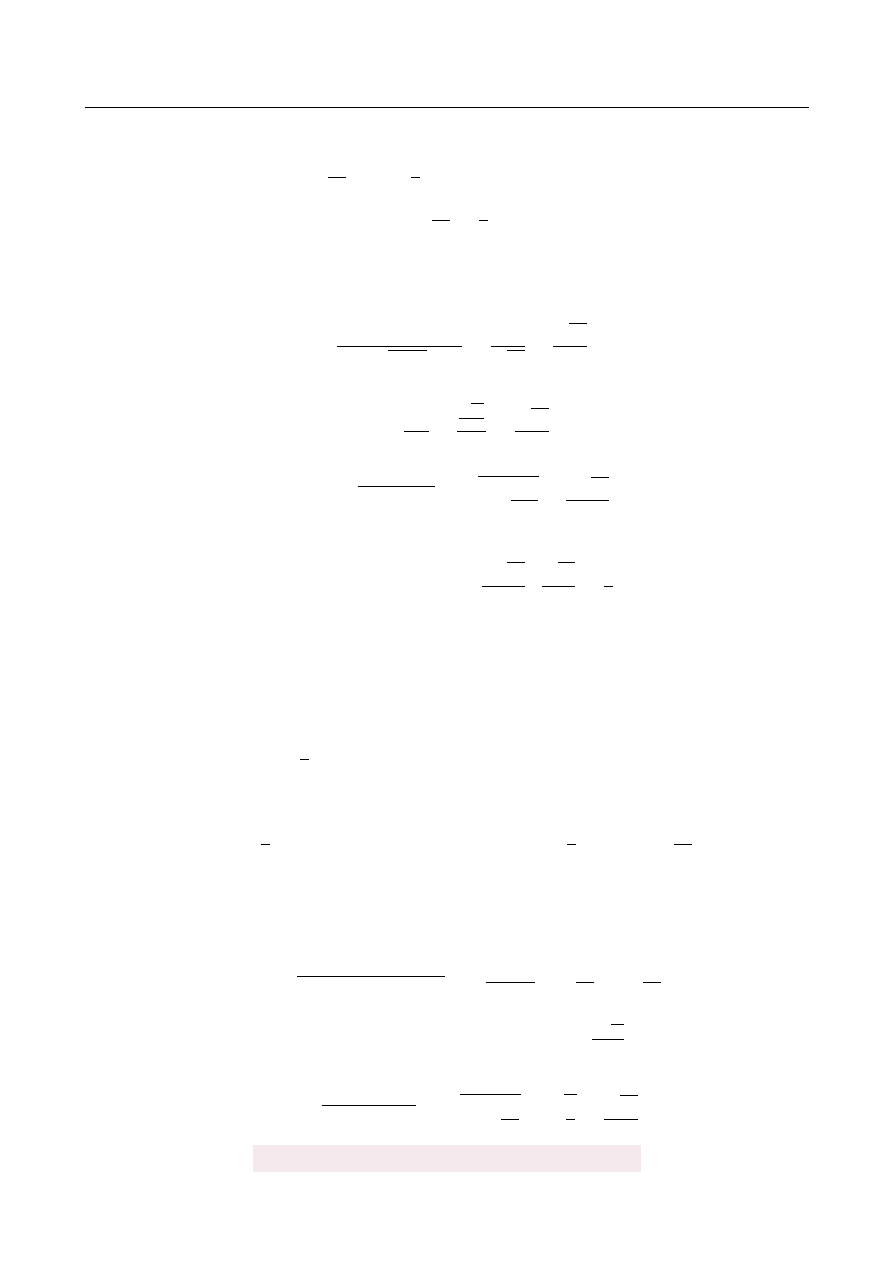
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Teraz korzystamy ze wzoru na pole z sinusem.
15
2
=
P
=
1
2
SA
·
SB
·
sin
]
ASB
sin
]
ASB
=
15
5
2
=
3
5
.
Sposób II
Tak jak w poprzednim sposobie obliczamy odległo´s´c punktu S od prostej AB.
h
=
| −
2
−
3
·
4
+
9
|
√
1
+
9
=
5
√
10
=
√
10
2
.
Mamy zatem
cos α
=
h
AS
=
√
10
2
5
=
√
10
10
.
St ˛
ad
sin α
=
p
1
−
cos
2
α
=
r
1
−
10
100
=
3
√
10
10
.
Teraz pozostało skorzysta´c ze wzoru na sin 2α.
sin 2α
=
2 sin α cos α
=
2
·
3
√
10
10
·
√
10
10
=
3
5
.
Zauwa ˙zmy, ˙ze w tym sposobie nie były nam potrzebne współrz˛edne punktów A i B.
Sposób III
Pole trójk ˛
ata ABS mo ˙zemy obliczy´c ze wzoru na pole trójk ˛
ata o wierzchołkach A
= (
x
A
, y
A
)
,
B
= (
x
B
, y
B
)
i C
= (
x
C
, y
C
)
.
P
ABC
=
1
2
|(
x
B
−
x
A
)(
y
C
−
y
A
) − (
y
B
−
y
A
)(
x
C
−
x
A
)|
.
W naszej sytuacji mamy
P
ABS
=
1
2
|(
3
+
6
)(
4
−
1
) − (
4
−
1
)(−
2
+
6
)| =
1
2
|
27
−
12
| =
15
2
.
Sinus obliczamy jak w poprzednim sposobie.
Sposób IV
Liczymy długo´s´c odcinka AB
AB
=
q
(
3
+
6
)
2
+ (
4
−
1
)
2
=
√
81
+
9
=
√
90
=
3
√
10.
Je ˙zeli wi˛ec przez M oznaczymy ´srodek odcinka AB to AM
=
3
√
10
2
. Dorysujmy wysoko´s´c
SM i oznaczmy
]
ASM
= ]
MSB
=
2α. Na mocy twierdzenia Pitagorasa w trójk ˛
acie AMS
mamy
SM
=
p
AS
2
−
AM
2
=
r
25
−
45
2
=
r
5
2
=
√
10
2
.
Materiał pobrany z serwisu
8

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Mamy wi˛ec
sin α
=
AM
SA
=
3
√
10
2
5
=
3
√
10
10
cos α
=
SM
SA
=
√
10
2
5
=
√
10
10
.
Teraz pozostało skorzysta´c ze wzoru na sin 2α.
sin
]
ASB
=
sin 2α
=
2 sin α cos α
=
2
·
3
√
10
10
·
√
10
10
=
3
5
.
Sposób V
Liczymy długo´s´c odcinka AB
AB
=
q
(
3
+
6
)
2
+ (
4
−
1
)
2
=
√
81
+
9
=
√
90
=
3
√
10.
Teraz korzystamy z twierdzenia cosinusów.
AB
2
=
SA
2
+
SB
2
+
2SA
·
SB cos
]
ASB
AB
2
=
2SA
2
+
2SA
2
cos
]
ASB
AB
2
=
2SA
2
(
1
+
cos
]
ASB
)
90
=
50
(
1
+
cos
]
ASB
)
/ : 50
1
+
cos
]
ASB
=
90
50
=
9
5
cos
]
ASB
=
4
5
.
Zatem
sin
]
ASB
=
p
1
−
cos
2
]
ASB
=
r
1
−
16
25
=
3
5
.
Odpowied´z:
3
5
Z
ADANIE
7
(4
PKT
.)
Wyka ˙z, ˙ze je ˙zeli liczby rzeczywiste a, b, c spełniaj ˛
a równo´s´c a
2
+
b
2
+
c
2
=
ab
+
bc
+
ca to
a
=
b
=
c.
R
OZWI ˛
AZANIE
Przekształcamy dan ˛
a równo´s´c tak, aby otrzyma´c pełne kwadraty.
a
2
+
b
2
+
c
2
=
ab
+
bc
+
ca
/
·
2
2a
2
+
2b
2
+
2c
2
−
2ab
−
2bc
−
2ac
=
0
(
a
2
−
2ab
+
b
2
) + (
b
2
−
2bc
+
c
2
) + (
c
2
−
2ac
+
a
2
) =
0
(
a
−
b
)
2
+ (
b
−
c
)
2
+ (
c
−
a
)
2
=
0.
Je ˙zeli suma kwadratów jest równa 0, to ka ˙zdy ze składników musi by´c zerem, czyli a
=
b i
b
=
c.
Materiał pobrany z serwisu
9
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
8
(4
PKT
.)
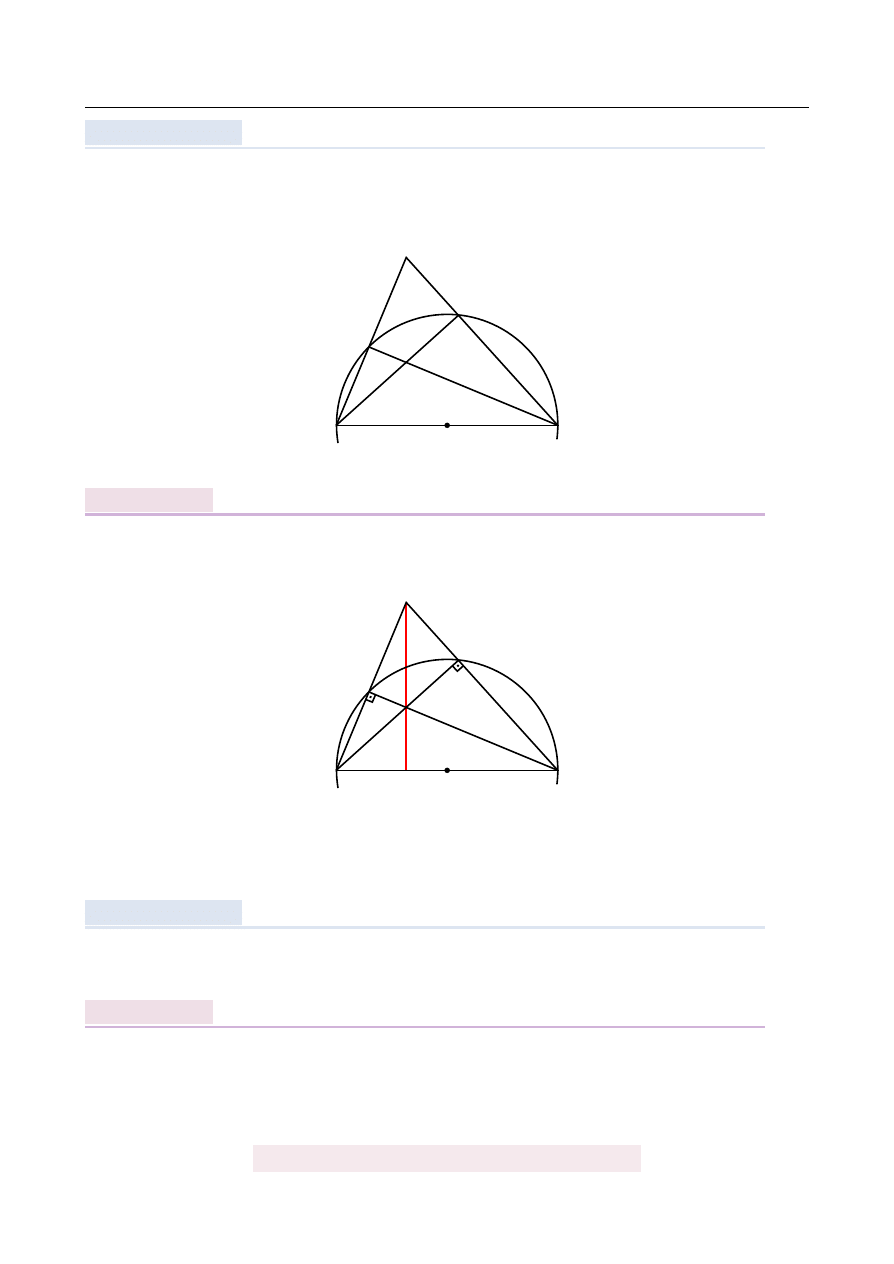
Na okr˛egu o ´srodku S wybrano punkty A, B, C i D w ten sposób, ˙ze prosta AB zawiera punkt
S, a proste AD i BC przecinaj ˛
a si˛e w punkcie E. Punkt M jest punktem wspólnym prostych
AC i BD. Wyka ˙z, ˙ze proste EM i AB s ˛
a prostopadłe.
A
B
E
D
C
M
S
R
OZWI ˛
AZANIE
Zauwa ˙zmy, ˙ze ka ˙zdy z k ˛
atów
]
ACB i
]
ADB jest oparty na ´srednicy, wi˛ec oba te k ˛
aty s ˛
a
proste.
A
B
E
D
C
M
S
To oznacza, ˙ze proste AC i BD s ˛
a wysoko´sciami trójk ˛
ata ABE. Jednak wszystkie trzy wy-
soko´sci w trójk ˛
acie przecinaj ˛
a si˛e w jednym punkcie, wi˛ec prosta EM jest trzeci ˛
a wysoko´sci ˛
a
trójk ˛
ata ABE. Jest wi˛ec ona prostopadła do prostej AB.
Z
ADANIE
9
(5
PKT
.)
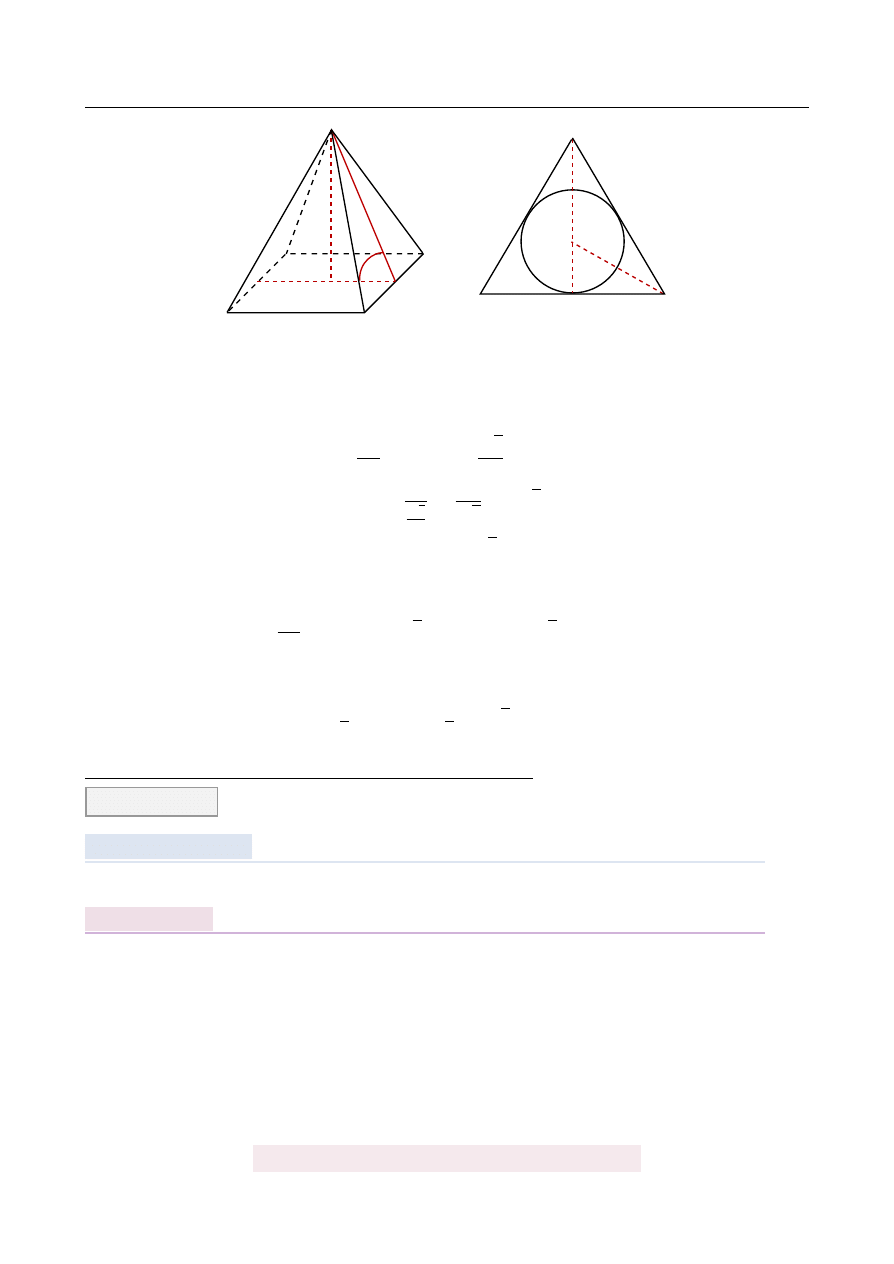
W ostrosłup prawidłowy czworok ˛
atny wpisano kul˛e o promieniu 2. ´Sciana boczna ostrosłu-
pa nachylona jest do płaszczyzny podstawy pod k ˛
atem 60
◦
. Oblicz obj˛eto´s´c tego ostrosłupa.
R
OZWI ˛
AZANIE
Zaczynamy od rysunku.
Materiał pobrany z serwisu
10
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
A
B
C
D
S
F
a
60
o
G
E
S
F
E
30
o
O
2
G
30
o
Podana informacja o promieniu kuli wpisanej w ostrosłup oznacza w szczególno´sci, ˙ze
promie ´n okr˛egu wpisanego w trójk ˛
at GES jest równy 2. To za´s pozwala łatwo wyliczy´c
długo´s´c kraw˛edzi podstawy. Patrzymy na trójk ˛
at FEO.
2
FE
=
tg 30
◦
=
√
3
3
FE
=
2
√
3
3
=
6
√
3
=
2
√
3
AB
=
2FE
=
4
√
3.
Z trójk ˛
ata FES wyliczamy długo´s´c wysoko´sci SF ostrosłupa.
SF
FE
=
tg 60
◦
=
√
3
⇒
SF
=
√
3FE
=
6.
Mo ˙zemy teraz obliczy´c obj˛eto´s´c ostrosłupa.
V
=
1
3
AB
2
·
SF
=
1
3
· (
4
√
3
)
2
·
6
=
96.
Odpowied´z: 96
Z
ADANIE
10
(6
PKT
.)
Ile jest liczb naturalnych siedmiocyfrowych, których suma cyfr jest równa 4?
R
OZWI ˛
AZANIE
Zastanówmy si˛e jaka mo ˙ze by´c najwi˛eksza cyfra liczby siedmiocyfrowej o sumie cyfr równej
4?
Oczywi´scie ˙zadna cyfra nie mo ˙ze by´c wi˛eksza od 4 i je ˙zeli jedn ˛
a z cyfr jest 4, to wszystkie
pozostałe cyfry musz ˛
a by´c zerami. Jest tylko jedna taka liczba: 4000000.
Je ˙zeli najwi˛eksz ˛
a cyfr ˛
a jest 3, to musi by´c jeszcze jedna jedynka i reszta to same zera.
Policzmy ile jest takich liczb. Pierwsz ˛
a cyfr˛e mo ˙zemy wybra´c na dwa sposoby (mo ˙ze to by´c
3 lub 1), a drug ˛
a niezerow ˛
a cyfr˛e mo ˙zemy umie´sci´c na jednej z 6 pozostałych pozycji. Jest
wi˛ec
2
·
6
=
12
Materiał pobrany z serwisu
11

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
takich liczb.
Je ˙zeli najwi˛eksz ˛
a cyfr ˛
a jest 2, to mamy dwie mo ˙zliwo´sci: albo s ˛
a dwie dwójki, albo jedna
dwójka i dwie jedynki. Jest 6 liczb z dwoma dwójkami (pierwsza musi sta´c na pocz ˛
atku, a
druga na jednym z pozostałych 6 miejsc). Policzmy, ile jest liczb z jedn ˛
a dwójk ˛
a i dwoma
jedynkami. Je ˙zeli dwójka jest na pocz ˛
atku, to pozostałe dwie jedynki mo ˙zemy umie´sci´c na
6
2
=
6
·
5
2
=
15
sposobów, jest wi˛ec 15 takich liczb. Je ˙zeli na pocz ˛
atku jest jedynka, to mo ˙zliwych liczb jest
6
·
5
=
30
(wybieramy miejsce dla jedynki i potem dla dwójki).
Ostatnia mo ˙zliwo´s´c to liczby składaj ˛
ace si˛e z czterech jedynek i trzech zer. Jedna jedynka
musi by´c pierwsz ˛
a cyfr ˛
a, a pozostałe 3 mo ˙zemy umie´sci´c na
6
3
=
6
·
5
·
4
2
·
3
=
20
sposobów.
W sumie s ˛
a wi˛ec
1
+
12
+
6
+
15
+
30
+
20
=
84
liczby spełniaj ˛
ace warunki zadania.
Odpowied´z: 84
Materiał pobrany z serwisu
12
Wyszukiwarka
Podobne podstrony:
26 03 11 A
26 03 11 R
2 Zal.11, projektowanie3 26 03 2012
Kardiologia wyklad 03 11 2011
TRENING 03 11 2009 DOLNOŚLĄSKI ZPN
Interna 26.03.2014, weterynaria, 4 rok, notatki 2014
pn 14 03 11 łożysko konia
dp 589 wstrzas2012 (czyli 2014 03 11)
2 Zal.12b, projektowanie3 26 03 2012
2003 03 11
5 krajoznawstwo (26.03.2011 r.), Krajoznastwo WSHGIT
wykład 13 - 26.03.2009, FARMACJA, ROK 5, TPL 3, Zachomikowane
26 03 2011
03 11 2013 Choroba wysokościowa
ppst wykład 3 (26 03) w p
więcej podobnych podstron