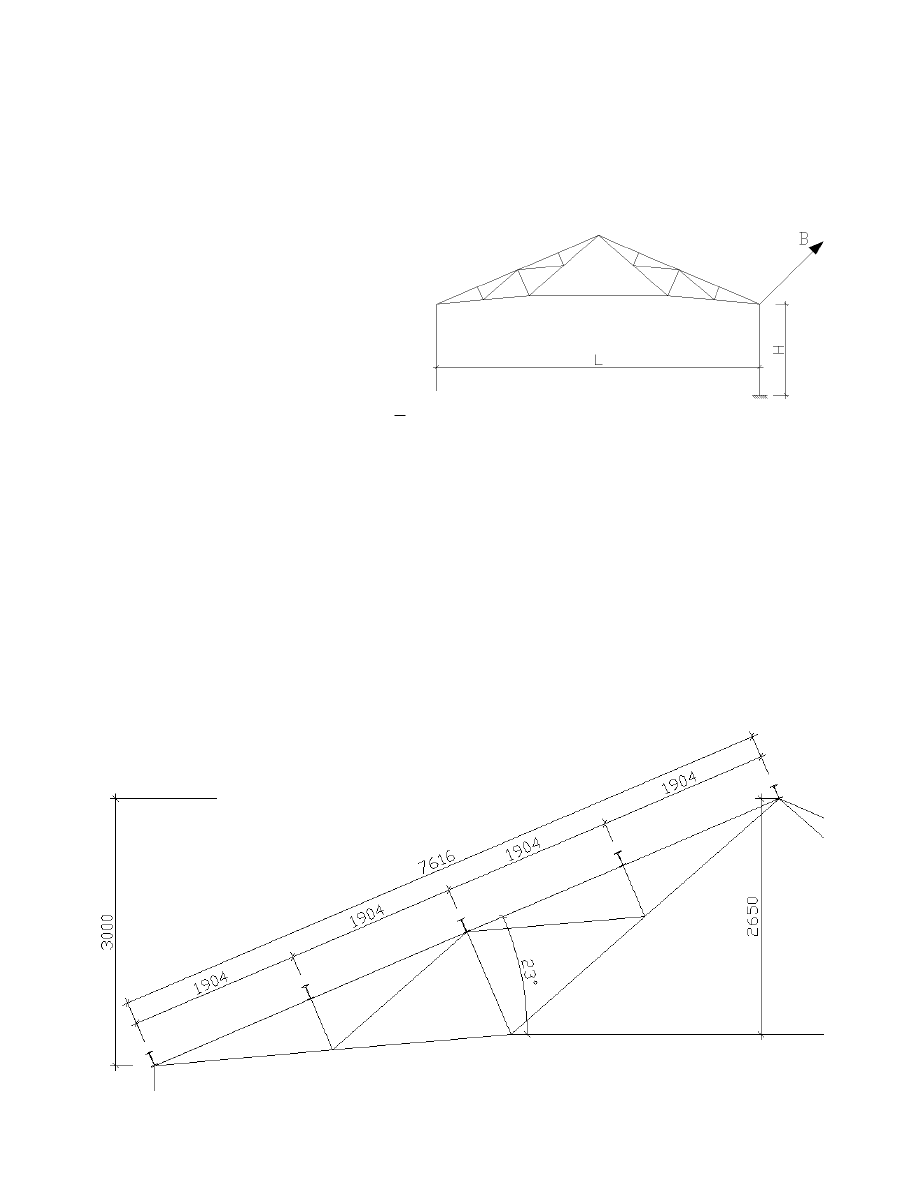
Projekt dachu hali o konstrukcji stalowej

Założenia projektowe:

rozpiętość nawy (szerokość
budynku):

L

14.0

m

=

podłużny rozstaw słupów:

e

5.0

m

=

całkowita długość budynku:

B

10

e

⋅

50

m

⋅

=

=

wysokość słupa

(przyjęto)

:

h

4.0

m

=

wysokość w okapie:

ho

h

4

m

=

=

rozstaw ram:

e

5

m

=

rozstaw rygli

(przyjęto)

:

ar

h

4

1

m

=

=

strefa obciążenia śniegiem:

I

strefa obciążenia wiatrem:

I

Wstępny dobór wymiarów dźwigara kratowego:

wysokość w kalenicy

•

dźwigara:

hk

3.0

m

=

nachylenie połaci dachowej:

αd

23

deg

=

rozstaw płatwi:

a

1.904

m

=

wysokość od okapu do kalenicy:

hok

hk

3

m

=

=

1

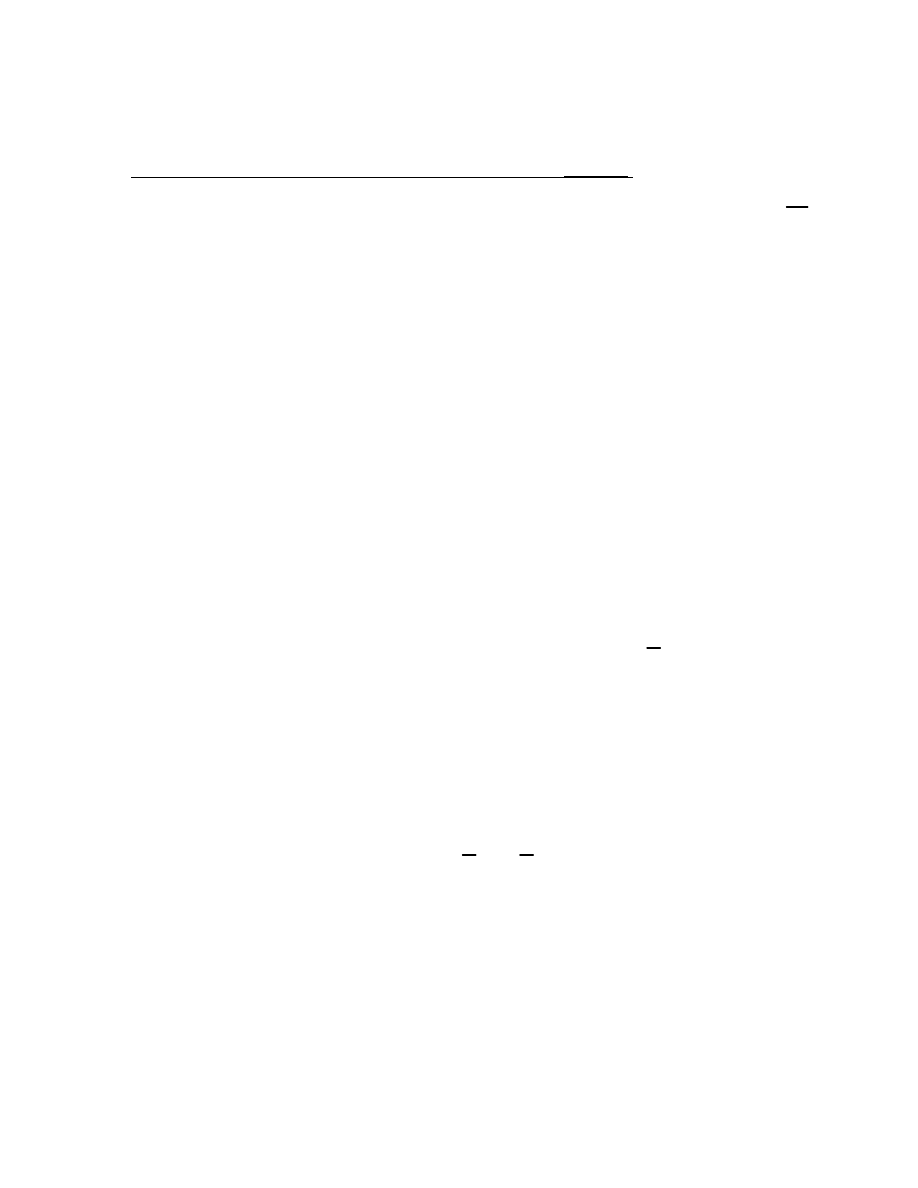
wysokość hali w kalenicy:

H

h

hok

+

7

m

=

=

Gatunek stali z której są wykonane elementy konstrukcji S235JR :

Granica plastyczności stali:

fy

235

MPa

=

G

80.770

GPa

8.077

10

7

×

kN

m

2

⋅

=

=

Wytrzymałość stali na rozciąganie

fu

410

MPa

=

Moduł sprężystości:

E

210

GPa

=

1. Zestawienie obciążeń

1.1. Oddziaływania zmienne

1.1.1. Obciażenie wiatrem

Obliczenia przeprowadzono na podstawie normy PN-EN 1991-1-4:

•

Eurokod 1 Oddziaływania na konstrukcje. Część 1-4: Oddziaływania ogólne -
Oddziaływania wiatru

Bazowa prędkość wiatru

•

Rozpatrywany obiekt znajduje się w I strefie obciążenia wiatrem na wysokości nie
przekraczającej 300 m n.p.m

vb.0

22

m

s

=

wartość podstawowa bazowej prędkości wiatru:

przyjęto najbardziej niekorzystny współczynnik
kierunkowy wiatru:

cdir

1.0

=

cseason

1.0

=

współczynnik sezonowy:

bazowa prędkość wiatru:

vb

cdir cseason

⋅

vb.0

⋅

1.0 1.0

⋅

22

m

s

⋅

⋅

=

22

m

s

=

=

Wysokość odniesienia

•

Budynek którego wysokość H jest mniejsza niż B, należy traktować jako jedną część o
wysokości odniesienia równej:

ze

H

7

m

=

=

Kategoria terenu

•

2

Przyjęto, że teren odpowiada kategorii II, więc zgodnie z normą:

z0

0.05

m

=

zmin

2

m

=

Wartość charakterystycznego szczytowego ciśnienia prędkości wiatru

•

współczynnik turbulencji:

k1

1.0

=

współczynnik rzeźby terenu:

c0

1.0

=

intensywność turbulencji:

Iv

k1

c0 ln

ze
z0













⋅

0.202

=

=

współczynnik chropowatości:

z

ze

7

m

=

=

cr

z

10













0.17

0.941

=

=

średnia prędkość wiatru:

vm

cr c0

⋅

vb

⋅

20.706

m

s

=

=

wartość charaterystyczna szczytowego ciśnienia
prędkości wiatru:

q

1.25

kg

m

3

=

qp

1

7

Iv

+

(

)

0.5

⋅

q

⋅ v

m

2

⋅

1

7 0.202

⋅

+

(

)

0.5

⋅

1.25

kg

m

3

⋅

⋅

20.706

m

s

⋅









2

⋅

=

0.647

kN

m

2

⋅

=

=

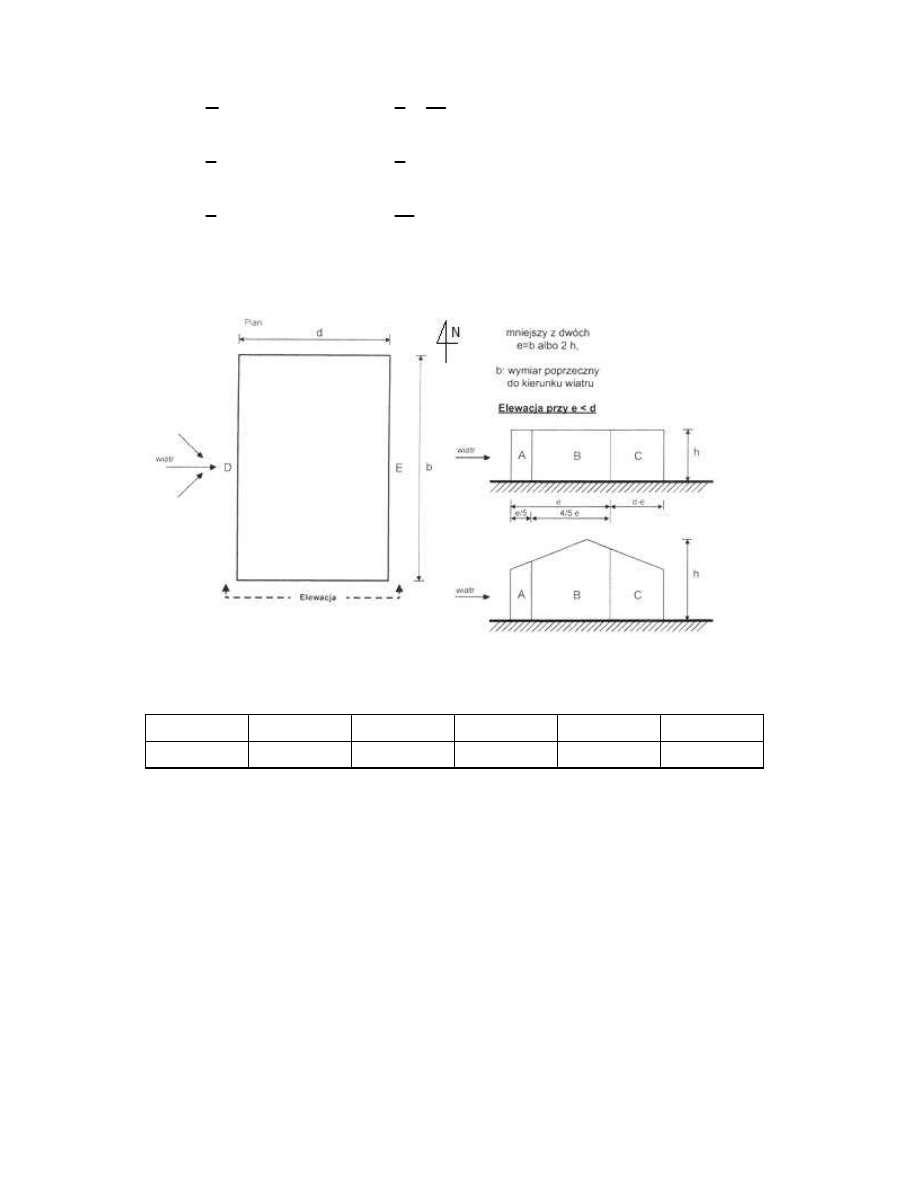
Współczynniki ciśnienia zewnętrznego w przypadku wiatru wiejącego prostopadle do

•

budynku (Θ = 0

o

)

Ściany pionowe:

e = min(b = B ; 2 * h) = min (50,0m ; 2 * 7,00m) = 14,00 m = d = L = 14,0m

e

14.00

m

=

Proporcje budynku

d

L

14

m

=

=

3

H

d

0.5

=

d

2

e

10

−

5.6

m

=

e

5

2.8

m

=

e

4

3.5

m

=

4

5

e

⋅

11.2

m

=

e

10

1.4

m

=

d

e

−

0

m

=

Wartość współczynników ciśnienia zewnętrznego dla ścian pionowych

Pole

A

B

C

D

E

c

pe,10

-1,2

-0,8

-0,5

0,75

-0,4

Dach dwuspadowy:

4

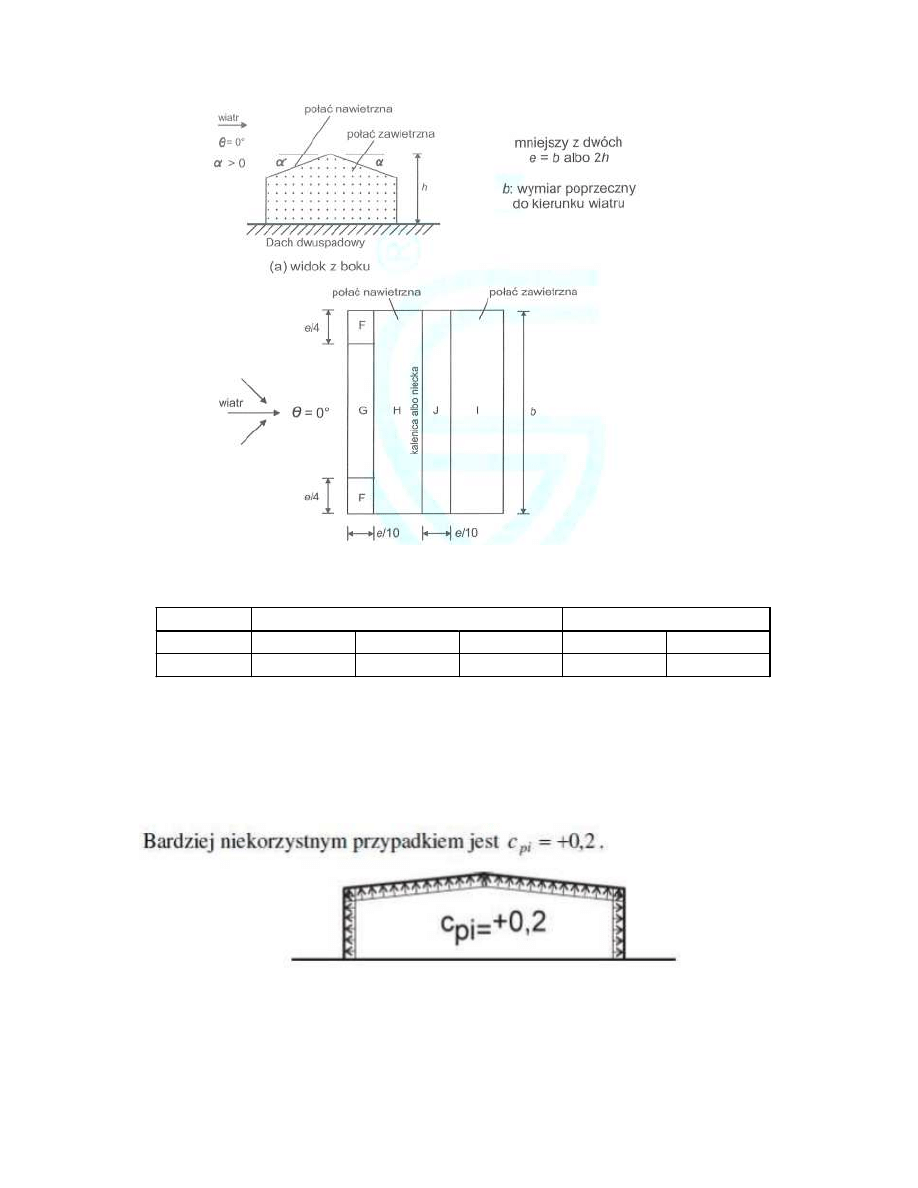
Wartość współczynników ciśnienia zewnętrznego dla połaci

αd

23

deg

⋅

=

Połać nawietrzna

Połać zawietrzna

Pole

F

G

H

I

J

c

pe,10

-0,7

-0,65

-0,25

-0,4

-0,75

Współczynniki ciśnienia wewnętrznego w przypadku wiatru wiejącego prostopadle do

•

budynku

Przyjęto bardziej niekorzystną wartość współczynnika ciśnienia wewnętrznego,
powiekszającą ssanie na połaci dachu.

cpi

0.20

=

ODDZIAŁYWANIE WIATRU

Oddziaływanie wiatru wiejącego prostopadle do budynku

5

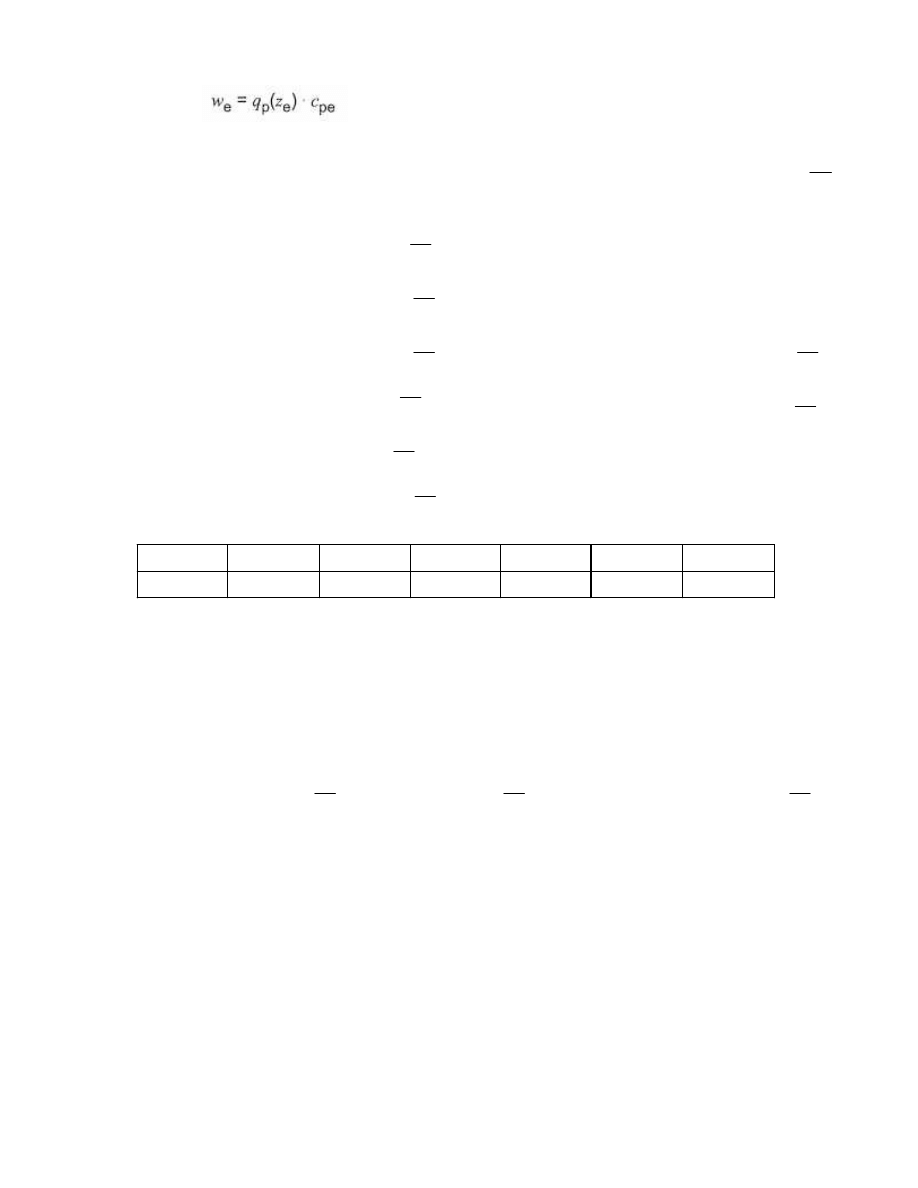
(5.1)

Przyjmując oddziaływanie wiatru bierzemy pod uwagę rozstaw płatwi/rygli

qp

0.647

kN

m

2

⋅

=

we

qp ze

( )

cpe cpi

+

(

)

⋅

a

⋅

=

cpe

rozstaw płatwi:

a

1.904

m

=

we.D

Cpe.0.D cpi

+

(

)

qp ar

⋅

0.615

kN

m

⋅

=

=

rozstaw rygli:

ar

1

m

=

we.G

Cpe.0.G cpi

−

(

)

qp a

⋅

1.047

−

kN

m

⋅

=

=

we.H

Cpe.0.H cpi

−

(

)

qp a

⋅

0.554

−

kN

m

⋅

=

=

we.A

Cpe.0.A cpi

+

(

)

qp ar

⋅

0.647

−

kN

m

⋅

=

=

we.I

Cpe.0.I cpi

−

(

)

qp a

⋅

0.493

−

kN

m

⋅

=

=

we.B

Cpe.0.B cpi

+

(

)

qp ar

⋅

0.388

−

kN

m

⋅

=

=

we.J

Cpe.0.J cpi

−

(

)

qp a

⋅

1.17

−

kN

m

⋅

=

=

we.E

Cpe.0.E cpi

−

(

)

qp ar

⋅

0.388

−

kN

m

⋅

=

=

Pole

D

G

H

I

J

E

w

e,0

0,615

- 1,047

- 0,554

- 0,493

- 1,17

- 0,388

Pole "F" pomija się przy rozpatrywaniu ramy w środkowej części hali

Z uwagi, że pole G występuję tylko na skraju dachu na odcinku e/10 = 1,4m
do obliczeń bierzemy pole H jako najbardziej obciążone

wiatr parcie

we.D

0.615

kN

m

⋅

=

we.H

0.554

−

kN

m

⋅

=

wiatr ssanie

we.E

0.388

−

kN

m

⋅

=

6

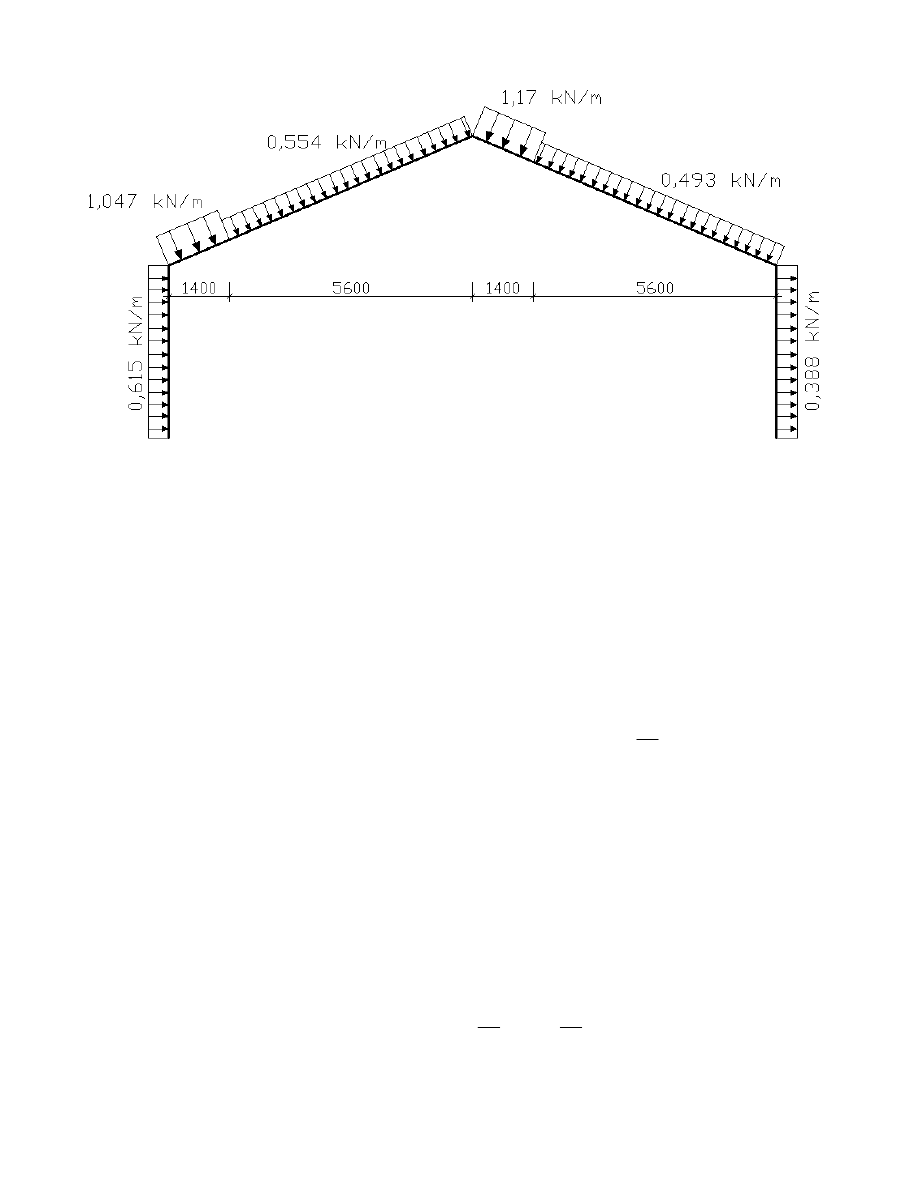
1.1.2. Obciażenie śniegiem

Obliczenia przeprowadzono na podstawie normy PN-EN 1991-1-3:

•

Eurokod 1 Oddziaływania na konstrukcje. Część 1-3: Oddziaływania ogólne - Obciążenie
śniegiem

Rozpatrywany obiekt znajduje się w I strefie obciążenia śniegiem gruntu, na terenie

•

normalnym, na którym nie występuje znaczące przenoszenie śniegu przez wiatr na
budowlę z powodu ukształtowania, terenu, innych budowli lub drzew

wartość charakterystyczna obciążenia śniegiem
gruntu:

sk

0.7

kN

m

2

=

współczynnik kształtu dachu dla nachylenia
połaci dachu 0

o

< α < 30

o

:

μ1

0.8

=

współczynnik ekspozycji:

Ce

1.0

=

współczynnik termiczny:

Ct

1.0

=

Obciążenie charakterystyczne powierzchniowe

•

Oddziaływanie śniegu zostało zebrane na wewnętrzną ramę budynku:

sch

μ1 Ce Ct

⋅

(

)

⋅

sk

⋅

0.8 1.0 1.0

⋅

⋅

0.7

kN

m

2

⋅

⋅

=

0.56

kN

m

2

⋅

=

=

Obciążenie obliczeniowe powierzchniowe

•

7

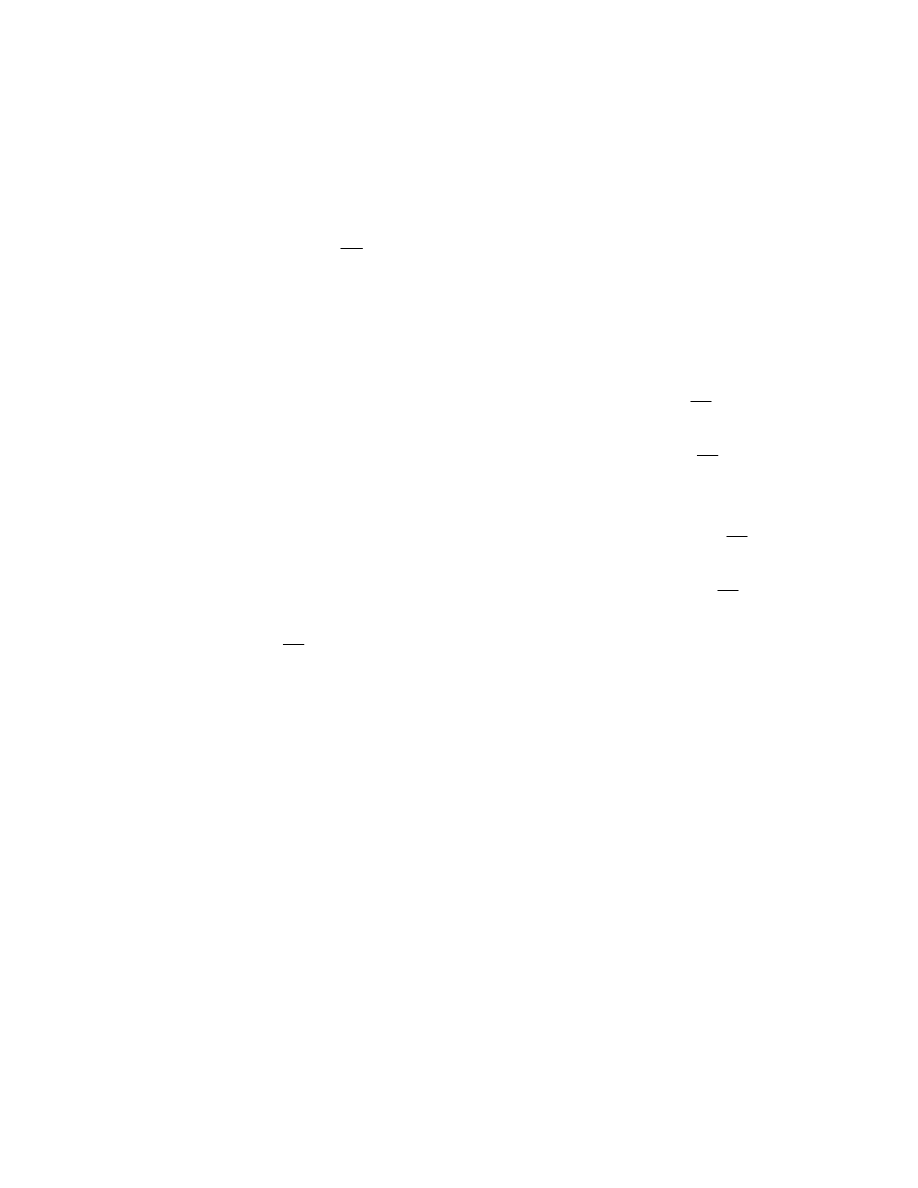
Obciążenie obliczeniowe powierzchniowe

Współczynnik obliczenbiowy dla obciążenia śniegiem zgodnie z normą wynosi:

γs

1.5

=

a więc wartość obliczeniowa obciążenia śniegiem jest równa:

so

sch γs

⋅

0.84

kN

m

2

⋅

=

=

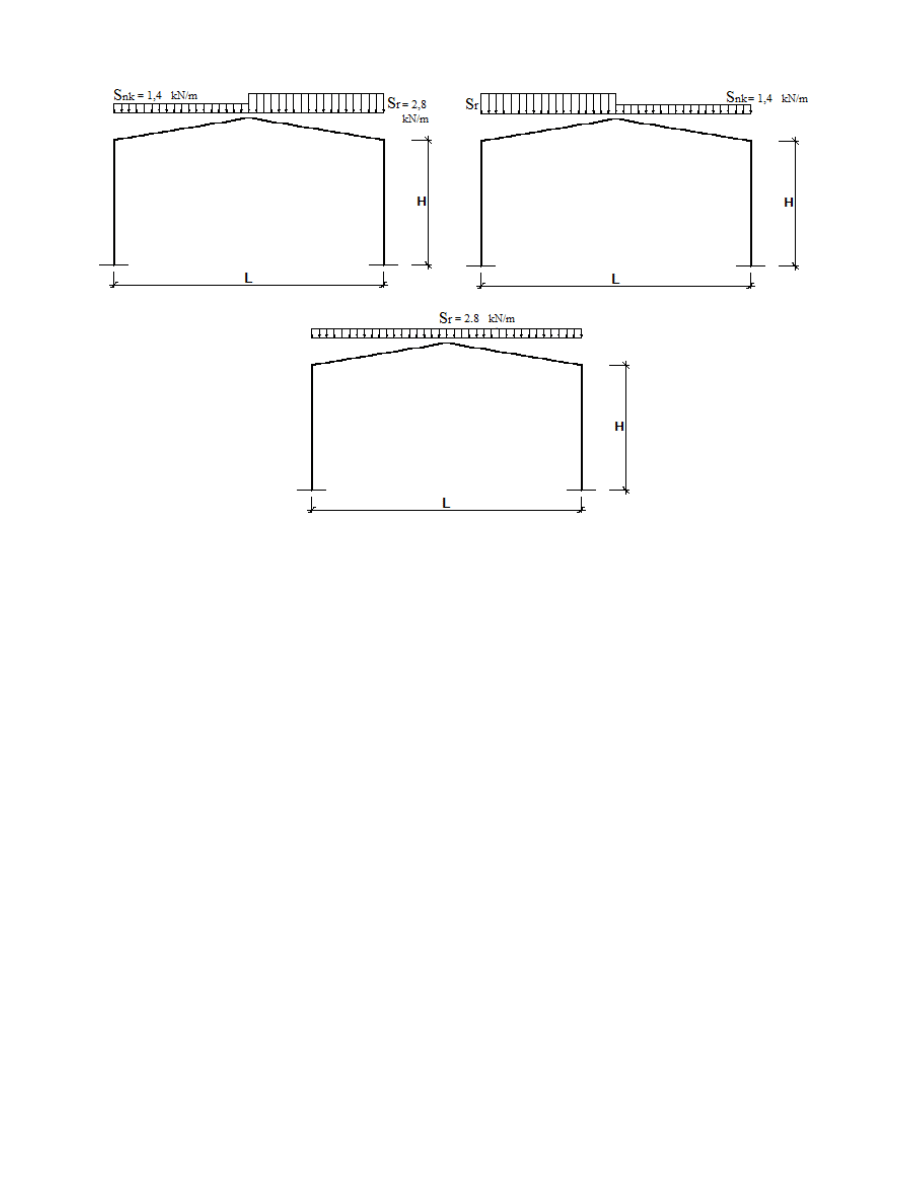
Obciążenie połaci zewnętrznych - dla dachu dwuspadowego stosuje się dwa przypadki

•

obciążeń

Przypadek I - równomierne obciążenie śniegiem

równomierne obciążenie śniegiem

.
.

zebrane z fragmentu połaci przy okapie

sr

sch e

⋅

2.8

kN

m

⋅

=

=

sro

0.5sr

1.4

kN

m

⋅

=

=

Przypadek II - nierównomierne obciążenie śniegiem

(dwa warianty lustrzane)

nierównomierne obciążenie śniegiem

.
.

zebrane z fragmentu połaci przy okapie

snk

0.5 sch

⋅

e

⋅

1.4

kN

m

⋅

=

=

snko

0.5snk

0.7

kN

m

⋅

=

=

sr

2.8

kN

m

⋅

=

gdzie:

e

5

m

=

- rozstaw ram

8

9

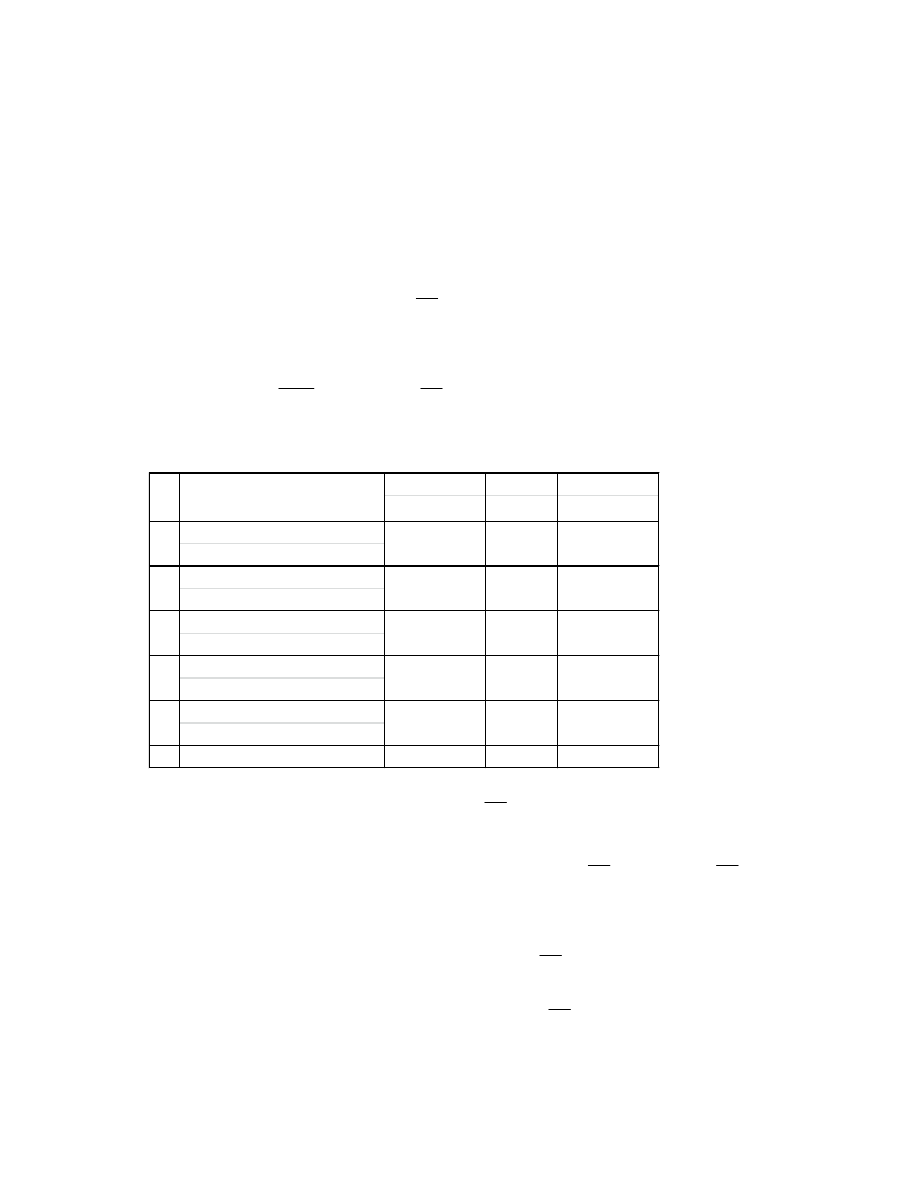
1.2.2. Oddziaływania stałe

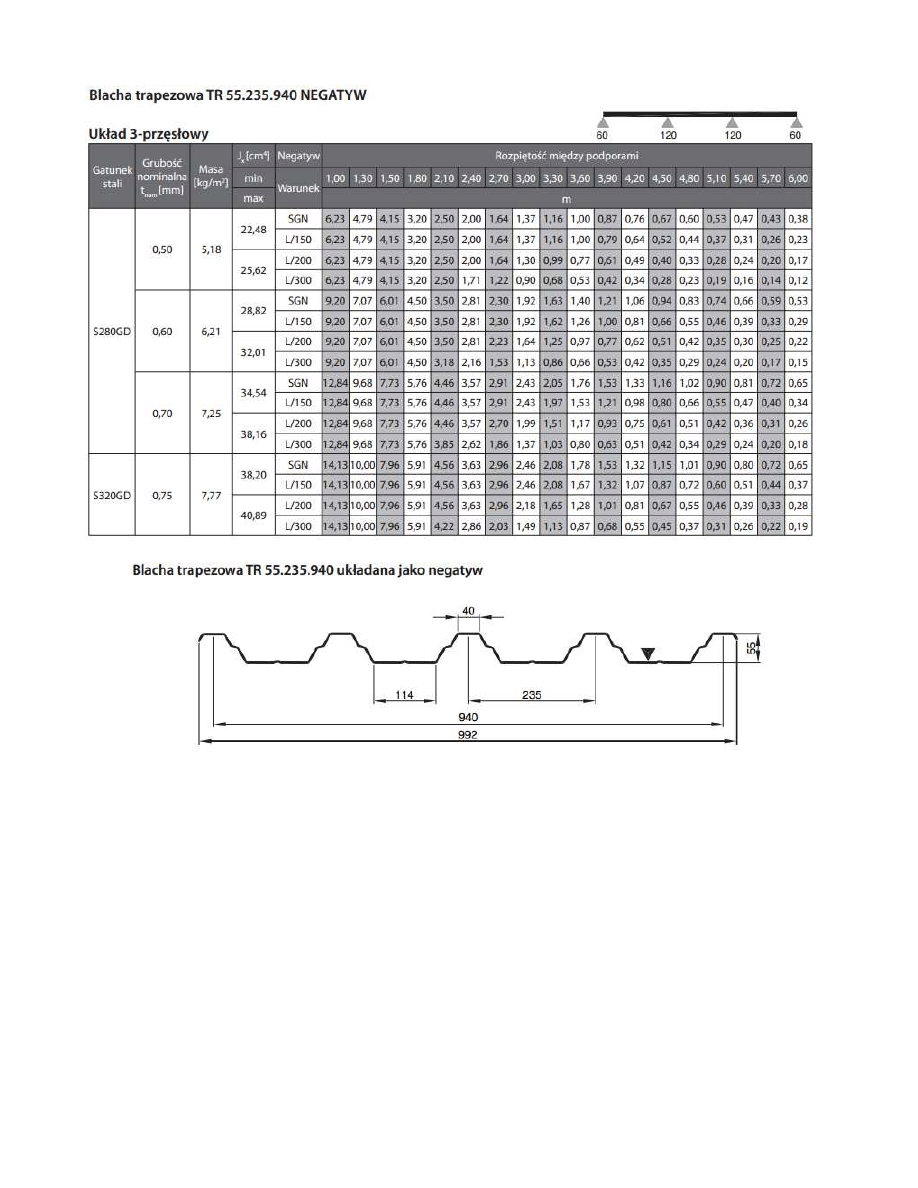
1.2.2.1. Dobór pokrycia dachowego

Najniekorzystniejsze obciążenie od śniegu i wiatru działające na pokrycie dachowe

a

1.904

m

=

rozstaw płatwi

śnieg równomierny:

qśnieg

so cos αd

( )

⋅

0.773

kN

m

2

⋅

=

=

ssanie wiatru

qwiatr

we.H

a

1.5

⋅

0.437

−

kN

m

2

⋅

=

=

Zestawienie obciążeń stałych - wstępnie przyjęto blachę trapezową T55x750x0,88

Obc. charakt. współcz.

Obc. obl.

[kN/m

2

]

bezpiecz

[kN/m

2

]

Blacha trapezowa
T55x750x0,88
Folia paroizolacyjna
0,2 mm
Wełna mineralna twarda
12 cm
Papa podkładowa

Papa nawierzchniowa termiczna

5,2 mm

SUMA

0,219

-

0,295

0,107

Lp.

Rodzaj obciążenia

1

2

5

0,049

0,040

0,022

0,001

3

4

1,35

1,35

1,35

1,35

1,35

0,144

0,001

0,029

0,054

0,066

wartość charakterystyczna

gdach.

0.219

kN

m

2

=

wartość obliczeniowa

gdach

gdach.

1.35

⋅

0.219

kN

m

2

⋅

1.35

⋅

=

0.296

kN

m

2

⋅

=

=

Suma obciążeń

(wart. obliczeniowe)

na połać dachową:

parcie -

qśnieg gdach

+

1.069

kN

m

2

⋅

=

ssanie -

qwiatr gdach

+

0.141

−

kN

m

2

⋅

=

Ostatecznie dobrano: Blacha trapezowa TR 55.235.940 NEGATYW

10

11

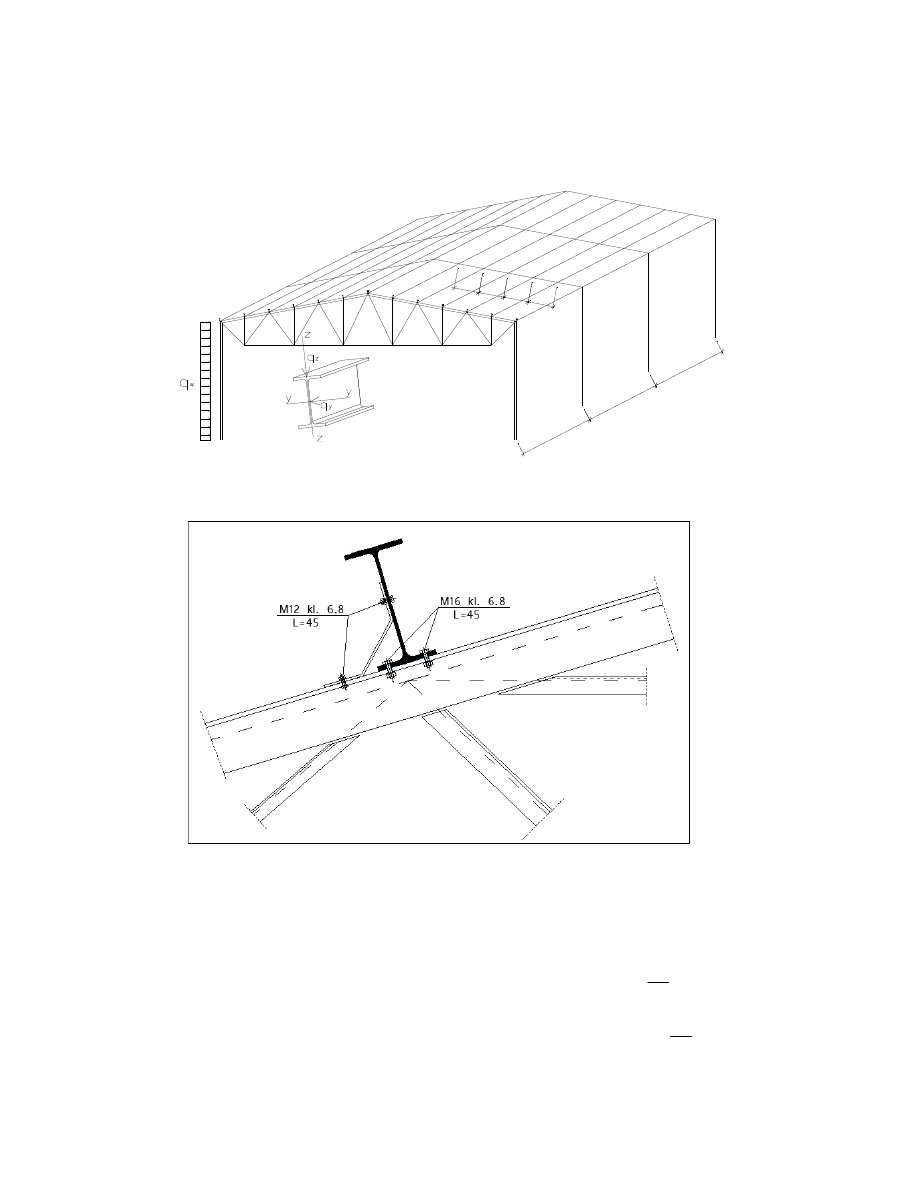
2. Dobór płatwi dachowej

2.1. Założenia oraz wyznaczenie sił wewnętrzych występujących w płatwi

a

a

s

a

s

a

s

a

a

a

rozpiętość płatwi

.

rozstaw płatwi

as

e

5

m

=

=

a

1.904

m

=

Rys. po łączenia płatwi z wiąz are m

Obciążenie płatwi

•

Obciążenie stałe:

gp

0.158

kN

m

=

ciężar własny płatwi

(przyjęto IPE160)

ciężar pokrycia dachowego

gdach

0.296

kN

m

2

⋅

=

12

Obciążenie zmienne:

obciążenie wiatrem

qwiatr

0.437

−

kN

m

2

⋅

=

obciążenie śniegiem

so

0.84

kN

m

2

⋅

=

Obciążenia działające na płatew:

•

siła działająca względem osi y

qzd

qwiatr a

⋅

gdach a

⋅

gp

+

(

)

1.35

⋅

so a

⋅

+





cos

αd

( )

⋅

+

1.537

kN

m

⋅

=

=

wart.obliczeniowa

qzk

qwiatr a

⋅

(

)

1.5

gdach a

⋅

gp

+

sch a

⋅

+

(

)

cos

αd

( )

⋅

+

1.091

kN

m

⋅

=

=

wart.charakterystyczna

qzdS

gdach a

⋅

gp

+

(

)

1.35

⋅





cos

αd

( )

⋅

0.896

kN

m

⋅

=

=

od obc. stałego - wartość obliczeniowa

od obc. zmiennego - wartość obliczeniowa

qzdZ

qwiatr a

⋅

so a

⋅

( )

cos

αd

( )

⋅

+

0.641

kN

m

⋅

=

=

qzdZś

so a

⋅

( )

cos

αd

( )

⋅

1.472

kN

m

⋅

=

=

od obc. śniegiem - wartość obliczeniowa

od obc. stałego -
- wartość charakterystyczna

od obc. zmiennego -
- wartość charakterystyczna

qzkS

gdach a

⋅

gp

+

(

)

cos

αd

( )

⋅

0.664

kN

m

⋅

=

=

qzkZ

qwiatr a

⋅

(

)

1.5

sch a

⋅

(

)

cos

αd

( )

⋅

+

0.427

kN

m

⋅

=

=

qzkZś

sch a

⋅

(

)

cos

αd

( )

⋅

0.981

kN

m

⋅

=

=

od obc. śniegiem -
- wartość charakterystyczna

Ponieważ oddziaływanie wiatru pomniejsza max. siły wewnętrze nie bierzemy
wiatru pod uwagę:

qzd

gdach a

⋅

gp

+

(

)

1.35

⋅

so a

⋅

+





cos

αd

( )

⋅

2.368

kN

m

⋅

=

=

wart.obliczeniowa
bez wiatru

qzk

gdach a

⋅

gp

+

sch a

⋅

+

(

)

cos

αd

( )

⋅

1.645

kN

m

⋅

=

=

wart.charakterystyczna
bez wiatru

siła działająca względem osi z

13

qyd

gdach a

⋅

gp

+

(

)

1.35

⋅

so a

⋅

+





sin

αd

( )

⋅

1.005

kN

m

⋅

=

=

wart.obliczeniowa

qyk

gdach a

⋅

gp

+

(

)

sch a

⋅

+





sin

αd

( )

⋅

0.698

kN

m

⋅

=

=

wart.charakterystyczna

qydS

gdach a

⋅

gp

+

(

)

1.35

⋅





sin

αd

( )

⋅

0.38

kN

m

⋅

=

=

od obc. stałego - wartość obliczeniowa

od obc. zmiennego - wartość obliczeniowa

qydZ

so a

⋅

( )

sin

αd

( )

⋅

0.625

kN

m

⋅

=

=

od obc. stałego -
- wartość charakterystyczna

od obc. zmiennego -
- wartość charakterystyczna

qykS

gdach a

⋅

gp

+

(

)

sin

αd

( )

⋅

0.282

kN

m

⋅

=

=

qykZ

sch a

⋅

(

)

sin

αd

( )

⋅

0.417

kN

m

⋅

=

=

Sprawdzenie nośności na zginanie:

MEd

qzd as

2

⋅

8

2.368

kN

m

⋅

5

m

⋅

(

)

2

⋅

8

=

7.4

kN m

⋅

⋅

=

=

MEd

Wy

fy

≤

Wy.potrz

MEd

fy

≥

7.4

kN

⋅

m

⋅

235

MPa

⋅

=

31.489

cm

3

⋅

=

Jako płatew przyjęto wstępnie IPE160, którego charakterystyka geometryczna jest
następująca:

A

20.1

cm

2

=

Wpl.y

124

cm

3

=

Wy

109

cm

3

=

>

Wy.potrz

31.489

cm

3

⋅

=

h

16

cm

=

Wpl.z

26.1

cm

3

=

bw

8.2

cm

=

Iy

869

cm

4

=

tw

0.50

cm

=

Iz

68.3

cm

4

=

tf

0.74

cm

=

Iw

3960

cm

6

=

r

0.9

cm

=

It

3.6

cm

4

=

Wstępne sprawdzenie ugięcia:

14

unet.fin

as

200

5

m

⋅

200

=

25

mm

⋅

=

=

uinst

5

384

qzk as

4

⋅

E Iy

⋅

⋅

5

384

1.645

kN

m

⋅

5

m

⋅

(

)

4

⋅

210

GPa

⋅

869

cm

4

⋅

⋅

⋅

=

7.336

mm

⋅

=

=

uinst

7.336

mm

⋅

=

<

unet.fin

25

mm

⋅

=

Warunek spełniony

przyjęto IPE160

Siły wewnętrzne występujące w płatwi

(obliczenia przeprowadzono w programie SOLDIS

•

Siły wewnętrzne od obciążeń prostopadłych do osi z płatwi

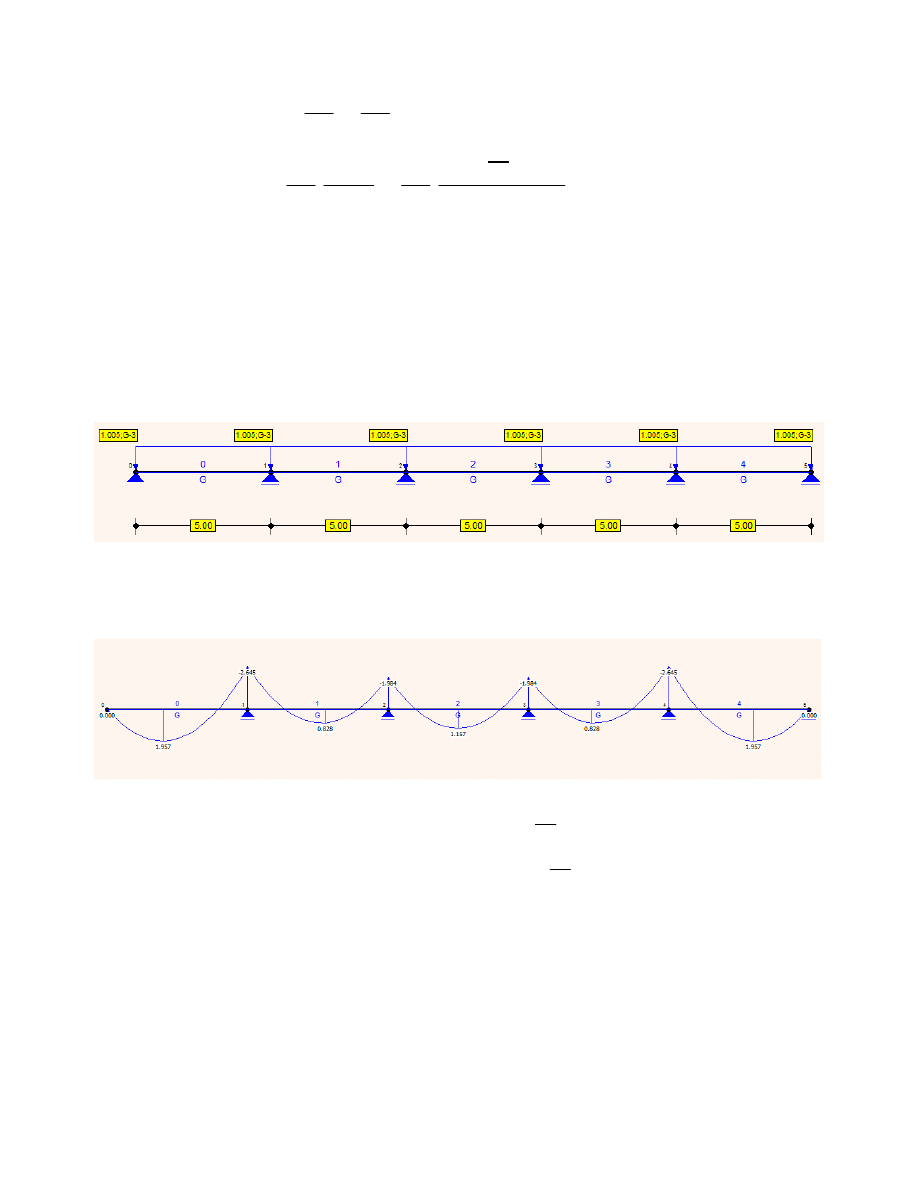
Schemat statyczny płatwi jako belki ciągłej

schemat obciążeń 1

Siły wewnetrzne występujące w płatwi

Momenty zginające (M

z,Ed

)

Sprawdzenie z tablic Winklera:

Mz.Ed.podW

0.105

qyd

⋅

as

2

⋅

0.105 1.005

kN

m

⋅

⋅

5

m

⋅

(

)

2

⋅

=

2.638

kN m

⋅

⋅

=

=

Mz.Ed.przW

0.0781

qyd

⋅

as

2

⋅

0.0781 1.005

kN

m

⋅

⋅

5

m

⋅

(

)

2

⋅

=

1.962

kN m

⋅

⋅

=

=

Siły poprzeczne (V

z,Ed

)

15

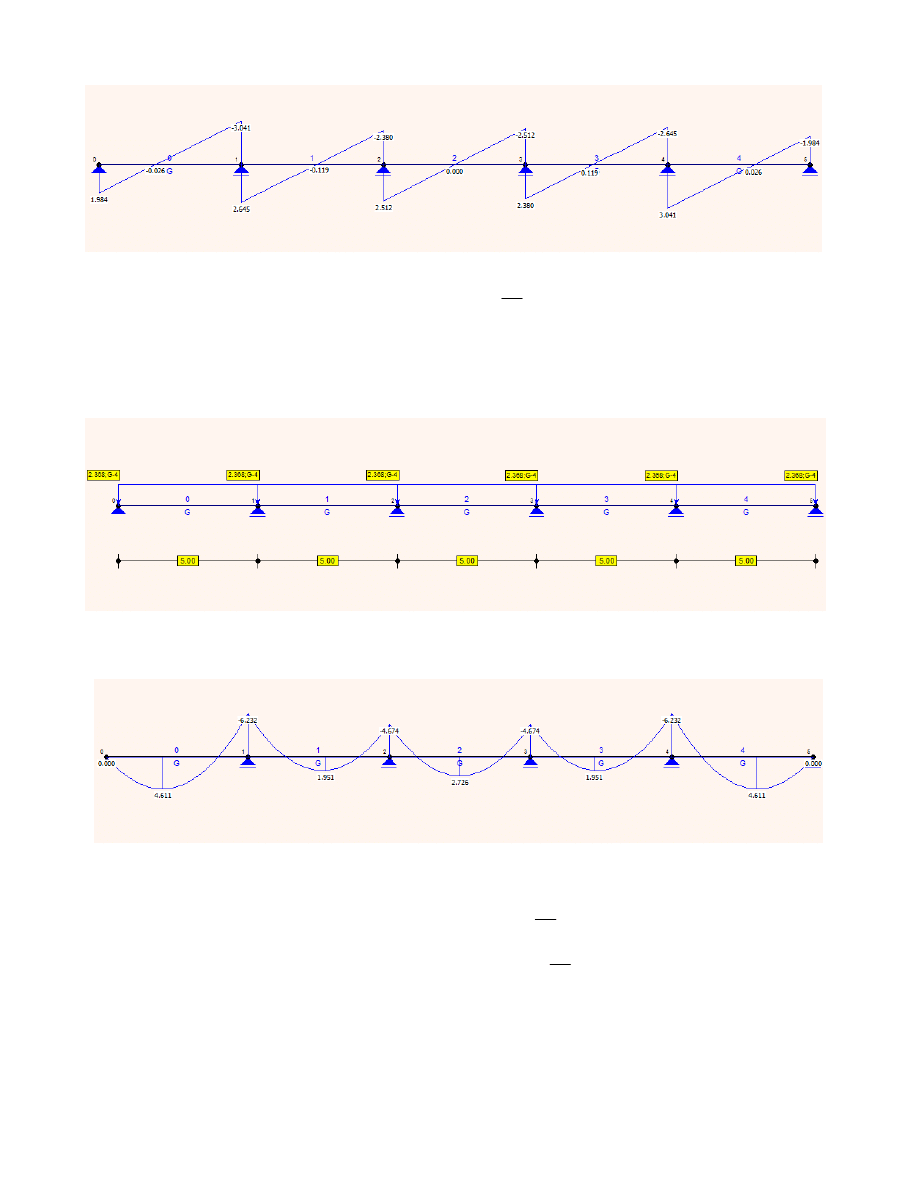
Sprawdzenie z tablic Winklera:

Vz.Ed.W

0.606

qyd

⋅

as

⋅

0.606 1.005

kN

m

⋅

⋅

5

m

⋅

⋅

=

3.045

kN

⋅

=

=

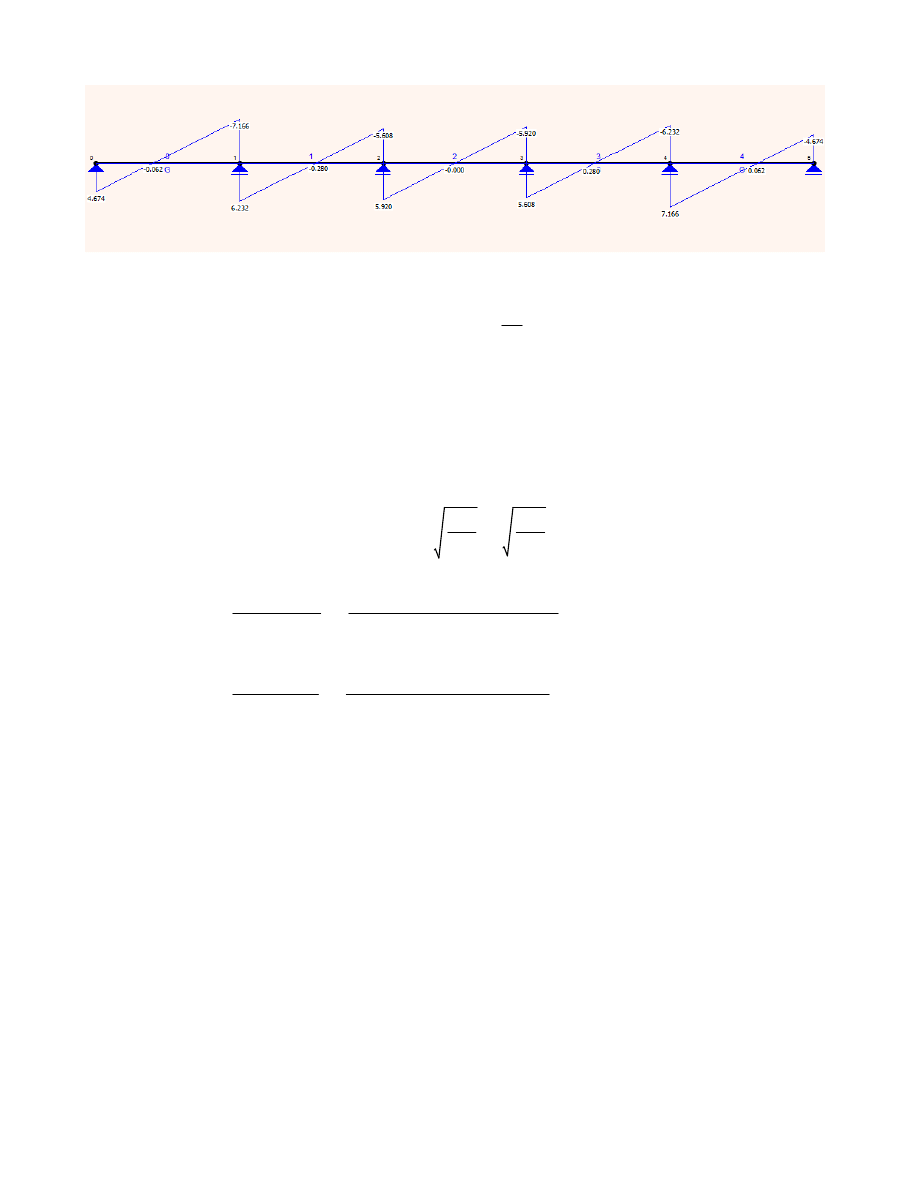
Siły wewnętrzne od obciążeń prostopadłych do osi y płatwi

Schemat statyczny płatwi jako belki ciągłej

schemat obciążeń 1

Siły wewnetrzne występujące w płatwi

Momenty zginające (M

y,Ed

)

Sprawdzenie z tablic Winklera:

My.Ed.podW

0.105

qzd

⋅

as

2

⋅

0.105 2.368

kN

m

⋅

⋅

5

m

⋅

(

)

2

⋅

=

6.216

kN m

⋅

⋅

=

=

My.Ed.przW

0.0781

qzd

⋅

as

2

⋅

0.0781 2.368

kN

m

⋅

⋅

5

m

⋅

(

)

2

⋅

=

4.624

kN m

⋅

⋅

=

=

Siły poprzeczne (V

y,Ed

)

16

Sprawdzenie z tablic Winklera:

Vy.Ed.W

0.606

qzd

⋅

as

⋅

0.606 2.368

kN

m

⋅

⋅

5

m

⋅

⋅

=

7.175

kN

⋅

=

=

Klasa przekroju płatwi przy zginaniu

Względem osi y-y

•

współczynnik

ε

235

fy.

235

235

=

1

=

=

- środnik

h

2

tf r

+

(

)

⋅

−

tw

16

cm

⋅

2 0.74

cm

⋅

0.9

cm

⋅

+

(

)

⋅

−

0.50

cm

⋅

=

25.44

=

<

72

ε

⋅

72

=

- półka

bw tw

−

2r

−

2tf

8.2

cm

⋅

0.50

cm

⋅

−

2 0.9

cm

⋅

⋅

−

2 0.74

cm

⋅

⋅

=

3.986

=

<

9

ε

⋅

9

=

Przekrój spełnia wymagania dla klasy 1

Sprawdzenie warunku nośności na zginanie

Maksymalne momenty zginające występujące w płatwi

My.Ed

6.232

kN m

⋅

⋅

=

Mz.Ed

2.645

kN m

⋅

⋅

=

Obliczeniowa nośność przekroju na zginanie:

γM0

1

=

17

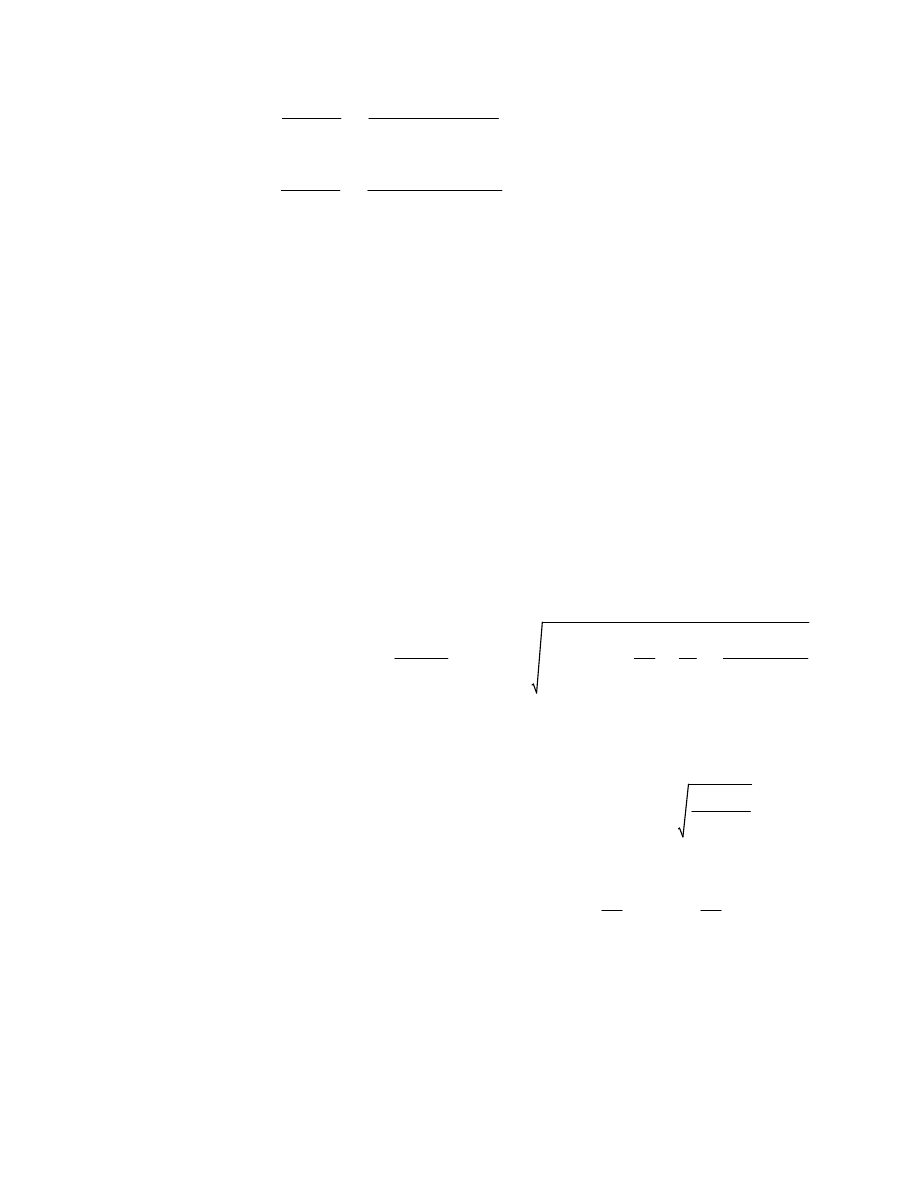
My.Rd

Wpl.y fy

⋅

γM0

124

cm

3

⋅

235

MPa

⋅

⋅

1

=

29.14

kN m

⋅

⋅

=

=

Mz.Rd

Wpl.z fy

⋅

γM0

26.1

cm

3

⋅

235

MPa

⋅

⋅

1

=

6.134

kN m

⋅

⋅

=

=

Sprawdzenie nośności z uwagi na zwichrzenie

Obliczenie momentu krytycznego

•

współczynniki zależne od obciążenia warunków
podparcia na końcach

C1

1.285

=

C2

1.562

=

współczynniki długości efektywnej:

ponieważ stopka ściskana
nie jest stężona bocznie

kz

1

=

ponieważ przekrój podporowy
nie może ulegać swobodnemu spaczeniu

kw

1

=

odległość od punktu przyłożenia obciążenia do
środka ścinania przekroju

zg

h

0.5

⋅

80

mm

⋅

=

=

bez podwieszenia

Mcr.0

C1

π

2

E

⋅ I

z

⋅

kz as

⋅

(

)

2

















⋅

C2

−

zg

⋅

C2 zg

⋅

(

)

2

kz

kw













2

Iw

Iz

⋅

+

















kz as

⋅

(

)

2

G

⋅

It

⋅

π

2

E

⋅ I

z

⋅

+

+

















⋅

=

as

5

m

=

Mcr.0

10.535

kN m

⋅

⋅

=

Krzywa zwichrzenia

•

smukłość względna przy zwichrzeniu bez podwieszenia

λLT0

Wpl.y fy

⋅

Mcr.0

1.663

=

=

smukłość graniczna przy zwichrzeniu

λLT.0

0.4

=

krzywa zwichrzenia

a

gdyż

h

bw

2

≤

h

bw

1.951

=

parametr imperfekcji

αLT

0.21

=

parametr poprawkowy

β

0.75

=

parametr krzywej zwichrzenia bez podwieszenia

ϕLT0

0.5 1

αLT λLT0 λLT.0

−

(

)

⋅

+

β λLT0

2

⋅

+









0.5 1

0.21 1.663

0.4

−

(

)

⋅

+

0.75 1.663

2

⋅

+









⋅

=

1.67

=

=

18

współczynnik zwichrzenia (bez podwieszenia)

χLT0

1

ϕLT0

ϕLT0

2

β λLT0

2

⋅

−

+

1

1.67

1.67

2

0.75 1.663

2

⋅

−

+

=

0.398

=

=

< 1

χLT min

1

1

λLT

2

,













<

1

λLT0

2

0.362

=

Maksymalne momenty zginające występujące w płatwi

My.Ed

6.232

kN m

⋅

⋅

=

Mz.Ed

2.645

kN m

⋅

⋅

=

Obliczeniowa nośność przekroju na zginanie:

My.Rd

Wpl.y fy

⋅

γM0

124

cm

3

⋅

235

MPa

⋅

⋅

1

=

29.14

kN m

⋅

⋅

=

=

Mz.Rd

Wpl.z fy

⋅

γM0

26.1

cm

3

⋅

235

MPa

⋅

⋅

1

=

6.134

kN m

⋅

⋅

=

=

Nośność przekroju na zginanie

bez podwieszenia

My.Ed

χLT0 My.Rd

⋅













Mz.Ed
Mz.Rd













+

0.969

=

< 1

warunek spełniony

Nośność obliczeniowa płatwi na ścinanie (dla IPE160)

ciężar płatwi

gp

0.158

kN

m

⋅

=

Siła tnąca występująca w płatwi

VEd

7.166

kN

⋅

=

Warunek stateczności miejscowej przy ścinaniu

hw

h

2

tf r

+

(

)

−

16

cm

⋅

2 0.74

cm

⋅

0.9

cm

⋅

+

(

)

⋅

−

=

127.2

mm

⋅

=

=

η

1

=

hw

tw

25.44

=

<

72

ε

η

⋅

72

=

Środnik nie jest wrażliwy na niestateczność przy ścinaniu

Pole przekroju czynnego przy ścinaniu dla dwuteownika walcowanego wynosi

Av

A

2

bw

⋅

tf

⋅

−

tw 2r

+

(

)

tf

⋅

+

9.666

cm

2

⋅

=

=

Obliczeniowa nośność przekroju na ścinanie:

19

Vpl.Rd

Av fy

⋅

3

γM0

⋅

131.146

kN

⋅

=

=

Nośność przekroju na ścinanie

Vz.Ed

Vpl.Rd

0.023

=

< 1,0

warunek został spełniony

Nośność przekroju na zginanie ze ściskaniem

współczynniki równoważnego stałego momentu

dla przechyłowej postaci wyboczenia

Cmy

0.9

=

Cmz

0.9

=

współczynniki interakcji

kyy

Cmy

0.9

=

=

Wpływ ścinania na nośność przy zginaniu
można pominąć bo nośność przekroju nie ulega
redukcji wskutek wyboczenia przy ścinaniu, a
siła poprzeczna nie przekracza 50% nośności
plastycznej przekroju przy ścinaniu

kzz

Cmz

0.9

=

=

kyz

0.6 kzz

⋅

0.54

=

=

kzy

0.6

kyy

⋅

0.54

=

=

kyy My.Ed

⋅

χLT0 My.Rd

⋅













α

kyz Mz.Ed

⋅

Mz.Rd













β

+

0.9 6.232

kN

⋅

m

⋅

⋅

0.398 29.14

kN

⋅

m

⋅

⋅













0.54 2.645

kN

⋅

m

⋅

⋅

6.134

kN

⋅

m

⋅













2

+

=

0.538

=

< 1,0

warunek został spełniony

kzy My.Ed

⋅

χLT0 My.Rd

⋅













α

kzz Mz.Ed

⋅

Mz.Rd













β

+

0.54 6.232

kN

⋅

m

⋅

⋅

0.398 29.14

kN

⋅

m

⋅

⋅













0.9 2.645

kN

⋅

m

⋅

⋅

6.134

kN

⋅

m

⋅













2

+

=

0.441

=

< 1,0

warunek został spełniony

gdzie: α = 1

β = 2

- parametry interakcji przy dwukierunkowym zginaniu

Stan graniczny użytkowalności

Qkz

qzkS qzkZś

+

0.664

kN

m

⋅

0.981

kN

m

⋅

+

=

1.645

kN

m

⋅

=

=

Ugięcie belki od obciążenia stałego

uinst.G

0.5 5

⋅ q

zkS

⋅

as

4

⋅

384

E

⋅ I

y

⋅

0.5 5

⋅

0.664

kN

m

⋅

⋅

5

m

⋅

(

)

4

⋅

384 210

GPa

⋅

⋅

869

cm

4

⋅

⋅

=

1.481

mm

⋅

=

=

Ugięcie belki od obciążenia zmiennego

20

uinst.Q

0.75 5

⋅ q

zkZ

⋅

as

4

⋅

384

E

⋅ I

y

⋅

0.75 5

⋅

0.427

kN

m

⋅

⋅

5

m

⋅

(

)

4

⋅

384 210

GPa

⋅

⋅

869

cm

4

⋅

⋅

=

1.428

mm

⋅

=

=

Ugięcie belki całkowite

uinst

uinst.G uinst.Q

+

2.909

mm

⋅

=

=

Ugięcie belki dopuszczalne

unet.fin

as

200

5

m

⋅

200

=

25

mm

⋅

=

=

uinst

2.909

mm

⋅

=

<

unet.fin

25

mm

⋅

=

Warunek spełniony

przyjęto ostatecznie IPE160

21

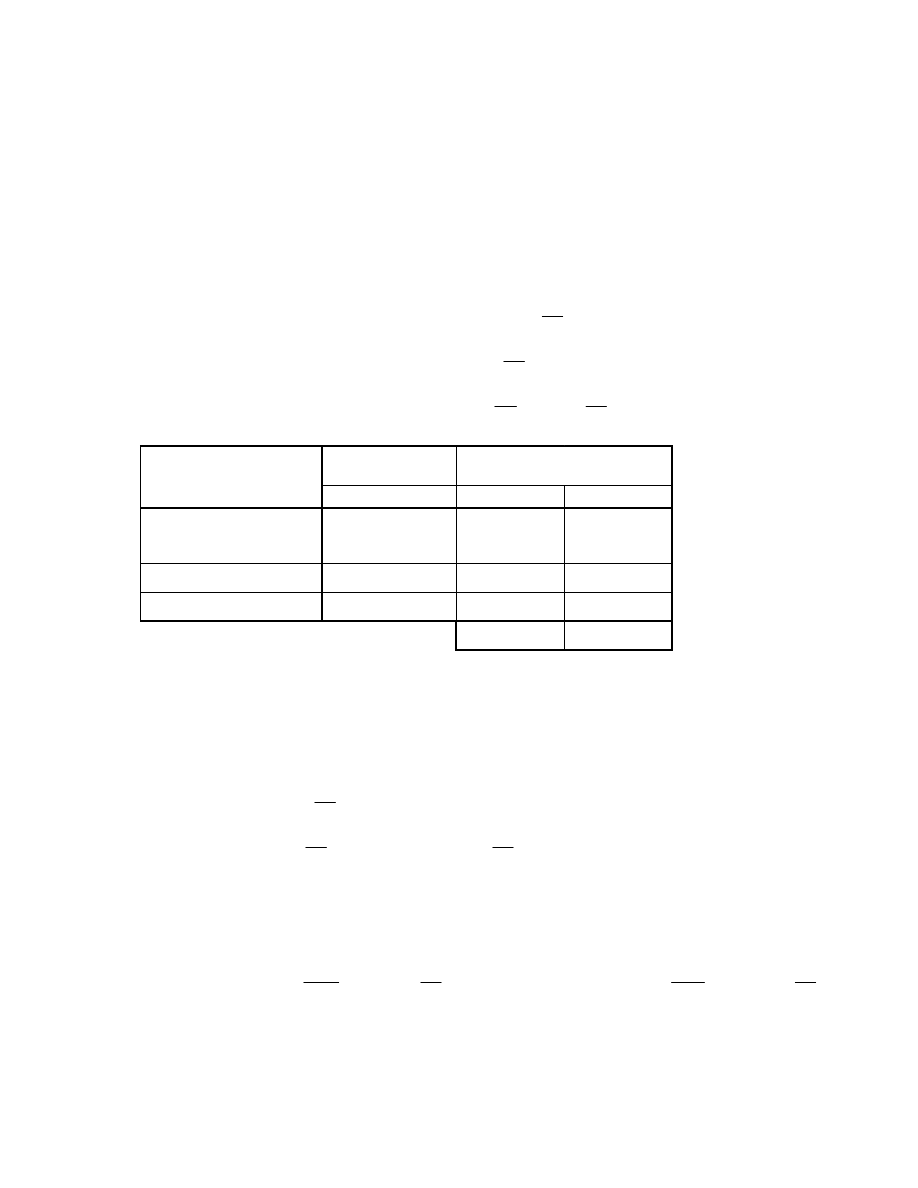
3. Wiązar kratowy

3.1. Końcowe zestawienie obciążeń stałych i zmiennych na dźwigar dachowy ramy
wewnętrznej

3.1.1. Obciążenia stałe (wartość charakterystyczna)

Wartości obciążeń stałych

a

1.904

m

=

rozstaw płatwi

Obciążenie od płyty dachowej

gdach. a

⋅

0.417

kN

m

⋅

=

Obciążenie od płatwi dachowej

gp

0.158

kN

m

⋅

=

Obciążenie od instalacji

gi

a

0.3

⋅

kN

m

2

0.571

kN

m

⋅

=

=

Odległość między

ramami

[m]

[kN/m]

[kN]

Pokrycie dachowe

5,0

1,038

5,190

Płatew IPE 160

5,0

0,158

0,790

Obciążenie od instalacji

5,0

0,826

4,130

g

ch

10,110

Materiał

Obciążenie charakterystyczne

3.1.2. Obciążenie wiatrem (wartość charakterystyczna)

Oddziaływanie wiatru wiejącego prostopadle do budynku ( wg. pkt. 1.1.1.) -

•

przyjęto wartość najbardziej niekorzystną

we.H

0.554

−

kN

m

⋅

=

we.D

0.615

kN

m

⋅

=

we.E

0.388

−

kN

m

⋅

=

Obciążenie wiatrem działające na ramę węwnętrzną

qw.dach

we.H e

⋅

2.771

−

kN

⋅

=

=

parcie

qw.ściana.p

we.D

ar

e

⋅

3.073

kN

m

⋅

=

=

ssanie

qw.ściana.s

we.E

ar

e

⋅

1.941

−

kN

m

⋅

=

=

gdzie:

e

5

m

=

rozstaw ram

ar

1

m

=

rozstaw rygli

3.1.3. Obciążenie śniegiem (wartość charakterystyczna)

22

3.1.3. Obciążenie śniegiem (wartość charakterystyczna)

Obciążenie śniegiem wg pkt. 1.2.1.2.

sch

0.56

kN

m

2

⋅

=

Obciążenie śniegiem dźwigara ramy wewnętrznej

qś

sch e

⋅ a

⋅

0.56

kN

m

2

⋅

5

m

⋅

⋅

1.904

m

⋅

⋅

=

5.331

kN

⋅

=

=

23

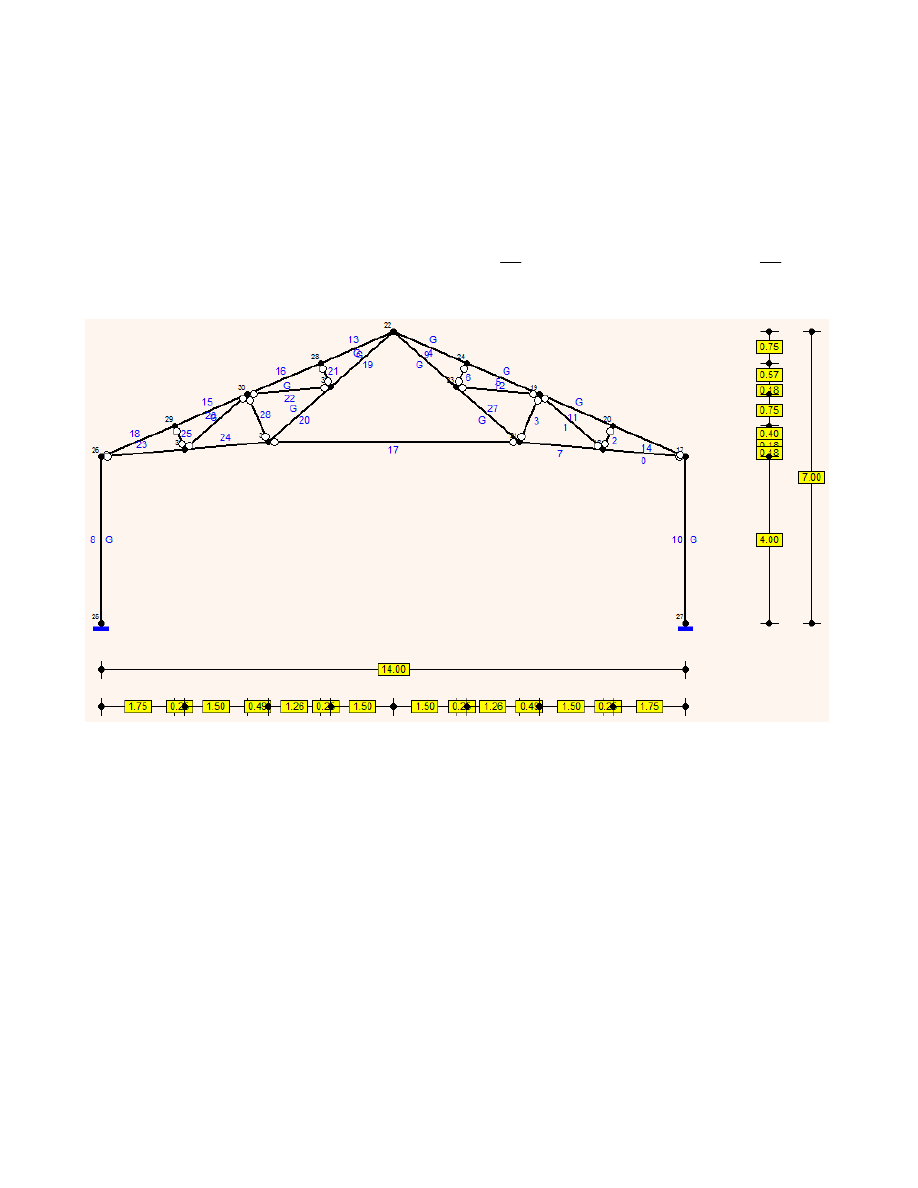
3.2. Wyznaczenie sił wewnętrznych działąjących na ramę wewnętrzną

Siły wewnętrzne w ramie wyznaczono przy pomocy programu SOLDIS

Obciążenie stałe

gch

1.35

⋅

13.649

kN

⋅

=

Obciążenie wiatrem

qw.dach

1.5

⋅

4.157

−

kN

⋅

=

qw.ściana.p

1.5

⋅

4.609

kN

m

⋅

=

qw.ściana.s

1.5

⋅

2.911

−

kN

m

⋅

=

Obciążenie śniegiem

qś

1.5

⋅

7.997

kN

⋅

=

Schemat statyczny ramy

3.2.1. Kombinacja 1

24

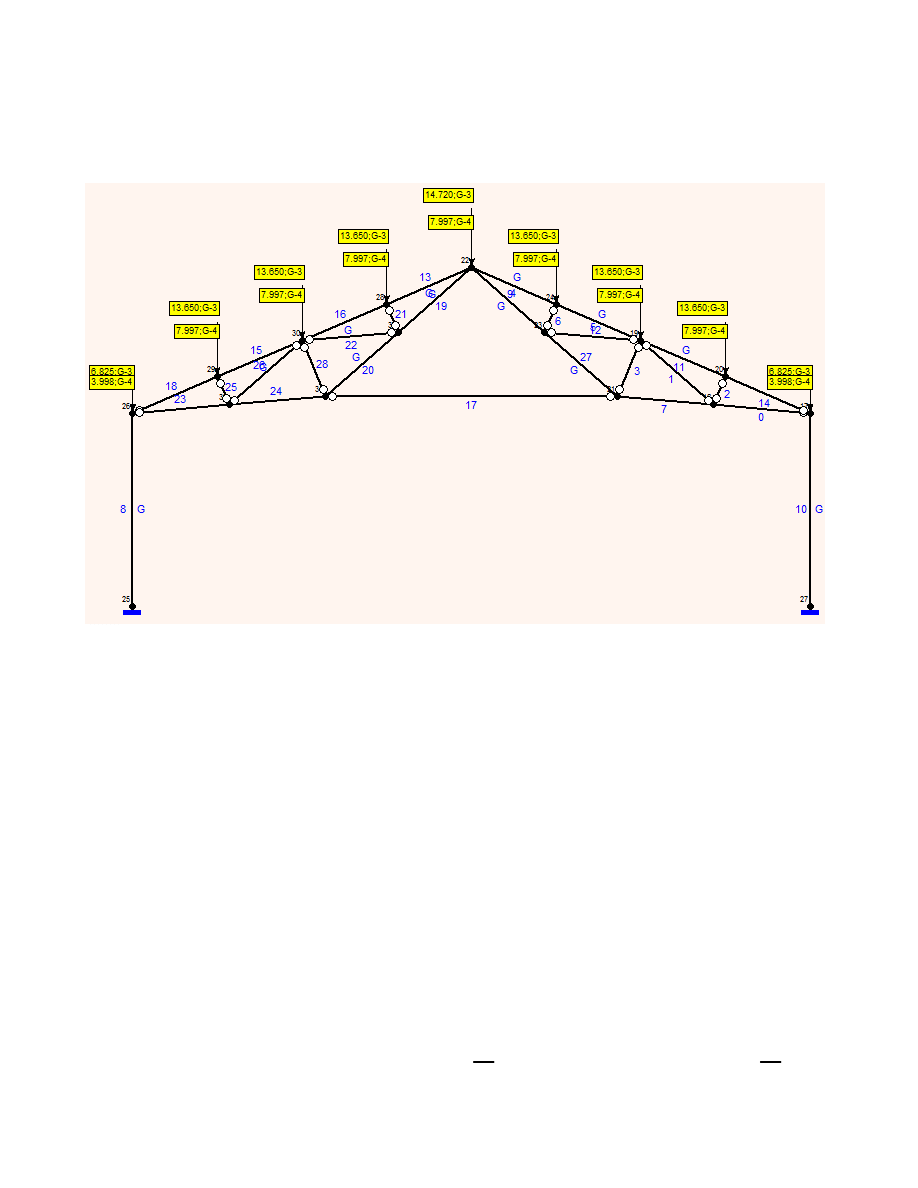
1.35

gch

⋅

1.5

qś

⋅

+

1.35 10.110

kN

⋅

⋅

1.5 5.331

kN

⋅

⋅

+

=

21.645

kN

⋅

=

- obciążenie stałe i śnieg

obciążenie dodatkowe
od drugiej płatwi w kalenicy

1.35

gch

⋅

1.35 10.110

kN

⋅

⋅

=

1.365

10

4

×

N

=

1.35

gp

⋅

e

⋅

1.067

kN

⋅

=

1.5

qś

⋅

1.5 5.331

kN

⋅

⋅

=

7.997

10

3

×

N

=

Obciążenie ramy

Wyniki w raporcie z obliczeń: Raport SOLDIS - Kombinacja 1

pas górny

Nmax1

190.830

−

kN

=

pręt nr 18

pas dolny

Nmax1

192.537kN

=

pręt nr 24

pas dolny

wewnętrzny

Nmax1

71.497kN

=

pręt nr 20

krzyżulce

Nmax1

41.726

−

kN

=

pręt nr 22

słupki

Nmax1

15.993

−

kN

=

pręt nr 28

3.2.2. Kombinacja 2

1.35

gch

⋅

1.5

qw.dach

⋅

+

- obciążenie stałe i wiatr

gdzie:

1.35

gch

⋅

1.35 10.110

kN

⋅

⋅

=

13.649

kN

⋅

=

1.5

qw.dach

⋅

4.157

−

kN

⋅

=

1.5

qw.ściana.p

⋅

4.609

kN

m

⋅

=

1.5

qw.ściana.s

⋅

2.911

−

kN

m

⋅

=

25

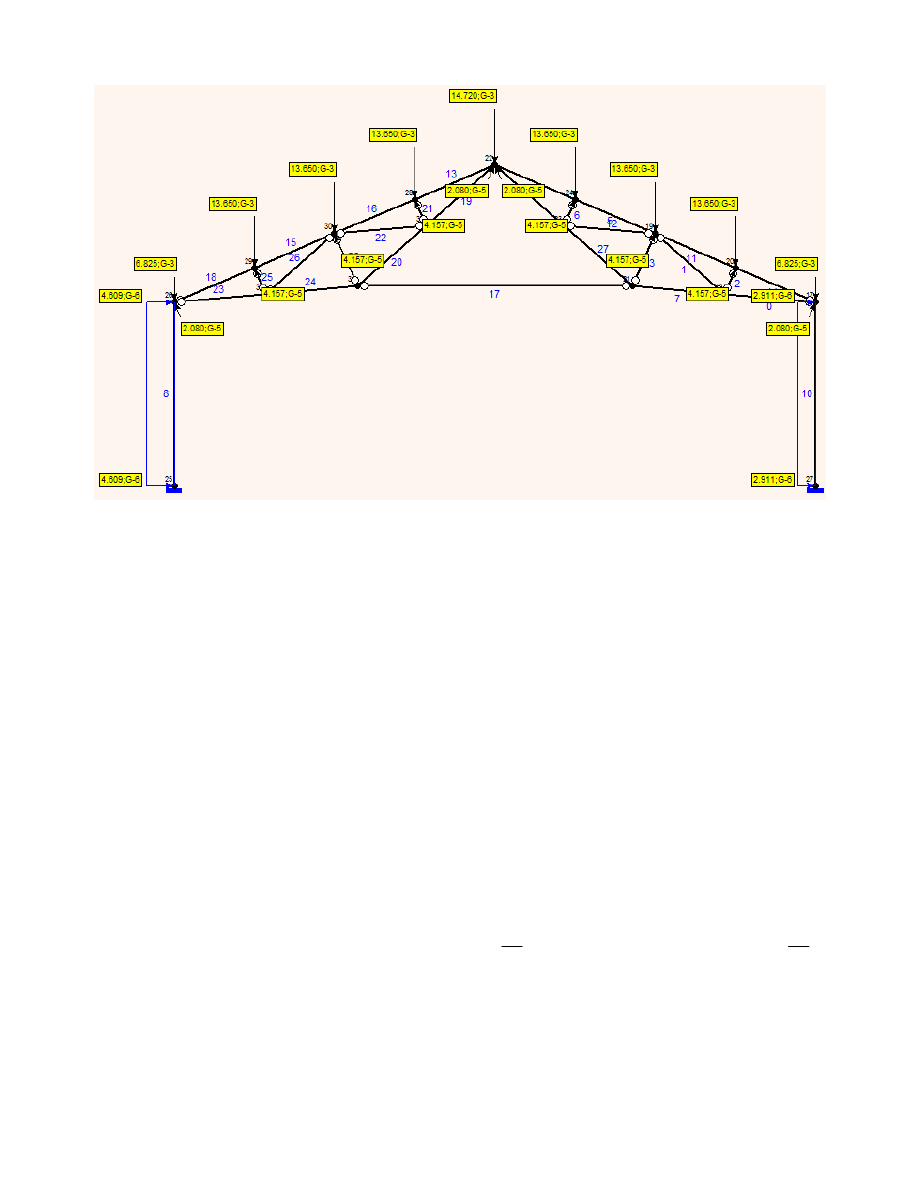
Obciążenie ramy

Wyniki w raporcie z obliczeń: Raport SOLDIS - Kombinacja 2

pas górny

Nmax2

87.537

−

kN

=

pręt nr 18

pas dolny

Nmax2

88.634kN

=

pręt nr 24

pas dolny

wewnętrzny

Nmax2

31.026kN

=

pręt nr 20

krzyżulce

Nmax2

18.520

−

kN

=

pręt nr 22

słupki

Nmax2

6.290

−

kN

=

pręt nr 28

3.2.3. Kombinacja 3

1.35

gch

⋅

1.5

qś

⋅

+

1.5 0.6

⋅

qw

⋅

+

- obciążenie stałe, śnieg i wiatr

gdzie:

1.35

gch

⋅

1.35 10.110

kN

⋅

⋅

=

13.649

kN

⋅

=

1.5

qś

⋅

7.997

kN

⋅

=

1.5 0.6

⋅

qw.dach

⋅

2.494

−

kN

⋅

=

1.5 0.6

⋅

qw.ściana.p

⋅

2.765

kN

m

⋅

=

1.5 0.6

⋅

qw.ściana.s

⋅

1.747

−

kN

m

⋅

=

Obciążenie ramy

26

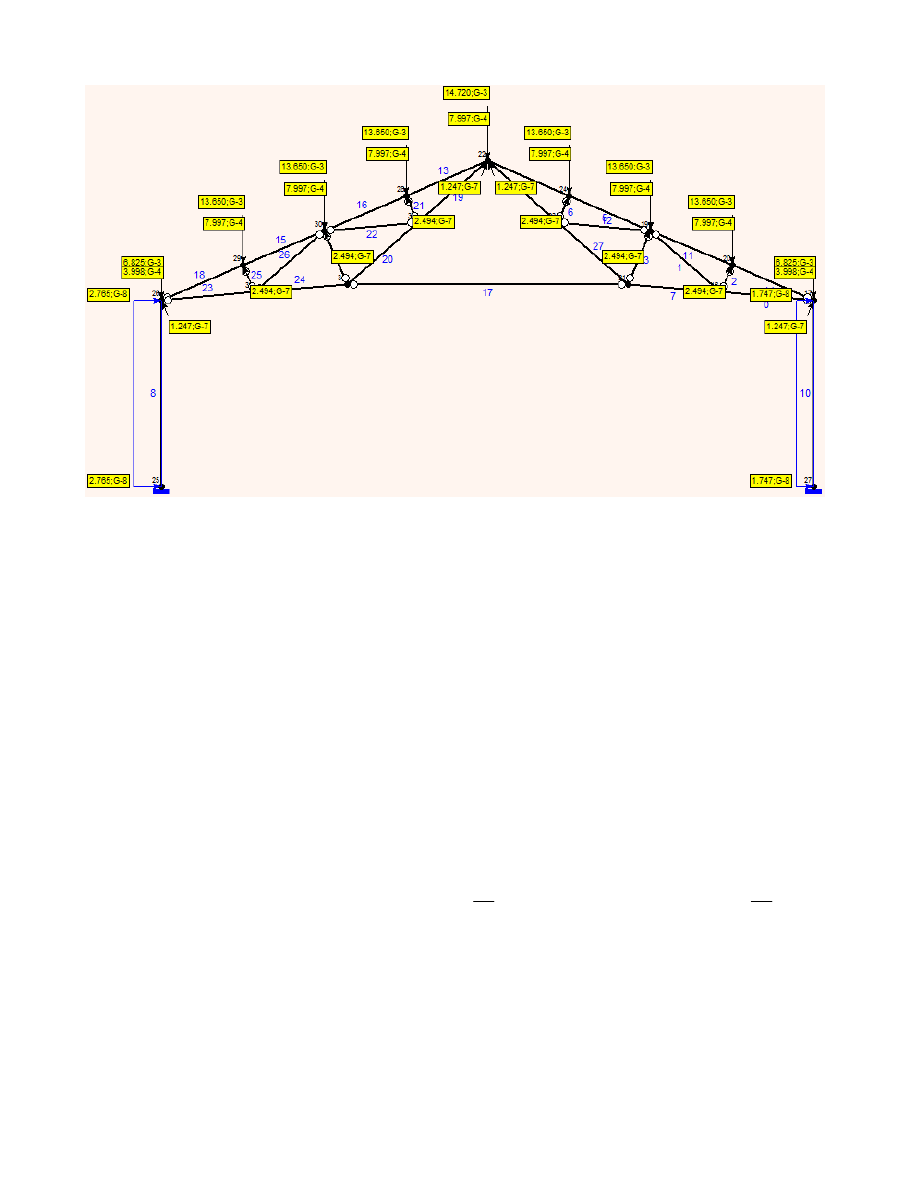
Wyniki w raporcie z obliczeń: Raport SOLDIS - Kombinacja 3

pas górny

Nmax2

170.856

−

kN

=

pręt nr 18

pas dolny

Nmax2

172.531kN

=

pręt nr 24

pas dolny

wewnętrzny

Nmax2

63.028kN

=

pręt nr 20

krzyżulce

Nmax2

36.965

−

kN

=

pręt nr 22

słupki

Nmax2

13.746

−

kN

=

pręt nr 28

3.2.4. Kombinacja 4

1.35

gch

⋅

1.5

qw

⋅

+

1.5 0.5

⋅

qś

⋅

+

- obciążenie stałe, wiatr i śnieg

gdzie:

1.35

gch

⋅

1.35 10.110

kN

⋅

⋅

=

13.649

kN

⋅

=

1.5

qw.dach

⋅

4.157

−

kN

⋅

=

1.5

qw.ściana.p

⋅

4.609

kN

m

⋅

=

1.5

qw.ściana.s

⋅

2.911

−

kN

m

⋅

=

1.5 0.5

⋅

qś

⋅

3.998

kN

⋅

=

Obciążenie ramy

27

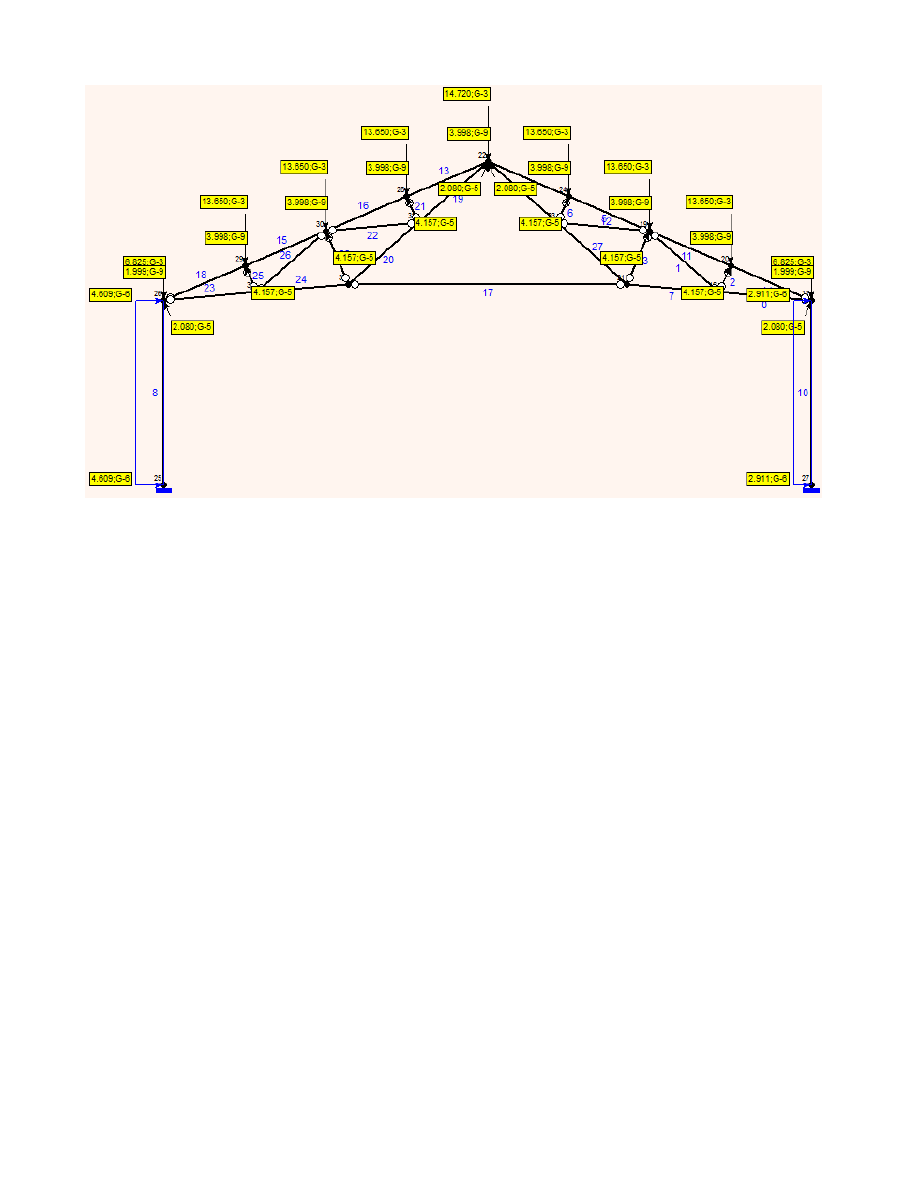
Wyniki w raporcie z obliczeń: Raport SOLDIS - Kombinacja 4

pas górny

Nmax2

127.599

−

kN

=

pręt nr 18

pas dolny

Nmax2

129.736kN

=

pręt nr 24

pas dolny

wewnętrzny

Nmax2

44.793kN

=

pręt nr 20

krzyżulce

Nmax2

27.620

−

kN

=

pręt nr 22

słupki

Nmax2

8.761

−

kN

=

pręt nr 28

Maksymalne siły występują w kombinacji 1:

pas górny

NmaxG

190.830

−

kN

=

pręt nr 18

pas dolny

NmaxD

192.537kN

=

pręt nr 24

pas dolny

wewnętrzny

NmaxDw

71.497kN

=

pręt nr 20

krzyżulce

NmaxK

41.726

−

kN

=

pręt nr 22

słupki

NmaxS

15.993

−

kN

=

pręt nr 28

28

3.3. Wymiarowanie elementów dźwigara

wg PN-EN 1993-1-1

Momenty zginające występujące w układzie są tak małe, że aż marginalne w wymiarowaniu
pasów, słupków, krzyżulców w kratownicy. Zatem nie bierzemy ich po uwagę w wymiarowaniu
elementów dźwigara.

Pas górny: (ściskanie)

Jako najbardziej wytężony przekrój przyjęto do wymiarowania pas górny nr 18

Założono, że płatwie zabezpieczają przed wyboczeniem względem osi z (nieprzesuwnych punktów
podparcia), a słupki i krzyżulce wzgl. osi y zatem długości wyboczeniowe wynoszą:

ly

2 190.4

⋅

cm

3.808

m

=

=

lz

190.4

cm

=

siła ściskająca:

NEd

190.83

kN

=

fy

235

MPa

⋅

=

γM0

1

=

- smukłość powinna spełniać warunek

λ

250

≤

stąd

l

250

i

<

ly

250

1.523

cm

⋅

=

lz

250

0.762

cm

⋅

=

- nośność obliczeniowa przekroju przy osiowym ściskaniu

NcRd

określona jest wzorem:

NcRd

γM0 A

⋅

fy

⋅

=

(wzór 6.10)

- przekrój próbny obliczono ze wzoru:

A

NEd

γM0 fy

⋅

≥

A

8.12

cm

2

⋅

=

- dane geometryczne pojedyńczego kształtownika

HEA 120

A

25.3

cm

2

=

R

12

mm

=

b

120

mm

=

tf

8.0

mm

=

c

0.5

b

⋅

R

−

48

mm

⋅

=

=

iy

4.89

cm

=

iz

3.02

cm

=

- klasa przekroju:

ε

235

MPa

fy

=

ε

1

=

9

ε

⋅

9

=

>

c

tf

6

=

Przekrój spełnia warunki dla klasy 1

(Tablica 5.2)

Nośność charakterystyczna przekroju przy ściskaniu:

NcRd

A fy

⋅

γM0

25.3

cm

2

⋅

235

MPa

⋅

⋅

1

=

594.55

kN

⋅

=

=

Wartość odniesienia do wyznaczenia smukłości względnej:

29

λ1

π

E

fy

93.913

=

=

Długość wyboczeniowa w rozpatrywanej płaszczyźnie wyboczenia elementu:

μ

1

=

Lcr

μ ly

⋅

3.808

m

⋅

=

=

μ ly

⋅

Smukłość względna przy wyboczeniu giętnym dla osi 'y' i 'z':

p. 6.3.1.3

iy

4.89

cm

⋅

=

λy

Lcr

iy λ1

⋅

380.8

cm

⋅

4.89

cm

⋅

93.913

⋅

=

0.829

=

=

iz

3.02

cm

⋅

=

λz

Lcr

iz λ1

⋅

380.8

cm

⋅

3.02

cm

⋅

93.913

⋅

=

1.343

=

=

Parametr imperfekcji wg krzywej zwichrzenia (Tabela 6.1 i Tabela 6.2):

a dla y-y

b dla z-z

αy

0.21

=

αz

0.34

=

Parametr krzywej niestateczności:

ϕy

0.5 1

αy λy

0.2

−

(

)

⋅

+

λy

( )

2

+









0.5 1

0.21 0.829

0.2

−

(

)

⋅

+

0.829

2

+









⋅

=

0.91

=

=

ϕz

0.5 1

αz λz

0.2

−

(

)

⋅

+

λz

( )

2

+









0.5 1

0.34 1.343

0.2

−

(

)

⋅

+

1.343

2

+









⋅

=

1.596

=

=

Współczynnik wyboczeniowy (wzór 6.49):

χy

1

ϕy

ϕy

2

λy

2

−

+

1

0.91

0.91

2

0.829

2

−

+

=

0.778

=

=

χz

1

ϕz

ϕz

2

λz

2

−

+

1

1.596

1.596

2

1.343

2

−

+

=

0.407

=

=

Sprawdzenie warunku nośności:

γM1

1

=

NbRd.y

χy NcRd

⋅

γM1

0.778 594.55

kN

⋅

⋅

1

=

462.56

kN

⋅

=

=

NbRd.z

χz NcRd

⋅

γM1

0.407 594.55

kN

⋅

⋅

1

=

241.982

kN

⋅

=

=

30

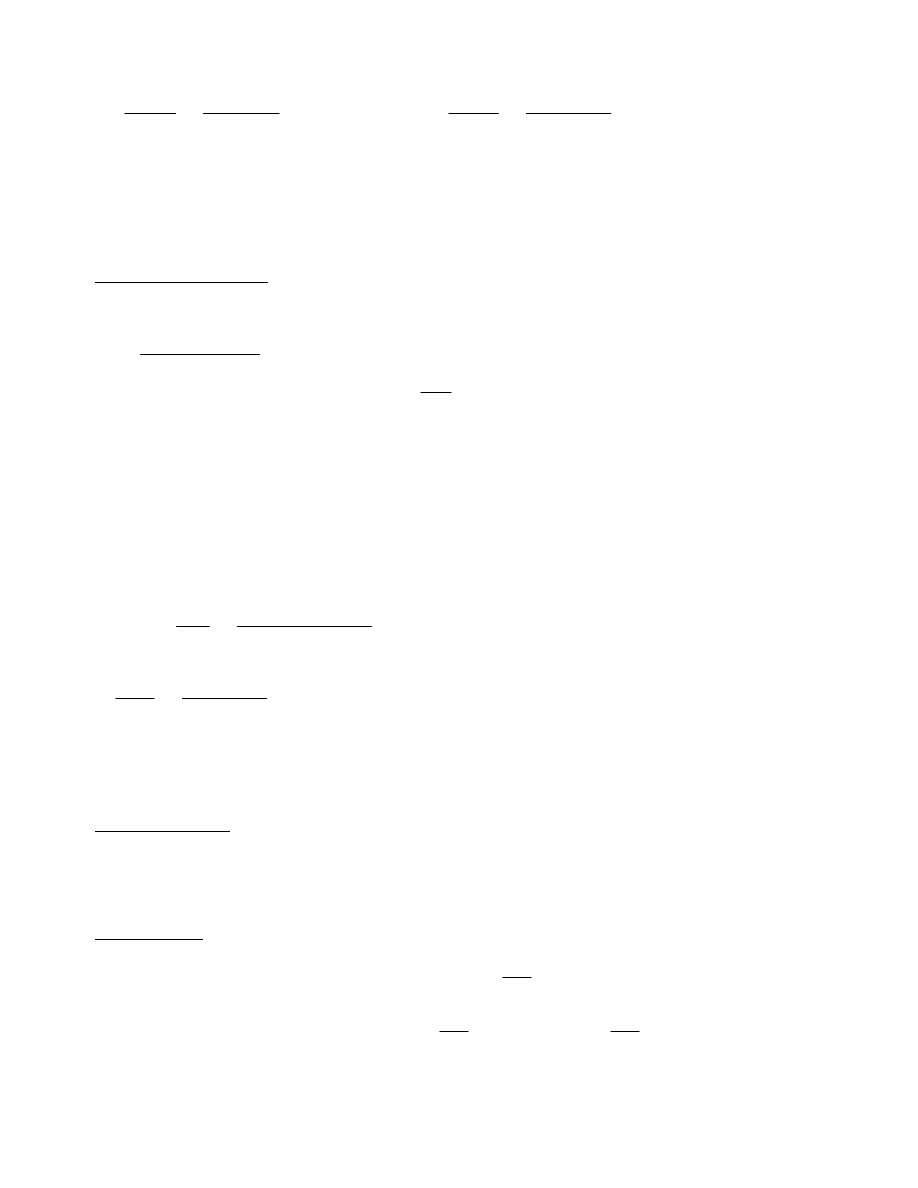
NEd

NbRd.y

190.83

kN

⋅

462.56

kN

⋅

=

0.413

=

< 1

NEd

NbRd.z

190.83

kN

⋅

241.982

kN

⋅

=

0.789

=

< 1

(wzór 6.46)

WARUNEK SPEŁNIONY

na całej długości pasa górnego przyjęto HEA 120

Pas dolny:(rozciąganie)

- max siła rozciągajaca w pręcie nr 24

siła rozciągająca

NEd

192.537

kN

=

wstępny dobór przekroju z warunku

A

NEd

fy

=

A

8.193

cm

2

⋅

=

dane geometryczne pojedyńczego kształtownika

HEA 100

A

21.2

cm

2

=

bf

100

mm

=

tf

8.0

mm

=

Nośność charakterystyczna przekroju przy rozciąganiu:

NcRd

A fy

⋅

γM0

21.2

cm

2

⋅

235

MPa

⋅

⋅

1

=

498.2

kN

⋅

=

=

NEd

NcRd

192.537

kN

⋅

498.2

kN

⋅

=

0.386

=

< 1

WARUNEK SPEŁNIONY

na całej długości pasa dolnego przyjęto HEA 100

Słupki: (ściskanie)

Jako najbardziej wytężony przekrój przyjęto do wymiarowania słupek nr 28

ly

125

cm

=

lz

125

cm

=

siła ściskająca:

NEd

15.993

kN

=

fy

235

MPa

⋅

=

γM0

1

=

- smukłość powinna spełniać warunek

λ

250

≤

stąd

l

250

i

<

ly

250

0.5

cm

⋅

=

lz

250

0.5

cm

⋅

=

- nośność obliczeniowa przekroju przy osiowym ściskaniu

NcRd

określona jest wzorem:

31

NcRd

γM0 A

⋅

fy

⋅

=

(wzór 6.10)

- przekrój próbny obliczono ze wzoru:

A

NEd

γM0 fy

⋅

≥

A

0.681

cm

2

⋅

=

- dane geometryczne pojedyńczego kształtownika

RK 40x40x4

A

5.59

cm

2

=

R

4

mm

=

b

40

mm

=

t

4.0

mm

=

c

b

2 t

R

+

(

)

−

24

mm

⋅

=

=

i

1.45

cm

=

- klasa przekroju:

ε

235

MPa

fy

=

ε

1

=

33

ε

⋅

33

=

>

c

t

6

=

Przekrój spełnia warunki dla klasy 1

(Tablica 5.2)

Nośność charakterystyczna przekroju przy ściskaniu:

NcRd

A fy

⋅

γM0

5.59

cm

2

⋅

235

MPa

⋅

⋅

1

=

131.365

kN

⋅

=

=

Wartość odniesienia do wyznaczenia smukłości względnej:

λ1

π

E

fy

93.913

=

=

Długość wyboczeniowa w rozpatrywanej płaszczyźnie wyboczenia elementu:

μ

1

=

Lcr

μ ly

⋅

125

cm

⋅

=

=

Smukłość względna przy wyboczeniu giętnym dla osi 'y' i 'z':

p. 6.3.1.3

i

1.45

cm

⋅

=

λy

Lcr

i

λ1

⋅

125

cm

⋅

1.45

cm

⋅

93.913

⋅

=

0.918

=

=

Parametr imperfekcji wg krzywej zwichrzenia (Tabela 6.1 i Tabela 6.2):

a dla y-y

αy

0.21

=

Parametr krzywej niestateczności:

ϕy

0.5 1

αy λy

0.2

−

(

)

⋅

+

λy

( )

2

+









0.5 1

0.21 0.918

0.2

−

(

)

⋅

+

0.918

2

+









⋅

=

0.997

=

=

32

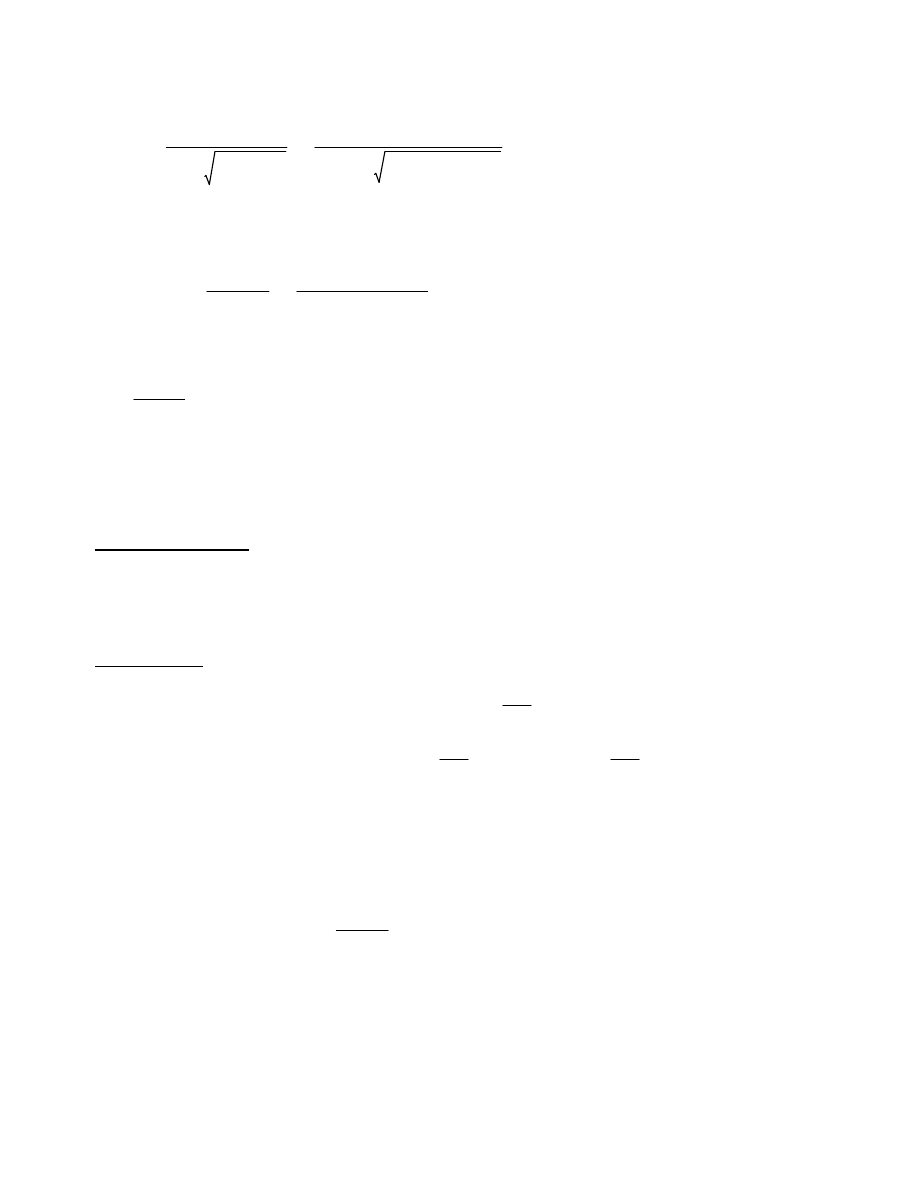
Współczynnik wyboczeniowy (wzór 6.49):

χy

1

ϕy

ϕy

2

λy

2

−

+

1

0.997

0.997

2

0.918

2

−

+

=

0.722

=

=

Sprawdzenie warunku nośności:

γM1

1

=

NbRd.y

χy NcRd

⋅

γM1

0.722 131.365

kN

⋅

⋅

1

=

94.846

kN

⋅

=

=

NEd

15.993

kN

⋅

=

NEd

NbRd.y

0.162

=

< 1

(wzór 6.46)

WARUNEK SPEŁNIONY

na słupki przyjęto RK 40x40x4

Krzyżulce:(ściskanie)

Jako najbardziej wytężony przekrój przyjęto do wymiarowania krzyżulec nr 22

ly

200.4

cm

=

lz

200.4

cm

=

siła ściskająca:

NEd

41.726

kN

=

fy

235

MPa

⋅

=

γM0

1

=

- smukłość powinna spełniać warunek

λ

250

≤

stąd

l

250

i

<

ly

250

0.802

cm

⋅

=

lz

250

0.802

cm

⋅

=

- nośność obliczeniowa przekroju przy osiowym ściskaniu

NcRd

określona jest wzorem:

NcRd

γM0 A

⋅

fy

⋅

=

(wzór 6.10)

- przekrój próbny obliczono ze wzoru:

A

NEd

γM0 fy

⋅

≥

A

1.776

cm

2

⋅

=

- dane geometryczne pojedyńczego kształtownika

RK 40x40x4

A

5.59

cm

2

=

R

4

mm

=

b

40

mm

=

t

4.0

mm

=

c

b

2 t

R

+

(

)

−

24

mm

⋅

=

=

i

1.45

cm

=

33

- klasa przekroju:

ε

235

MPa

fy

=

ε

1

=

33

ε

⋅

33

=

>

c

t

6

=

Przekrój spełnia warunki dla klasy 1

(Tablica 5.2)

Nośność charakterystyczna przekroju przy ściskaniu:

NcRd

A fy

⋅

γM0

5.59

cm

2

⋅

235

MPa

⋅

⋅

1

=

131.365

kN

⋅

=

=

Wartość odniesienia do wyznaczenia smukłości względnej:

λ1

π

E

fy

93.913

=

=

Długość wyboczeniowa w rozpatrywanej płaszczyźnie wyboczenia elementu:

μ

1

=

Lcr

μ ly

⋅

200.4

cm

⋅

=

=

Smukłość względna przy wyboczeniu giętnym dla osi 'y' i 'z':

p. 6.3.1.3

i

1.45

cm

⋅

=

λy

Lcr

i

λ1

⋅

200.4

cm

⋅

1.45

cm

⋅

93.913

⋅

=

1.472

=

=

Parametr imperfekcji wg krzywej zwichrzenia (Tabela 6.1 i Tabela 6.2):

a dla y-y

αy

0.21

=

Parametr krzywej niestateczności:

ϕy

0.5 1

αy λy

0.2

−

(

)

⋅

+

λy

( )

2

+









0.5 1

0.21 1.472

0.2

−

(

)

⋅

+

1.472

2

+









⋅

=

1.717

=

=

Współczynnik wyboczeniowy (wzór 6.49):

χy

1

ϕy

ϕy

2

λy

2

−

+

1

1.717

1.717

2

1.472

2

−

+

=

0.384

=

=

Sprawdzenie warunku nośności:

γM1

1

=

NbRd.y

χy NcRd

⋅

γM1

0.384 131.365

kN

⋅

⋅

1

=

50.444

kN

⋅

=

=

34

NEd

41.726

kN

⋅

=

NEd

NbRd.y

0.827

=

< 1

(wzór 6.46)

WARUNEK SPEŁNIONY

na krzyżulce przyjęto RK 40x40x4

35

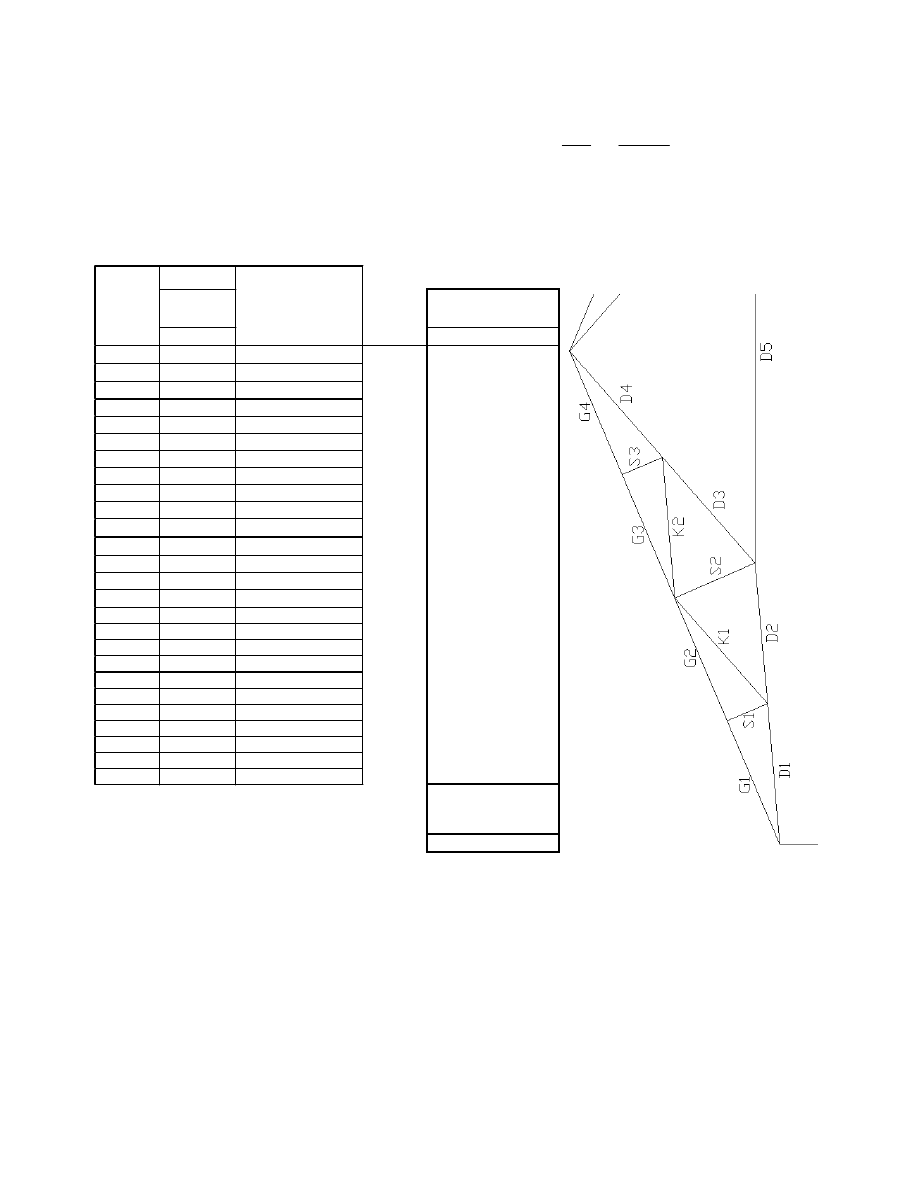
3.3.1 Sprawdzenie stanu SGU

ufin

23.7

mm

=

odczytane z raportu SOLDIS SGU

unet

L

250

14.0

m

⋅

250

=

56

mm

⋅

=

=

ufin

23.7

mm

⋅

=

<

unet

56

mm

⋅

=

WARUNEK SPEŁNIONY

3.3.2 Tabela doboru przekrojów

Długość pręta

L

i

masa

ciężar

elementu

m

kN/m

kN

G1

1,904

HEA 120

0,1990

0,379

G2

1,904

HEA 120

0,1990

0,379

G3

1,904

HEA 120

0,1990

0,379

G4

1,904

HEA 120

0,1990

0,379

G5

1,904

HEA 120

0,1990

0,379

G6

1,904

HEA 120

0,1990

0,379

G7

1,904

HEA 120

0,1990

0,379

G8

1,904

HEA 120

0,1990

0,379

…

…

…

D1

2,004

HEA 100

0,1670

0,335

D2

2,004

HEA 100

0,1670

0,335

D3

2,004

HEA 100

0,1670

0,335

D4

2,004

HEA 100

0,1670

0,335

D5

6,015

HEA 100

0,1670

1,005

…

…

…

K1

2,004

RK 40x40x4

0,0439

0,088

K2

2,004

RK 40x40x4

0,0439

0,088

K3

2,004

RK 40x40x4

0,0439

0,088

K4

2,004

RK 40x40x4

0,0439

0,088

…

…

…

S1

0,625

RK 40x40x4

0,0439

0,027

S2

1,250

RK 40x40x4

0,0439

0,055

S3

0,625

RK 40x40x4

0,0439

0,027

S4

0,625

RK 40x40x4

0,0439

0,027

S5

1,250

RK 40x40x4

0,0439

0,055

S6

0,625

RK 40x40x4

0,0439

0,027

SUMA

5,946

5%

6,243

nr pręta

Przekrój pręta

z dodatkiem 5% na spoiny

36

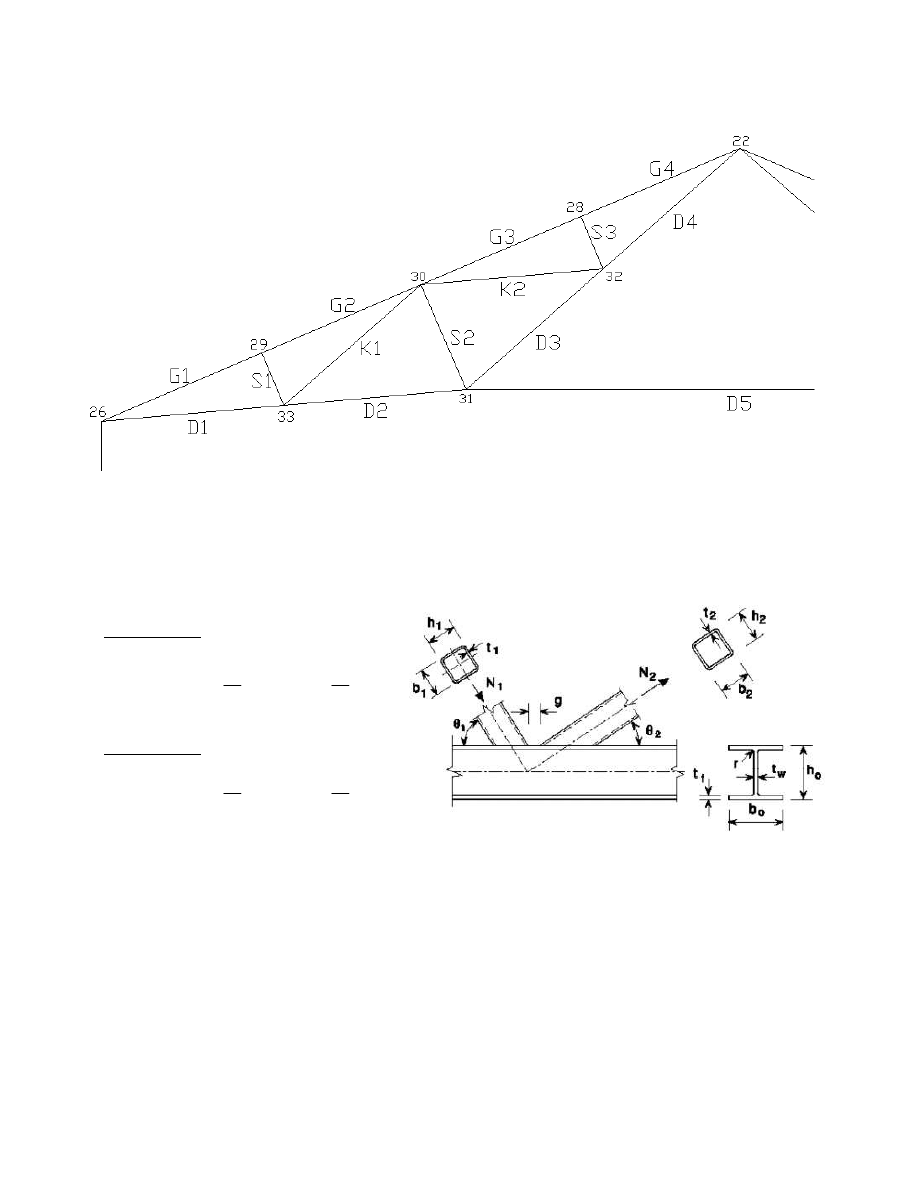
Numeracja prętów i węzłów w kratownicy

3.4. Obliczenia nośności węzłów w skratowaniu:

Zakres ważności formuł obliczeniowych węzłów spawanych:

Węzeł T, Y, X i K, N z odstępem wg. EN 1993-1-8:2005+AC:2005 7.6, Tablica 7.20, Tablica 7.21:

RK 40x40x4:

b1

40

mm

=

t1

4

mm

=

krzyżulec K1 K2

,

b1

t1

10

=

b1

t1

50

<

RK 40x40x4:

b2

40

mm

=

t2

4

mm

=

słupek

S2

b2

t2

10

=

b2

t2

50

<

tablica 7.21 węzeł K

3.4.1. Nośności obliczeniowe węzłów spawanych między prętami górnego
skratowania

:

37

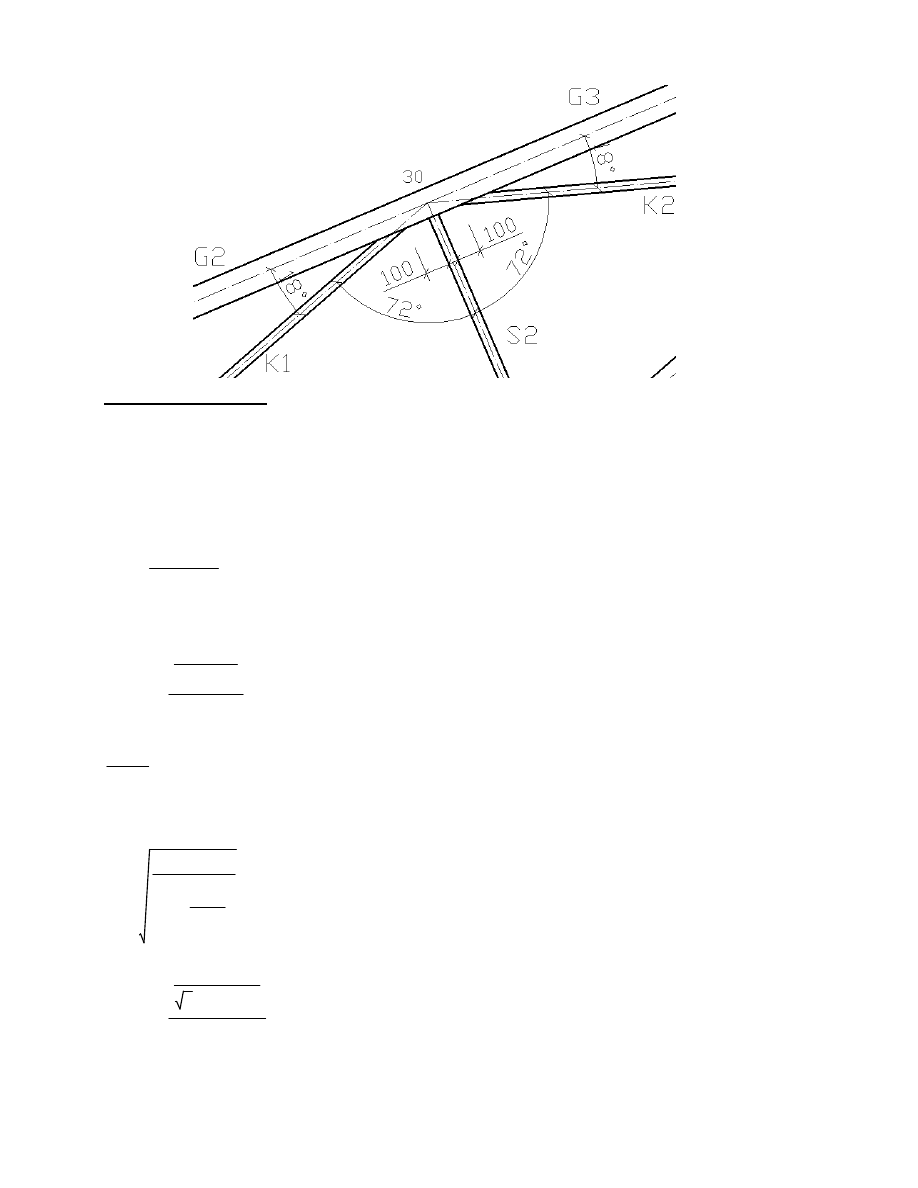
Węzeł 30 pręt 22 (K2):

θ30.1

18

deg

=

θ30.2

90

deg

=

fy0

235

MPa

=

γM5

1.0

=

h0

114

mm

=

b0

120

mm

=

tf

8

mm

=

tw

5

mm

=

Właściwości przekroju HEA 120:

A0

25.3

cm

2

=

r

12

mm

=

NEd.1

41.726

kN

=

Siła występująca w skratowaniu

g

100

mm

=

odstęp

bw

b1

sin

θ30.1

(

)

5

tf r

+

(

)

⋅

+

22.944

cm

⋅

=

=

>

2

t1

⋅

10

tf r

+

(

)

⋅

+

20.8

cm

⋅

=

stąd:

Niestateczność środnika pasa:

bw

20.8

cm

=

Ni.Rd

fy0 tw

⋅

bw

⋅

sin

θ30.1

(

)

γM5

790.895

kN

⋅

=

=

tab. 7.21

NEd.1

Ni.Rd

0.053

=

WARUNEK SPEŁNIONY

Nośność na ścięcie pasa:

α

1

1

4

g

2

⋅

3

tf

2

⋅

+

















0.069

=

=

Av

A0

2

α

−

(

)

b0

⋅

tf

⋅

−

tw

2

r

+

(

)

tf

+

9.084

cm

2

⋅

=

=

Nl.Rd

fy0 Av

⋅

3

sin

θ30.1

(

)

⋅

γM5

398.822

kN

⋅

=

=

38

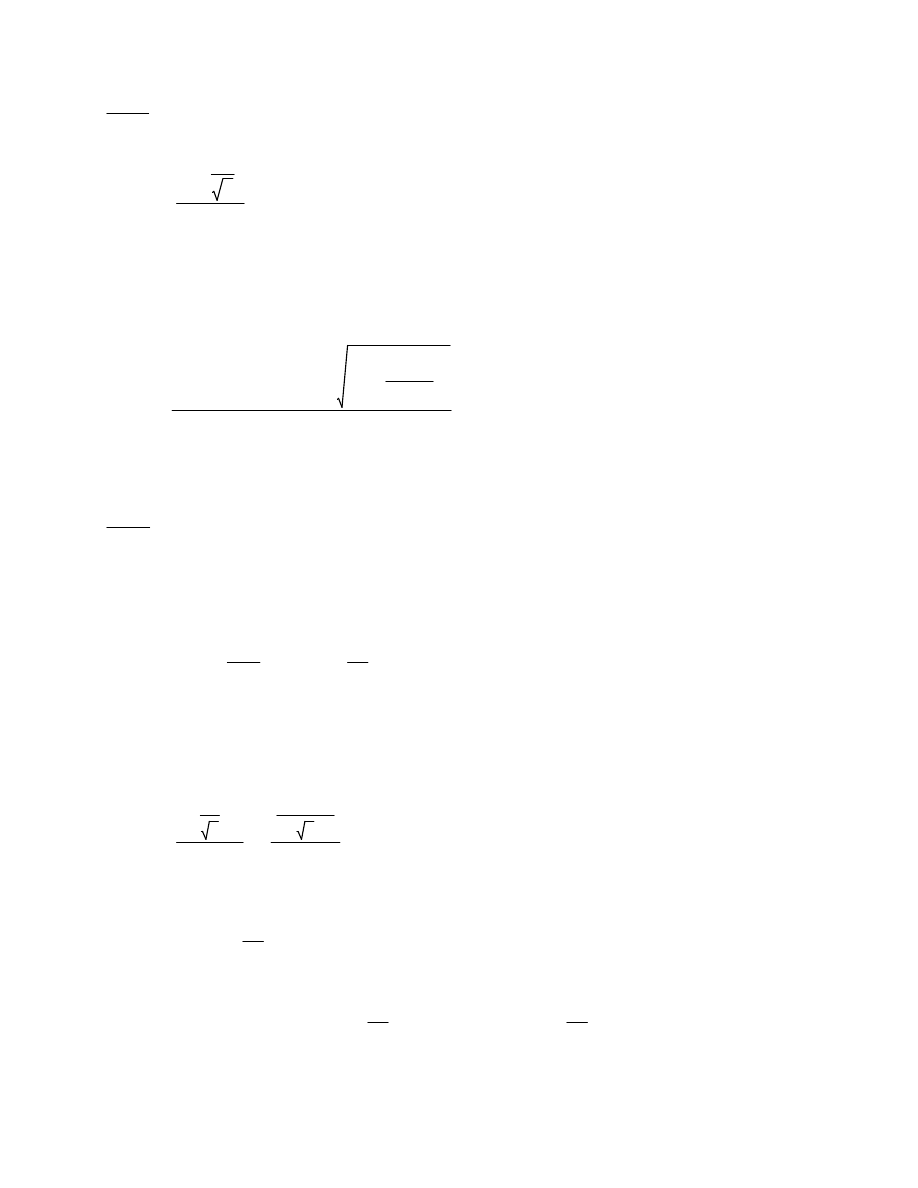
NEd.1

Nl.Rd

0.105

=

WARUNEK SPEŁNIONY

Vpl.Rd

Av

fy

3













⋅

γM0

123.243

kN

⋅

=

=

VEd.1

NEd.1

=

VEd

VEd.1 sin θ30.1

(

)

⋅

12.894

kN

⋅

=

=

N0.Rd

A0 Av

−

(

)

fy0

⋅

Av fy0

⋅

1

VEd

Vpl.Rd













2

−

⋅

+

γM5

593.379

kN

⋅

=

=

N0.Ed

437.185kN

=

siła w pasie

N0.Ed
N0.Rd

0.737

=

WARUNEK SPEŁNIONY

Metoda uproszczona obliczania nośności spoin pachwinowych

pkt 4.5.3.3 PN-EN 1993-1-8

leff.s

4

b1

⋅

160

mm

⋅

=

=

długość spoiny łączącej skratowanie z pasem kratownicy

Fw.Ed

NEd.1

1

leff.s

⋅

260.788

kN

m

⋅

=

=

wartość obliczeniowa siły na jednostkę długości spoiny

a

3

mm

=

przyjęta grubość spoiny pachwinowej

βw

0.8

=

współczynnik korelacji dla stali S235

Tablica 4.1 PN-EN 1993-1-8

γM2

1.25

=

współczynnik częściowy

Tablica 2.1 PN-EN 1993-1-8

fvw.d

fu

3

βw γM2

⋅

410

MPa

⋅

3

0.8 1.25

⋅

=

2.367

10

8

×

Pa

⋅

=

=

Fw.Rd

fvw.d a

⋅

2.367

10

8

×

Pa

⋅

3

mm

⋅

⋅

=

=

fvw.d a

⋅

Fw.Rd

710.141

kN

m

⋅

=

Fw.Ed Fw.Rd

≤

Fw.Ed

260.788

kN

m

⋅

=

<

Fw.Rd

710.141

kN

m

⋅

=

WARUNEK SPEŁNIONY

39

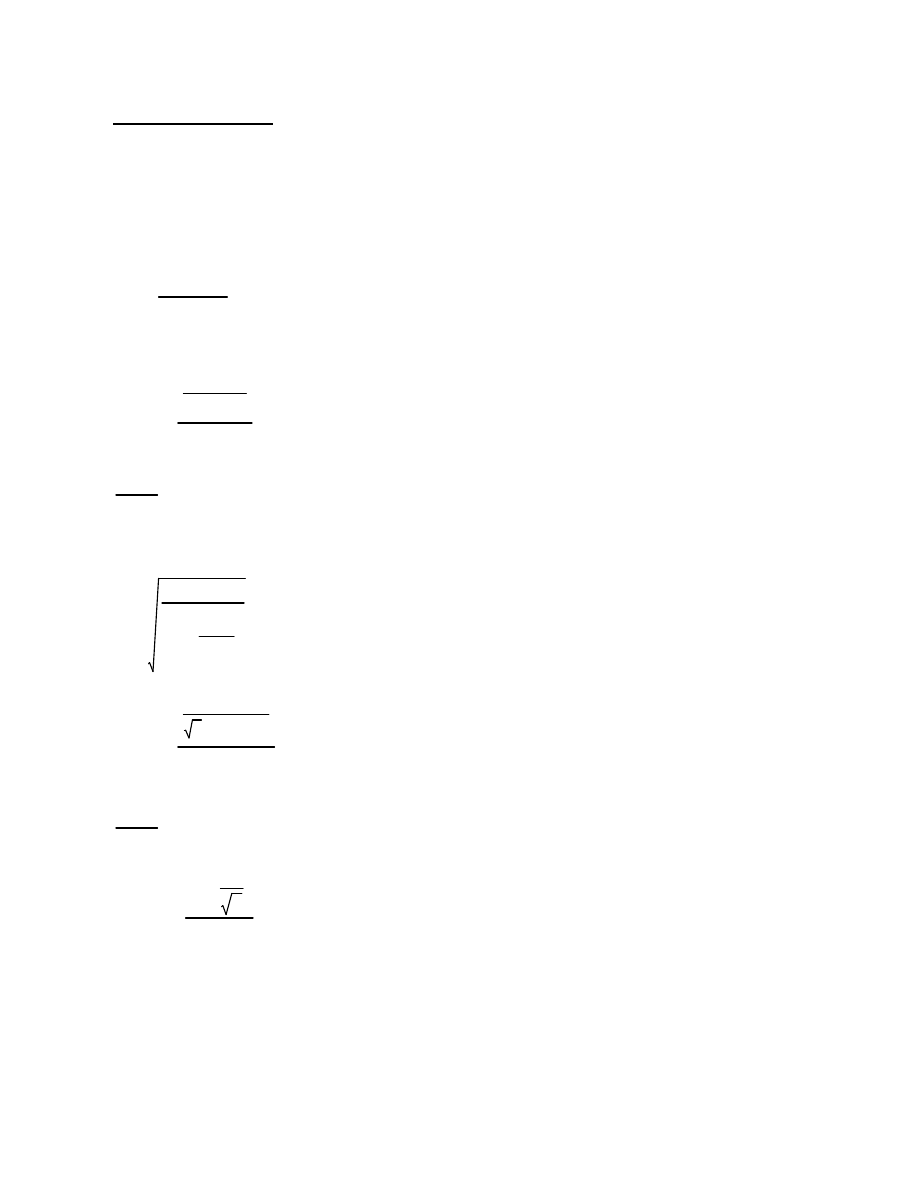
Węzeł 30 pręt 28 (S2):

θ30.1

18

deg

=

θ30.2

90

deg

=

fy0

235

MPa

=

γM5

1.0

=

h0

114

mm

=

b0

120

mm

=

tf

8

mm

=

tw

5

mm

=

Właściwości przekroju HEA 120:

A0

25.3

cm

2

=

r

12

mm

=

NEd.1

15.993

kN

=

Siła występująca w skratowaniu

g

100

mm

=

odstęp

bw

b1

sin

θ30.2

(

)

5

tf r

+

(

)

⋅

+

14

cm

⋅

=

=

<

2

t1

⋅

10

tf r

+

(

)

⋅

+

20.8

cm

⋅

=

stąd:

Niestateczność środnika pasa:

bw

14

cm

⋅

=

Ni.Rd

fy0 tw

⋅

bw

⋅

sin

θ30.2

(

)

γM5

164.5

kN

⋅

=

=

tab. 7.21

NEd.1

Ni.Rd

0.097

=

WARUNEK SPEŁNIONY

Nośność na ścięcie pasa:

α

1

1

4

g

2

⋅

3

tf

2

⋅

+

















0.069

=

=

Av

A0

2

α

−

(

)

b0

⋅

tf

⋅

−

tw

2

r

+

(

)

tf

+

9.084

cm

2

⋅

=

=

Nl.Rd

fy0 Av

⋅

3

sin

θ30.1

(

)

⋅

γM5

398.822

kN

⋅

=

=

NEd.1

Nl.Rd

0.04

=

WARUNEK SPEŁNIONY

Vpl.Rd

Av

fy

3













⋅

γM0

123.243

kN

⋅

=

=

VEd.1

NEd.1

=

VEd

VEd.1 sin θ30.2

(

)

⋅

15.993

kN

⋅

=

=

40

N0.Rd

A0 Av

−

(

)

fy0

⋅

Av fy0

⋅

1

VEd

Vpl.Rd













2

−

⋅

+

γM5

592.745

kN

⋅

=

=

N0.Ed

182.303

kN

=

siła w pasie

N0.Ed
N0.Rd

0.308

=

WARUNEK SPEŁNIONY

Metoda uproszczona obliczania nośności spoin pachwinowych

pkt 4.5.3.3 PN-EN 1993-1-8

leff.s

4

b1

⋅

160

mm

⋅

=

=

długość spoiny łączącej skratowanie z pasem kratownicy

Fw.Ed

NEd.1

1

leff.s

⋅

99.956

kN

m

⋅

=

=

wartość obliczeniowa siły na jednostkę długości spoiny

a

3

mm

=

przyjęta grubość spoiny pachwinowej

βw

0.8

=

współczynnik korelacji dla stali S235

Tablica 4.1 PN-EN 1993-1-8

γM2

1.25

=

współczynnik częściowy

Tablica 2.1 PN-EN 1993-1-8

fvw.d

fu

3

βw γM2

⋅

410

MPa

⋅

3

0.8 1.25

⋅

=

2.367

10

8

×

Pa

⋅

=

=

Fw.Rd

fvw.d a

⋅

2.367

10

8

×

Pa

⋅

3

mm

⋅

⋅

=

=

fvw.d a

⋅

Fw.Rd

710.141

kN

m

⋅

=

Fw.Ed Fw.Rd

≤

Fw.Ed

99.956

kN

m

⋅

=

<

Fw.Rd

710.141

kN

m

⋅

=

WARUNEK SPEŁNIONY

41

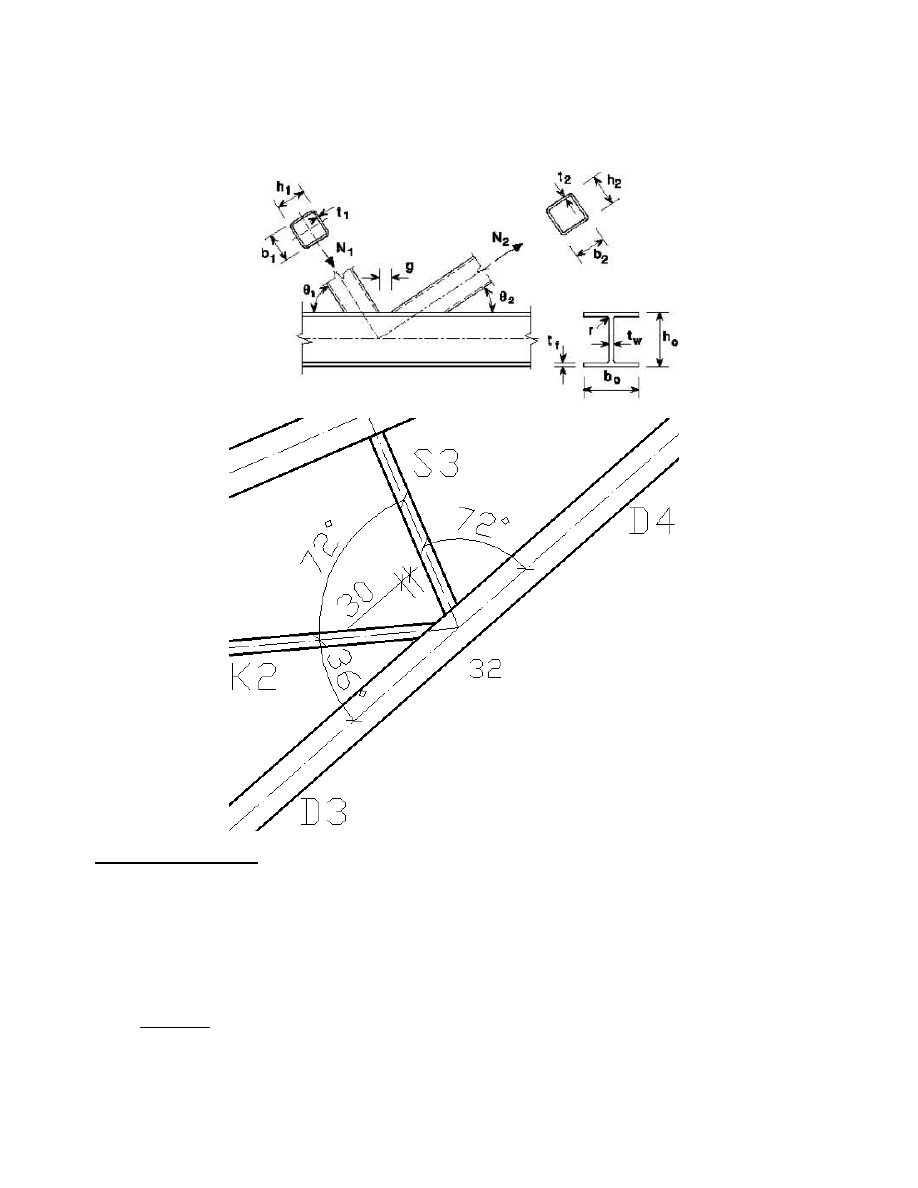
3.4.2. Nośności obliczeniowe węzłów spawanych między prętami dolnego
skratowania

:

tablica 7.21 węzeł K z odstępem

Węzeł 32 pręt 22 (K2):

θ32.1

36

deg

=

θ32.2

72

deg

=

fy0

235

MPa

=

γM5

1.0

=

h0

96

mm

=

b0

100

mm

=

tf

8

mm

=

tw

5

mm

=

Właściwości przekroju HEA 100

A0

21.2

cm

2

=

r

12

mm

=

NEd.1

41.726

kN

=

g

30

mm

=

bw

b1

sin

θ32.1

(

)

5

tf r

+

(

)

⋅

+

16.805

cm

⋅

=

=

<

2

t1

⋅

10

tf r

+

(

)

⋅

+

20.8

cm

⋅

=

stąd:

Niestateczność środnika pasa:

bw

16.805

cm

⋅

=

42

Ni.Rd

fy0 tw

⋅

bw

⋅

sin

θ32.1

(

)

γM5

335.941

kN

⋅

=

=

tab. 7.21

NEd.1

Ni.Rd

0.124

=

WARUNEK SPEŁNIONY

Nośność na ścięcie pasa:

α

1

1

4

g

2

⋅

3

tf

2

⋅

+

















0.225

=

=

Av

A0

2

α

−

(

)

b0

⋅

tf

⋅

−

tw

2

r

+

(

)

tf

+

9.32

cm

2

⋅

=

=

Nl.Rd

fy0 Av

⋅

3

sin

θ32.1

(

)

⋅

γM5

215.135

kN

⋅

=

=

NEd.1

Nl.Rd

0.194

=

WARUNEK SPEŁNIONY

Vpl.Rd

Av

fy

3













⋅

γM0

126.453

kN

⋅

=

=

VEd.1

NEd.1

=

VEd

VEd.1 sin θ32.1

(

)

⋅

24.526

kN

⋅

=

=

N0.Rd

A0 Av

−

(

)

fy0

⋅

Av fy0

⋅

1

VEd

Vpl.Rd













2

−

⋅

+

γM5

494.041

kN

⋅

=

=

N0.Ed

71.497

kN

=

siła w pasie

N0.Ed
N0.Rd

0.145

=

WARUNEK SPEŁNIONY

Metoda uproszczona obliczania nośności spoin pachwinowych

pkt 4.5.3.3 PN-EN 1993-1-8

43

leff.s

4

b1

⋅

160

mm

⋅

=

=

długość spoiny łączącej skratowanie z pasem kratownicy

Fw.Ed

NEd.1

1

leff.s

⋅

260.788

kN

m

⋅

=

=

wartość obliczeniowa siły na jednostkę długości spoiny

a

3

mm

=

przyjęta grubość spoiny pachwinowej

Fw.Rd

fvw.d a

⋅

2.367

10

8

×

Pa

⋅

3

mm

⋅

⋅

=

=

fvw.d a

⋅

Fw.Rd

710.141

kN

m

⋅

=

Fw.Ed

Fw.Rd

≤

Fw.Ed

260.788

kN

m

⋅

=

<

Fw.Rd

710.141

kN

m

⋅

=

WARUNEK SPEŁNIONY

Węzeł 32 Pręt 21 (S3):

NEd.2

2.984

kN

=

bw

b2

sin

θ32.2

(

)

5

tf r

+

(

)

⋅

+

=

bw

14.206

cm

⋅

=

<

2

t1

⋅

10

tf r

+

(

)

⋅

+

20.8

cm

⋅

=

Niestateczność środnika pasa:

Ni.Rd

fy0 tw

⋅

bw

⋅

sin

θ32.2

(

)

γM5

175.509

kN

⋅

=

=

NEd.2

Ni.Rd

0.017

=

WARUNEK SPEŁNIONY

Nośność na ścięcie pasa:

α

1

1

4

g

2

⋅

3

tf

2

⋅

+

















0.225

=

=

Av

A0

2

α

−

(

)

b0

⋅

tf

⋅

−

tw

2

r

+

(

)

tf

+

9.32

cm

2

⋅

=

=

Nl.Rd

fy0 Av

⋅

3

sin

θ32.2

(

)

⋅

γM5

132.961

kN

⋅

=

=

NEd.2

Nl.Rd

0.022

=

WARUNEK SPEŁNIONY

44

Vpl.Rd

Av

fy

3













⋅

γM0

126.453

kN

⋅

=

=

VEd.2

NEd.2

=

VEd

VEd.2 sin θ32.2

(

)

⋅

=

N0.Rd

A0 Av

−

(

)

fy0

⋅

Av fy0

⋅

1

VEd

Vpl.Rd













2

−

⋅

+

γM5

498.145

kN

⋅

=

=

N0.Ed

71.497

kN

=

siła w pasie

N0.Ed
N0.Rd

0.144

=

WARUNEK SPEŁNIONY

Metoda uproszczona obliczania nośności spoin pachwinowych

pkt 4.5.3.3 PN-EN 1993-1-8

leff.s

4

b2

⋅

160

mm

⋅

=

=

długość spoiny łączącej skratowanie z pasem kratownicy

Fw.Ed

NEd.2

1

leff.s

⋅

18.65

kN

m

⋅

=

=

wartość obliczeniowa siły na jednostkę długości spoiny

a

3

mm

⋅

=

przyjęta grubość spoiny pachwinowej

Fw.Rd

fvw.d a

⋅

2.367

10

8

×

Pa

⋅

3

mm

⋅

⋅

=

=

fvw.d a

⋅

Fw.Rd

710.141

kN

m

⋅

=

Fw.Ed

Fw.Rd

≤

Fw.Ed

18.65

kN

m

⋅

=

<

Fw.Rd

710.141

kN

m

⋅

=

WARUNEK SPEŁNIONY

Zniszczenie skratowania:

γ

b0

2

tf

⋅

6.25

=

=

β

1

0.03

γ

⋅

−

≤

β

b1 b1

+

b2

+

b2

+

4

b0

⋅

0.4

=

=

<

1

0.03

γ

⋅

−

0.813

=

WARUNEK SPEŁNIONY

g

tf

20

28

β

−

<

g

tf

3.75

=

<

20

28

β

−

8.8

=

WARUNEK SPEŁNIONY

45

należy sprawdzić czy nastapi zniszczenie skratowania:

b1

40

mm

⋅

=

h1

b1

40

mm

⋅

=

=

b2

40

mm

⋅

=

h2

b2

40

mm

⋅

=

=

b1 h1

+

2

t1

⋅

−

7.2

cm

⋅

=

peff

tw

2

r

+

7

tf

⋅

fy
fy

⋅

+

8.5

cm

⋅

=

=

<

stąd:

peff

7.2

cm

=

b2 h2

+

2

t2

⋅

−

7.2

cm

⋅

=

Ni.Rd

2

fy

⋅

t1

⋅

peff

γM5

⋅

135.36

kN

⋅

=

=

NEd.2

Ni.Rd

0.022

=

< 1

WARUNEK SPEŁNIONY

46