Adam Paweł Zaborski

Project “The development of the didactic potential of Cracow University of Technology in the range of

modern construction” is co-financed by the European Union within the confines of the European Social Fund

and realized under surveillance of Ministry of Science and Higher Education.

5. Simple beams

Introduction

Differential relationships between cross-section forces

In the case of straight beam we have the boundary value problem (BVP)

1

:

)

(

)

(

),

(

)

(

),

(

)

(

2

2

x

q

x

x

M

x

q

x

x

Q

x

Q

x

x

M

−

=

⇒

−

=

=

d

d

d

d

d

d

The order of the bending moment equation is two orders greater than the continuous loading, see the table
below.

continuous loading

bending moment equation (diagram)

q

= 0, no continuous loading

linear

q(x)

= const.

2

nd

order (nonlinear, 2

nd

order parabola)

q(x)

is linearly variable

3

rd

order (nonlinear, 3

rd

order parabola)

It results from the sign convention, that the bending moment diagram convexes in the sense of the
continuous loading. Moreover, the bending moment maximum is attained at the section where the shear
force vanishes.

Example

2.0

30 kN

15 kN/m

25 kNm

2.5

2.0

3.5

2.0

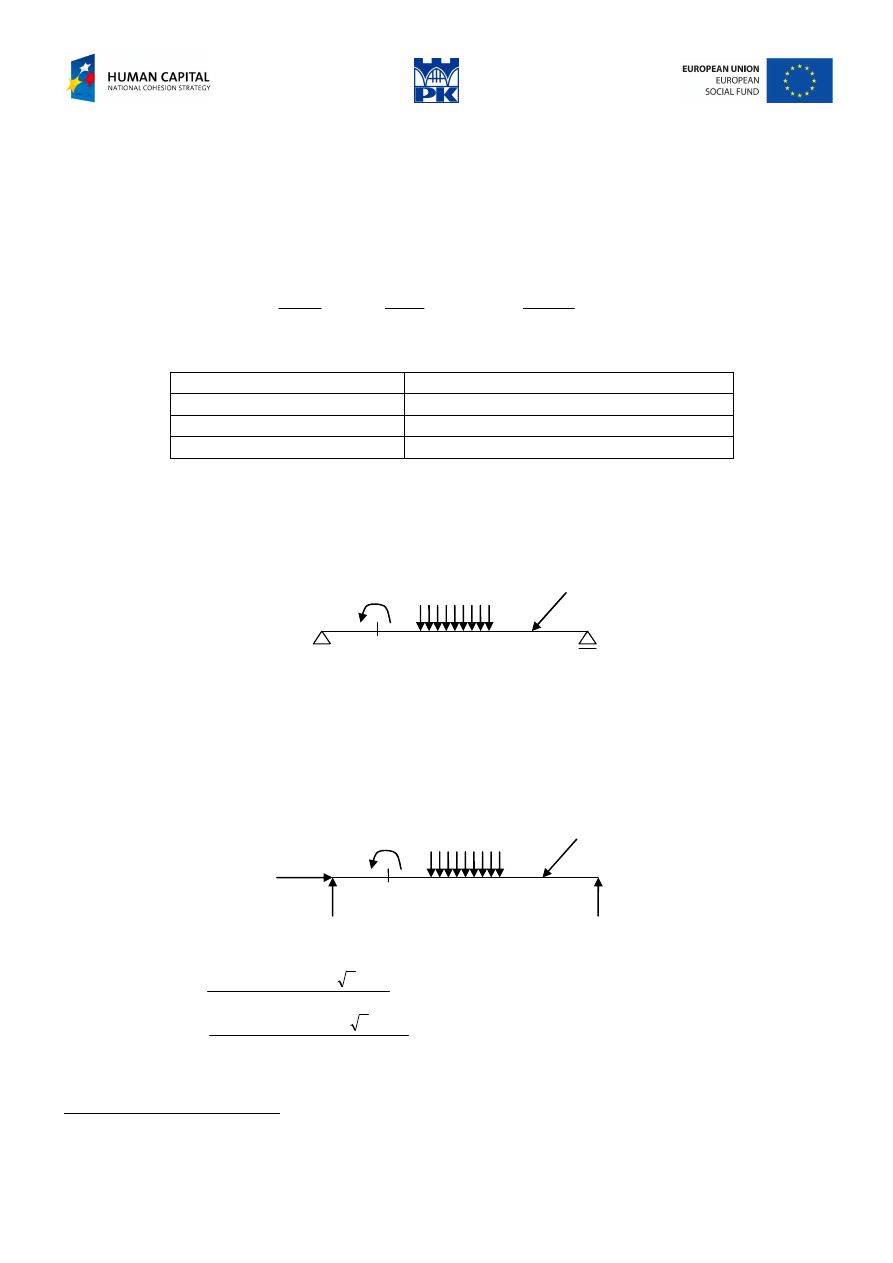
Fig. 5.1 Simply supported beam

Write cross-section equations and draw their diagrams for the beam in Fig. 5.1. If not stated, the
dimensions are in [m] and the angle is 45 degrees.

Solution

Beam reactions:

R

B

H

A

V

A

2.0

30 kN

15 kN/m

25 kNm

2.5

2.0

3.5

2.0

Fig. 5.2 Beam with reactions

∑

=

⋅

+

⋅

⋅

+

=

⇒

=

78

.

30

12

2

2

/

2

30

75

.

5

5

.

3

15

25

0

A

B

V

M

kN

∑

=

⋅

+

⋅

⋅

+

−

=

⇒

=

94

.

42

12

10

2

/

2

30

25

.

6

5

.

3

15

25

0

B

A

R

M

kN

21

.

21

0

=

⇒

=

∑

A

H

X

kN

Verification:

1

Boundary value problem – a differential equation (or set of equations) with the boundary conditions (BCs). For the equation of

n

-th order there are n BCs.

Adam Paweł Zaborski

Project “The development of the didactic potential of Cracow University of Technology in the range of

modern construction” is co-financed by the European Union within the confines of the European Social Fund

and realized under surveillance of Ministry of Science and Higher Education.

∑

≈

=

−

=

−

+

=

−

−

+

⋅

=

0

01

.

0

72

.

73

71

.

73

72

.

73

21

.

21

5

.

52

94

.

42

78

.

30

2

/

2

30

5

.

3

15

Y

, OK!

Cross-section forces equations:

5

.

2

0

<

< x











−

=

=

=

=

=

[kN]

[kN]

[kNm]

21

.

21

)

(

78

.

30

)

(

95

.

76

)

5

.

2

(

,

0

)

0

(

,

78

.

30

)

(

x

N

x

Q

M

M

x

x

M

5

.

4

5

.

2

<

< x











−

=

=

=

=

−

=

[kN]

[kN]

[kNm]

21

.

21

)

(

78

.

30

)

(

5

.

113

)

5

.

4

(

,

95

.

51

)

5

.

2

(

,

25

78

.

30

)

(

x

N

x

Q

M

M

x

x

M

8

5

.

4

<

< x

(

)

















−

=

−

=

=

−

⋅

−

=

=

=

−

−

−

=

[kN]

[kN]

[kNm]

21

.

21

)

(

72

.

21

)

8

(

,

78

.

30

)

5

.

4

(

),

5

.

4

(

15

78

.

30

)

(

4

.

129

)

8

(

,

5

.

113

)

5

.

4

(

,

2

5

.

4

15

25

78

.

30

)

(

2

x

N

Q

Q

x

x

Q

M

M

x

x

x

M

(due to change of shear force’s sign, we calculate the bending moment extremum)

[kNm]

1

.

145

)

552

.

6

(

,

552

.

6

0

)

(

=

=

→

=

M

x

x

Q

(we use continuous loading resultant)

10

8

<

< x











−

=

=

⋅

=

=

=

−

⋅

⋅

−

−

=

[kN]

[kN]

[kNm]

21

.

21

72

21

5

3

15

78

30

93

.

85

)

10

(

,

4

.

129

)

8

(

),

25

.

6

(

5

.

3

15

25

78

.

30

)

(

N(x)

.

-

.

-

.

Q(x)

M

M

x

x

x

M

(for the last interval we use another coordinate,

1

x

)

2

0

1

<

< x











≡

−

≅

−

=

−

−

=

=

−

=

=

≅

=

=

=

0

)

,

94

.

42

93

.

42

2

/

2

30

72

.

21

10

94

.

42

)

(

)

10

(

88

.

85

)

2

(

,

0

)

0

(

,

94

.

42

)

(

1

1

1

1

N(x

OK

(

:

ver.

[kN],

[kNm]

V

)-P

x

Q

x

Q

x

M

M

M

x

x

M

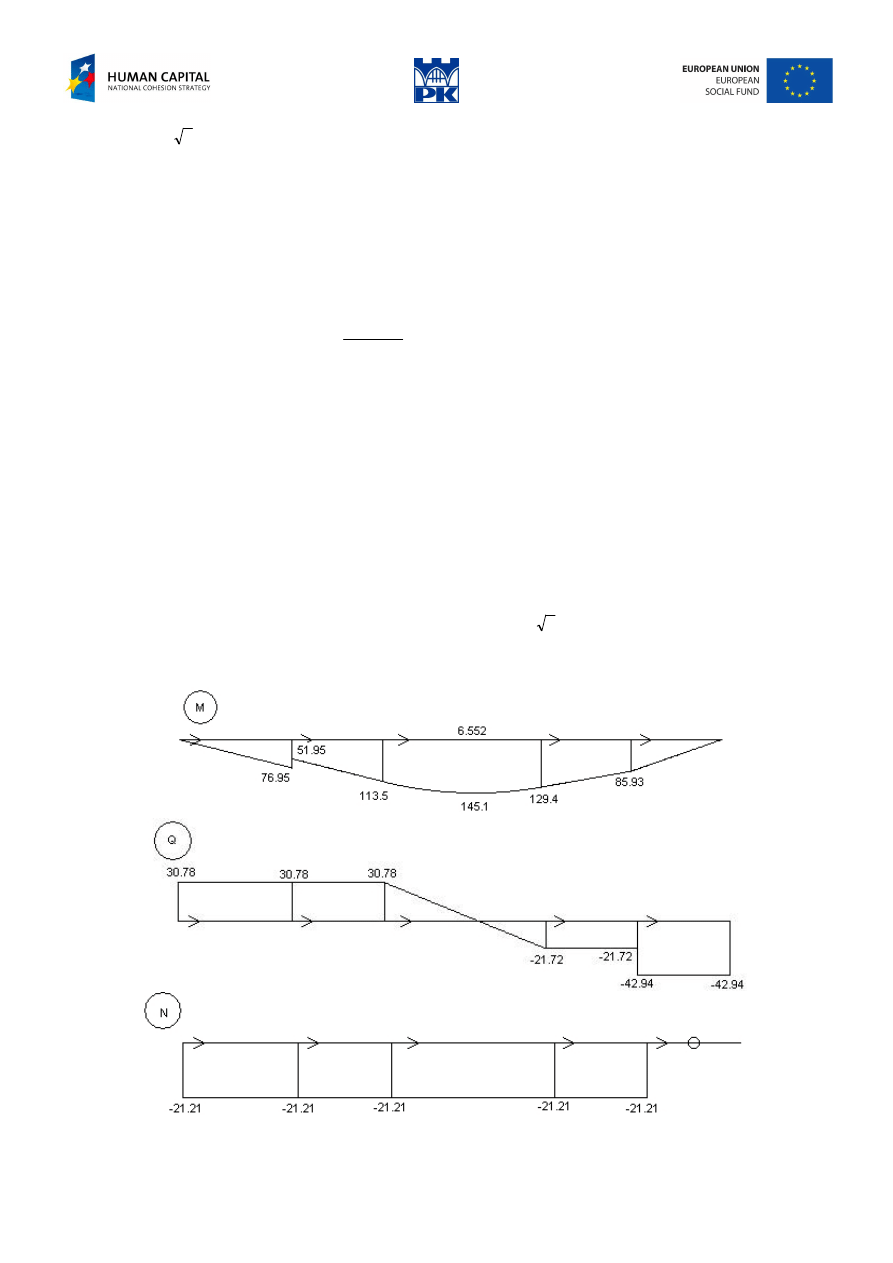
Cross-section forces diagrams:

Fig. 5.3 Cross-section forces diagrams

Adam Paweł Zaborski

Project “The development of the didactic potential of Cracow University of Technology in the range of

modern construction” is co-financed by the European Union within the confines of the European Social Fund

and realized under surveillance of Ministry of Science and Higher Education.

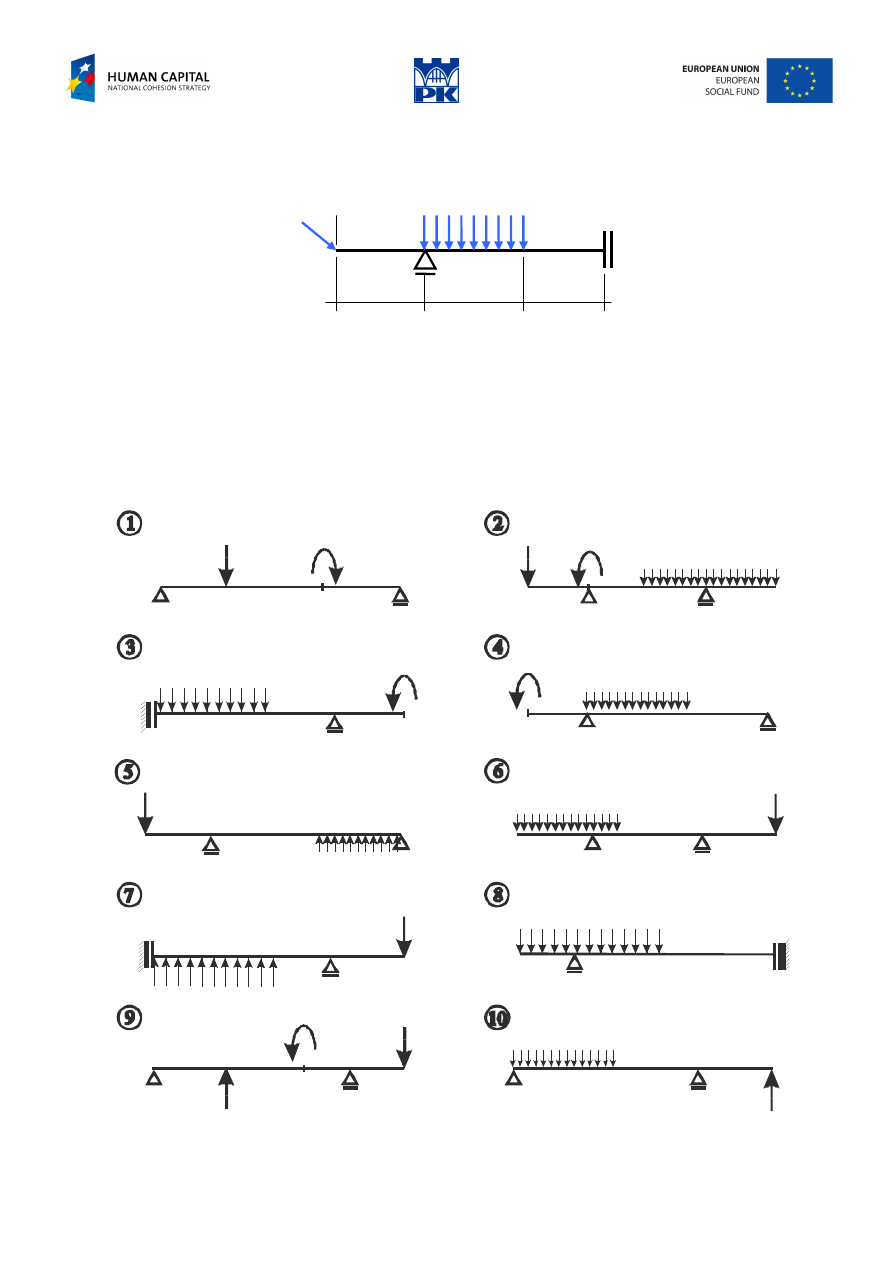
Workshop theme

Construct the cross-section forces diagrams for the beam in Fig. 5.4.

α

q

P

a

b

c

Fig. 5.4 Simple beam

Input data:
P

= ...........(10÷150 kN),

α

= ........(15°÷75°), q = .........(10÷80 kN/m), a = ......, b = ..., c = ......(1÷3.5 m)

Review problems

Simple beams

Fig. 5.5 Simple beams – review problems

Adam Paweł Zaborski

Project “The development of the didactic potential of Cracow University of Technology in the range of

modern construction” is co-financed by the European Union within the confines of the European Social Fund

and realized under surveillance of Ministry of Science and Higher Education.

Addendum

Hints

Tip: There are two typical students’ errors:

−

an incomplete section; section does not determine the subsets properly, in effect the subsets are not

disjoint

−

a section without suitable internal forces or cross-section forces

Tip: The best proportion of the diagram is the height/length ratio = 1/3 (approx.)