
Adam Paweł Zaborski
Project “The development of the didactic potential of Cracow University of Technology in the range of
modern construction” is co-financed by the European Union within the confines of the European Social Fund
and realized under surveillance of Ministry of Science and Higher Education.
14. Stress state
Introduction
Definitions
The stress vector
i
p
is internal forces’ density in the plane with outer normal
i
n
, parallel to the axis of the
coordinate system.
The stress tensor
ij
σ
is a matrix of stress vector components written in the given coordinate system:
j
ij
i
n
p
σ
=
The components of the stress tensor in the new coordinate system may be computed by the transformation
formula:
– in index notation:
kl
jl
ik
ij
a
a
σ
=
σ
– in matrix notation:
T
A
Σ
A
Σ
⋅
⋅
=
'
where:
–
ij
σ
is a stress matrix with normal stress on the diagonal and shear stress elsewhere:
4
4
4
3
4
4
4
2
1
4
4
4
3
4
4
4
2
1
notation)
ng
(engineeri
z
zy
zx
yz
y
yz
xz
xy
x
notation)
c
(scientifi
σ
τ
τ
τ
σ
τ
τ
τ
σ
=
σ
σ
σ
σ
σ
σ
σ
σ
σ
=
σ
33
32
31
23
22
21
13
12
11
ij
The first index specifies the direction of the outer unit normal of the section plane. The second index
specifies the stress direction.
A matrix can be the stress matrix if it fulfills the partial differential equations (PDE) of internal equilibrium
(Navier’s equations):
0
0
0
=
+
∂
σ
∂
+
∂
τ
∂
+
∂
τ
∂
=
+
∂
τ
∂
+
∂
σ
∂
+
∂
τ
∂
=
+
∂
τ
∂
+
∂
τ
∂
+
∂
σ
∂
z
z
yz
xz
y
yx
y
xy
x
xx
xy
x
P
z
y
x
P
z
y
x
P
z
y
x
,
(
)
x
y
x
j
i
P
i
j
ij
,
,
,
,
0
,
=
=
+
σ
and the static boundary conditions:
z
z
y
yz
x
xz
z
z
yz
y
y
x
xy
y
z
xz
y
xy
x
x
x
n
n
n
q
n
n
n
q
n
n
n
q
σ
+
τ
+
τ
=
τ
+
σ
+
τ
=
τ
+
τ
+
σ
=
,
(
)
z
y
x
j
i
n
q
j
ij
i
,
,
,
,
=
σ
=
Stress state analysis
The main goal of the stress state analysis is to find such directions of the sections where the stresses values
are extreme. This happens when the outer normal and the stress vector are parallel, and leads to the
eigenvalues problem:
(
)
0
=
λδ
−
σ
→
λ
=
σ
j
ij
ij
i
j
ij
v
v
v
.
The set of algebraic linear equation system has non-zero (non-trivial) solution if and only if the main
determinant of the system is zero. From this condition we get a cubic equation for the principal stress
values:

Adam Paweł Zaborski
Project “The development of the didactic potential of Cracow University of Technology in the range of
modern construction” is co-financed by the European Union within the confines of the European Social Fund
and realized under surveillance of Ministry of Science and Higher Education.
0
3
2
2
1
3
=
−
σ
+
σ
−
σ
I
I
I
.
The stress matrix in the principal directions is diagonal and the shear components are zero. From algebra
we know that the principal normal stresses are extreme and the principal directions are perpendicular:
4
4
4
3
4
4
4
2
1
4
4
4
3
4
4
4
2
1
)
3
,
2
,
1
(
)
,
,
(
0
0
0
0
0
0
in
3
2
1
in
z
zy
zx
yz
y
yz
xz
xy
x
σ
σ
σ
⇒
σ
τ
τ
τ
σ
τ
τ
τ
σ
z
y
x
Mohr’s circles
The domain of possible results due to the transformation of a coordinate system is illustrated by Mohr’s
circles, Fig. 14.1 with the shaded region.
τ
xy
2α
σ
2
σ
τ
σ
1
σ
y
σ
x
σ
3
Fig. 14.1 Mohr’s circles
Examples
Three-dimensional state of stress
The stress matrix and the outer normal vector of a section are given. Determine the principal directions and
stresses, the normal and tangential components of the stress vector for the section.
−
−
−
=
σ
120
60
40
60
85
17
40
17
240
ij
,
(
)
2
,
2
,
7
−
n
Solution
We calculate the invariants:
205
120
85
240
)
(
1
=
−
+
=
σ
=
ij
I
tr
24089
120
40
40
240
120
60
60
85
85
17
17
240
2
−
=
−
+
−
+
−
−
=
I
3494920
60
40
85
17
40
120
40
60
17
17
120
60
60
85
240
)
det(
3
=
−
⋅
+
−
−
⋅
+
−
⋅
=
σ
=
ij
I
The cubic equation:
0
3494920
24089
205
2
3
=
−
σ
⋅
−
σ
⋅
−
σ
has the roots:
1
.
141
,
0
.
101
,
1
.
245
3
2
1
−
=
σ
=
σ
=
σ
.
The principal directions are given by the transformation matrix:
Adam Paweł Zaborski
Project “The development of the didactic potential of Cracow University of Technology in the range of
modern construction” is co-financed by the European Union within the confines of the European Social Fund
and realized under surveillance of Ministry of Science and Higher Education.
3
2
1
z
y
x
a
ij
−
−
=
9583
.
0
2686
.
0
9583
.
0
2627
.
0
9624
.
0
0689
.
0
1123
.
0
0404
.
0
9929
.
0
.
We calculate the length of the normal vector:
8730
.
3
4
4
7
=
+
+
=
n
and we normalize the vector (to obtain unit normal vector)
)
5164
.
0
,
5164
.
0
,
6831
.
0
(
−
n
The stress vector is:
)
3
.
120
,
30
.
1
,
5
.
134
(
p
n
p
i
ij
j
→
σ
=
its length:
5
.
180
=
p
the normal component of the stress vector is:
45
.
30
=
=
⋅
=
σ
i
i
n
p
n
p
and the tangential component is:
9
.
177
2
2
=
σ
−
=
τ
p
Plane stress
For the given stress tensor, determine principal stresses and directions.
−
=
σ
10
16
16
40
T
.
Solution
The principal stresses for the plane state of stress are:
68
.
14
16
2
10
40
2
10
40
2
2
68
.
44
16
2
10
40
2
10
40
2
2
2
2
2
2
2
2
2
2
2
1
−
=
+
+
−
−
=
τ
+
σ
−
σ
−
σ
+
σ
=
σ
=
+
+
+
−
=
τ
+
σ
−
σ
+
σ
+
σ
=
σ
y
x
y
x
y
x
y
x
y
x
y
x
,
The principal directions:
)
7
.
73
(
,
286
.
1
4175
.
3
16
40
68
.
14
tan
)
3
.
16
(
,
285
.
0
2925
.
0
16
40
68
.
44
tan
2
2
2
1
1
1
°
−
−
=
α
⇒
−
=
−
−
=
τ
σ
−
σ
=
α
°
=
α
→
=
−
=
τ
σ
−
σ
=
α
y
x
x
y
x
x
The transformation matrix and the stress tensor in principal directions are, cf. Fig. 14.2:
9598
.
0
2808
.
0
2808
.
0
9598
.
0
2
y
x
x
−
−
=
σ
68
.
14
0
0
68
.
44
T
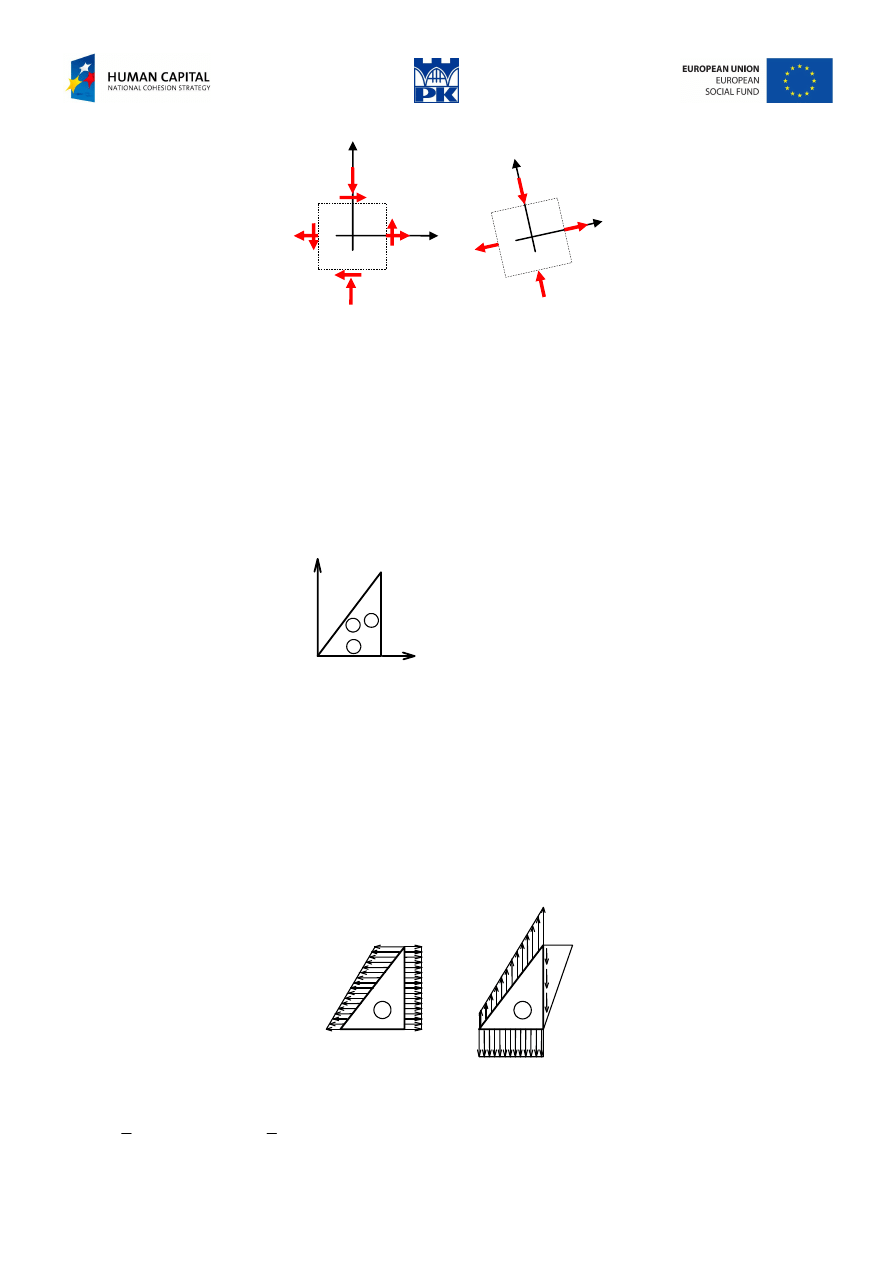
Adam Paweł Zaborski
Project “The development of the didactic potential of Cracow University of Technology in the range of
modern construction” is co-financed by the European Union within the confines of the European Social Fund
and realized under surveillance of Ministry of Science and Higher Education.
14.68
14.68
44.68
44.68
x
16
10
10
16
16
16
40
40
2
1
y
Fig. 14.2 Plane state of stress
or, in 3D notation:
0
1
0
9598
.
0
0
2808
.
0
2808
.
0
0
9598
.
0
3
2
1
z
y
x
−
−
−
−
=
σ
68
.
14
0
0
0
0
0
0
0
68
.
44
T
Static boundary conditions
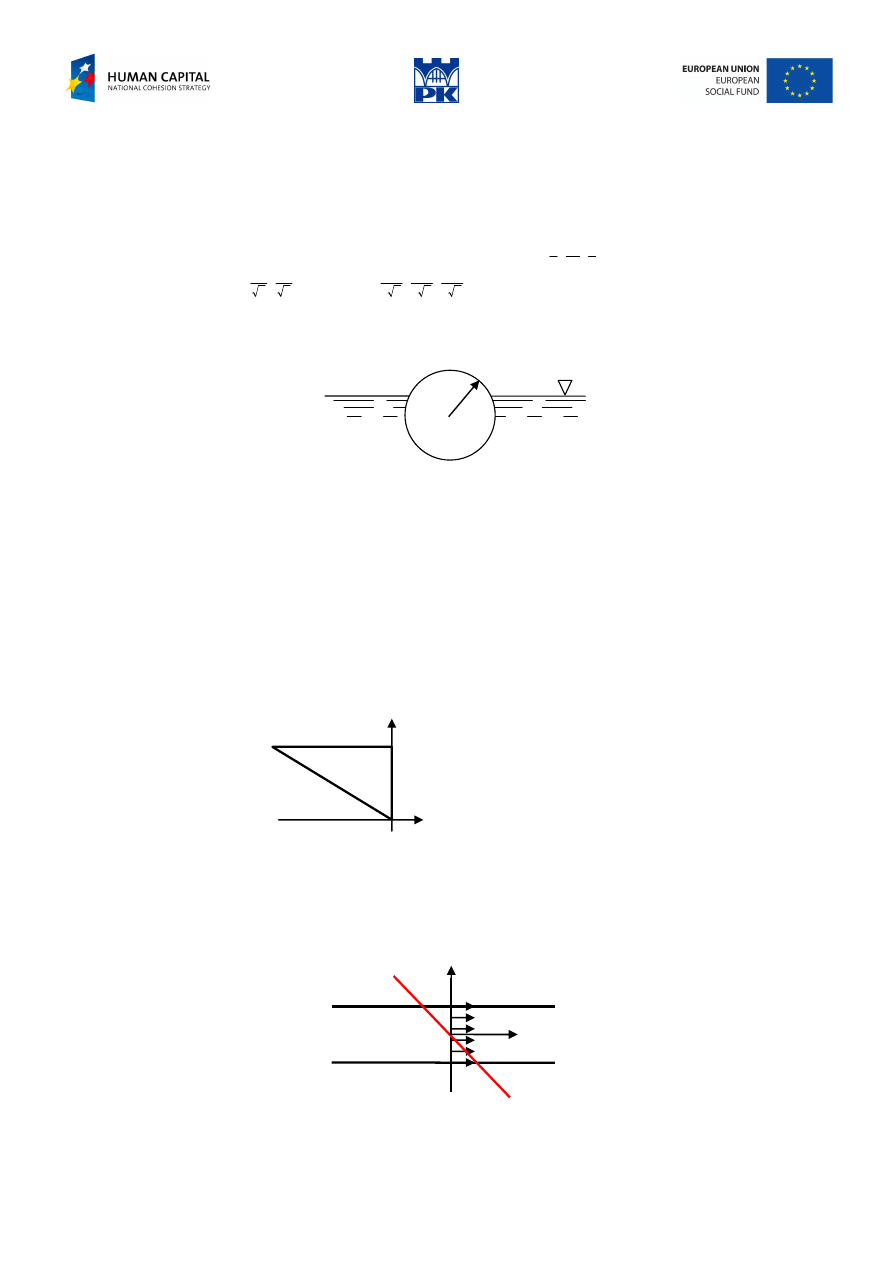
Given the stress tensor, determine the mass forces and the boundary loading of the shield.
.
x
y
4
3
3
2
1
−
−
=
σ
8
2
2
5
y
y
T
Fig. 14.3 Shield and stress state
Solution
The mass forces from Navier’s equations are: P (2, 0)
σ
+
τ
=
τ
+
σ
=
y
y
x
y
x
y
y
y
x
x
x
x
n
n
q
n
n
q
the boundary (1):
8
,
0
2
)
1
,
0
(
−
=
=
=
→
−
y
x
q
y
q
n
the boundary (2):
y
q
q
y
x
2
,
5
)
0
,
1
(
−
=
=
→
n
the boundary (3):
8
.
4
6
.
1
,
2
.
1
4
5
)
6
.
0
,
8
.
0
(
+
=
−
−
=
→
−
y
q
y
q
y
x
n
The loading is drawn in Fig. 14.4.
q
nx
q
ny
5
5
-8
-8
-8.8
-4
4.8
11.2
-8
Fig. 14.4 The loading of the shield
The checking of the solution:
0
4
3
2
1
2
4
5
5
)
4
8
.
8
(
2
1
=
⋅
⋅
⋅
+
⋅
+
⋅
+
⋅
−
=
∑
X
,OK, similarly:
∑
∑
=
=
=
=
0
,
0
K
K
o
M
Y
Adam Paweł Zaborski
Project “The development of the didactic potential of Cracow University of Technology in the range of
modern construction” is co-financed by the European Union within the confines of the European Social Fund
and realized under surveillance of Ministry of Science and Higher Education.
Workshop theme
1) The stress matrix is given:
−
=
σ
10
40
0
40
20
20
0
20
30
T
MPa.
Determine: a) normal stress on the section plane with the normal
(
)
3
1
3
2
3
2
,
,
−
v
, b) shear stress in the plane
parallel to the vectors:
(
)
0
,
,
2
1
2
1
1
v
and
(
)
2
3
4
2
3
1
2
3
1
2
,
,
−
v
. Interpret the obtained results graphically.
2) Write the boundary conditions on the side surface of floating a wooded column. Assume the draught
greater than the radius of the cylinder, Fig. 14.5
R
Fig. 14.5 Floating wooded column
Review problems
1) Given the plane stress matrix, find principal stresses and their directions. Illustrate the stress state before
the transformation and after this.
=
σ
0
150
150
0
T
[MPa]
2) Given the stress state and the shield shape with dimensions, Fig. 14.6, determine the mass forces and the
loading on the boundary.
y
x
3
4
−
−
=
σ
y
x
x
xy
T
5
7
7
2
Fig.
14.6 Plane stress state
3) There is uniaxial stress state in the cross-section plane of a bar,
150
=
σ
x
[MPa]. Determine the stress
components in the plane turned by 45 degrees along z axis, Fig. 14.7.
y
x
Fig. 14.7 Uniaxial stress state

Adam Paweł Zaborski
Project “The development of the didactic potential of Cracow University of Technology in the range of
modern construction” is co-financed by the European Union within the confines of the European Social Fund
and realized under surveillance of Ministry of Science and Higher Education.
Addendum
Glossary
outer (exterior) unit normal – wersor normalnej zewnętrznej
stress vector – wektor naprężenia
load vector – wektor obciążenia
stress matrix – macierz naprężenia
stress tensor – tensor naprężenia
normal stress – naprężenia normalne
shear stress – naprężenia styczne
internal balance equations – równania równowagi wewnętrznej
static boundary conditions – statyczne warunki brzegowe
stress state analysis – analiza stanu naprężenia
Mohr’s circles – koła Mohra
Wyszukiwarka
Podobne podstrony:
C07 design 14 AZ
C07 design 11 AZ
C07 design 12 AZ
C07 design 08 AZ
C07 design 02 AZ
C07 design 03 AZ
C07 design 09 az
C07 design 05 AZ
C07 design 10 AZ
C07 design 06 AZ
C07 design 01 AZ
C07 design 03 AZ
C07 design 02 AZ
C07 design 09 AZ
C07 design 10 AZ
C07 design 01 AZ
C07 design 06 AZ
C07 design 08 AZ
C07 design 15 AZ
więcej podobnych podstron