A. Zaborski, No no graniczna przekroju

Graniczna no no spr ysta i plastyczna przekroju

Przykład 1
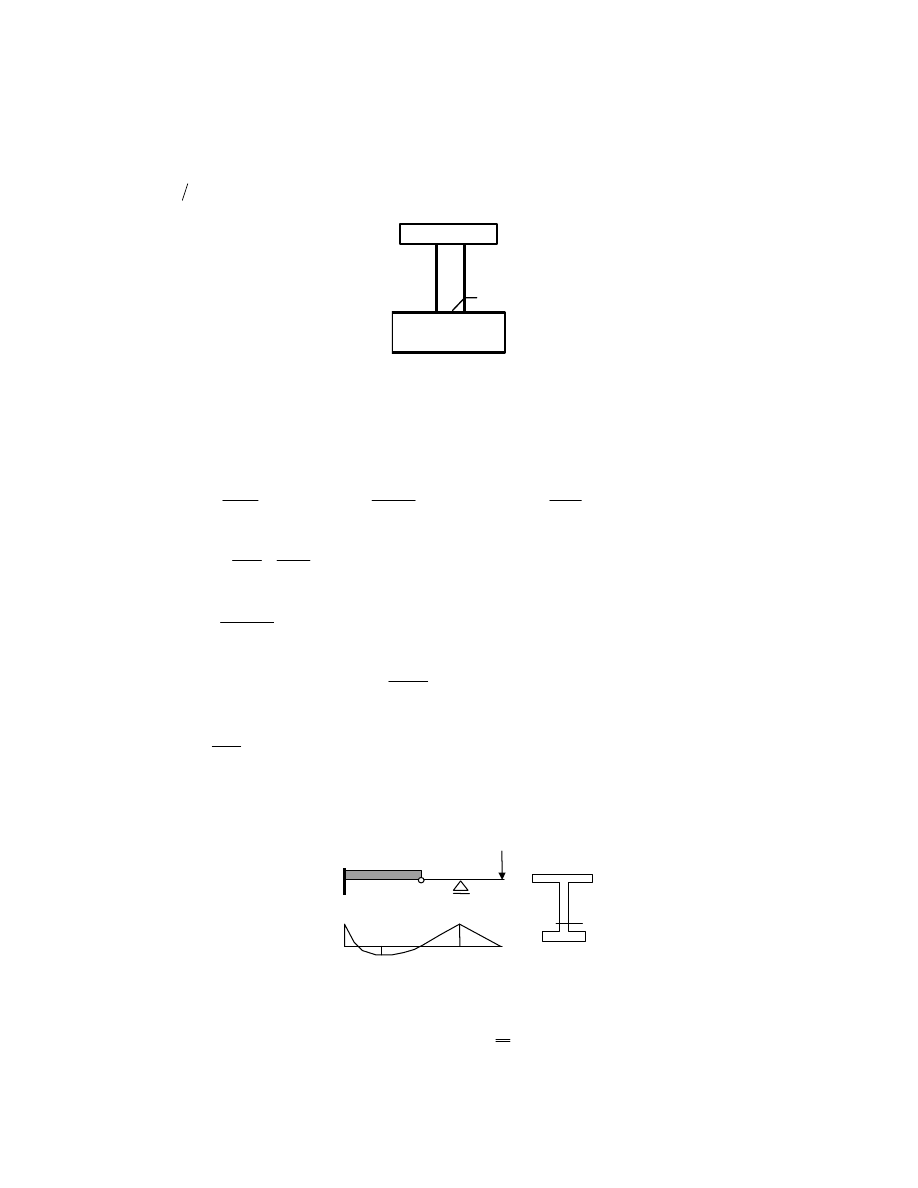
Okre li stosunek wska nika plastycznego do wska nika spr ystego dla przekroju:

s W W

pl

spr

=

.

2

3

3

1.5

1

4

Rozwi zanie:
pole powierzchni: F = 15.5 cm

2

rodek ci ko ci: z

c

= 2.60 cm

główny centralny moment bezwładno ci:

(

)

(

)

(

)

65

.

55

5

.

5

6

.

2

3

12

1

3

5

.

3

6

.

2

3

5

.

1

12

3

5

.

1

1

6

.

2

2

4

12

2

4

2

3

2

3

2

3

=

−

×

+

×

+

−

×

×

+

×

+

−

×

×

+

×

=

y

J

cm

4

wska nik spr ysty:

37

.

16

4

.

3

65

.

55

max

=

=

=

z

J

W

y

spr

cm

3

poło enie osi oboj tnej w stanie granicznym plastycznym (o przechodzi przez doln półk ):

6625

.

0

6

.

2

4

5

.

15

5

.

0

0

−

=

−

×

=

z

cm

wska nik plastyczny:

28

.

25

2

9375

.

1

6

.

2

4

9375

.

1

2

2

1

=

−

×

×

×

=

=

y

pl

S

W

cm

3

wynik ko cowy:

544

.

1

=

=

spr

pl

W

W

s

Podobne wyniki uzyskujemy z programu „przekrój” ( A. Zaborski)

Przykład – obci enie dwuparametrowe
Okre li no no graniczn spr yst i plastyczn belki jak na rysunku:

a

10a

7a

M

1

q

2l

l

l

P

M

2

M

3

a

5a

a

Rozwi zanie:
poło enie osi centralnej i osi oboj tnej:

R

a

W

a

z

a

z

c

3

0

90

,

7

,

5

.

6

=

=

=

A. Zaborski, No no graniczna przekroju

ekstremalne momenty zginaj ce:

Pl

M

l

q

P

q

P

x

M

ql

P

l

M

q

P

−

=

≤

≤

=

=

−

=

3

2

2

1

),

2

0

dla

(

,

2

)

(

),

(

2

belka zamieni si w mechanizm, je li utworzy si jeden przegub plastyczny - zakładamy jego

istnienie w kolejnych przekrojach ekstremalnych momentów, otrzymuj c:

e

R

W

ql

P

l

M

M

≤

−

≤

)

(

2

1

,

e

R

W

q

P

M

M

≤

≤

2

2

2

, je li ponadto

l

q

P

2

0

≤

≤

,

e

R

W

Pl

M

M

≤

≤

3

Po wprowadzeniu bezwymiarowych parametrów obci e :

e

e

R

W

ql

s

R

W

Pl

p

2

,

≡

≡

,

ograniczenia mo emy zapisa :

5

.

0

≤

− s

p

, sk d:

,

,

5

.

0

s

p

s

p

≥

≤

−

(1a)

oraz:

,

,

5

.

0

p

s

s

p

>

≤

+

−

(1b),

2

2

≤

s

p

, (2a), gdy

2

0

≤

≤

s

P

, (2b)

1

,

1

1

−

≥

≤

≤

p

p

p

, (3).

Ograniczenia przedstawiono na wykresie. Warunek (2b), istnienia ekstremum momentu w

przekroju (2), oraz warunek (2a), przekroczenia no no ci w tym przekroju, daj ograniczenia

poza zaznaczonym obszarem: (2a) ma zastosowanie jedynie dla spełnionego (2b), tj. wtedy

gdy linia (2a) jest "ponad" (2b) - na lewo i na prawo od zaznaczonego obszaru. Tak wi c oba

warunki (2) ł cznie nie wnosz dodatkowego ograniczenia na rozwi zanie i obszar

zakreskowany na wykresie wyznacza zakres dopuszczalnych obci e .

1a

1b

3b

3a

2b

2a

1

0.5

0.5

p

s

-0.5

-1