Obliczenia półosi napędowych

FORD B-MAX 1.4 TITANIUM

Półoś odciążona

m1

777.75

:=

Tnet

125

:=

id

1

:=

ib1

3.58

:=

ig

4.25

:=

iz

1

:=

ηz

1

:=

ηc

1

:=

rd

0.287

:=

g

9.8

:=

μx

0.85

:=

Rm

1650

:=

Realizacja obliczeń

Kmr

0.1

:=

χ

Kmr 1

+

2

:=

χ

0.55

=

λ1

0.8

:=

Moment skęcajacy półosi przy jeździe na biegu 1 z wykorzystaniem maksymalnego momentu

T2n

Tnet id

⋅

ib1

⋅

ig

⋅

ηc

⋅

χ

⋅

:=

T2n 1.046 10

3

×

=

Sila napedowa na kole

F2n

T2n

rd

:=

F2n 3.645 10

3

×

=

Reakcja pionowa działajaca na na koło, przy rozpedzaniu samochodu, N

R2n

m1 g

⋅

λ1

⋅

2

:=

R2n 3.049 10

3

×

=

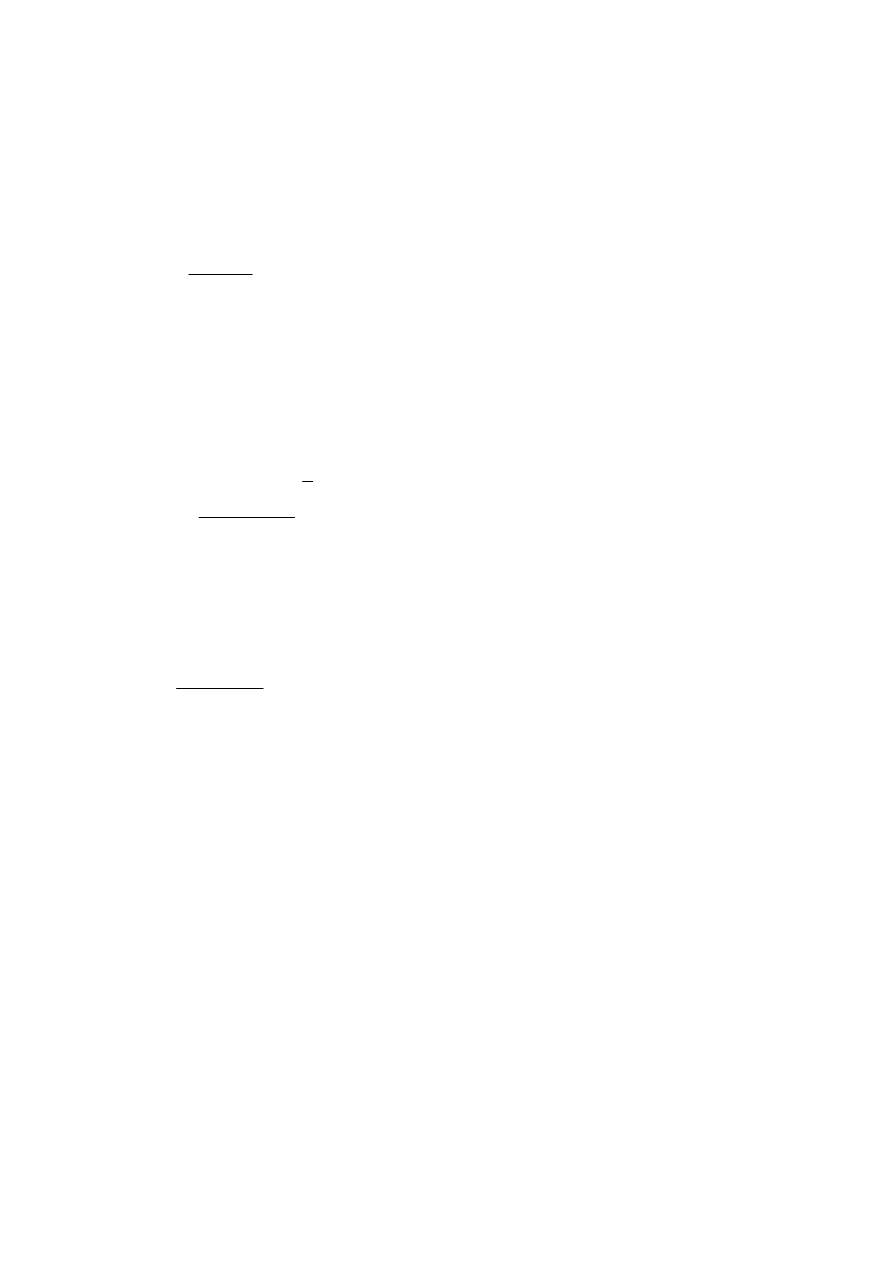
Graniczny moment od przyczepnosci dla kola napedowego

N m

⋅

T2μ

R2n μx

⋅

rd

⋅

iz ηz

⋅

:=

T2μ 743.75

=

T2max

T2n

:=

Dopuszczalne naprezenia skrecajace, MPa

τdop

0.6 Rm

⋅

:=

τdop 990

=

Minimalna średnica polosi, mm

dmin

T2max

0.2

τdop 10

6

⋅









⋅

















1

3

10

3

⋅

:=

dmin 17.416

=

Ostatecznie przyjmujemy średnice półosi, mm

d

42

:=

Naprezenia skrecajoce polos, MPa

τs

T2max

0.2 d 10

3

−

⋅

(

)

3

⋅

10

6

−

⋅

:=

τs 70.594

=

Porownanie napezen z wartosciasmi dopuszczalnymi

τdop 990

=

τs τdop

≤

Półoś nieodciążona

m1k

93.45

:=

Tnet

112.8

:=

ib1

3.58

:=

id

1

:=

ig

4.25

:=

ηc 1

=

rd

0.287

:=

g

9.8

=

μx 0.85

=

μy

1

:=

hs

0.6

:=

l1

1.324

:=

b1

1.588

:=

b2

1.585

:=

λ

1.2

:=

c

38

:=

Rm

1650

:=

Przypadek obciazenia 1 - maksymalna siła wzdłużna

Kmr 0.1

=

χ

Kmr 1

+

2

:=

χ

0.55

=

λ2

1.2

:=

Moment skęcajacy półosi przy jeździe na biegu 1 z wykorzystaniem maksymalnego momentu,
Nm

T2n

Tnet id

⋅

ib1

⋅

ig

⋅

ηc

⋅

χ

⋅

:=

T2n 943.939

=

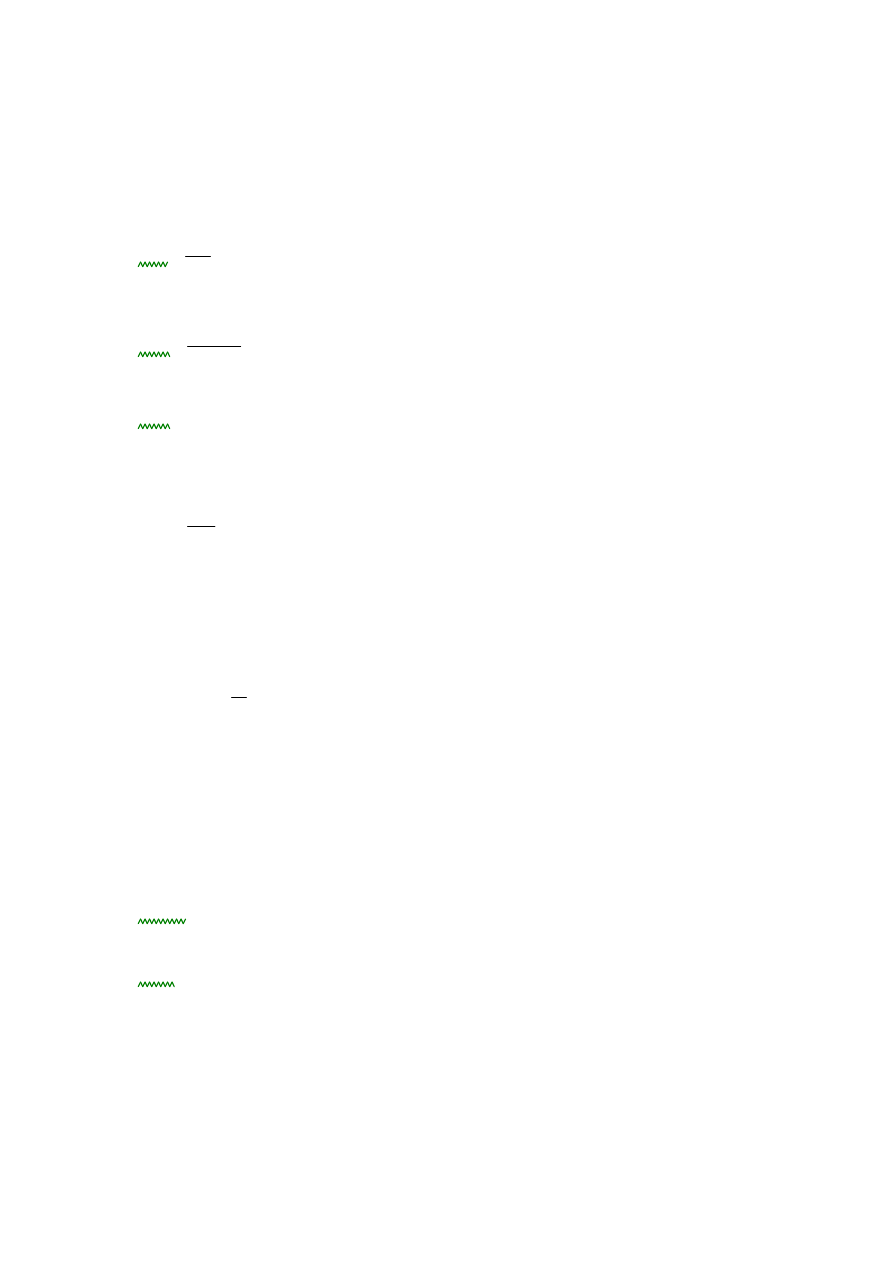
Sila napedowa na kole, N

F2n

T2n

rd

:=

F2n 3.289 10

3

×

=

Reakcja pionowa działajaca na na koło, przy rozpedzaniu samochodu, N

R2n

m1 g

⋅

λ2

⋅

2

:=

R2n 4.573 10

3

×

=

Graniczny moment od przyczepnosci, dla kola napedowego,

N

T2μ

R2n μx

⋅

rd

⋅

:=

T2μ 1.116 10

3

×

=

Sila obwodowa na kole pochodzaca od momentu Tμ2, N

F2μ

T2μ

rd

:=

F2μ 3.887 10

3

×

=

Maksymalna sila pionowa, zginajaca polos, N

F2p

R2n m1k g

⋅

−

:=

F2p 3.657 10

3

×

=

Wspolczynnik odciazenia kol tylnych samochodu przy hamowaniu

λ2h

1

μx

hs

l1

⋅

−

:=

λ2h 0.615

=

Maksymalna pionowa reakcja dzialajaca na kolo podczas hamowania, N

R2h

m1 g

⋅

λ2h

⋅

:=

R2h 4.686 10

3

×

=

Wartosc m aksymalnej s ily hamowania na kole osi tylnej, N

F2h

R2h μx

⋅

:=

F2h 3.983 10

3

×

=

Do obliczen polosi przyjmije sie moment

T2max

T2n

:=

Dopuszczalne naprezenia skrecajace, MPa

τdop

0.6 Rm

⋅

:=

τdop 990

=

Minimalna srednica polosi z warunku na skrecanie, mm

dmin

T2max

0.2

τdop 10

6

⋅









⋅

















1

3

10

3

⋅

:=

dmin 16.83

=

Dopuszczane naprezenia na zginanie, MPa

σdop

0.6 Rm

⋅

:=

σdop 990

=

Wypadkowa sila zginajaca polos, wywolana dzialaniem sil napedowych, N

Fwn

F2p

2

F2n

2

+

:=

Fwn 4.919 10

3

×

=

Wypadkowa sila zginajaca polos, wywolana dzialaniem sil hamowania, N

Fwh

R2h

2

F2h

2

+

:=

Fwh 6.15 10

3

×

=

Do obliczeń polosi na zginanie przyjmujemy sile wypadkowa

Fw

Fwh

:=

Minimalna srednica polosi oliczona z warunku na zginanie, mm

d1g

c 10

3

−

⋅









Fw

⋅

0.1

σdop 10

6

⋅









⋅

















1

3

10

3

⋅

:=

d1g 13.315

=

Przypadek obciazenia 2 - maksymalna sila boczna

Sily obwodowe (napedowa i hamujaca) sa rowne zeru

Reakcja boczna działajaca na kolo (polos) zewnetrzne, N

F2Yz

μy m1

⋅

g

⋅

2

1

2

μy

⋅

hs

⋅

b2

+













⋅

:=

F2Yz 6.696 10

3

×

=

Reakcja robocza działajaca na kolo (polos) wewnetrzne, N

F2Yw

μy m1

⋅

g

⋅

2

1

2

μy

⋅

hs

⋅

b2

−













⋅

:=

F2Yw 925.694

=

Sila pionowa działajaca na polos kola zewnetrznego, N

F2z

m1 g

⋅

2

1

2

μy

⋅

hs

⋅

b2

+













⋅

m1k g

⋅

−

:=

F2z 5.78 10

3

×

=

Sila pionowa działajaca na polos kola wewnetrznego, N

F2w

m1 g

⋅

2

1

2

μy

⋅

hs

⋅

b2

−













⋅

m1k g

⋅

−

:=

F2w 9.884

=

Minimalna średnica polosi obliczona z warunku na zginanie, mm

d2Y

F2Yz rd

⋅

F2z c 10

3

−

⋅









⋅

−

0.1

σdop 10

6

⋅









⋅

















1

3

10

3

⋅

:=

d2Y 25.81

=

Przypadek obciazenia 3 - maksymalna sila pionowa

Przy uderzeniu kola o nawierzchnie drogi pionowa reakcja na kole okreslona jest zaleznoscia

kd

1.75

:=

Rg

m1 g kd

⋅

(

)

2

:=

Rg 6.669 10

3

×

=

Maksymalna sila pionowa, zginajaca polos, N

Fg

m1 g

⋅

2

kd

⋅

m1k g

⋅

−

:=

Fg 5.753 10

3

×

=

Minimalna srednica polosi obliczona z warunku na zginanie, mm

d3g

Fg c 10

3

−

⋅









⋅

0.1

σdop 10

6

⋅









⋅

















1

3

10

3

⋅

:=

d3g 13.022

=

Dobór średnicy półosi

obliczenia polosi dla roznych przypadkow obciazenia daly nastepujace wyniki:

Przypadek 1
- z warunku na skręcanie, mm

d1sk

16.2

:=

- z warunku na zginanie, mm

d1g 13.315

=

Przypadek 2
- z warunku na zginanie, mm

d2Y

26.2

:=

Przypadek 3
- z warunku na zginanie, mm

d3g

13.3

:=

Dla obliczenia koncentracji naprezen i ze wzgledu na rozmiary wielowypustow
zakladamy srednice polosi, mm

d

30

:=

Końcowe sprawdzenie naprężeń

Naprezenia zginajace polos dla przypadku 1, MPa

σ1

c10

3

−









F2p

2

F2n

2

+

⋅

0.1 d 10

3

−

⋅

(

)

3

⋅

10

6

−

⋅

:=

σ1 69.226

=

Naprezenia skrecajace polos dla przypadku 1, MPa

τ1

T2max

0.2 d 10

3

−

⋅

(

)

3

⋅

10

6

−

⋅

:=

τ1 174.803

=

Naprezenia zastepcze dla przypadku 1, MPa

σ1z

σ1

2

4

τ1

2

⋅

+

:=

σ1z 356.395

=

Naprezenia zginajace polos dla przypadku obciazenia 2, MPa

σ2g

F2Yz rd

⋅

F2z c 10

3

−

⋅









⋅

−

0.1 d 10

3

−

⋅

(

)

3

⋅

















10

6

−

⋅

:=

σ2g 630.433

=

Naprezenia zginajace polos dla przypadku obciazenia 3, MPa

σ3g

Fg c 10

3

−

⋅









⋅

0.1 d 10

3

−

⋅

(

)

3

⋅

















10

6

−

⋅

:=

σ3g 80.974

=

Naprężenia σ

1z

=357 MPa, σ

2g

=

631 MPa oraz σ3

g

=81 MPa są mniejsze od naprężeń

dopuszczalnych σ

dop

=990 MPa.