1

Metoda Elementów

Metoda Elementów

Sko czonych

Sko czonych

ZAGADNIENIA DYNAMIKI

ZAGADNIENIA DYNAMIKI

3

Równanie ruchu dla

Równanie ruchu dla

zagadnienia dynamicznego

zagadnienia dynamicznego

M ¨q+C q+K q=0

gdzie:

M

macierz bezw adno ci

o wymiarze n

×n ,

C

macierz t umienia

o wymiarze n

×n ,

K

macierz sztywno ci

o wymiarze n

×n ,

q

wektor uogólnionych przemieszczen×1,

Q

wektor uogólnionych si wymuszaj cych

n×1,

n

liczba stopni swobody dynamicznej.

4

Podzia zagadnie dynamicznych

Podzia zagadnie dynamicznych

5

6

7

8

Zagadnienie w asne -

Zagadnienie w asne -

problem matematyczny

problem matematyczny

9

jest to rozwi zanie liniowego

jest to rozwi zanie liniowego

jednorodnego uk adu równa

jednorodnego uk adu równa

postaci:

postaci:

10

Mamy nietrywialne rozwi zanie,

Mamy nietrywialne rozwi zanie,

je eli

je eli

co prowadzi do wielomianowego

co prowadzi do wielomianowego

równania N-tego stopnia

równania N-tego stopnia

11

Je eli macierz A jest dodatnio

Je eli macierz A jest dodatnio

okre lona (tzn.:

okre lona (tzn.:

x

x

T

T

Ax

Ax

>

>

0

0

dla

dla

dowolnego

dowolnego

x

x

) to wszystkie

) to wszystkie

pierwiastki s rzeczywiste i

pierwiastki s rzeczywiste i

dodatnie:

dodatnie:

12

Zagadnienie w asne liniowego uk adu

Zagadnienie w asne liniowego uk adu

dynamicznego bez t umienia

dynamicznego bez t umienia

Rozwa amy drgania swobodne uk adu

Rozwa amy drgania swobodne uk adu

liniowego bez t umienia:

liniowego bez t umienia:

C

C

0

0

,

,

b

b

0

0

13

Uogólniony problem w asny

Uogólniony problem w asny

14

15

Po rozwi zaniu równania

Po rozwi zaniu równania

otrzymujemy

otrzymujemy

16

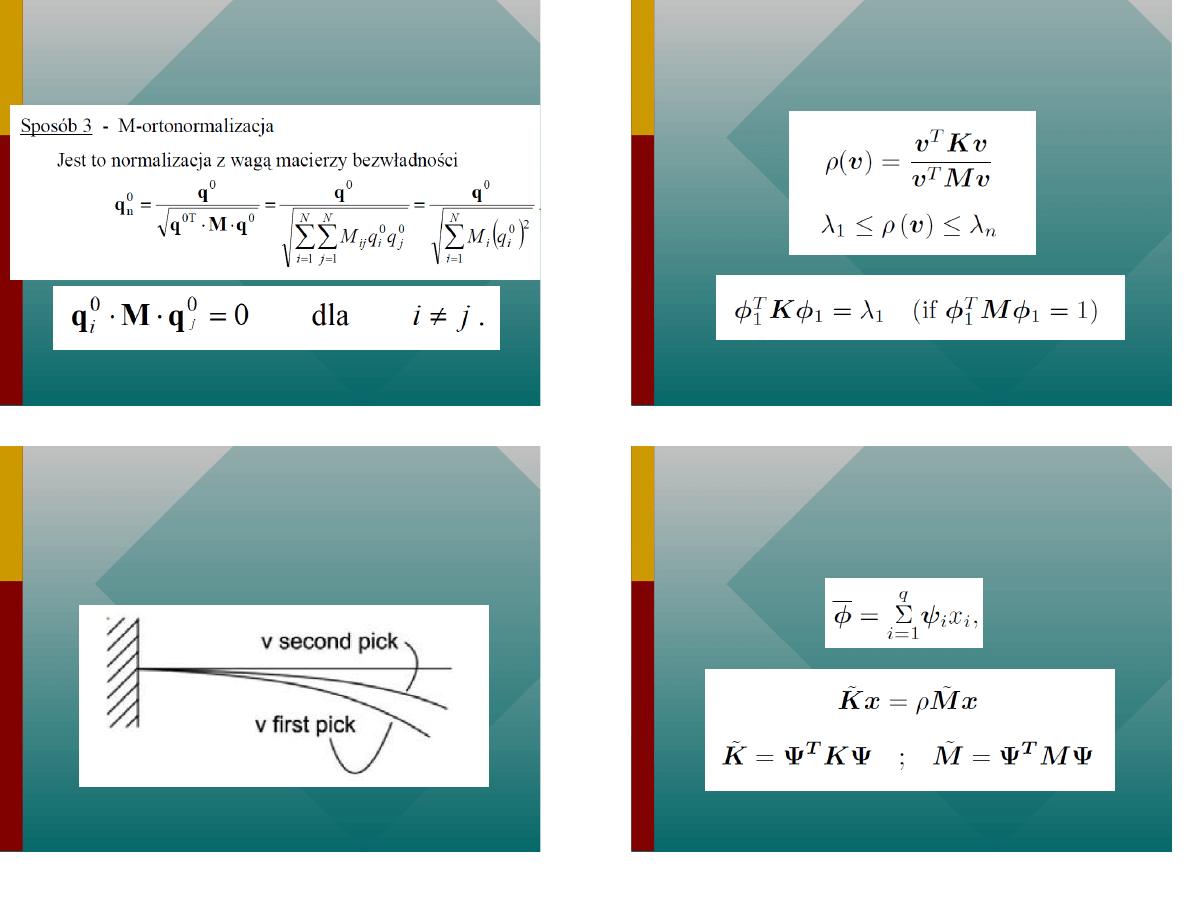
Normowanie wektora w asnego

Normowanie wektora w asnego

Wektory w asne otrzymuje si z dok adno ci

Wektory w asne otrzymuje si z dok adno ci

do sta ego mno nika. Cz sto dokonuje si

do sta ego mno nika. Cz sto dokonuje si

odpowiedniego skalowania:

odpowiedniego skalowania:

17

18

19

Metoda Rayleigha-Ritza

Metoda Rayleigha-Ritza

20

21

22

Do czego s u y analiza

Do czego s u y analiza

zagadnienia w asnego?

zagadnienia w asnego?

1.

Opisuje drgania swobodne konstrukcji.

2.

Problem rezonansu.

3.

Znajomo form i cz sto ci w asnych pozwala

na wykonanie analizy modalnej, tzn.
rozseparowanie zagadnienia wzgl dem tzw.

wspó rz dnych modalnych.

4.

Z widma cz sto ci drga w asnym mo emy

wyci gn szereg wniosków co do zachowania si

konstrukcji pod wp ywem obci e o charakterze

harmonicznym.

23

Zagadnienia dynamiczne

Zagadnienia dynamiczne

nieustalone

nieustalone

24

Ca kowanie numeryczne

Ca kowanie numeryczne

„krok po kroku”

„krok po kroku”

25

Ca kowanie metod ró nic

Ca kowanie metod ró nic

sko czonych

sko czonych

26

Metoda Newmarka

Metoda Newmarka

Równanie ruchu w chwili: t + t

27

28

Metoda modalna

Metoda modalna

29

30

Macierzowe równanie separuje

Macierzowe równanie separuje

si na N zwyczajnych równa

si na N zwyczajnych równa

ró niczkowych

ró niczkowych