Opracował: Mateusz Antoniak i Karol Frasz

Budownictwo – Drogi, Ulice i Lotniska

IV rok, sem. VII

Charakterystyka i klasyfikacja metod obliczeniowych

- I PODEJŚCIE (KONTYNUALNE):

Rozwiązanie większości problemów inżynierskich, polega na wyznaczaniu pól (czyli funkcji) różnych
wielkości , (tzn.: przemieszczeń, naprężeń, odkształceń).

Pole interesującej nas wielkości w rozpatrywanym ciele, określone jest przez nieskomplikowaną liczbę
parametrów (jest bowiem funkcją każdego, z nieskończonej liczby punktów materialnych należących do
tego układu). Takie podejście do rozwiązywania zagadnień inżynierskich nazywa się kontynualnym,
gdyż wprowadza jako model ciała – odkształcalne kontinuum. (metody rozwiązywania tego typu
zagadnień nazywamy metodami analitycznymi).

Metody analityczne są bardzo dokładne ale mało efektywne, (tzn.: mają ograniczone zastosowanie
praktyczne, gdyż odnoszą się do układów liniowych, prostych warunków podparcia i
nieskomplikowanej geometrii – a większość układów z inżynierskiego punktu widzenia jest nieciągła,
nieliniowa, nietypowo obciążona, o skomplikowanej strukturze geometrycznej i nieciągłości
materiałów).

- II PODEJŚCIE (DYSKRETNE):

Badanie reakcji układu bardziej się uprości, jeśli przemieszczenia nie będą wyznaczane we wszystkich
punktach ciała, ale tylko w skończonej ich liczbie. Takie podejście do rozwiązywania zagadnień
inżynierskich nazywa się dyskretnym, gdyż wymaga dyskretyzacji układu.

Proces dyskretyzacji układu, przekształca opis poszukiwanego pola (czyli funkcji), wyrażonej przez
nieskończoną liczbę parametrów w opis wyrażony przez skończoną ich liczbę (metody rozwiązywania
tego typu zagadnień nazywamy metodami numerycznymi (komputerowymi) – metody przybliżone.

Wśród nich wyróżniamy:

- MRS – metody różnic skończonych,
- MES – metody elementów skończonych,
- MEB – metody elementów brzegowych,
- MECZ – metody elementów czasoprzestrzennych.

Modelowanie problemów inżynierskich

Etapy modelowania

- modelowanie fizyczne,

- modelowanie matematyczne,

- modelowanie dyskretne,

- modelowanie numeryczne,

- programowanie,

- przygotowanie danych wyjściowych do obliczeń,

- wykonanie obliczeń,

- weryfikacja wyników

- Model fizyczny

Proces tworzenia modelu fizycznego polega na pewnej idealizacji układu rzeczywistego (opiera się w
dużej mierze na intuicji i doświadczeniu inżyniera). W tworzeniu modelu fizycznego uwzględniamy
tylko te cechy układu rzeczywistego, które według nas odgrywają istotną rolę. Model fizyczny,
powstaje więc w wyniku przeprowadzenia uproszczeń, które sprawiają, że staje się on łatwiejszy od
analizy układu rzeczywistego. Trafność przyjętego modelu fizycznego najczęściej decyduje o zgodności
wyników uzyskanych z obliczeń z wynikami pomiarów.

- Zbyt uproszczony model fizyczny – pomija istotne cechy układu rzeczywistego,

- Zbyt złożony model fizyczny – prowadzi do trudności matematycznych.

Opracował: Mateusz Antoniak i Karol Frasz

Budownictwo – Drogi, Ulice i Lotniska

IV rok, sem. VII

(właściwy model fizyczny stanowi kompromis między tymi trudnościami a dokładnością wyników
obliczeń).

- Założenia upraszczające:

- uproszczenie geometrii układu – złożone kształty układu rzeczywistego, upraszczamy do brył
złożonych z walców, stożków lub prętów,
- założenie o jednorodności materiałów – np. taka sama gęstość materiałów,
- założenie o idealnej sztywności i nieważkości – gdy element ma sztywność wielokrotnie większą od
pozostałych (bryły nieodkształcalne) bądź wielokrotnie mniejszą masę ( brak ciężaru własnego),
- założenie liniowych charakterystyk właściwości fizycznych układu, (np. Prawo Hooke’a) –
linearyzacja nieliniowych charakterystyk – znacznie upraszcza obliczenia, ponieważ pozwala na
zastosowanie zasady superpozycji.
- niezmienność czasowa parametrów fizycznych układu – pominięcie procesu starzenia, zużycia i
zmęczenia.
- pominięcie małoistotnych oddziaływań – siły Coriolisa, przyciągania księżyca, zmian temperatury

- Model matematyczny

Modelem matematycznym, nazywamy równania opisujące model fizyczny. Na podstawie poczynionych
założeń przy budowie modelu fizycznego budowany jest model matematyczny układu w postaci równań
algebraicznych i różniczkowych z warunkami brzegowymi. Model ten z jednej strony powinien
zawierać najistotniejsze czynniki a z drugiej strony musi być stosunkowo łatwy do obliczeń.

Model matematyczny może przyjmować różne formy, począwszy od prostych równań algebraicznych
po złożone równania, wymagające specjalistycznych programów komputerowych.

- Model dyskretny

Modele fizyczne składają się zwykle z elementów , których parametry rozłożone są w sposób ciągły.
Równanie charakteryzujące te modele, są równaniami różniczkowymi cząstkowymi. Rozwiązanie
takich równań jest bardzo trudne, a czasami wręcz niemożliwe, dlatego też ciągły model fizyczny,
zastępuje się modelem, w którym parametry maja charakter skupiony. Proces ten nazywa się
dyskretyzacji a otrzymany model, modelem dyskretnym.

W wyniku dyskretyzacji otrzymujemy model, który wcześniej opisany jest równaniami różniczkowymi
zwyczajnymi, z pochodnymi względem czasu lub równaniami algebraicznymi. Do najważniejszych i
najbardziej powszechnych modeli dyskretyzacji należą: MRS, MES, MECZ

Istnieją dwa sposoby dyskretyzacji:

- dyskretyzacji matematyczna, polega na dyskretyzacji równań opisujących dany problem
(MRS).
- dyskretyzacji fizyczna, polega na podziale rozpatrywanego układu na skończoną liczbę
elementów o podobnym kształcie.

- Model numeryczny

Tworzenie tego modelu polega na wyborze algorytmów numerycznych, służących do rozwiązania
równań modelu dyskretnego.

Tworzenie modelu numerycznego, wymaga znajomości nowoczesnych technik komputerowych.

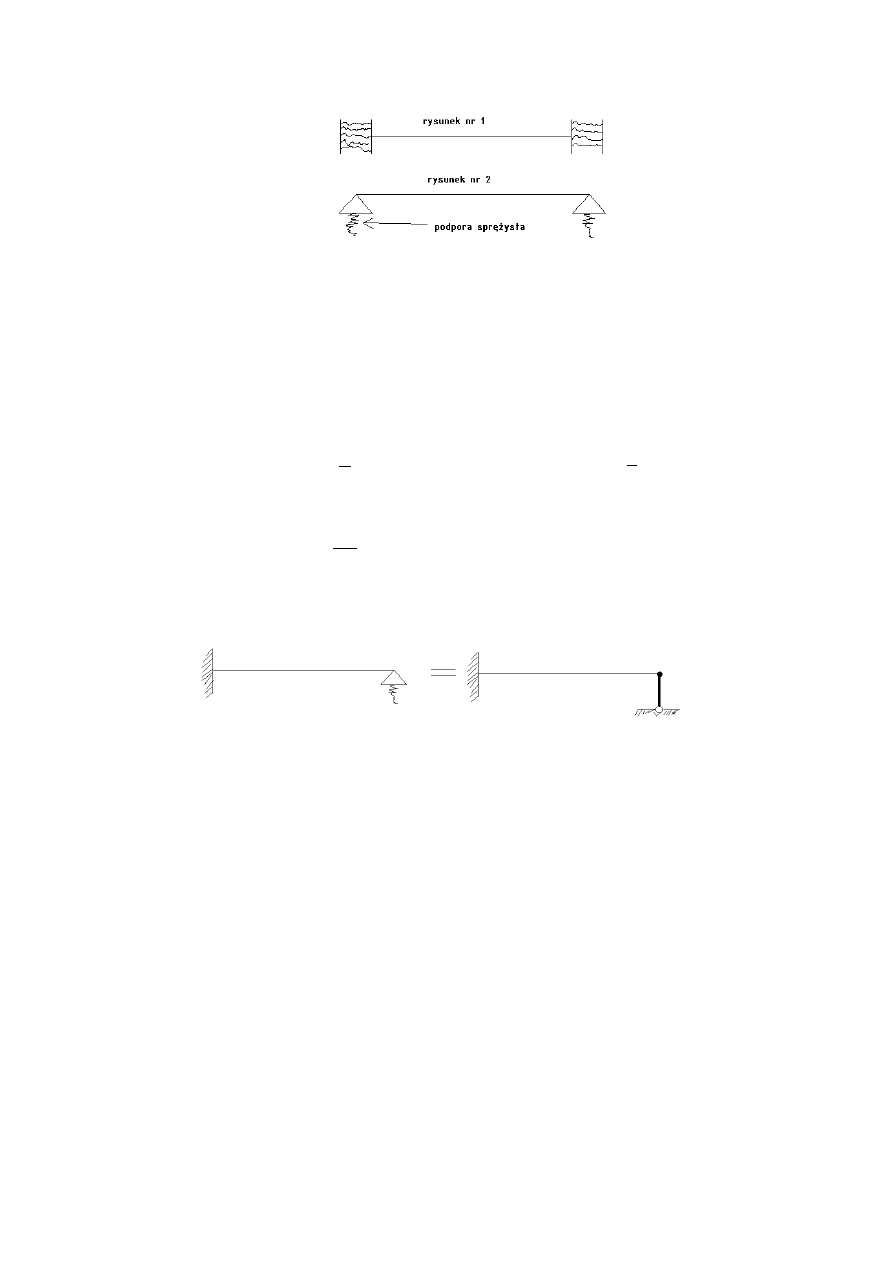
Dobór modelu fizycznego w konstrukcjach prętowych

Dobór odpowiedniego schematu statycznego zależy od rodzaju ściany, w którym umieszczone są końce
belki a także od tego, w jaki sposób belka ze ścianą została połączona. Rola projektanta pola na
podjęciu decyzji odnośnie schematu statycznego i tym samym podjęciu ryzyka związanego z
bezpieczeństwem konstrukcji.

Opracował: Mateusz Antoniak i Karol Frasz

Budownictwo – Drogi, Ulice i Lotniska

IV rok, sem. VII

Wyżej przedstawione schematy mogą być przyjęte, gdy projektant dysponuje odpowiednimi badaniami
doświadczalnymi, lub gdy przeprowadza odpowiednią symulację komputerową, dzięki której może
ustalić najbardziej odpowiednią podatność podpory.

Modelując podparcia ustrojów prętowych, przypisujemy im odpowiednie stopnie swobody w węzłach.
Np. usuwając wszystkie stopnie swobody w węźle otrzymujemy sztywne zamocowanie pręta w
podporze. Aby wymodelować podporę podatną, umieszcza się w podporze sprężynę o zadanej
sztywności, która jest charakterystyką tej sprężyny.

Sztywnością sprężyny nazywamy stosunek uogólnionej siły czynnej do odpowiadającej jej
uogólnionego przemieszczenia.

q

Q

K =

- odwrotność sztywności to jej podatność

K

1

=

Najprostszym sposobem modelowania podpory sprężystej jest jej przegubowe podparcie za pomocą
podatnego pręta. Sztywność tej podpory wyraża się następującą zależnością:

l

E A

k =

, gdzie: EA – sztywność pręta, l – długość pręta

Sztywność podpory w takim przypadku reguluje się sztywnością podłużną pręta. Przyjmując możliwie
najmniejszą, ale skończoną jego długość. W przypadku gdy podpora jest niepodatna, wielkość EA,
przyjmuje się jak największą, ale skończoną.

Opracował: Mateusz Antoniak i Karol Frasz

Budownictwo – Drogi, Ulice i Lotniska

IV rok, sem. VII

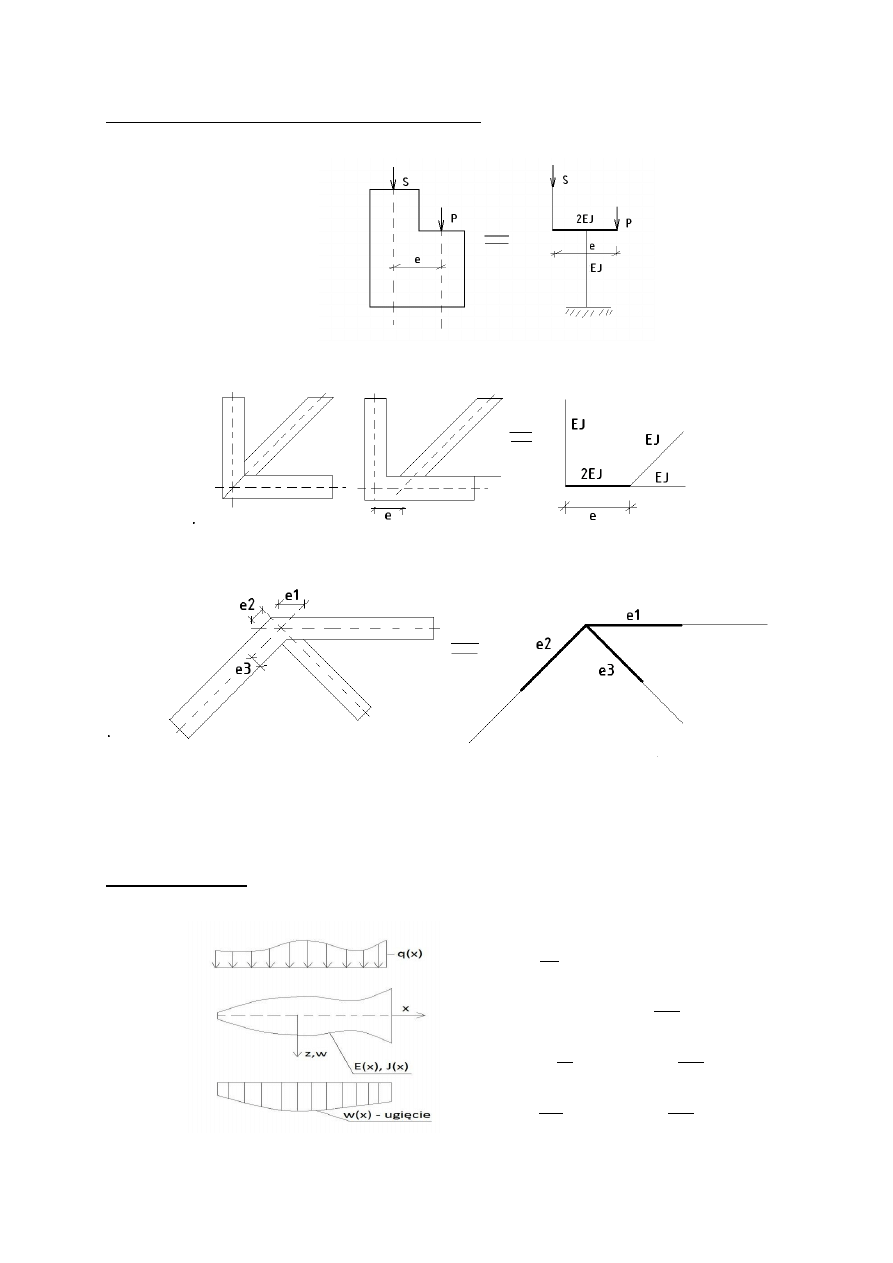
Przypadki szczególne modelowania konstrukcji prętowych

- Słup o zmiennej skokowo wysokości przekroju poprzecznego

- Osie prętów kratownicy nie schodzą się w jednym węźle

- Modelowanie węzłów w konstrukcjach prętowych

Na rysunku wyżej widać, że mniejszy moment uzyskiwany jest na przęsłach niż na węzłach. Węzły
konstrukcji prętowej są elementami o bardzo dużej sztywności w porównaniu do prętów schodzących
się do węzła.
W konstrukcji płaskiej, węzeł stanowi tarcze a w konstrukcji przestrzennej bryłę

Dyskretyzacja układu

- Dyskretyzacja matematyczna (MRS)

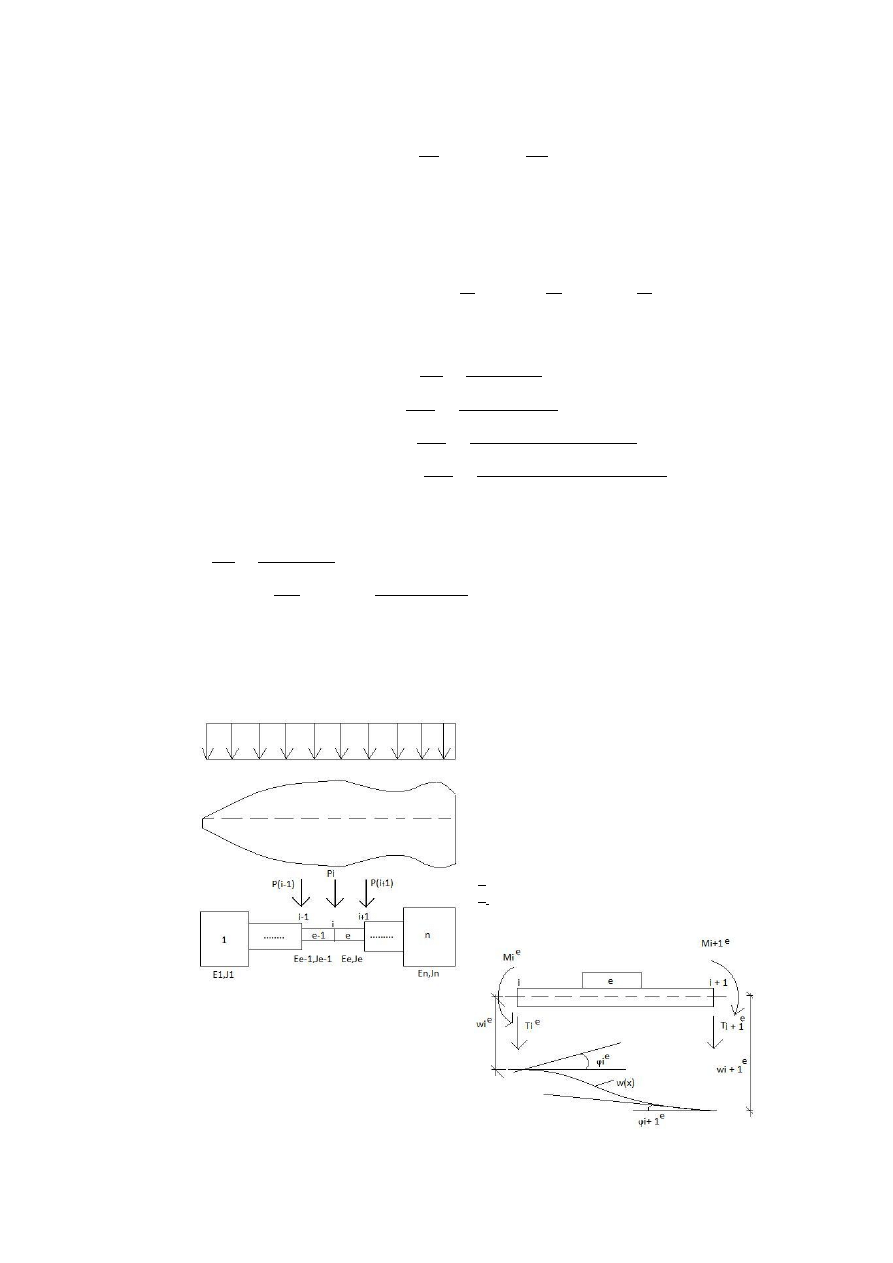
Belkę zginaną opisuje następujący zestaw równań:

φ(x) =

𝑑𝑤

𝑑𝑥

M(x) =

−𝐸(𝑥) ∙ 𝐽(𝑥) ∙

𝑑

2

𝑤

𝑑𝑥

2

T(x) =

−

𝑑

𝑑𝑥

𝐸 𝑥 ∙ 𝐽 𝑥 ∙

𝑑

2

𝑤

𝑑𝑥

2

q(x) =

𝑑

2

𝑑𝑥

2

𝐸 𝑥 ∙ 𝐽 𝑥 ∙

𝑑

2

𝑤

𝑑𝑥

2

Opracował: Mateusz Antoniak i Karol Frasz

Budownictwo – Drogi, Ulice i Lotniska

IV rok, sem. VII

Modelem matematycznym, przedstawionego powyżej modelu fizycznego belki zginanej w
płaszczyźnie XZ, jest równanie q(x) =

𝑑

2

𝑑𝑥

2

𝐸 𝑥 ∙ 𝐽 𝑥 ∙

𝑑

2

𝑤

𝑑𝑥

2

Dyskretyzacja będzie polegała na zastąpieniu operatów różniczkowych (pochodnych) przez
odpowiadające im operaty różnicowe (ilorazy różnicowe). W wyniku czego, równanie różniczkowe
sprowadzone zostanie do zestawu równań algebraicznych.

Poszukiwana funkcja w(x) rozpisujemy w szereg potęgowy Taylora w otoczeniu punktu x=0

𝑤 𝑥 = 𝑤 0 + 𝑤

𝐼

0 ∙

𝑥

1

1!

+ 𝑤

𝐼𝐼

0 ∙

𝑥

2

2!

+ 𝑤

𝐼𝐼𝐼

0 ∙

𝑥

3

3!

+

Po długich żmudnych przekształceniach otrzymujemy wzory na:

- I RS (pierwsza różnica skończona) =

∆𝑤

𝑖

∆𝑥

=

−𝑤

𝑖−1

+𝑤

𝑖+1

2𝜆

- II RS (druga różnica skończona) =

∆

2

𝑤

𝑖

∆𝑥

2

=

𝑤

𝑖−1

−2𝑤

𝑖

+𝑤

𝑖+1

𝜆

2

- III RS (trzecia różnica skończona) =

∆

3

𝑤

𝑖

∆𝑥

3

=

−𝑤

𝑖−2

+2𝑤

𝑖−1

−2𝑤

𝑖+1

+𝑤

𝑖+2

2𝜆

3

- IV RS (czwarta różnica skończona) =

∆

4

𝑤

𝑖

∆𝑥

4

=

𝑤

𝑖−2

−4𝑤

𝑖−1

+6𝑤

𝑖

−4𝑤

𝑖+1

+𝑤

𝑖+2

𝜆

4

Zatem można przyjąć następujące wzory:

φ

i

=

∆𝑤

𝑖

∆𝑥

=

−𝑤

𝑖−1

+𝑤

𝑖+1

2𝜆

M

i

=

−𝐸

𝑖

∙ 𝐽

𝑖

∙

∆

2

𝑤

𝑖

∆

𝑥

2

= −𝐸

𝑖

∙ 𝐽

𝑖

∙

𝑤

𝑖−1

−2𝑤

𝑖

+𝑤

𝑖+1

𝜆

2

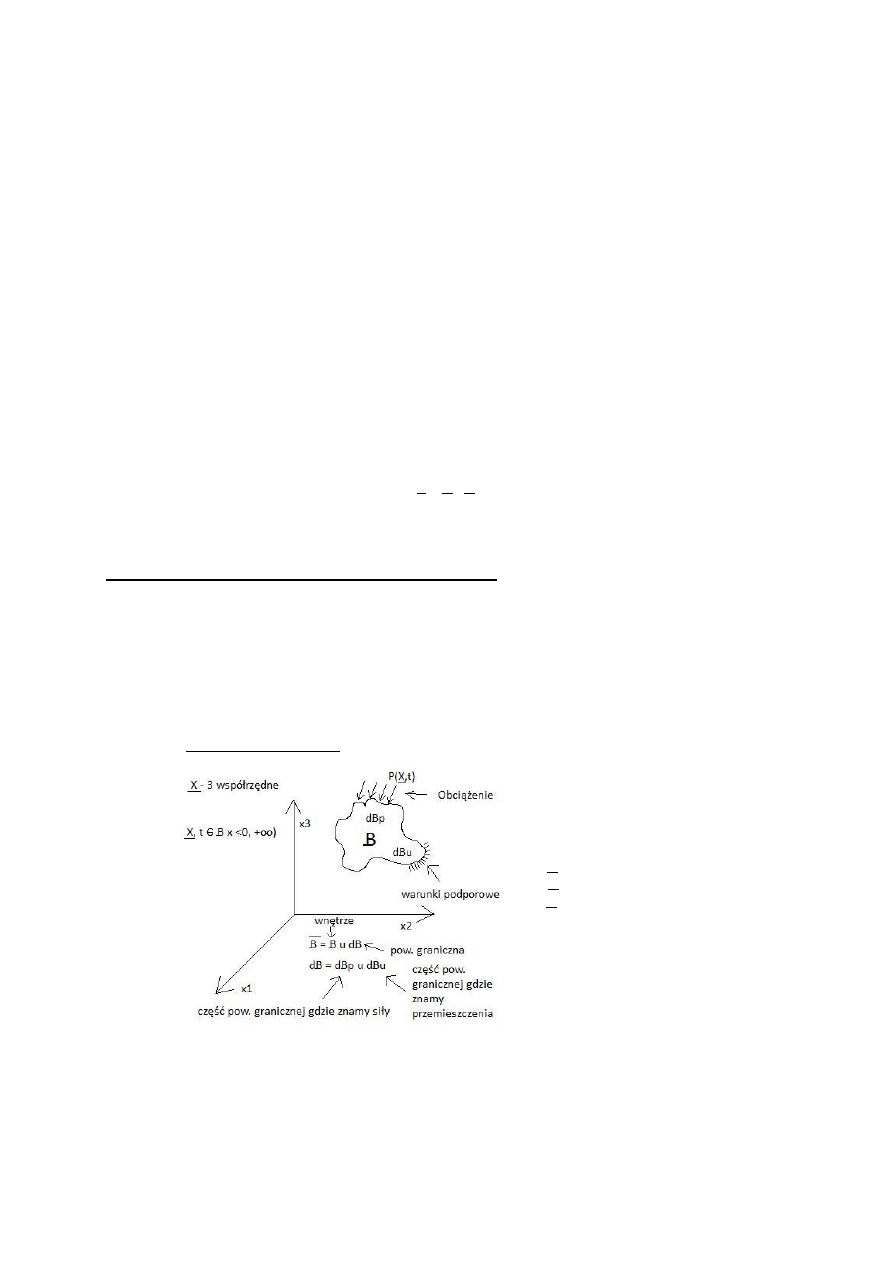
- Dyskretyzacja fizyczna modelu ciągłego (MES)

Dyskretyzacja fizyczna związana jest z MES i w wyniku tej dyskretyzacji układ kontynualny
zostaje zastąpiony modelem dyskretnym.

- model dyskretny składa się z elementów, które
stanowią część układu kontynualnego o
uproszczonych charakterystykach geometrycznych
i fizycznych (E

e

= constans i J

e

= constans)

oraz zbioru węzłów w których elementy te są ze
sobą połączone.

- obciążenie sprowadzamy do węzłów:

P = col { P

1

, P

2

, …, P

i

, … ,P

n

}, gdzie

P

i

– zawiera składowe siły i momenty (obciążenia

zewnętrzne)

Opracował: Mateusz Antoniak i Karol Frasz

Budownictwo – Drogi, Ulice i Lotniska

IV rok, sem. VII

Na podstawie znanych z wytrzymałości materiałów zależności różniczkowych, możemy napisać
odpowiednie związki pomiędzy parametrami statycznymi (siłami) a parametrami geometrycznymi
(przemieszczeniami) w nast. sposób:

𝑇

𝑖

𝑒

𝑀

𝑖

𝑒

𝑇

𝑖+1

𝑒

𝑀

𝑖+1

𝑒

=

𝑘

11

𝑘

12

𝑘

21

𝑘

22

𝑘

13

𝑘

14

𝑘

23

𝑘

24

𝑘

31

𝑘

32

𝑘

41

𝑘

42

𝑘

33

𝑘

34

𝑘

43

𝑘

44

∙

𝜑

𝑖

𝑒

𝑤

𝑖

𝑒

𝜑

𝑖+1

𝑒

𝑤

𝑖+1

𝑒

Po długotrwałych wyprowadzeniach wzorów, dla każdego węzła i po uwzględnieniu warunków
brzegowych otrzymujemy następujące układy równań algebraicznych.

P

1

= 𝑘

11

r

1

+ 𝑘

12

r

2

+ 𝑘

13

r

3

+ ⋯ + 𝑘

1n

r

n

P

2

= 𝑘

21

r

1

+ 𝑘

22

r

2

+ 𝑘

23

r

3

+ ⋯ + 𝑘

2n

r

n

.
.
.

P

n

= 𝑘

n1

r

1

+ 𝑘

n

r

2

+ 𝑘

n3

r

3

+ ⋯ + 𝑘

nn

r

n

Ostatecznie:

P = K

∙ X

Po rozwiązaniu układu równań, otrzymujemy zbiór przemieszczeń poszczególnych węzłów ES,
będących opisem linii ugięcia.

Zagadnienie początkowo brzegowe w mechanice ciała stałego

Zagadnienie początkowo brzegowe w mechanice ciała stałego możemy sformułować na dwa różne
sposoby:

a) Sformułowanie lokalne – znane są wówczas równania różniczkowe i algebraiczne opisujące

badany problem,

b) Sformułowanie globalne – znane są równania całkowe opisujące badanu problem,

Sformułowanie problemu

Pod wpływem zmiennych czasie i przestrzeni
oddziaływań zewnętrznych, w ciele
powstanie pole przemieszczeń, naprężeń i
odkształceń, gdzie:

u (X, t) – przemieszczenia

ζ (X, t) – naprężenia
ε (X, t) – odkształcenia

Opracował: Mateusz Antoniak i Karol Frasz

Budownictwo – Drogi, Ulice i Lotniska

IV rok, sem. VII

Siły masowe

Sformułowanie lokalne - polega na wyprowadzeniu kompletu równań różniczkowych i algebraicznych

opisujących wybrane zagadnienie oraz warunków brzegowych i początkowych.
Ważne jest, aby równania te spełnione były w każdym punkcie obszaru. Warunki
brzegowe natomiast muszą obowiązywać na jego brzegu.

- Równania równowagi – są równaniami różniczkowymi cząstkowymi, stąd do ich rozwiązania są

potrzebne warunki brzegowe i początkowe

𝜕𝜎

11

𝜕𝑥

1

+

𝜕𝜎

12

𝜕𝑥

2

+

𝜕𝜎

13

𝜕𝑥

3

+ 𝜌𝑓

1

= 𝜌𝑢

1

𝜕𝜎

21

𝜕𝑥

1

+

𝜕𝜎

22

𝜕𝑥

2

+

𝜕𝜎

23

𝜕𝑥

3

+ 𝜌𝑓

12

= 𝜌𝑢

2

𝜕𝜎

31

𝜕𝑥

1

+

𝜕𝜎

32

𝜕𝑥

2

+

𝜕𝜎

33

𝜕𝑥

3

+ 𝜌𝑓

3

= 𝜌𝑢

3

𝜕𝜎

𝑖𝑗

𝜕𝑥

𝑗

+ 𝜌𝑓

𝑖

= 𝜌𝑢

𝑖

, gdzie X, t

𝜖 B x <0, oo)

- Równania geometryczne

𝜀

11

=

𝜕𝑢

1

𝜕𝑥

1

; 𝜀

22

=

𝜕𝑢

2

𝜕𝑥

12

; 𝜀

33

=

𝜕𝑢

3

𝜕𝑥

3

𝜀

12

=

1
2

𝜕𝑢

1

𝜕𝑥

2

+

𝜕𝑢

2

𝜕𝑥

1

; 𝜀

13

=

1
2

𝜕𝑢

1

𝜕𝑥

3

+

𝜕𝑢

3

𝜕𝑥

1

; 𝜀

23

=

1
2

𝜕𝑢

2

𝜕𝑥

3

+

𝜕𝑢

3

𝜕𝑥

2

gdzie:

𝜀

𝑖𝑗

=

1
2

𝜕𝑢

𝑖

𝜕𝑥

𝑗

+

𝜕𝑢

𝑗

𝜕𝑥

𝑖

oraz

X, t

𝜖 B x <0, oo)

- Równania fizyczne (związki konstytutywne)

- ciało anizotropowe:

𝜎

𝑖𝑗

= 𝐶

𝑖𝑗𝑘𝑙

∙ 𝜀

𝑘𝑙

, gdzie: i, j = 1,2,3 oraz X, t

𝜖 B x <0, oo)

- ciało izotropowe:

-

𝜆, μ – stałe materiałowe Lameg’o

- δ

i, j

– delta Kronecker’a =

1 𝑑𝑙𝑎 𝑖=1
0 𝑑𝑙𝑎 𝑖≠𝑗

-

e – dylatacje (pierwszy niezmiennik stanu odkształcenia), e =

𝜀

11

+

𝜀

22

+

𝜀

33

𝜎

11

= 2𝜇𝜀

11

+ 𝜆𝑒; 𝜎

22

= 2𝜇𝜀

22

+ 𝜆𝑒; 𝜎

33

= 2𝜇𝜀

33

+ 𝜆𝑒,

𝜎

12

= 2𝜇𝜀

12

;

𝜎

13

= 2𝜇𝜀

13

;

𝜎

23

= 2𝜇𝜀

23

;

𝜎

𝑖𝑗

= 2𝜇𝜀

𝑖𝑗

+ 𝜆δ

ij

𝑒, gdzie i,j = 1,2,3 oraz oraz X, t 𝜖 B x <0, oo)

Przy czym:

Siły bezwładności

Tensor ujmujący parametry materiałowe

Tensor ujmujący odkształcenia

Tensor ujmujący naprężenia

Opracował: Mateusz Antoniak i Karol Frasz

Budownictwo – Drogi, Ulice i Lotniska

IV rok, sem. VII

𝜀

11

=

1

𝐸

[𝜎

11

− 𝜐(𝜎

22

+ 𝜎

33

]; 𝜀

22

=

1

𝐸

[𝜎

22

− 𝜐(𝜎

11

+ 𝜎

33

]; 𝜀

33

=

1

𝐸

[𝜎

11

− 𝜐(𝜎

11

+ 𝜎

22

]

𝜀

12

=

1+𝜐

𝐸

𝜎

12

=

𝜎

12

2𝜇

;

𝜀

13

=

1+𝜐

𝐸

𝜎

13

=

𝜎

13

2𝜇

;

𝜀

23

=

1+𝜐

𝐸

𝜎

23

=

𝜎

23

2𝜇

𝜀

𝑖𝑗

=

1

𝐸

(1 + 𝜐)𝜎

𝑖𝑗

− 𝜐δ

ij

𝜎

𝑟𝑟

, gdzie 𝜎

𝑟𝑟

= 𝜎

11

+ 𝜎

22

+ 𝜎

33

oraz

𝜇 =

𝐸

2(1+𝜐)

- Warunki brzegowe:

- typu statycznego

P

1

=

𝜎

11

n

1

+

𝜎

12

n

2

+

𝜎

13

n

3

P

2

=

𝜎

21

n

1

+

𝜎

22

n

2

+

𝜎

23

n

3

P

3

=

𝜎

31

n

1

+

𝜎

32

n

2

+

𝜎

33

n

3

P

i

=

𝜎

ij

n

j

, gdzie i,j = 1,2,3; n

j

= cosα < (N, x

j

) oraz X, t

𝜖 B x <0, oo)

- typu geometrycznego

𝑢

𝑖

= 𝑢

𝑖

, gdzie i = 1,2,3 oraz X, t

𝜖 Bu x <0, oo)

- Warunki początkowe:

𝑢

𝑖

= 𝑢

0

oraz X, t

𝜖 B x <0>

𝑢

𝑖

= 𝑢

0

Sformułowanie globalne - związane jest z sformułowaniem wariacyjnym. Sformułowanie to jest

wymagane przy rozwiązaniu zagadnienia za pomocą metod numerycznych( np.
MES lub MECZ). Przejście do sformułowania globalnego może być realizowane na
różne sposoby. Mogą być do tego celu stosowane np. metody wariacyjne lub
minimalizacja funkcjonalności.

Zalety

- równanie pól oraz warunki brzegowe są otrzymywane wprost z zasad wariacyjnych,

- sformułowanie wariacyjne umożliwia skoncentrowanie w 1 wyrażeniu wielu równań
opisujących badany problem.

W ramach przeprowadzanych wykładów wykorzystamy metody wariacyjne, stosując równania pracy
wirtualnej. Parametr wyjścia do wyprowadzenia równania pracy wirtualnej są różniczkowe równania
równowagi oraz statyczne warunki brzegowe.

𝜎

𝑖𝑗

+ 𝜌𝑓

𝑖

− 𝜌𝑢

𝑖

= 0 - różniczkowe równania równowagi

oraz

𝑃

𝑖

− 𝜎

𝑖𝑗

n

j

= 0 – statyczne warunki brzegowe

Równania równowagi powinny być spełnione w każdym punkcie obszaru oraz w każdej chwili „t”.
Sens tych równań nie zmieni się jeżeli pomnożymy je przez wariacje przemieszczeń

δ

ui

oraz

scałkujemy po obszarze ciała.

Def. wariacji przemieszczeń – nazywamy przemieszczenie wirtualne

δ

ui

≝

0 x ϵ

𝜕𝐵𝑢

dowolna, x ϵ B

−

𝜕𝐵𝑢

Opracował: Mateusz Antoniak i Karol Frasz

Budownictwo – Drogi, Ulice i Lotniska

IV rok, sem. VII

Cechy wariacji:

- przemieszczenia nieskończenie małe,

- przemieszczenia niezależne od obciążeń,

- przemieszczenia kinematyczne dopuszczalne, czyli zgodne z więzami ograniczającymi ciało.

( 𝜎

𝑖𝑗

+ 𝜌𝑓

𝑖

− 𝜌𝑢

𝑖

)δ

ui

dB = 0

( 𝑃

𝑖

− 𝜎

𝑖𝑗

n

j

)δ

ui

δ

uj

d(

𝜕

B)

Po scałkowaniu wyżej wymienionych wyrażeń, otrzymujemy, że:

𝑢

𝑖𝑗

= 𝜀

𝑖𝑗

+ 𝜔

𝑖𝑗

oraz

δ𝑢

𝑖𝑗

= δ𝜀

𝑖𝑗

+ δ𝜔

𝑖𝑗

Powyższe równości informują nas o tym, że tensor naprężenia oraz wariancja tensora odkształcenia

δ𝜀

𝑖𝑗

są tensorami symetrycznymi. Wariancja obrotu odkształcenia

δ𝜔

𝑖𝑗

jest tensorem antysymetrycznym.

Iloczyn tensora symetrycznego i tensora antysymetrycznego = 0

Dyskretyzacja modelu obliczeniowego – idealizacji geometrii układu podlegają również warunki podparcia i

obciążenia. W szczególności obciążenia ciągłe zastępujemy układem
sił skupionych w węzłach elementu skończonego. Elementy
skończone są w węzłach, dlatego spełniony jest warunek ciągłości
przemieszczeń. Na brzegach elementów skończonych, tej ciągłości
nie gwarantujemy, stąd w procesie deformacji, może pojawić się
między elementami szczelina. Aby zminimalizować wymiar
szczeliny wprowadza się węzły pośrednie. Gęstość podziału
konstrukcji na elementy skończone oraz liczba węzłów decyduje o
dokładności metody. Im gęstszy podział obszaru na elementy
skończone tym więcej mamy równań dla dokładniejsze obliczenia. W
węzłach zakładamy liczbę stopni swobody, które stanowią
podstawowy układ niewiadomych w metodzie elementów
skończonych.

Analiza elementu skończonego

Analiza elementu skończonego sprowadza się do ustalenia związku pomiędzy siłami oddziaływującymi
w węzłach a przemieszczeniami tych węzłów. Tworzymy więc macierz sztywności K, którą tę
zależność opisuje. Analizowane funkcje w obszarze elementu skończonego (przemieszczenia) wyrażone
są przez parametry węzłowe.

Zależności te można przedstawić w nast. postaci:

u

i

e

(x,t) = Φ

iα

e

(x) * r

α

(t) oraz x,t Є β < 0, ∞) ,gdzie:

u

i

e

- pole przemieszczeń w obszarze elementu skończonego ( w dowolnym punkcie)

gdzie:

- i= 1,2,3
- Φ

iα

e

- funkcje kształtu ( decyduje o dokładności)

- r

α

– przemieszczenie węzłowe

- α= 1,2,3,… s

∙w

- w- liczba węzłów elementu skończonego
- s - liczba stopni swobody w węźle
- e - numer elementu skończonego
- Ω - pole elementu skończonego
- x- przestrzeń
- t- czas

Opracował: Mateusz Antoniak i Karol Frasz

Budownictwo – Drogi, Ulice i Lotniska

IV rok, sem. VII

Powyższa zależność, stanowi przybliżone określenie pola przemieszczeń w obszarze elementu
skończonego w dowolnym punkcie w funkcji przemieszczeń jego węzłów. Właściwy dobór funkcji
kształtu, jest zagadnieniem podstawowym w analizie elementu skończonego i jednocześnie
zagadnieniem najtrudniejszym. Właściwy dobór tej funkcji w zasadniczy sposób decyduje o
dokładności metody elementów skończonych (MES)

Przy wyborze funkcji kształtu decyduje:

- kryterium zgodności przemieszczeń- funkcja kształtu musi być tak dobrana aby zapewnić
ciągłość przemieszczeń węzła obszaru elementu skończonego oraz w jego węzłach,

- kryterium sztywności- funkcja kształtu musi być tak dobrana aby podczas ruchu układu bryły
sztywnej, nie powstały w nim żadne naprężenia ani odkształcenia.

Związek pomiędzy siłami oddziaływania w węzłach elementu skończonego a przemieszczeniami tych
węzłów, przyjmuje nast. postać

-zagadnienie brzegowe: K

e

∙ r

e

= P

e

-zagadnienie początkowo brzegowe: M

e

∙ 𝑟

𝑒

+ C

e

∙ 𝑟

𝑒

+ K

e

∙ r

e

= P

e

- M - macierze bezwładności mas ES,
- C - macierz tłumienia dla elementu skończonego ES,
- U- macierz sztywności elementu skończonego ES,
- P - macierz- wektor obciążeń węzłów elementu skończonego o wymiarze (s

∙w) ∙1 ES,

- r-wektor przemieszczeń węzłów elementu skończonego o wymiarze (s

∙w) ∙1,

-

𝑟

𝑒

- przyspieszenie przemieszczeń węzłów ES,

-

𝑟

𝑒

- prędkość przemieszczeń węzłów ES.

Analiza całego układu (analiza konstrukcji)

Etap ten polega ma zszywaniu poszczególnych elementów końcowych w całość, przy wykorzystaniu
warunku ciągłości przemieszczeń i warunku równowagi węzłów.

W wyniku czego, otrzymujemy:

- układ równań algebraicznych ( dla zagadnienia brzegowego), lub
- układ równań różniczkowych zwyczajnych ( dla zagadnienia początkowego).

K

∙ r = P, oraz

M

∙ r + C∙ r + K∙r = P



Uwzględnienie warunków brzegowych

M, C, K – macierze globalne układu

Układ równań K

∙ r = P ma taką cechę, gdy macierz kolumna-wektor (r) zawiera oprócz

nieznanych przemieszczeń węzłów , również te przemieszczenia które znamy (tam gdzie
mamy zadane warunki podporowe). Wektor (P), oprócz znanych zadanych sił, zawiera również
nieznane reakcje podporowe. W takim przypadku, macierz sztywności (K), jest macierzą
osobliwą, czyli jej wyznacznik jest równy = 0. Aby pozbyć się tej osobliwości, należy do
układu równań K

∙ r = P wprowadzić więzy kinematyczne ograniczające ruch naszego układu.



Rozwiązanie układu równań algebraicznych lub różniczkowych zwyczajnych

W wyniku tego otrzymujemy przemieszczenia węzłów, czyli parametry węzłowe.

Opracował: Mateusz Antoniak i Karol Frasz

Budownictwo – Drogi, Ulice i Lotniska

IV rok, sem. VII

Charakterystyka modelu skończonego:

1) Przemieszczenia:

𝑢

𝑖

𝑒

= 𝑢

𝑖

𝑒

𝑥, 𝑡 = 𝜙

𝑖𝛼

𝑒

𝑥 𝑟

𝛼

(𝑡), gdzie i=1,2,3 oraz α=1,2,3,…,w∙s

2) Odkształcenia:

𝐵

𝑖𝑗

𝛼

=

1
2

[𝜙

𝑖𝛼,𝑗

𝑒

+𝜙

𝑗 𝛼,𝑖

𝑒

]

3) Naprężenia:

𝜎

𝑖𝑗

𝑒

= 𝑐

𝑖𝑗𝑘𝑙

𝑒

∙ 𝐵

𝑘𝑙 𝛼

𝑒

∙ 𝑟

𝛼

4) Wariancje:

- Przemieszczenia:

δ

ui

e

= 𝜙

𝑖𝛽

𝑒

∙ δ

rβ

- Odkształcenia:

δ

ε,j

e

= 𝐵

𝑖𝑗𝛽

𝑒

∙ δ

rβ

Na podstawie wyższych zależności, można stwierdzić, że funkcja kształtu

𝜙 i 𝐵 nie zależą od

przemieszczeń.

Równanie pracy wirtualnej - Równanie pracy wirtualnej piszemy dla każdego elementu

skończonego. Elementów skończonych mamy skończoną liczbę (E), stąd musimy
sumować (tzn. dokonać agregacji) wszystkich elementów skończonych.

Po dyskretyzacji ośrodka ciągłego, czyli podziale na elementy skończone, równanie pracy
wirtualnej przyjmuje następującą postać:

𝜌

𝑒

𝑓

𝑖

𝑒

δ

ui

e

d𝛺𝑒 − 𝜌

𝑒

𝑢

𝑖

𝑒

δ

ui

e

d𝛺𝑒 + 𝑃

𝑖

𝑒

𝑓

𝑖

𝑒

δ

ui

e

(𝜕𝛺𝑒) − 𝜎

𝑖𝑗

𝑒

δ

εij

e

𝑑𝛺𝑒

𝜕𝛺𝑒

𝜕𝛺𝑒

𝛺𝑒

𝛺𝑒

𝐸

𝑒=1

= 0

𝑀

Która po agregacji przyjmuje postać następującego równania:

𝑀 ∙ 𝑟 + 𝐾 ∙ 𝑟 − 𝑃 = 0 – równanie różniczkowe dla zagadnienia początkowo brzegowego
𝐾 ∙ 𝑟 = 𝑃 – równanie różniczkowe dla zagadnienia brzegowego

Cechy macierzy M i K:

- macierze są pasmowe (wstęgowe),
- macierze są symetryczne względem głównej przekątnej,
- gdy wyznacznik macierzy k=0, to układ jest zmienny, jeśli k

≠0 to układ jest

geometrycznie niezmienny.

Agregacja macierzy sztywności i bezwładności mas

Macierze po agregacji nazywamy macierzami globalnymi. Równani ruchu przyjmuje postać
zagadnienie początkowo brzegowego

𝑀 ∙ 𝑟 + 𝐾 ∙ 𝑟 = 𝑃

Macierze sztywności w układzie współrzędnych globalnych:

𝐾

𝑒

= 𝑇

𝑒𝑇

∙ 𝐾

∙ 𝑇

𝑒