Metoda Elementów

Metoda Elementów

Sko czonych

Sko czonych

P yty i pow oki

P yty i pow oki

2

2

M

M

odel przemieszczeniowy dla

odel przemieszczeniowy dla

zagadnie

zagadnie

statyki

statyki

X, U

Y, V

Z, W

V

S

i

F

Y

i

F

X

i

F

Z

i

f

Y

B

f

X

B

f

Z

B

3

3

4

4

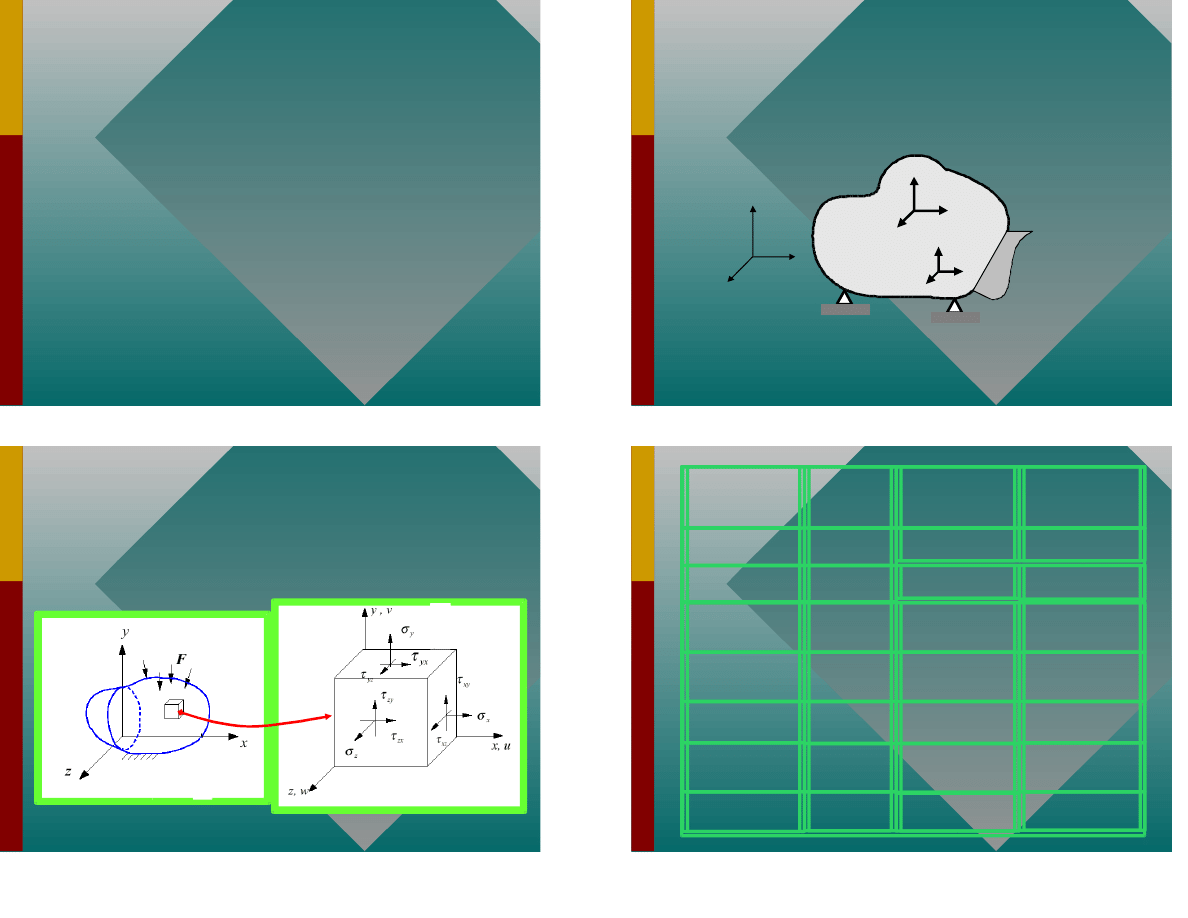
Zagadnienie

Sk adowe

przemie-

szcze

Wektor

odkszta ce

Wektor

napr e

Pr t kratowy

u

[e

xx

]

[s

xx

]

Belka

w

[k

xx

]

[M

xx

]

P aski

stan

napr en

ia

u, v

[e

xx

e

yy

g

xy

]

[s

xx

s

yy

t

xy

]

P aski stan

odksztacenia

u, v

[e

xx

e

yy

g

xy

]

[s

xx

s

yy

t

xy

]

Osiowo-
symetryczne

u, v

[e

xx

e

yy

g

xy

e

zz

]

[s

xx

s

yy

t

xy

s

zz

]

Trójwymiarowe

u, v, w

[e

xx

e

yy

e

zz

g

xy

g

yz

g

zx

]

[s

xx

s

yy

s

zz

t

xy

t

yz

t

zx

]

Zginanie p yty

w

[k

xx

k

yy

k

xy

]

[M

xx

M

yy

M

xy

]

5

5

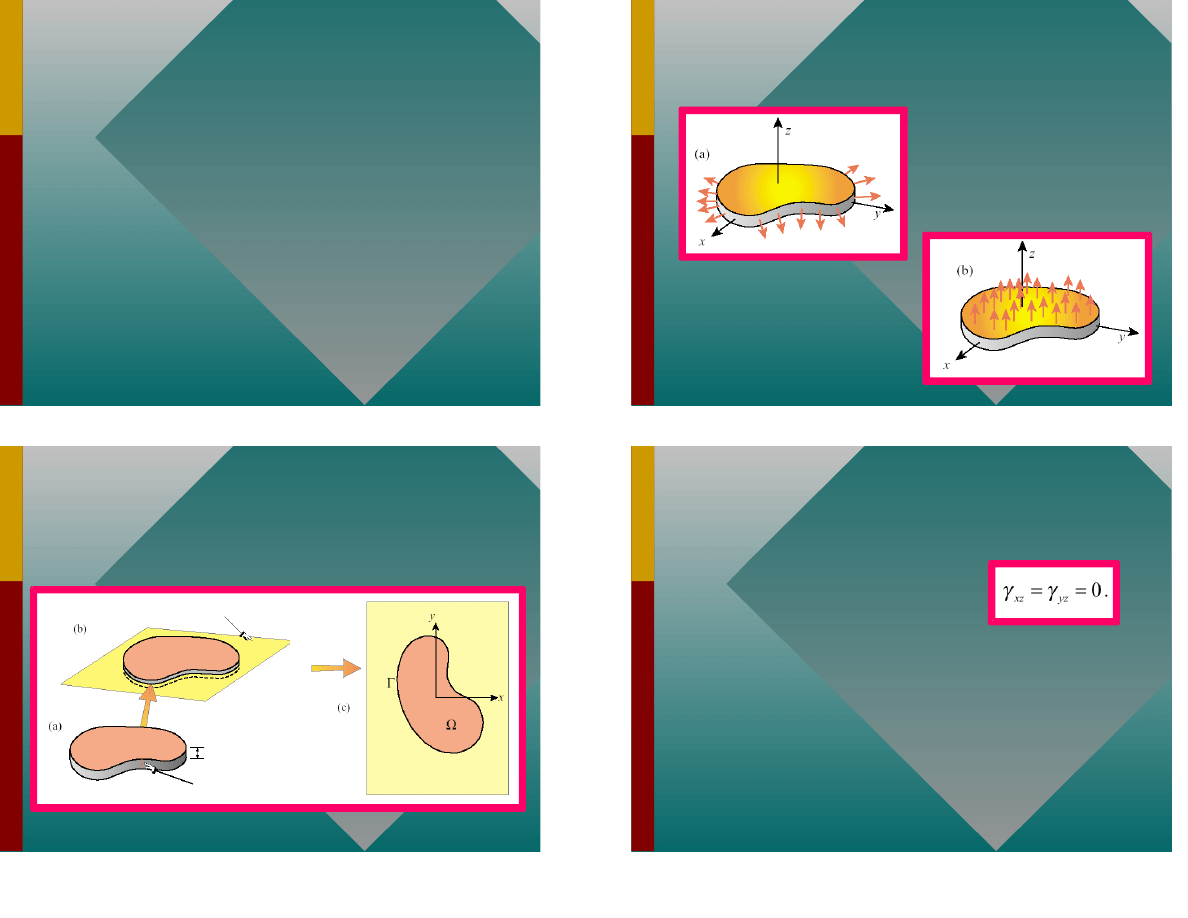
Za o enia modelu p yty

Za o enia modelu p yty

•

P aska p aszczyzna

P aska p aszczyzna

•

Obci enie prostopad e do powierzchni p yty

Obci enie prostopad e do powierzchni p yty

•

Dominuj cy wp yw zginania

Dominuj cy wp yw zginania

•

Ugi cie p yty jest ma e w porównaniu z

Ugi cie p yty jest ma e w porównaniu z

grubo ci

grubo ci

•

p aszczyzna rodkowa zamienia si w

p aszczyzna rodkowa zamienia si w

powierzchni rodkow bez zmiany d ugo ci

powierzchni rodkow bez zmiany d ugo ci

elementów i k tów mi dzy nimi

elementów i k tów mi dzy nimi

6

6

P yta – stan tarczowy i zgi ciowy

P yta – stan tarczowy i zgi ciowy

7

7

Idealizacja p yty – model 2D

Idealizacja p yty – model 2D

Powierzchnia rodkowa

Model

matematyczny

Grubo

h

Model

fizyczny

8

8

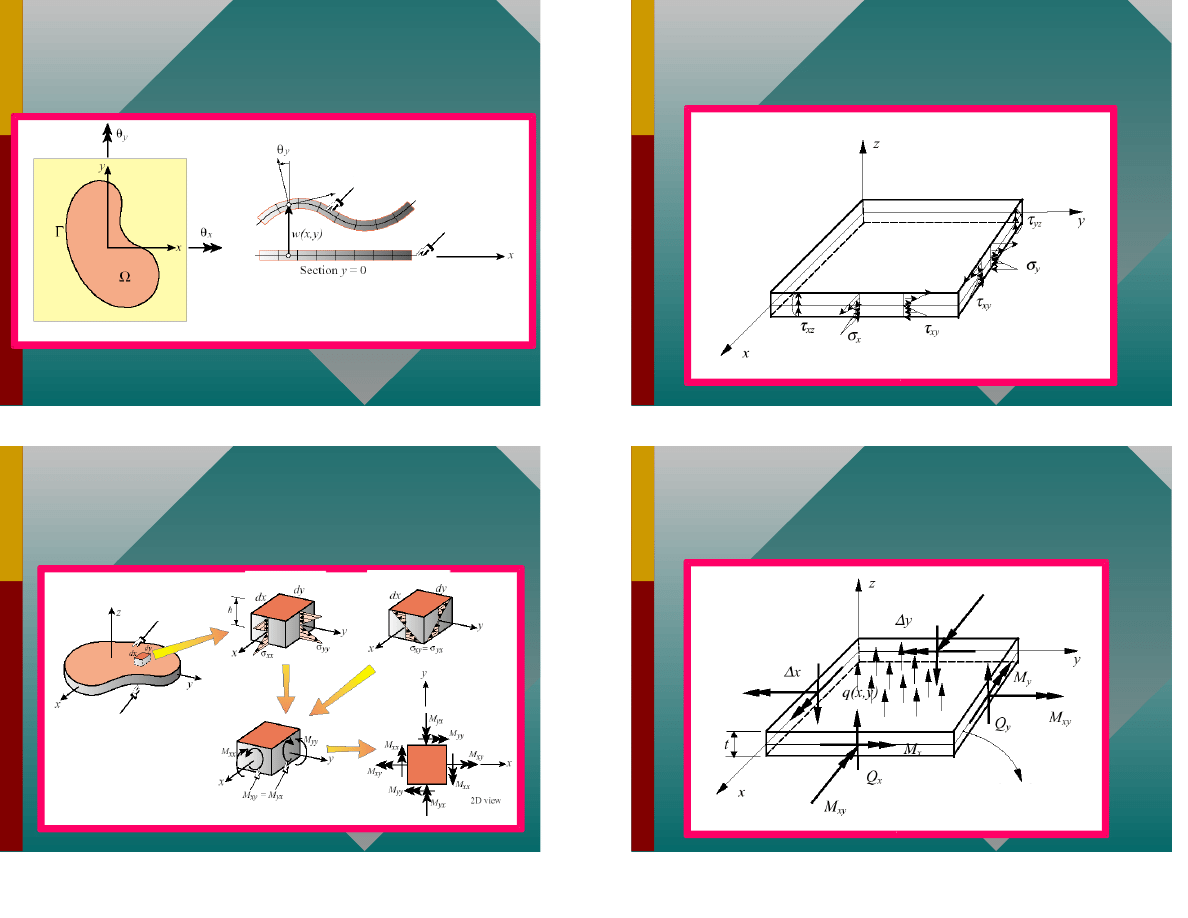
Proste, prostopad e do p aszczyzny rodkowej

Proste, prostopad e do p aszczyzny rodkowej

w nieodkszta conej p ycie, zostaj po jej

w nieodkszta conej p ycie, zostaj po jej

odkszta ceniu proste i prostopad e do

odkszta ceniu proste i prostopad e do

powierzchni rodkowej.

powierzchni rodkowej.

Odkszta cenia warstw równoleg ych do

Odkszta cenia warstw równoleg ych do

powierzchni rodkowej w kierunku

powierzchni rodkowej w kierunku

prostopad ym do tej powierzchni s pomijalne.

prostopad ym do tej powierzchni s pomijalne.

Teoria p yt cienkich

Teoria p yt cienkich

(Kirchhoffa)

(Kirchhoffa)

Hipotezy:

Hipotezy:

9

9

Kinematyka p yty Kirchhoffa

Kinematyka p yty Kirchhoffa

Powierzchnia

rodkowa

Odkszta cona

powierzchnia

10

10

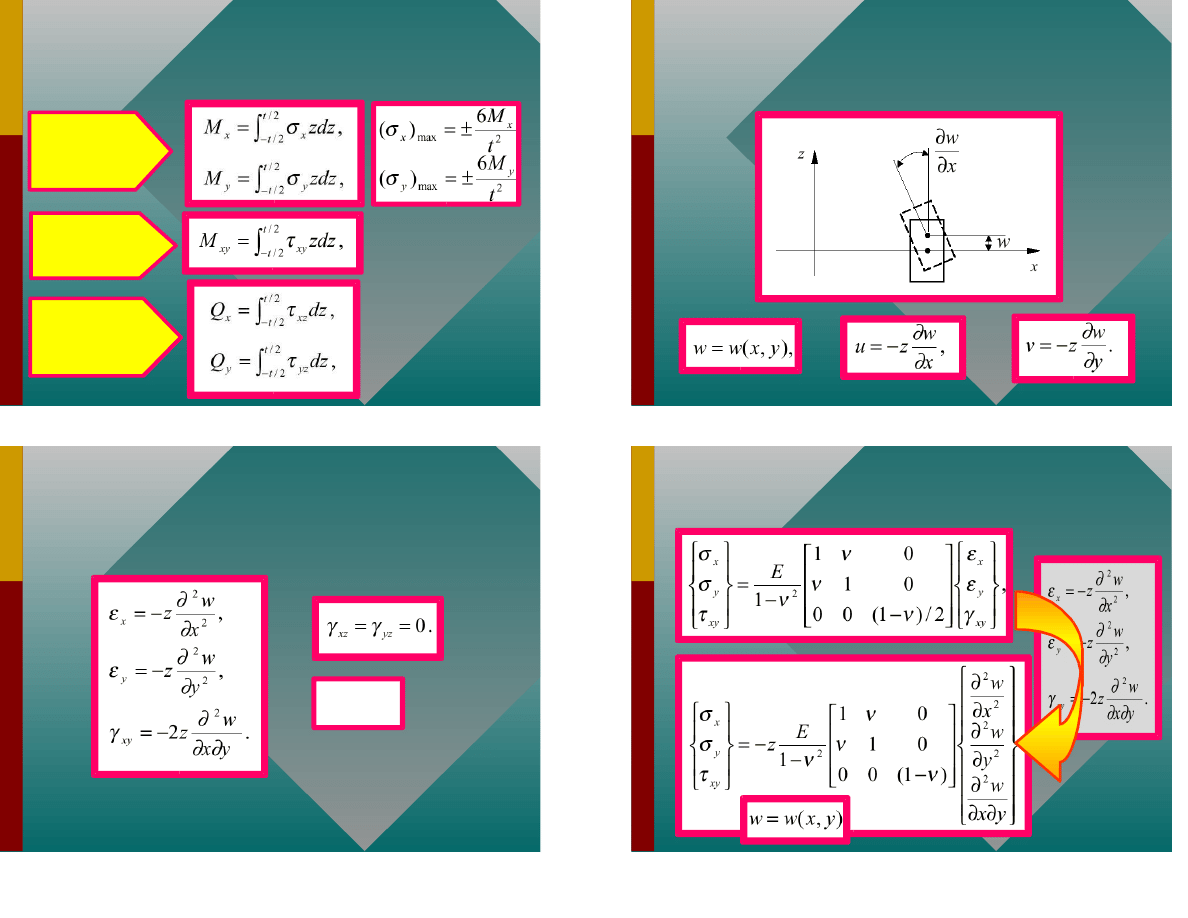
Napr enia

Napr enia

11

11

Napr enia uogólnione

Napr enia uogólnione

Powierzchnia górna

Powierzchnia dolna

Napr enia normalne

Napr enia styczne

Momenty zginaj ce

12

12

Si y wewn trzne w p ycie

Si y wewn trzne w p ycie

Powierzchnia rodkowa

13

13

Si y i momenty

Si y i momenty

Momenty

Momenty

zginaj ce

zginaj ce

Moment

Moment

skr caj cy

skr caj cy

Si y

Si y

poprzeczne

poprzeczne

14

14

Przemieszczenia

Przemieszczenia

15

15

Odkszta cenia

Odkszta cenia

ε

z

= 0

Teoria

Teoria

spr ysto ci

spr ysto ci

16

16

Zwi zki fizyczne

Zwi zki fizyczne

17

17

18

18

Równanie równowagi

Równanie równowagi

gdzie

gdzie

sztywno

sztywno

p yty

p yty

porównaj

porównaj

belka

belka

p yta

p yta

19

19

Si y poprzeczne i momenty

Si y poprzeczne i momenty

20

20

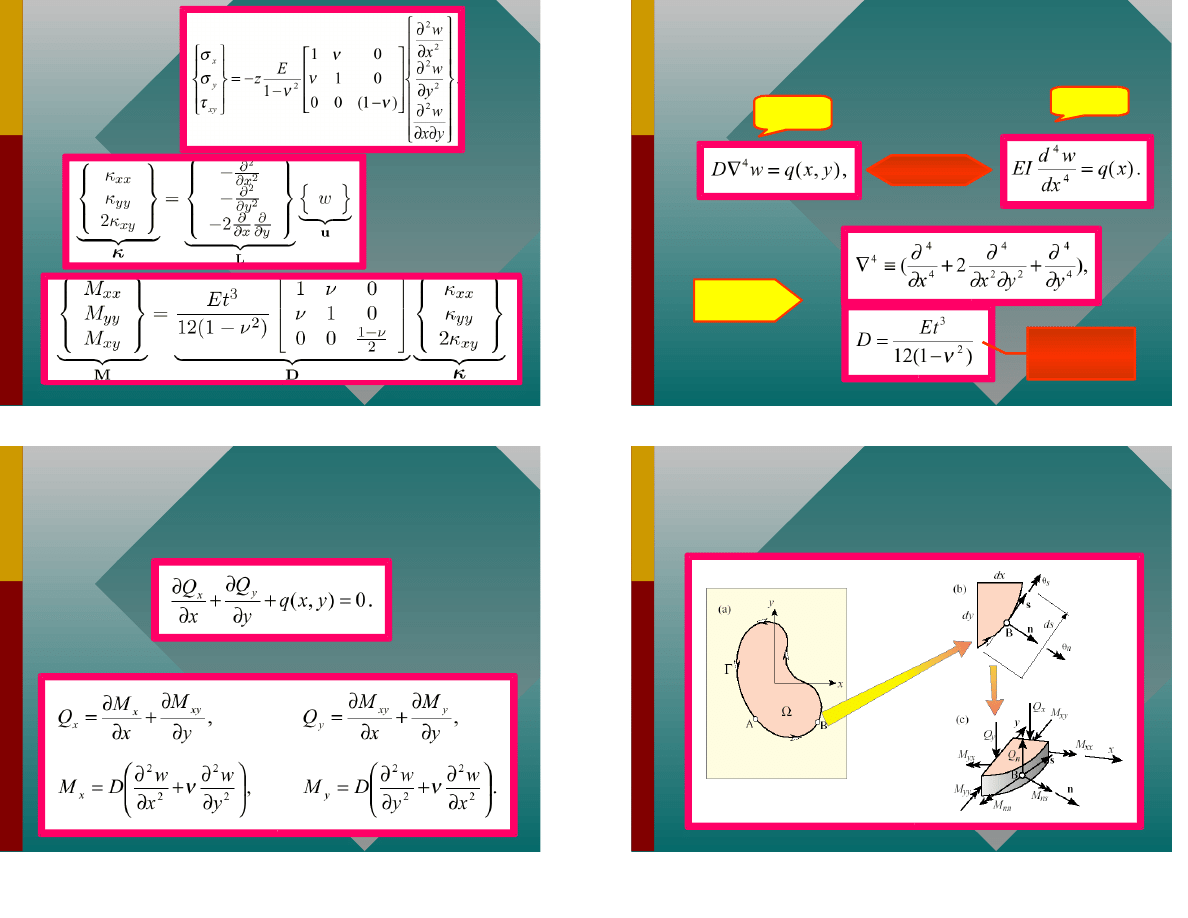
Warunki brzegowe

Warunki brzegowe

21

21

Warunki brzegowe

Warunki brzegowe

brzeg

brzeg

utwierdzony

utwierdzony

brzeg

brzeg

przegubowy

przegubowy

brzeg

brzeg

swobodny

swobodny

22

22

Wp yw M

Wp yw M

xy

xy

na reakcj w rogu

na reakcj w rogu

23

23

Dyskretyzacja

Dyskretyzacja

24

24

Elementy sko czone

Elementy sko czone

Element 4-w z owy

Element 4-w z owy

Powierzchnia rodkowa

Stopnie swobody w w le

Stopnie swobody w w le

25

25

Funkcje kszta tu dla elementu

Funkcje kszta tu dla elementu

26

26

Element 8-w z owy

Element 8-w z owy

27

27

Teoria p yt redniej grubo ci

Teoria p yt redniej grubo ci

(Mindlina)

(Mindlina)

4

4

t/L>1/10

t/L>1/10

Proste, prostopad e do p aszczyzny rodkowej

Proste, prostopad e do p aszczyzny rodkowej

w nieodkszta conej p ycie, zostaj po jej

w nieodkszta conej p ycie, zostaj po jej

odkszta ceniu proste i prostopad e do

odkszta ceniu proste i prostopad e do

powierzchni rodkowej.

powierzchni rodkowej.

Odrzucona zostaje hipoteza:

Odrzucona zostaje hipoteza:

Wyst pi wi c odkszta cenie postaciowe:

Wyst pi wi c odkszta cenie postaciowe:

28

28

Przemieszczenia

Przemieszczenia

Nowe zmienne:

Nowe zmienne:

x

x

,

,

y

y

29

29

Odkszta cenia

Odkszta cenia

30

30

gdzie

gdzie

oraz

31

31

Elementy sko czone

Elementy sko czone

Stopnie swobody w w le

Stopnie swobody w w le

32

32

Pow oki

Pow oki

Si y membranowe

Si y membranowe

+ momentowe

+ momentowe

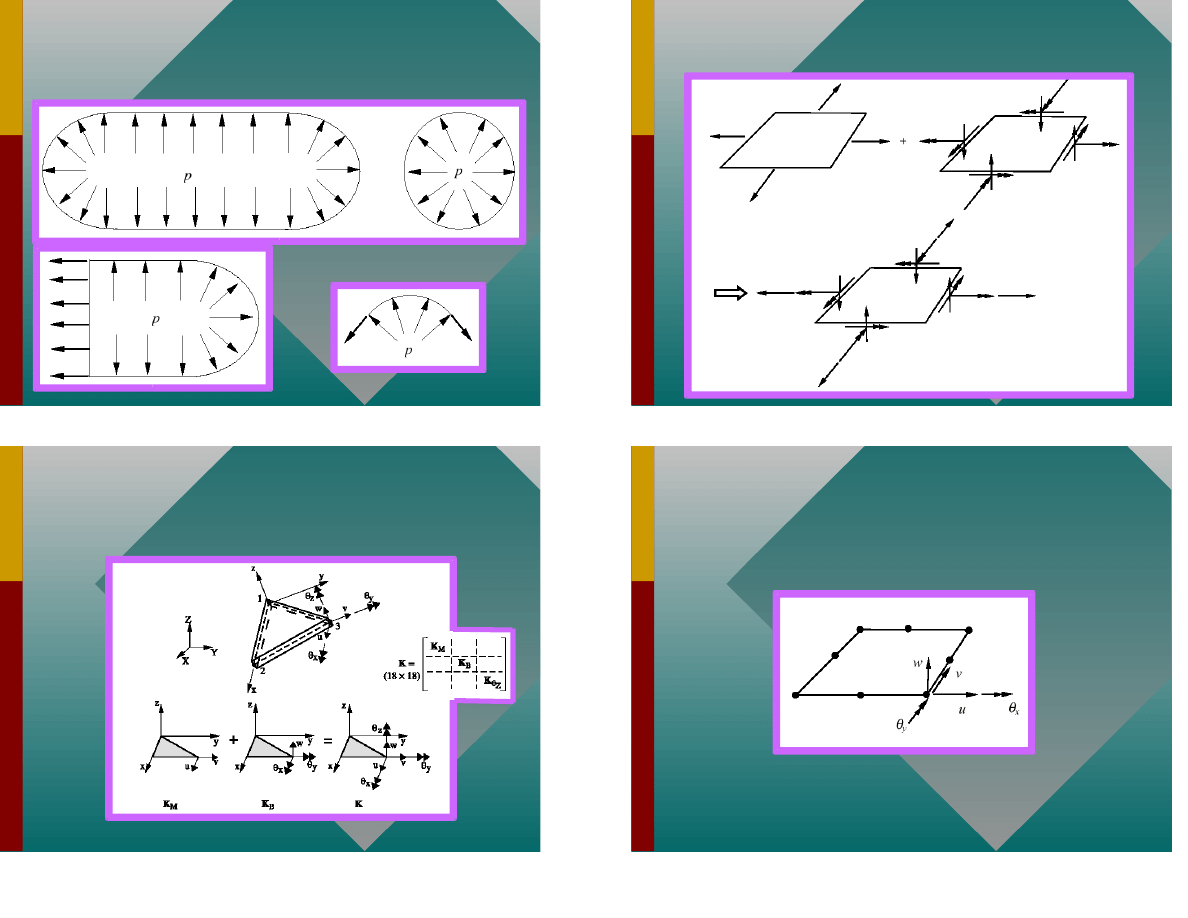
33

33

Zbiornik

Zbiornik

34

34

Elementy pow okowe

Elementy pow okowe

Element p aski stan napr

enia

Element p ytowy

Element pow okowy

35

35

Element trójk tny

Element trójk tny

36

36

Element Q8

Element Q8

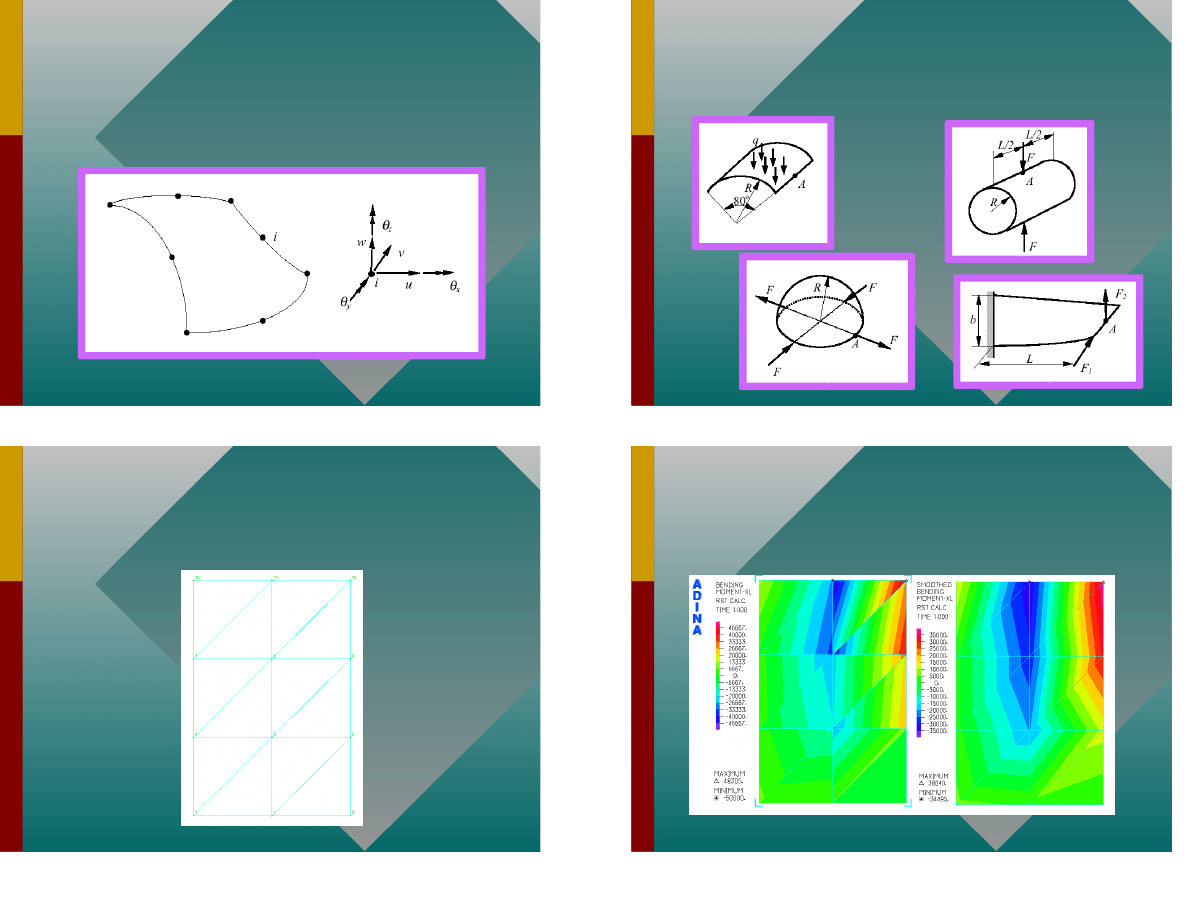
37

37

Element krzywoliniowy

Element krzywoliniowy

38

38

Przyk ady testowe

Przyk ady testowe

39

39

Siatka – elementy trójk tne

Siatka – elementy trójk tne

40

40

Moment zginaj cy M

Moment zginaj cy M

xx

xx

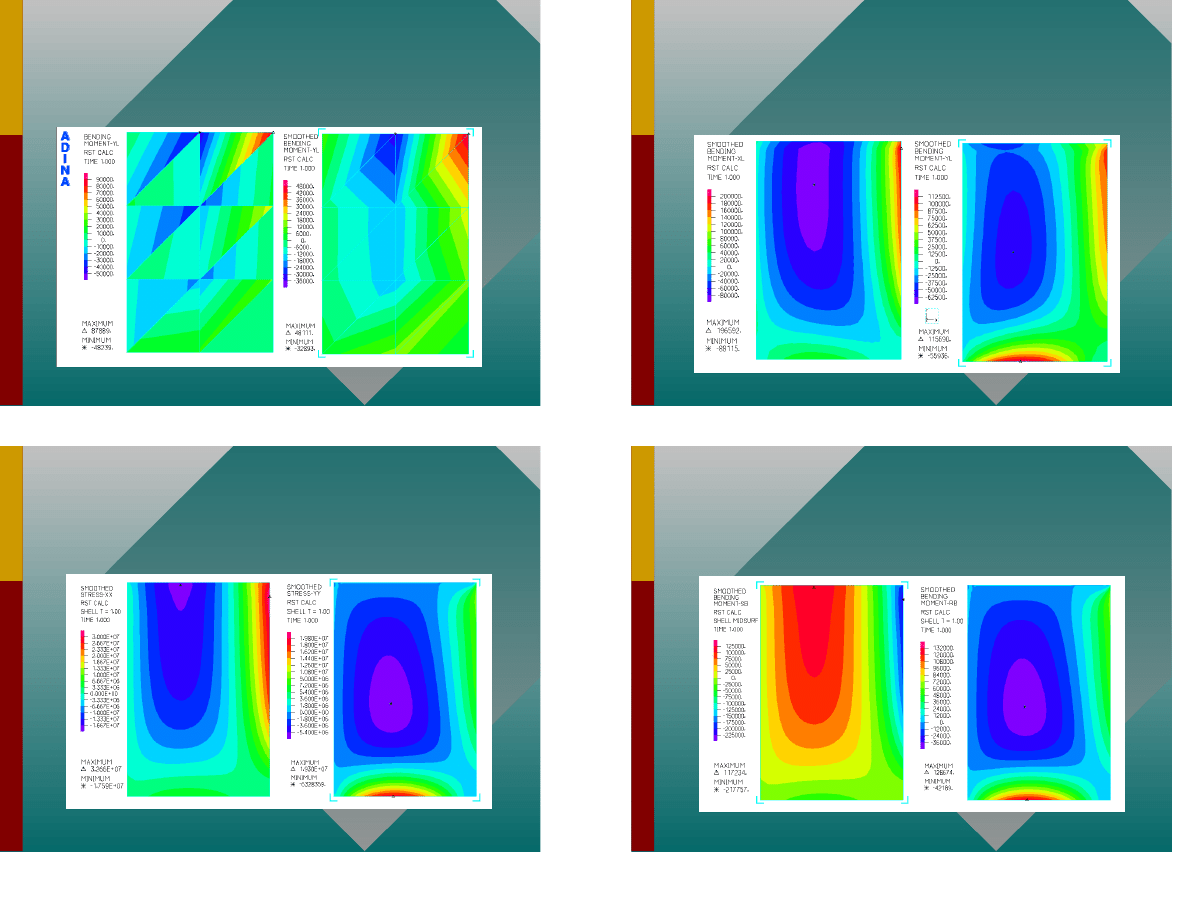
41

41

Moment zginaj cy M

Moment zginaj cy M

yy

yy

42

42

Momenty – g stsza siatka

Momenty – g stsza siatka

43

43

Pow oka

Pow oka

44

44

Pow oka

Pow oka

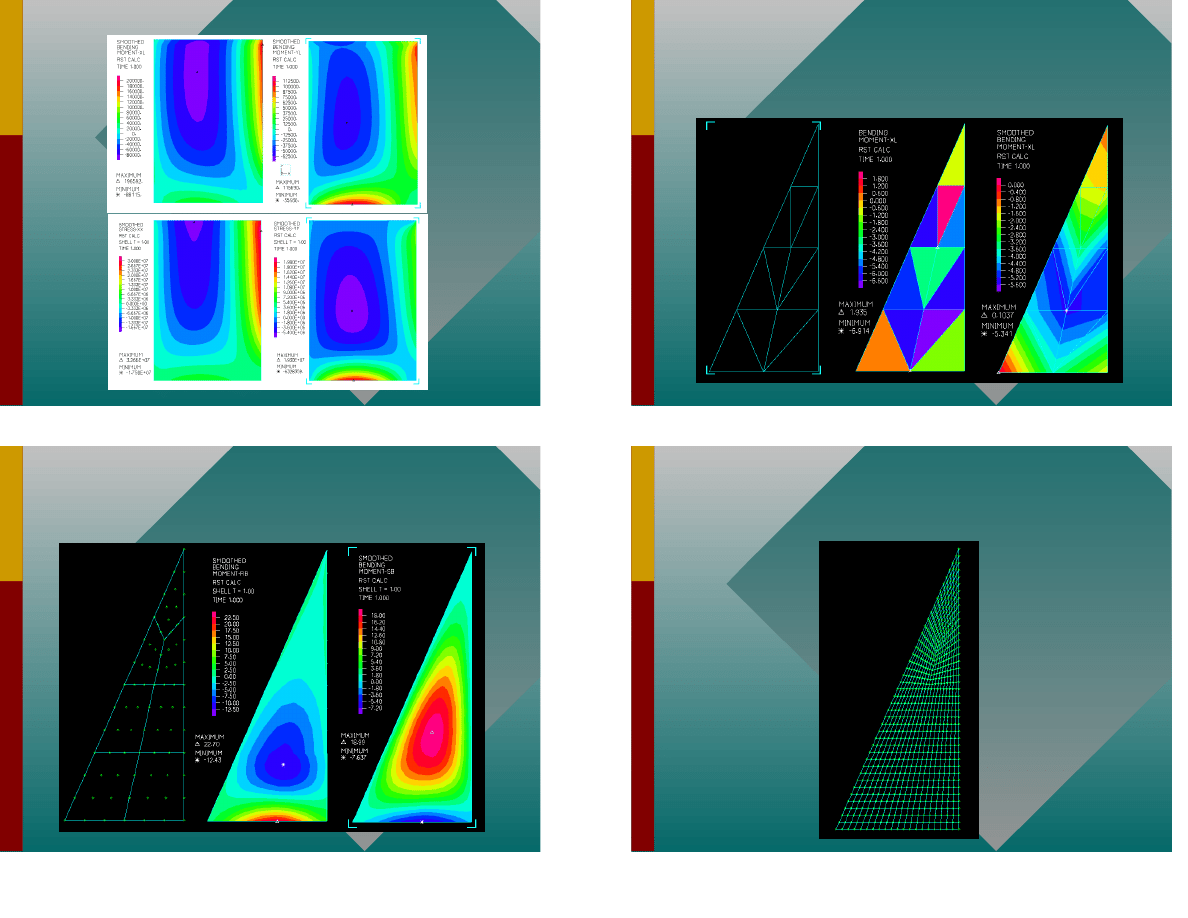
45

45

46

46

P yta trójk tna

P yta trójk tna

47

47

Elementy pow okowe

Elementy pow okowe

48

48

P yta trójk tna – siatka elementów

P yta trójk tna – siatka elementów

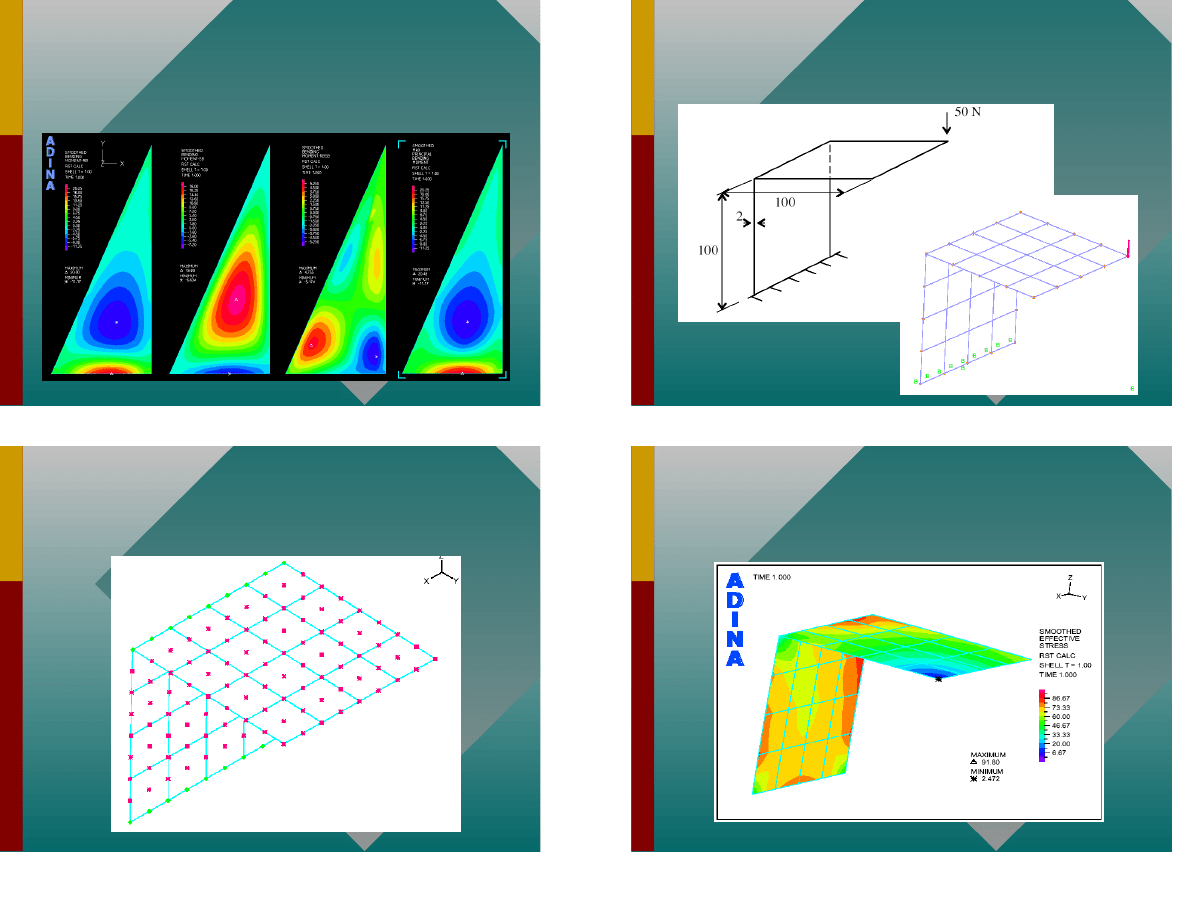
49

49

Wyniki

Wyniki

50

50

P yta naro na

P yta naro na

51

51

Siatka elementów sko czonych

Siatka elementów sko czonych

52

52

Napr enia zredukowane

Napr enia zredukowane

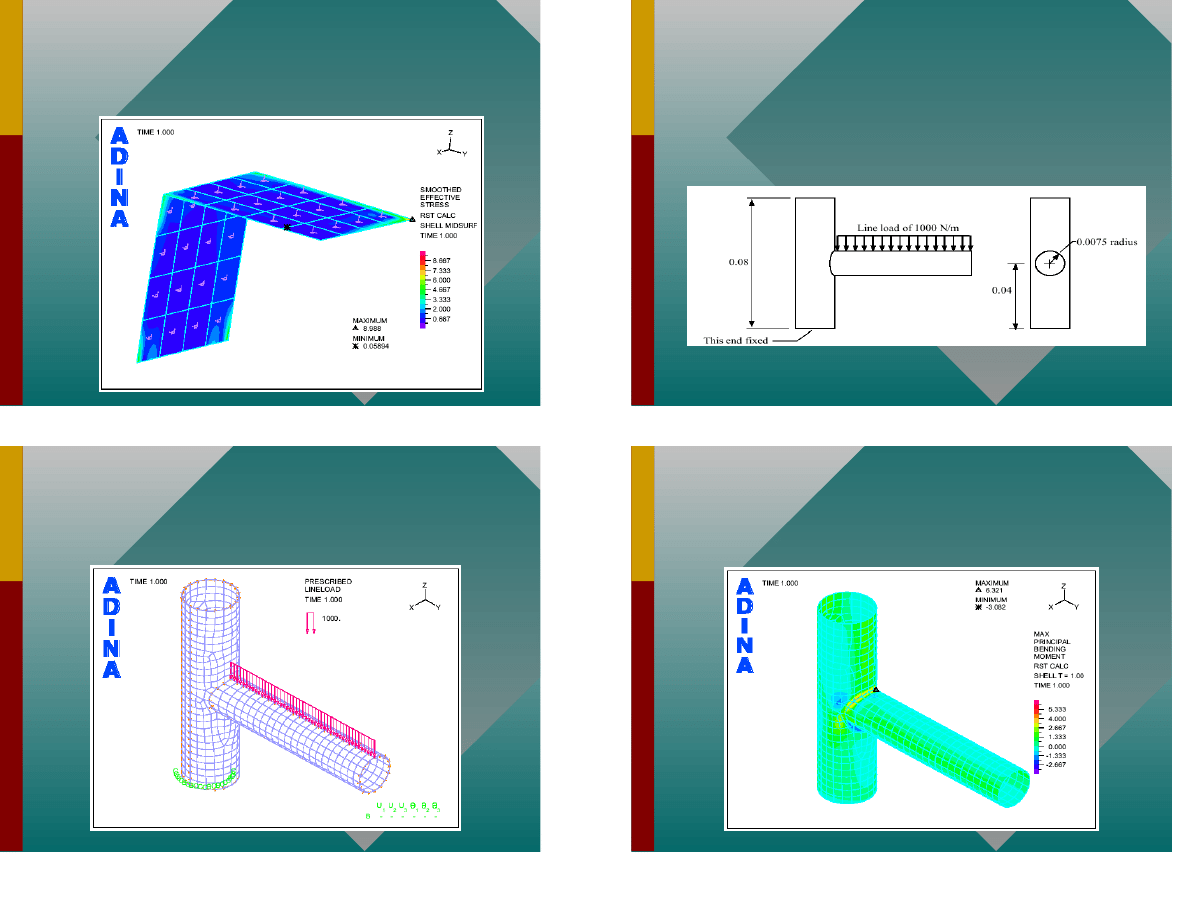
53

53

Napr enia w p aszczy nie

Napr enia w p aszczy nie

rodkowej

rodkowej

54

54

Po czenie pow okowe

Po czenie pow okowe

55

55

Model mes

Model mes

56

56

Moment - 1

Moment - 1

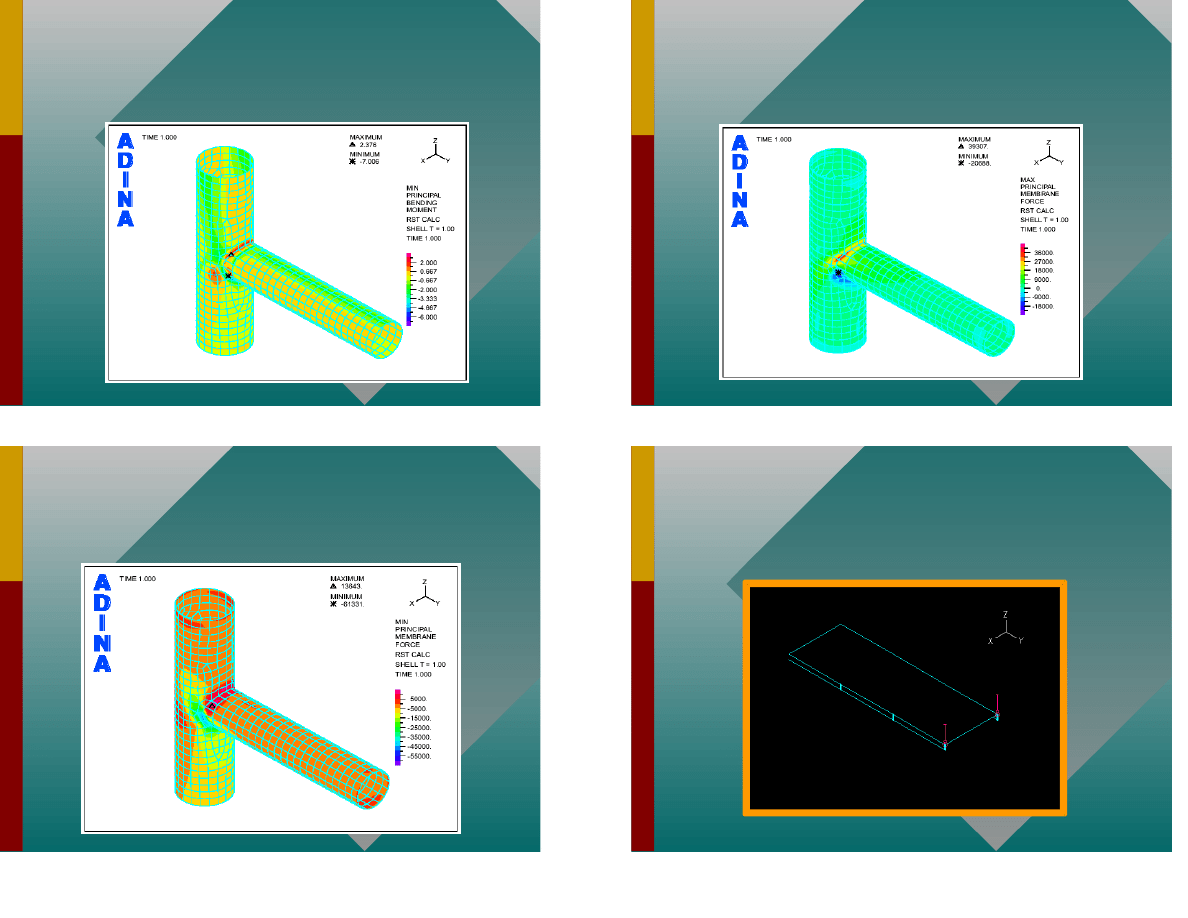
57

57

Moment - 2

Moment - 2

58

58

Si y membranowe - 1

Si y membranowe - 1

59

59

Si y membranowe - 2

Si y membranowe - 2

60

60

P yta z ebrami

P yta z ebrami

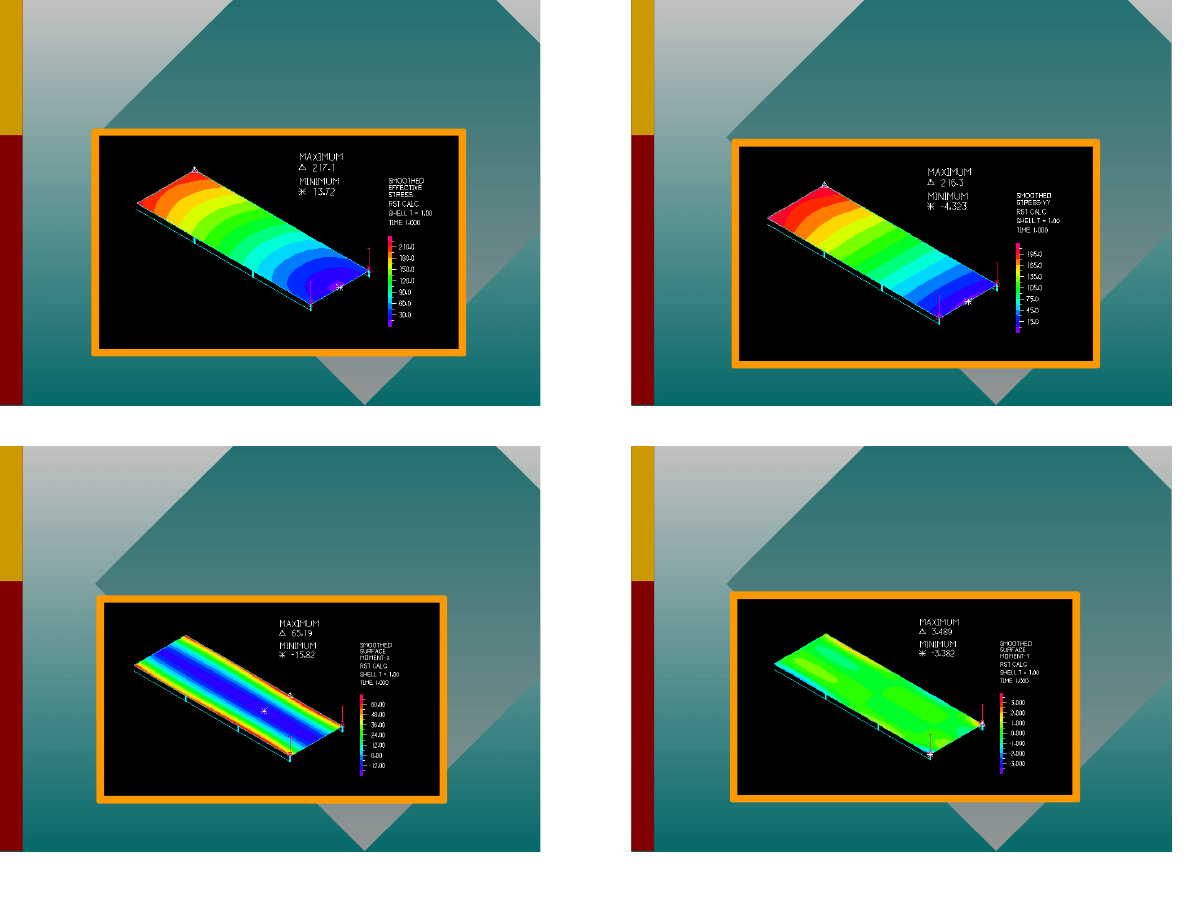
61

61

Napr enia zredukowane

Napr enia zredukowane

62

62

Napr enia normalne

Napr enia normalne

s

s

yy

yy

63

63

Moment zginaj cy M

Moment zginaj cy M

xx

xx

64

64

Moment zginaj cy M

Moment zginaj cy M

yy

yy