1

POLITECHNIKA

POZNAŃSKA

LABORATORIUM

Z

ENERGOELEKTRONIKI

ROK AKADEMICKI

2007/2008

WYDZIAŁ ELEKTRYCZNY
ROK STUDIÓW 2007 / 2008
SEMESTR 1; ROK 1
KIERUNEK: ELEKTROTECHNIKA
II STOPNIA

NR ĆWICZENIA 2

Filtry aktywne RC

PROWADZĄCY

dr inż. J. Piłaciński

WYKONUJACY ĆW.

1.

Piotr Fabian

2.

Andrzej Witkowski

3.

4.

5.

Grupa ćwiczeniowa 2

DATA WYKONANIA ĆW

08-12-2007

DATA ODDANIA SPR.

19-01-2008

ZALICZENIE :

2

1.

Wprowadzenie

Filtry aktywne RC to układy liniowe i stacjonarne realizowane za pomocą elementu
aktywnego, na który założono sprzężenie zwrotne zbudowane z elementów biernych R i C.
Elementem aktywnym najczęściej jest wzmacniacz operacyjny. Elementy bierne
sprzężenia zwrotnego kształtują charakterystykę amplitudowo częstotliwościową całego
układu filtru. Sprzężenie zwrotne odpowiedzialne za kształt charakterystyki amplitudowo-
częstotliwościowej może być zarówno dodatnie jak i ujemne. Elementem czynnym
(aktywnym) jest wzmacniacz operacyjny µA741 z ujemnym sprzężeniem zwrotnym
dobranym dla wymaganego wzmocnienia k.

2.

Cel ćwiczenia

Celem ćwiczenia było zbadanie charakterystyk amplitudowo-częstotliwościowych
podstawowych filtrów aktywnych RC w różnych konfiguracjach. Elementem aktywnym
jest wzmacniacz operacyjny uA 741. Elementy bierne sprzężenia zwrotnego natomiast
kształtują charakterystykę amplitudowo-częstotliwościową całego badanego układu. W
ć

wiczeniu, do badania filtrów wykorzystano człony kwadraturowe (tzn. dwubiegunowe)

zrealizowane w konfiguracji z dodatnim sprzężeniem zwrotnym.

Głównym celem ćwiczeniem jest przerysowanie odpowiedzi filtru na skok napięcia
u(t)=1(t). Podać czas narastania i określić ewentualne przeregulowanie.

Zestaw przyrządów:
- zestaw laboratoryjny ETS-7000
- oscyloskop dwukanałowy
- płytka testowa PT8
- generator NDN DF 1642B
3.

Przebieg ćwiczenia

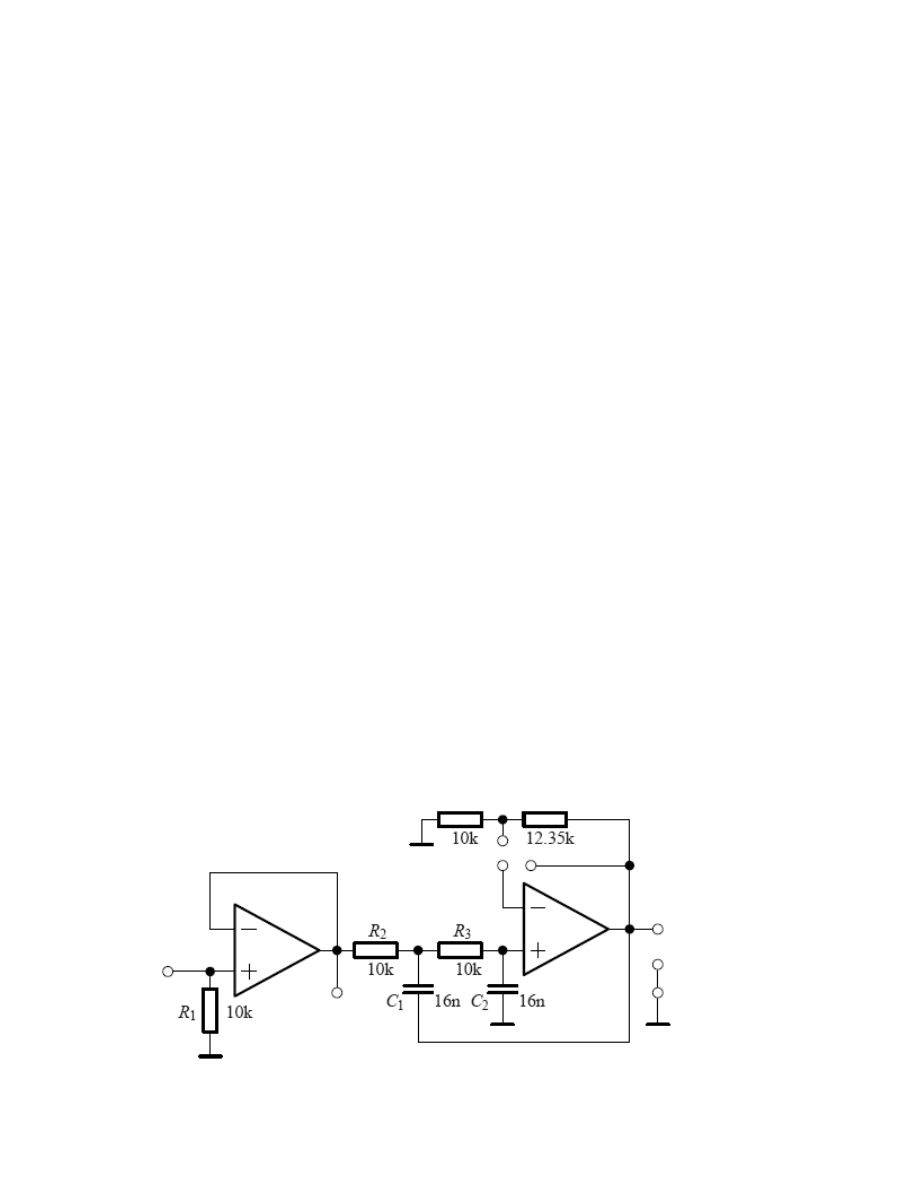
Część pierwsza – Filtr dolnoprzepustowy rzędu II o tłumieniu krytycznym (1 kHz).

Rysunek 1

3

:

1

10

16

gdzie

k

R

k

C

nF

=

=

Ω

=

Charakterystyka amplitudowo – częstotliwościowa:

2

1

| ( ) |

( )

U

K s

f f

U

=

=

Wyniki pomiarów napięcia wejściowego U1 oraz wyjściowego U2 dla filtru
dolnoprzepustowego, II rzędu:

Tabela 1. Tabela pomiarowa dla filtru II-rzędu

Lp. f[Hz]

U1[V]

U2[V]

Ku[dB]

1.

3

3,5

3,4

-0,25

2.

5

3,5

3,46

-0,10

3.

7

3,5

3,51

0,02

4.

10

3,5

3,5

0,00

6.

30

3,5

3,52

0,05

7.

50

3,5

3,52

0,05

9.

100

3,5

3,51

0,02

10.

200

3,5

3,45

-0,12

11.

300

3,5

3,3

-0,51

12.

500

3,5

2,9

-1,63

13.

700

3,5

2,4

-3,28

14.

800

3,5

2,1

-4,44

15.

850

3,5

2,05

-4,65

16.

900

3,5

1,95

-5,08

17.

950

3,5

1,88

-5,40

18.

970

3,5

1,73

-6,12

19.

1000

3,5

1,68

-6,38

20.

1100

3,5

1,62

-6,69

21.

1200

3,5

1,49

-7,42

22.

1300

3,5

1,32

-8,47

23.

1500

3,5

1,17

-9,52

24.

2000

3,5

0,75

-13,38

25.

3000

3,5

0,3

-21,34

26. 10000

3,5

0,02

-44,86

4

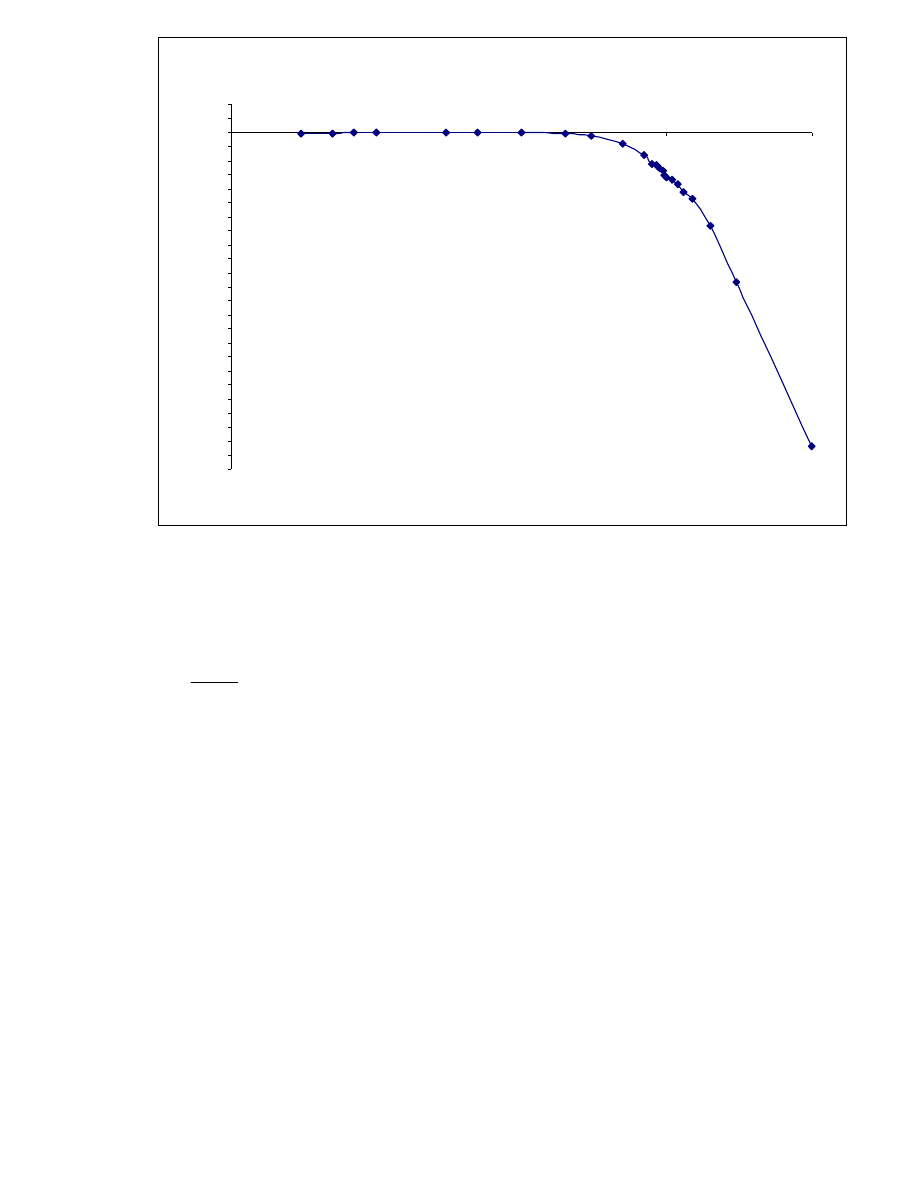
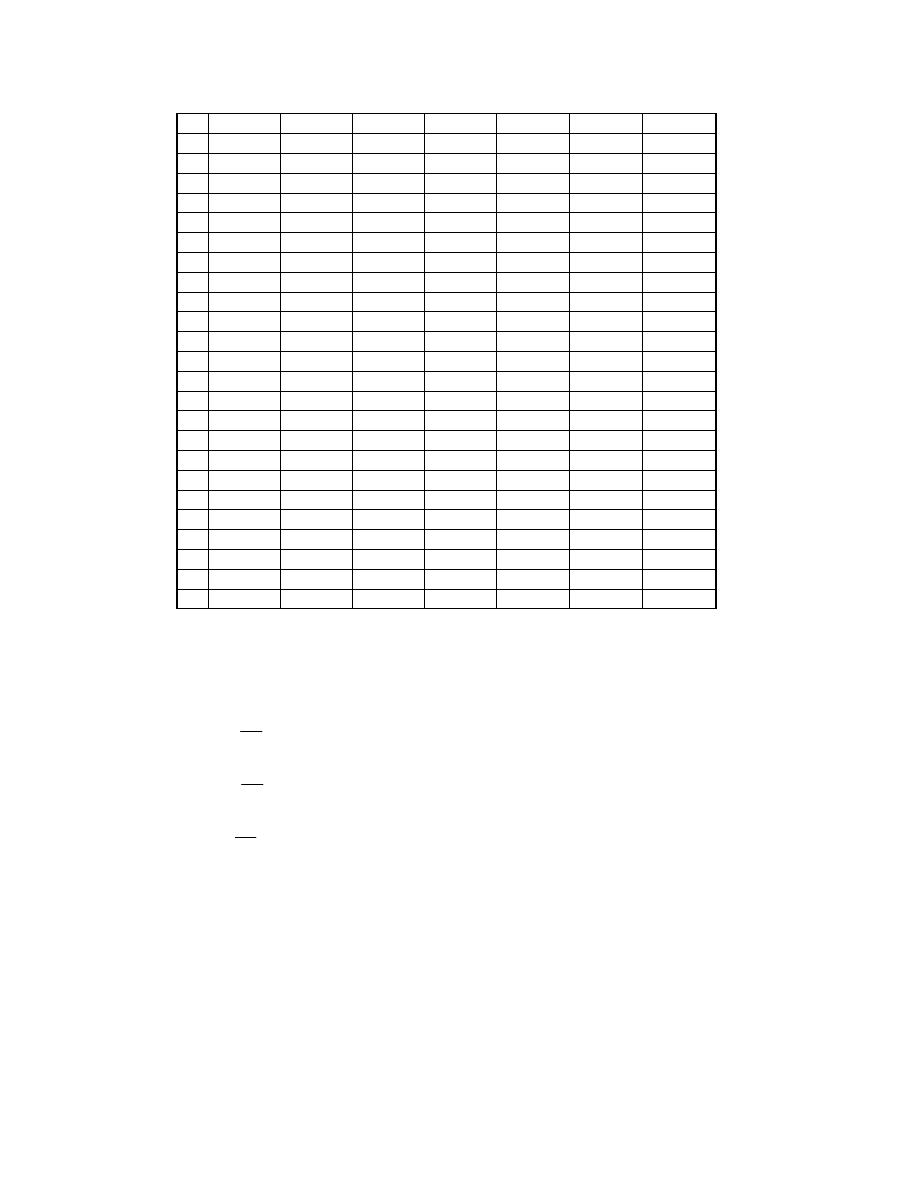
Z otrzymanych wyników wyrysowano charakterystykę amplitudowo – częstotliwościową.

Filtr o tł umieniu krytycz nym II rz ędu

-0,25

-0,10 0,02 0,00

0,05

0,05

0,02

-0,12

-0,51

-1,63

-3,28

-4,44

-4,65

-5,08

-5,40

-6,12

-6,38

-6,69

-7,42

-8,47

-9,52

-13,38

-21,34

-44,86

-48

-46

-44

-42

-40

-38

-36

-34

-32

-30

-28

-26

-24

-22

-20

-18

-16

-14

-12

-10

-8

-6

-4

-2

0

2

4

1

10

100

1000

10000

f[Hz]

K

u

[d

B

]

Wykres 1. Charakterystyka amplitudowo - częstotliwościowa dla filtru

dolnoprzepustowego II rzędu

Metodą regresji liniowej dopasowano prostą do liniowej części wykresu (do opadającej
części charakterystyki). Otrzymana prosta ma równanie: K = -0,0044 × f -1,89. Na tej
podstawie zostało wyliczone nachylenie asymptotyczne : -39,11[dB/dec].

1

1

2

g

f

kHz

RC

π

=

≈

-

częstotliwość graniczna teoretyczna

700

800

g

Hz

f

Hz

<

<

-

przedział w jakim znajduje się częstotliwość graniczna dla

badanego układu.

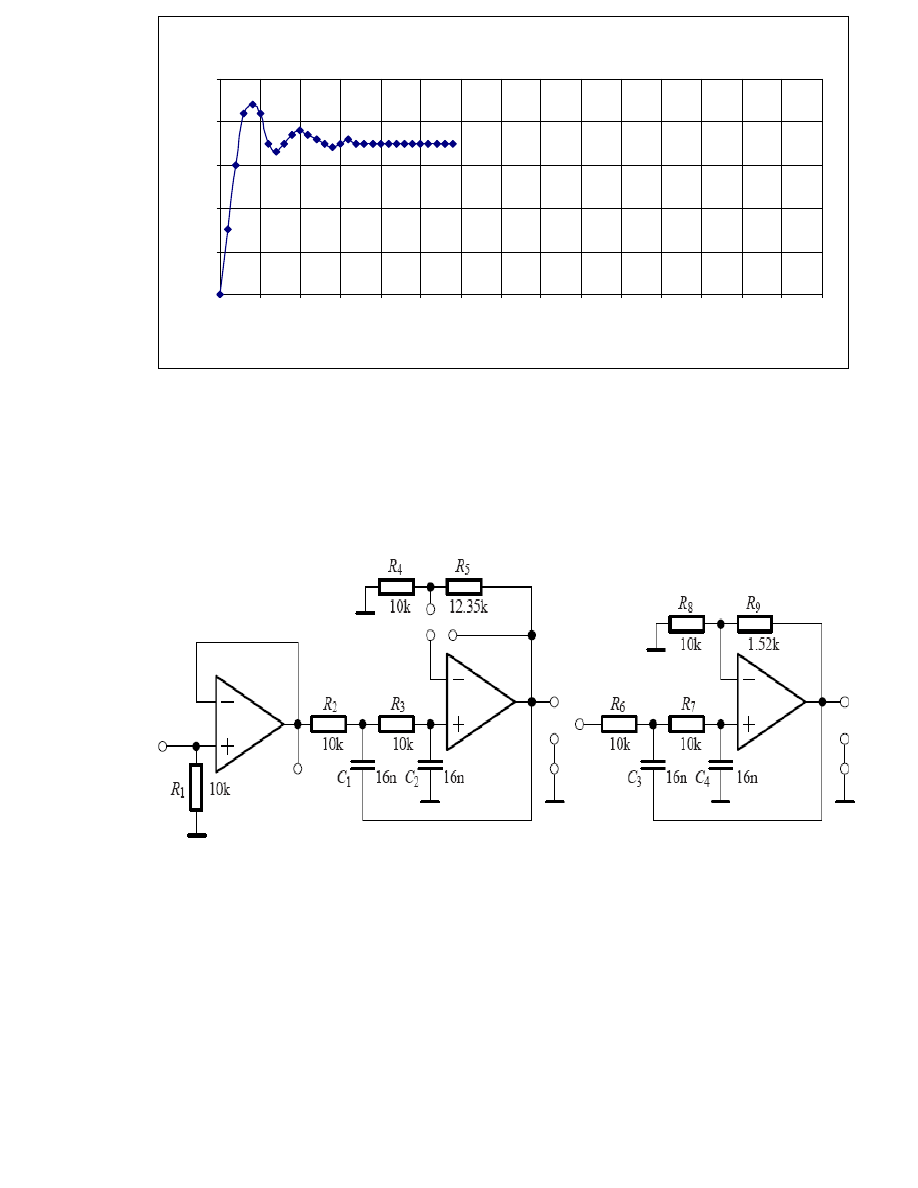
5

Odpowiedź na skok jednostkowy

0,00

1,50

3,00

4,20

4,40

4,20

3,50

3,30

3,50

3,70

3,80

3,70

3,60

3,50

3,40

3,50

3,60

3,50

3,50

3,50

3,50

3,50

3,50

3,50

3,50

3,50

3,50

3,50

3,50

3,50

0

1

2

3

4

5

0

0,2

0,4

0,6

0,8

1

1,2

1,4

1,6

1,8

2

2,2

2,4

2,6

2,8

3

[m s]

[V

]

Wykres 2. Odpowiedź na skok jednostkowy - filtru II rzędu

Czas narastania sygnału wyjściowego na zadany skok jednostkowy jest równy:

90% 10% 0,36

0,04

0,32

n

t

ms

ms

ms

=

−

=

−

=

Część druga – Filtr dolnoprzepustowy Butterworth’a rzędu IV (1 kHz).

1

2

:

2,235
1,152

10

16

gdzie

k

k

R

k

C

nF

=

=

=

Ω

=

6

Charakterystyki amplitudowo – częstotliwościowe:

Tabela 2. Tabela pomiarowa dla filtru IV-rzędu

Lp. f[Hz]

U1[V]

U2[V]

U3[V]

K1 [dB]

K2 [dB]

K [dB]

1.

10

1,8

3,9

4,5 6,715842 1,242958

7,9588

2.

20

1,8

4,02

4,53 6,979071 1,037443 8,016514

3.

30

1,8

4,02

4,53 6,979071 1,037443 8,016514

4.

50

1,8

4,02

4,53 6,979071 1,037443 8,016514

5.

70

1,8

4,04

4,54 7,022177

1,01349 8,035667

6.

100

1,8

4,05

4,54

7,04365 0,992017 8,035667

7.

200

1,8

4,09

4,51 7,129016 0,849065 7,978081

8.

300

1,8

4,03

4,3 7,000651 0,563268 7,563919

9.

500

1,8

3,93

3,73 6,782401 -0,45367 6,328727

10.

600

1,8

3,5

3,11 5,775911 -1,02615 4,749758

11.

700

1,8

3,12

2,47 4,777642 -2,02915 2,748489

12.

800

1,8

2,71

1,91 3,553936 -3,03872 0,515217

13.

850

1,8

2,38

1,71 2,426089 -2,87162 -0,44553

14.

900

1,8

2,31

1,52 2,166789 -3,63537 -1,46858

15.

950

1,8

2,11

1,31 1,380199 -4,14022 -2,76002

16.

1000

1,8

2,01

1,15 0,958471 -4,84996 -3,89149

17.

1050

1,8

1,87

1,03 0,331382 -5,18009 -4,84871

18.

1100

1,8

1,76

0,91

-0,1952 -5,72943 -5,92462

19.

1200

1,8

1,52

0,74 -1,46858 -6,25224 -7,72082

20.

1300

1,8

1,36

0,59 -2,43467 -7,25374 -9,68841

21.

1500

1,8

1,14

0,42 -3,96735 -8,67311 -12,6405

22.

1700

1,8

0,95

0,31 -5,55098 -9,72724 -15,2782

23.

2000

1,8

0,74

0,18 -7,72082 -12,2792

-20

24.

3000

1,8

0,39

0,04 -13,2842 -19,7801 -33,0643

Z otrzymanych pomiarów (Tabela 2) wyrysowano charakterystyki amplitudowo –
częstotliwościowe:

2

1

1

3

2

2

3

1

) |

( ) |

( );

) |

( ) |

( );

) | ( ) |

( ).

U

a

K s

f f

U

U

b

K s

f f

U

U

c

K s

f f

U

=

=

=

=

=

=

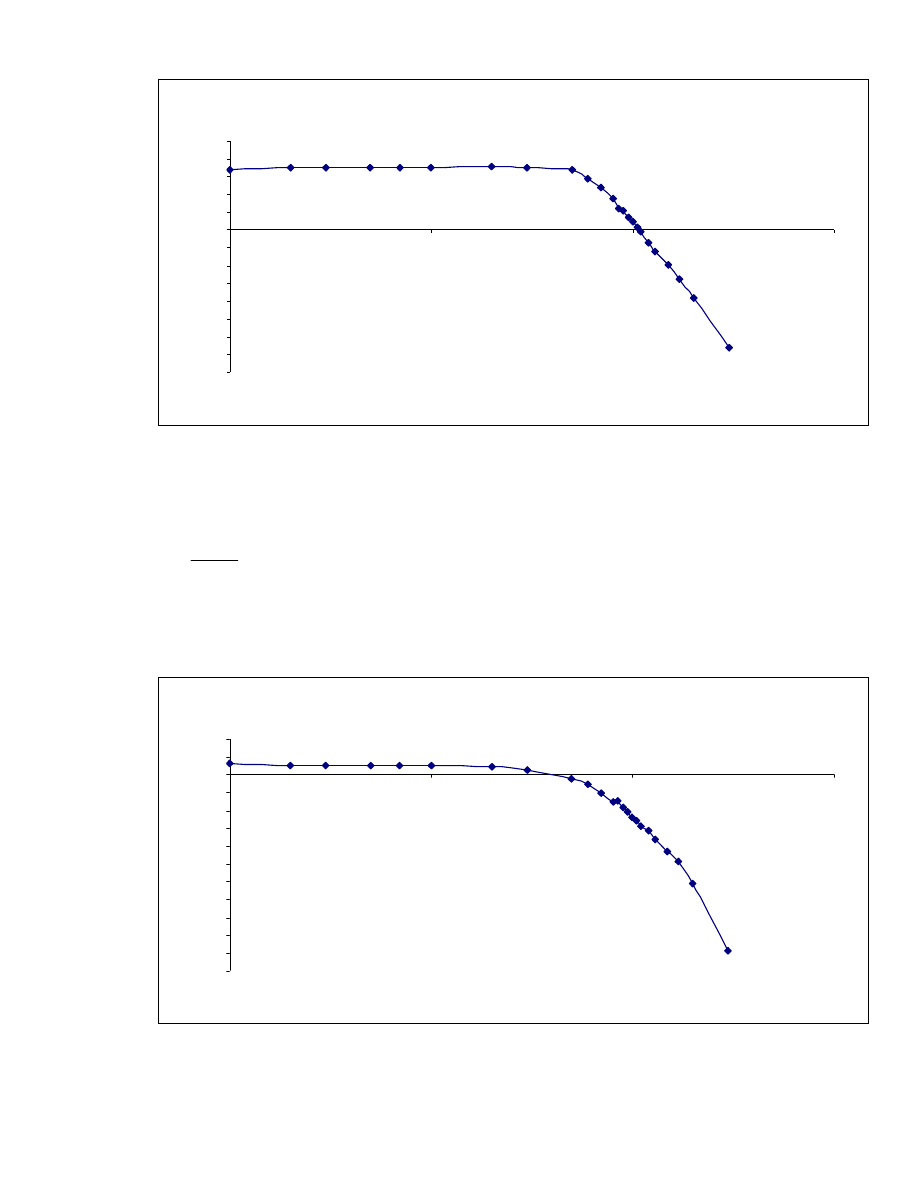
7

a)

Zależ ność wz mocnienia K1 od cz ęstotliwości f

6,72

6,98

6,98

6,98

7,02

7,04

7,13

7,00

6,78

5,78

4,78

3,55

2,43

2,17

1,38

0,96

0,33

-0,20

-1,47

-2,43

-3,97

-5,55

-7,72

-13,28

-16

-14

-12

-10

-8

-6

-4

-2

0

2

4

6

8

10

10

100

1000

10000

f[Hz]

K

u

[d

B

]

Wykres 3. Zależność wzmocnienia K1 od częstotliwości f

Metodą regresji liniowej dopasowano prostą do liniowej części wykresu (do opadającej
części charakterystyki). Otrzymana prosta ma równanie: K = -0,0053 × f +8,56. Na tej
podstawie zostało wyliczone nachylenie asymptotyczne : -41,44[dB/dec].

1

1

2

g

f

kHz

RC

π

=

≈

-

częstotliwość graniczna teoretyczna

700

g

f

Hz

≈

-

wartość uzyskana na podstawie pomiaru

b)

Zależ ność wz mocnienia K2 od cz ęstotliwości f

1,24

1,04

1,04

1,04

1,01

0,99

0,85

0,56

-0,45

-1,03

-2,03

-3,04

-2,87

-3,64

-4,14

-4,85

-5,18

-5,73

-6,25

-7,25

-8,67

-9,73

-12,28

-19,78

-22

-20

-18

-16

-14

-12

-10

-8

-6

-4

-2

0

2

4

10

100

1000

10000

f[Hz]

K

u

[d

B

]

Wykres 4. Zależność wzmocnienia K2 od częstotliwości f

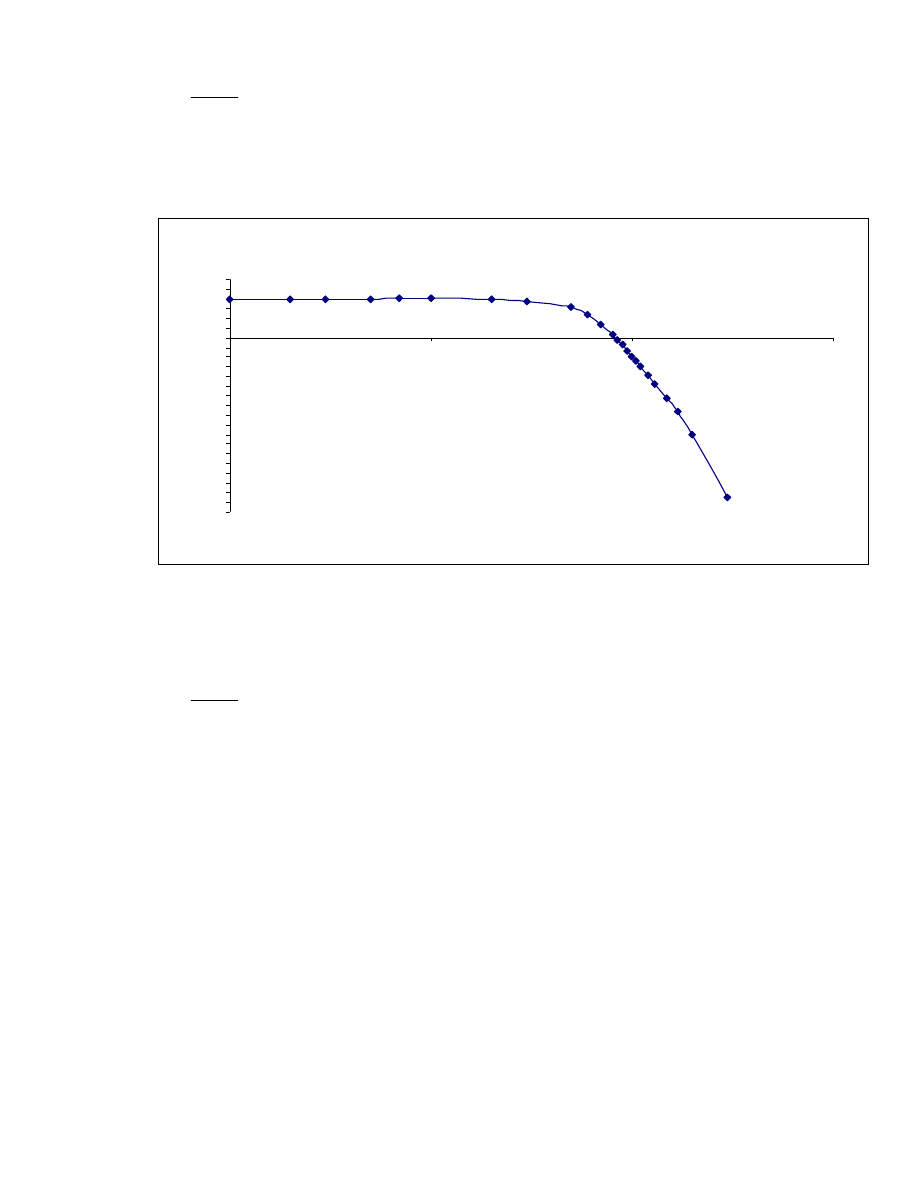
8

Metodą regresji liniowej dopasowano prostą do liniowej części wykresu (do opadającej
części charakterystyki). Otrzymana prosta ma równanie: K = -0,0055 × f +6,07. Na tej
podstawie zostało wyliczone nachylenie asymptotyczne : -45,30[dB/dec].

1

1

2

g

f

kHz

RC

π

=

≈

-

częstotliwość graniczna teoretyczna

650

g

f

Hz

≈

-

wartość uzyskana na podstawie pomiaru

b)

Zależ ność wz mocnienia K od cz ęstotliwości f

7,96

8,02

8,02

8,02

8,04

8,04

7,98

7,56

6,33

4,75

2,75

0,52

-0,45

-1,47

-2,76

-3,89

-4,85

-5,92

-7,72

-9,69

-12,64

-15,28

-20,00

-33,06

-36

-34

-32

-30

-28

-26

-24

-22

-20

-18

-16

-14

-12

-10

-8

-6

-4

-2

0

2

4

6

8

10

12

10

100

1000

10000

f[Hz]

K

u

[d

B

]

Wykres 5. Zależność wzmocnienia K od częstotliwości f

Metodą regresji liniowej dopasowano prostą do liniowej części wykresu (do opadającej
części charakterystyki). Otrzymana prosta ma równanie: K = -0,0099 × f +5,55. Na tej
podstawie zostało wyliczone nachylenie asymptotyczne : -79,50[dB/dec].

1

1

2

g

f

kHz

RC

π

=

≈

-

częstotliwość graniczna teoretyczna

650

g

f

Hz

≈

-

wartość uzyskana na podstawie pomiaru

9

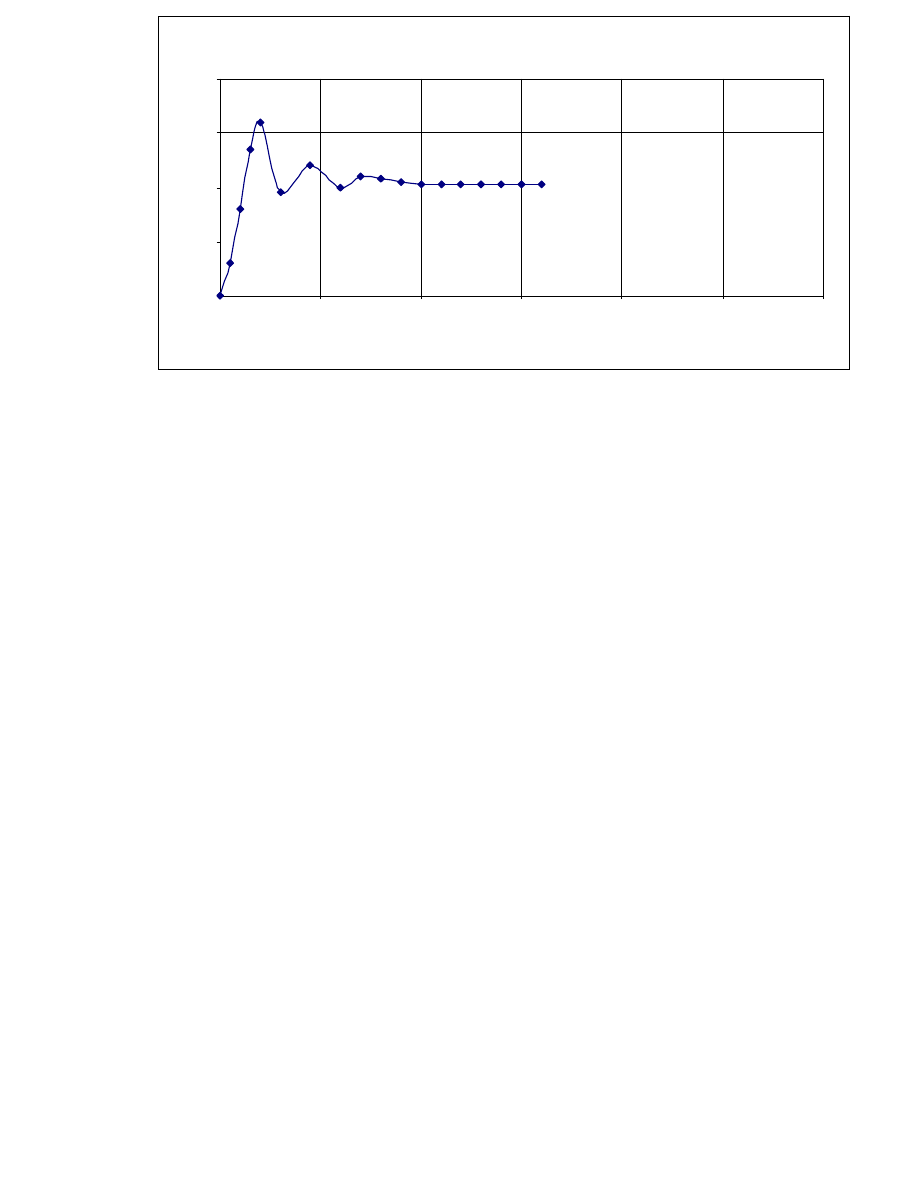
Odpowiedź na skok jednostkowy

0,00

1,20

3,20

5,40

6,40

3,80

4,80

4,00

4,40 4,30

4,20 4,10 4,10 4,10 4,10 4,10 4,10 4,10

0

2

4

6

8

0

0,5

1

1,5

2

2,5

3

[m s]

[V

]

Wykres 4. Odpowiedź na skok jednostkowy - filtru IV rzędu

Czas narastania sygnału wyjściowego na zadany skok jednostkowy jest równy:

90% 10% 0,33

0,05

0,28

n

t

ms

ms

ms

=

−

=

−

=

4.

Podsumowanie

Celem ćwiczenia było zbadanie układów: filtra dolnoprzepustowego – rzędu II i filtra
Butterworth’a rzędu IV dolnoprzepustowego.
Filtr Butterworth’a ma charakterystykę, która na możliwie długim odcinku przebiega
poziomo i załamuje się dopiero przy częstotliwości fg. Odpowiedz impulsowa ma znaczne
oscylacje wzrastające z rzędem.
Można zauważyć, że czas narastania nie zależy zbyt silnie od rzędu lub typu filtru i ma
wartość ~ (1/3fg ). Natomiast czas opóźnienia i przerost zależą silnie od rzędu filtru.