W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

O

PIS RUCHU

,

DRGANIA WŁASNE TŁUMIONE

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymper

Rys.11.2

Olga Kopacz, Adam Łodygowski, Krzysztof Tymber,

Michał Płotkowiak, Wojciech Pawłowski

Konsultacje naukowe: prof. dr hab. Jerzy Rakowski

Poznań 2002/2003

OPIS RUCHU

1. 1. Opis ruchu

Przypuśćmy, że mamy układ jak na rysunku

obok (rys.11.1). Zgodnie z zasadą d’Alemberta równanie
równowagi można zapisać:

( )

( )

0

..

=

+

t

q

t

q

m

κ

(11.1)

( )

( )

0

2

..

=

+

t

q

t

q

ω

(11.2)

gdzie:

m

κ

ω =

2

,

2

2

..

dt

d

=













i :

−

m

masa

[ ]

kg

−

q

przemieszczenie w czasie

−

κ

sztywność podpory









m

N

.

Rozwiązaniem jest funkcja

( )

⇒

+

=

t

q

t

q

t

q

c

s

ω

ω

cos

sin

( )

(

)

ϕ

ω +

=

t

A

t

q

sin

,

przy czym kąt

ϕ

-to kąt fazowy. Stałe

ϕ

,

A

wyznaczymy z dwóch warunków

początkowych:

np.

1

0

)

( )

a

q

t

=

⇒

=

0

0

2

0

)

( )

0

0

0

0

.

=

=

⇒

=

=

t

dt

dq

q

t

Z warunków tych otrzymujemy:

(

)

a

A

a

A

A

A

a

=

⇒

=

⇒

=

+

=

2

sin

sin

0

sin

π

ϕ

ϕ

Rys.11.1

W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

S

ZCZEGÓLNE PRZYPADKI ŁUKÓW

,

STOPIEŃ STAT

.

NIEWYZNACZALNOŚCI

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymper

(

)

(

)

2

0

cos

0

cos

0

cos

π

ϕ

ϕ

ϕ

ω

ω

ω

ϕ

ω

=

⇒

=

⇒

+

⋅

=

⇒

+

=

A

t

A

dt

dq

Zatem dla warunków początkowych j.w otrzymujemy pełne rozwiązanie postaci:

( )

t

a

t

a

t

q

ω

π

ω

cos

2

sin

=











 +

=

(11.3)

gdzie:

a

-amplituda drgań, to max. wartość przemieszczenia(wychylenia) w stosunku do

położenia równowagi,

ω

-to częstość kołowa drgań własnych (zakładamy brak czynników zaburzających, czyli

nie występuje tłumienie)

[ ]

s

rd

, jest cechą indywidualną każdego ciała (

Jest stała!

)

Uwaga!

Nie ma związku między amplitudą a częstością kołową!

Zgodnie z rozwiązaniem (wzór 11.3) nasza kulka powróci do swego położenia po czasie
odpowiadającym

π

2

. Podstawmy tą wartość do naszego rozwiązania:

( )

(

)

(

)

[

]

T

t

t

t

a

t

q

+

=























 +

=

+

=

ω

ω

π

ω

π

ω

cos

2

cos

2

cos

gdzie

ω

π

2

=

T

to okres drgań, czyli czas dzielący dwa identyczne stany rozpatrywanego

ciała (łatwiej można to sobie wyobrazić patrząc na rysunek 11.2).

Zadanie 1
Wyznaczyć częstość kołową elementu.

♦

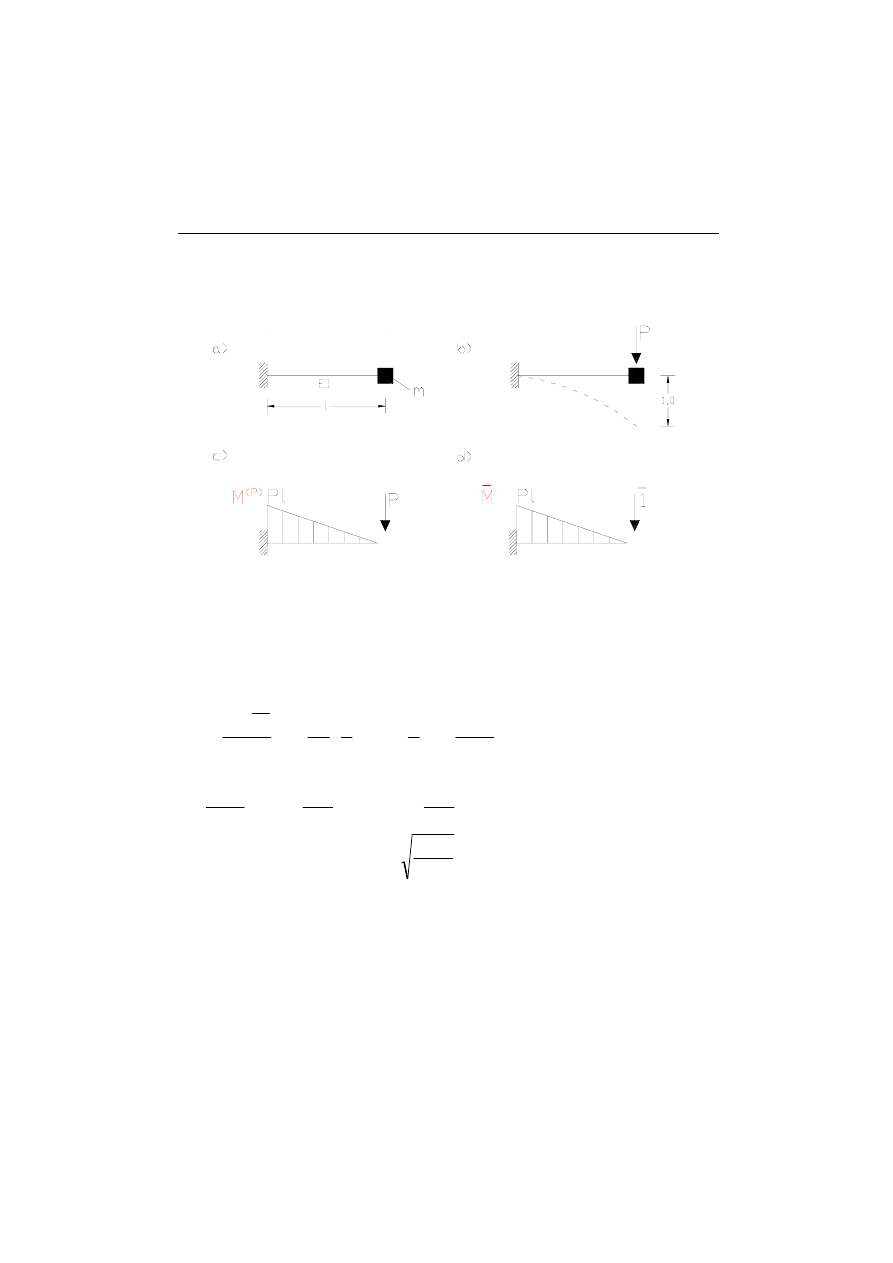
Powiedzmy, że mamy układ jak na rysunku (rys.11.3) z jednym stopniem swobody.
Zakładamy, że masa belki jest znikomo mała w stosunku do nałożonej masy
(powstały w ten sposób błąd będzie bardzo mały i nieistotny dla dalszych
rozważań). Częstość kołowa wyrażana jest wzorem:

m

κ

ω =

(11.4)

W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

S

ZCZEGÓLNE PRZYPADKI ŁUKÓW

,

STOPIEŃ STAT

.

NIEWYZNACZALNOŚCI

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymper

Sztywność belki wyznaczymy korzystając z pracy wirtualnej. W miejscu masy m
przykładamy taką siłę P, która spowoduje jednostkowe ugięcie belki (rys.11.3b) stąd
i

δ

równe będzie 1. Wykonujemy wykresy momentów od zadanej siły P i siły

jedynkowej (rys.11.3c i d)otrzymując:

EI

l

P

l

l

l

P

EI

ds

EI

M

M

3

3

2

2

1

1

3

⋅

=













⋅

⋅

⋅

=

⋅

=

∫

δ

Przyrównując otrzymaną wartość do jedynki:

3

3

3

3

1

l

EI

P

EI

l

P

=

⇒

⋅

=

czyli

3

3

l

EI

=

κ

stąd szukana częstość kołowa wynosi:

3

3

l

m

EI

⋅

=

ω

(11.5)

♦

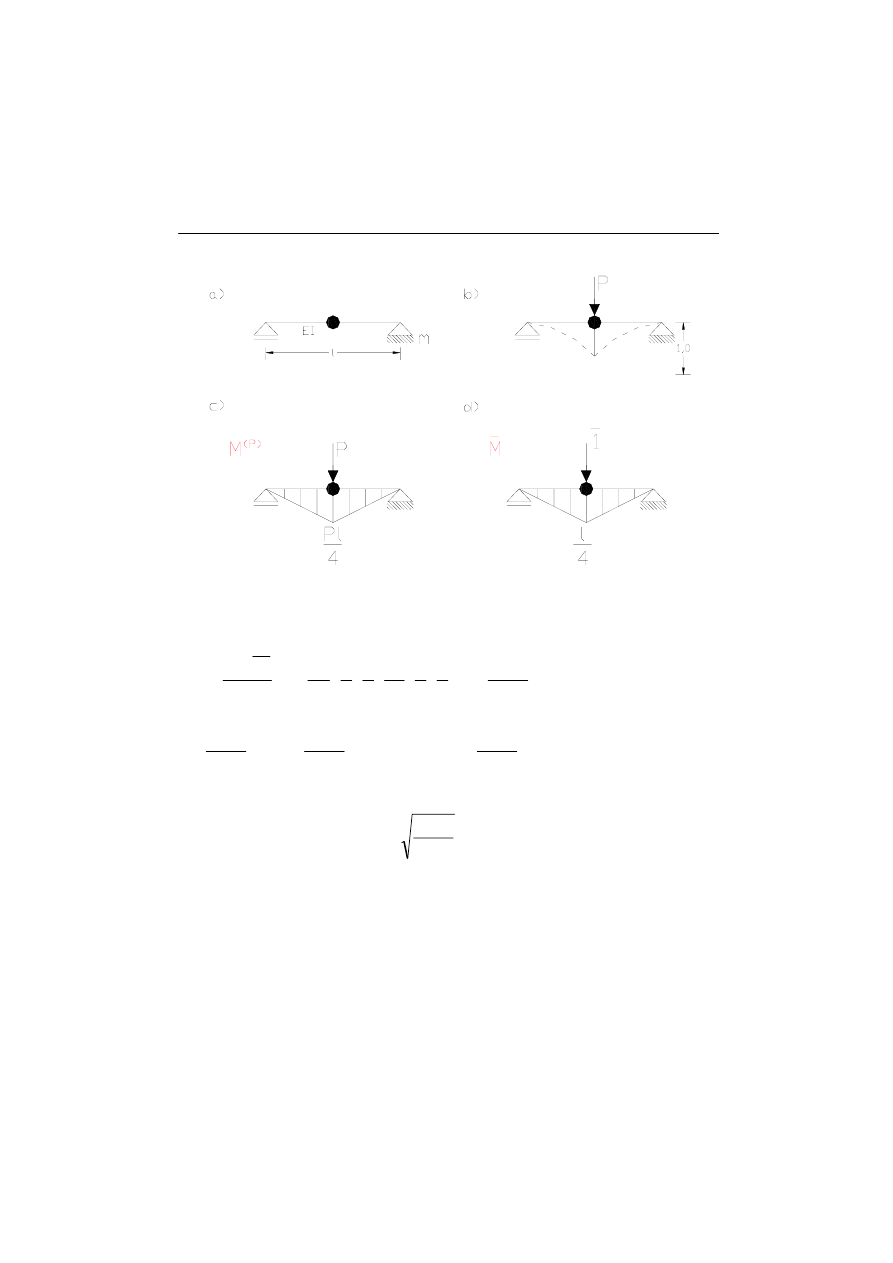
Zajmijmy się teraz belką swobodnie podpartą, której masę sprowadzimy do masy
skupionej umieszczonej w środku jej rozpiętości (rys.11.4). Sposób postępowania
jest analogiczny jak dla belki z przykładu pierwszego. Wykonujemy wykresy
momentów od zadanej siły P i siły jedynkowej.

Rys.11.3

W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

S

ZCZEGÓLNE PRZYPADKI ŁUKÓW

,

STOPIEŃ STAT

.

NIEWYZNACZALNOŚCI

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymper

EI

l

P

l

Pl

l

EI

ds

EI

M

M

48

2

4

3

2

4

2

2

1

1

3

⋅

=













⋅

⋅

⋅

⋅

=

⋅

=

∫

δ

ponieważ :

3

3

48

48

1

l

EI

P

EI

l

P

=

⇒

⋅

=

czyli

3

48

l

EI

=

κ

stąd szukana częstość kołowa

wynosi:

3

48

l

m

EI

⋅

=

ω

(11.6)

przy czym

A

l

m

⋅

⋅

=

ρ

(A-pole przekroju poprzecznego belki).

1. 2. Drgania własne, tłumione.

Tłumienie drgań jest wynikiem działania sił oporu oznaczanych jako

R

. Siły te działają

w ruchu zwanym Voigt. Zakładany w nim tłumienie lekkie (wiskotyczne)
proporcjonalne do prędkości ruch, co zapisujemy:

)

(

~`

t

q

c

R

•

⋅

Rys.11.4

W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

S

ZCZEGÓLNE PRZYPADKI ŁUKÓW

,

STOPIEŃ STAT

.

NIEWYZNACZALNOŚCI

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymper

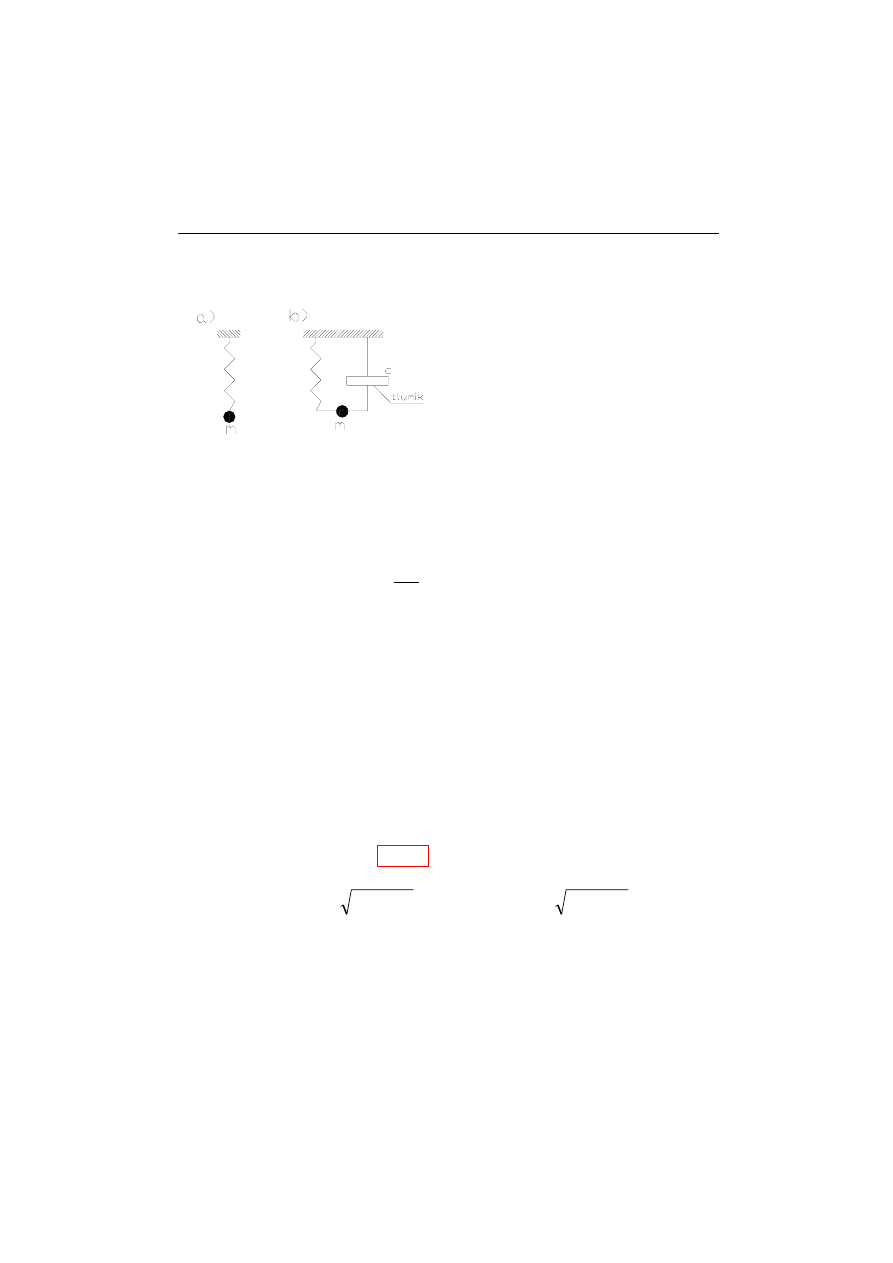
Na rysunku (rys.11.5) widzimy ciało o masie m drgające swobodnie (bez tłumienia) i
podczas tłumienia drgań.

a)drgania własne-układ o jednym
stopniu swobody

b)drgania własne tłumione

Równanie ruch z uwzględnieniem tłumienia przyjmuje postać:

0

)

(

)

(

)

(

=

+

⋅

+

⋅

•

•

•

t

t

q

c

t

q

m

κ

(11.7)

gdzie

c

-stała tłumienia

przy wprowadzeniu zmiennej

m

c

2

=

ρ

równanie przechodzi do postaci:

0

)

(

)

(

2

)

(

2

=

⋅

+

⋅

+

•

•

•

t

q

t

q

t

q

ω

ρ

(11.8)

−

ρ

współczynnik tłumienia drgań.

Rozwiązaniem równania ruchu (wzór11.8) będzie funkcja postaci:

rt

Ae

t

q

=

)

(

.

Podstawiając ją do równania otrzymamy równanie charakterystyczne postaci:

0

2

2

2

=

+

⋅

+

ω

ρ

r

r

(11.9)

Rozwiązując je możemy otrzymać trzy przypadki:

(

)









=

>

<

⇒

−

=

−

=

∆

0

0

0

4

4

4

2

2

2

2

ω

ρ

ω

ρ

♦

Rozważamy małe tłumienia

ω

ρ <

Możliwe są dwa rozwiązania:

2

2

1

ρ

ω

ρ

−

−

−

=

i

r

2

2

2

ρ

ω

ρ

−

+

−

=

i

r

Rozwiązującą funkcją jest funkcja postaci:

)

sin(

)

(

1

ϕ

ω

ρ

+

=

−

t

Ae

t

q

t

(11.10)

co jest równoważne rozwiązaniu:

)

sin

cos

sin(

)

(

2

1

t

c

t

c

e

t

q

t

ω

ω

ρ

+

=

−

(11.11)

Rys.11.5

W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

S

ZCZEGÓLNE PRZYPADKI ŁUKÓW

,

STOPIEŃ STAT

.

NIEWYZNACZALNOŚCI

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymper

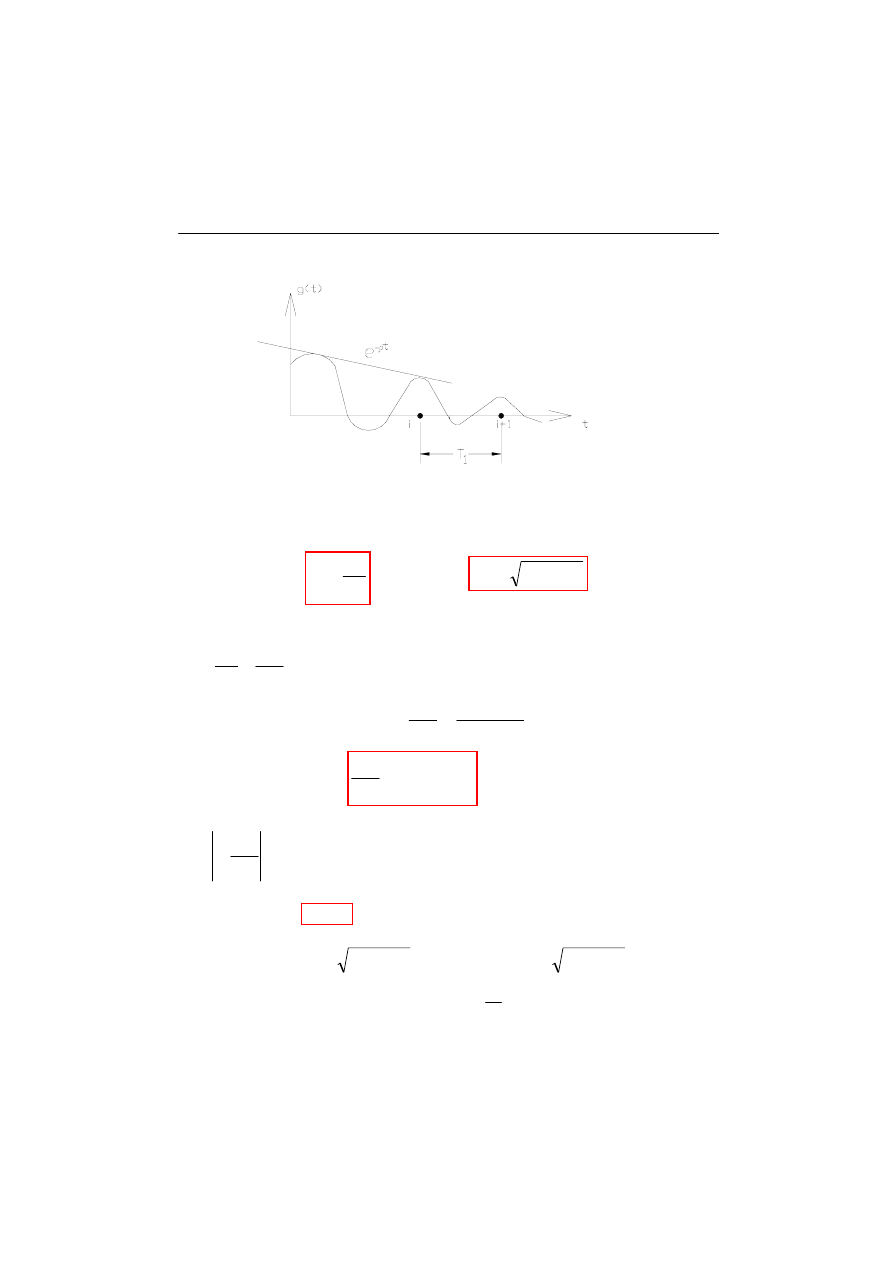
Wykres (rys.11.6) poniżej obrazuje funkcję rozwiązującą (wzór 11.10):

gdzie:

−

1

T

okres drgań własnych tłumionych wynoszący:

1

1

2

ω

π

=

T

a

2

2

1

ρ

ω

ω

−

=

Miarą tłumienia jest to z jaką szybkością następuje redukcja amplitudy, czyli relacja
między dwiema kolejnymi amplitudami podobnych stanów. I tak:

1

1

2

ω

π

=

T

i

i

q

q

1

+

.Podstawiając do funkcji rozwiązującej (11.10) otrzymujemy:]

przy założeniu, że:

1

)

sin(

1

=

+

e

t

ω

(

)

⇒

=

−

+

−

+

t

T

t

i

i

Ae

Ae

q

q

ρ

ρ

1

1

λ

ρ

−

−

+

=

=

e

e

q

q

T

i

i

1

1

(11.12)

przy czym

−

⋅

=

=

+

1

1

ln

T

q

q

i

i

ρ

λ

logarytmiczny dekrement mienia.

♦

Silne tłumienie

ω

ρ >

Możliwe są dwa rozwiązania:

2

2

1

ρ

ω

ρ

−

−

−

=

r

2

2

2

ρ

ω

ρ

−

+

−

=

r

Funkcja rozwiązująca przyjmuje postać:

)

(

)

(

1

2

1

1

t

sh

c

ch

c

e

t

q

t

ω

ω

ρ

+

=

−

(11.13)

Rys.11.5

W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

S

ZCZEGÓLNE PRZYPADKI ŁUKÓW

,

STOPIEŃ STAT

.

NIEWYZNACZALNOŚCI

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymper

gdzie:

2

2

1

ω

ρ

ω

−

=

W tym przypadku wykres funkcji rozwiązującej wygląda następująco (rys.11.6):

♦

W trzecim ostatnim przypadku gdy

ω

ρ =

funkcja rozwiązująca jest postaci:

)

(

)

(

2

1

c

t

c

e

t

q

t

+

=

−

ρ

(11.14)

a jej wykres jest taki jak przy silnym tłumieniu(rys.11.6).

Rys.11.6