W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

P

RACA SIŁ WEWNĘTRZNYCH W PRĘTACH

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymber

1

Olga Kopacz, Adam Łodygowski, Wojciech Pawłowski,

Michał Płotkowiak, Krzysztof Tymber

Konsultacje naukowe: prof. dr hab. J

ERZY

R

AKOWSKI

Poznań 2002/2003

MECHANIKA BUDOWLI 2

PRACA SIŁ WEWNĘTRZNYCH W PRĘTACH

Praca sił normalnych

Siła

normalna

przypomnienie (N):

Jest to siła działająca wzdłuż osi pręta, decydując o rozciąganiu bądź ściskaniu elementu.
Innymi słowy, to suma naprężeń normalnych na powierzchni całego przekroju:

∫

=

A

dA

N

σ

(2.1)

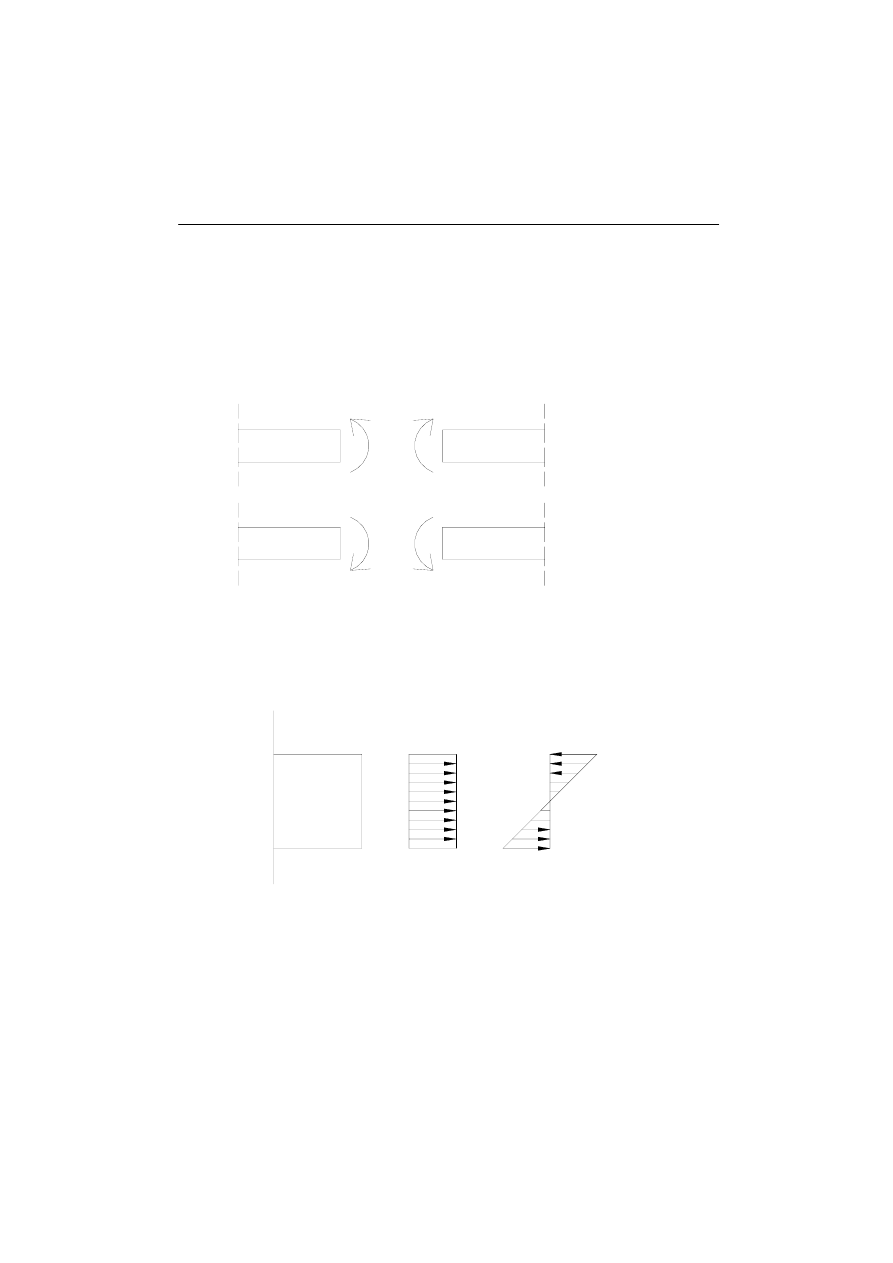
Rys. 1.

Umowne znakowanie siły normalnej

W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

P

RACA SIŁ WEWNĘTRZNYCH W PRĘTACH

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymber

2

Korzystając ze wzoru (2.1) i prawa Hooke’a można napisać zależności dla wycinaka
pręta o długości ds:

ds

Rys. 2.

Przyrost długości pręta

ds

A

E

N

N

N

dL

A

E

N

E

ds

u

u

A

dA

N

N

N

N

N

A

N

N

⋅

⋅

⋅

=

∆

⋅

⋅

=

⋅

=

=

↔

∆

=

∆

=

⋅

=

=

∫

2

1

2

1

σ

ε

ε

σ

σ

Gdzie
E- moduł Younga
A- pole powirzchni
przekroju

Całkowita praca siły normalnej w pręcie o długości l:

∫

⋅

=

l

N

ds

A

E

N

L

0

2

2

1

(2.2)

Element pracy siły normalnej:

ds

A

E

N

dL

N

⋅

=

2

2

1

(2.3)

W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

P

RACA SIŁ WEWNĘTRZNYCH W PRĘTACH

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymber

3

Praca momentów zginających
Moment zginający

przypomnienie: Def

∫

⋅

=

A

zdA

z

M

)

(

σ

(2.4)

Jest to para sił równo oddalonych od siebie, których wynikiem działania jest ściskanie
części włókien i rozćiąganie pozostałych.:

M<0
rozciąganie górnych włókien

M>0
rozciąganie dolnych włókien

Rys. 3. Umowne znakowanie momentó zginających

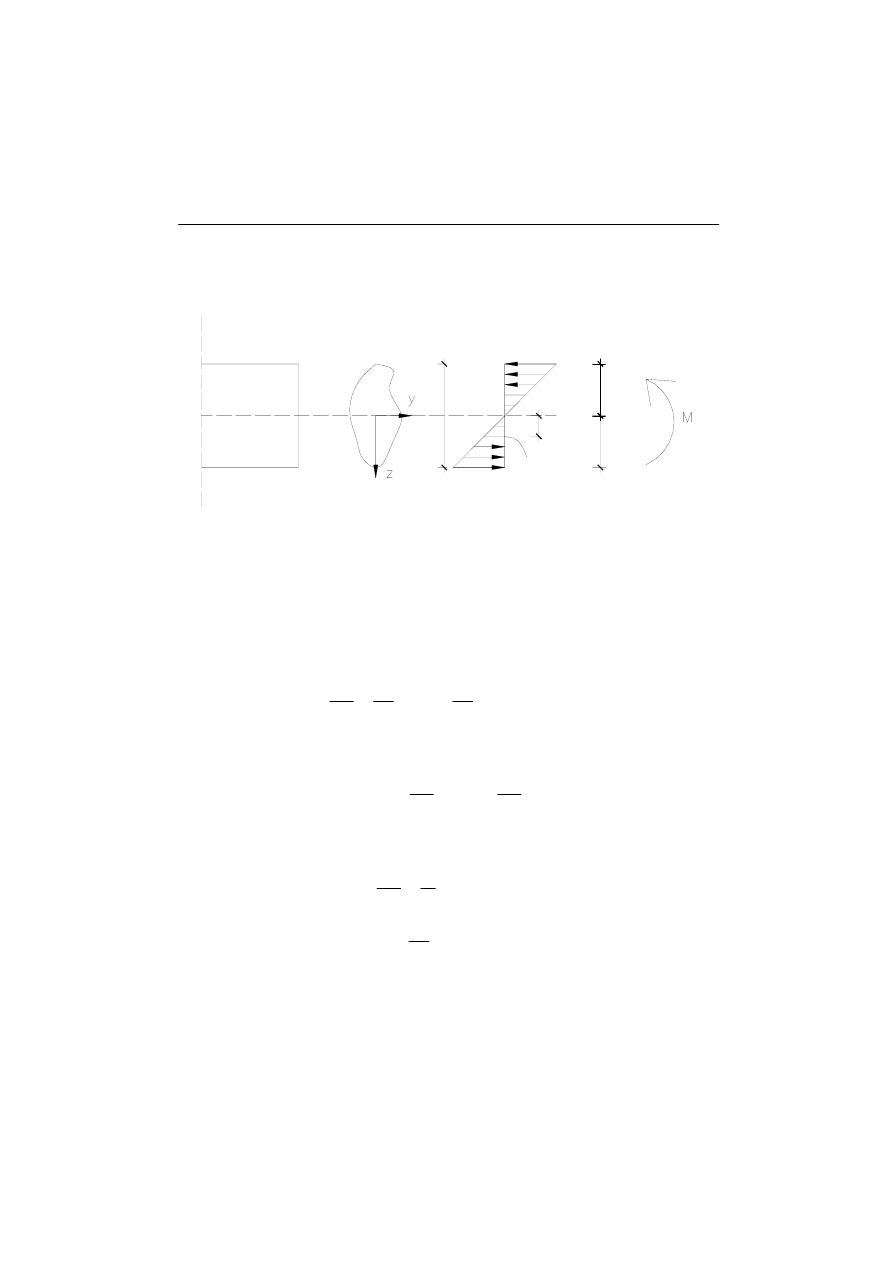
W przekroju występują naprężenia stałe (od siły normalnej) i zmienne (od momentu
zginającego)

stałe

naprężenia
normalne

zmienne

naprężenia

od momentu

Rys. 4. Naprężenia stałe i zmienne

W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

P

RACA SIŁ WEWNĘTRZNYCH W PRĘTACH

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymber

4

h

g

h

d

z

h

Naprężenia występujące od momentu zginającego decydują o ściskaniu części włókien i
rozciąganiu pozostałej części:

σ

z

= σ

Rys. 5. Naprężenia zmienne od momentu zginającego

Górna rzędna naprężenia od momentu σ

g

Górna rzędna naprężenia od momentu σ

d

Korzystając ze wzoru (2.4) i zależności geometrycznych (twierdzenie Talesa)
otrzymujemy:

d

d

d

d

z

h

z

h

z

σ

σ

σ

σ

=

→

=

(2.5)

y

d

d

A

d

d

A

z

I

h

dA

z

h

zdA

M

σ

σ

σ

∫

∫

=

⋅

=

=

2

(2.6)

Wobec tego:

z

I

M

z

h

y

d

d

⋅

=

=

σ

σ

σ

(2.7)

W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

P

RACA SIŁ WEWNĘTRZNYCH W PRĘTACH

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymber

5

dx=ds

z

promień
krzywizny

Biegun

chwilowego
obrotu

2

∆

na wysokości z

Rys. 6. Nieskończenie mały element, poddany momentowi zginającemu

ρ- promień krzywizny,

2

ϕ

d

- połowa kąta zawartego między promieniami krzywizny,

ρ

ϕ

ϕ

ρ

ds

d

d

ds

=

→

=

(2.8)

Przyrost długości ds jest symetryczny względem promienia krzywizny, dlatego przyrośt
po jednej stronie wynosi:

z

d

zd

d

z

∆

=

=

∆

=

∆

ϕ

ϕ

ϕ

2

2

(2.9)

Przyrost ds jest odkształceniem liniowym, dlatego korzystając z prawa Hooke’a można
zapisać relacje między przyrostem włókna a naprężeniami.

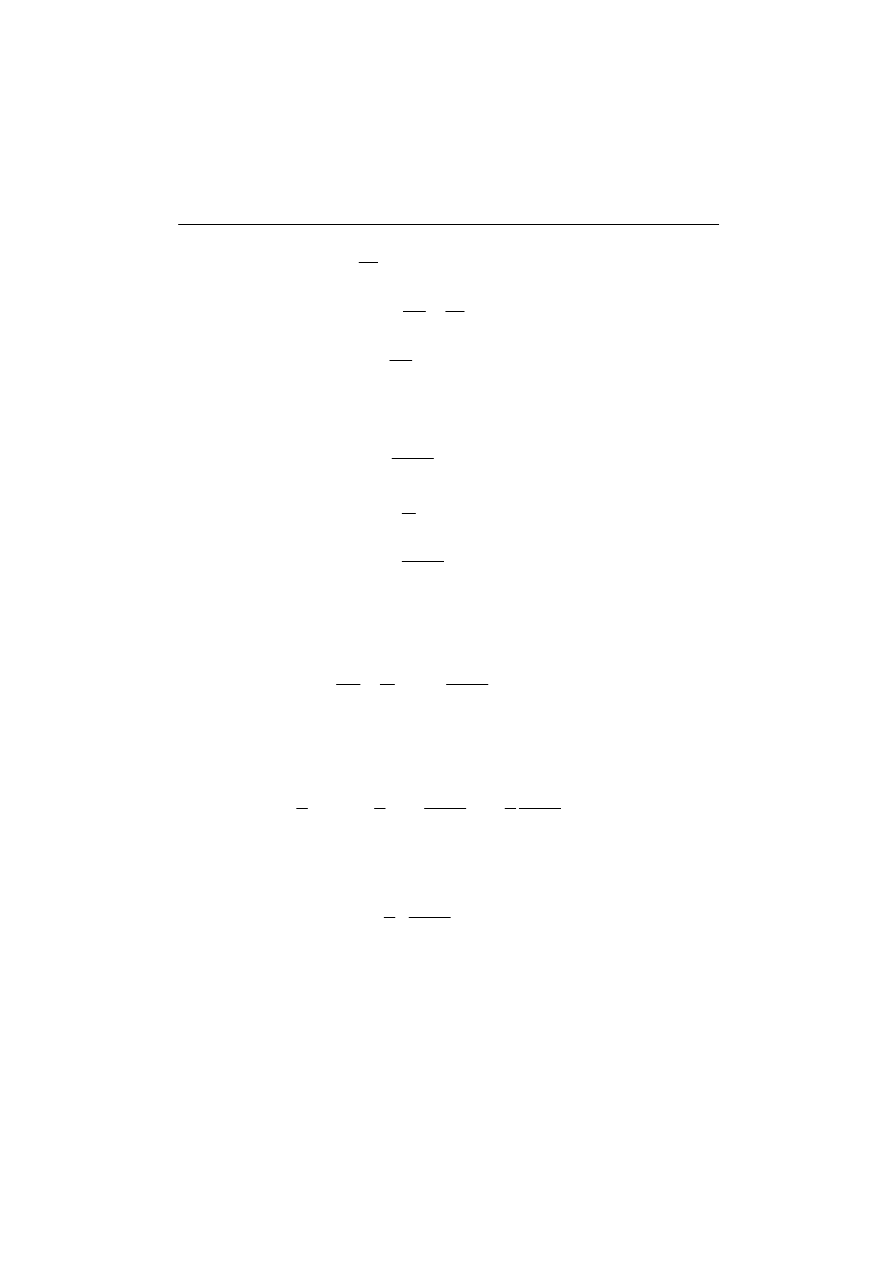
W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

P

RACA SIŁ WEWNĘTRZNYCH W PRĘTACH

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymber

6

ds

E

ds

E

ds

z

z

z

z

σ

σ

ε

ε

=

∆

∆

=

=

=

∆

)

(

(2.10)

Podstawiając wzór na naprężenie (2.7) i na kąt obrotu (2.9) otrzymujemy:

ds

I

E

M

d

z

d

ds

I

E

z

M

y

y

⋅

=

∆

=

⋅

⋅

=

∆

ϕ

ϕ

(2.11)

Wykorzystując wzór (2.11) i prawo Hooke’a otrzymujemy relację między krzywizną (χ)
a momentem:

y

I

E

M

ds

d

⋅

=

=

=

χ

ρ

ϕ

1

(2.12)

χ- to odwrotność promienia krzywizny.

Element pracy momentu zginającego, który działa na obrocie wynosi:

ds

I

E

M

ds

I

E

M

M

Md

dL

y

y

M

⋅

=

⋅

⋅

⋅

=

⋅

=

2

2

1

2

1

2

1

ϕ

(2.13)

Całkowita praca momentu w pręcie o długości l:

∫

⋅

=

l

y

M

ds

I

E

M

L

0

2

2

1

(2.14)

W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

P

RACA SIŁ WEWNĘTRZNYCH W PRĘTACH

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymber

7

Praca sił poprzecznych

Siła poprzeczna

przypomnienie

Siła poprzeczna jest sumą wszystkich naprężeń stycznych w przekroju
Indeks pierwszy określa płaszczyznę na jakiej działa siła
Indeks drugi określa kierunek dodatniej osi naprężeń stycznych

)

(

)

(

z

b

I

z

S

T

dA

T

y

y

xz

xz

A

xz

xz

⋅

⋅

=

=

∫

τ

τ

(2.15)

W powyższym siła działa na płaszczyźnie x o kierunku z.
System znakowania siły poprzecznej

T<0

kręci odciętą

częścią w lewo

T>0

kręci odciętą

częścią w prawo

Rys. 7. System znakowania siły poprzecznej

W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

P

RACA SIŁ WEWNĘTRZNYCH W PRĘTACH

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymber

8

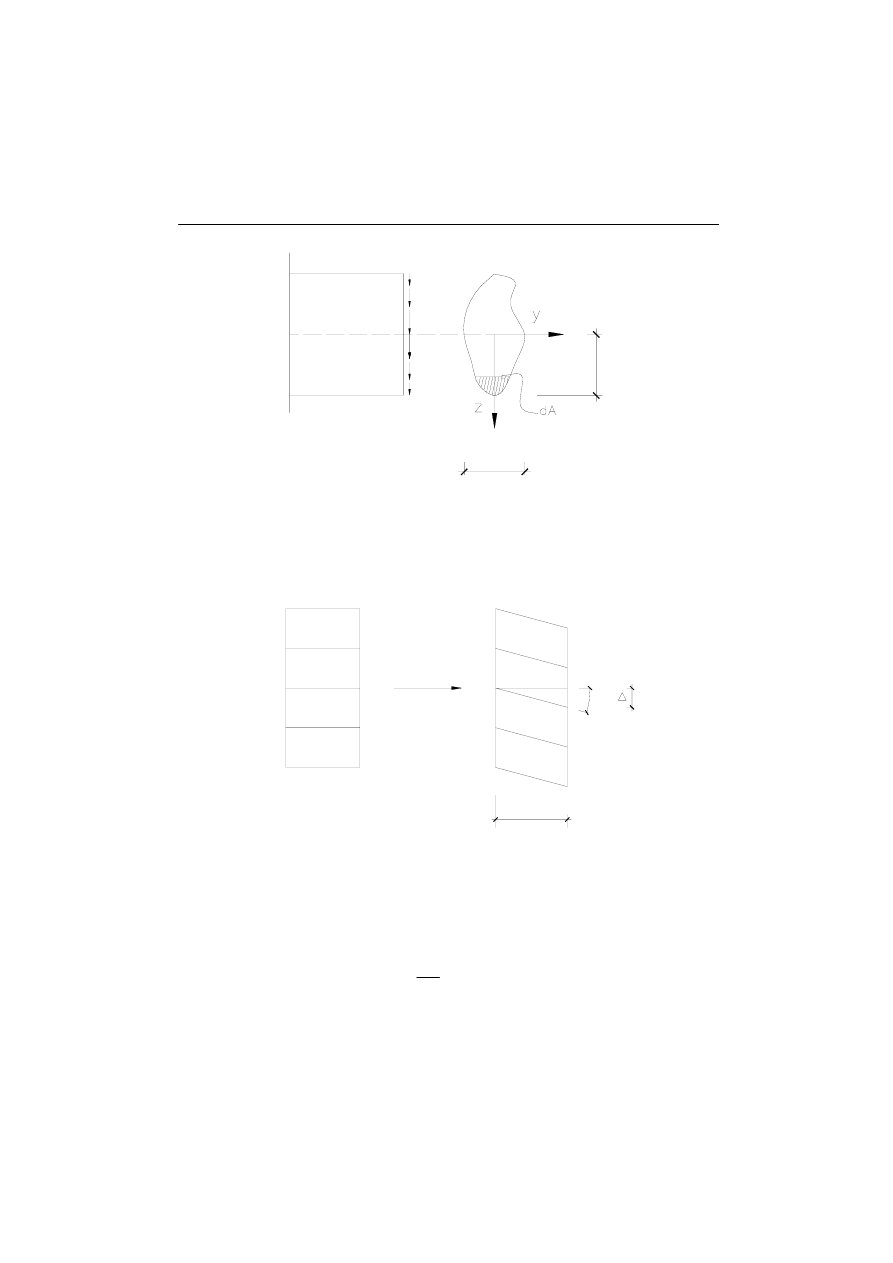
ds

b(z)

h

d

Rys. 8. Rysunek poglądowy działania siły poprzecznej

Wynikiem działania sił stycznych jest deformacja przedstawiona na rysunku (w
zdecydowanej przesadzie)

xz

γ

Rys. 9. Rezultaty działania siły poprzecznej na elemencie: a) γ- kąt odkształcenia
postaciowego, b) ∆- wynik działania sił stycznych

G

ds

t

xz

xz

xz

τ

γ

γ

=

=

∆

(2.16)

We wzorze (2.16) G jest modułem odkształcenia postaciowego Kirchhoffa.

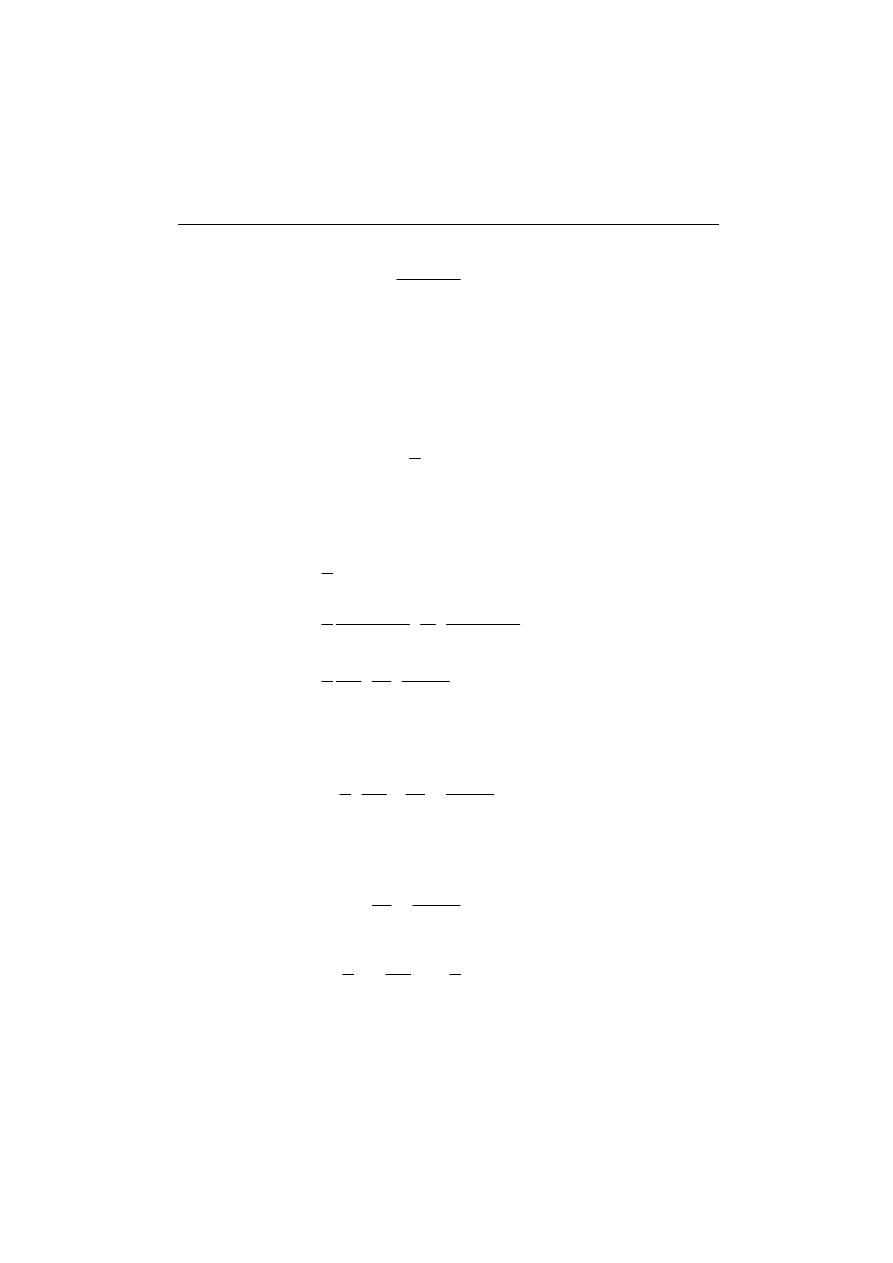
W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

P

RACA SIŁ WEWNĘTRZNYCH W PRĘTACH

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymber

9

(

)

ν

+

⋅

=

1

2

E

G

(2.17

E- moduł Younga, ν- współczynnik Poissona
Równanie pracy jest przedstawione wyłącznie dla poletka dA, w którym występują
elementy siły poprzecznej. Jeżeli chciałoby się otrzymać całkowitą pracę, należałoby
zsumować wszystkie poletka dA- czyli scałkować.

T

T

dT

dL

dA

dT

∆

=

=

2

1

τ

(2.18)

Przyrost pracy elementu siły poprzecznej przypadającej na poletko dA leżące na włóknie
b(z) dla elementarnego wycinka pręta o długości ds.

dAds

z

b

z

S

I

A

GA

T

L

d

dAds

z

b

I

z

S

T

G

z

b

I

z

S

T

L

d

ds

dA

L

d

y

T

y

y

xz

y

y

xz

T

xz

xz

T

)

(

)

(

2

1

)

(

)

(

1

)

(

)

(

2

1

2

1

2

2

2

3

3

3

⋅

⋅

⋅

=

⋅

⋅

⋅

⋅

⋅

⋅

=

⋅

=

γ

τ

(2.19)

Przyrost pracy całej siły poprzecznej w przekroju dla wycinka ds:































⋅

⋅

⋅

=

∫

A

y

T

dA

z

b

z

S

I

A

GA

T

dL

)

(

)

(

2

1

2

2

2

(2.20)

Wprowadzamy upraszczający zapis na ścinanie:

∫

⋅

⋅

=

dA

z

b

z

S

I

A

y

)

(

)

(

2

2

κ

(2.21)

ds

T

ds

GA

T

T

dL

śr

T

γ

κ

⋅

⋅

=

⋅

⋅

=

2

1

2

1

(2.22)

W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

P

RACA SIŁ WEWNĘTRZNYCH W PRĘTACH

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymber

10

Wzór (2.23) w nawiązaniu do poprzednich (praca N i praca M) można przez analogię
zinterpretować jako pracę siły poprzecznej na uśrednionym przemieszczeniu wwołanym
odkształceniem postaciowym (γ

śr

ds)

A

T

G

G

śr

śr

κ

τ

γ

⋅

=

=

1

1

(2.23)

Całkowita praca na długości pręta z uwzględnieniem współczynnika ścinania wynosi:

∫

⋅

=

l

T

ds

GA

T

L

0

2

2

1

κ

(2.24

Podsumowanie

Rodzaje występujących sił w przekroju
F-

uogólniona siła,

∆-

uogólnione przemieszczenie











∆

∆

⇒









⋅

⋅

⋅

=

∆

=

→









=

T

N

śr

d

d

d

ds

s

ds

s

ds

ds

s

s

s

T

M

N

s

F

ϕ

γ

χ

ε

δ

)

(

)

(

)

(

)

(

)

(

)

(

)

(

(2.25)

Wszystkie współczynniki charakteryzują się bardzo podobną strukturą- siła/ sztywność
(na rozciąganie, zginanie, ścinanie)

GA

T

EI

M

EA

N

śr

κ

γ

χ

ε

=

=

=

(2.26)

Wzór na całkowitą pracę sił wewnętrznych jest sumą prac tych wszystkich sił w pręcie:

∫

∫

∫

⋅

+

⋅

+

⋅

=

l

l

l

ds

GA

T

ds

EA

N

ds

EI

M

L

0

2

0

2

0

2

2

1

2

1

2

1

κ

(2.27)

W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

P

RACA SIŁ WEWNĘTRZNYCH W PRĘTACH

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymber

11