Mechanika Gruntów i fundmantowanie

Dane do projektu:

γa

1.4



współczynnik bezpieczeństwa dla obciążeń

Obciążenia charakterystyczne - kombinacja 1

Obciążenia obliczeniowe - kombinacja 1

Pk1 974kN



Pd1 Pk1 γa



1363.6 kN







Mk1 93kN m





Md1 Mk1 γa



130.2 kN m









Tk1 19kN



Td1 T

k1

γa



26.6 kN







Obciążenia charakterystyczne - kombinacja 2

Obciążenia obliczeniowe - kombinacja 2

Pk2 882kN



Pd2 Pk2 γa



1234.8 kN







Mk2 133kN m





Md2 Mk2 γa



186.2 kN m









Tk2 48kN



Td2 T

k2

γa



67.2 kN







Warstwy gruntowe:

ρw

1000

kg

m

3



Gęstość wody

Ciężar objetościowy wody

γw

ρw g



9.807

kN

m

3







Woda gruntowa

Poziom nawiercony

hw.naw 4.7m



Poziom ustalony

hw.ust 4.7m



Warstwa 1: FSa Piasek drobny

Konsystencja (grunt spoisty)

IL1

0.27



ID1 0



Miąższość

h1

2.1m



ρ

2670

kg

m

3



Tablica 2 PN-81/B-03020

Gęstość objetościowa gruntu

Ciężar objętościowy gruntu

γ1

ρ

g



26.184

kN

m

3







Spójność gruntu

cu1 29.03kPa



Kąt tarcia wewnętrznego

ϕ1

17deg



Edometryczny moduł ściśliwości pierwotnej M01 31293kPa



Edometryczny moduł ściśliwości wtórnej

M1

41714kPa



Warstwa 2a: siCl (b) Iły pylaste

IL2

0.15



ID2 0



Zagęszczenie (grunt niespoisty - sypki)

h2

2.3m



Miąższość

Tablica 2 PN-81/B-03020

Gęstość objetościowa gruntu

ρ2

2750

kg

m

3



Ciężar objętościowy gruntu

γ2

ρ2 g



26.968

kN

m

3







Spójność gruntu

cu2 33.45kPa



Kąt tarcia wewnętrznego

ϕ2

19.2deg



Edometryczny moduł ściśliwości pierwotnej M02 41944kPa



Edometryczny moduł ściśliwości wtórnej

M2

55911kPa



Warstwa 3a: Sa - Piasek

Konsystencja (grunt spoisty)

IL3

0



ID3 0.58



Miąższość

h3

0.3m



Tablica 2 PN-81/B-03020

Gęstość objetościowa gruntu

ρ3

2650

kg

m

3



Ciężar objętościowy gruntu

γ3a

ρ3 g



γw



16.181

kN

m

3







Spójność gruntu

cu3 0kPa



Kąt tarcia wewnętrznego

ϕ3

33.5deg



Edometryczny moduł ściśliwości pierwotnej M03 108603kPa



Edometryczny moduł ściśliwości wtórnej

M3

120670kPa



Warstwa 3b: Piasek Sa z uwzględnieniem wody

Zagęszczenie (grunt niespoisty - sypki)

h3.1 2.6m h3



2.3 m





Miąższość

Ciężar objętościowy gruntu

γ3b

ρ3 g



γw



16.181

kN

m

3







Warstwa 4:

Gr żwir- z uwzględnieniem wody

Zagęszczenie (grunt niespoisty - sypki)

IL4

0



ID4 0.58



Tablica 2 PN-81/B-03020

Gęstość objetościowa gruntu

ρ4

1750

kg

m

3



Ciężar objętościowy gruntu

γ4

ρ4 g



γw



7.355

kN

m

3







Spójność gruntu

cu4 0kPa



Kąt tarcia wewnętrznego

ϕ4

39deg



Edometryczny moduł ściśliwości pierwotnej M04 169565kPa



Edometryczny moduł ściśliwości wtórnej

M4

169565kPa



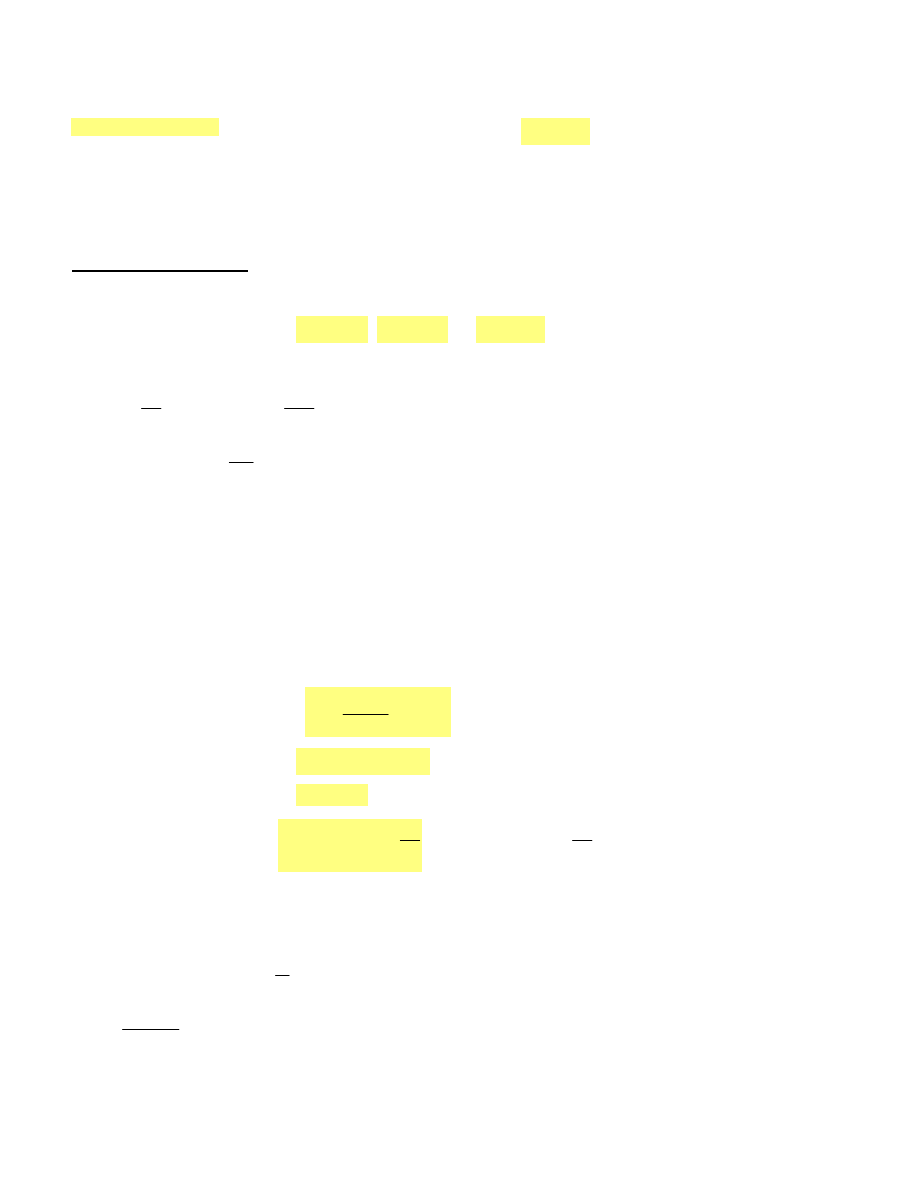
Określenie głębokości posadowienia z uwagi na przemarzanie gruntu

Lokalizacja : Kielce

głębokość przemarzania

hz 1.2m



Przyjmuję

D

1.9m



D

hz



1



D

0.5m



1



warunki spełnione

Kombinacja nr 1

SPRAWDZENIE STANU GRANICZNEGO NOŚNOŚCI

Dane geometryczne fundamentu: B1 1.6m



L1

1.6m



hf

0.5m



Mimośrody B` i L`

eB.max

B1

6

0.267 m





eB

Md1

Pd1

0.095 m





eB eB.max



1



ML 0kN m





eL

ML
Pd1

0





Efektywna szerokość fundamentu:

B'

B1 2 eB





1.41 m





Efektywna długość fundamentu:

L'

L1 2 eL





1.6 m





Efektywne pole powierzchni fundamentu:

A'

B' L'



2.254 m

2





Określenie nośności podłoża pod fundamentem:

φ' kąt tarcia wewnętrznego [rad]

φ

'

π ϕ2



180deg

0.335





c'

cu2 33.45 kPa







Kohezja (spójność)

Poziom posadowienia D

D

1.9 m



γk

γ2 26.968

kN

m

3







q'

D γk



51.24

kN

m

2







Ciężar objętościowy gruntu:

Współczynniki dla nośności:

Nq

e

π

tan φ'

( )



tan 45deg

φ

'

2



















2



5.913





Nc

Nq 1







tan φ'

( )

14.108





N

γ

2 Nq 1









tan φ'

( )



3.422





Nachylenie podstawy fundamentu:

Fundament posadowiony poziomo:

α

0deg



bq

1

α

tan φ'

( )





(

)

2

1





bc bq

1

bq







Nc tan φ'

( )





1





b

γ

bq 1





Kształt fundamentu dla prostokąta:

sq

1

B'
L'









sin φ'

( )





1.29





s

γ

1

0.3

B'
L'













0.736





sc

sq Nq



1







Nq 1



1.349





Siła pozioma T działa w kierunku B`:

mb

2

B'
L'



















1

B'
L'











1.532





Nachylenia obciążenia spowodowanego obciążeniem poziomym H:

iq

1

Tk1

Pk1 A' c'



1

tan φ'

( )























mb

0.976





i

γ

1

Tk1

Pk1 A' c'



1

tan φ'

( )























mb 1



0.96





ic iq

1

iq







Nc tan φ'

( )





0.971





Jednostkowy charakteryczny opór graniczny podłoża w warunkach z odpływem:

qf

c' Nc



bc



sc

 ic



q' Nq



bq



sq



iq





0.5 γk



B'

 N

γ



b

γ



s

γ



i

γ





1.045

10

3



kPa







Wartość charakterystyczna oporu podłoża:

Rk

A' qf



2.356

10

3



kN







Wartość obliczeniowa oporu podłoża:

Rd

Rk
1.4

1.683

10

3



kN







Sprawdzenie warunków nośności:

Pd1 Rd



1



Pd1

Rd

0.81



Td1 Rd



1



Td1

Rd

0.016



Warunki spełnione dla przyjętych wymiarów stopy fundamentowej.

B1 1.6m



L1 1.6m



hf 0.5m



Warunek na odrywanie:

Wskaźnik wytrzymałości:

Wx

B1

2

L1

6



0.683 m

3







qmin

Pd1

B1 L1



Md1

Wx



341.934 kPa







qmin 0



1



Warunek spełniony.

Kombinacja nr 2

SPRAWDZENIE STANU GRANICZNEGO NOŚNOŚCI

Dane geometryczne fundamentu: B2 1.6m



L2

1.6m



hf2 0.5m



Mimośrody B` i L`

eB.max

B2

6

0.267 m





eB

Md2

Pd2

0.151 m





eB eB.max



1



ML 0kN m





eL

ML
Pd1

0





Efektywna szerokość fundamentu:

B'

B2 2 eB





1.3 m





Efektywna długość fundamentu:

L'

L2 2 eL





1.6 m





Efektywne pole powierzchni fundamentu:

A'

B' L'



2.077 m

2





Określenie nośności podłoża pod fundamentem:

φ' kąt tarcia wewnętrznego [rad]

φ

'

π ϕ2



180deg

0.335





c'

cu2 33.45 kPa







Kohezja (spójność)

Poziom posadowienia D

D

1.9 m



γk

γ2 26.968

kN

m

3







q'

D γk



51.24

kN

m

2







Ciężar objętościowy gruntu:

Współczynniki dla nośności:

Nq

e

π

tan φ'

( )



tan 45deg

φ

'

2



















2



5.913





Nc

Nq 1







tan φ'

( )

14.108





N

γ

2 Nq 1









tan φ'

( )



3.422





Nachylenie podstawy fundamentu:

Fundament posadowiony poziomo:

α

0deg



bq

1

α

tan φ'

( )





(

)

2

1





bc bq

1

bq







Nc tan φ'

( )





1





b

γ

bq 1





Kształt fundamentu dla prostokąta:

sq

1

B'
L'









sin φ'

( )





1.267





s

γ

1

0.3

B'
L'













0.757





sc

sq Nq



1







Nq 1



1.321





Siła pozioma T działa w kierunku B`:

mb

2

B'
L'



















1

B'
L'











1.552





Nachylenia obciążenia spowodowanego obciążeniem poziomym H:

iq

1

Tk2

Pk2 A' c'



1

tan φ'

( )























mb

0.932





i

γ

1

Tk2

Pk2 A' c'



1

tan φ'

( )























mb 1



0.891





ic iq

1

iq







Nc tan φ'

( )





0.918





Jednostkowy charakteryczny opór graniczny podłoża w warunkach z odpływem:

qf

c' Nc



bc



sc

 ic



q' Nq



bq



sq



iq





0.5 γk



B'

 N

γ



b

γ



s

γ



i

γ





970.518 kPa







Wartość charakterystyczna oporu podłoża:

Rk

A' qf



2.016

10

3



kN







Wartość obliczeniowa oporu podłoża:

Rd

Rk
1.4

1.44

10

3



kN







Sprawdzenie warunków nośności:

Pd2 Rd



1



Pd2

Rd

0.857



Td2 Rd



1



Td2

Rd

0.047



Warunki spełnione dla przyjętych wymiarów stopy fundamentowej.

B2 1.6m



L2 1.6m



hf 0.5m



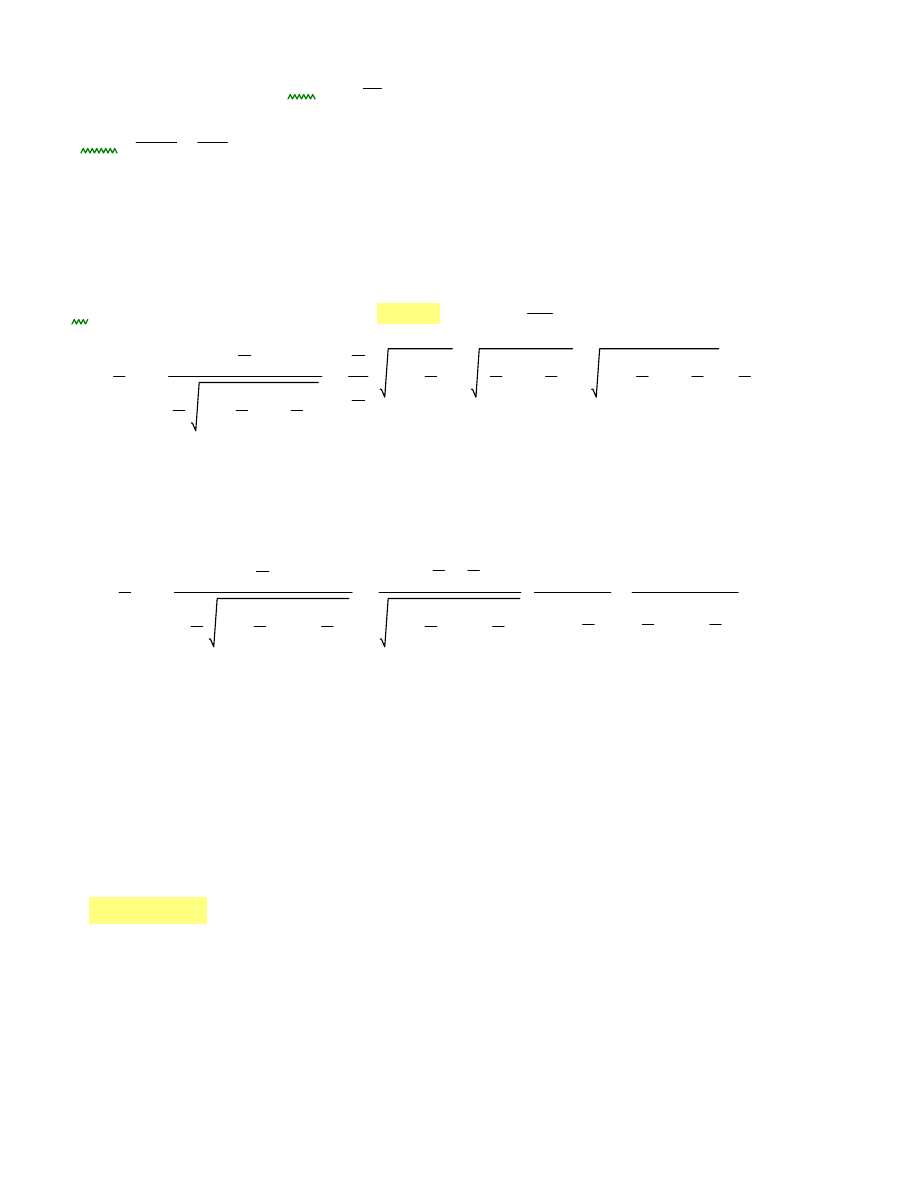
Warunek na odrywanie:

Wskaźnik wytrzymałości:

Wx

B2

2

L2

6



0.683 m

3







qmin

Pd2

B2 L2



Md2

Wx



209.59 kPa







qmin 0



1



Warunek spełniony.

STAN GRANICZNY UŻYTKOWALNOŚCI DLA KOMBINACJI NR 1
Obliczenie osiadań

Wyznaczenie współczynnika zaniku naprężeń:

L

L1 1.6m





B

B1 1.6m





Z

3.4m



q

Pk1
B L



380.469 kPa







ηs Z

( )

2

π

atan

L

B

Z
B

1

L
B









2



Z
B









2





























Z

B

L

B

1

Z
B









2



L
B









2

Z
B









2





1

L
B









2



Z
B









2





Z
B















































σzq

q ηs Z

( )



0.034 MPa







- naprężenie wywołane ciężarem fundamentu

Wyznaczenie współczynnika rozkładu naprężeń:

ηm Z

( )

2

π

atan

L

B

2

Z
B



1

L
B









2



4

Z
B









2































2

L
B











Z
B











1

L
B









2



4

Z
B









2





1

1

4

Z
B









2





1

L
B









2

4

Z
B









2



















































σDρ

D γ2



0.051 MPa







naprężenie na poziomie posadowienia fundamentu

σz.ρ

σDρ ηm Z

( )



4.959

10

3





MPa







odprężenie

σzs

σz.ρ



naprężenie wtórne

σzd

σzq σzs



0.029 MPa







naprężenie dodatkowe

σzp

γ1 h1



γ2 h2





γ3a h3





γ3b h3.1





0.159 MPa







naprężenie pierwotne na poziomie

0.2 σzp



0.032 MPa





0.2σzp σzd



1



Warunek spełniony

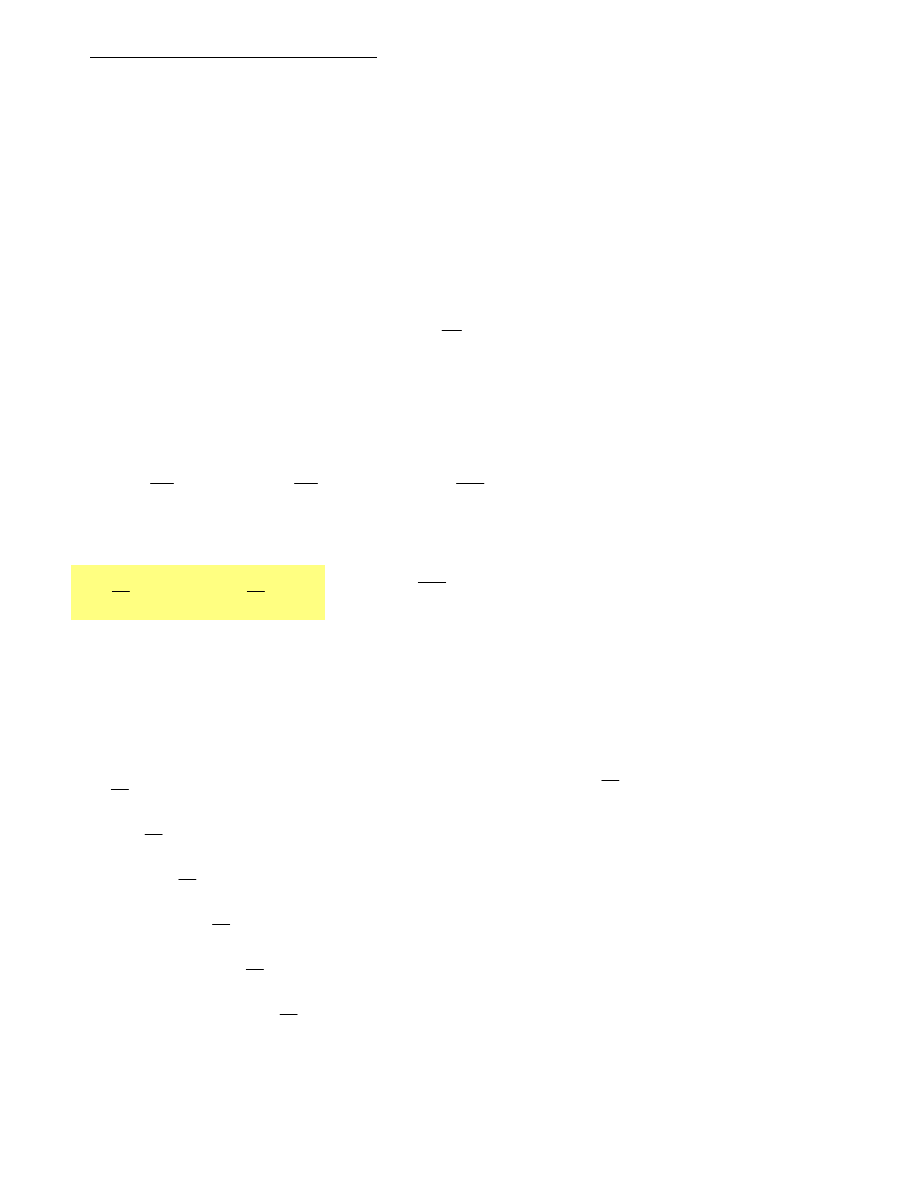
Podział gruntu na warstwy obliczeniowe:

Głębokość posadowienia

D

1.9 m



Miąższości warstw

h1 2.1m



h2 2.3m



h3 0.3m



h3.1 2.3m



Głębokość do której wyznaczamy warstwy obliczeniowe

Z

3.4 m



h4

Z

h1 D



h2



h3.1



h3









1.7



m





Maxymalna grubość warstwy obliczeniowej:

W0

B1

2

0.8 m





Miąższości warstw obliczeniowych

Warstwa 2a:

Warstwa 2b:

Warstwa 3:

Ilość warstw obliczeniowych:

n2

ceil

h2

W0













3





n3

ceil

h3

W0













1





n4

ceil

h3.1

W0













3





Grubość warstw obliczeniowych (Warstwy wyznaczamy od poziomu posadowienia D):

d5

h3.1

n4

0.767 m





d1

h2
n2

0.767 m





d4

h3
n3

0.3 m





d6

d5 0.767 m





d2

d1 0.767 m





d7

d5 0.767 m





d3

d2 0.767 m





Odległości od poziomu posadowienia do środka warstw:

z7

d1 d2



d3



d4



d5



d6



d7

2



4.517 m





z1

d1

2

0.383 m





z2

d1

d2

2



1.15 m





z3

d1 d2



d3

2



1.917 m





z4

d1 d2



d3



d4

2



2.45 m





z5

d1 d2



d3



d4



d5

2



2.983 m





z6

d1 d2



d3



d4



d5



d6

2



3.75 m





Naprężenia pierwotne na granicach warstw obliczeniowych

σzρ1

σDρ d1 γ2





0.072 MPa







σzρ2

σzρ1 d2 γ2





0.093 MPa







σzρ3

σzρ2 d3 γ2





0.113 MPa







σzρ4

σzρ3 d4 γ3a





0.118 MPa







σzρ5

σzρ4 d5 γ3b





0.131 MPa







σzρ6

σzρ5 d6 γ3b





0.143 MPa







σzρ7

σzρ6 d7 γ3b





0.155 MPa







Odprężenia w środkach warstw obliczeniowych:

Wyznaczenie współczynnika rozkładu naprężeń:

σz.ρ1

σDρ ηm z1

 



0.048 MPa







ηm z1

 

0.937



ηm z2

 

0.507



σz.ρ2

σDρ ηm z2

 



0.026 MPa







ηm z3

 

0.257



σz.ρ3

σDρ ηm z3

 



0.013 MPa







ηm z4

 

0.173



σz.ρ4

σDρ ηm z4

 



8.855

10

3





MPa







ηm z5

 

0.123



σz.ρ5

σDρ ηm z5

 



6.282

10

3





MPa







ηm z6

 

0.081



σz.ρ6

σDρ ηm z6

 



4.139

10

3





MPa







ηm z7

 

0.057



σz.ρ7

σDρ ηm z7

 



2.917

10

3





MPa







Naprężenia wtórne w środkach warstw obliczeniowych:

σzs1

σz.ρ1 0.048 MPa







σzs5

σz.ρ5 6.282 10

3





MPa







σzs2

σz.ρ2 0.026 MPa







σzs6

σz.ρ6 4.139 10

3





MPa







σzs3

σz.ρ3 0.013 MPa







σzs7

σz.ρ7 2.917 10

3





MPa







σzs4

σz.ρ4 8.855 10

3





MPa







Naprężenia w środkach warstw obliczeniowych

σzq1

q ηs z1

 



0.278 MPa







σzq5

q ηs z5

 



0.042 MPa







ηs z1

 

0.731



ηs z5

 

0.112



σzq2

q ηs z2

 



0.147 MPa







σzq6

q ηs z6

 



0.029 MPa







ηs z2

 

0.386



ηs z6

 

0.076



σzq7

q ηs z7

 



0.021 MPa







ηs z3

 

0.216



σzq3

q ηs z3

 



0.082 MPa







ηs z7

 

0.054



ηs z4

 

0.152



σzq4

q ηs z4

 



0.058 MPa







Naprężenia dodatkowe w środkach warstw obliczeniowych

σzd1

σzq1 σzs1



0.23 MPa







σzd5

σzq5 σzs5



0.036 MPa







σzd2

σzq2 σzs2



0.121 MPa







σzd6

σzq6 σzs6



0.025 MPa







σzd7

σzq7 σzs7



0.018 MPa







σzd3

σzq3 σzs3



0.069 MPa







σzd4

σzq4 σzs4



0.049 MPa







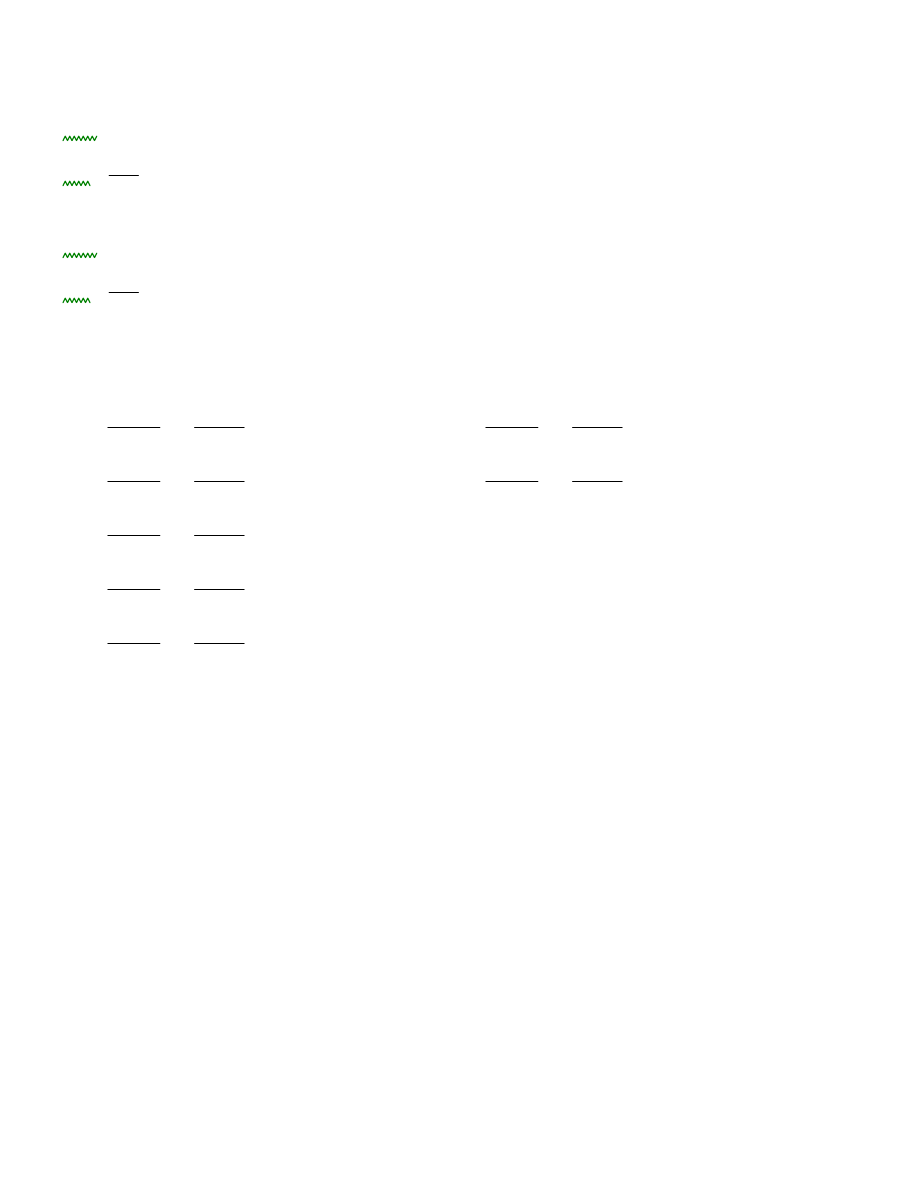
Parametry odksztakłceniowe warstw obliczeniowych

Dla warstw obliczeniowych z warstwy drugiej:

M02

74.73



MPa IL2

3



148.47MPa IL2

2





120.16MPa IL2





47.626MPa



32.69 MPa







M1

M01

0.9

34.77 MPa







Dla warstw obliczeniowych z warstwy trzeciej:

M02

74.73



MPa IL3

3



148.47MPa IL3

2





120.16MPa IL3





47.626MPa



47.626 MPa







M2

M02

0.9

52.918 MPa







Obliczenie spodziewanych osiadań

λ

1



Budowa trwa dłużej niż rok

s01

σzd1 d1



M01

λ

σzs1 d1



M1





0.67 cm







s06

σzd6 d6



M02

λ

σzs6 d6



M2





0.046 cm







s02

σzd2 d2



M01

λ

σzs2 d2



M1





0.354 cm







s07

σzd7 d7



M02

λ

σzs7 d7



M2





0.033 cm







s03

σzd3 d3



M01

λ

σzs3 d3



M1





0.198 cm







s04

σzd4 d4



M01

λ

σzs4 d4



M1





0.055 cm







s05

σzd5 d5



M02

λ

σzs5 d5



M2





0.067 cm







s0

s01 s02



s03



s04



s05



s06



s07



1.422 cm







s0 5cm



warunek spełniony

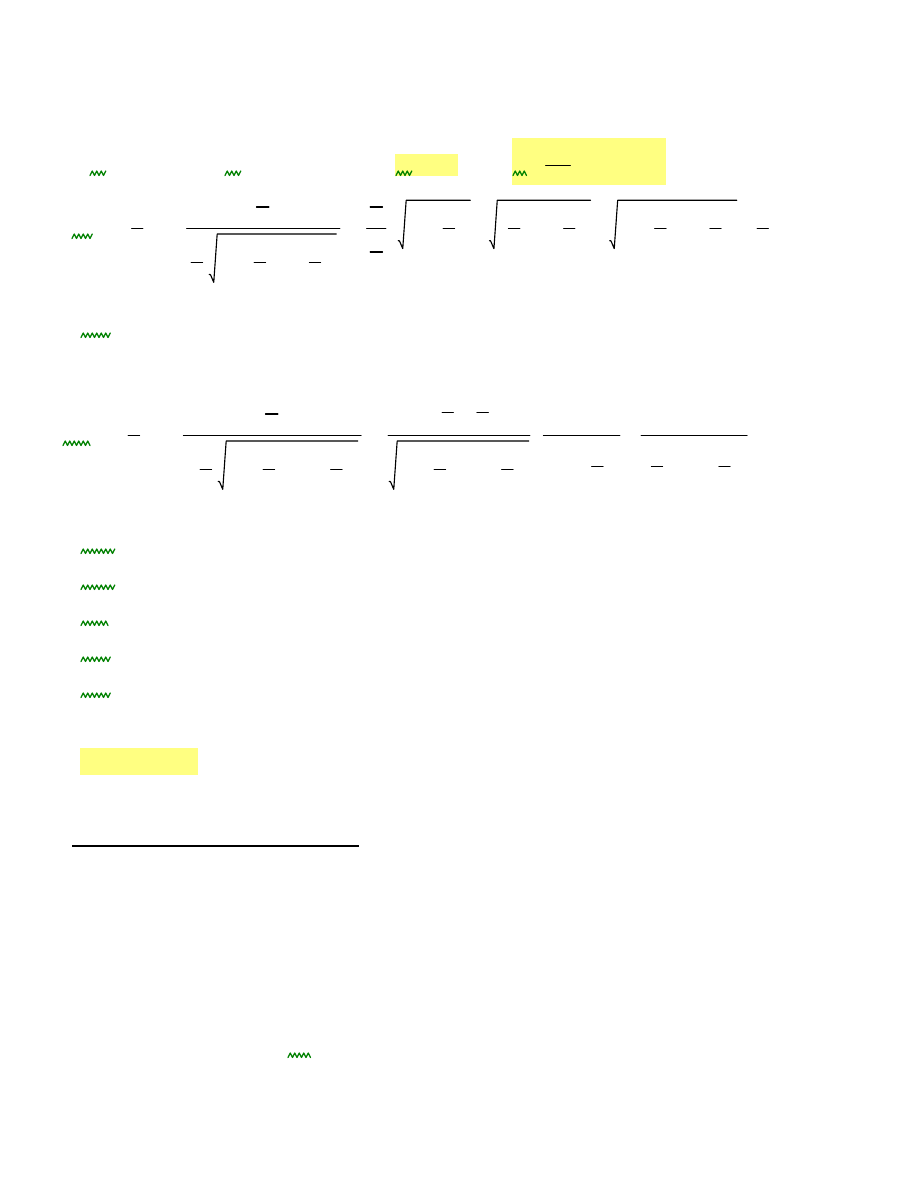
STAN GRANICZNY UŻYTKOWALNOŚCI DLA KOMBINACJI NR 2
Obliczenie osiadań

Wyznaczenie współczynnika zaniku naprężeń:

L

L2 1.6m





B

B2 1.6m





Z

3.4m



q

Pk2
B L



344.531 kPa







ηs Z

( )

2

π

atan

L

B

Z
B

1

L
B









2



Z
B









2





























Z

B

L

B

1

Z
B









2



L
B









2

Z
B









2





1

L
B









2



Z
B









2





Z
B















































σzq

q ηs Z

( )



0.031 MPa







- naprężenie wywołane ciężarem fundamentu

Wyznaczenie współczynnika rozkładu naprężeń:

ηm Z

( )

2

π

atan

L

B

2

Z
B



1

L
B









2



4

Z
B









2































2

L
B











Z
B











1

L
B









2



4

Z
B









2





1

1

4

Z
B









2





1

L
B









2

4

Z
B









2



















































σDρ

D γ2



0.051 MPa







naprężenie na poziomie posadowienia fundamentu

σz.ρ

σDρ ηm Z

( )



4.959

10

3





MPa







odprężenie

σzs

σz.ρ



naprężenie wtórne

σzd

σzq σzs



0.026 MPa







naprężenie dodatkowe

σzp

γ1 h1



γ2 h2





γ3a h3





γ3b h3.1





0.159 MPa







naprężenie pierwotne na poziomie

0.2 σzp



0.032 MPa





0.2σzp σzd



1



Warunek spełniony

Podział gruntu na warstwy obliczeniowe:

Głębokość posadowienia

D

1.9 m



Miąższości warstw

h1 2.1m



h2 2.3m



h3 0.3m



h3.1 2.3m



Głębokość do której wyznaczamy warstwy obliczeniowe

Z

3.4 m



h4

Z

h1 D



h2



h3.1



h3









1.7



m





Maxymalna grubość warstwy obliczeniowej:

W0

B2

2

0.8 m





Miąższości warstw obliczeniowych

Warstwa 2a:

Warstwa 2b:

Warstwa 3:

Ilość warstw obliczeniowych:

n2

ceil

h2

W0













3





n3

ceil

h3

W0













1





n4

ceil

h3.1

W0













3





Grubość warstw obliczeniowych (Warstwy wyznaczamy od poziomu posadowienia D):

d5

h3.1

n4

0.767 m





d1

h2
n2

0.767 m





d4

h3
n3

0.3 m





d6

d5 0.767 m





d2

d1 0.767 m





d7

d5 0.767 m





d3

d2 0.767 m





Odległości od poziomu posadowienia do środka warstw:

z7

d1 d2



d3



d4



d5



d6



d7

2



4.517 m





z1

d1

2

0.383 m





z2

d1

d2

2



1.15 m





z3

d1 d2



d3

2



1.917 m





z4

d1 d2



d3



d4

2



2.45 m





z5

d1 d2



d3



d4



d5

2



2.983 m





z6

d1 d2



d3



d4



d5



d6

2



3.75 m





Naprężenia pierwotne na granicach warstw obliczeniowych

σzρ1

σDρ d1 γ2





0.072 MPa







σzρ2

σzρ1 d2 γ2





0.093 MPa







σzρ3

σzρ2 d3 γ2





0.113 MPa







σzρ4

σzρ3 d4 γ3a





0.118 MPa







σzρ5

σzρ4 d5 γ3b





0.131 MPa







σzρ6

σzρ5 d6 γ3b





0.143 MPa







σzρ7

σzρ6 d7 γ3b





0.155 MPa







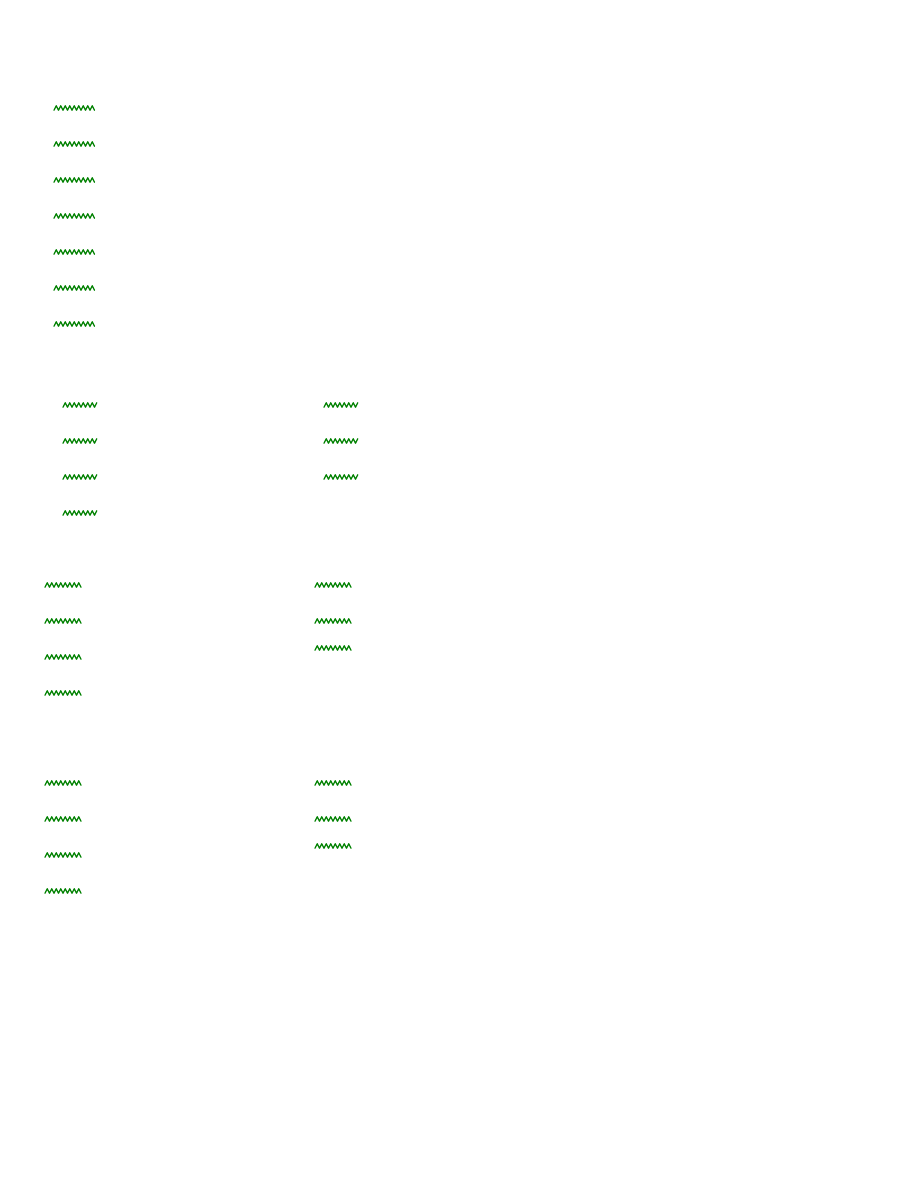
Odprężenia w środkach warstw obliczeniowych:

Wyznaczenie współczynnika rozkładu naprężeń:

σz.ρ1

σDρ ηm z1

 



0.048 MPa







ηm z1

 

0.937



ηm z2

 

0.507



σz.ρ2

σDρ ηm z2

 



0.026 MPa







ηm z3

 

0.257



σz.ρ3

σDρ ηm z3

 



0.013 MPa







ηm z4

 

0.173



σz.ρ4

σDρ ηm z4

 



8.855

10

3





MPa







ηm z5

 

0.123



σz.ρ5

σDρ ηm z5

 



6.282

10

3





MPa







ηm z6

 

0.081



σz.ρ6

σDρ ηm z6

 



4.139

10

3





MPa







ηm z7

 

0.057



σz.ρ7

σDρ ηm z7

 



2.917

10

3





MPa







Naprężenia wtórne w środkach warstw obliczeniowych:

σzs1

σz.ρ1 0.048 MPa







σzs5

σz.ρ5 6.282 10

3





MPa







σzs2

σz.ρ2 0.026 MPa







σzs6

σz.ρ6 4.139 10

3





MPa







σzs3

σz.ρ3 0.013 MPa







σzs7

σz.ρ7 2.917 10

3





MPa







σzs4

σz.ρ4 8.855 10

3





MPa







Naprężenia w środkach warstw obliczeniowych

σzq1

q ηs z1

 



0.252 MPa







σzq5

q ηs z5

 



0.038 MPa







ηs z1

 

0.731



ηs z5

 

0.112



σzq2

q ηs z2

 



0.133 MPa







σzq6

q ηs z6

 



0.026 MPa







ηs z2

 

0.386



ηs z6

 

0.076



σzq7

q ηs z7

 



0.019 MPa







ηs z3

 

0.216



σzq3

q ηs z3

 



0.075 MPa







ηs z7

 

0.054



ηs z4

 

0.152



σzq4

q ηs z4

 



0.052 MPa







Naprężenia dodatkowe w środkach warstw obliczeniowych

σzd1

σzq1 σzs1



0.204 MPa







σzd5

σzq5 σzs5



0.032 MPa







σzd2

σzq2 σzs2



0.107 MPa







σzd6

σzq6 σzs6



0.022 MPa







σzd7

σzq7 σzs7



0.016 MPa







σzd3

σzq3 σzs3



0.061 MPa







σzd4

σzq4 σzs4



0.044 MPa







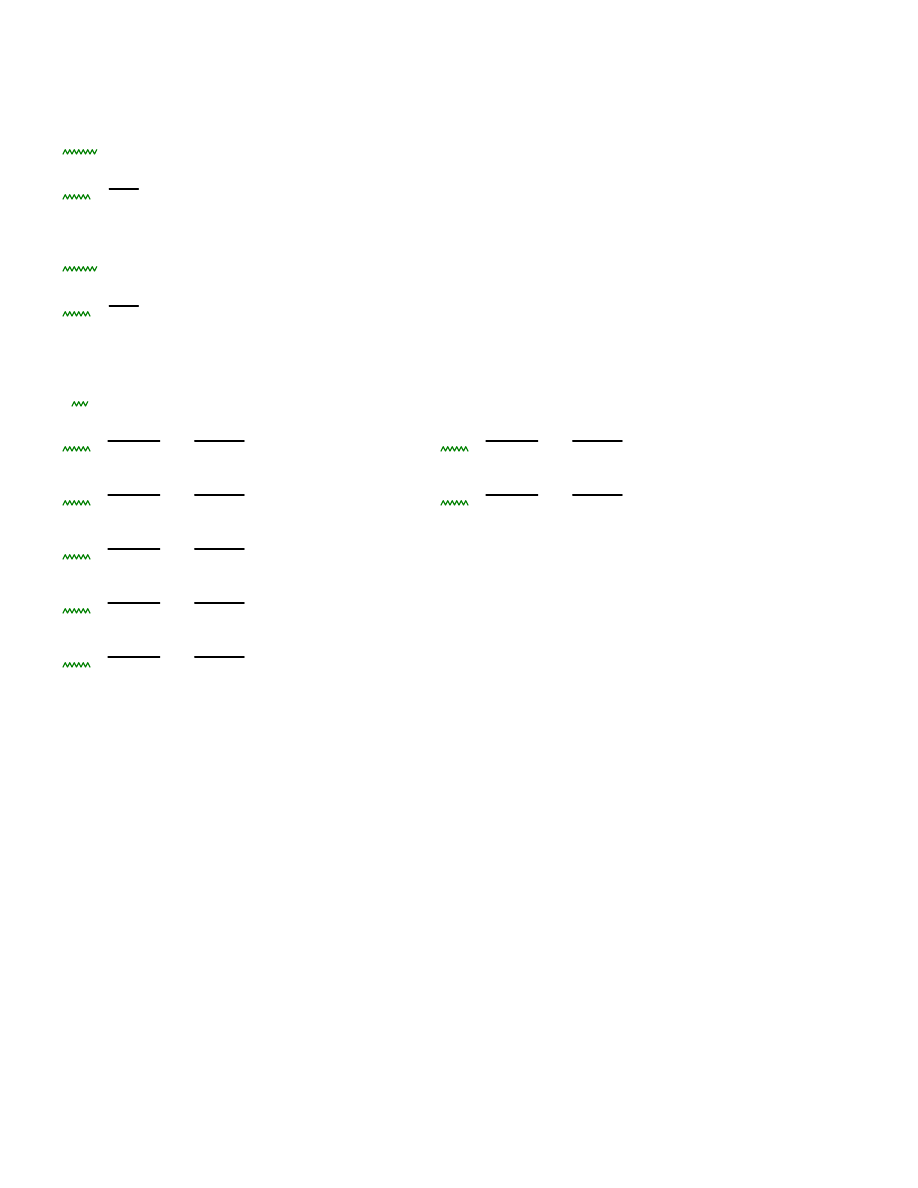
Parametry odksztakłceniowe warstw obliczeniowych

Dla warstw obliczeniowych z warstwy drugiej:

M02

74.73



MPa IL2

3



148.47MPa IL2

2





120.16MPa IL2





47.626MPa



32.69 MPa







M1

M01

0.9

34.77 MPa







Dla warstw obliczeniowych z warstwy trzeciej:

M02

74.73



MPa IL3

3



148.47MPa IL3

2





120.16MPa IL3





47.626MPa



47.626 MPa







M2

M02

0.9

52.918 MPa







Obliczenie spodziewanych osiadań

λ

1



Budowa trwa dłużej niż rok

s01

σzd1 d1



M01

λ

σzs1 d1



M1





0.605 cm







s06

σzd6 d6



M02

λ

σzs6 d6



M2





0.041 cm







s02

σzd2 d2



M01

λ

σzs2 d2



M1





0.32 cm







s07

σzd7 d7



M02

λ

σzs7 d7



M2





0.03 cm







s03

σzd3 d3



M01

λ

σzs3 d3



M1





0.179 cm







s04

σzd4 d4



M01

λ

σzs4 d4



M1





0.049 cm







s05

σzd5 d5



M02

λ

σzs5 d5



M2





0.061 cm







s00 s01 s02



s03



s04



s05



s06



s07



1.285 cm







s00 5cm



warunek spełniony

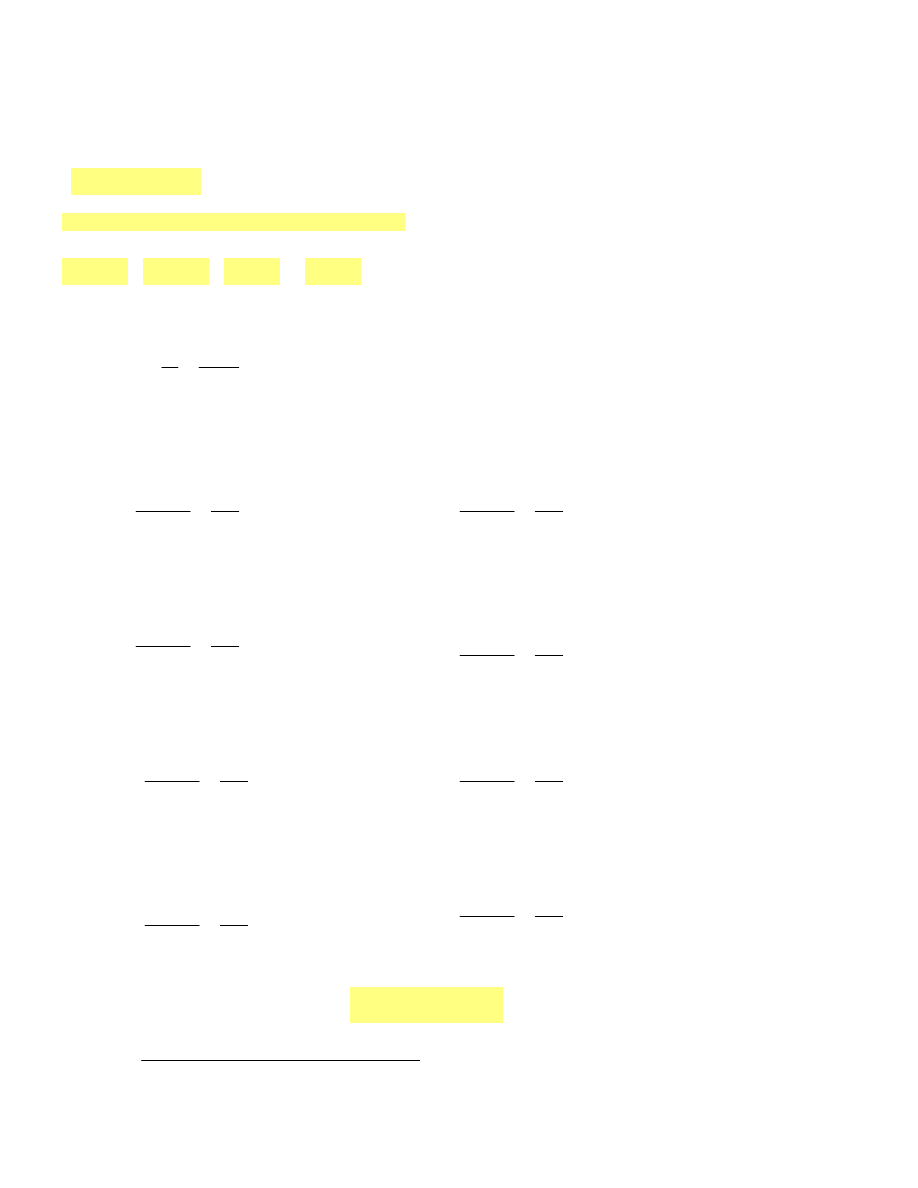
Osiadanie dla kombinacji nr 1:

s0 14.22 mm





Osiadanie dla kombinacji nr 2:

s00 12.854 mm





Wybrano większe osiadanie:

s1

s0 14.22 mm







Współrzędne poszczególnych stóp fundamentowych

l1

3.5m



l2

4.5m



l3

8m



l4

6m



Wzór na obliczenie poszczególnych osiadań:

S0

si

xi

10

yi

xi 1





















si

Osiadanie dla stopy nr 2:

Osiadanie dla stopy nr 3:

x2

0



y2

l4 6 m





x3

l2 4.5m





y3

l4 6 m





s2

s1

y2

x2 1m



x2

10m

















85.323 mm







s3

s1

y3

x3 1m



x3

10m

















21.912 mm







Osiadanie dla stopy nr 4:

Osiadanie dla stopy nr 5:

x4

l1



3.5



m





y4

0m



x5

0m



y5

0m



s4

s1

y4

x4 1m



x4

10m

















4.977



mm







s5

s1

y5

x5 1m



x5

10m

















0 mm







Osiadanie dla stopy nr 6:

Osiadanie dla stopy nr 7:

x6

l2 4.5m





y6

0m



x7

l1



3.5



m





y7

l3



8

 m





s6

s1

y6

x6 1m



x6

10m

















6.399 mm







s7

s1

y7

x7 1m



x7

10m

















40.528 mm







Osiadanie dla stopy nr 8:

Osiadanie dla stopy nr 9:

x8

0m



y8

l3



8

 m





x9

l2 4.5m





y9

l3



8

 m





s9

s1

y9

x9 1m



x9

10m

















14.285



mm







s8

s1

y8

x8 1m



x8

10m

















113.764



mm







Średnie osiadanie budowli:

Pole powierzchni stopy fundamentowej: F1 B1 L1



2.56 m

2





sśr F1

s1 s2



s3



s4



s5



s6



s7



s8



s9







9 F1





3.929 mm







10. Przechylenie Budowli=> Uklad przyjmuję w środku ciężkości

x1

l1



3.5



m





y1

l4 6 m





x1

2

12.25 m

2



y1

2

36 m

2



x1 y1



21

 m

2



s1 y1



0.085 m

2



s1 x1



0.05



m

2



x2

0



y2

l4 6 m





x2

2

0



y2

2

36 m

2



x2 y2



0



s2 y2



0.512 m

2



s2 x2



0



x3

l2 4.5m





y3

l4 6 m





x3

2

20.25 m

2



y3

2

36 m

2



x3 y3



27 m

2



s3 y3



0.131 m

2



s3 x3



0.099 m

2



x4

l1



3.5



m





y4

0m



x4

2

12.25 m

2



y4

2

0



x4 y4



0



s4 y4



0



s4 x4



0.017 m

2



x5

0m



y5

0m



x5

2

0



y5

2

0



x5 y5



0



s5 y5



0



s5 x5



0



x6

l2 4.5m





y6

0m



x6

2

20.25 m

2



y6

2

0



x6 y6



0



s6 y6



0



s6 x6



0.029 m

2



x7

l1



3.5



m





y7

l3



8

 m





x7

2

12.25 m

2



y7

2

64 m

2



x7 y7



28 m

2



s7 y7



0.324



m

2



s7 x7



0.142



m

2



x8

0m



y8

l3



8

 m





x8

2

0



y8

2

64 m

2



x8 y8



0



s8 y8



0.91 m

2



s8 x8



0



x9

l2 4.5m





y9

l3



8

 m





x9

2

20.25 m

2



y9

2

64 m

2



x9 y9



36

 m

2



s9 y9



0.114 m

2



s9 x9



0.064



m

2



s

s1 s2



s3



s4



s5



s6



s7



s8



s9



0.035 m





x

x1 x2



x3



x4



x5



x6



x7



x8



x9



3 m





y

y1 y2



y3



y4



y5



y6



y7



y8



y9



6

 m





X

x1

2

x2

2



x3

2



x4

2



x5

2



x6

2



x7

2



x8

2



x9

2



97.5 m

2





Y

y1

2

y2

2



y3

2



y4

2



y5

2



y6

2



y7

2



y8

2



y9

2



300 m

2





xy

x1 y1



x2 y2





x3 y3





x4 y4





x5 y5





x6 y6





x7 y7





x8 y8





x9 y9





2

 m

2





xs

x1 s1



x2 s2





x3 s3





x4 y4





x5 y5





x6 y6





x7 s7





x8 s8





x9 s9





0.157



m

2





ys

y1 s1



y2 s2





y3 s3





y4 s4





s5 y5





s6 y6





y7 s7





y8 s8





y9 s9





1.429 m

2





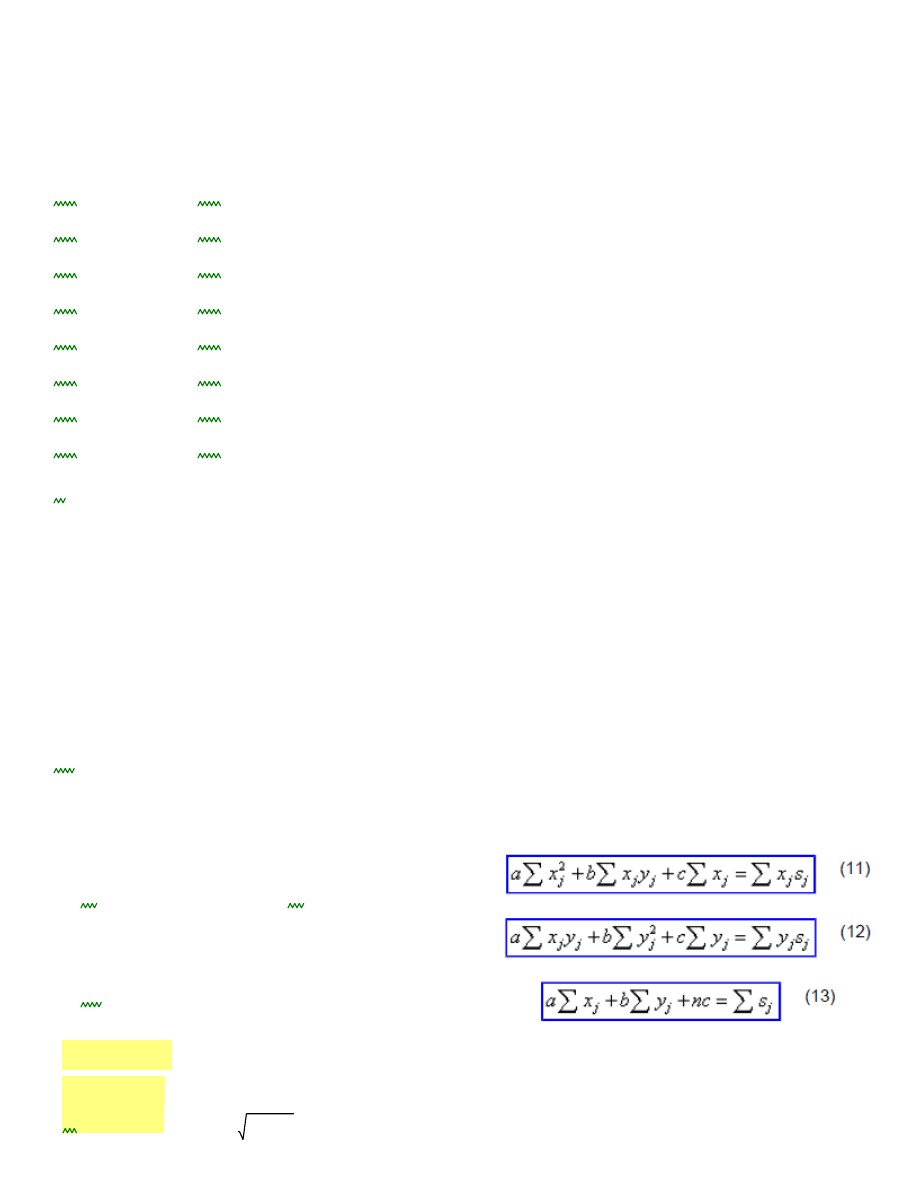
Ilość stóp fundamentowych w budynku:

n

9



C

X

xy

x

xy

Y

y

x

y

n



















Z

xs

ys

s



















W

C

1



Z



1.752



10

3





4.907

10

3





7.784

10

3





























a

1.752



10

3







θdop

0.003



Przechylenie budowli:

b

4.907 10

3







c

7.784 10

3







θ

a

2

b

2



4.584i

10

3









warunek niespełniony

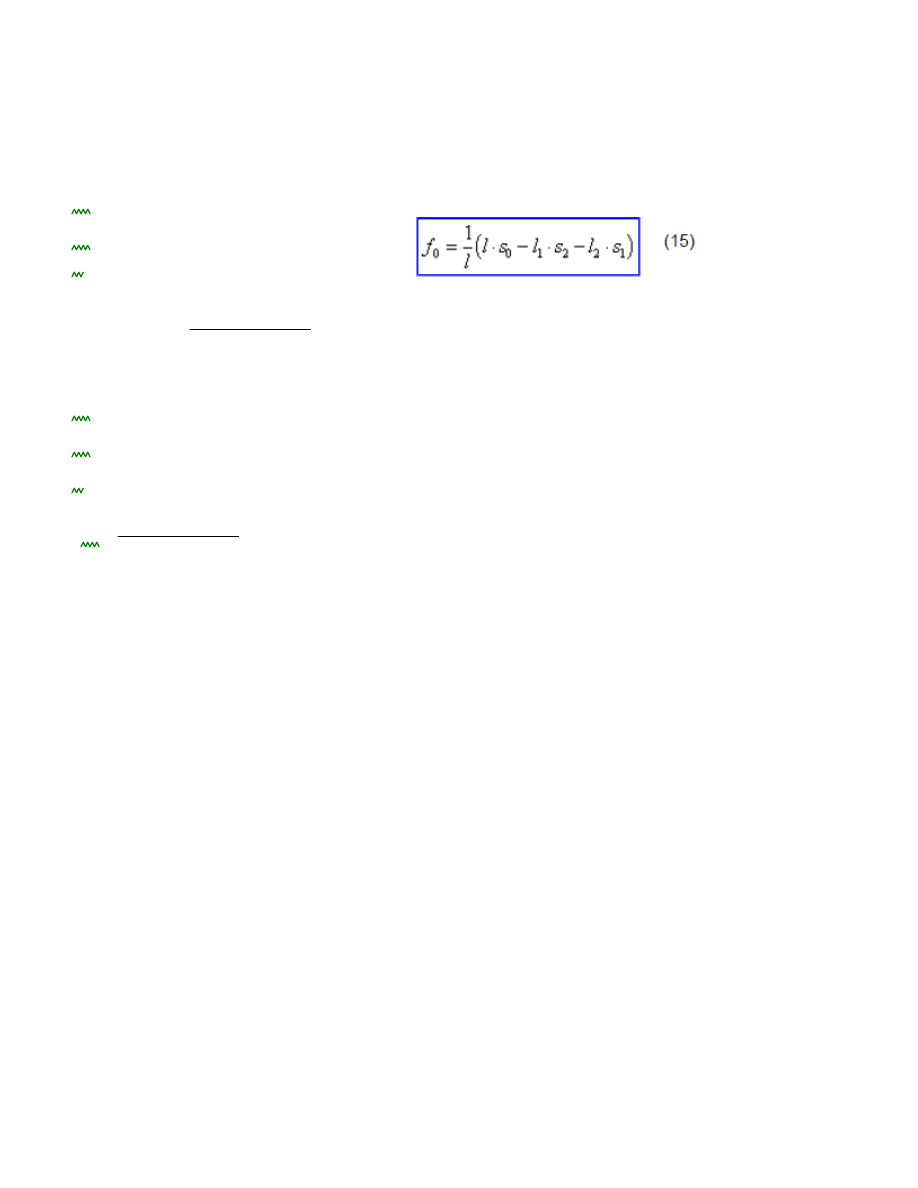
11. Strzałka ugięcia budowli

f0.dop

1cm



-dopuszczalna strzałka ugięcia (PN-80/B-03020 tab.4.)

Strzałka ugięcia na linii 1-2-3

l1

12.6m



l2

6.3m



l

l1 l2



18.9 m





f0

s2 l s3 l1





s1 l2





l

6.597 cm







f0 f0.dop



0



warunek
niespełniony

Strzałka ugięcia na linii 1-4-7

l3

7.2m



l4

7.2m



l

l3 l4



14.4 m





f0

s4 l s1 l3





s7 l4





l

3.235



cm







f0 f0.dop



1



warunek został
spełniony

Gdy h4 > 0 to musimy wziac jeszcze z 4 warstwy