Anna  Ociepa   Gr.1 

Zad 1. 

a)  

𝜕𝑑

𝜕𝑖

=

𝜕

𝜕𝑖

 

𝑖

𝑖+1

  =

1+𝑖−𝑖

(1+𝑖)

2

=

1

(1+𝑖)

2

 

 

b)  

𝜕𝑑

 𝑚  

𝜕𝑑

=

𝜕

𝜕𝑑

 𝑘 1 −  1 − 𝑑

𝑘

   = 

= 𝑘 ∙

1
𝑘

(1 − 𝑑)

1

𝑘−1

= (1 − 𝑑)

1

𝑘−1

 

 

c)  

𝜕𝑑
𝜕𝛿

=

𝜕

𝜕𝛿

 1 −

1

𝑒

𝛿

  =

𝑒

𝛿

𝑒

2𝛿

=

1

𝑒

𝛿

 

 

 

d)  

𝜕𝛿

𝜕𝑖

=

𝜕

𝜕𝑖

(ln 1 + 𝑖 ) =

1

1+𝑖

 

 

e)  

𝜕𝛿
𝜕𝑣

=

𝜕

𝜕𝑣

 ln  

1
𝑣

   = −

1

𝑣

2

∙ 𝑣 = −

1
𝑣

  

 

 

Zad 2. 

Z treści zadania: 

𝛿 𝑡  = 3 ∙ 5

𝑡

  

𝑖

4

=

𝑎(4)
𝑎(3)

− 1 

Korzystam ze wzoru: 

Z poniższego równania wyznaczam d : 

1 + 𝑖 =

1

1−𝑑

     stąd     𝑑 =

𝑖

1+𝑖

 

 

 

 

Z poniższego równania wyznaczam 𝑑

(𝑚)

 : 

1

(1−

𝑑(𝑚 )

𝑘

)

𝑘

=

1

1−𝑑

    stąd  𝑑

(𝑚)

= 𝑘 1 −  1 − 𝑑

𝑘

  

 

Z poniższego równania wyznaczam d : 

1

1−𝑑

= 𝑒

𝛿

    stąd    𝑑 = 1 −

1

𝑒

𝛿

 

Z poniższego równania wyznaczam 𝛿 : 

1 + 𝑖 = 𝑒

𝛿

     stąd    𝛿 = ln⁡

(1 + 𝑖) 

Z poniższego równania wyznaczam 𝛿 : 

1
𝑣

= 𝑒

𝛿

    stąd   𝛿 = ln⁡

(

1
𝑣

) 

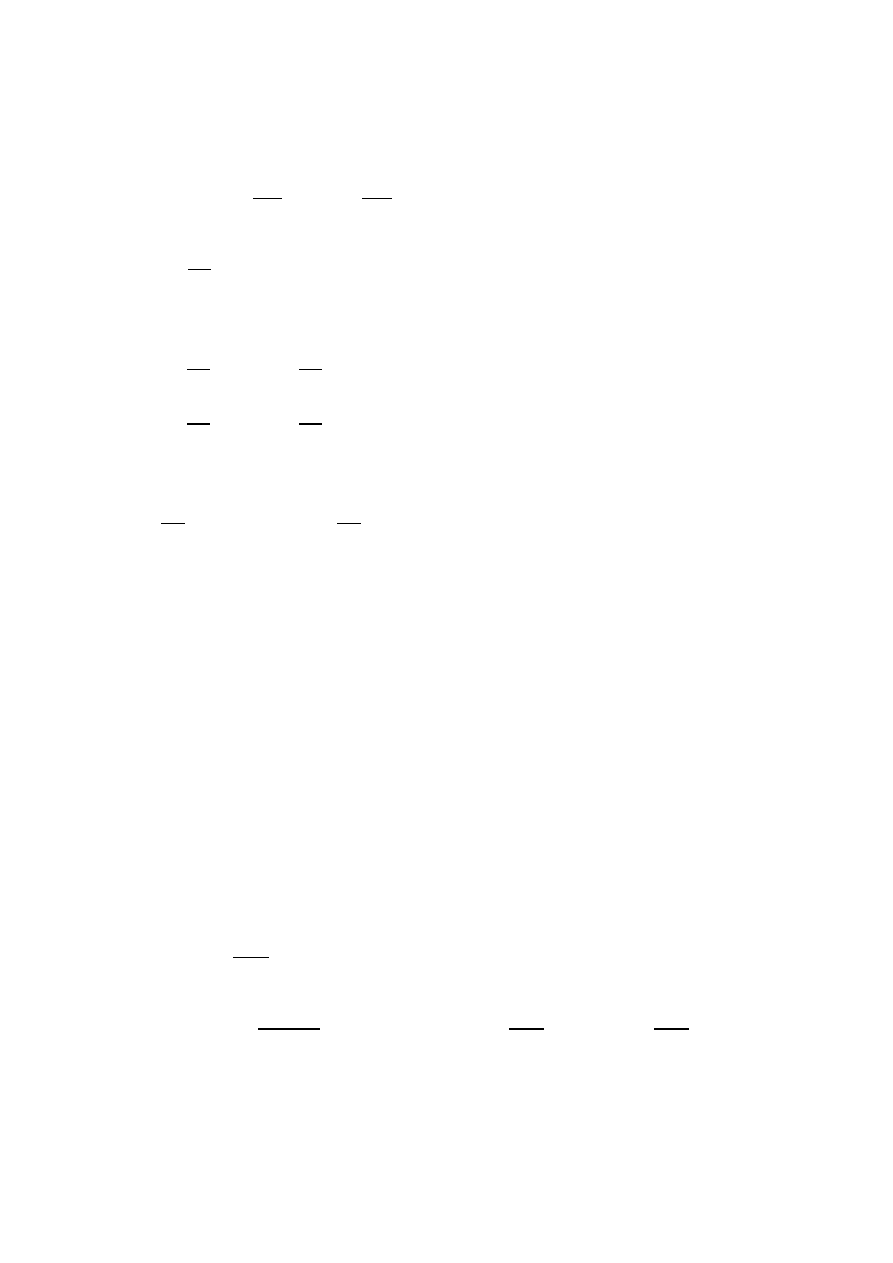
𝑎 𝑇  = 𝑒

  𝛿 𝑡 𝑑𝑡

𝑇

0

 

  3 ∙ 5

𝑡

  dt =

𝑇

0

3 ∙

1

ln5

∙ 5

𝑡

|

0

𝑇

=

3

𝑙𝑛5

(5

𝑇

− 1) 

𝑎 𝑇  = 𝑒

3

𝑙𝑛5(5

𝑇

−1)

 

Podstawiam  T=4  i  T=3 : 

𝑎 4  = 𝑒

3

𝑙𝑛5(5

4

−1)

= 𝑒

3

𝑙𝑛 5∙624

 

𝑎 3  = 𝑒

3

𝑙𝑛5(5

3

−1)

= 𝑒

3

𝑙𝑛 5∙124

 

Stąd: 

𝑖

4

= 𝑒

3

𝑙𝑛5 624−124 

− 1 = 𝑒

3

𝑙𝑛5∙500

− 1 

𝑖

4

≈ 𝑒

923

− 1  

 

Zad 3. 

𝐾

4

= $1000 - Kapitał koocowy 

n=3,5  - czas inwestycji w latach 

𝑑

(12)

= 10%  - nominalna stopa dyskonta 

k=12  - ilośd podokresów 

 

𝐾 = 𝐾

𝑛

∙ (1 −

𝑑

 𝑘 

𝑘

)

𝑛∙𝑘

 

𝐾 = 1000 ∙  1 −

1

10 ∙ 12

 

3,5∙12

= 1000 ∙  1 −

1

120

  = 1000 ∙  

119
120

 

42

= 1000 ∙ 0,70366 

𝐾 = $703,66 

 

Zad 4. 

𝑖

 2 

= 8% 

k=2 

Z poniższego równania wyznaczam i, a następnie podstawiam dane wartości : 

1 + 𝑖 = (1 +

𝑖

(𝑘)

𝑘

)

𝑘

 

𝑖 =  1 +

𝑖

 𝑘 

𝑘

 

𝑘

− 1 

𝑖 =  1 +

𝑖

 2 

2

 

2

− 1 

𝑖 = 8,16% 

Z treści zadania tworzę równanie: 

−5000 −

𝑋

(1 + 𝑖)

1

+

3000

(1 + 𝑖)

5

+

10000

(1 + 𝑖)

10

= 0 

Z którego wyznaczam X : 

𝑋 =  1 + 𝑖   

3000

 1 + 𝑖 

5

+

10000

 1 + 𝑖 

10

− 5000  

I podstawiając     𝑖 = 8,16%   otrzymuję kwotę X : 

𝑋 = 1720,35 

 

Zad 5. 

Z treści zadania: 

156,85

 1 + 𝑖 

3

=

100

(1 + 𝑖)

3

+

200

(1 + 𝑖)

6

 

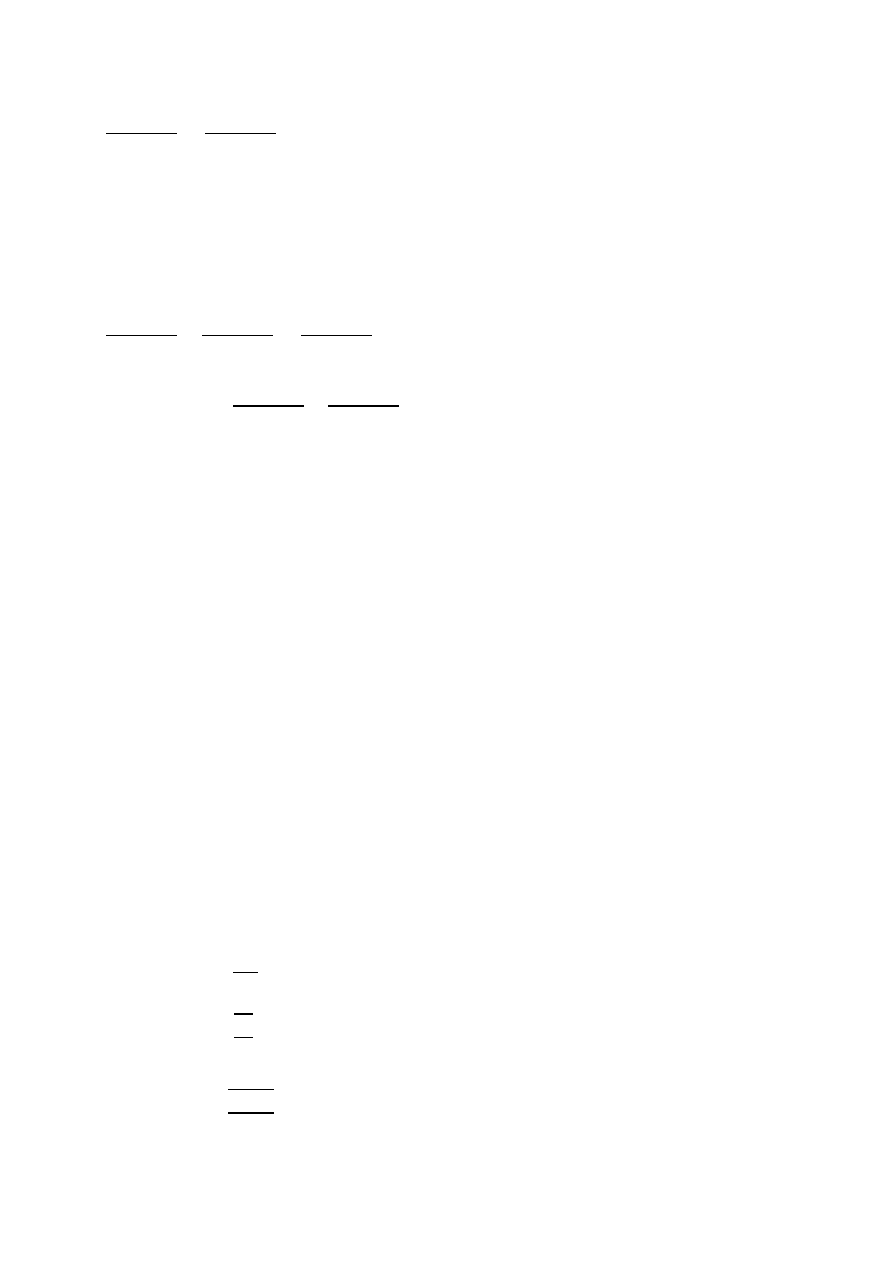
56,85

 1 + 𝑖 

3

=

200

(1 + 𝑖)

6

 

 1 + 𝑖 

3

∙ 56,85 = 200 

𝑖 = 52,09% 

Z poniższego równania wyznaczam X : 

300

(1 + 𝑖)

0

+

200

(1 + 𝑖)

4

=

𝑋

(1 + 𝑖)

6

 

𝑋 =  1 + 𝑖 

6

 

300

 1 + 𝑖 

0

+

200

 1 + 𝑖 

4

  

Podstawiając    𝑖 = 52,09%  otrzymuję szukane X : 

𝑋 = $4175,59 

 

Zad 6. 

𝐾 = $100  - kapitał początkowy

 

n=5  - liczba lat 

𝐾

𝑛

= $180,61  - kapitał koocowy 

k=4  - ilośd kapitalizacji 

𝑖

 𝑘 

  - nominalna stopa oprocentowania 

 

Z poniższego równania wyznaczam  𝑖

(𝑘)

 : 

𝐾

𝑛

= 𝐾 ∙ (1 +

𝑖

 𝑘 

𝑘

)

𝑛∙𝑘

  

𝑖

 𝑘 

= 𝑘 ∙    

𝐾

𝑛

𝐾

𝑛 ∙𝑘

− 1    Podstawiam wartości : 

𝑖

 4 

= 4 ∙    

180,61

100

20

− 1   

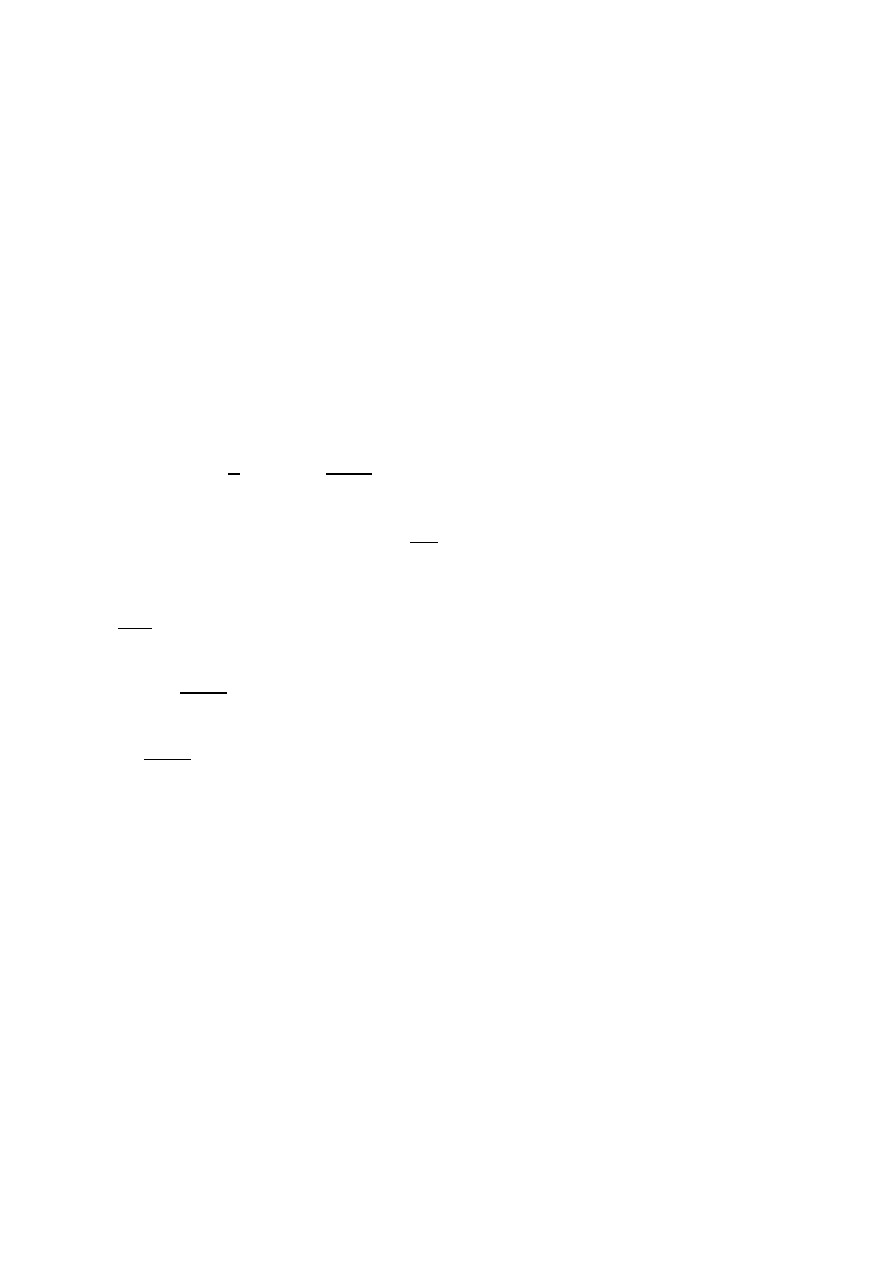
𝑖

 4 

= 0,12 

𝑖

 4 

= 12% 

 

Zad 7. 

𝛿

𝑡

= 𝑐 ∙ 𝑡

2

 

Z definicji nominalnej stopy oprocentowania ciągłego mamy :  

𝐾 10  = 𝐾 0  ∙ 𝑒

  𝑐∙𝑡

2

 𝑑𝑡

10

0

 

  𝑐 ∙ 𝑡

2

 𝑑𝑡 =

𝑐
3

10

0

∙ 𝑡

3

|

0

10

=

1000

3

∙ 𝑐 

Mamy równania  𝐾 10  = 𝐾(0) ∙ 𝑒

1000

3

∙𝑐

       i   z treści zadania    3 ∙ 𝐾 10  =

𝐾(0)      stąd: 

𝑒

1000

3 ∙𝑐

= 3 

ln 3  =

1000

3

∙ 𝑐 

𝑐 =

3

1000

∙ ln3 

𝑐 = 0,0033 

 

Zad 8. 

Z treści zadania tworzę równanie:  

5000 =   2𝑋(1 + 𝑖)

𝑘

+   𝑋(1 + 𝑖)

𝑛

15

𝑛=1

5

𝑘=1

 

Podstawiam    𝑖 = 5% 

5000 =   2𝑋(1,05)

𝑘

+   𝑋(1,05)

𝑛

15

𝑛=1

5

𝑘=1

 

5000 = 𝑋(2 ∙  (1,05)

𝑘

+  (1,05)

𝑛

)

15

𝑛=1

5

𝑘=1

 

i wyznaczam X : 

𝑋 =

5000

2 ∙  

(1,05)

𝑘

+  

(1,05)

𝑛

)

15

𝑛=1

5

𝑘=1

 

Rozbijam mianownik ze wzoru na sumę szeregu geometrycznego : 

𝑋 =

5000

2 ∙ 1,05 ∙

1 − 1,05

5

1 − 1,05 + 1,05 ∙

1 − 1,05

15

1 − 1,05

 

Stąd szukana kwota X wynosi : 

𝑋 = 1756,89 

 

Zad 9. 

Z treści zadania : 

𝐾

5

= 100000 ∙  1 + 0,05 

5

∙  1 + 0,03  

𝐾

5

≈ 131457 

𝐾

5

=   𝑅 ∙ (1 +

𝑖

 12 

12

)

𝑘

60

𝑘=1

 

131457 = 𝑅 ∙  (1 +

𝑖

 12 

12

)

𝑘

60

𝑘=1

 

𝑅 =

131457

 

 1 +

𝑖

 12 

12  

𝑘

60

𝑘=1

 

Podstawiam   

𝑖

 12 

12

=

6%

12

= 0,005  : 

𝑅 =

131457

 

 1 + 0,005 

𝑘

60

𝑘=1

 

𝑅 =

131457

 

 1,005 

𝑘

60

𝑘=1

 

Rozbijam mianownik ze wzoru na sumę szeregu geometrycznego : 

𝑅 =

131457

1.005 ∙

1 − 1,005

60

1 − 1,005

 

Stąd szukane R wynosi : 

𝑅 = 1874,77