2
Cel üwiczenia
Pomiar zalenoci oporu próbek od temperatury, wyznaczenie temperaturowego współczynnika
rezystancji dla metali i przerwy energetycznej dla półprzewodników wystpujcych wród próbek.
Wprowadzenie
Jeeli midzy dwoma punktami ciała wytworzymy rónic potencjałów (przyłoymy napicie) to
wewntrz ciała pojawi si pole elektryczne. Jeli w tym ciele istniej swobodne ładunki - noniki prdu (m.in.
elektrony, jony a take tzw. dziury w półprzewodnikach) to pole elektryczne wprawia je w ruch. Taki przepływ
ładunków nazywamy prdem elektrycznym. Noniki prdu mog mie ładunek ujemny lub dodatni. Ciała
wyróniajce si dobrym przepływem prdu nazywamy przewodnikami prdu. Typowymi przewodnikami s
metale.
Metale s to ciała stałe, których atomy posiadaj jeden lub dwa elektrony walencyjne. Przy łczeniu si
takich atomów, elektrony walencyjne trac bezporedni kontakt ze swoimi atomami i staj si swobodnymi
nonikami prdu, tzn. mog swobodnie porusza si po całej objtoci próbki. Natomiast atomy, które utraciły
elektrony staj si jonami, które wykonuj drgania wokół ich połoenia równowagi.
Innym typem materiału jest półprzewodnik., którego przewodno właciwa prdu nie jest tak wysoka
jak w przypadku dobrych przewodników oraz którego nie mona zaliczy do dielektryków, gdy w porównaniu
z nimi ma znacznie wiksz przewodno.
Zaleno koncentracji noników od temperatury róni si istotnie dla metali i półprzewodników. W
przypadku metali koncentracja nie zaley od temperatury i jest rzdu koncentracji atomów. Wzrost temperatury
powoduje zwikszanie prawdopodobiestwa zderzenia si swobodnych noników prdu (elektronów w metalu) z
drgajcymi atomami, przez co zmniejsza si ruchliwo elektronów, a tym samym nastpuje wzrost oporu.
Zatem opór metalu wyranie ronie ze wzrostem temperatury. W przypadku półprzewodników zwikszanie
temperatury powoduje wykładniczy wzrost liczby noników mogcych bra udział w przewodnictwie.
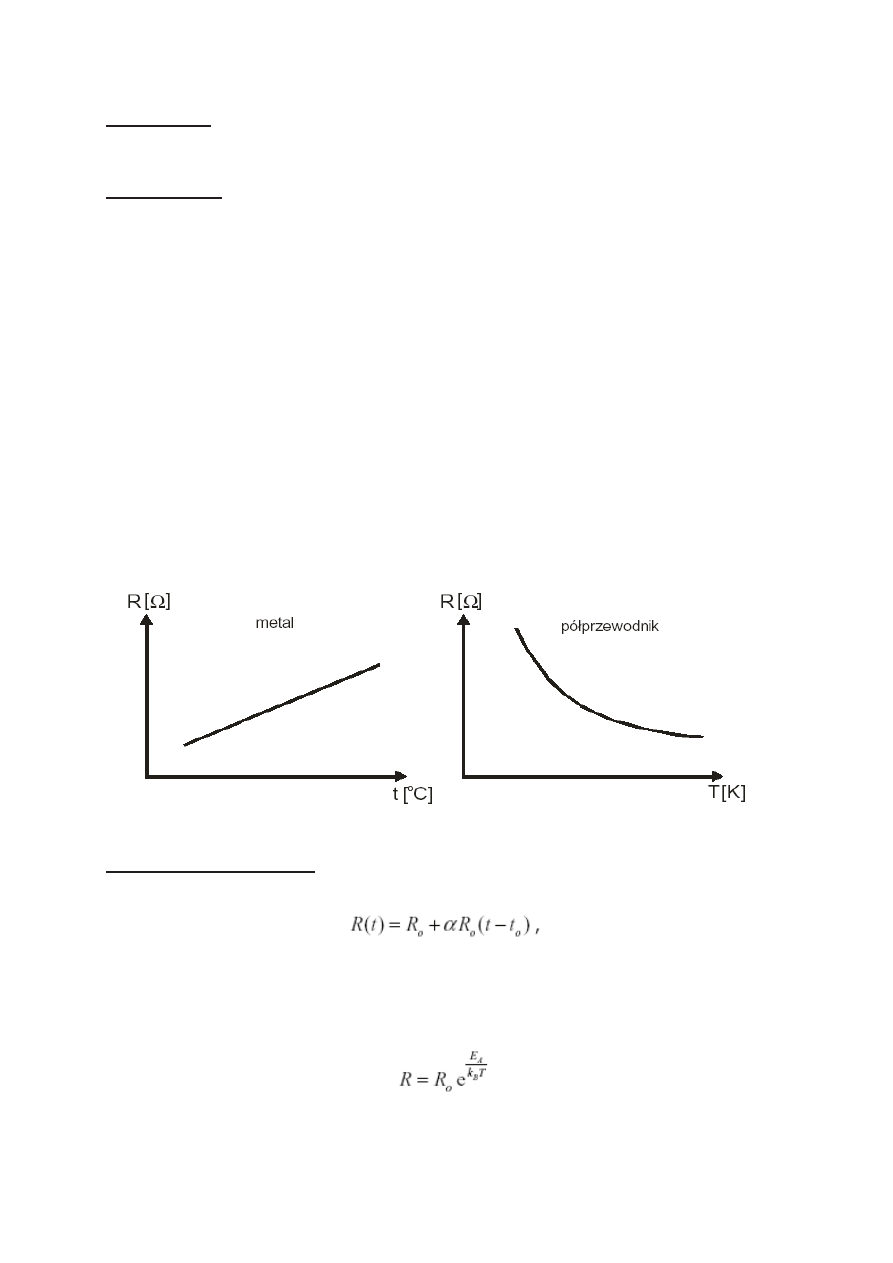
Wynikajc z powyszych obserwacji zaleno oporu dla metali i półprzewodników przedstawiaj
ponisze wykresy.
Wykres 1. ZaleĪnoĞü oporu od temperatury dla metali
Wykres 2.ZaleĪnoĞü oporu od temperatury dla
półprzewodników
Układ i metody pomiarowe
Do opracowania wyników pomiarów skorzystamy z okrelonych zalenoci fizycznych.
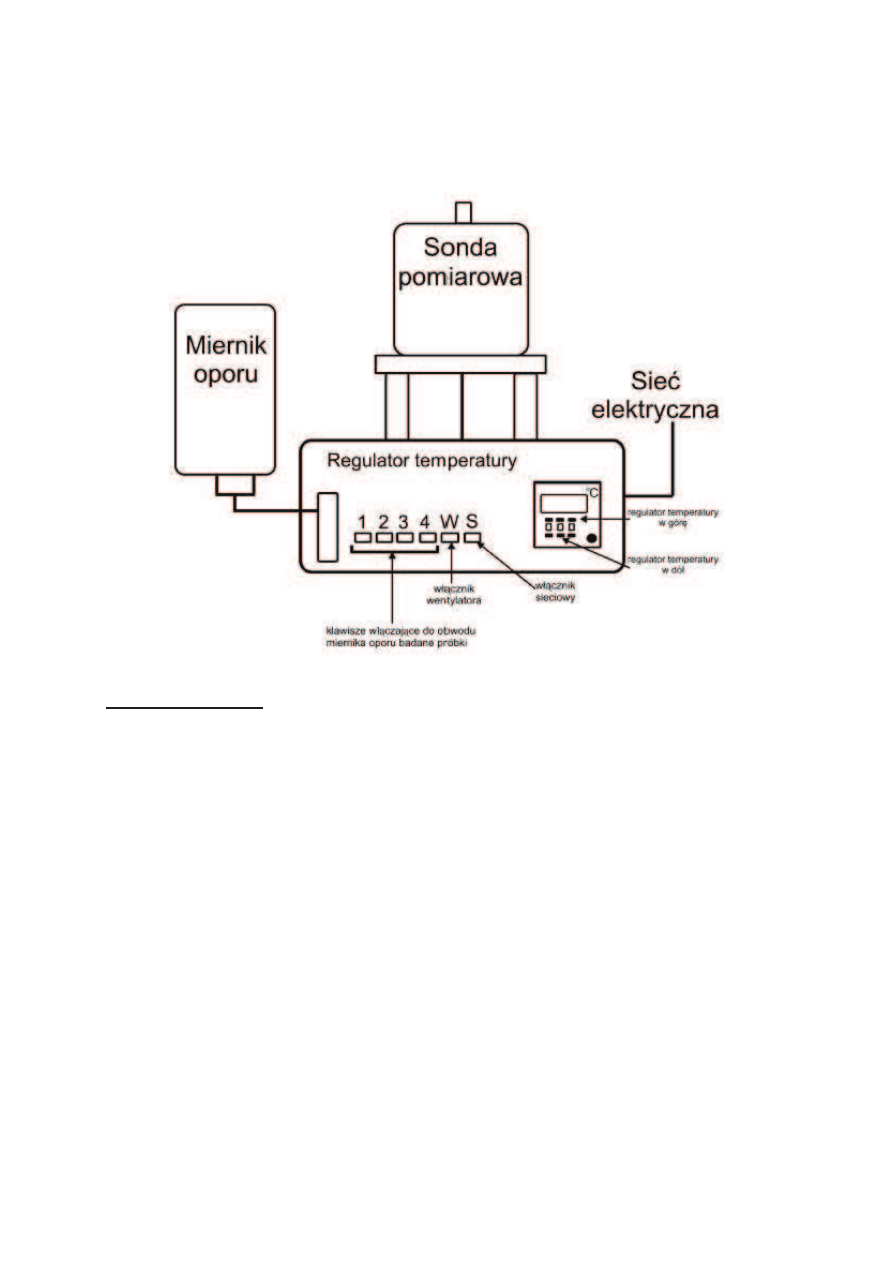
W przypadku metali opór wzrasta liniowo ze wzrostem temperatury, zgodnie z wyraeniem:
gdzie: t
o
– temperatura pocztkowa pomiarów [
o
C], R
o
– opór metalu w temperaturze pocztkowej [], –
temperaturowy współczynnik oporu, t – temperatura mierzona [
o
C]. Na podstawie powyszego wzoru obliczymy
temperaturowy współczynnik oporu .
W przypadku półprzewodników koncentracja noników prdu ronie ekspotencjalnie wraz ze wzrostem
temperatury, tak wic opór próbki z półprzewodnika bdzie malał wraz z jej wzrostem. Zaleno oporu
półprzewodnika od temperatury jest funkcj wykładnicz:
gdzie: R
o
– stała zalena od rodzaju półprzewodnika i jego rozmiarów, T – temperatura [K], k
B
– stała
Boltzmana, E
A
– energia aktywacji.
3
Logarytmujc to równanie oraz przyjmujc skal (1/T) na osi ox oraz lnR na osi oy, powinnimy
otrzyma liniow zaleno oporu od temperatury, która pozwoli nam wyznaczy energi aktywacji
półprzewodnika przy pomocy regresji liniowej.
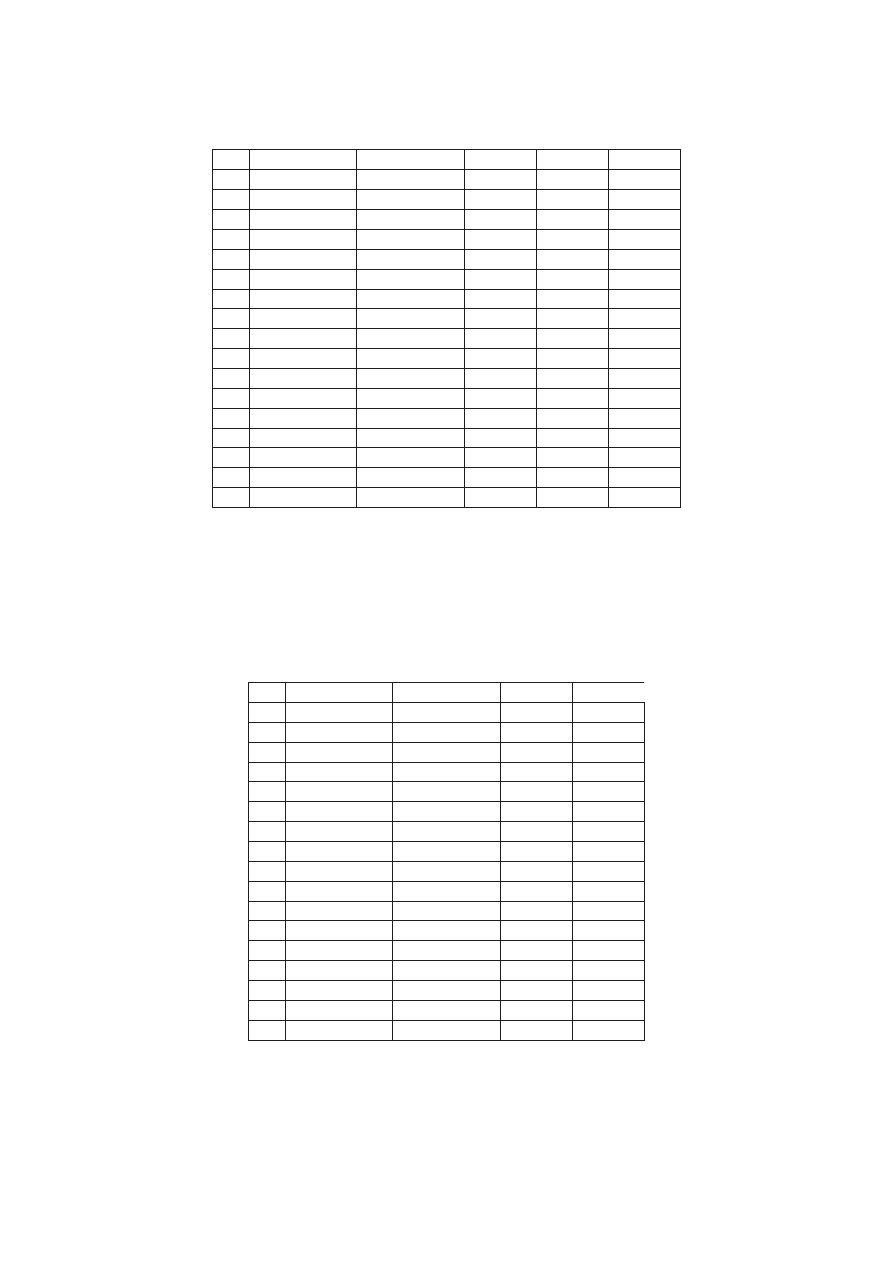
Układ, w którym zostały dokonane pomiary prezentuje poniszy rysunek:
Rys. 1. Schemat układu pomiarowego
Pomiary i obliczenia
Opór próbek mierzylimy kolejno dla temperatur z zakresu 30 ÷ 110
o
C zmieniajc j co 5
o
C.
Rozpoczynajc prac nie wiedzielimy, które próbki s metalami, a które półprzewodnikami.
Pomiary zostały przeprowadzone przy pomocy przyrzdów:
Sondy pomiarowej zawierajcej grzejnik,
regulator temperatury oraz badane próbki, a take miernika oporu – model METEX M-3850. Charakterystyki
w/w przyrzdów:
•
METEX M-3850 dla zakresów 400 ÷ 4 k , na których były robione pomiary, posiada
dokładno:
± 0,5% rdg + dgt, gdzie rdg - warto odczytana, dgt – rozdzielczo urzdzenia
•
dokładno czujnika temperatury, w który jest wyposaona Sonda:
± 1
o
C
Odczytanie ustabilizowanego oporu próbek nie było łatwym zadaniem, poniewa próbki nagrzewały si
szybko, chłodziły nieco wolniej. W wyniku cigłych zmian temperatury mierzony opór zmieniał si do
dynamicznie.
4
Wyniki pomiarów przedstawia Tabela 1:
Tabela 1. Pomiary oporu próbek wraz ze wzrostem temperatury
Lp
T [
o
C]
R
1
[k]
R
2
[]
R
3
[]
R
4
[]
1.
30
1,991
51,9
30,2
111,7
2.
35
2,024
47,8
27,3
113,4
3.
40
2,067
42,8
23,8
115,2
4.
45
2,126
37,9
20,4
117,1
5.
50
2,182
33,6
17,6
118,8
6.
55
2,236
29,4
15,3
120,6
7.
60
2,284
27,1
14,0
122,8
8.
65
2,348
23,8
11,9
124,1
9.
70
2,389
22,2
1,1
126,3
10.
75
2,443
19,8
9,6
127,9
11.
80
2,488
18,4
8,8
129,6
12.
85
2,545
16,7
7,8
131,2
13.
90
2,599
15,3
7,0
133,1
14.
95
2,639
14,2
6,5
134,7
15.
100
2,701
13,0
5,8
136,5
16.
105
2,764
11,8
5,1
138,3
17.
110
2,818
11,0
4,9
140,3
Na podstawie powyszych pomiarów moemy wysun pierwszy wniosek. W przypadku próbek nr 2 i
3 wraz ze wzrostem temperatury opór maleje. S to zatem półprzewodniki. Natomiast w próbkach nr 1 i 4 opór
ronie wraz z temperatur – czyli mamy do czynienia z metalami.
Dla próbek które s metalami rysujemy wykresy zalenoci oporu od temperatury (T-T
0
). Metod
regresji liniowej obliczamy parametry prostej. Dokładn analiz przeprowadzimy dla próbki nr 1. Dane do
wykresu dla próbki nr 1 przedstawia Tabela 2:
Tabela 2. Dane do sporządzenia wykresu zaleĪnoĞci dla próbki 1
Lp
(T-T
0
) [
o
C]
¨(T-T
0
) [
o
C]
R
1
(t) [] ¨R
1
(t) []
1.
0
1
1991,00
10,96
2.
5
1
2024,00
11,12
3.
10
1
2067,00
11,34
4.
15
1
2126,00
11,63
5.
20
1
2182,00
11,91
6.
25
1
2236,00
12,18
7.
30
1
2284,00
12,42
8.
35
1
2348,00
12,74
9.
40
1
2389,00
12,95
10.
45
1
2443,00
13,22
11.
50
1
2488,00
13,44
12.
55
1
2545,00
13,73
13.
60
1
2599,00
14,00
14.
65
1
2639,00
14,20
15.
70
1
2701,00
14,51
16.
75
1
2764,00
14,82
17.
80
1
2818,00
15,09
Warto R
1
(t) uzyskujemy z dokładnoci Multimetru METEX M-3850. Przykładowe obliczenia dla
pierwszego pomiaru dla próbki nr 1:
( )
Ω
≈
+
⋅
=
∆
96
,
10
1
1991
%
5
,
0
1
t
R
Dla pozostałych próbek obliczenia zostały wykonane analogicznie, majc na uwadze zakresy, na
których zostały wykonane pomiary.
5
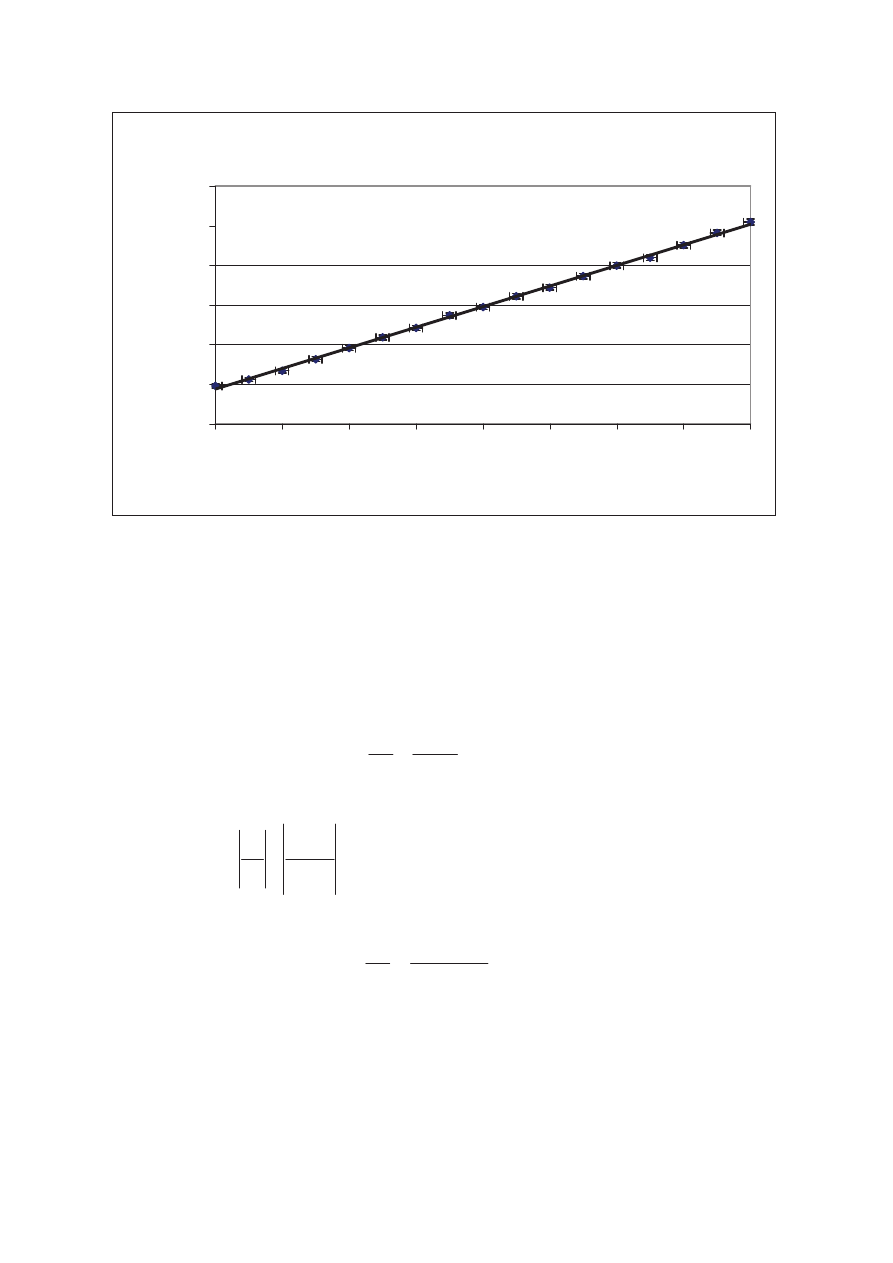
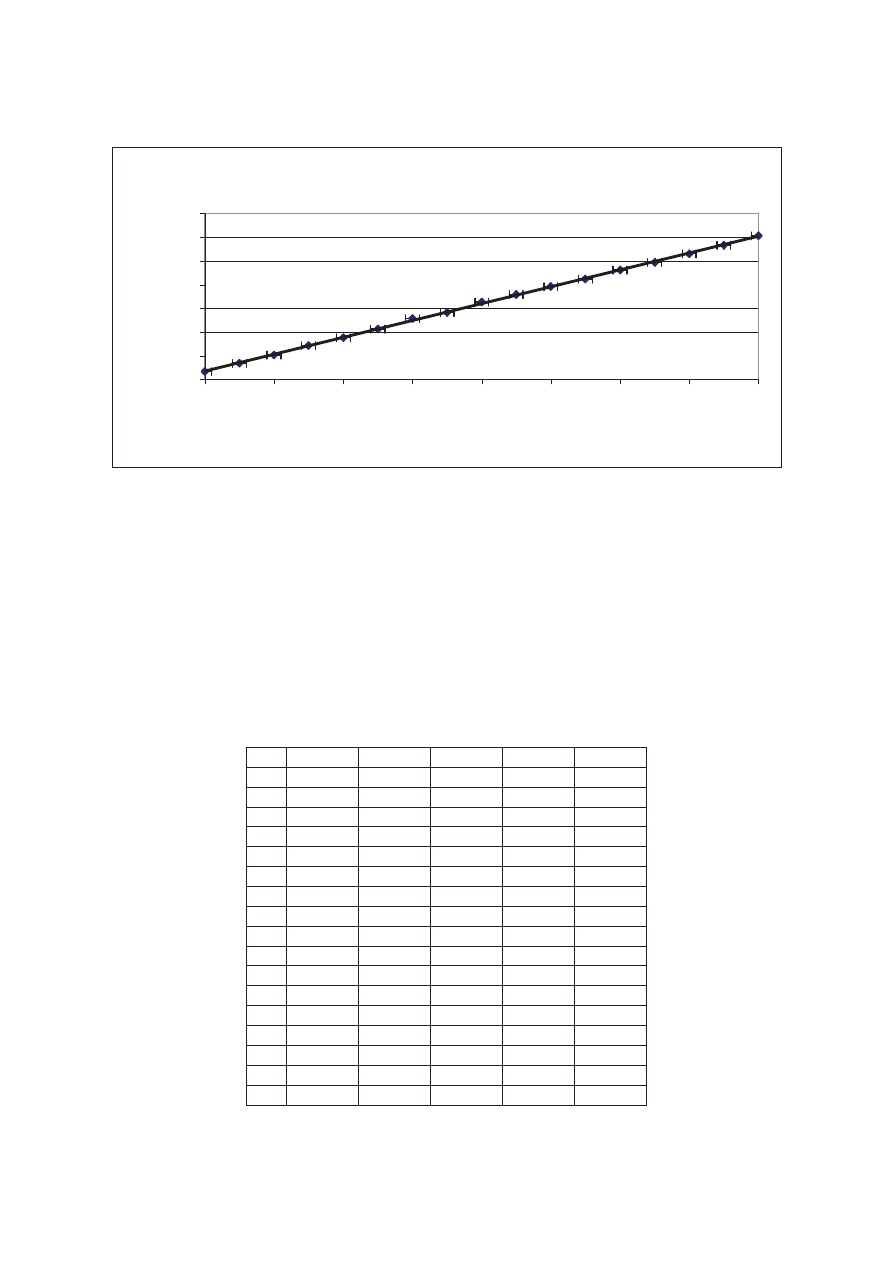
Wykres 3. ZaleĪnoĞü oporu od temperatury dla próbki nr 1
y = 10,423x + 1973,9
R
2
= 0,999
1800
2000
2200
2400
2600
2800
3000
0
10
20
30
40
50
60
70
80
Temperatura (T - T
o
) [
o
C]
O
p
ó
r
R
1
(t
)
[
?
]
Wykres 3 przedstawia zaleno oporu od temperatury dla próbki nr 1. Wyznaczona przy pomocy
arkusza kalkulacyjnego Excel oraz programu Regresja.pas na poziomie ufnoci 0,3096 linia trendu
charakteryzuje si równaniem:
R(t) = 10,423t + 1973,9
Współczynnik R
2
wynosi 0.999, co oznacza, e zaprezentowana zaleno jest idealnie liniowa.
Potwierdza to nasze wczeniejsze przypuszczenia i obserwacje, e pomiar dotyczył przewodnika metalowego.
Program Regresja.pas wyznaczył nam dodatkowo niepewnoci współczynników tej prostej. Wynosz one
odpowiednio a = 0,007784 oraz b = 3,651.
Kolejnym krokiem naszych działa jest obliczenie temperaturowego współczynnika metalu .
1
0052
,
0
1991
423
,
10
−
=
=
=
K
o
R
a
α
Warto niepewnoci temperaturowego współczynnika oporu metalu wynosi:
1
0000327
,
0
2
1991
/
96
,
10
*
423
,
10
1991
/
00774
,
0
2
0
0
0
−
≈
+
=
∆
⋅
+
∆
=
∆
K
R
R
a
R
a
α
Błd wzgldny okrelenia temperaturowego współczynnika oporu metalu wynosi:
0,63%
0,0052
0,0000327
=
=
=
6
Dla próbki nr 4 wykonano obliczenia analogicznie. Wyniki zostały zaprezentowane poniej:
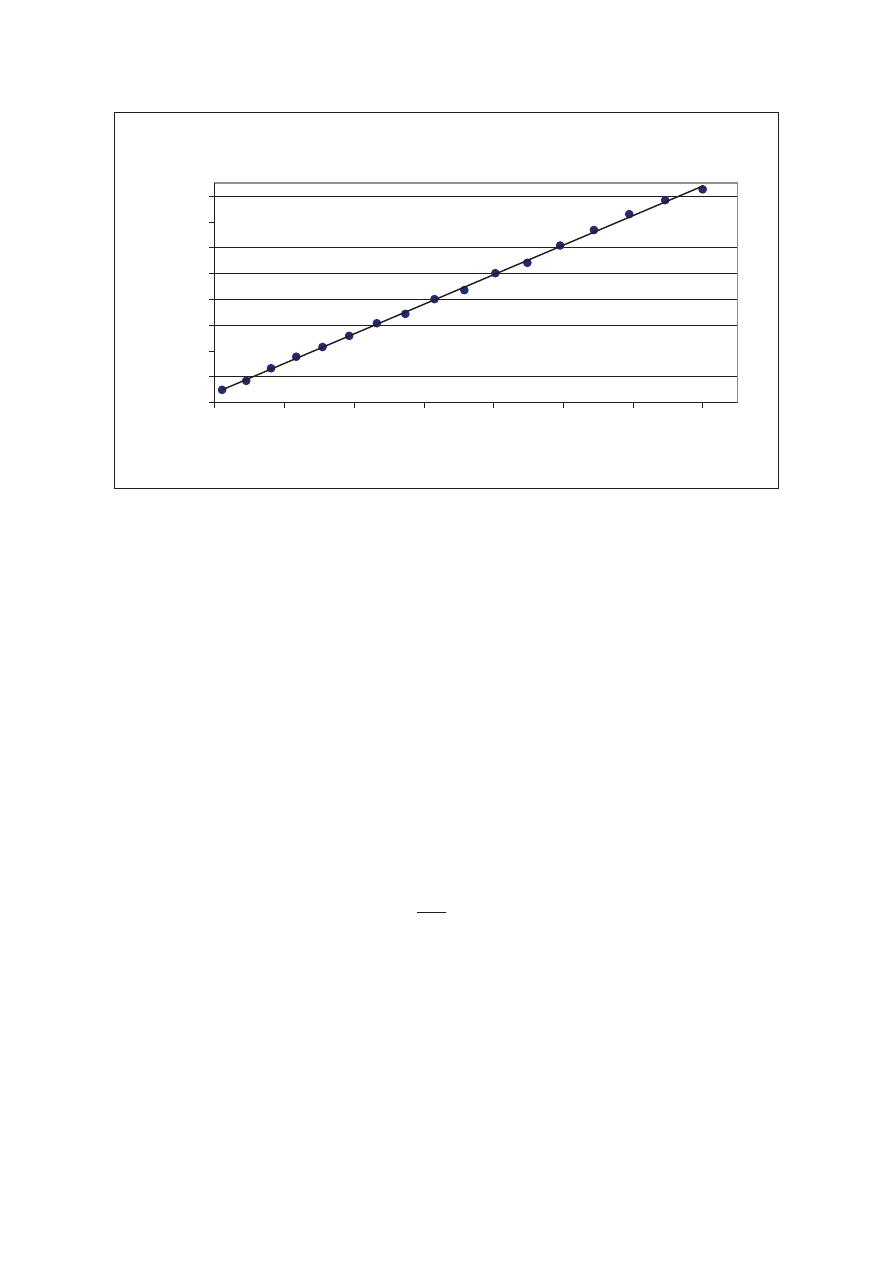
Wykres 4. ZaleĪnoĞü oporu od temperatury dla próbki nr 4
y = 0,3555x + 111,75
R
2
= 0,999
110,0
115,0
120,0
125,0
130,0
135,0
140,0
145,0
0
10
20
30
40
50
60
70
80
Temperatura (T - T
o
) [
o
C]
O
p
ó
r
R
4
(t
)
[?
]
R(t) = 0,3555t + 111,75
R
2
= 0,999
a = 0,001632
b = 0,07656
= 0,032 K
-1
= 0,000033373 K
-1
= 1%
Nastpnie przeszlimy do analizy zachowa półprzewodników. Dokładn analiz przeprowadzimy dla
próbki nr 2. Ponownie przystpujemy do wyznaczenia prostej regresji liniowej, tym razem rysujc wykres
zalenoci lnR od 1/T.
Dane potrzebne do sporzdzenia wykresu i oblicze przedstawia Tabela 3:
Tabela 3. Dane do sporządzenia wykresu zaleĪnoĞci dla próbki 2
Lp
T[
o
C]
T [K]
1/T [1/K]
R
2
[]
LnR
2
1.
30
303
0,00330
51,9
3,949
2.
35
308
0,00325
47,8
3,867
3.
40
313
0,00319
42,8
3,757
4.
45
318
0,00314
37,9
3,635
5.
50
323
0,00310
33,6
3,515
6.
55
328
0,00305
29,4
3,381
7.
60
333
0,00300
27,1
3,300
8.
65
338
0,00296
23,8
3,170
9.
70
343
0,00292
22,2
3,100
10.
75
348
0,00287
19,8
2,986
11.
80
353
0,00283
18,4
2,912
12.
85
358
0,00279
16,7
2,815
13.
90
363
0,00275
15,3
2,728
14.
95
368
0,00272
14,2
2,653
15.
100
373
0,00268
13,0
2,565
16.
105
378
0,00265
11,8
2,468
17.
110
383
0,00261
11,0
2,398
7
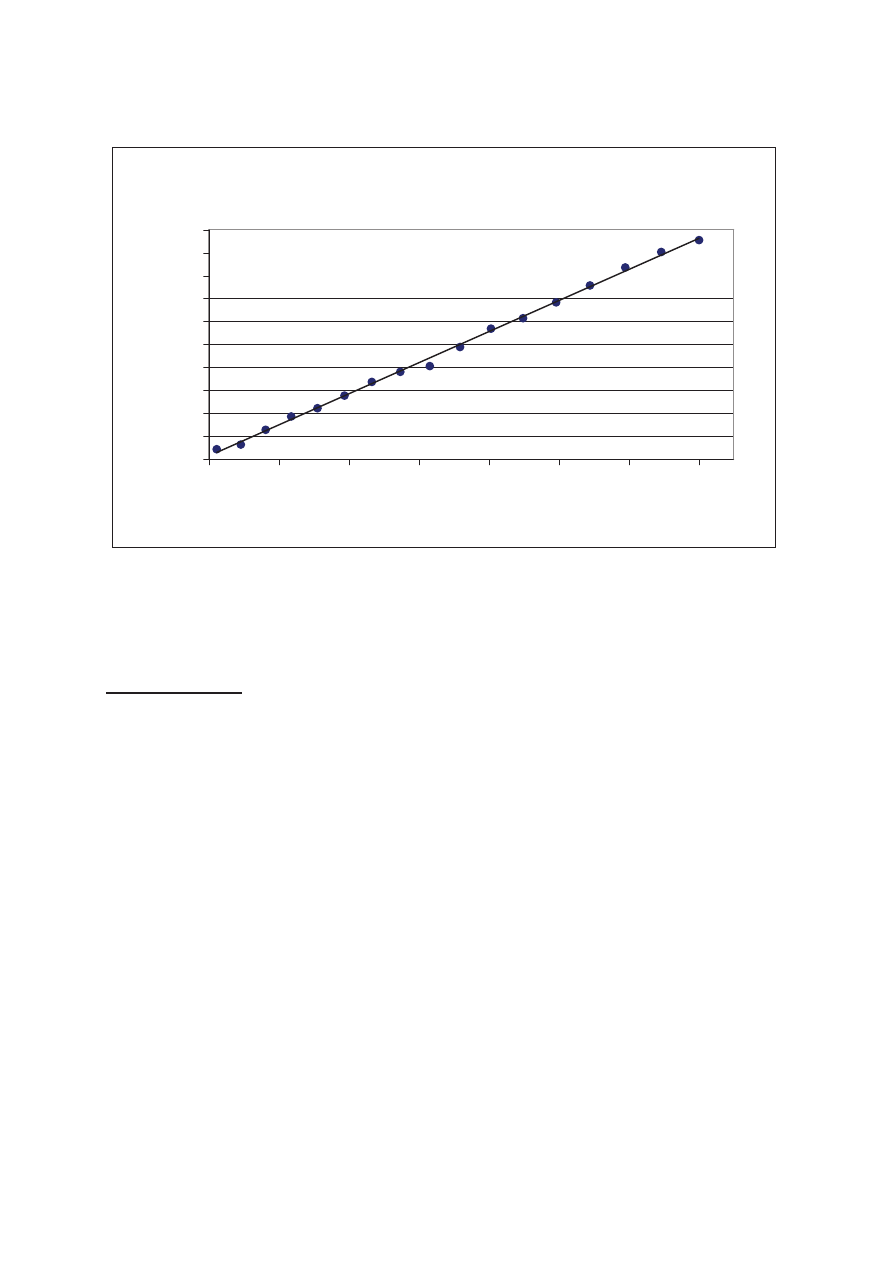
Wykres 5. ZaleĪnoĞü temperatury od oporu dla próbki nr 2
y = 2289,5x - 3,5799
R
2
= 0,999
2,30
2,50
2,70
2,90
3,10
3,30
3,50
3,70
3,90
0,0026
0,0027
0,0028
0,0029
0,0030
0,0031
0,0032
0,0033
Temperatura 1/T [1/K]
O
p
ó
r
ln
R
2
[?
]
Wykres przedstawia zaleno oporu od temperatury dla półprzewodnika. Wyznaczona przy pomocy
arkusza kalkulacyjnego Excel oraz programu Regresja.pas na poziomie ufnoci 0,02088 linia trendu
charakteryzuje si równaniem:
lnR(1/T) = 2289,5 1/T – 3,5799
Współczynnik R
2
wynosi 0,999, co oznacza, e zaprezentowana zaleno jest niemal idealnie liniowa.
Pozwoli nam to stosunkowo dokładnie obliczy warto energii aktywacji. Program Regresja.pas wyznaczył
nam dodatkowo niepewnoci oblicze współczynników tej prostej. Wynosz one odpowiednio:
a = 37,6 b = 0,06022
Obliczamy warto energii aktywacji (k
B
= 1,38 * 10
-23
J/K – stała Boltzmanna)
E
A
= k
B
* a = 1,38 * 10
-23
J/K * 2289,5 K = 3,1595 * 10
-20
J
Dzielimy przez warto ładunku elektronu e = 1,602 * 10
-19
C
E
A
= 3,1595 * 10
-20
J / 1,602 * 10
-19
C = 0,1972 eV.
Niepewno wartoci energii aktywacji wynosi:
E
A
= |k
B
| * a = 5,1888 * 10
-22
J = 3,2390 * 10
-3
eV
Błd wzgldny okrelenia wartoci energii aktywacji wynosi:
%
64
,
1
=
∆
=
A
A
E
E
ε
8
Dla próbki nr 3 wykonano obliczenia analogicznie. Wyniki zostały zaprezentowane poniej:
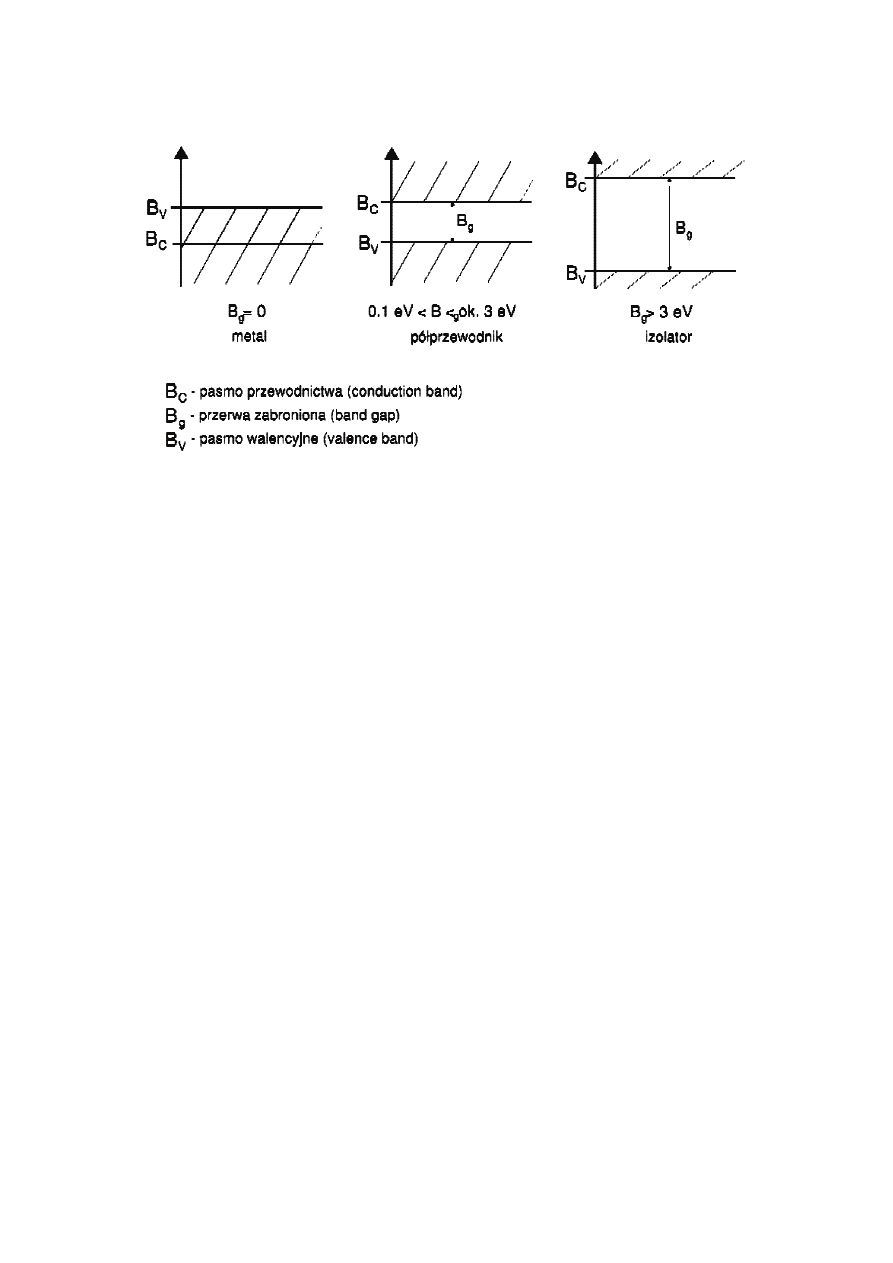
Wykres 6. ZaleĪnoĞü oporu od temperatury próbki nr 3
y = 2707,4x - 5,5099
R
2
= 0,998
1,50
1,70
1,90
2,10
2,30
2,50
2,70
2,90
3,10
3,30
3,50
0,0026 0,0027 0,0028 0,0029 0,0030 0,0031 0,0032 0,0033
Temperatura 1/T [1/K]
O
p
ó
r
ln
R
3
[
?
]
lnR(1/T) = 2707,4 1/T – 5,5099
a = 37,02 b = 0,0187
E
A
= 3,7362 * 10
-20
J = 0,2332 eV
E
A
= 5,1088 * 10
-22
J = 3,2 * 10
-3
eV
= 1,37%
Wnioski koĔcowe
Pomiary przeprowadzilimy na 4 rónych próbkach, nie wiedzc czy s to metale, czy te
półprzewodniki. Zanotowane w Tabeli 1 wyniki oraz znajomo zalenoci przedstawionej na wykresach we
wprowadzeniu teoretycznym do wiczenia pozwoliły wywnioskowa, e próbki nr 2 i 3 s półprzewodnikami,
natomiast próbki nr 1 i 4 to metale. Po przeprowadzonych obliczeniach utwierdzamy si tylko w rozpoznaniu
próbek. Dodatkowo potwierdzilimy na wykresach, e zarówno dla przewodników jak i półprzewodników
zaleno oporu od temperatury, przy odpowiednich oznaczeniach osi, mona przedstawi liniowo.
Z danych dla próbek, które jak ustalilimy s metalami, wyznaczylimy temperaturowe współczynnik
oporu, wyniosły one odpowiednio:
•
dla próbki nr 1:
= 0,0052 ± 0,000033 K
-1
•
dla próbki nr 4:
= 0,0032 ± 0,000034 K
-1
Korzystajc z tablic fizycznych moemy spróbowa okreli rodzaj metalu, z których były wykonane
próbki. I tak dla próbki nr 1 temperaturowy współczynnik oporu pokrywa si z tablicowym współczynnikiem
oporu temperaturowego dla wolframu, a uzyskana przez nas warto dla próbki nr 4 ley najbliej stali, której
współczynnik oporu wynosi 3,3 * 10
-3
K
-1
. Naley tu zaznaczy, e współczynniki z tablic uwzgldniały
przyrostu oporu w zakresie od 0
o
C do 100
o
C. A górn granic naszych pomiarów było 110
o
C.
Dla półprzewodników energia aktywacji wyniosła odpowiednio:
•
dla próbki nr 2:
E
A
= 0,1972 ± 3,239 * 10
-3
eV
•
dla próbki nr 3:
E
A
= 0,2332 ± 3,200 * 10
-3
eV
9
Mieci si to w przedziale pasma wzbronionego dla półprzewodników, wic przypuszczamy, e
oszacowalimy je poprawnie:
Rys. 2. Porównanie układu pasm
(ħródło: http://pl.wikipedia.org/wiki/Półprzewodniki)
S to wartoci na tyle niedue, e mona „w ciemno” powiedzie, e s to półprzewodniki
domieszkowe. Porównujc otrzymane wyniki z tablicami, moemy spróbowa zidentyfikowa te substancje.
Najbliszym dla próbki nr 2 wynikiem odczytanym z tablic jest przerwa energetyczna równa 0,2 eV i warto ta
naley do tellurku antymonu (Sb
2
Te
3
). Natomiast otrzymany wynik dla próbki nr 3 ley najbliej tablicowej
wartoci przerwy energetycznej selenka ołowiu (PbSe).
Błdy i niepewnoci naszych pomiarów wynikaj głównie z trudnoci z ustabilizowaniem temperatury
próbek, a take z dokładnoci odczytów z termometru, którego niepewno przyjlimy ± 1
o
C, mimo, e
dokładno podziałki wynosiła 0,1
o
C. Wartoci błdów pomiarowych oporu były stosunkowo niewielkie (<1%).