WYDZIAŁ ETI PG

Katedra Systemów Elektroniki Morskiej

Laboratorium Obwodów i Sygnałów

LINIA TRANSMISYJNA

Opracował: Witold Szkudliński

na podstawie materiałów Andrzeja Leśnickiego

Gdańsk 2011

© Witold Szkudliński: L

INIA TRANSMISYJNA

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_TLine_2011.pdf Modyfikacje 2011: M. Makowski, C. Stefański

Laboratorium OiS

(sieciowe)

KSEM/626Ea

Wersja 2011

-2-

1.1.

Wstęp

Linia transmisyjna jest z punktu widzenia teorii obwodów czwórnikiem symetrycznym

o stałych rozłożonych. Obwód jest obwodem o stałych rozłożonych, jeżeli jego wymiary są porów-
nywalne z długością fali (lub większe). W praktyce porównuje się wymiar ݈ (długość np. linii) z war-
tością 0.1ߣ, gdzie ߣ jest długością fali. Należy rozumieć to w ten sposób, że jeśli rozmiary ukła-
du/elementu są dostatecznie duże względem

భ

భబ

długości fali to ten układ/element jest ukła-

dem/elementem o stałych rozłożonych. Wynika z tego, z drugiej strony, że każdy układ dla dosta-
tecznie dużej częstotliwości pobudzenia (czyli dostatecznie małej długości fali) staje się układem
o stałych rozłożonych. Na przykład w komputerze pracującym z częstotliwością taktowania 3 GHz
długość fali wynosi ߣ= 10 cm i przyrząd o długości 1 cm jest elementem o stałych rozłożonych.
Z kolei w akustyce na częstotliwości 1 kHz długość fali wynosi ߣ= 34 cm i pudło o długości ݈=

ߣ= 17

cm jest rezonatorem półfalowym. Te dwa przykłady pokazują jak często mamy do czynienia
w praktyce z obwodami o stałych rozłożonych.

W dotychczasowym kursie przedmiotu Obwody i Sygnały (sem.2) przyjmowaliśmy zazwyczaj

(przeciwstawne) założenie o układzie o stałych skupionych czyli takim, którego rozmiary są dosta-
tecznie małe względem

భ

భబ

długości fali (inaczej rozmiary układu są na tyle małe, że w rozwiązaniu

nie występuje zależność od zmiennych przestrzennych (ݔ, ݕ, ݖ) a jedynie od czasu lub częstotliwo-
ści).

Same linie transmisyjne służą do przesyłania, opóźniania i kształtowania sygnałów elektrycz-

nych oraz, rzadziej, do realizacji za pomocą takiego elementu indukcyjności, pojemności, trans-
formatora impedancji lub rezonatora, czyli obwodu rezonansowego o znacznej dobroci.

1.2.

Linia długa

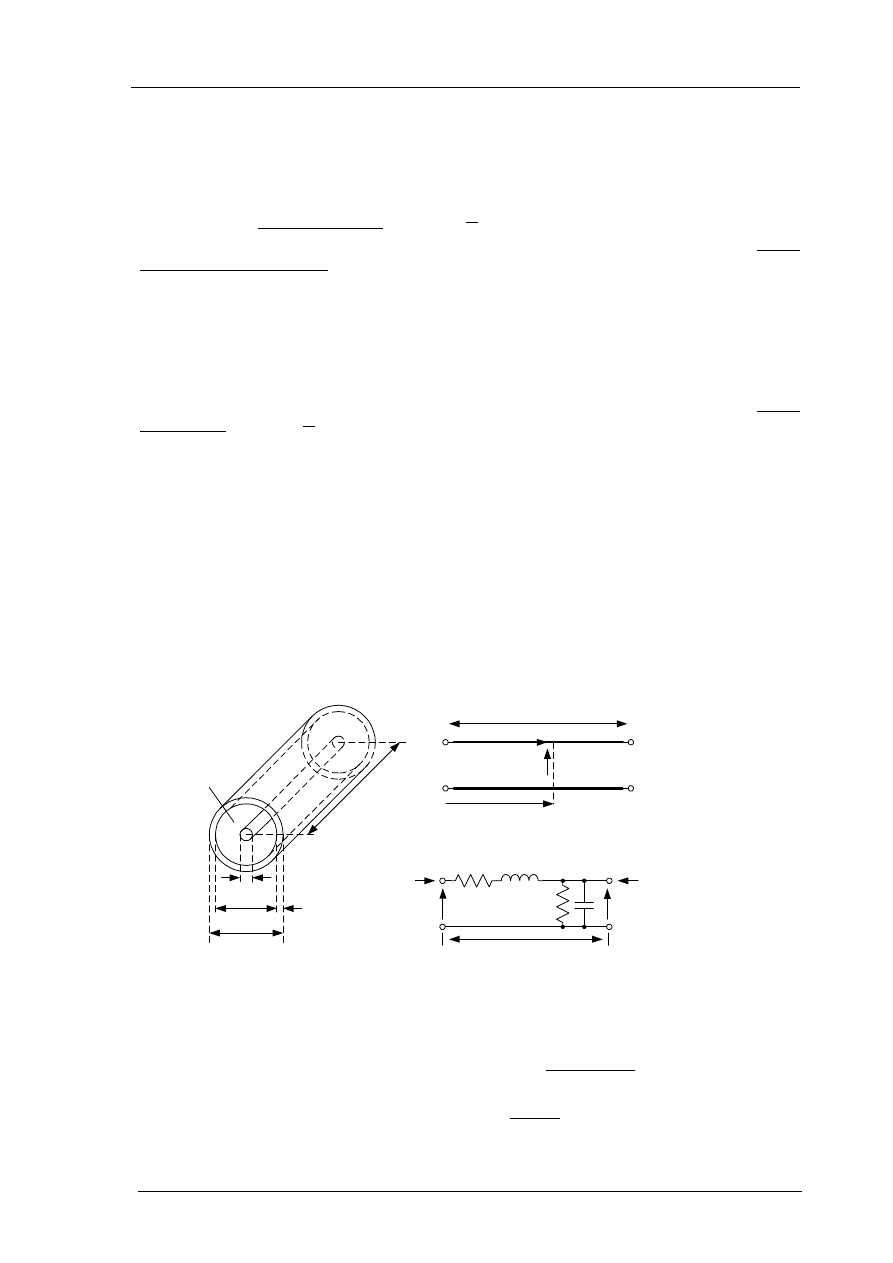
Linia długa (linia transmisyjna) to element, którego długość ݈ jest porównywalna z długo-

ścią fali (rys. 1.1). Linia taka jest obwodem o stałych rozłożonych i w równaniach elektrycznych
dla prądów i napięć obwodu wystąpi dodatkowa zmienna będąca współrzędną zmian wzdłuż
linii. Linia długa charakteryzuje się określoną rezystancją szeregową strat , indukcyjnością ,
konduktancją równoległą strat i pojemnością na jednostkę długości . Zakłada się, że linia dłu-
ga jest jednorodna, tj. parametry jednostkowe , ܮ, ܩ, ܥ są stałe wzdłuż linii (nie zależą od ݔ).

Rys. 1.1. Linia współosiowa: a) konstrukcja linii; b) obwód elektryczny odcinka linii długiej;

c) schemat zastępczy nieskończenie krótkiego odcinka linii

Wyprowadzimy teraz równania opisujące linię długą. Dla nieskończenie krótkiego odcinka

∆x

(rys. 1.1c) równania wynikające z I i II prawa Kirchhoffa mają następującą postać

t

t

x

x

u

x

C

t

x

x

u

x

G

t

x

i

t

x

x

i

∂

∂

)

,

(

)

,

(

)

,

(

)

,

(

∆

∆

∆

∆

∆

+

−

+

−

=

−

+

(1.1)

t

t

x

i

x

L

t

x

i

x

R

t

x

u

t

x

x

u

∂

∂

)

,

(

)

,

(

)

,

(

)

,

(

∆

∆

∆

−

−

=

−

+

1

2r

2

2r

3

2r

g

r

ε

ε

ε

0

=

l

a)

b)

c)

(

)

λ

1

,

0

>

l

)

,

(

t

x

i

)

,

(

t

x

u

l

x

≤

≤

0

1

1

′

2

2

′

)

,

(

t

x

i

)

,

(

t

x

x

i

∆

+

)

,

(

t

x

x

u

∆

+

)

,

(

t

x

u

x

x

∆

+

x

0

→

∆

x

L

R

G

C

© Witold Szkudliński: L

INIA TRANSMISYJNA

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_TLine_2011.pdf Modyfikacje 2011: M. Makowski, C. Stefański

Laboratorium OiS

(sieciowe)

KSEM/626Ea

Wersja 2011

-3-

Dzieląc obustronnie równania (1.1) przez zmienną

x

∆

, otrzymuje się w granicy przy

0

→

∆x

równania różniczkowe cząstkowe linii długiej

t

t

x

i

L

t

x

i

R

x

t

x

u

t

t

x

u

C

t

x

u

G

x

t

x

i

∂

∂

∂

∂

∂

∂

∂

∂

)

,

(

)

,

(

)

,

(

)

,

(

)

,

(

)

,

(

−

−

=

−

−

=

(1.2)

Metoda rozwiązywania równań postaci (1.2) zależy od postaci pobudzenia . W przypadku, gdy
pobudzenie jest sinusoidalnym napięciem

t

U

t

x

u

t

u

m

x

ω

cos

)

,

(

)

(

1

0

1

=

=

=

(1.3)

to w stanie ustalonym napięcie w przekroju położonym w odległości x od początku linii o nieskoń-
czonej długości

)

cos(

)

,

(

1

x

t

U

t

x

u

x

m

β

ω

α

−

≅

−

e

(1.4)

gdzie:

• stała

λ

π

β

2

=

ma sens przesunięcia fazowego na jednostkę długości w

]

/m

[

lub

]

rad/m

[

°

,

• stała

α

to tłumienie sinusoidy w [Neperach/m].

W praktyce często tłumienie w linii podaje się nie w [Neperach/m] tylko w [dB/m], gdzie

α

α

α

α

α

⋅

≅

⋅

=

=

=

−

686

.

8

)

log

20

(

log

20

log

20

1

1

]

/

[

e

e

e

U

U

m

m

m

dB

(1.5a)

α

α

e

=

]

/

/

[

m

V

V

(1.5b)

]

/

/

[

]

/

[

log

20

m

V

V

m

dB

α

α

=

(1.5c)

W przypadku pobudzenia sinusoidalnym napięciem postaci (1.3) prąd w linii w stanie ustalonym
jest również sinusoidalny , przy czym iloraz amplitud zespolonych dla sinusoidalnych napięcia
i prądu będziemy, jak zwykle, nazywali impedancją

)

(

)

(

)

(

x

I

x

U

x

Z

=

(1.6)

Traktując linię o skończonej długości l jako czwórnik możemy wprowadzić pojęcie impedancji

charakterystycznej Z

c

czwórnika, czyli impedancji, która włączona jako obciążenie na wyjście

linii daje impedancję wejściową równą również Z

c.

c

Z

Z

in

Z

Z

c

=

=

2

(1.7)

W szczególności impedancja wejściowa jednorodnej nieskończenie długiej linii transmisyjnej jest
zawsze równa Z

c

.

Wspomniane powyżej parametry linii zależą w praktyce od częstotliwości pobudzenia sinusoidal-
nego w sposób przedstawiony na rys.1.2

Rys.1.2. Zmiany parametrów linii długiej w funkcji częstotliwości

0

C

L

R

=

0

G

R

ω

( )

ω

c

Z















+

=

0

0

0

2

1

GR

R

R

α

RG

( )

ω

α

0

ω

0

ω

α

0

t

tg

=

α

( )

ω

β

LC

ω

β

=

a)

b)

c)

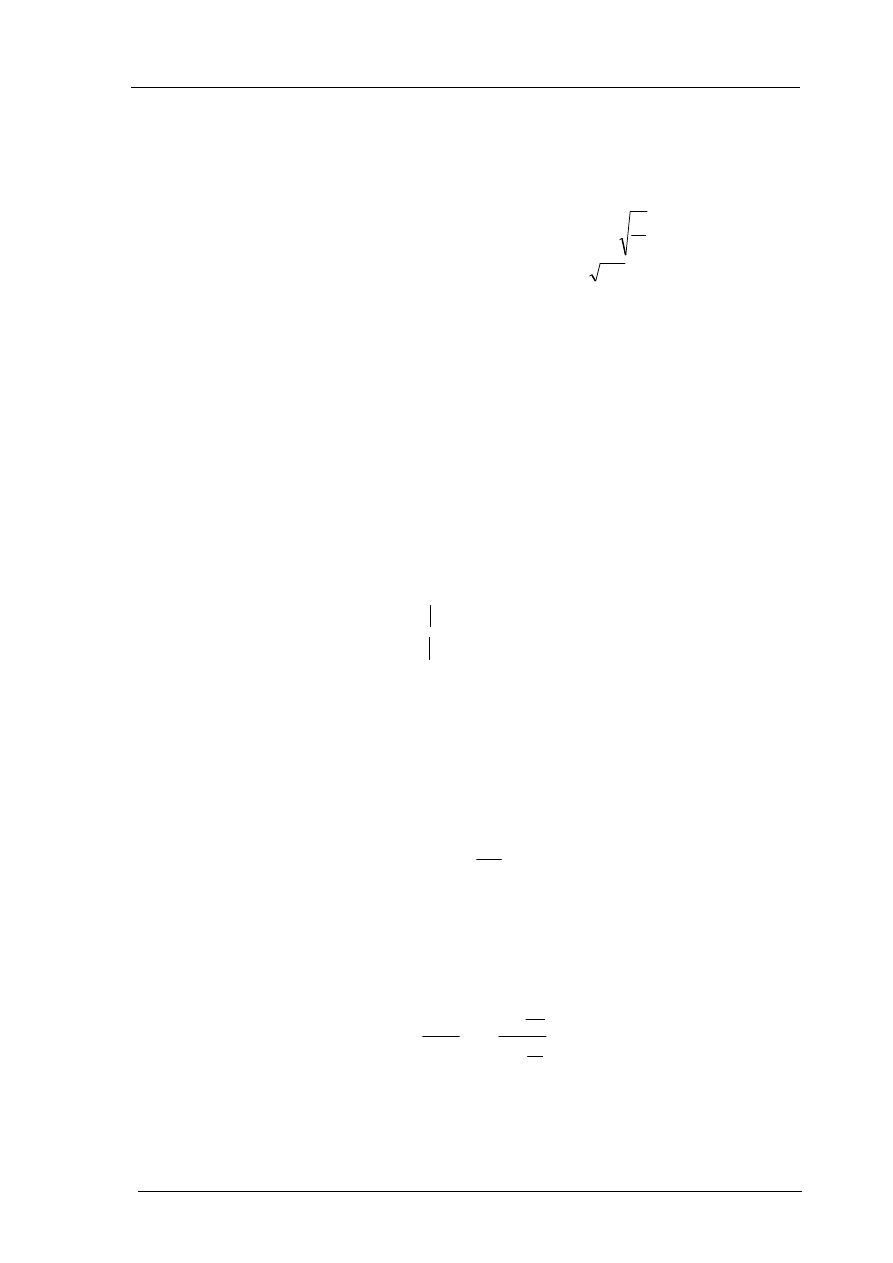
© Witold Szkudliński: L

INIA TRANSMISYJNA

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_TLine_2011.pdf Modyfikacje 2011: M. Makowski, C. Stefański

Laboratorium OiS

(sieciowe)

KSEM/626Ea

Wersja 2011

-4-

Widzimy, że począwszy od pewnej, dostatecznie dużej częstotliwości, moduł impedancji charakte-
rystycznej jest w przybliżeniu niezależny od częstotliwości i dodajmy, że impedancja ta jest rze-
czywista. Przesunięcie (opóźnienie) fazowe

β

począwszy od pewnej częstotliwości w przybliżeniu

liniowo zmienia się z częstotliwością.

Dla ݂ > ݂

௠௜௡

:

impedancja charakterystyczna

]

[

0

Ω

C

L

R

Z

c

=

≅

(1.8)

opóźnienie jednostkowe

]

[

0

s/m

LC

t

x

=

stała fazowa

]

[rad/m

ox

t

ω

β

≅

opóźnienie w całej linii

=

o

t

݈

]

[

0

s

x

t

⋅

Bardzo ważną właściwością jest liniowość przesunięcia fazowego

β

, gdyż w takim przypadku

opóźnienie czasowe ݐ

௢

(opóźnienie na osi czasu to pochodna charakterystyki fazowej) każdej skła-

dowej widmowej przenoszonego przez linię sygnału jest stałe. Gdy opóźnienie oraz tłumienie są
stałe to kształt np. impulsu na wyjściu jest taki sam jak kształt impulsu na wejściu linii (linia nie-
zniekształcająca).

Ogólnie, linia nie zawsze, a w pewnych przypadkach nigdy, nie jest obciążana impedancją

charakterystyczną. Za to często tłumienie w linii może być do pominięcia w pierwszym przybliże-
niu rozważań. W przypadku, gdy przesuwający się wzdłuż linii (wymiar ݔ) sygnał napotyka w prze-
kroju wyjściowym różną od charakterystycznej impedancję obciążenia ܼ

ଶ

, to powoduje to skoko-

wą zmianę relacji pomiędzy napięciem i prądem. Przyjęto taką zmianę ujmować w ten sposób, że
uważa się, iż (w stanie ustalonym) sinusoidy napięcia i prądu w skończonej i niedopasowanej (ܼ

ଶ

różne od ܼ

௖

) linii są reprezentowane przez amplitudy zespolone :

y

y

y

y

I

I

y

I

U

U

y

U

β

β

α

β

β

α

j

j

j

j

e

e

e

e

−

−

+

=

−

−

+

=

−

=

+

=

0

0

)

(

~

)

(

~

(1.9)

Powyższy zapis zakłada linię bezstratną (

ߙ = 0), co ma sens dla linii o dostatecznie małych

stratach.

W obydwu równaniach (1.9) pierwsza składowa to amplituda zespolona fali przesuwającej się

od źródła do obciążenia zaś druga składowa to amplituda zespolona fali powrotnej (przesuwającej
się od obciążenia do źródła). Ze względu na łatwe do określenia warunki brzegowe na końcu linii
dogodnie było wprowadzić nową zmienną ݕ = ݔ − ݈ , co oznacza, że początek linii to ݕ = −݈, zaś
na końcu ݕ = 0.

Dodatkowo, zgodnie z poprzednio przedstawionym rozumowaniem

+

+

=

I

U

Z

c

(1.10)

W przekroju końcowym linii może występować stan dopasowania ࢆ

૛

= ࢆ

ࢉ

i wtedy

0

0

=

=

−

−

I

U

(1.11)

czyli w linii dopasowanej nie występuje fala powrotna . W ogólnym przypadku impedancja w
przekroju wyjściowym (ݔ = ݈, ݕ = 0)

+

−

+

−

−

+

=

=

2

2

2

2

1

1

)

0

(

~

)

0

(

~

2

I

I

U

U

c

Z

I

U

Z

(1.12)

Jednocześnie w przekroju wejściowym (ݔ = 0, ݕ = −)

© Witold Szkudliński: L

INIA TRANSMISYJNA

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_TLine_2011.pdf Modyfikacje 2011: M. Makowski, C. Stefański

Laboratorium OiS

(sieciowe)

KSEM/626Ea

Wersja 2011

-5-

l

l

l

l

β

β

2

2

2

2

2

2

1

1

)

(

~

)

(

~

j

j

e

e

−

+

−

−

+

−

−

+

=

−

−

=

I

I

U

U

c

in

Z

I

U

Z

(1.13)

Wyrażenie (1.12) jest oczywiście słuszne także dla skrajności (

∞

=

=

2

2

,

0 Z

Z

).

1

1

0

2

2

2

2

2

2

2

2

2

2

+

=

=

⇒

∞

=

−

=

=

⇒

=

+

−

+

−

+

−

+

−

I

I

U

U

Z

I

I

U

U

Z

(1.14)

Iloraz zespolonej amplitudy fali padającej oraz fali odbitej nosi nazwę współczynnika odbicia

c

c

Z

Z

Z

Z

I

I

U

U

+

−

=

=

=

+

−

+

−

2

2

2

2

2

2

2

Γ

(1.15)

Po podstawieniu (1.15) do (1.13) otrzymuje się użyteczną postać wyrażenia na impedancję wej-
ściową linii bezstratnej

l

l

β

β

Γ

Γ

2

2

2

2

1

1

j

j

e

e

−

−

−

+

=

c

in

Z

Z

(1.16)

W przypadku linii zwartej na końcu (

Γ

2

=−1) impedancja wejściowa jest (czysto) urojona:

0

0

2

t

tg

Z

tg

Z

Z

c

c

Z

in

ω

β

j

j

=

⋅

=

=

l

(1.17)

Zatem dostatecznie krótka linia bezstratna zwarta na końcu wykazuje na wejściu impedancję

o tym samym charakterze co cewka indukcyjna. W praktyce dobroć takiej indukcyjności jest rzędu
100-500.

Dodajmy jeszcze, że analogicznie do definicji (1.15), można wprowadzić definicję współczyn-

nika odbicia na wejściu linii

c

c

Z

Z

Z

Z

+

−

=

1

1

1

Γ

(1.18)

gdzie ܼ

ଵ

to impedancja wewnętrzna źródła sygnału na wejściu.

1.3.

Przenoszenie impulsów przez linię transmisyjną

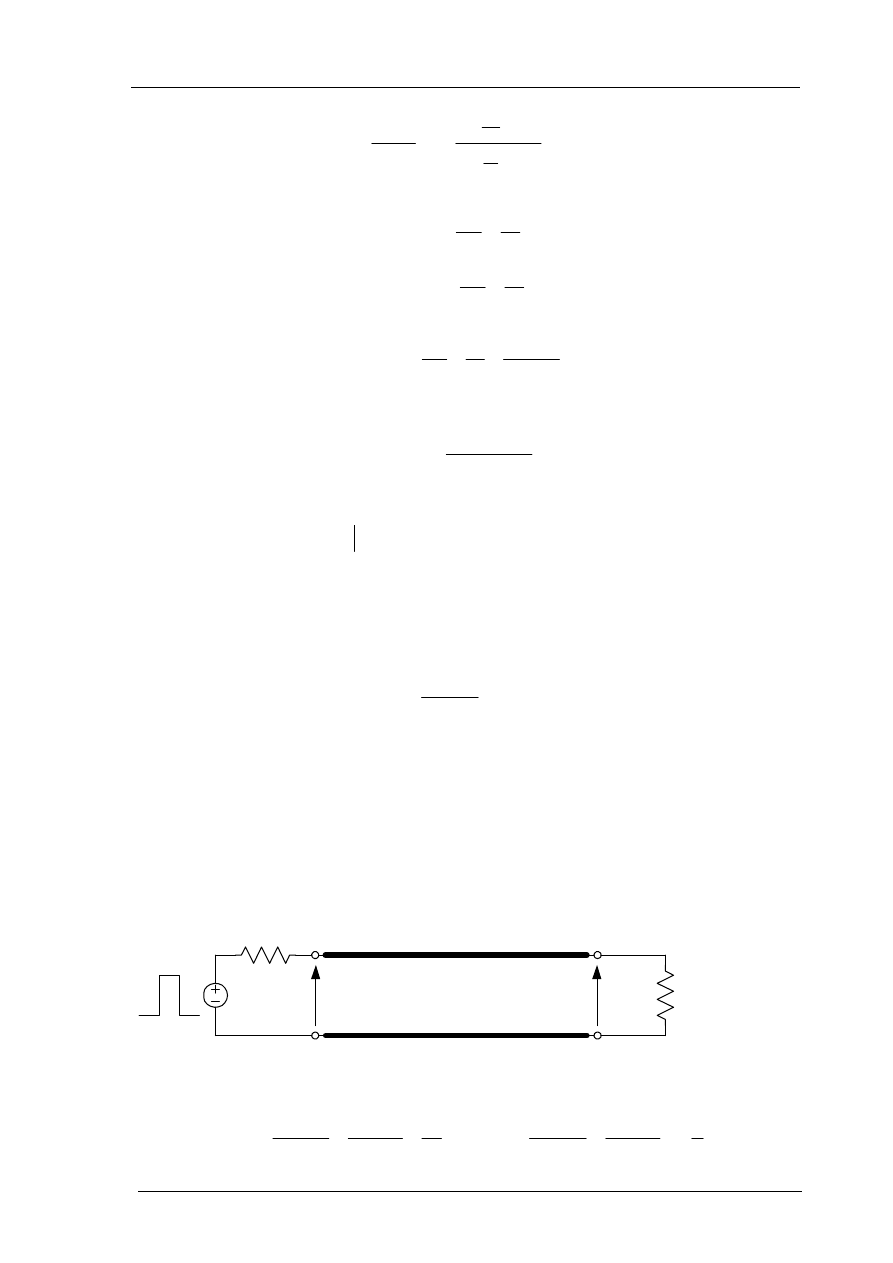
Weźmy pod uwagę przedstawioną na rys.1.3 linię transmisyjną przez którą jest transmitowa-

ny pojedynczy impuls o czasie trwania

τ, ze źródła o wewnętrznej rezystancji

R

1

do obciążenia o rezystancji R

2

. Linia nie jest dopasowana ani na wejściu ani na wyjściu i współ-

czynniki odbicia mają wartości (patrz rysunek)

Rys.1.3. Transmisja pojedynczego impulsu przez niedopasowaną linię transmisyjną

4

1

50

30

50

30

,

13

3

50

80

50

80

2

2

2

1

1

1

−

=

+

−

=

+

−

=

=

+

−

=

+

−

=

c

c

c

c

Z

Z

Z

Z

Z

Z

Z

Z

Γ

Γ

m

l

50

=

V

E

5

=

Ω

=

=

80

1

1

R

Z

Ω

=

=

30

2

2

R

Z

( )

t

u

1

( )

t

u

2

Ω

=

=

50

0

R

Z

c

(

)

dB

e

a

085

,

1

13

,

1

0

=

s

t

µ

25

,

0

0

=

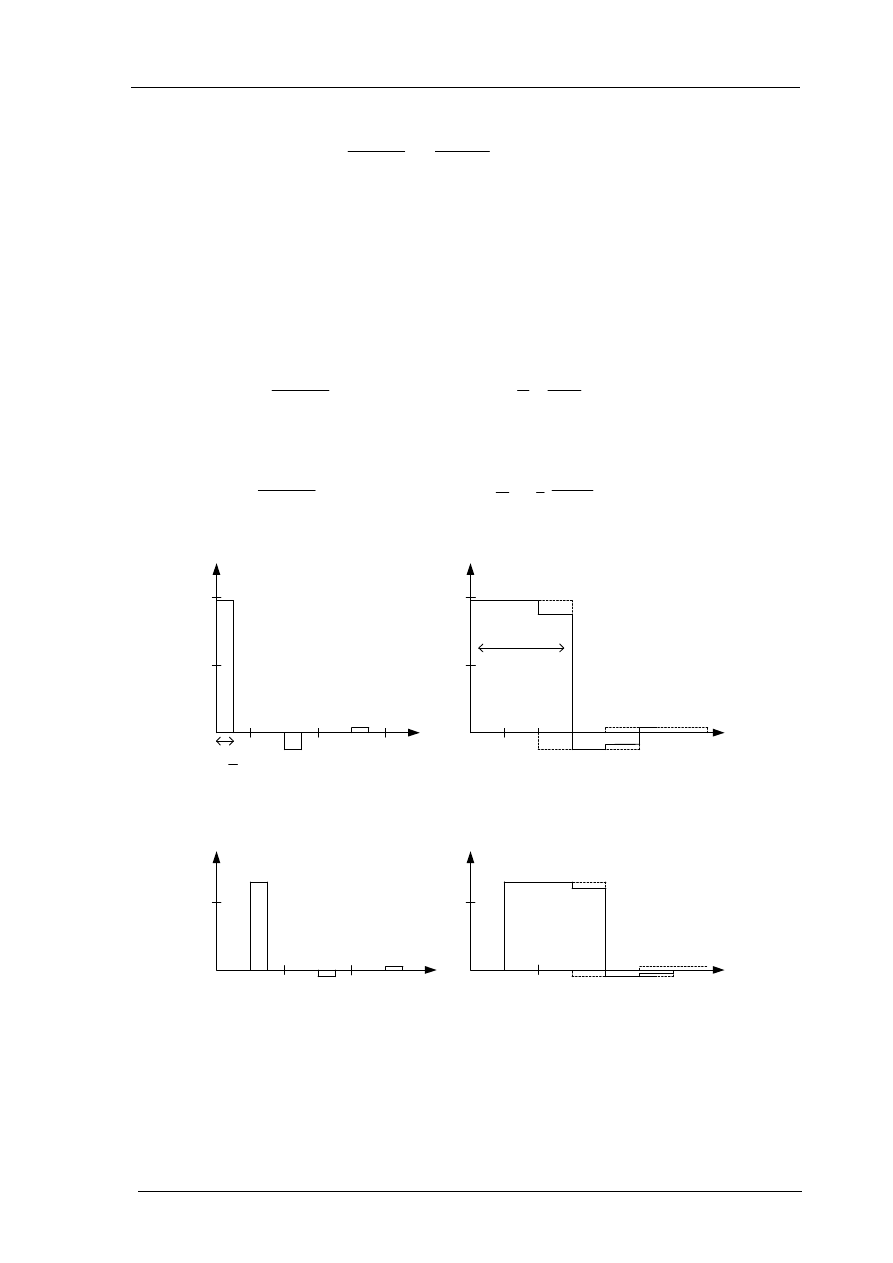
© Witold Szkudliński: L

INIA TRANSMISYJNA

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_TLine_2011.pdf Modyfikacje 2011: M. Makowski, C. Stefański

Laboratorium OiS

(sieciowe)

KSEM/626Ea

Wersja 2011

-6-

W chwili czasu

0

=

t

jest obserwowany na wejściu linii impuls prostokątny o amplitudzie

τ

<

<

=

+

=

+

=

t

Z

R

Z

E

t

u

c

c

0

923

.

1

50

80

50

5

)

(

1

)

0

(
1

V

Należy wyjaśnić dlaczego, niezgodnie ze wzorem (1.16), uznano, że impedancja wejściowa linii
z rys.1.3 jest równa Z

c

, przecież wzór (1.16) wskazuje, na liczbę zespoloną. Zauważmy jednak, że

rozważania prowadzące do wzoru (1.16) dotyczą linii w sinusoidalnym stanie ustalonym, a aktual-
ny przypadek dotyczy stanu przejściowego przy pobudzeniu impulsem: „ źródło sygnału począt-
kowo nie odróżnia linii o skończonej długości od linii nieskończenie długiej bo sygnał dotrze na
koniec (x=l) dopiero po czasie t

o

, a jeszcze drugie tyle zużyje na ewentualny powrót do wejścia”

Impuls dociera do niedopasowanego końca (współczynnik odbicia

Γ

2

) linii po czasie

s

t

µ

25

.

0

0

=

nieco tylko stłumiony (zakładamy, że wszystkie składniki widma tłumione są i opóźniane tak samo
więc kształt impulsu zostaje zachowany – patrz rozdział 1.2)

τ

Γ

+

<

<

=

⋅













−

⋅

=

+

+

=

−

−

0

0

2

1

0

)

1

(
2

,

276

.

1

13

.

1

1

4

1

1

923

.

1

)

1

(

)

(

t

t

t

Z

R

Z

E

t

t

u

o

a

c

c

V

e

W przypadku R

2

<Z

c

napięcie na wyjściu wskutek niedopasowania maleje (prąd rośnie).

Odbity częściowo od końca linii impuls znowu pojawia się opóźniony i stłumiony na wejściu linii

(

)

( )

(

)

τ

Γ

Γ

+

<

<

−

=

−

⋅

=

+

+

=

−

⋅

−

0

0

13

.

1

1

4

1

13

16

2

2

1

1

0

)

2

(
1

2

2

,

46

.

0

923

.

1

1

)

2

(

2

t

t

t

V

Z

R

Z

E

t

t

u

o

a

c

c

e

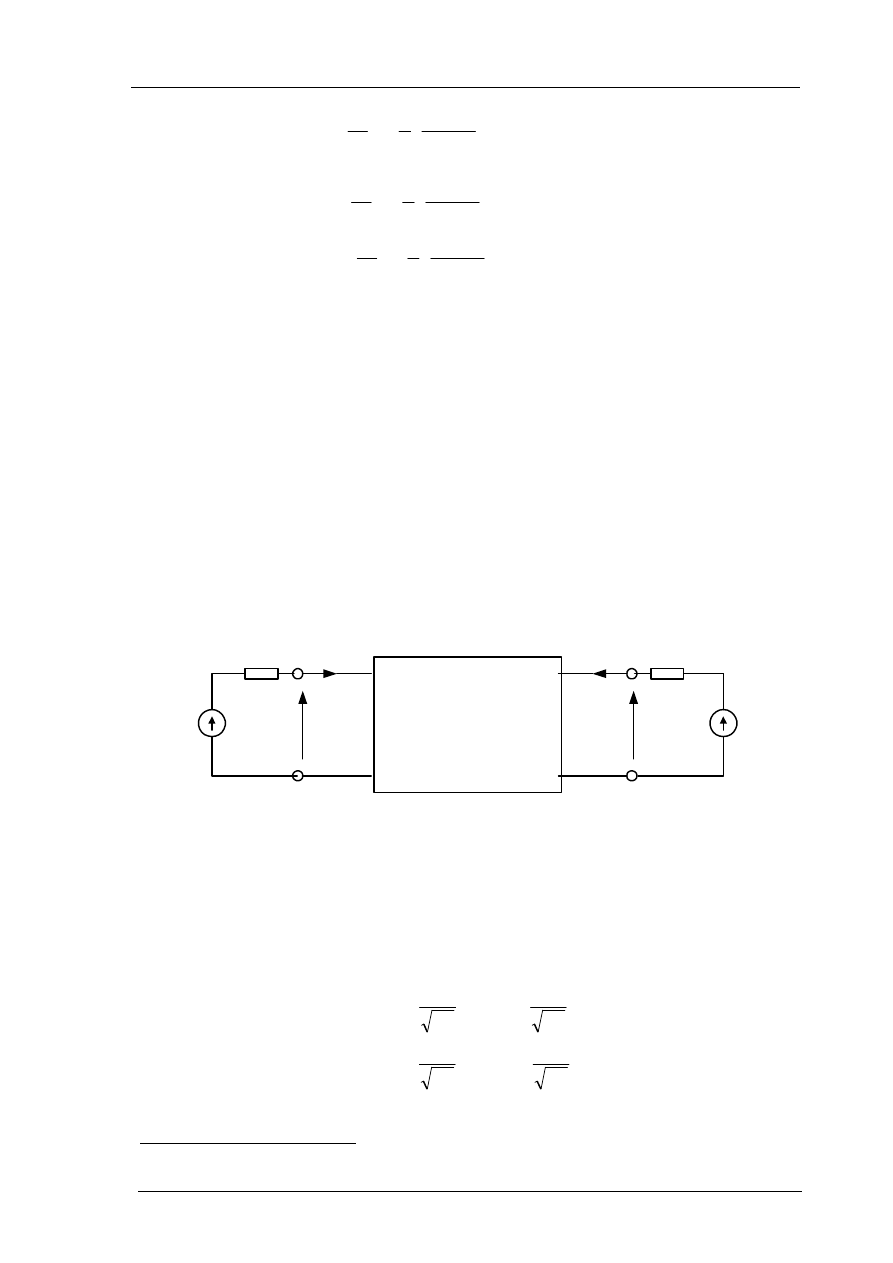
Rys. 1.4. Przebiegi napięciowe na wejściu i wyjściu linii :

a) dla impulsu (wąskiego) o czasie trwania

τ

=t

o

/2,

b) dla impulsu (szerokiego) o czasie trwania

τ

=3t

o

Kontynuując obliczenia w podobny sposób wyznacza się amplitudy kolejnych wędrujących po linii
wersji pierwotnego impulsu

0

2

1

t

=

τ

( )

(

)

0

3

2

3t

t

u

−

( )

(

)

0

5

2

5t

t

u

−

( )

(

)

0

1

2

t

t

u

−

( )

t

u

2

( )

(

)

0

3

2

3t

t

u

−

( )

(

)

0

5

2

5t

t

u

−

( )

(

)

0

1

2

t

t

u

−

( )

t

u

2

t

t

0

0

V

276

,

1

V

058

,

0

−

V

0026

,

0

V

1

V

1

0

t

0

3t

0

5t

0

t

0

3t

V

1

V

1

V

2

V

2

t

t

0

t

0

2t

0

4t

0

0

0

t

0

2t

( )

t

u

1

( )

t

u

1

V

923

,

1

V

46

,

0

−

V

021

,

0

( )

( )

t

u

0

1

( )

(

)

0

2

1

2t

t

u

−

( )

(

)

0

4

1

4t

t

u

−

( )

( )

t

u

0

1

( )

(

)

0

2

1

2t

t

u

−

( )

(

)

0

4

1

4t

t

u

−

a)

b)

0

3t

=

τ

© Witold Szkudliński: L

INIA TRANSMISYJNA

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_TLine_2011.pdf Modyfikacje 2011: M. Makowski, C. Stefański

Laboratorium OiS

(sieciowe)

KSEM/626Ea

Wersja 2011

-7-

τ

+

<

<

−

=













−













=

−

0

0

2

0

)

3

(
2

3

3

,

058

.

0

)

13

.

1

(

1

4

1

13

3

276

.

1

)

3

(

t

t

t

V

t

t

u

τ

+

<

<

=













−













−

=

−

0

0

2

0

)

4

(
1

4

4

,

021

.

0

)

13

.

1

(

1

4

1

13

3

46

,

0

)

4

(

t

t

t

V

t

t

u

τ

+

<

<

=













−













−

=

−

0

0

2

0

)

5

(
2

5

5

,

0026

.

0

)

13

.

1

(

1

4

1

13

3

058

.

0

)

5

(

t

t

t

V

t

t

u

Przedstawione powyżej przeliczenia efektu „wędrowania” impulsu wskutek niedopasowania obu
końców linii zostały graficznie przedstawione na rys.1.4

1.4.

Parametry rozproszenia

1

[S

i k

]

Parametry rozproszenia, to zestaw czterech parametrów czwórnika dość znacznie różnią-

cy się od parametrów typu [࢟], [ࢠ] czy [ࢎ] wiążących ze sobą prądy i napięcia dla obu czwórniko-
wych wrót. W definicjach tych ostatnich istotna rolę grają definicje oparte o zwarcie i rozwarcie
wrót. Jednak dla przebiegów sinusoidalnych o znacznych częstotliwościach realizacja zwarcia, czy
też rozwarcia jest związana ze znacznymi trudnościami lub wręcz niemożliwa. Definicje parame-
trów rozproszenia oparte są nie na zwarciu czy rozwarciu, a na obciążeniu wrót czwórnika re-
zystancją, która może w znaczącej mierze poprawiać warunki stabilności systemu.
Weźmy pod uwagę czwórnik przedstawiony na rys.1.5. Może to być obiekt o stałych rozłożonych
np. linia transmisyjna, ale może być również tranzystorowy wzmacniacz o dostatecznie małych
rozmiarach na to, aby potraktować go jako obiekt o stałych skupionych. Rezystancja R

0

, to w tym

przypadku tzw. rezystancja odniesienia .

1

U

2

U

1

1

b

a

⇐

⇒

⇒

⇐

2

2

b

a

1

I

2

I

0

R

0

R

1

E

2

E

[ ]

k

i

s

Rys.1.5. Wielkości związane z definicjami parametrów rozproszenia

]

[

k

i

s

Oprócz prądów i napięć mamy wielkości, które nazwiemy napięciową falą padającą (

2

1

,a

a

)

oraz napięciowa falą odbitą, czy też rozproszoną (

)

,

2

1

b

b

. Równania czwórnikowe z parametrami

rozproszenia mają postać:

2

22

1

21

2

2

12

1

11

1

a

s

a

s

b

a

s

a

s

b

+

=

+

=

(1.19)

gdzie wielkości falowe

(

)

2

1

2

1

,

,

,

b

b

a

a

zdefiniujemy jako

0

2

2

0

1

1

0

2

2

0

1

1

,

,

R

U

b

R

U

b

R

U

a

R

U

a

−

−

+

+

=

=

=

=

(1.20)

1

rozdział o charakterze poszerzającym (jego tematyka może w pewnych latach być pomijana w realizacji ćwiczenia)

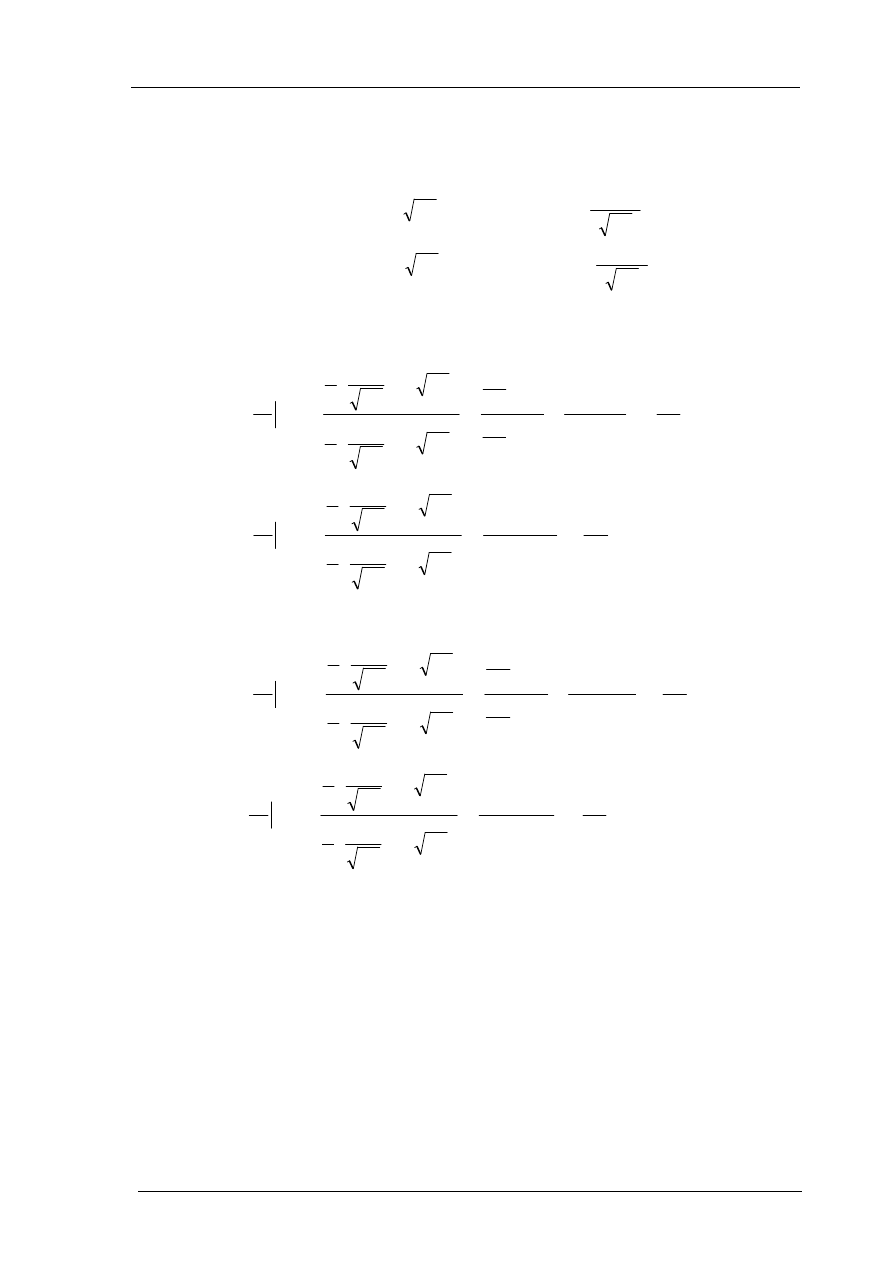
© Witold Szkudliński: L

INIA TRANSMISYJNA

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_TLine_2011.pdf Modyfikacje 2011: M. Makowski, C. Stefański

Laboratorium OiS

(sieciowe)

KSEM/626Ea

Wersja 2011

-8-

Nietrudno zauważyć, że wielkości { ܽ

௜

,ܾ

௜

} reprezentujące fale padającą i odbitą, podniesione do

kwadratu maja sens i wymiar mocy jeśli tylko napięcia występujące we wzorach (1.20) to wartości
skuteczne.
Z kolei napięcia i prądy w przekrojach wejścia i wyjścia

0

2

2

2

2

2

0

2

2

2

2

2

0

1

1

1

1

1

0

1

1

1

1

1

,

)

(

,

,

)

(

R

b

a

I

I

I

R

b

a

U

U

U

R

b

a

I

I

I

R

b

a

U

U

U

−

=

−

=

+

=

+

=

−

=

−

=

+

=

+

=

−

+

−

+

−

+

−

+

(1.21)

Przejdźmy do definicji pomiarowych parametrów macierzy rozproszenia.
Parametry s

11

i s

21

definiujemy w warunkach

pobudzania tylko wejścia, czyli E

2

=0.

W takich warunkach:

1

2

0

1

1

2

0

1

0

1

0

2

0

2

0

1

2

21

1

1

0

0

0

1

1

0

1

1

0

1

0

1

0

1

0

1

0

1

1

11

2

2

2

1

2

1

1

2

2

1

2

1

2

2

E

U

R

I

U

U

R

I

R

U

R

I

R

U

a

b

s

E

U

R

Z

R

Z

R

I

U

R

I

U

R

I

R

U

R

I

R

U

a

b

s

a

in

in

a

=

+

=















+















−

=

=

−

=

+

−

=

+

−

=















+















−

=

=

=

=

(1.22a)

Parametry s

22

i s

12

definiujemy w warunkach

pobudzania tylko wyjścia, czyli E

1

=0.

W takich warunkach:

2

1

0

2

2

1

0

2

0

2

0

1

0

1

0

2

1

12

2

2

0

0

0

2

2

0

2

2

0

2

0

2

0

2

0

2

0

2

2

22

2

2

2

1

2

1

1

2

2

1

2

1

1

1

E

U

R

I

U

U

R

I

R

U

R

I

R

U

a

b

s

E

U

R

Z

R

Z

R

I

U

R

I

U

R

I

R

U

R

I

R

U

a

b

s

a

out

out

a

=

+

=















+















−

=

=

−

=

+

−

=

+

−

=















+















−

=

=

=

=

(1.22b)

Jak widać, definicje (1.22) prowadzą do bardzo łatwo mierzalnych ilorazów napięć w obwodach,
w których badany czwórnik jest zawsze obciążony obustronnie rezystancją odniesienia ܴ

0

.

Każda zmiana rezystancji odniesienia

ܴ

0

powoduje automatycznie, że dla tego samego czwórnika

pomiary współczynników rozproszenia muszą być wykonane ponownie.

1.5.

Opis badanego układu

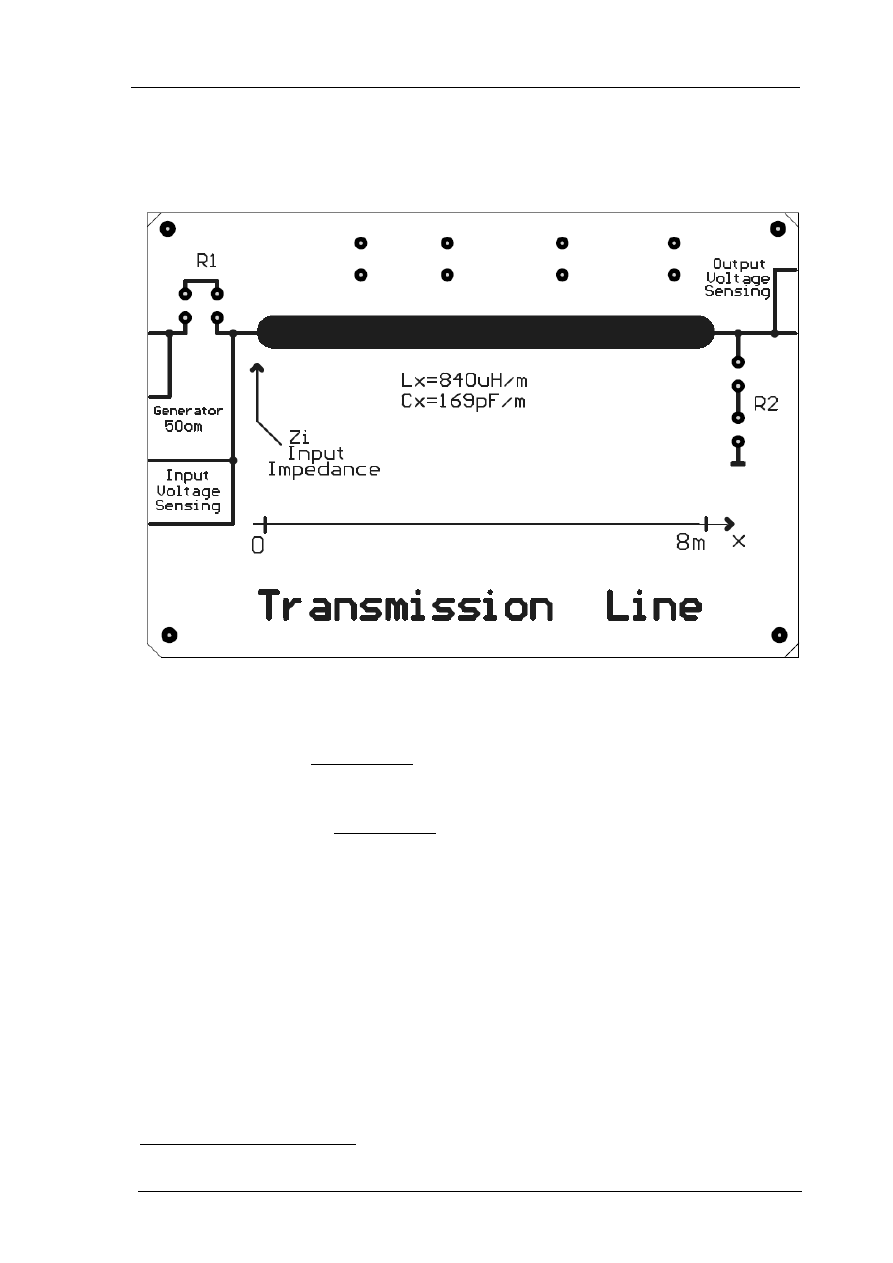
Do dyspozycji wykonawcy ćwiczenia jest pulpit operacyjny przedstawiony na rys.1.6. Za-

sadniczym elementem pulpitu jest linia transmisyjna, dla której z góry znane są parametry jed-
nostkowe: indukcyjność L

x

=840 uH/m oraz pojemność C

x

=169 pF/m. Długość tej linii wynosi l=8m,

ale tylko jej 10cm wycinek jest przedstawiony do oglądu, natomiast sama linia jest zamknięta we-
wnątrz obudowy. Linia jest uzupełniona potrzebną liczbą gniazd do podłączenia generatora sy-
gnałów (PCG10 lub PCGU1000) i oscyloskopu (PCS500 lub PCSU1000) oraz rezystorów obciążają-
cych (R

1

, R

2

). Wymienione rezystory znajdują się na przenośnych wtykach ze zwarciami oraz rezy-

storami regulowanymi (0-10k

Ω)

Ω)

Ω)

Ω). Użyta linia transmisyjna jest specjalnego typu o podwyższonej

© Witold Szkudliński: L

INIA TRANSMISYJNA

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_TLine_2011.pdf Modyfikacje 2011: M. Makowski, C. Stefański

Laboratorium OiS

(sieciowe)

KSEM/626Ea

Wersja 2011

-9-

indukcyjności na metr, co owocuje stosunkowo dużym opóźnieniem na jednostkę długości linii i,
niestety, również stosunkowo dużą wartością modułu impedancji charakterystycznej, wyraźnie
większą od impedancji popularnych linii dla standardu telewizyjnego (75

Ω) lub pomiarowego

(50

Ω).

Rys. 1.6. Widok pulpitu operacyjnego

1.6.

Przykładowe pytania kontrolne

1)

Podaj definicję (słowną plus wzory) długości fali elektromagnetycznej w linii?

2)

Badana w ćwiczeniu ośmiometrowa linia transmisyjna ma indukcyjność jednostkową

840uH/m oraz pojemność jednostkową 169pF/m. Oblicz, jaką w przybliżeniu rezystancję

charakterystyczną w omach ma badana linia.

3)

Badana w ćwiczeniu ośmiometrowa linia transmisyjna ma indukcyjność jednostkową

840uH/m oraz pojemność jednostkową 169pF/m. Oblicz, jakie w przybliżeniu opóźnienie im-

pulsu w mikrosekundach wprowadza badana linia.

4)

Zdefiniuj tzw. współczynnik odbicia na końcu linii. Ile wynosi wartość liczbowa tego współ-

czynnika dla: a) linii dopasowanej na końcu, b) linii zwartej na końcu, c) linii rozwartej na

końcu.

5)

W jakich warunkach impuls prostokątny wprowadzony na wejście linii pojawi się ponownie w

przekroju wejściowym . W przypadku gdy się pojawia, to po jakim czasie?

Kolejne pytania – równie ważne – znajdzie Czytelnik w naszej witrynie

2

.

2

http://www.eti.pg.gda.pl/katedry/ksem/pracownicy/Czeslaw.Stefanski/PomoceDydaktyczne/11_ObwodyIsygnaly_semIII/